0 引　言

水下航行器离开载体时，保持水下载体的姿态稳定尤为重要，由于航行器与海水的重量差以及海水灌入容器内所形成水锤效应对载体姿态控制会产生不利影响，而水下容器不同的开启角度所引起的底部压力和进水量也不同。在公开发表的文献中，关于开启角度的研究大多集中于盖体结构受力影响分析^[1]，对于开启角度不同所引起的底部压力和进水量变化的研究很少。本文采用Mixture多相流计算模型^[2]求解气液两相流场，对水下航行器离开容器的过程进行数值模拟，研究了不同开启角度的条件下底部压力及容器进水量的变化情况。

1 数学建模 1.1 物理模型

水下航行器离开容器^[3]的物理模型如图1所示，由水下容器、航行器、海水域3部分所组成。航行器初始位置位于容器内，海水域为容器盖口与海平面之间的区域，为方便建模选取海水域直径为10倍容器直径的范围。水下航行器离开载体时，产生复杂的气液两相流。由于物理模型的非轴对称性，本文采用1:1面对称三维建模。

1.2 控制方程

采用Fluent软件对流场进行计算，选用欧拉-欧拉多相流模型中的Mixture模型，Mixture模型通过求解混合物的连续方程、动量方程、能量方程、次要相的体积分数方程以及相对速度的代数方程来模拟多相流。

1）连续方程

$\frac{\partial }{{\partial t}}\left( {{\rho _m}} \right) + \nabla \cdot \left( {{\rho _m}{{\overrightarrow \upsilon }_m}} \right) = 0{\text{。}}$

式中： ${\overrightarrow \upsilon _m}$ 为质量平均速度， ${\overrightarrow \upsilon _m} = \displaystyle\frac{{\sum\nolimits_{k = 1}^n {{\alpha _k}{\rho _k}{{\overrightarrow \upsilon }_k}} }}{{{\rho _m}}}$ ；ρ_m为混合物的密度， ${\rho _m} = \sum\limits_{k = 1}^n {{\alpha _k}{\rho _k}} $ ；α_k为第k相的体积分数。

2）动量方程

多相流动量方程通过叠加各相的动量方程获得：

$\begin{aligned} \frac{\partial }{{\partial t}}\left( {{\rho _m}{{\overrightarrow \upsilon }_m}} \right) + & \nabla \cdot \left( {{\rho _m}{{\overrightarrow \upsilon }_m}{{\overrightarrow \upsilon }_m}} \right) = - \nabla p + \nabla \cdot \left[ {{\mu _m}\left( {\nabla {{\overrightarrow \upsilon }_m} + \overrightarrow \upsilon _m^T} \right)} \right] +\\ & {\rho _m}\overrightarrow g +\overrightarrow F + \nabla \cdot \left( {\sum\limits_{k = 1}^n {{\alpha _k}{\rho _k}{{\overrightarrow \upsilon }_{dr,k}}{{\overrightarrow \upsilon }_{dr,k}}} } \right){\text{。}}\end{aligned}$

式中：n为第n相； $\overrightarrow F $ 为质量力；μ_m为混合物的粘性； ${\mu _m} = \sum\limits_{k = 1}^n {{\alpha _k}{\mu _k}} $ ； ${\overrightarrow \upsilon _{dr,k}}$ 为次要相k的漂移速度， ${\overrightarrow \upsilon _{dr,k}} = {\overrightarrow \upsilon _k} - {\overrightarrow \upsilon _m}$ 。

3）能量方程

$\frac{\partial }{{\partial t}}\sum\limits_{k = 1}^n {{\alpha _k}{\rho _k}{E_k}} \!+\! \nabla \cdot \left( {\sum\limits_{k = 1}^n {{\alpha _k}{{\overrightarrow \upsilon }_k}\left( {{\rho _k}{E_k} + p} \right)} } \right) \!=\! \nabla \cdot \left( {k{}_{eff}\nabla T} \right) \!+\! {S_E}{\text{。}}$

式中：k_eff为有效传导率（ $\sum {{\alpha _k}\left( {{k_k} + {k_t}} \right)} $ ），k_t为湍流热容；方程右侧第一项代表了根据热传导而产生的能量传递；S_E为其他的体积热源。对于可压缩相， ${E_k} = {h_k} - \displaystyle\frac{p}{{{\rho _k}}} + \frac{{\upsilon _k^2}}{2}$ ；对于不可压缩相， ${E_k} = {h_k}$ ，h_k为第k相的热焓。

4）相对速度与漂移速度

相对速度的定义为：次要相（p）相对于主要相（q）的速度。

${\overrightarrow \upsilon _{pq}} = {\overrightarrow \upsilon _p} - {\overrightarrow \upsilon _q},$

任意相（k）的质量分数定义为 ${c_k} = \displaystyle\frac{{{\alpha _k}{\rho _k}}}{{{\rho _m}}}$ 。

漂移速度通过下式与相对速度之间进行联系：

${\overrightarrow \upsilon _{dr,p}} = {\overrightarrow \upsilon _{pq}} - \sum\limits_{k = 1}^n {{c_k}{{\overrightarrow \upsilon }_{qk}}} $ 。

5）次要相的体积分数方程

从次要相p的连续方程中，可以获得次要相的体积分数方程：

$\frac{\partial }{{\partial t}}\left( {{\alpha _p}{\rho _p}} \right) \!+\! \nabla \cdot \left( {{\alpha _p}{\rho _p}{{\overrightarrow \upsilon }_m}} \right) \!=\! - \nabla \cdot \left( {{\alpha _p}{\rho _p}{{\overrightarrow \upsilon }_{dr,p}}} \right) \!+\!\! \sum\limits_{q = 1}^n {\left( {{{\dot m}_{qp}} \!-\!\! {{\dot m}_{pq}}} \right)} {\text{。}}$

6）RNG k-ε湍流模型方程

在RNG k-ε湍流模型^[4]中，通过在大尺度运动和修正后的粘度项体现小尺寸的影响，而这些小尺度运动有系统地从控制方程中去除，所得到的k方程和ε方程如下：

$\begin{array}{l}\displaystyle\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} + \rho \varepsilon ,\\[10pt]\displaystyle\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) + \frac{{C_{1\varepsilon }^*\varepsilon }}{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}{\text{。}}\end{array}$

$ \begin{aligned}{\text{式中：}}\quad\quad\quad & {\mu _{eff}} = \mu + {\mu _i};\\[3pt]& {\mu _i} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon };\\[3pt]& {C_\mu } = 0.0845,{\alpha _k} = {\alpha _\varepsilon } = 1.39;\\[3pt]& C_{1\varepsilon }^* = {C_{1\varepsilon }} - \frac{{\eta \left( {1 - \eta /{\eta _0}} \right)}}{{1 + \beta {\eta ^3}}};\\[3pt]& {C_{1\varepsilon }} = 1.42,{C_{2\varepsilon }} = .68;\\& \eta = {\left( {2{E_{ij}} \cdot {E_{ij}}} \right)^{1/2}}\frac{k}{\varepsilon };\\[3pt]& {E_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right);\\[3pt]& {\eta _0} = 4.377;\beta = 0.012 {\text{。}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\end{aligned}$

2 仿真方法 2.1 控制方程离散

对流体进行计算时，采用有限体积法^[5]对控制方程进行离散，其基本思路是将计算区域划分为网格，使每个网格点周围有一个互不重复的控制体积，将待解控制方程对每一个控制体积积分，从而得到一组离散方程。

水下容器、水下航行器、盖体等壁面附近采用增强型壁面函数，以便于海水压力梯度的引入，网格更新采用域动分层法^[6]。

2.2 仿真算法

对离散后的控制方程组进行耦合求解，本文采用Simple算法（求解压力耦合方程组的半隐式方法），它属于压力修正法的一种，其核心是采用“预测-修正”的过程，在交错网格的基础上来计算压力场，从而达到求解N-S方程的目的。

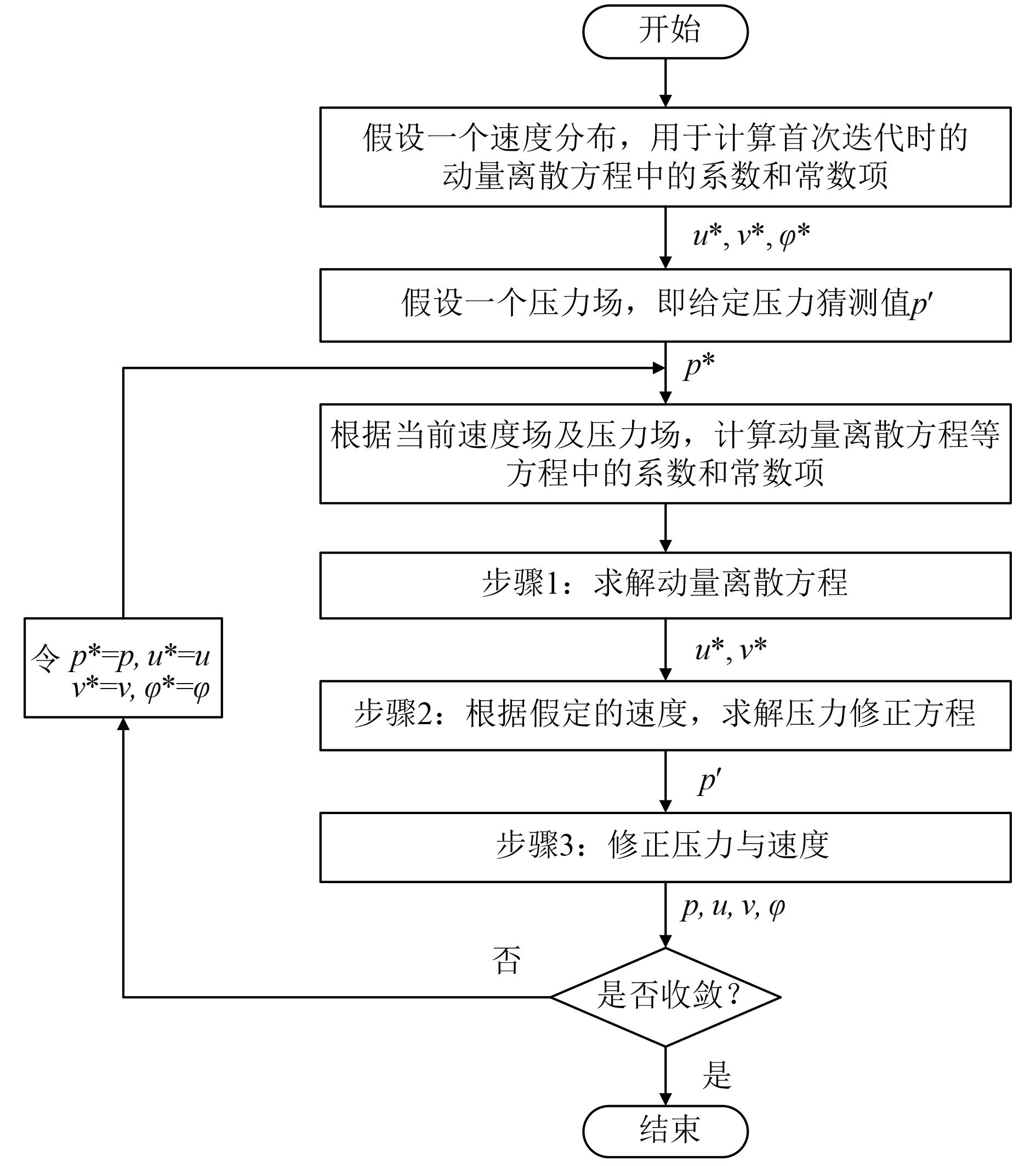
Simple算法的基本思想如下：对于给定的压力场（可以是假定的值或是上一次迭代计算所得到的结果），求解离散形式的动量方程，得到速度场。因为压力场是假定的或不精确的，这样得到的速度场一般不满足连续方程，因此必须对给定的压力场加以修正。修正的原则是与修正后的压力场相对应的速度场能满足这一迭代层次上的连续方程。据此原则，将由动量方程的离散形式所规定的压力与速度的关系代入连续方程的离散形式，从而得到压力修正方程，由压力修正方程得出压力修正值。接着，根据修正后的压力场，求得新的速度场。然后检查速度场是否收敛，若不收敛，用修正后的压力值作为给定的压力场，开始下一层次的计算，如此反复，直到获得收敛的解，求解步骤如图2所示。

3 仿真结果与分析 3.1 不同开启角度对容器底部压力和容器内进水量的影响

航行器位于指定深度，以给定的速度向上运动，为研究不同开启角度对容器底部压力和容器内进水量的影响，对盖体开启角度为α₁，α₂，α₃（90°＜α₁＜α₂＜α₃）的约束状态进行数值计算。

图3所示为3种开启角度下航行器在整个运动过程中容器底部压力随时间的变化曲线。由曲线可知，3种工况下容器底部压力分别在t₁，t₂，t₃时刻达到峰值P₁，P₂，P₃，且t₁＜t₂＜t₃，P₁＞P₂＞P₃，说明盖体开启角度越小，容器底部压力峰值越大，且达到峰值的时刻越早。

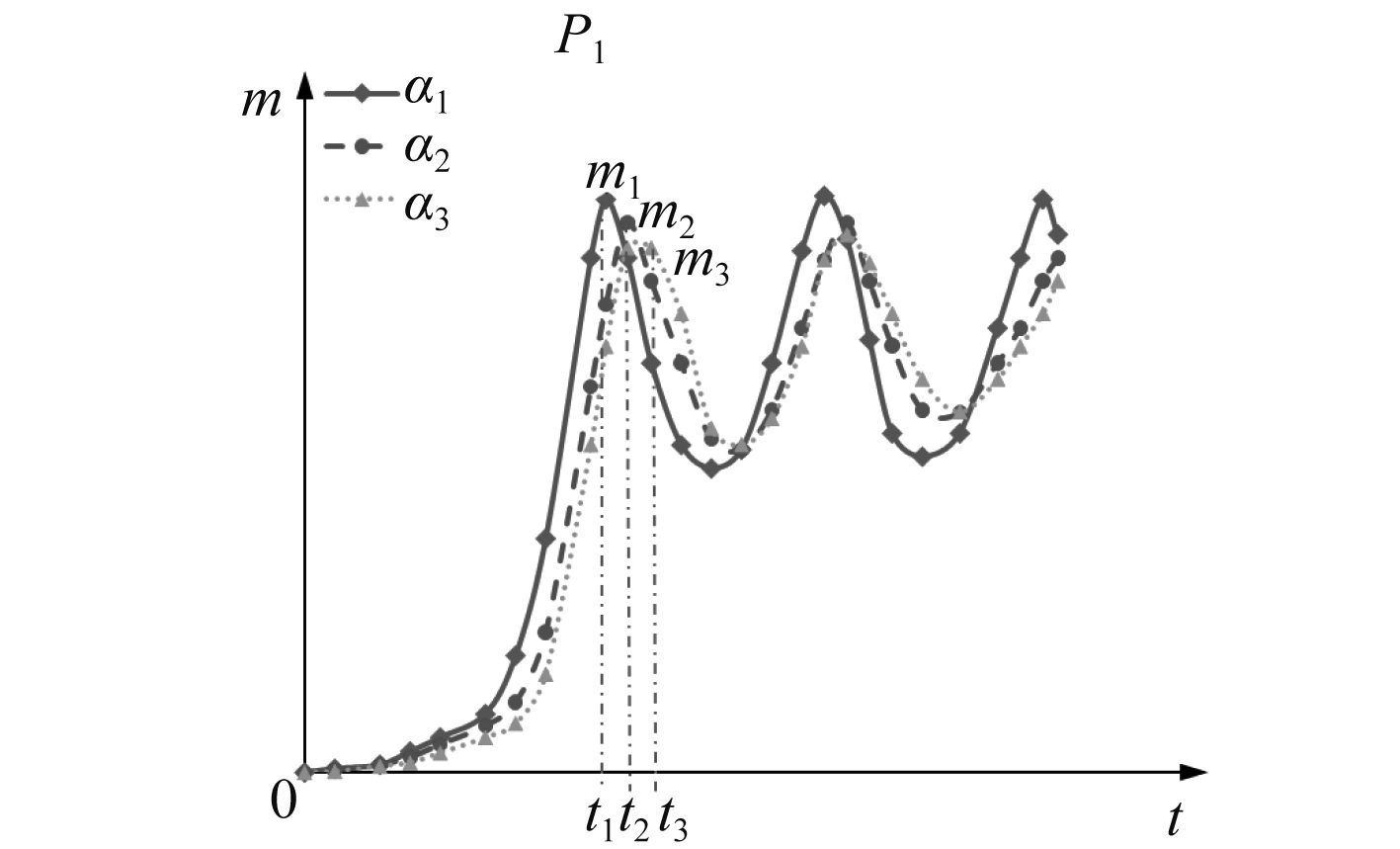
图4所示为3种开启角度下容器内进水量随时间的变化曲线。由曲线可知，3种工况下容器内进水量分别在t₁，t₂，t₃时刻达到峰值m₁，m₂，m₃，且t₁＜t₂＜t₃，m₁＞m₂＞m₃，说明盖体开启角度越小，容器内进水量越大，且达到峰值的时刻越早。

结合图3和图4可知，开盖角度为α₁时，容器底部压力曲线和进水量曲线震荡最剧烈，峰值最大，随着开盖角度的增加，两者震荡幅度均有所减缓，峰值也略有降低。据此可判断，开盖角度越小，海水进入容器的流速越大，对容器底部的冲击作用力越大，水锤现象^[7]越明显。

3.2 容器底部压力和容器内进水量变化机理分析

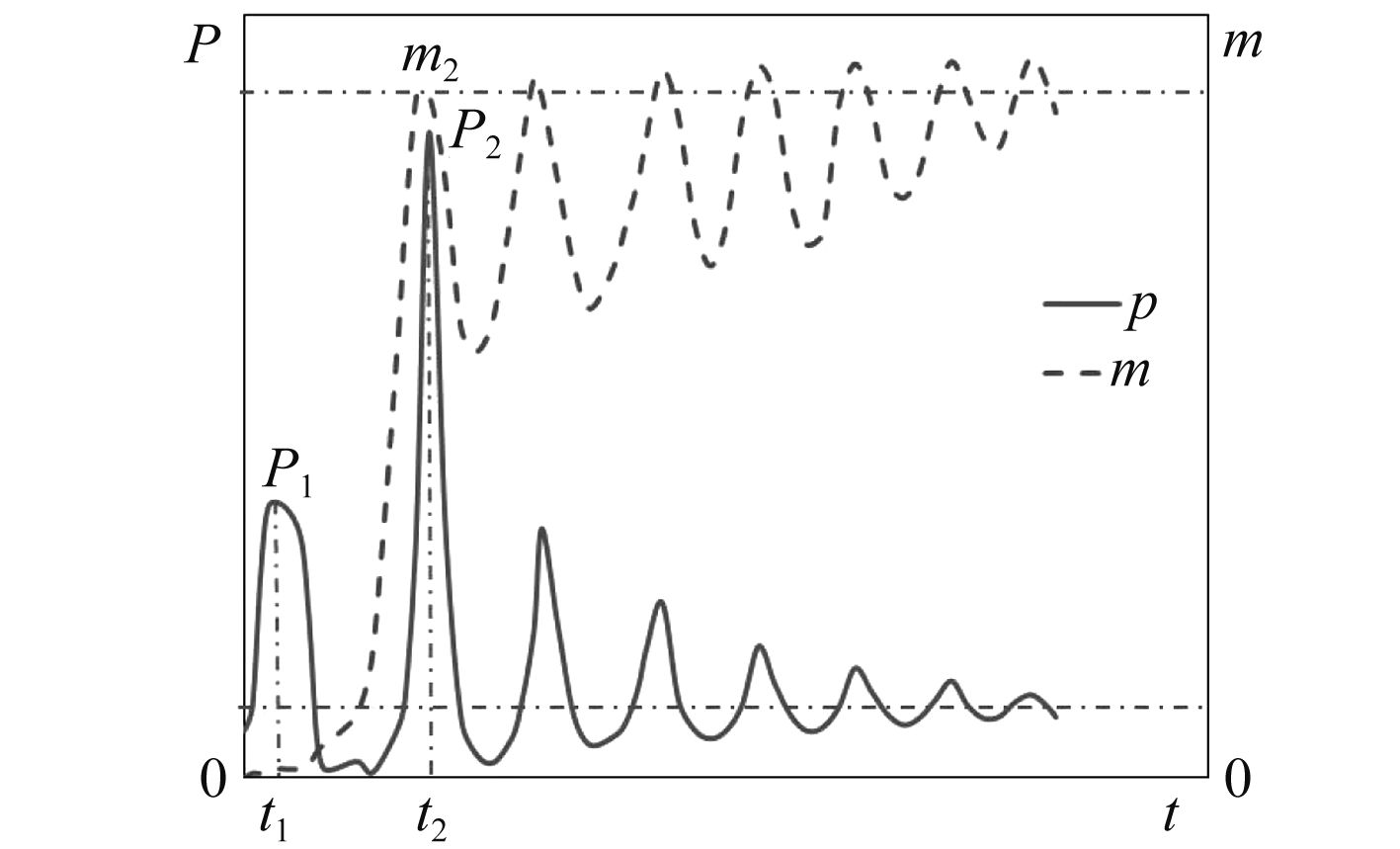
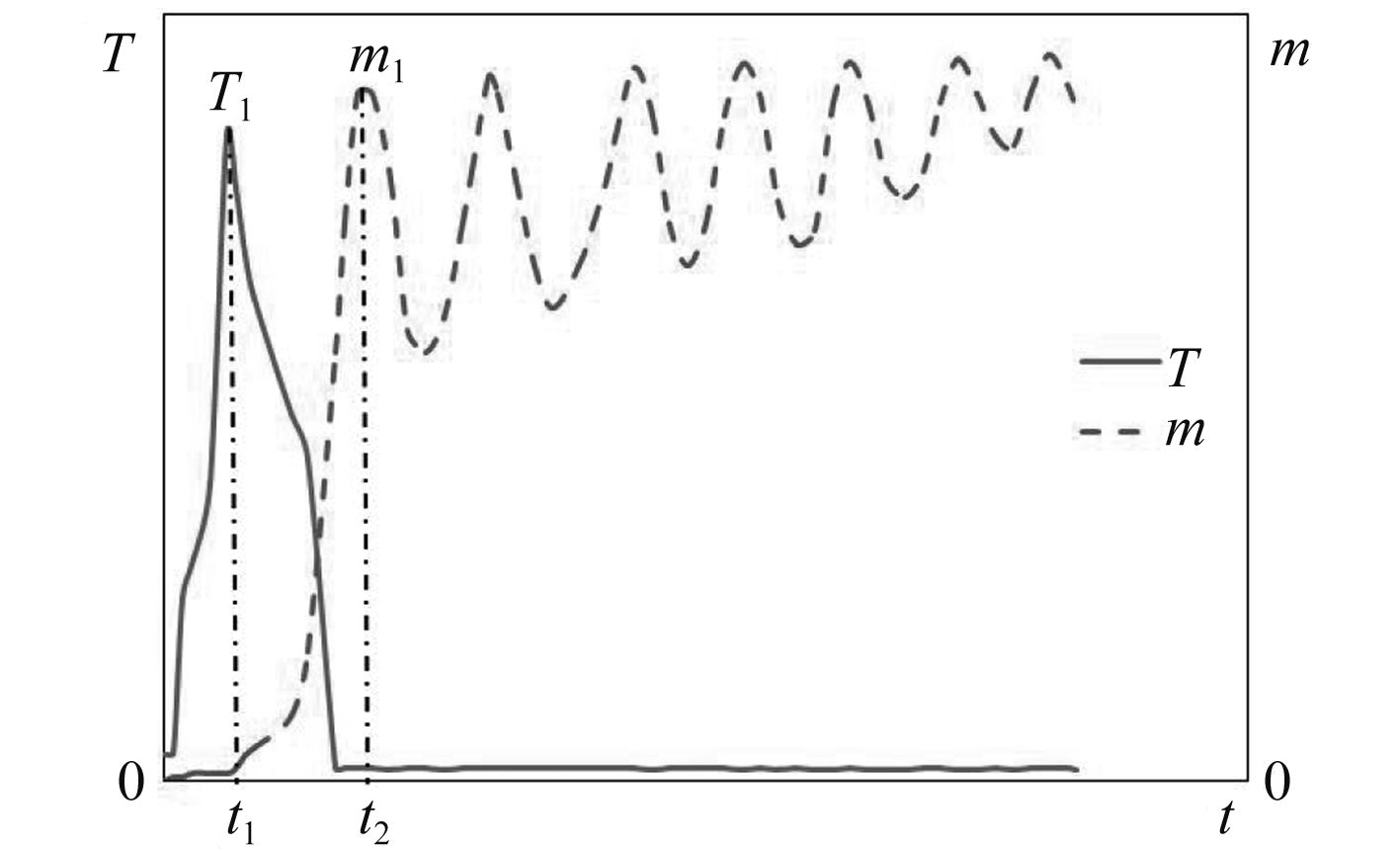
为研究容器底部压力和容器内进水量变化规律，延长约束状态仿真时间。图5和图6所示为开盖角度α₁时，容器底部压力和容器内进水量、容器底部温度和容器内进水量随时间变化曲线。由曲线可知，在容器内动力系统的作用下，底部压力和温度在t₁时刻出现第一个峰值P₁和T₁，之后随着航行器离开载体的运动而急剧下降，同时海水开始进入容器内。海水受重力作用逐渐压缩动力系统的残余气体从而产生压缩波^[8]，压缩波互相叠加，使底部压力达到第2个峰值P₂，并形成第1次水锤效应，此时容器内进水量达到第1个峰值m₁，容器底部温度降至最低并保持稳定。压缩波撞击容器底部后开始反弹为膨胀波，将容器内的海水排挤出容器外。从图中可看出，进水量m在逐渐减小，同时底部压力降低。之后底部压力和进水量在海水压力、压缩波、膨胀波的作用下继续按此规律变化，随着能量的损失以及海水、气体压力差值的不断减小，水锤效应逐渐减弱，底部压力峰值也逐渐减弱并趋于稳定，容器内进水量同样也逐步趋于稳定。

4 结　语

本文采用Mixture两相流计算模型，通过设定不同的容器开启角度，对水下航行器离开容器过程中容器底部压力和容器内进水量进行仿真计算，仿真结果表明：

1）容器开启角度越小，底部压力和进水量越大，且震荡越剧烈；底部压力较进水量的波动幅度更大；随着时间的推移，两者逐渐趋于稳定；

2）容器底部压力震荡所产生的水锤现象是由海水压力和残余气体压力两者互相作用所产生的压缩波冲击容器底部而引起的；

3）进水量的变化是由于压缩波、膨胀波所引起的底部压力波动而引起的，在压缩波形成过程中，进水量逐渐增加，压缩波在底部反弹为膨胀波后，将容器内海水排挤出容器外，进水量减少。

所得到的研究成果可为水下容器总体设计、系统使用流程优化提供理论支撑。