跨介质航行器具有空防能力强、隐蔽性好,环境适应性强、任务可达性好的特点,在未来军事领域中有着极其可观的应用前景[1]。跨介质航行器要跨越水、气2种介质的交界面,具有复杂的非定常、非线性流体动力特性,在入水过程中,会受到入水抨击以及空泡溃灭载荷的影响,因而承受巨大的冲击载荷和水动力弯矩。
目前,大多采用低速出入水的策略来回避跨介质武器系统研究中高速跨介质出现的难题,对结构入水冲击载荷的研究也以低速为主。目前对低速结构入水过程的砰击已经进行了很多仿真计算,得到了不同结构物,如空投鱼雷、舰船等的冲击载荷及动态响应[2 – 7]。对于高速入水,M.Park等[8]基于无粘势流理论,利用切片法,分析计算了高速入水冲击载荷,王永虎等[9]研究了斜入水高速冲击,采用精确形体法,得到了入水初始状态条件和入水冲击载荷之间的关系以及入水过程中的转动力矩的变化规律,但没有考虑空气垫效应,会使其计算结果偏大。
随着应用研究的不断深入、基础理论和研究手段的不断完善,迫切需要开展高速出入水和水面滑跳等跨介质航行器流体动力基础和弹道控制技术研究。当航行器入水速度达到100 m/s以上时,入水空泡内部气体不再是单纯的降压过程,而且还有相变过程。航行器入水冲击载荷以及自然空泡溃灭时的高速冲击给航行器壳体的局部强度带来巨大挑战。高速抨击和自然空泡溃灭引起载荷是工程应用中面临的最大难题。超空泡研究表明,特殊设计的超空泡航行器外形可以减阻一个量级,而通气超空泡比自然超空泡具有更稳定的特性[10]。高速抨击引起的冲击载荷有望通过超空泡减阻削弱,而空泡溃灭引起的载荷则可以通过通气方法得以解决。
本文在超空泡理论研究的基础上,开展跨介质航行器高速入水的建模与仿真分析研究,通过数值模拟开展高速入水的通气降载技术研究。
1 计算模型 1.1 动网格模型动网格模型(Dynamic Mesh Model)可用于模拟流体域边界随时间改变的问题。在Fluent中,网格的更新过程由程序根据迭代步中边界的变化情况自动完成。
相对于不能计算弹体转动情况的水面上升法,动网格方法与真实情况最大程度接近,可用于模拟非定常高速入水过程[10 – 11]。
动态分层法(Layering)是一种应用网格合并/分裂实现网格更新的方法。运动边界向下方运动时,网格处于拉伸状态,当
| ${h_{\max }} > (1 + {\alpha _s}){h_{ideal}}$ |
满足时,网格层j会被分裂成2层。
式中,
| ${h_{\min }} < {\alpha _c}{h_{ideal}}$ |
满足时,第j层网格会与第i层网格合并。
式中:
在Fluent中提供的多相流模型中,VOF不支持相间的穿插,而且不兼容Singhal空化模型,而混合模型(Mixture Model)允许相之间互相贯穿,允许相以不同的速度运动,可用于模拟多相流,包括各相不同速度的、各相以相同速度运动的、以及有强烈耦合的各向同性的多相流模拟。
混合模型的连续性方程为
| $\frac{\partial }{{\partial t}}({\rho _m}) + \nabla \cdot ({\rho _m}{{{v}}_{{m}}}) = 0{\text{。}}$ |
式中:
在Fluent中进行2次开发,利用自编程序进行流场弹道耦合计算,在实时输出模型运动参数的同时,完成模型入水非定常流场计算,流场-弹道耦合计算各模块的流程见图1。
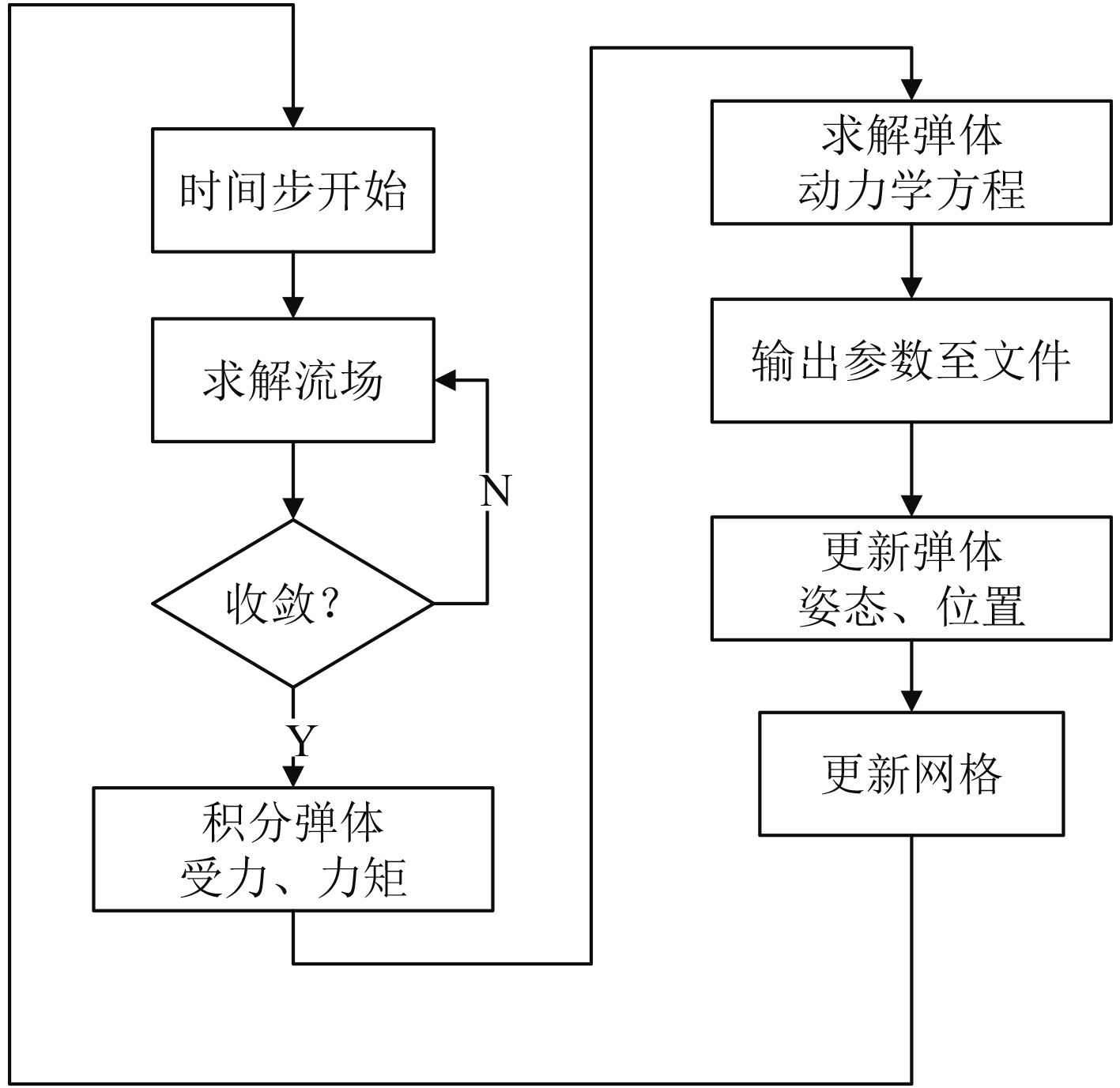
|
图 1 流场-弹道耦合计算流程 Fig. 1 Calculation flow diagram of flow field-ballistic coupling |
本文的计算对象为具有细长前锥段的超空泡航行器模型,肩部具有通气狭缝,外形如图2所示。

|
图 2 计算对象 Fig. 2 Computing object |
计算域划分情况及边界条件设置如图3所示。
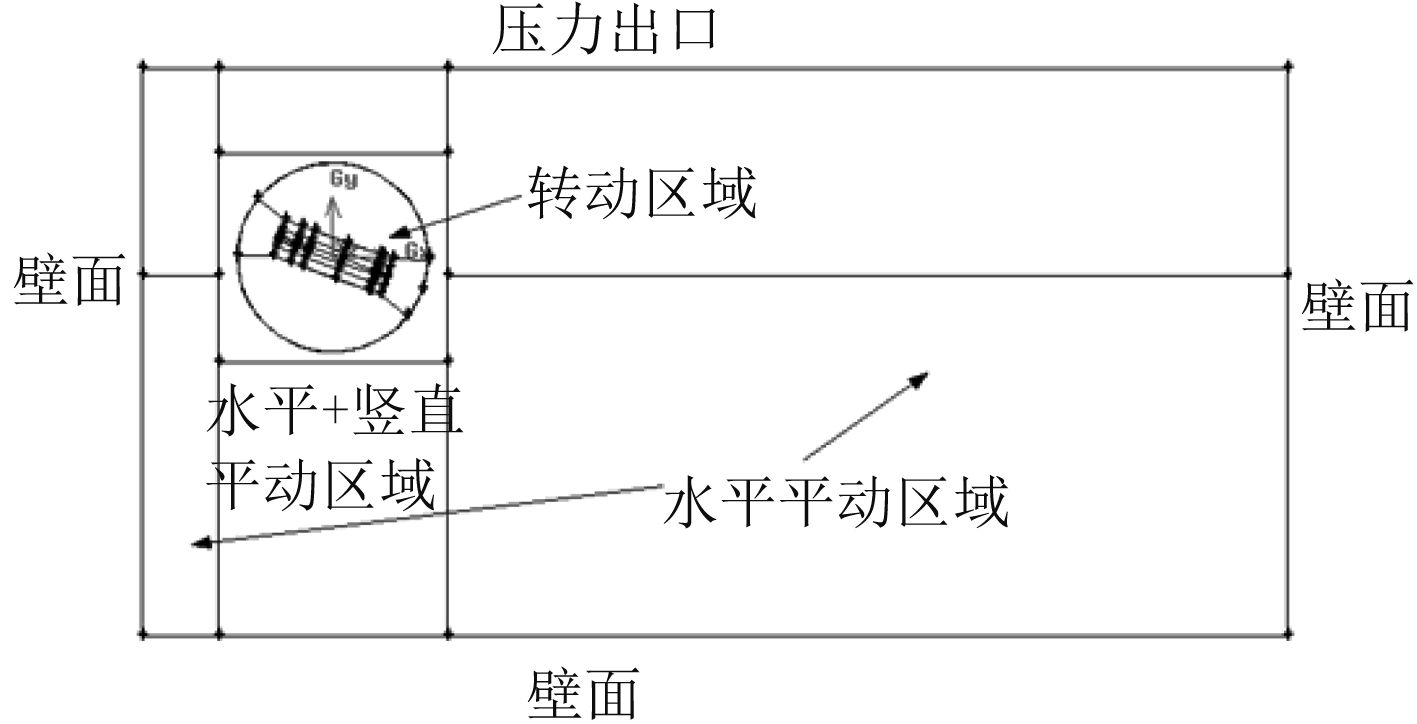
|
图 3 计算区域及边界条件设置 Fig. 3 Calculated zone and boundary condition |
从图3可以看出,计算域共包括3个流体运动区域:转动区域、水平+竖直平动区域、水平平动区域。计算域顶部为压力边界,其它远场为壁面边界。弹体肩部的通气狭缝,为压力边界,如图4所示。

|
图 4 通气口边界条件 Fig. 4 Vent boundary condition |
对图3所示计算域进行网格划分,划分结果如图5所示,不同区域间网格通过接口边界条件来连接。水平+竖直平动区域、水平平动区域均使用六面体网格,动网格更新方式采用Layering方式;而在转动区域,航行器的贴体网格为结构化网格,之外的网格为四面体网格,以消减六面体网格由于方向性而导致的不规则界面。在贴近航行体可能出现空化的地方以及水气自由附近加密网格,以更精确更清晰地捕捉空泡及自由面边界。

|
图 5 网格划分 Fig. 5 Grid dividing |
对超空泡航行器20°高速斜入水过程进行仿真计算,通过UDF求解航行器的运动方程,得到了不同速度和通气与否时的超空泡航行器在各个时刻所受到的力和力矩,受力-时间历程曲线如图6所示。

|
图 6 不同速度与通气条件下的弹体受力曲线 Fig. 6 Hydro-dynamic parameter |
1)通气对轴向冲击载荷的影响
由图6(a)可以看出,不通气时,航行器入水过程中轴向力出现了2处峰值,第1处在空化器入水后,第2处在锥段完全入水后。这是由于航行器前段为细长锥形,前端面面积较小,空化器入水时的峰值不是很明显,在入水时产生的冲击力峰值被随后不断增大的轴向水动力所掩盖。轴向力最大的峰值出现在锥段完全入水后。由此可见,细长锥形航行器在高速入水时可以很好地缓冲入水冲击,将最大轴向力出现的峰值降低、时间延后、冲击峰宽度展宽。
而通气后,轴向力的第1个冲击峰值出现在航行器头部触水时,并缓慢增大。轴向力没有明显的第2个冲击峰值,或者说第二轴向冲击峰变得平缓;当整个航行器全部入水后,由于弹尾抨击空泡壁,形成低头力矩,使航行器的轴向力减小。
对比不同速度下的轴向力曲线,冲击载荷峰值随入水速度的增大显著增大,峰值出现的时间随入水速度的增大前移;相同速度时,不通气时的冲击峰值较窄。模型重0.3 kg,经计算可知,在速度为80 m/s时,峰值由不通气的330 N降为通气后的150 N,降幅达到54.5%。轴向冲击过载由110 g降为50 g;速度为100 m/s时,峰值由不通气的410 N降为通气后的250 N,降幅达到39%。轴向冲击过载由136.67 g降为83.3 g;速度为120 m/s时,峰值由不通气的540 N降为通气后的330 N,降幅达到38.9%。轴向冲击过载由180 g降为110 g。
速度较低时,轴向降载效果更好,原因是通气后形成超空泡流型。在速度较低(80 m/s)时,航行器始终包裹在空泡中,而在较高速度时(100 m/s和120 m/s),由于迎流面沾湿,形成了抬头力矩。
2)通气对法向冲击载荷的影响
由图6(b)可以看出,不通气时,航行器倾斜入水初期,产生法向冲击力,是由于航行器头部前端面和下表面沾湿引起的。在较低速度下(80 m/s和100 m/s),法向力逐渐增大,这是由于航行器迎流面全沾湿;而在较高速度下(120 m/s),入水后形成自然超空泡,航行器迎流面包裹在超空泡中,尾部沾湿,法向力也大幅降低。
通气后,法向力的第1个峰值出现在航行器斜入水初期,是航行器前端面沾湿引起的。随后,弹尾滑水形成法向力。在较低速度下(80 m/s),法向力也逐渐降低,是由于通气形成了超空泡流型,使航行器迎流面被气体包裹,而在较高速度下(100和120 m/s),法向力大幅增大,是由于通气抑制了自然空化,从而弹体迎流面沾湿。
对比不同速度下的法向力曲线,头部入水冲击法向力峰值随着入水速度的增大而增大,峰值出现的时间随入水速度增大前移。通气后,在速度为80 m/s时,形成了超空泡,减小了弹体沾湿面积,法向力和法向过载大幅度降低,法向力由470 N降为120 N,法向过载由157 g降为40 g,降幅达到74.5%;在速度为100 m/s时,法向力和法向过载有所降低,但降低并不明显;而在速度为120 m/s时,法向力和法向过载不但没有降低,而且大幅度增加。这是由于在斜入水初期,航行器头部前端面和下表面沾湿,产生法向冲击力,航行器入水后形成自然超空泡,之后航行器迎流面锥段包裹在超空泡中,法向力降低并趋于平缓。由于通气,形成超空泡流型,在较高速度(120 m/s)条件下,通气抑制了自然空化,航行器迎流面沾湿,形成抬头力矩,法向力大幅增大。
3)通气对俯仰力矩的影响
不通气时,由于速度很高,形成超空泡流型。航行器斜入水初期,力矩的第1个峰值是由于航行器头部下表面触水形成的抬头力矩,航行器头部形成局部负攻角形成低头力矩冲击峰。由于自然超空泡的形成,航行器尾部抨击下空泡壁形成抬头力矩峰值。
通气后,抬头力矩冲击峰出现在航行器斜入水初期,航行器头部触水,前端面沾湿,而在航行器头部入水后,通气形成超空泡流型,不再提供抬头力矩。在较低速度下(80 m/s),由于航行器迎流面包裹在气泡内,而尾部沾湿,力矩很快稳定。低头力矩平抑了抬头力矩;在较高速度下(100和120 m/s),抬头力矩出现了第2个峰值,是由于通气抑制了自然空化,弹体迎流面锥段沾湿,弹体尾部抨击下空泡壁形成的,之后力矩趋于稳定,是由于尾部迎流面沾湿,形成低头力矩,平抑了抬头力矩。
对比不同速度下的俯仰力矩曲线,无论通气与否,头部入水冲击力矩峰值随入水速度增大而显著增大,而且入水速度的越大,俯仰力矩峰值出现的时间越早,脉冲宽度越窄,与冲击阶段相比,头部入水后的俯仰力矩为小量。通气后,80 m/s速度时,入水初期的抬头力矩峰值也有所降低,由15.5 Nm,降为9.5 Nm,降幅达到38.7%;100 m/s和120 m/s速度时,入水初期的抬头力矩峰值几乎与不通气时相同,分别为19.3 Nm,19.2 Nm和31.3 Nm,30.3 Nm。
3.2 空化器直径对入水冲击载荷的影响由3.1节的分析可知,通气可以有效地降低轴向过载,而对于法向过载,只有在较低速条件下才有效,而在速度较高的条件下,不但不能降载,反而会使入水冲击载荷大幅度升高。这是由于空化器直径太小而造成的。由于空化器直径很小,入水空泡比较瘦削,由于通气,抑制了自然空泡的形成,因而造成包裹不住整个弹体,从而使前锥段的迎流面沾湿,进而使法向过载大幅度增大。因此有必要分析空化器直径对入水冲击载荷的影响。
图7给出了20°入水角,120 m/s入水速度,不通气/通气条件下,以及空化器直径放大1.1倍通气条件下的受力曲线对比。
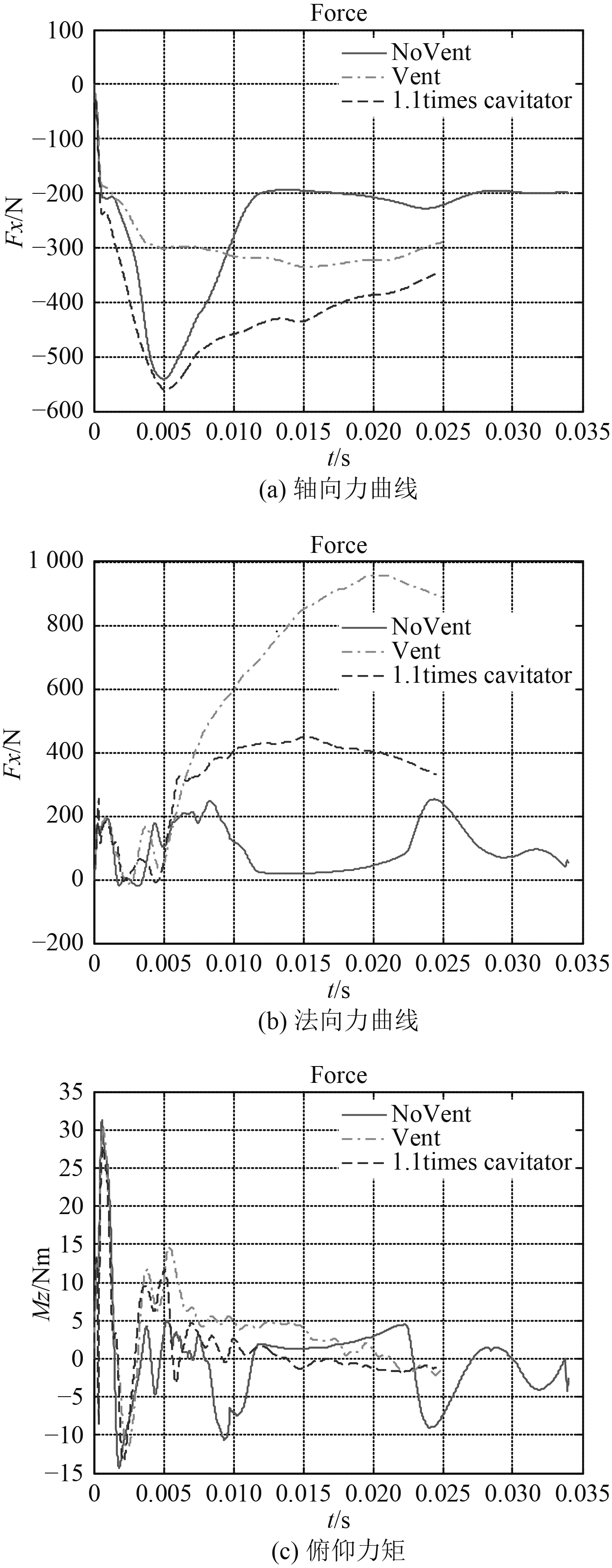
|
图 7 受力参数对比 Fig. 7 Hydro-dynamic parameter |
从图7中可以看出,增大空化器直径到1.1倍后,法向过载有较大幅度降低,但仍高于不通气时的法向过载。而对于轴向过载,空化器增大后,不但不能降载,反而更高于不通气时的轴向过载。对于俯仰力矩,空化器增大后,入水初期峰值几乎相同,之后,略低于通气情况下的力矩,仍比不通气时的力矩大。也就是由于增大空化器引入的过载要比通气降低的载荷大得多,尤其是轴向过载。因此,对于具有细长前锥段的超空泡航行器,利用增大空化器直径来降载是不可行的。
4 结 语本文仿真分析了具有细长前锥段的超空泡航行器,在不同速度下,通气/不通气条件下的高速入水流场,分析了通气对弹体流体动力参数的影响,得出以下结论:
1)具有细长前锥段的超空泡航行器在高速入水时,可以有效缓冲冲击过载,比常规的鱼雷、导弹等钝头体能耐受更高的入水速度;2)通气可以有效地降低轴向载荷,过载降幅可达38%以上,但是通气对降低入水初期的抬头力矩峰值作用不大;3)通气对法向过载的降载效果与速度有关,速度较低时有很好地降载效果,但在很高速度时,不但不能降载而且会使过载大幅度增加;4)增大空化器能够降低法向过载,但由此引入的轴向载荷要大于通气的降载。
| [1] | ROCK G, JONATHAN E. Submersible Aircraft Concept Design Study. Naval Surface Warfare Center. |
| [2] |
夏斌, 陈震, 肖熙. 弹性平底海洋结构物入水冲击的仿真分析[J]. 中国海洋平台, 2005 : 2.
XIA Bin, CHEN Zhen, XIAO Xi. THE SIMULATION ANALYSIS OF THE SLAMMING OF ELASTIC FLAT-BOTTOM MARINE STRUCTURE[J]. Chinese Ocean, 2005 : 2. |
| [3] |
陈小平, 滕蓓, 张晓杰, 等. 二维楔形体入水砰击的数值仿真[J]. 舰船科学技术, 2010. 1: 120-123.
CHEN Xiao-ping, TENG Bei, ZHANG Xiao-jie, et al. Num erical simulation aboutwater entry of 2D wedge bodies[J]. Ship Science and Technology, 2010. 1: 120-123. |
| [4] |
卢炽华, 郑际嘉. 刚性细长柱体倾斜姿态落水冲击的附加质量法[J]. 华中理工大学学报, 1996, 24 (8): 89–93.
LU Chi-hua, ZHENG Ji-jia. A study of water impact against a rigid slender cylinder falling obliquely with the added masses method[J]. Journal of Huazhong University of Science and Technology, 1996, 24 (8): 89–93. |
| [5] |
江松青, 李永池, 陈正翔. 侧向不均匀冲击下环向加筋圆柱壳的动力响应[J]. 计算力学学报, 2001, 18 (4): 443–448.
JIANG Song-qing, LI Yong-chi, CHEN Zheng-xiang. Dynamic response of ring-stiffened cylindrical shells under non-uniform lateral impact[J]. Chinese Journal of Computational Mechanics, 2001, 18 (4): 443–448. |
| [6] | XU L, TROESCH A W, PETERSON R. Asymmetric hydrodynamic impact and dynamic response of vessels[J]. Journal of Offshore Mechanics and Arctic Engineering, 1999, 121 (2): 83–89. DOI: 10.1115/1.2830082 |
| [7] | BATTISTIN D, IAFRATI A. A numerical model for the jet flow generated by water impact[J]. Journal of Engineering Mathematics, 2004, 48 : 353–374. DOI: 10.1023/B:engi.0000018173.66342.9f |
| [8] | PARK M, JUNG Y, PARK W. Numerical study of the impact force and ricochet behaviour of high speed water entry bodies[J]. Computers & Fluids, 2003, 32 : 939–951. |
| [9] |
王永虎, 石秀华, 李文哲, 李强. 斜入水高速冲击的理论建模及缓冲分析[J]. 机械科学与技术, 2008, 27 (6): 766–769.
WANG Yong-hu, SHI Xiu-hua, LI Wen-zhe, LI Qiang. Modeling and cushioning analysis of oblique water entry with high velocity[J]. MechanicalScience and Technology for Aerospace Engineering, 2008, 27 (6): 766–769. |
| [10] |
袁绪龙, 朱珠. 预置舵角对高速入水弹道和流体动力的影响[J]. 应用力学学报, 2015 (1): 11–16.
YUAN Xu-long, ZHU Zhu. Influence of preset rudder angle on trajectory and hydro-dynamic at high-speed water-entry[J]. Chinese Journal of Applied Mechanics, 2015 (1): 11–16. DOI: 10.11776/cjam.32.01.A001 |
| [11] |
袁绪龙, 张宇文. 水下高速航行体典型空化器多相流CFD分析[J]. 弹箭与制导学报, 2005, 25 (1): 53–59.
YUAN Xu-long, ZHANG Yu-wen. Multi-phase CFD analysis of typical cavitator for high-speed supercavitatig underwater vehicle[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2005, 25 (1): 53–59. |
 2017, Vol. 39
2017, Vol. 39
