传统的一些船用旋转设备,如螺旋桨、尾轴、推力轴承所组成的一套旋转设备,通常由振源、转动构件、弹性构件、传力结构、壳体组成,振源产生静力和脉动力,脉动力由振源,经转动构件、弹性构件、传力结构传递给了设备的壳体,最终通过壳体作用到船体基座和船体,引起船体振动[1 – 3]。为了减小传递到船体的激振力,以减弱振动,研究在传力结构和壳体之间安装隔振器,使壳体或船体基座之前的所有结构得到整体隔振。随着舰艇隐身性要求的提高,很多船用旋转设备都应该采取上述隔振措施,为此,设计一种由橡胶减振元件和金属件构成的橡胶隔振器,橡胶减振元件夹在2个金属连接板中间,隔振器由2个弹性防松圈、螺栓、4个橡胶减振元件组成,4个橡胶减振元通过2个弹性防松圈和螺栓与2块板固接,一块板的振动经过弹性构件的衰减传递到另一块板,达到隔振的目的。它的优点在于:
1)通常橡胶金属减振器要求橡胶和金属粘接在一起,橡胶件与金属件除破坏外不会脱开。而文中设计的隔振器橡胶元件结构形式统一,构型简单,与其他构件,如连接金属板、弹性防松圈及其他橡胶元件等没有粘连在一起,因此,拆卸方便、适应性强。
2)安装时,通过螺栓调节施加到隔振系统的预紧力,就可以保证在工作时隔振系统各个组件之间不脱开、不分离。
3)材料和结构的复杂性决定了只能通过实验确定大多数隔振器的性能[4 – 8],而文中设计的隔振器是由橡胶件和金属件构成,因此,能够采用数值计算的方式确定其性能,效率高,成本低。
分析隔振系统工作原理,建立系统线性动力学分析模型,得到系统的初始参数,然后设计优化算法,采用非线性有限元法进行数值计算。
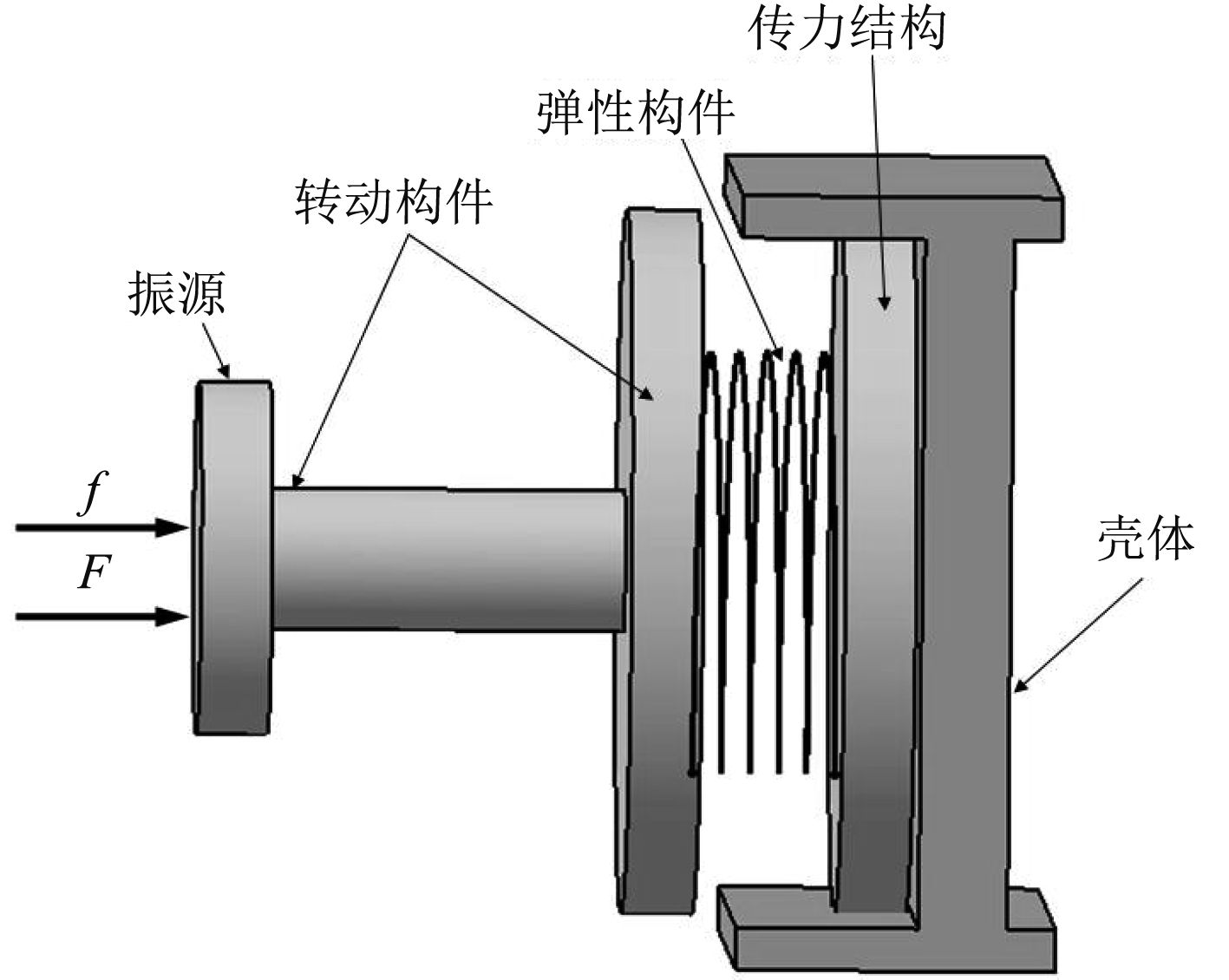
1 隔振系统简化模型及减振理论传统的一些船用旋转设备的工作过程可简化成如图1所示的形式,图1中的弹性构件指的是转动构件在高速旋转时产生的油膜,或是刚度相对较小的结构、隔振器等,f,F分别为振源产生的沿水平方向的脉动力和静力。
|
图 1 船用旋转设备工作过程示意图 Fig. 1 Schematic diagram of rotating equipment working process |
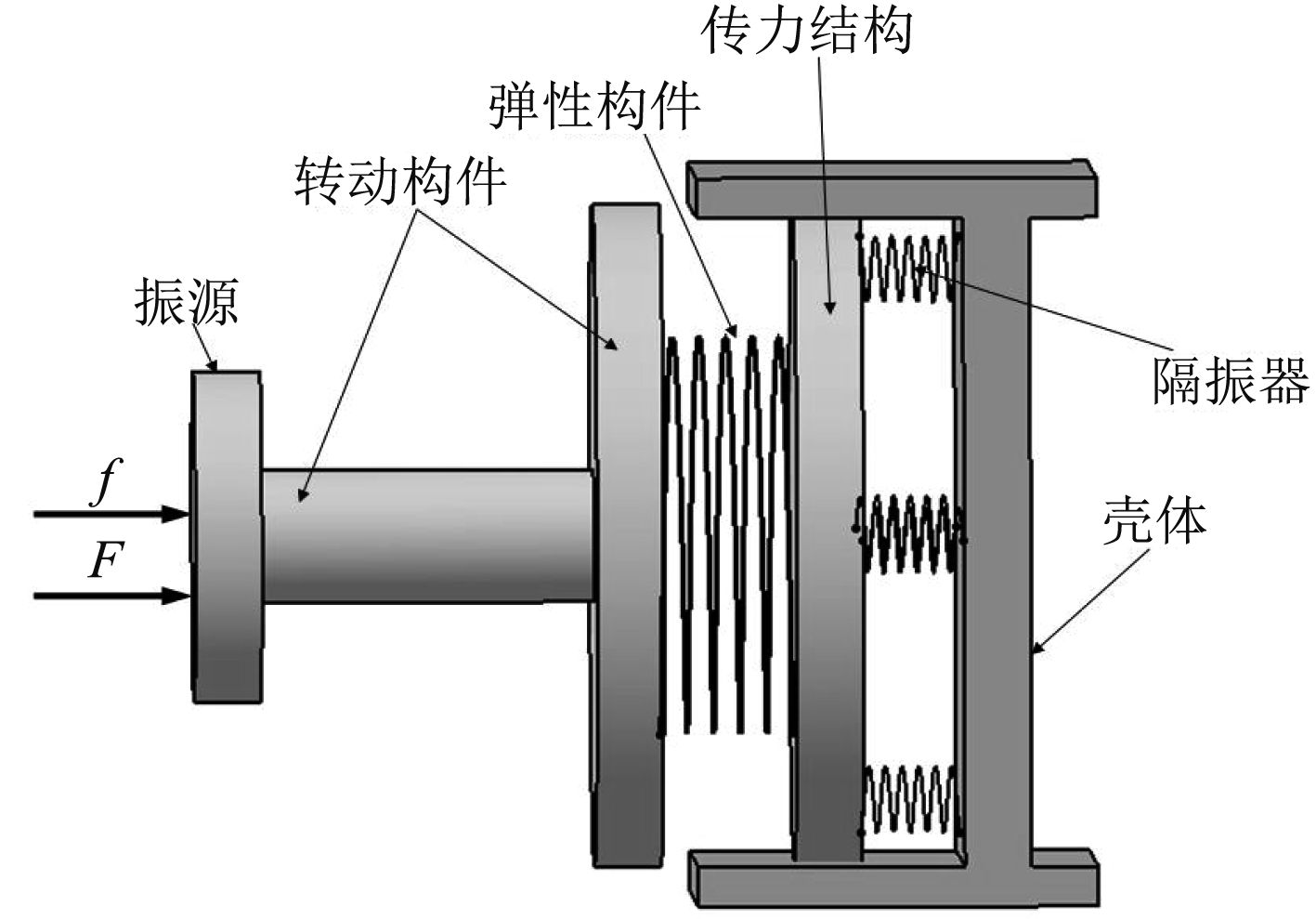
脉动力f的传递路径如图2所示。在传力结构和壳体之间安装隔振器,使设备壳体之前的所有结构得到整体隔振,如图3所示。脉动力f的传递路径发生改变,如图4所示。

|
图 2 脉动力f的传递路径 Fig. 2 Transmission path of fluctuating force f |
|
图 3 整体隔振效果图 Fig. 3 Overall effect of isolating system figure |

|
图 4 脉动力f的传递路径 Fig. 4 Transmission path of fluctuating force f |
在隔振器的设计中,首先将图3所示隔振系统简化为线性系统,得到系统的初始参数,然后用非线性有限元法,进行橡胶隔振器的设计计算。
图3所示的隔振系统中,弹性构件为油膜,其刚度按线性处理。与金属结构相比,橡胶刚性很小,因此可用图5所示的2个自由度集中质量系统来简化图3所示的复杂隔振系统,2个集中质量分别指转动构件质量m1、传力结构质量m2,激振力为沿水平方向的脉动力

|
图 5 两自由度集中质量隔振系统模型 Fig. 5 Model of two freedom lumped mass isolating vibration system |
图5所示的2个自由度集中质量系统运动方程为:
| $\left\{ {\begin{array}{*{20}{l}}\!\!\! {{m_1}{{\ddot y}_1} + {c_1}{{\dot y}_1} - {c_1}{{\dot y}_2} + {k_1}{y_1} - {k_1}{y_2} = {f_0}\sin (\omega t)}\text{,}\\\!\!\! {{m_2}{{\ddot y}_2} - {c_1}{{\dot y}_1} + ({c_1} + {c_2}){{\dot y}_2} - {k_1}{y_1} + ({k_1} + {k_2}){y_2} = 0}\text{。}\end{array}} \right.$ | (1) |
令
| $ \omega _n^2 \!=\! \frac{{\omega _1^2}}{2}\left[ {(1 \!+\! \frac{{{m_1}}}{{{m_2}}} \!+\! \frac{{\omega _2^2}}{{\omega _1^2}}) \! \pm \! \sqrt {{{(1 \!+\! \frac{{{m_1}}}{{{m_2}}}\! +\! \frac{{\omega _2^2}}{{\omega _1^2}})}^2} \!-\! 4\frac{{\omega _2^2}}{{\omega _1^2}}} } \right]\text{。}$ | (2) |
用
| $\left\{ \begin{array}{l}\!\!\!\! {f_0}\sin (\omega t) = {\mathop{\rm Re}\nolimits} (f(\omega ).{e^{{\rm{j}}\omega t}})\text{,} \\\!\!\!\! {y_1}(t) = {\mathop{\rm Re}\nolimits} ({Y_1}(\omega ).{e^{{\rm{j}}\omega t}}) = {\mathop{\rm Re}\nolimits} ({H_1}(\omega ) \cdot f(\omega ).{e^{{\rm{j}}\omega t}})\text{,}\\\!\!\!\! {y_2}(t) = {\mathop{\rm Re}\nolimits} ({Y_2}(\omega ).{e^{{\rm{j}}\omega t}}) = {\mathop{\rm Re}\nolimits} ({H_2}(\omega ) \cdot f(\omega ).{e^{{\rm{j}}\omega t}})\text{,}\\\!\!\!\! {f_{{{T}}0}}\sin (\omega t) \!=\! {\mathop{\rm Re}\nolimits} ({f_T}(\omega ).{e^{{\rm{j}}\omega t}}) \!=\! {\mathop{\rm Re}\nolimits} ({H_3}(\omega ) \cdot f(\omega ).{e^{{\rm{j}}\omega t}})\text{。}\!\!\!\!\!\!\!\!\!\!\!\end{array} \right.$ | (3) |
将式(3)代入式(1),得到频响函数
| ${Y_2} = {f_0} \cdot \left| {{H_2}(\omega )} \right|\text{,}$ | (4) |
| ${T_A} = 20\log (\frac{{{f_{T0}}}}{{{f_0}}}) = 20\log (\left| {{H_3}(\omega )} \right|)\text{。}$ | (5) |
减振元件的橡胶要求有良好的耐油、消音、隔振及缓冲能力,能耐一定温度、性能稳定,制造方便、易于制成所需形状,单位面积的承载能力大以及使用寿命长等,文中减振元件的橡胶材料主要成分是氯丁橡胶[9]。
橡胶材料的应变能函数W用Mooney-Rivlin方程来表达[9]:
| $W\left( {{I_1},{I_2}} \right) = {C_{10}}\left( {{I_1} - 3} \right) + {C_{01}}\left( {{I_2} - 3} \right)\text{,}$ | (6) |
橡胶材料的本构模型是非线性的,可表示为:
| $\sigma = - pI + 2\left( {\frac{{\partial W}}{{\partial {I_1}}} + {I_1}\frac{{\partial W}}{{\partial {I_2}}}} \right)B - 2\frac{{\partial W}}{{\partial {I_2}}}{B^2}\text{,}$ | (7) |
式中:
| ${I_1} = tr\left( B \right),{I_2} = \left[ {{I_1}^2 - tr\left( {{B^2}} \right)} \right]/2,{I_3} = \det \left( B \right)\text{。}$ | (8) |
对于不可压缩橡胶材料,
在有限元中两参数的Mooney-Rivlin模型需要定义Rivlin因数C10,C01和材料压缩性参数d。对橡胶进行拉伸试验,用曲线拟合应力、应变的试验数据,从而得到Rivilin因数C10=0.465 2 MPa,C01=0.433 MPa,根据文献[9],可取
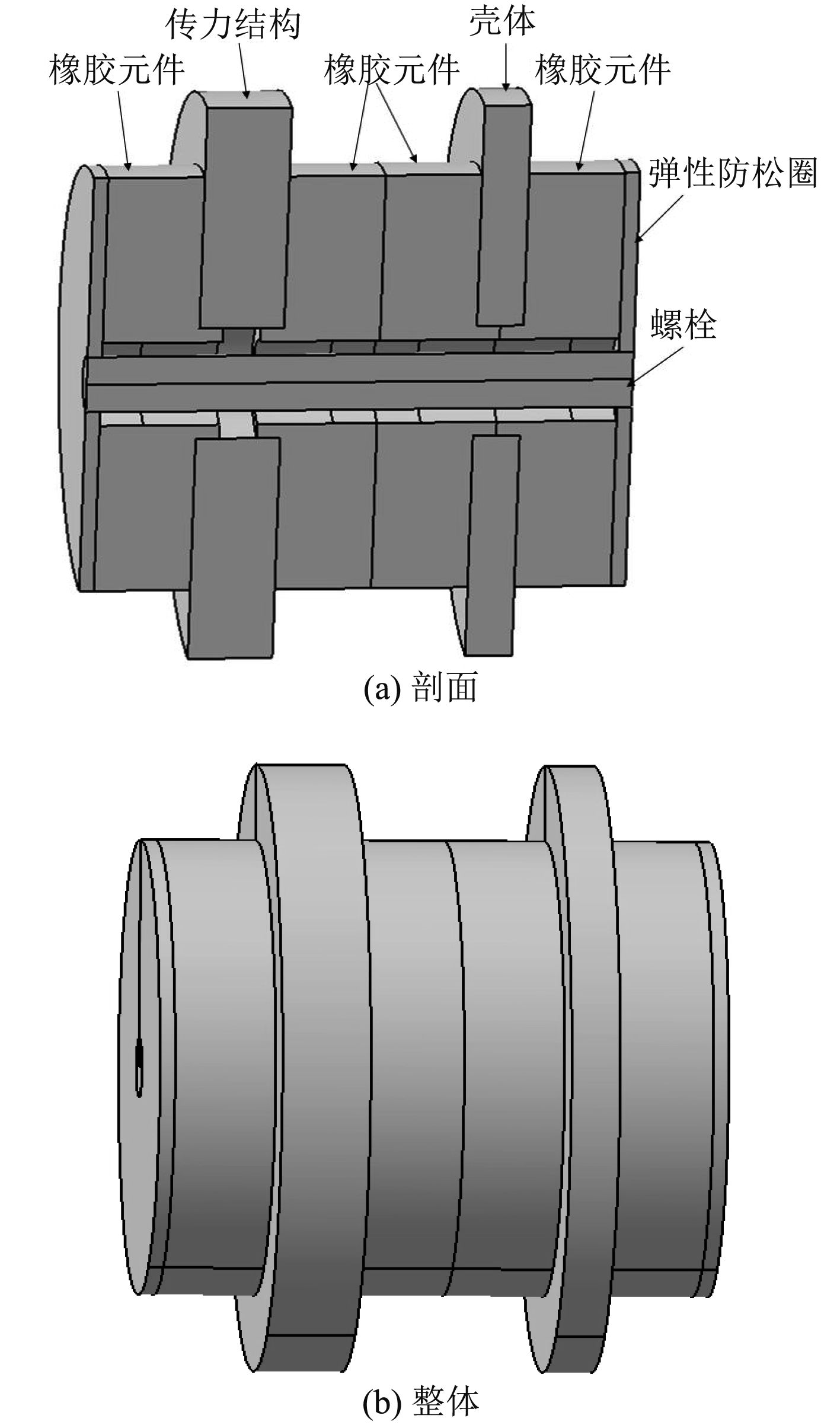
根据旋转设备的传力结构和壳体之间的空间情况确定隔振器的基本尺寸、基本构型,用第1节中隔振系统简化模型确定系统的初始参数。隔振器的初始结构形式如图6所示。
|
图 6 隔振器的初始结构形式 Fig. 6 Isolator initial configuration |
设计的隔振器沿水平方向安装,壳板固定在船体结构上,脉动力从传力结构经过橡胶件传递到壳板,传力结构及其前面的设备被整体隔振,隔振器的内径应足够大,以保证正常工作时橡胶减振元件始终与螺杆处于分离状态,隔振器的最大外径控制在135 mm以内,传力结构与壳板之间橡胶元件总高度不超过60 mm,激振力f的频率28~70 Hz,隔振系统的固有频率小于激振力频率的1/2,即小于14 Hz,隔振系统的其他参数如表1所示。
|
|
表 1 系统参数 Tab.1 Parameters of propulsion system |
一般地,设备型号决定了油膜的刚度大小,当无法根据设备型号确定油膜的刚度时,往往按以前用过的相关船用设备的油膜刚度来决定,文中的研究中,取油膜在水平方向的刚度为
| ${k_1} \leqslant 3.32 \times {10^8}\;{\rm{N/m}}{\text{。}}$ |
根据隔振系统一阶固有频率小于14 Hz的要求,对系统进行编程求解,得出动刚度:
| ${k_2} \leqslant 1.81 \times {10^6}\;{\rm{N/m,}}$ |
氯丁橡胶的动态系数d=1.5~2.5,这里取d=1.5,因此静刚度取。
| ${k_s} = {k_2}/1.5 = 1.20 \times {10^6}\;{\rm{N/m}}\text{。}$ |
螺栓预紧力使隔振系统产生较大的静变形、非线性的橡胶减振元件材料决定了数值计算应该采用非线性有限元法[10 – 12],金属构件与橡胶减振元件的连接关系由接触算法确定[12],优化设计的最终目标是使隔振系统的构型、尺度满足系统的隔振要求。
以隔振系统的刚度为目标函数的优化设计如下:
设计变量:螺栓预紧力
目标函数:隔振系统的刚度,且在满足要求的情况下尽可能小。
约束条件:隔振器的最大外径控制在135 mm以内,传力结构与壳板之间橡胶元件总高度不超过60 mm;静态下的压缩变形<15%,动态下的压缩变形<5%,正常工作时橡胶减振元件与螺杆不能接触,金属材料的屈服极限是590 MPa,氯丁橡胶的屈服极限是15~20 MPa。
根据设计变量的取值范围,设计多种方案,采用枚举法,按下面3个步骤进行优选:
1)分3个阶段:第1阶段是螺栓预紧力由0逐步增大到最大的系统变形计算过程;第2阶段在螺栓预紧力最大的状态下,将静载荷由0逐步增大到最大,施加到传力结构上;第3阶段计算隔振器水平方向静刚度;
2)在螺栓预紧状态下,计算隔振系统在水平方向的一阶振动固有频率;
3)根据一阶振动固有频率,计算隔振器水平方向动刚度值。
根据枚举法中方案数量,重复步骤1~步骤3的过程,选出最优的设计方案。
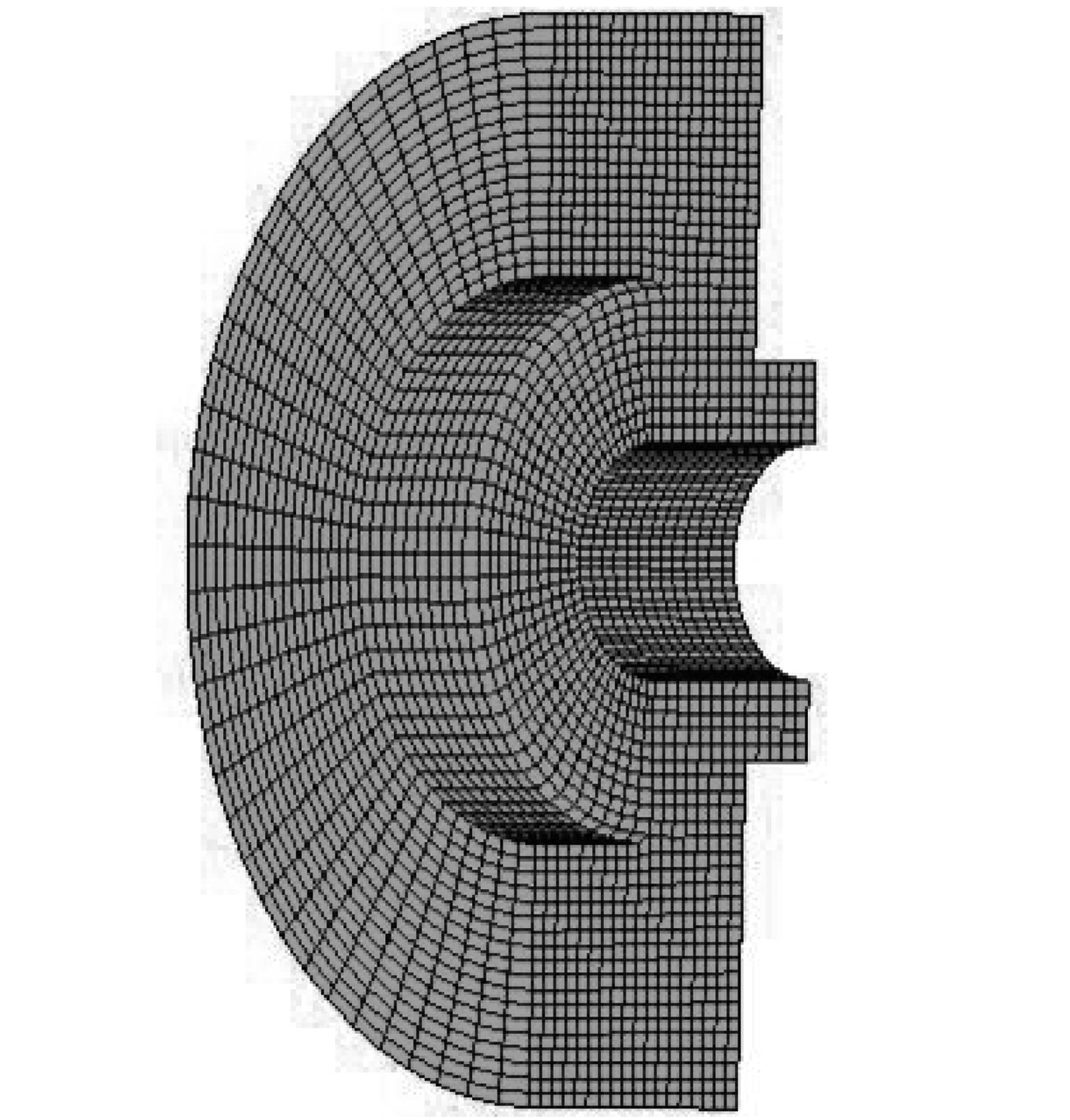
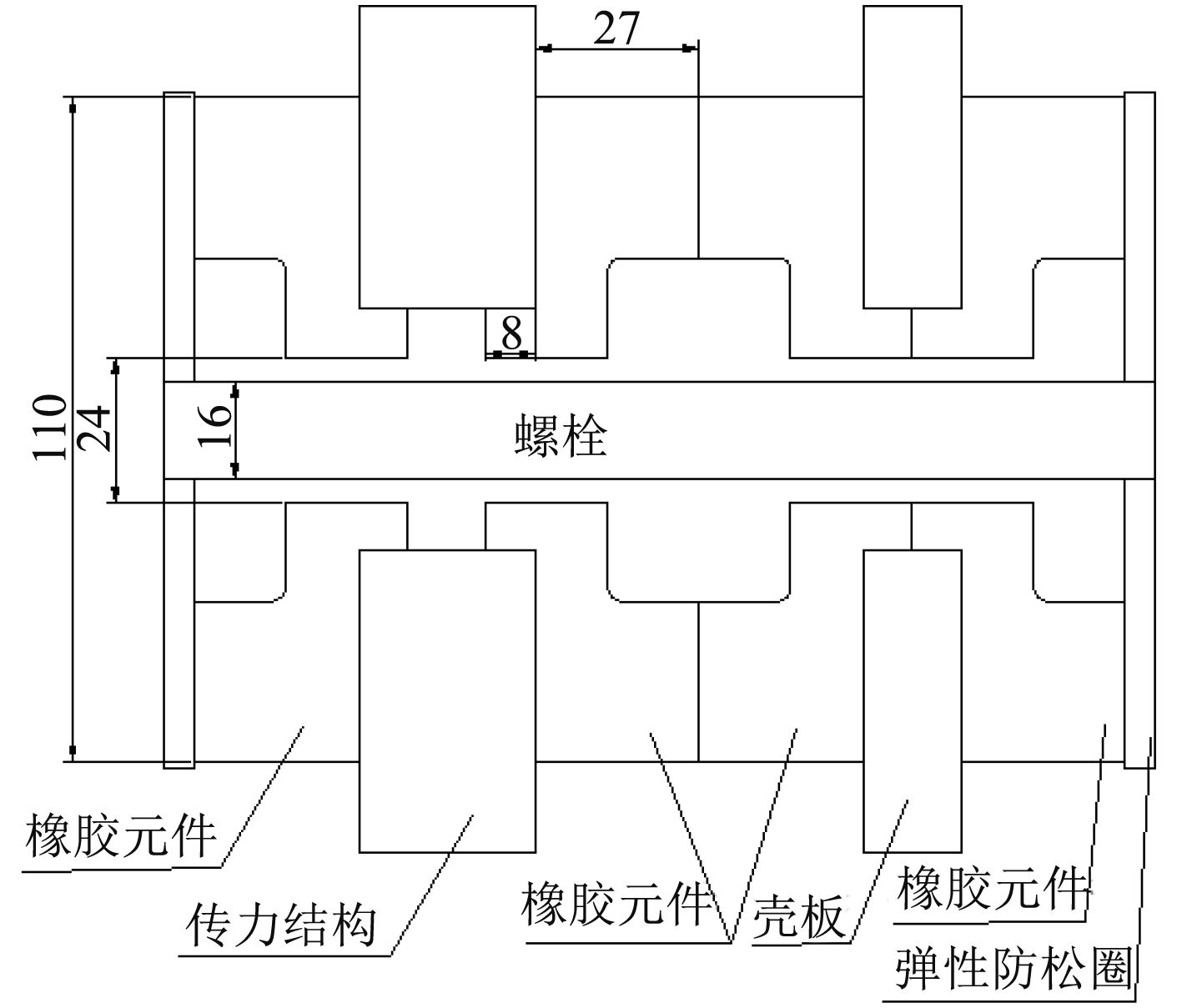
隔振器优化设计过程的核心是橡胶减振元件的构型优化,减振元件外形如图7所示,每个隔振器包含4个橡胶减振元件,隔振器的整体装配图如图8所示,图9表示基本尺寸。
|
图 7 橡胶减振元件外形 Fig. 7 Configuration of the rubber elememt |

|
图 8 隔振器的整体装配图 Fig. 8 Assembling drawing of the isolator |
|
图 9 隔振器的基本尺寸 Fig. 9 Detail sizes of the isolator |
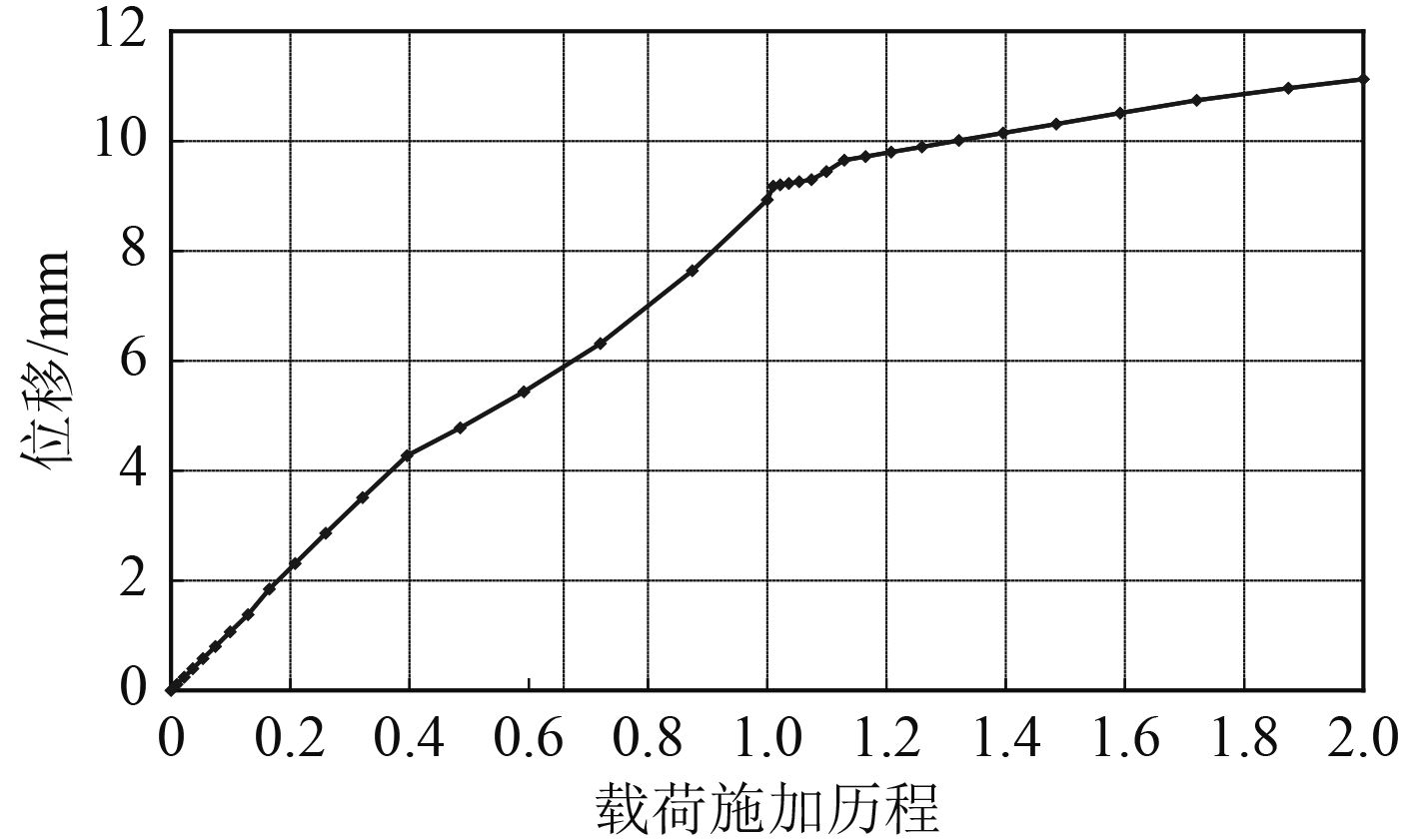
在6 500 N螺栓预紧力的作用下,在水平方向,整个隔振器产生15.4 mm的压缩变形,橡胶件总的压缩率为14.3%,在预紧状态下,在传力结构上施加2 210.0 N水平静载荷,传力结构在整个加载历程中与壳板之间的水平方向相对位移如图10所示,时间轴的0~1.0阶段表示螺栓预紧力的加载历程,时间轴的1.0~2.0阶段表示水平静载荷的加载历程,在这个阶段,传力结构相对壳板的位移为1.92 mm,因此隔振器在水平方向的平均静刚度为:
| ${k_s} = 2\;210.0/1.92 = 1.151 \times {10^6}\;{\rm{N/m}}{\text{。}}$ |
|
图 10 传力结构在水平方向的相对位移 Fig. 10 Comparative displacement of the transmitting force structure in the horizontal direction |
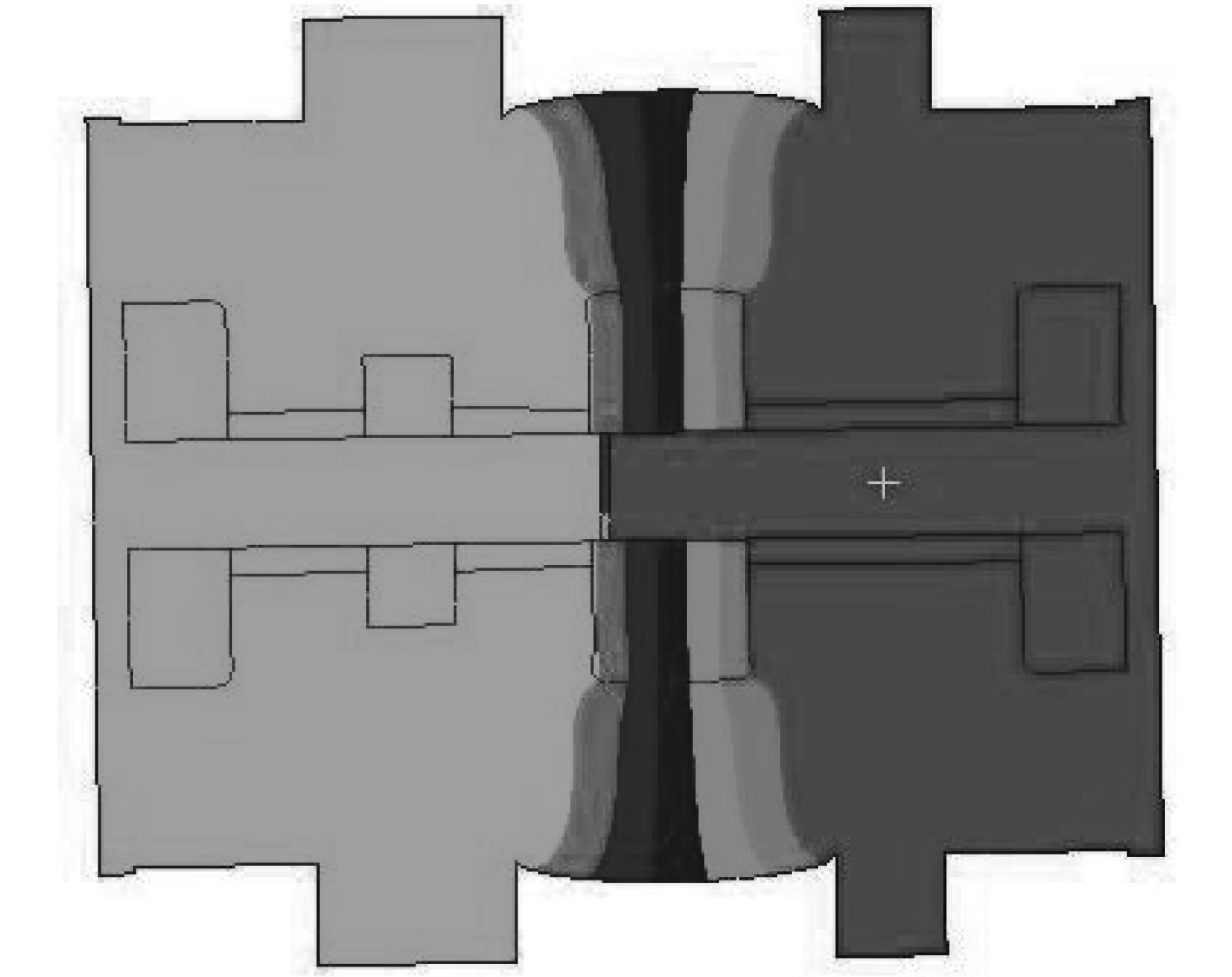
由上述分析可知,隔振器的刚度ks和k2都比油膜的刚度小很多,所以图3中的转动构件可以认为刚性固定在传力结构上,因此,图3所示两自由度隔振系统可以简化成如图8的单自由度系统形式,只是传力结构的质量是其自身质量与转动构件之和,这样可以通过分析该简化系统的固有振动特性得到隔振器动刚度k2。在螺栓预紧状态下,隔振器水平方向振动的一阶固有频率fn是13.3 Hz,振型如图11所示。
|
图 11 隔振器水平方向一阶振型 Fig. 11 First horizontal vibration model |
由动刚度计算下式:
| ${k_2} = ({m_1} + {m_2}){(2\pi {f_n})^2}\text{。}$ | (9) |
可得k2=1.709×106 N/m,满足3.1节中k2≤1.81×106 N/m的要求。
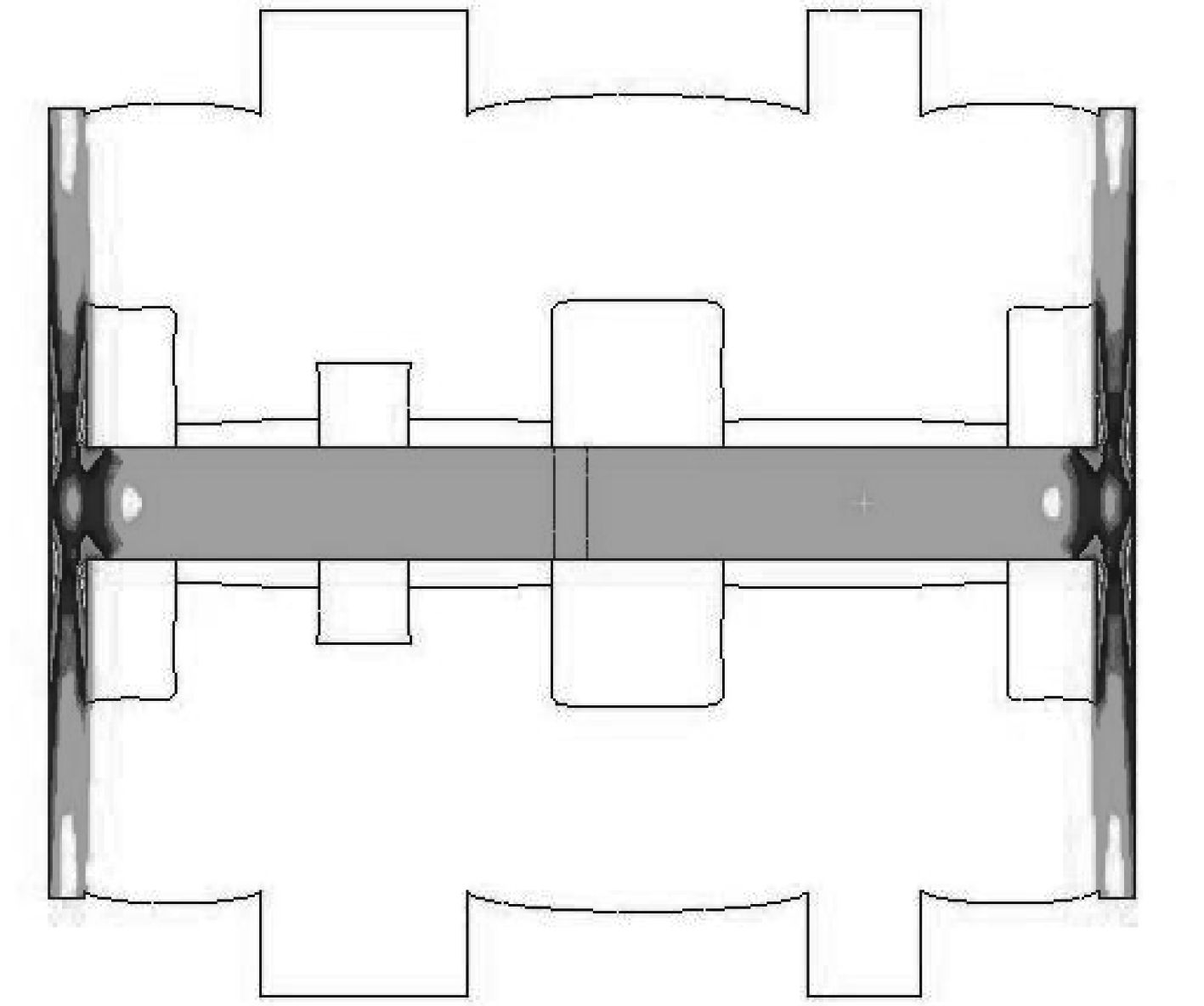
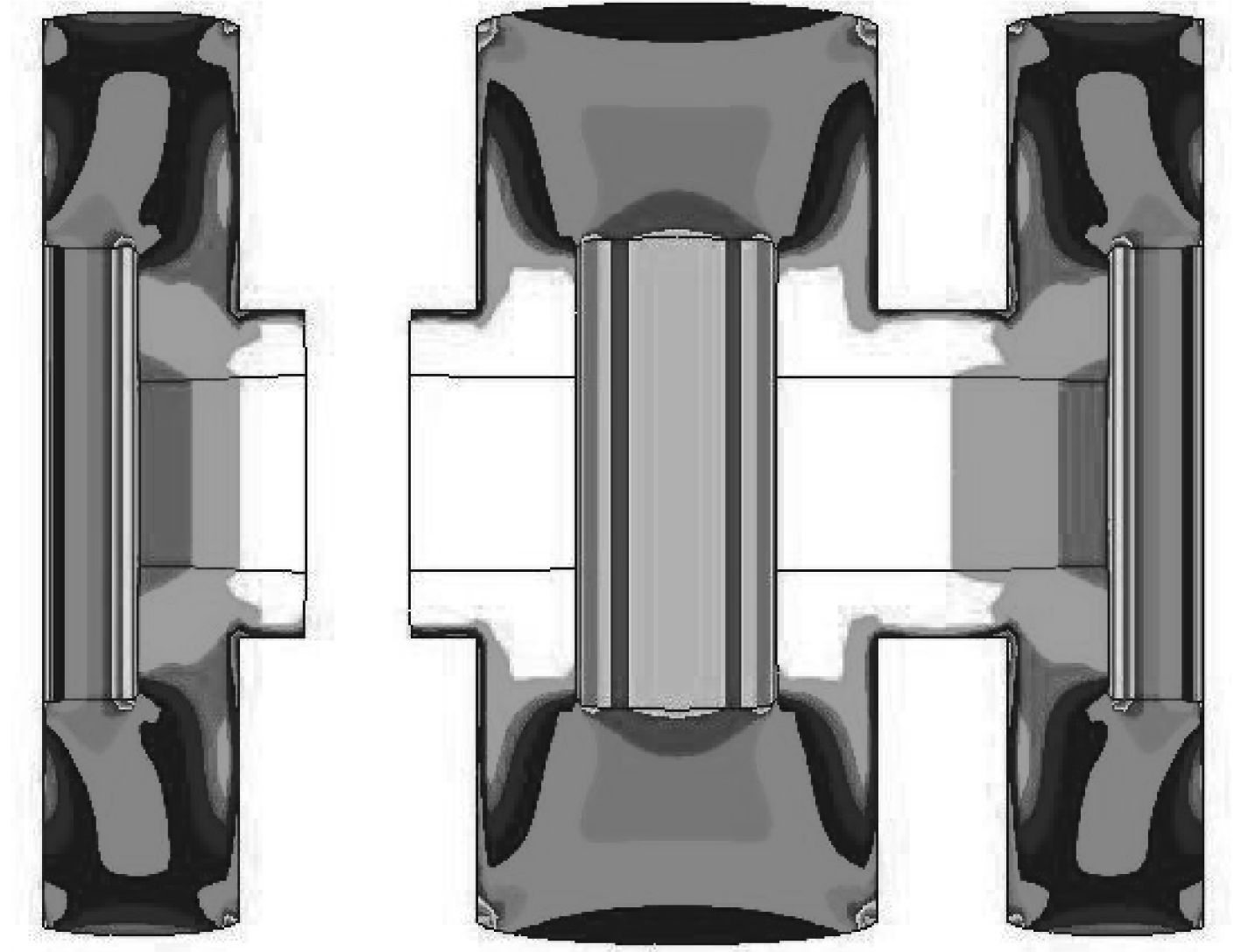
在螺栓预紧力和水平静载荷的共同作用下,隔振器的压缩变形如图12所示。可以看出,橡胶减振元件与弹性防松圈、前后连接板之间基本上没有滑移、保持接触状态;橡胶减振元件与螺栓之间最小间离为1.5 mm,保证了两者之间在隔振系统产生最大变形时不会接触、隔振器能正常工作。图13和图14分别表示隔振器整体、橡胶减振元件的应力云图,金属构件的最大Mises应力为415.0 MPa,橡胶减振元件最大应力在与金属结构接触位置的角点处,大小是3.66 MPa,满足强度要求。

|
图 12 隔振器的压缩变形 Fig. 12 Horizontal compression deformation of rubber isolator |
|
图 13 隔振器的应力云图 Fig. 13 MISES stress of rubber isolator |
|
图 14 橡胶减振元件的应力云图 Fig. 14 MISES stress of rubber elemrnts |
传统的一些船用旋转设备将脉动力通过设备壳体直接作用到船体而加剧船体振动,为了减小这种脉动力的传递,研究并设计一套安装在传力结构和壳体之间的橡胶隔振器,计算结果表明:
1)对于类似上述结构形式的橡胶隔振器,文中的设计方法可行,即先采用线性系统设计系统初始参数,然后用非线性数值计算方法对橡胶隔振器进行优化设计,确定最终参数;
2)本文设计的橡胶隔振器满足实际的使用要求,能够正常工作。
3)设计橡胶金属隔振器时,在隔振器的材料和结构不是非常复杂的情况下,采用本文所述的数值仿真的优化设计方法既实用又高效。
| [1] | FAHY F, GARDONIO P. Sound and structural vibration [M]. UK: Academic Press, 2007: 277–596. |
| [2] | 马光宗, 蔡承德. 船舶振动基础与实用计算[M]. 北京: 人民交通出版社, 1981. |
| [3] |
敬刘凯, 吴文伟. 带主动动力吸振器的浮筏隔振系统自适应控制仿真分析[J]. 船舶力学, 2014, 18 (8): 989–995.
JING Liu-kai, WU Wen-wei. Simulation of vibration control based on the multi-channel self-adaptive feed forward law for the floating raft system with AVAs[J]. Journal of Ship Mechanics, 2014, 18 (8): 989–995. |
| [4] |
孙伟, 李以农. 橡胶隔振器非线性动态特性建模及实验研究[J]. 振动与冲击, 2012, 31 (23): 71–76.
SUN Wei, LI Yi-nong. Dynamic modeling and test for a nonlinear rubber damper[J]. Journal of Vibration and Shock, 2012, 31 (23): 71–76. DOI: 10.3969/j.issn.1000-3835.2012.23.013 |
| [5] |
王文杰. 船用橡胶弹性元件力学特性试验研究[D]. 北京: 中国舰船研究院, 2013.
WANG Wen-jie. Study of the experiment of the mechanics characteristics of marine rubber elastic isolator [J]. Beijing: China Ship Development and Design Center, 2013. |
| [6] |
何小静, 上官文斌. 橡胶隔振器静态力-位移关系计算方法的研究[J]. 振动与冲击, 2012, 31 (11): 91–97.
HE Xiao-jing, SHANGGUAN Wen-bin. Calculating methods for force versus displacement relation of a rubber isolator[J]. Journal of Vibration and Shock, 2012, 31 (11): 91–97. |
| [7] |
金晶, 张振山. 一种橡胶隔振圈动刚度计算方法[J]. 鱼雷技术, 2012, 20 (4): 124–127.
JIN Jing, ZHANG Zhen-shan. Dynamic stiffness calculation method for rubber ring isolator[J]. Torpedo Technology, 2012, 20 (4): 124–127. |
| [8] |
曾诚, 华宏星. 非线性橡胶隔振器的冲击特性研究[J]. 噪声与振动控制, 2012 (4): 20–24.
ZENG Cheng, HUAN Hong-xing. Study on shock response characteristics of nonlinear rubber isolator[J]. Noise and Vibration Control, 2012 (4): 20–24. |
| [9] | GENT A N, Engineering with rubber, Chemical Industry Press, Beijing, 2002. |
| [10] |
周振凯, 徐兵. 橡胶隔振器大变形有限元分析[J]. 振动与冲击, 2013, 32 (5): 171–175.
ZHOU Zhen-kai, XU Bing. Large deformation finite element analysis of rubber isolator[J]. Journal of Vibration and Shock, 2013, 32 (5): 171–175. |
| [11] |
唐振寰, 罗贵火. 含橡胶隔振器隔振系统动态特性研究[J]. 南京航空航天大学学报, 2014, 46 (20): 285–291.
TANG Zhen-huan, LUO Gui-huo. Dynamic characteristics of vibration system including rubber isolator[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46 (20): 285–291. |
| [12] | 杨剑, 张璞. 新编MD Nastran 有限元实例教程[M]. 北京: 机械工业出版社, 2008: 102–204. |
 2017, Vol. 39
2017, Vol. 39
