0 引　言

船舶数量的急剧增长，排放性问题引起了国内外专家学者及政府机构的广泛关注，国际海事组织（IMO）和地方区域性保护组织对船舶尾气排放做了严格的规定，尤其是2016年实施的《MARPOL》公约第三阶段对船舶排放提出了更加严格的要求；新造船舶能效设计指数（EEDI）强调了建设绿色、环保、高效的新型船舶。燃油动力船舶具有其固有的优势，但其很难满足日益严格的国际海事法规的要求，因此迫切需要开发新型动力船舶满足日益严格的相关排放性要求。柴电混合动力船舶是柴油机和轴带发电机（船舶电站）混合推进的新型推进方式^[1]，包含PTO/PTI运行模式，船舶正常航行时使用轴带发电机，可充分利用主机的储备功率，使主机运行在高效率状态，可提升主机利用率10%～15%，而且轴带发电机可以完全或者部分替代发电机，大大提高了船舶运营的经济性；加速、港口、内河航行等机动航行时，与柴油机共同推进，大大增强了船舶的操纵性；港口、冰区等环保特殊要求的区域，采用PTI模式，使船舶能够满足严格的国际法规；主机发生故障丧失动力时，采用电力推进模式，大大提高了动力系统的可靠性^[2-3]。船舶动力^[1]设备是船舶安全航行的生命保障，因此其可靠性、环保性、经济性、操纵性受到船东、船级社、国际海事组织的普遍关注，目前尚未有专门的组织机构采用专业的方法对混合动力船舶性能做出综合评估，本文利用层次分析法和隶属云理论将定性指标转化为定量指标对柴电混合动力系统进行综合评估。

柴电混合动力系统在实际运行中由于受到人为因素、设备因素、环境因素等诸多因素的影响，存在一定的不确定性和随机性。目前主流的评估方法有层次分析法、模糊综合评判法、系统分析法等，各种方法具有各自的优点，但缺少客观、有效的定量定性转化模型，若采用纯数学模型，便忽略了评估目标的不确定性与随机性，降低了事物的客观性^[4]。云理论已广泛用于航天、科技、商业等方面的性能评估。隶属云模型由我国工程院院士李德毅提出，它基于各种不确定性，综合考虑各因素，通过统一的数学表达式，采用定量的数学评估模型描述定性概念，能够较为准确的描述系统的模糊性和随机性，具有较高的客观性^{[4 – 6]}。云模型综合评估采用概率统计的方法，避免了人为评价的个人倾向性，因而能够客观准确的对柴电混合动力船舶动力系统做出综合评价。

1 混合动力船舶动力系统评估模型

动力系统提供持续可靠动力是确保船舶安全航行的关键因素，柴电混合动力作为一种新的动力方式，具有极大的技术和经济优势，有着广阔的应用前景和应用范围。针对船舶营运过程的关键指标因素，建立柴电混合动力船舶综合评估指标体系（A）包括以下内容：

1）经济性指标（B₁），即柴电混合动力船舶在运营中所要支付总的经济费用。经济性指标是船东考虑的主要因素，也是船舶运营中的核心因素，主要包含制造费用、燃料费用、维修费用，由于柴电混合动力包含变频器，推进电机、齿轮箱等设备，制造费用相对柴油机推进的船舶高，但轴带发电机又可以充分利用主机功率，使主机处于高效率状态，因此大大降低了发电机组的燃料费用，大大增加了经济性。经研究表明虽然电力推进的初期投资比直接推进模式高10%～20%，但整个综合电力推进系统的维修量和维修费用可降低17%左右。从而实现电能综合管理，既减少了综合运行费用，又减少了排放污染^[7]。

2）可靠性（B₂）是船舶安全航行的生命保障，是指机器设备稳定运行和发生故障的概率。船舶安全航行必须保证一定的可靠性，柴电混和动力系统中的电力推进系统与柴油动力系统共同推进，大大增加了船舶在极端条件下的可靠性。电力推进更多的采用故障率低、安全可靠的电子元件，大大降低了动力系统的故障率，并且采用电力推进更易于自动化操作，降低了人为故障的发生，有效降低机器设备的振动与噪声，提高了机械性能；

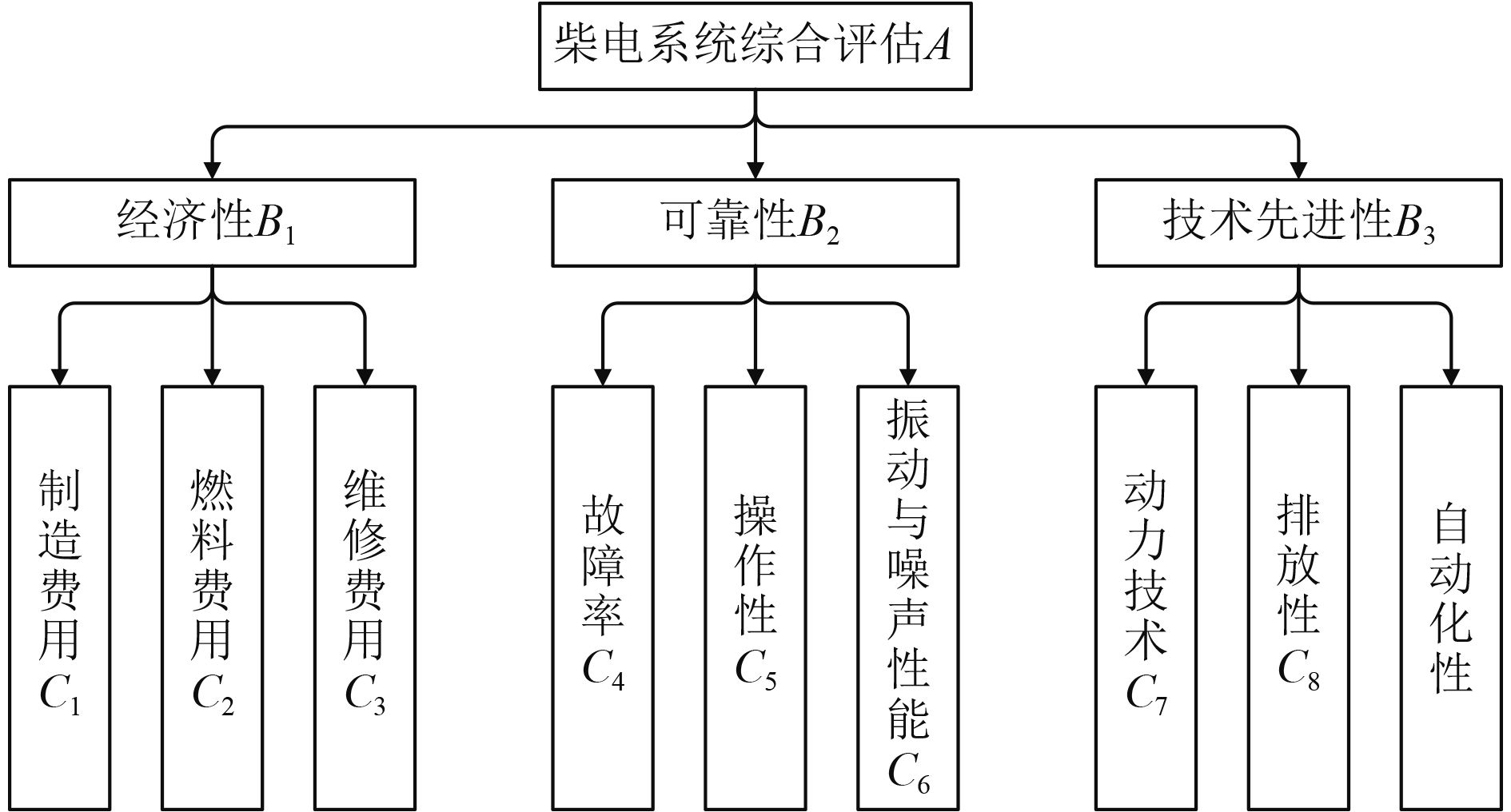
3）技术先进性（B₃）是柴电混合动力相对于柴油机推进动力的优越性。柴电混合动力可以采用电力推进和柴油机共同推进，避免柴油机极端情况下超负荷运行，为船舶提供强大的功率储备；也可以独立采用电力推进模式，适应对环保有严格要求的码头、港湾等特殊区域，可以大大减少船舶污染气体的排放^{[2, 7]}，极大地满足国际海事法规对排放性的严格要求；同时，电力推进更多的使用电子元器件，利于船舶实现自动化控制。柴电混合动力装置层次模型如图1所示。

2 建立AHP-云模型柴电混合动力评估数学模型 2.1 层次分析法（AHP）

对柴电混合动力系统进行模型化处理，分析目标影响因子，根据属性确立层次隶属关系，搭建因素递阶层次结构模型。高层次指标因素通过一定的准则支配约束下一层次的指标因素，同层因素之间相互独立、互不影响。根据评估需求，主要由目标层、准则指标层、方案层（处于最低层）等指标层构成。根据Satty法则对同层次指标因素相对重要性两两进行比较，构造指标因素的判断矩阵（A），求取该判断矩阵的最大特征值 ${\lambda _{\max }}$ 及最大特征向量w_i，各层次进行一致性检验，并对最大特征向量进行归一化处理，得到各指标因素的相对权重值。各因素构成的判断矩阵为：

$ A = \left[ {\begin{aligned}{\begin{aligned}{\displaystyle\frac{{{W_1}}}{{{W_1}}}}&{\displaystyle\frac{{{W_1}}}{{{W_2}}}}\\{\displaystyle\frac{{{W_2}}}{{{W_1}}}}&{\displaystyle\frac{{{W_2}}}{{{W_2}}}}\end{aligned}}&{\begin{aligned}L&{\displaystyle\frac{{{W_1}}}{{{W_n}}}}\\L&{\displaystyle\frac{{{W_2}}}{{{W_n}}}}\end{aligned}}\\{\begin{aligned}M&M\\{\displaystyle\frac{{{W_n}}}{{{W_1}}}}&{\displaystyle\frac{{{W_n}}}{{{W_2}}}}\end{aligned}}&{\begin{aligned}M&M\\L&{\displaystyle\frac{{{W_n}}}{{{W_n}}}}\end{aligned}}\end{aligned}} \right] = {\left( {{a_{ij}}} \right)_{n*n}}\text{。}$

(1)

层次分析法中，为了使数值型判断矩阵定量化和无量纲化，在进行比较时，引用1～9标度法，其具体含义如表1所示。

根据判断矩阵求出该矩阵的最大特征值 ${\lambda _{\max }}$ 和特征向量 ${w_i}\left( {{w_1},{w_2}, \ldots {w_n}} \right)$ ，进而进行一致性检验：

$CR = CI/RI,$

(2)

$CI = \left( {{\lambda _{\max }} - n} \right)/\left( {n - 1} \right)\text{。}$

(3)

式中： ${{\lambda _{\max }}}$ 为最大特征值；n为判断矩阵的阶数。

判断矩阵是否具有满意的一致性，引入平均随机一致性指标值RI，对于1～9阶判断矩阵，RI值通过大量随机试验统计分析得出，具体值可通过查表2得出。

当CR<0.1时，表明该判断矩阵具有良好的一致性，否则重新调整判断矩阵，直至满足相关一直性要求。将判断矩阵的最大特征向量进行无量纲化、归一化处理得到各指标的因素的相对权重值 ${w_i}\left( {{w_1},{w_2}, \ldots {w_n}} \right)$ 。

2.2 云模型 2.2.1 云模型的基本概念

云模型把随机性和模糊性结合起来，通过数字特征期望（E_x）、熵（E_n）、超熵（H_e）实现定性概念与定量概念的转化，揭示模糊性与随机性的关联性，表示特定定性概念的粒度，构成特定结构的发生器。云模型发生器有正向发生器和逆向发生器2种，正向云模型发生器由云滴产生数字特征（ ${E_x},{E_n},{H_e}$ ），逆向发生器由已知的多个云滴确定正态云模型的数值特征（ ${E_x},{E_n},{H_e}$ ）。期望（E_x），论域中最能代表定性概念的样本点，是隶属云的重心位置，反应了评价事物模糊概念的中心值；熵（E_n）反映了定性概念被接收值范围的大小，表现了一定的模糊性，其值越大，概念越模糊；超熵（H_e），熵的不确定性的量度，反映定性概念的随机性和云滴的离散程度，其值越大，云滴离散程度亦越大。

设论域X是一个集合X={x}， ${\mu _{\tilde A}}\left( X \right)$ 是论域X上的模糊集合 $\tilde A$ 的一个隶属函数：X→[0，1]，x∈X，即把论域X中的元素映射到实数[0，1]中。其中 ${\mu _{\tilde A}}\left( X \right)$ 是元素x隶属于模糊集合 $\tilde A$ 的程度，即x对 $\tilde A$ 的隶属度。隶属函数 ${\mu _{\tilde A}}\left( X \right)$ 是论域中所有元素属于模糊集 $\tilde A$ 的属度分布，隶属度x在X上的分布成为隶属云^[10]。

2.2.2 云模型各指标的数值特征

根据专家评估结果，组成决策矩阵，通过定性与定量语言的转化，提取n维数字型精确值的一个云模型的数字特征：

${E_x} = \left( {{E_{x1}} + {E_{x1}} + \ldots + {E_{xn}}} \right)/n,$

(4)

${E_n} \!=\! \left( {\max \left( {{E_{x1}},{E_{x2}} \ldots ,{E_{xn}}} \right) \!-\! \min \left( {{E_{x1}},{E_{x2}},{E_{xn}}} \right)} \right)/6\text{。}$

(5)

每个云模型都可以表示一个语言值指标，将n个语言值的云模型用一个一维综合云模型来表示：

$\begin{split}{E_x} = & \frac{{\left( {{E_{x1}}{E_{n1}} + {E_{x1}}{E_{n1}} + \ldots + {E_{x1}}{E_{n1}}} \right)}}{{{E_{x1}}}} + \\& {E_{x1}} + \ldots + {E_{xn}},\end{split}$

(6)

${E_n} = {E_{n1}} + {E_{n2}} + \ldots + {E_{nn}}\text{。}$

(7)

当指标为精确数字型时， ${E_{x1}} \sim {E_{nn}}$ 为指标的具体值，当指标为语言值型时， ${E_{x1}} \sim {E_{xn}}$ 为云模型的期望， ${E_{n1}} \sim {E_{nn}}$ 为云模型的熵。

2.2.3 云重心综合评估法

云重心综合评判法是将各指标用云模型来表示，形成一个一维综合云，对比综合云在理想状态下和特定状态下的偏离度，进行加权平均求得云模型目标层与理想值的偏离程度，计算出评估目标的归属度，判断指标的性能。

相应云的重要程度可用云重心来表示，系统信息发生变化云重心亦相应变化。云重心的表示式为：

$T = a \times b\text{。}$

(8)

式中：a为云重心位置，即云模型的期望值；b为云重心的高度，表示云滴的不同几何位置，通常情况下b取0.371。

理想状态下一个系统各指标的理想值是已知的，n维综合云的重心可用一个n维向量 ${T^0}\left( {T_1^0,T_2^0, \ldots ,T_n^0} \right)$ 来表示，a_i为理想云重心的值，云重心高度 ${b_i} = {w_i} \times 0.371$ 。当在某种条件下云重心的位置发生改变，此时新的n维综合云的重心向量为 $T'\left( {T_1',T_2', \ldots ,T_n'} \right)$ 。n维综合云重心与理想状态下云重心的差异用向量 ${T^G}\left( {T_1^G,T_2^G, \ldots ,T_n^G} \right)$ ，将综合云重心偏差向量归一化，得

$T_i^G = \left\{ {\begin{array}{*{20}{c}}{\displaystyle\frac{{\left( {T_i' - T_i^0} \right)}}{{T_i^0}},T_i' < T_i^0},\\{\displaystyle\frac{{\left( {T_i' - T_i^0} \right)}}{{T_i'}},T_i' \geqslant T_i^0},\end{array}} \right.\;\;\;i = 1,2, \ldots ,n\text{。}$

(9)

将归一化的各指标云重心向量乘以权重值并相加得综合云的总偏离度 $\theta $ （0≤ $\theta $ ≤1），偏离度越小，评估结果越完美。

$\theta = \mathop \sum \limits_{i = 1}^n {w_i} \times T_i^G,$

(10)

由加权偏离度θ获得综合云模型评估结果的归属度为:

$e = 1 - \left| \theta \right|\text{。}$

(11)

2.3 云模型评语集

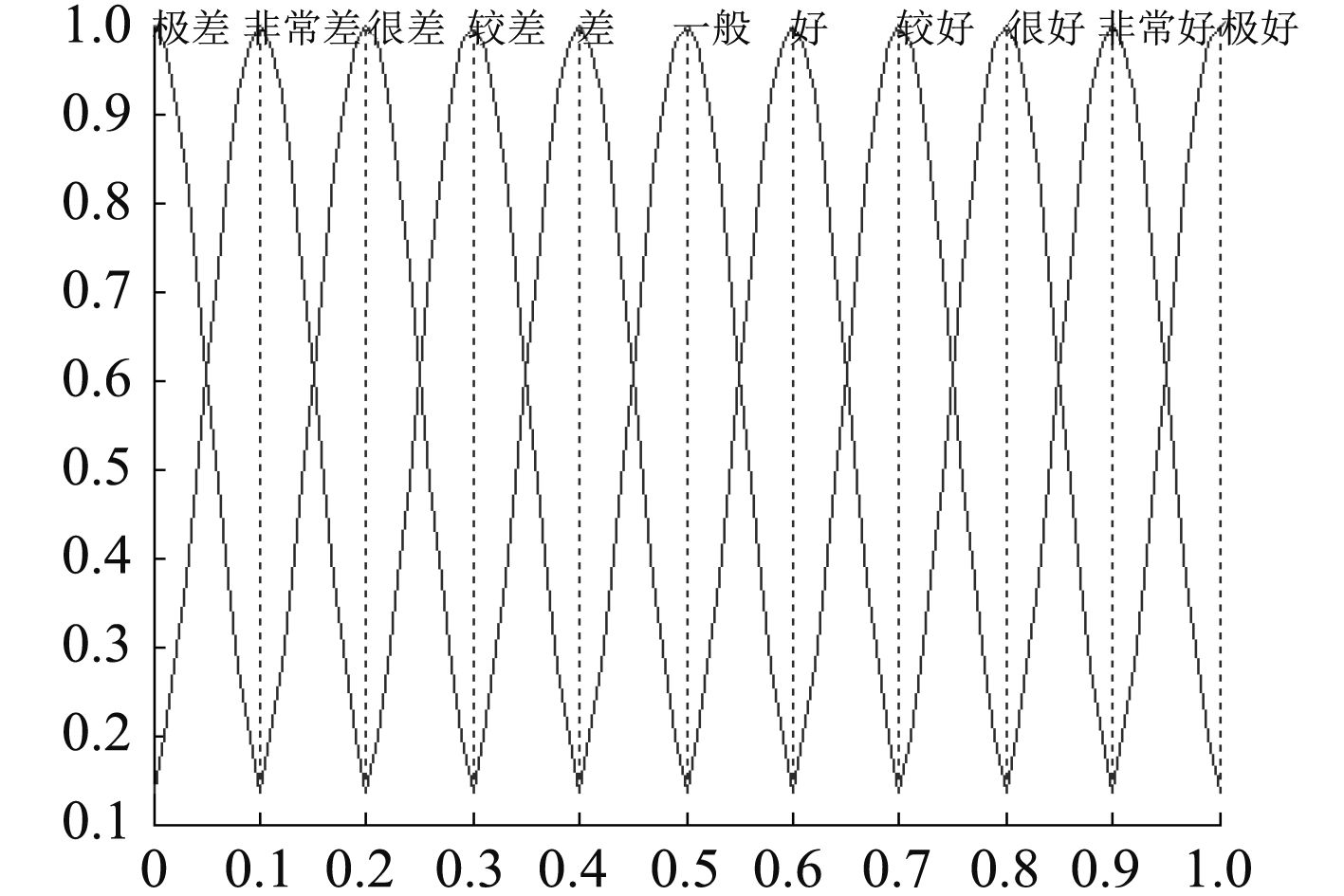
针对评估目标的特点，制定精度尽可能高的评语集的，通常云模型评语集V（极好，非常好，很好，较好，好，一般，差，较差，很差，非常差，极差）^[6]，每个评语值用云模型表示在一维线性坐标上，构成一维测评发生器，如图2所示。

3 模型计算分析 3.1 计算评估指标权重

选取某型调查船作为参考对象，采用单机单桨推进形式并接入轴带发电机（PTO/PTI）。其推进系统的参数如表3所示。

参考上述某型调查船柴电混合动力船舶各指标的性能特点，利用层次分析法结合1～9标度法，构造判断矩阵如表4所示。

由表4可知：

　　　　　　　　　 ${\lambda _{\max }}$ =8.965 9，

由式（3）得：

　　　　　 CI=∣（8.965 9–9）∣/（9–1）=0.004 26，

由式（2）得：

　　　　　　 CR=0.004 26/1.45=0.002 9<0.1。

上式表明柴电混合动力船舶指标层构成的判断矩阵满足良好的一致性，各技术指标权重如表5所示。

3.2 构建评估指标评语矩阵

针对参考对象柴电混合动力系统的特点，结合云模型隶属度函数，运用评语集语言，采用专家打分方式得到如下评语矩阵：

$ B = \left( {\begin{array}{*{20}{c}}{0.7}&{0.8}&{0.6}&{0.7}&{0.8}&{0.7}&{0.9}&{0.9}&{0.8}\\{0.5}&{0.9}&{0.5}&{0.5}&{0.7}&{0.6}&{0.8}&{0.9}&{0.8}\\{0.4}&{0.7}&{0.6}&{0.5}&{0.6}&{0.8}&{0.8}&{0.8}&{0.7}\\{0.6}&{0.7}&{0.7}&{0.6}&{0.5}&{0.5}&{0.8}&{0.8}&{0.7}\end{array}} \right)\text{。}$

由式（4）~式（5）求得各指标云模型的期望（E_x）和熵（E_n）。

3.3 指标云重心综合评判

基于云模型的船舶柴电混合动力系统评估，运用云模型描述指标性能，并进行相关云计算，求得理想状态下和特定状态下的云重心向量，得到综合云偏差值，求出混合动力船舶的归属度，评判其综合性能的优劣性。

根据评语集，理想状态下各指标的期望E⁰=（1，1，…，1），由式（8）求得理想状态下和特定状态下的云重心一维综合向量及综合云偏差向量如表6所示。

根据式（10）总偏离度 $\theta $ =0.302，表明该柴电混合动力船舶系统与理想值偏离度为0.302，归属度为0.698，综合各指标性能表明该评估模型具有较好的综合性能。

4 结　语

针对船舶柴电混合系统的各指标特点，建立层次云模型，利用隶属云相关理论客观、准确的对该模型进行综合评估，得出该模型具有良好的综合性能；该评估方法亦可以实现对船舶柴电混合动力多方案之间的优劣选择，通过对各方案归属度进行比较，得到最佳方案，为混合动力船舶的设计提供一定的理论和技术支撑。船舶柴电混合动力系统运用PTO/PTI技术，能够保证船舶主机在各种工况下处于良好的经济状态，同时船舶电站兼容岸电系统，能够满足排放性要求严格的码头、港湾、水域航行，具有良好的优越性；随着电子控制技术的发展，船舶柴电混合动力系统将会更加广泛的应用。