自升式海洋平台为由桩腿支撑在海面上方进行工程作业的海洋装备,现已广泛应用于石油、天然气等矿物资源的开采作业中。海洋平台工作环境恶劣,需要承受复杂的载荷,进而保证海洋平台的稳定性至关重要。海洋平台失稳状况主要有穿刺失稳、滑移失稳以及倾覆失稳。本文着重研究自升式海洋平台的抗滑移能力,抗滑移能力是指处于支撑状态下自升式平台,在最不利的组合载荷作用下,抵抗滑移的能力[1]。自升式平台依靠桩靴与地基土壤的相互作用来获得抗滑移阻力,抗滑移阻力主要来自于地基土壤的对桩靴的水平反作用力,而地基土所受的垂直载荷与水平载荷有着密切关系。
随着近海油气田的开采趋于饱和,油气勘探逐渐向深海发展,海平面上的环境和海底土质更加恶劣,导致平台发生滑移失效较高。1982年,在加拿大纽芬兰近岸油田作业的“海洋徘徊者”号钻井平台,遭遇时速高达190 km和浪高20 m的飓风,发生滑移倾覆,造成重大沉船事故。我国常根据CCS规范对平台进行抗滑移能力的评估,虽然考虑到平台所受到的水平载荷,能够为自升式钻井平台抗滑移力的校核提供部分理论参考。但是并未分析地基土壤流动产生的影响,并且海上平台所处的工作环境较为复杂,海底地基土壤环境参差交错,抗滑移力理论值难以与实际值相吻合,导致平台在作业过程中发生滑移事故。
本文以某自升式钻井平台中的桩腿和桩靴为研究对象,在抗滑移理论研究的基础上,借助有限元软件Abaqus,采用CEL方法,研究桩靴在复杂工作环境下与海底土壤的相互作用,模拟滑移过程中土壤的流动现象,分析平台的抗滑移能力,并与已有的理论值相比较,验证数值解的优越性,从而为自升式钻井平台的安全作业提供技术指导。
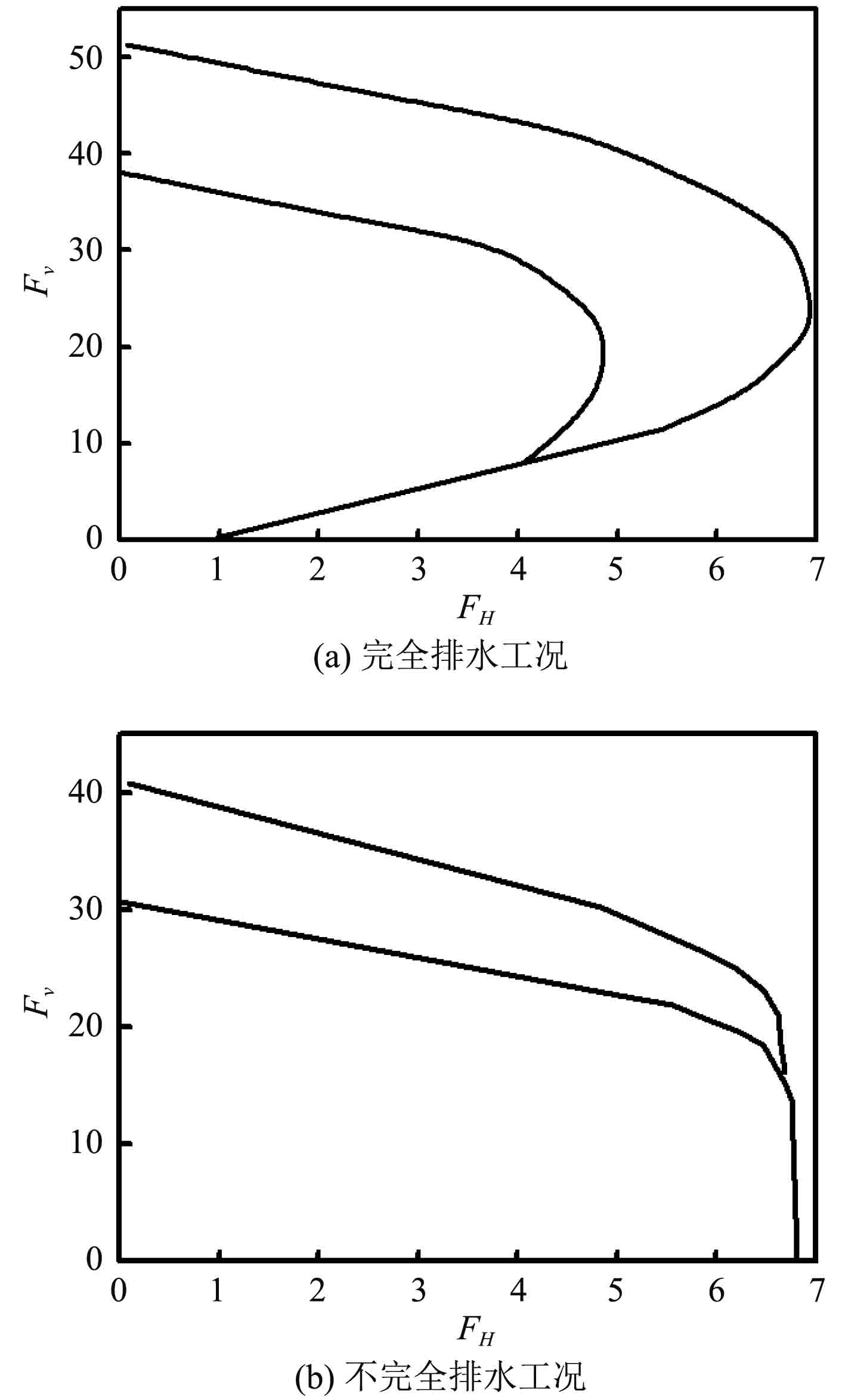
1 桩靴抗滑移能力理论分析 1.1 地基土与抗滑移能力自升式海洋平台所受到水平载荷包括风、海浪、海流等环境载荷。垂直载荷主要包括船体自身的固定载荷和水压、地压等环境载荷。水平载荷作用在桩腿上,对桩靴产生旋转力矩。所有水平载荷、垂直载荷以及弯矩自上而下由船体、桩腿和桩靴传递至地基土,引发桩土相互作用[4]。图1为挪威船级社依据经验获得的地基稳定曲线[3],该图描述分别描述了在完全排水与不排水状况下地基土不失稳所能承受的垂直载荷Fv与水平载荷FH之间的关系。图1(a)为完全排水状况下的地基稳定曲线,可见在曲线的下半段垂直载荷Fv数值较小时,水平载荷FH与垂直载荷Fv为正比线性关系;而当垂直载荷Fv足够大时,随垂直载荷Fv增大,水平载荷FH减小,地基土承载能力降低。图1(b)表述了在不排水情况下地基土的承载能力,当对地垂直载荷Fv为0或者数值较小时,临界水平载荷FH基本保持不变;当垂直载荷Fv足够大时,水平载荷FH随垂直载荷增加而减小。综述以上2种情况,当垂直载荷过大时,地基土所能承受的水平载荷数值较小,地基土水平方向上承载能力不足。
|
图 1 地基稳定曲线 Fig. 1 Stability curve of foundation soil |
根据对地基土承载能力的了解,本文在探讨桩靴抗滑移能力时,选择较小对地比压工况能更加有效地靠近自升式海洋平台的工作环境。
1.2 水平载荷理论值计算方法采用中国船级社在《海上移动式平台入级与制造规范》[5]所给出的相应公式。
风载荷主要由海风作用在船体、桩腿、工作楼等产生,具体计算公式:
| ${F_i} = 0.625{C_{si}}{C_{hi}}{V^2}{A_{pi}},$ | (1) |
式中:
水平载荷还主要包括海浪、海流对桩腿的水平作用力,其具体计算公式为:
| $F = 0.5\rho U{C_D}AdL + \rho {C_M}\pi dL/4{\text{。}}$ | (2) |
式中:
中国船级社(CCS)《海上移动式平台规范》中抗滑移力和衡准中给出:侧向滑移可能由水平力引起,滑移力计算方法为:
| ${F_H} = F + \sum {F_{Li}},$ | (3) |
式中:FH为环境力;F为风力;
抗滑移阻力RH由桩靴底部的土壤凝聚力Rc和桩靴周边摩擦力
| ${R_H} = {R_c} + {R_{cf}},{R_c} = G\tan \theta ,{R_{cf}} = {S_u}{A_{ms}}{\text{。}}$ | (4) |
式中:SU为土壤的剪切强度;G单个桩靴承受的自升式平台重量;
对抗滑安全系数KH的要求:
作业状态
自存状态
因而,为了更好地计算抗滑移力,本文在沿用理论公式的基础上,采用数值分析方法,模拟桩靴滑移过程,并将理论解与数值解进行对比分析。
2 桩-土系统的数值模型Abaqus软件能够对土体的变形和流动进行耦合分析,在Abaqus中使用欧拉网格来划分土体单元,可以模拟土壤在外力作用下的流动变形。
2.1 桩-土系统模型本文所研究的独立桩腿式自升式平台,每个桩腿都安装一个独立桩靴,该种自升式平台的桩靴插桩深度大,抗滑移能力强,一般对地比压在150~350 kPa。本文研究对象为典型桩靴,最大断面直径为6 m。利用ANSA软件对桩靴实体进行网格划分,以C3D8R网格对桩靴进行网格离散。由于桩靴滑移过程中,土壤相对桩靴的变形要大许多。因而在模拟桩靴滑移过程中,将桩靴整体结构设置为刚体,在桩腿处施加速度载荷完成加载。
考虑到土体的边界效应,土体直径选取6倍桩靴直径。土体网格采用欧拉网格离散,借鉴CEL方法进行分析,将土体网格设置为EC3D8R。土体完全包覆桩靴以此模拟独立桩腿式自升式平台桩靴入土深的状况,同时在桩靴滑移过程中模拟各个方向土体的变形。由于土体内部存在应力而从桩靴滑移初始过程中就会影响整个分析过程,因而模型建立需要在一开始平衡初始地应力,限制土壤底部变形,并设置土体边界条件。
在CEL法中,材料会在欧拉网格中流动,而实际桩靴滑移过程土壤的流动方向不确定。因此,为了真实模拟桩靴滑移过程中土壤流动,为土壤流动提供所需空间,本文采用完全包覆桩靴的土体来给土壤流动提供空间。桩靴滑移的数值模型如图2所示。

|
图 2 桩靴滑移数值模型 Fig. 2 Model used in simulation of anti-slide |
土体材料参数选取Hossain试验中所测得的参数[7]。其中硬质土比重为8.03 kN/m3,弹性模量19.2 MPa,抗剪强度为38.3 kPa,内摩擦角为8°。桩靴及桩腿材料参数:比重为20 kN/m3,弹性模量2e5 MPa。
2.3 边界条件及接触在土体模型底面施加全约束,顶面不施加约束。土体和桩靴之间的接触属性定义为“通用接触”。由于桩靴滑移路径相对较小,因此可以忽略桩土摩擦,其摩擦系数选为0。
2.4 载荷施加桩靴模型为一刚体,为模拟桩靴滑移过程,给桩靴模型施加一沿水平方向0.1 m/s的移动速度。自升式平台三桩系统承受自升式平台重量,平台空船重量4 010 t,单个桩靴承重设为1 337 t。
3 桩靴抗滑移结果分析与讨论 3.1 抗滑移阻力理论计算由土壤抗滑移阻力公式可知,抗滑移阻力与桩靴所受纵向载荷、桩土接触面积有关。在桩靴滑移过程中,桩靴所受到的抗滑移阻力不断变化。考虑到桩靴在稳定工作状态下滑移距离很小,且桩靴埋深大,桩靴与海底土壤接触面积为桩靴实际底面面积;三桩承重4 010 t,土壤内摩擦角为8°。式(4)各参数选择如下:G为单个桩靴承重,取1 337 t。
| ${R_c} = 1.88\;{\rm{MN}},{R_{cf}} = 0.29\;{\rm{MN}},{R_H} = 2.17\;{\rm{MN}}{\text{。}}$ |
因此,抗滑移阻力理论值为2.17 MN。
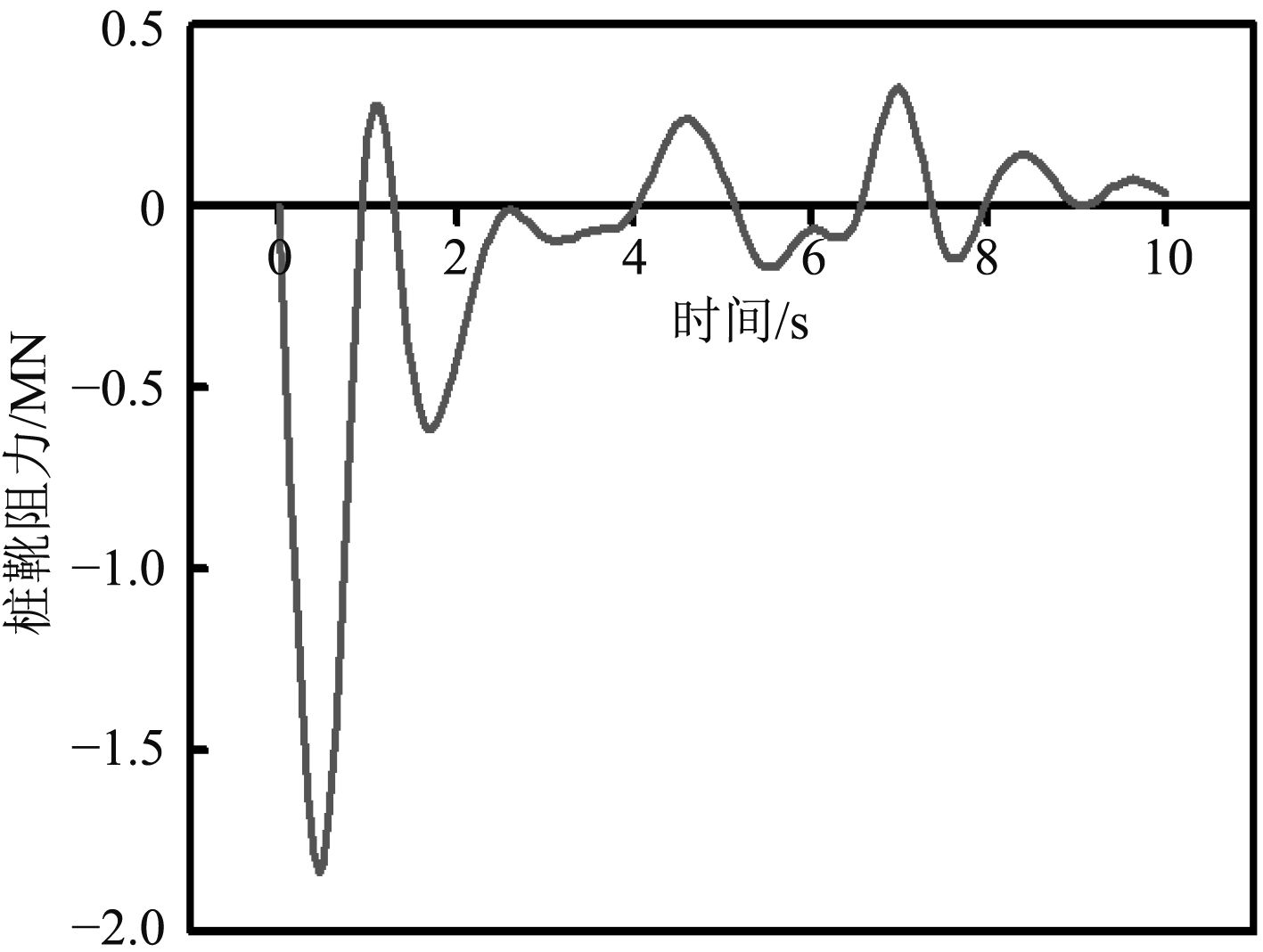
3.2 数值解结果分析将模型提交计算后,得到1条阻力曲线如图3所示。从图中可看出,当桩靴发生横向短距离快速位移时,桩靴滑移阻力迅速增长至最大;滑移距离增加后,阻力迅速降低,阻力变小并在0 kN上下浮动。桩靴抗滑移阻力数值解选取滑移过程中所受到的最大阻力为1.81 MN。
|
图 3 桩靴所受阻力曲线 Fig. 3 Resistance curve of spudcan |
为确保结果的准确性,本文将理论解与数值解进行比较。在本文所设定的工况下,桩靴抗滑移阻力理论解为2.17 MN,数值解为1.81 MN。数值解与理论解差值为354 kN。这是由于理论解公式依据土壤的粘附特性来推导抗滑移阻力,在计算过程中只是赋予公式某一状态下的土壤材料性质。而在桩靴滑移过程中,桩靴发生位移并挤压土壤,同时海水进入土壤,改变了土壤的剪切强度,容易造成误差,理论解较为保守。而桩靴抗滑移阻力的数值解是选取的在模拟桩靴发生微量滑移过程中桩靴所受到最大阻力,并且选用可以模拟土壤流动的EC3D8R来划分土壤,相比于理论解的静态求解,数值解更加有效的得到桩土互相挤压作用下,土壤所能提供的最大抗滑移阻力。
3.4 滑移过程中土壤的流动分析地基土壤在抵抗桩靴滑移过程中同样受力发生挤压、流动等变形,在数值解析过程中,模拟出土壤流动过程。
从图4可知,在桩靴微小滑移过程中,由于所选用的土体模型边界广,桩靴发生位移较小,滑移过程中只会影响周边土体,图中曲线可以反映土体的流动状况。如图4(a)所示,桩靴刚开始位移,在位移方向上产生抗滑移阻力,土体开始发生微小变形。如图4(b)所示,桩靴发生位移并受到最大抗滑移阻力,土体在位移方向上被挤压开始向上流动。如图4(c)所示,桩靴继续位移,土壤受挤压向桩靴上部流动。

|
图 4 土壤流动过程 Fig. 4 Flow process of soil |
为了更加准确地预测桩靴所受到的抗滑移阻力,本文采用中国船级社抗滑移稳性的理论计算方法,并在此基础上沿用该理论,结合CEL耦合方法,采用Abaqus建立数值模型,对初始条件进行限制,计算得出理论与数值解,并对两者进行比较,得出以下结论:
1)国内外学者对桩靴滑移理论的研究存在不足,传统理论公式中抗滑移阻力来自于土壤的粘附力和摩擦力,该方法只是在静态工况下以某一时刻的土壤材料属性来计算其抗滑移阻力,而桩靴在工作状态下会发生微小位移,同时土壤还会发生流动,容易产生误差。
2)数值解是以实际状况下模拟桩靴在微小滑移过程中,所得结果选取的是微小滑移过程中受到的最大阻力值,能够较为精确地得出抗滑移阻力。综合2种结果,2种不同方法得出的阻力都能够保证平台抗滑移稳性。与理论值相比,数值解能够更好的在动态下反映土壤的抗滑移属性,并且得到土壤的流动情况。
| [1] |
龚闽, 谭家华. 独立桩靴自升式平台抗滑能力计算方法研究[J]. 中国海洋台, 2004 (6): 23–27.
GONG Min, TAN Jia-hua. The methods research of calculating anti-sliding ability for jackups with separated spuncans[J]. China offshore Platform, 2004 (6): 23–27. |
| [2] |
周煜. 自升式海洋平台设计方案评价体系研究[D]. 大连: 大连理工大学, 2006.
ZHOU Yu. Research on the software of jack up estimation[D]. Dalian: Dalian University of Technology, 2006. |
| [3] | DnV. Classfictation Notes <FOUNDATIONS>[S]. 1992, 30(4). |
| [4] |
季春群, 孙东昌. 自升式平台上外载荷的分析计算[J]. 海洋工程, 1995, 3 : 19–24.
JI Chun-qun, SUN Dong-chang. The calculation an analysis of environment loads for jack-up rig[J]. The Ocean Engineering, 1995, 3 : 19–24. DOI: 10.3321/j.issn:0890-5487.1995.01.003 |
| [5] |
CCS. 海上移动式平台入级与建造规范[S], 1992.
CCS. Rules for construction and classification of mobile offshore drilling units[S], 1992. |
| [6] |
蔡宏. 海洋钻井平台稳定性分析研究[D]. 西安: 西安石油大学, 2011.
CAI Hong. Analysis and research on the stability of sea drilling platform[D]. Xi’an: Xi’an Shiyou University, 2011. |
| [7] | HOSSAIN. Cavity stability and bearing capacity of spudcan foundation on clay[C]//Offshore Technology Conference. Houston, OTC 17770. |
 2017, Vol. 39
2017, Vol. 39
