2. 船舶与海洋工程水动力湖北省重点实验室,湖北 武汉 430074;
3. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Hubei Key Laboratory of Naval Architecture & Ocean Engineering Hydrodynamics, Huazhong University of Science and Technology, Wuhan 430074, China;
3. Collaboration Innovation Center for Advanced Ship and Deep-Sea Exploration, CISSE, Shanghai 200240, China
近年来,随着航运业低运价、高油价情况的持续,各航运公司开始降低运营成本来提高生存竞争力。而在船舶的整个生命周期中,与燃油相关的成本占总成本的约40%~60%[1],此外国际海事组织(IMO)也对船舶的能效设计指数(EEDI)和营运指数(EEOI)作出规定以限制二氧化碳排放量,因此对船舶进行节能改造以降低油耗是提高竞争力的关键所在。
进行水动力性能优化是船舶节能减排的一个重要研究方向,主要包括对船舶进行线型优化、对已营运船舶进行球鼻首改装、安装节能装置和纵倾优化4个方面[2]。韩国大宇造船厂对超大型原油运输船(VLCC)进行型线优化,降低了5%的油耗;武汉理工大学对某渔船进行球鼻首改装,使设计状态下的总阻力降低了6%;节能装置则是在船舶的尾部安装整流鳍、舵球等整流装置以均匀螺旋桨进流,从而提高船舶的推进效率,但节能效果因船型和节能装置的不同而异,综合来说节能效率可达2%~8%[3];但线型优化、球鼻首改装通常仅只是针对特定的航速和吃水(通常是设计航速和设计吃水)下才会达到理想的节能效果[4],当船舶的航行姿态发生变化时节能效果便会降低甚至会引起油耗增加,安装节能装置虽然在一定程度上降低油耗,但会增加投资成本并降低船舶的营运效率,而纵倾优化是在保证船舶的排水量不变的情况下,通过调节装载或压载水来改变船体水下部分的流体线型和静水阻力从而降低油耗,既可用于绿色船舶的设计研发,又能用于现已营运的船舶,是未来绿色船舶的重要发展方向[5 – 7]。纵倾优化作为最容易实现的节能手段之一,既能降低油耗、提高营运优势又能减少对环境的污染,越来越受到重视[8 – 9]。
本文以某成品油船的阻力性能为优化指标,采用CATIA及ICEM软件,根据船体型线图及其型值参数,建立船体三维模型及控制域,划分结构性网格;采用CFD软件(Fluent)计算目标船在不同变纵倾状态下的阻力值,并与试验结果相比较,分析纵倾变化对船舶阻力性能的影响规律。结果表明:该方法可以确定船舶在不同吃水下的最优纵倾值,并为船舶的实际运营提供建议,从而提高船舶的节能减排率。
1 数学模型 1.1 建立模型本文以某46 000 t成品油轮为目标船,该船实际运营中存在多种工况,因此有必要开展纵倾优化工作以确定最优节能方案。该船具体船型参数及营运工况如表1所示。
|
|
表 1 油船基本参数 Tab.1 Basic parameters of oil tanker |
由于该船实际营运中存在较多工况,为了节约计算成本,本文选取实际运营中在设计航速下Vs=11 kn较为典型的3种工况(压载、设计吃水、满载)进行计算,同时考虑到船模试验中对水池长度、拖车速度、池壁干扰现象和堵塞效应的限制,取模型缩尺比λ=36以便于和试验结果进行对比。
|
|
表 2 油船计算工况 Tab.2 Calculating conditions of oil tanker |
在Catia的创成式曲面设计模块中,选择三维笛卡尔坐标系O-XYZ为建模坐标系,坐标轴定义为:以中线面、基平面和尾站面的交点为坐标原点,基平面与尾站面的交线为Y轴,指向右舷为正;中线面与尾站面的交线为Z轴,向上为正;Z轴服从右手坐标系[10]。根据目标船的型线图及型值表进行三维船体建模,并利用曲线光顺命令确保相邻的船体曲面光顺结合,建模效果如图1所示。

|
图 1 油船三维模型 Fig. 1 3D model of oil tanker |
RANS方程是粘性流体运动学和动力学的普适性控制方程[11],本文用它作为求解船体阻力的基本方程,其形式如下:
| $\begin{split}& \rho {f_i} + \displaystyle\frac{\partial }{{\partial {x_j}}}\left[ {{\mu _o}(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}) - \frac{2}{3}{\mu _o}\frac{{\partial {u_i}}}{{\partial {x_i}}}{\delta _{ij}}} \right] + \\& \displaystyle\frac{\partial }{{\partial {x_j}}}( - \rho \overline {{u_i}'{u_j}'} ) - \frac{{\partial p}}{{\partial {x_i}}} = \frac{{\partial (\rho {u_i})}}{{\partial t}} + \frac{{\partial (\rho {u_i}{u_j})}}{{\partial {x_i}}},\end{split}$ | (1) |
式中:ρ为流体密度;p为静压;fi为单位质量的质量力;ui,uj均为速度分量。
对RANS方程进行求解时,RNG k-ε湍流脉动耗散方程能更好地模拟船体周围的分离流、复杂流等二次流动:
| $\frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}[{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}] + {G_k} + \rho \varepsilon ,$ | (2) |
| $\frac{{\partial (\rho \varepsilon )}}{{\partial t}} \!+\! \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} \!=\! \frac{\partial }{{\partial {x_j}}}[{\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}] \!+\! \frac{{C_{1\varepsilon }^ * }}{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k},$ | (3) |
式中:
对于自由液面的波动,本文采用VOF法多相流模型进行模拟:
| $\frac{{\partial {a_q}}}{{\partial t}} + \frac{{\partial ({u_i}{a_q})}}{{\partial {x_i}}} = 0\;\;\;(q = 1,2),$ | (4) |
式中:a1,a2分别为空气相和水相的体积分数。
2 网格划分及计算策略网格划分是CFD模拟过程中用时较多的环节,也是影响数值计算的模拟精度、稳定性和收敛速度的关键因素之一,网格过密或过疏都会极大地影响计算结果。网格过疏,计算结果会与实际值相差较远甚至得到错误的计算值,网格过密,使计算量增大且计算难以收敛。
因此,本文在网格划分时使用了局部加密的方法,在远离船体周围流场的入口段和出口段,将其密度给予适当降低,以便于控制网格总数,而在船体附近曲率变化大的地方则逐步过渡加密,这样不仅能够提高计算精度,还能避免流场变化平缓区域的计算资源浪费[12]。
本文计算流域的选取为:入口距离船首一倍船长,出口距离船尾两倍船长,吃水方向距离船体底面一倍船长,船宽方向距离中纵剖面一倍船长,由于是数学模型,左右严格对称,因此为了节约计算成本,计算时只需取一半计算模型即可,网格总数约为110万。计算模型及网格划分效果如图2所示。

|
图 2 计算模型 Fig. 2 Computational model |

|
图 3 计算域网格划分 Fig. 3 Grid partition of calculation basin |
计算策略为:瞬态计算,船体中纵剖面所在的面设置为对称面,类型为SYMMETRY,动量、湍流动能和湍流耗散率均采用2阶迎风格式进行离散,入口为速度入口,出口为水流出口,流域的壁面设置为速度入口以模拟无限流场,来流速度与航速大小相同,方向相反,由于粘性流体在壁面处的应满足无滑移条件,故设置为不可穿透的WALL,如表3所示。
3 计算结果及分析 3.1 流场分析

|
图 4 纵倾状态下船体动压力云图 Fig. 4 Contours of dynamic pressure corresponding to trim variation |
|
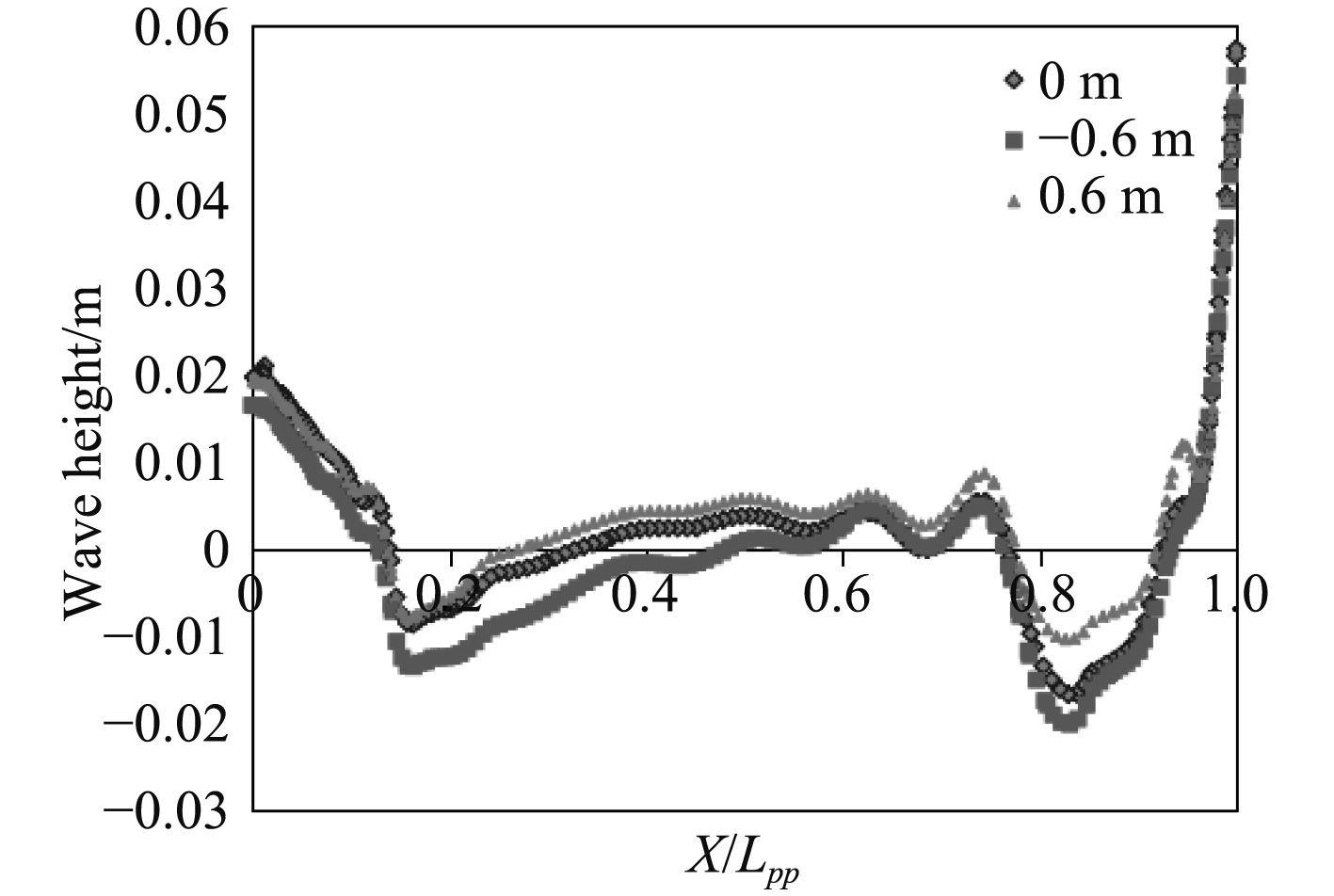
图 5 纵倾状态下船体表面波高图 Fig. 5 Wave height on ship surface corresponding to trim variation |
图4为设计吃水下D=10.2 m下尾倾0.6 m、平浮、及首倾0.6 m时的船体表面动压力云图及图及波高图。横向对比动压力云图中可以看出,从船首到船尾船体表面动压力云图先增大(一般在18~20站达到最大)后减小,在船尾处又略微增大,但明显小于船首动压力云图,这是由于水的粘性作用,使船体前后表面产生压力差,是产生粘压阻力的原因。
纵向对比还可以发现,首倾0.6 m下的船首动压力比平浮和尾倾下的明显小很多,说明纵倾对船体周围流场产生了显著影响。从波高图中可以看出,在船的首尾附近处产生波峰,兴波最为明显,这是兴波阻力产生的体现;尾倾状态下,首部和尾部的波浪均比首倾和平浮时有所降低,说明该状态下船体兴波阻力也有所减小。
3.2 CFD计算结果与试验结果的对比模型试验在华中科技大学船舶拖曳水池内进行,该水池的主要参数如下:长、宽、深分别为175 m×6 m×4 m,拖车加速度约为0.67 m/s,最大运行速度为8 m/s。船模缩尺比为36,表面进行光洁处理,为了使船模的边界层处于紊流状态,在19站处安装人工激流丝,船模及其在拖曳水池中的状态如图6所示。

|
图 6 船模及其在拖曳水池中的运动 Fig. 6 Ship model and its motion in towing tank |
|
|
表 3 边界条件计算策略 Tab.3 Calculation strategy of the boundary conditions |
为了验证CFD数值计算的可靠性,分别将3种吃水下各个纵倾状态的数值计算值Rm与试验值Rs进行对比,并绘制成纵倾-阻力曲线图。

|
图 7 CFD值与试验值的对比 Fig. 7 Comparisons between CFD calculation and experimental data |
如图7所示:虚线为CFD的数值计算数据,实线为船模拖曳试验结果。通过对比可以发现:虽然数值计算值与试验值有一定的差异(主要与计算域的选取、网格的划分、水温的不同有关),但总体而言数值计算值与试验值相差不大,且误差基本控制在4%范围内,满足工程精度的要求,同时CFD计算得到的纵倾-阻力变化规律与船模试验的变化规律表现出良好的一致吻合性,即用数值模拟方法来求解船舶的阻力性能可靠。
从图中还可以看出,在排水量和航速保持不变的情况下,船舶的阻力会随着纵倾状态而发生变化,从而验证了可以通过调节纵倾来降低船舶的节能减排率,为发展绿色船舶提供了新思路。纵倾值与阻力之间的具体变化规律与船舶的吃水有关,当船舶处于平均吃水Dm=7.8 m的压载状态时,船舶的水阻力随着尾倾值的增大而增大,适当首倾有利于减小水阻力,船舶在该工况下的最佳纵倾值为首倾0.5 m,具有3.34%的节能潜力;当船舶在设计吃水Dm=10.2 m时,水阻力随着首倾值的增大而减小,首倾和适当角度的尾倾有利于减小水阻力,船舶在该工况下的最佳纵倾值为首倾2 m,具有5.94%的节能潜力;当船舶在满载吃水Dm=12 m时,水阻力随着首倾值的增大而减小,随着尾倾的增大而增加,船舶在航行过程中应避免尾倾状态,该工况下的最佳纵倾值为首倾2 m,具有4.41%的节能潜力。
4 结 语综上所述,经过CFD数值模拟和船模试验验证,在保证船舶安全性与操纵性的范围内,利用调节船舶纵倾来降低船舶的阻力,提高节能减排率可行,并且观察得到了3个主要结论:
1)经过试验验证,利用CFD数值模拟船体周围流场并求解船体水阻力完全可行。
2)在排水量保持不变的情况下,纵倾状态的变化对船体水阻力产生一定的影响,但具体的影响规律与船舶的装载状态有关,一般情况下首倾可降低阻力,但当船舶处于设计吃水状态时适当角度的尾倾也可以降低阻力。
3)实船运行过程中存在多个工况,本文只研究了3个工况下的纵倾对阻力的影响规律,对其他状态的具体规律还需要进一步研究,以便能够提供较为全面的数据指导实船航行。
| [1] | ZONG Wei. Cost analysis and market assessment of energy efficiency improvement for a vessel[D]. Shanghai: Shanghai Jiao Tong University, 2014. |
| [2] | CHENG Zhining, CHEN Zhengshou, HUANG Conghan, et al. Research Progress about Additional Hydrodynamic Energy- Saving Devices of Ships[J]. Journal of Zhejiang Ocean University(Natural Science), 2016, 35 (1): 70–75. |
| [3] | ZHANG Xinxue, ZHAO Feng, WANG Chuanrong, et al. Research on the Development Strategy of Green Ship Technology[J]. Engineering Sciences, 2016, 18 (2): 66–71. |
| [4] | PERI D. Design Optimization of Ship Hulls Via CFD Techniques[J]. Journal of Ship Research, 2001, 45 (2): 140–149. |
| [5] | QIU Binbin. Ship Trim Optimization[J]. China Ship Survey, 2014 (2): 70–74. |
| [6] | HERMANS J. Optimization of inland shipping[J]. Journal of Scheduling, 2014, 17 (4): 305–319. DOI: 10.1007/s10951-013-0364-7 |
| [7] | SHERBAZ Salma, DUAN Wenyang. Ship Trim Optimization: Assessment of Influence of Trim on Resistance of MOERI Container Ship[J]. The Scientific World Journal, 2014 : 1–6. |
| [8] | LIU Yifan, ZHANG Jian, ZHANG Yuewen. Numerical Model of Ship Energy Efficiency with Trim Optimization[J]. Ship Engineering, 2015, 37 (12): 31–34. |
| [9] | ZHANG Jian. Study on ship energy efficiency based on trim optimization[D]. Dalian: Dalian Maritime University, 2015. |
| [10] | HYUN-SUK PARK, DAE-WON SEO. A study on resistance performance for various trim conditions and bulb shapes on a container ship under slow steaming[C]//Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St.John’s Newfoundland, Canada, 2015. |
| [11] | JISUN LEE, SEONOH YOO, SANGKYU CHOI, et al. Development and application of trim optimization and parametric study using an evaluation system (SoLuTion) based on the RANS for improvement of EEOI[C]//Proceedings of the ASME 2014 33th International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, California, USA, 2014. |
| [12] | MIAO Yuyue, SUN Jianglong. CFD Analysis of Hydrodynamic Performance of Propeller in Open Water[J]. Chinese Journal of Ship Research, 2011, 6 (5): 63–68. |
 2017, Vol. 39
2017, Vol. 39
