模态分析对结构动态力学性能设计具有十分重要的意义。一般来说由于空气对结构模态影响很小,处于空气中的结构模态分析可以不用考虑空气的影响,称之为结构的模态或干模态[1]。但有些结构,如盛液容器、水下航行器、水下管路等,流体对结构模态影响显著[2 – 3],模态计算必须考虑流体的影响,此时湿模态才是结构振动特性的真实表征。水下结构模态试验研究相对程序复杂,效率低,对有些大型结构来说,试验成本过高,因此水下结构模态的数值计算一直是研究重点。
早期,刘易斯、托德等[4]将船体等对水域流动的影响绘制成了图谱,并开展了一系列试验研究,由此提出了附加质量计算公式。钱勤等[5]虑结构变形对附连水质量的影响,利用势流理论推导了无限流场中无限长圆柱壳的附连水质量和振动的关系。科文-克劳夫斯基[6]研究了附连水计算的切片理论;J.A.Deruntz和T.L.Geers用结构浸水的边界元代替三维流场,通过边界积分法计算了结构附连水质量,但边界元法仅适用于规则结构的湿模态求解。
一般来说,影响水下结构固有频率的主要因素除了结构振动时和水域之间流固耦合效应外,还应考虑水下工作环境中由水压产生的结构预应力效应。对模态计算来说,预应力效应主要体现在结构刚度矩阵的变化[7 – 8],预应力状态下结构刚度矩阵可以通过非线性静力学分析获取。
流固耦合效应下的结构模态分析相对更为复杂,但随着声固耦合计算方法的发展,基于声固耦合算法的模态计算方法得到了迅速发展,并逐渐成熟成为水下结构湿模态计算的主流方法[9 – 10]。圆柱壳属工程应用中的一个经典结构,被广泛应用于船舶领域,潜艇主体段、水下航行器、管路等主要结构形式均为壳结构,本文将以该典型结构作为研究对象,探索不同预应力状态对结构模态频率的影响,最后借助Abaqus中的Acoustic(声学)单元C3D8R模拟流场,研究流固耦合效应对水下壳结构模态频率的影响。
1 水下结构模态计算方法水下结构预应力效应下的模态可以先通过静力学分析,在提取特定应力状态下结构刚度矩阵的基础上再进行模态计算,进而完成结构预应力模态仿真求解。
流固耦合效应下的结构模态可以使用声固耦合的方法计算。使用声-固耦合算法解决流固耦合问题时将流体计算区域视为声场,流场区域网格划分时选用声学单元,定义声场时材料给出密度ρ及其体积模量K。声固交界面满足“全沾湿、无滑移”假设[11],设置边界条件时将声场与结构交界面绑定约束。声固耦合方法的有限元方程为[12]:
| $ \begin{split}& \left[ {\begin{array}{*{20}{c}}{{{ M}_a}} & {{{ P}_a}{ A}}\\0 & {{{ M}_s}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{ P}\\{\ddot { U}}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{{{ C}_a}}\\0\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{ P}\\{\dot { U}}\end{array}} \right] + \\ & \left[ {\begin{array}{*{20}{c}}{{{ K}_a}} & 0\\0 & {{{ K}_s}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{ P}\\{ U}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0\\{{{ F}_a}}\end{array}} \right]{\text{。}}\end{split}$ | (1) |
式中:Ma,Ca,Ka分别为声场的总体质量,阻尼和刚度矩阵;Ms,Cs和Ks分别为结构的总体质量,阻尼和刚度矩阵。
2 某水下壳结构模态计算使用Abaqus前处理的壳建模功能建立某水下结构的三维壳模型,模型长约3.6 m,壁厚约12 mm。首先计算该壳模型空气中的模态,即不考虑流场的影响。为模拟壳结构在50 m,100 m水深工作时产生的外压对结构模态频率的影响,首先通过静力学分析求解0.5 MPa和1 MPa压强下壳结构应力状态,然后在静力学分析基础上,研究预应力对结构频率的影响。最后利用Abaqus内嵌的声固耦合方法研究壳体在流固耦合效应下的湿模态。
2.1 壳结构干模态计算对结构模型进行有限元壳单元网格划分,使用辛普森方法积分,设置5个积分点,有限元模型如图1所示。

|
图 1 水下壳体有限元模型 Fig. 1 The finite element model of an underwater shell |
选择线性摄动分析步,使用Lanczos方法对该模型进行模态计算,提取模态前20阶振型与固有频率。其中结构前两阶整体扁涨模态是重点关注的模态。壳体第1阶扁涨振型如图2所示,对应的频率为86.6 Hz。壳体第2阶扁涨振型如图3所示,对应频率为101.3 Hz。

|
图 2 1阶扁涨(86.6 Hz) Fig. 2 One order flat mode (86.6 Hz) |

|
图 3 2阶扁涨(101.3 Hz) Fig. 3 Two order flat mode(101.3 Hz) |
在模态分析中,动力学方程中的和载荷列阵为零,因而能够影响特征值的因素只有质量矩阵和刚度矩阵。因此为提取结构预应力状态下的固有频率,需要2个分析步:第1步进行结构静力学分析;第2步依据静力学分析结束时的结构刚度矩阵进行结构模态计算。需要注意的是Abaqus中线性静力学分析结束时结构的刚度矩阵和初始状态相比不发生任何变化。这将会导致无法提取预应力状态下的结构刚度矩阵。而如果静力学分析步是非线性的,则结构的刚度矩阵会随着迭代运算不断变化,这样非线性静力学分析结束时结构即为预应力状态下的结构刚度矩阵刚度。因此,预应力模态分析的模态分析务必在非线性静力学分析的基础上进行。
使用Abaqus非线性静力学分析功能对结构壳结构进行非线性应力分析,分别施加0.5 MPa和1 MPa压强,静力学分析结果如图4和图5所示。可以看出壳结构的应力集中部位为结构尾段,0.5 MPa工况下应力最高值为130 MPa。1 MPa工况时应力最高值达到了260 MPa。

|
图 4 0.5 MPa外压壳体应力状态 Fig. 4 The stress state when 0.5 MPa pressure on the shell |

|
图 5 1 Mpa外压壳体应力状态 Fig. 5 The stress state when 1MPa pressure on the shell |
在该非线性静力学分析的基础上建立线性摄动分析步进行模态计算,其步骤与非预应力模态计算相同。同样提取重点关注的前2阶扁涨振型模态频率,并将无预应力、0.5 MPa外压、1 MPa外压3种工况前两阶扁涨振型模态频率列为表1。可以看出外压产生的预应力效应使得壳体模态频率减小,当结构处于低应力状态时,预应力效应对模态计算结果影响很小,但随着预应力的增大,预应力效应对模态频率逐渐显著,1 MPa外压时前2阶扁涨振型的频率下降约10%。
|
|
表 1 预应力效应对壳体固有频率影响 Tab.1 Effect of pre-stress on the shell natural frequency |
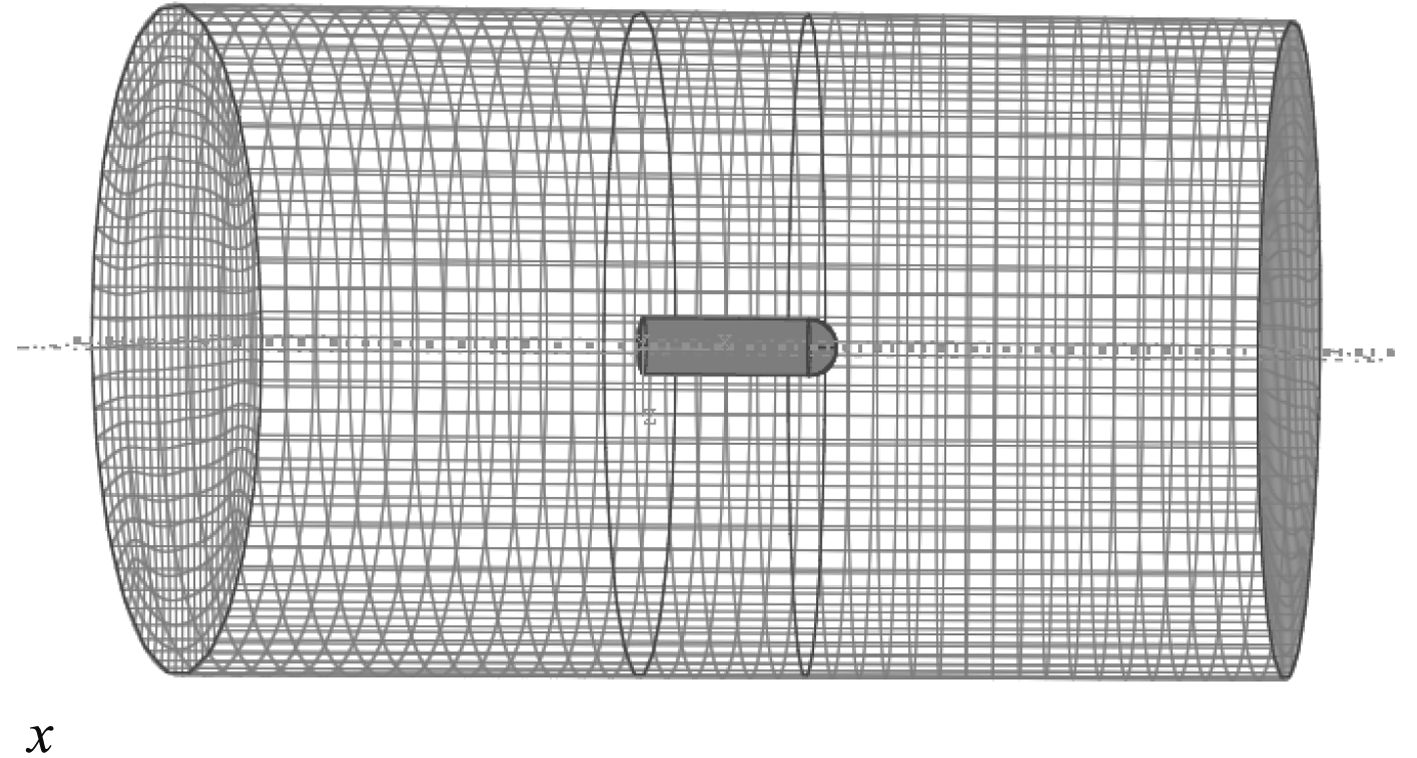
使用声固耦合方法计算湿模态时,流场尺寸一般不应小于结构尺寸的6倍。根据结构特征,建立流场模型并划分网格,模型如图6所示。将流场边界设置为无反射边界条件,将壳体外表面和流场绑定约束,
|
图 6 壳体声固耦合湿模态计算模型 Fig. 6 Acoustic solid interaction wet mode calculation model of the shell |
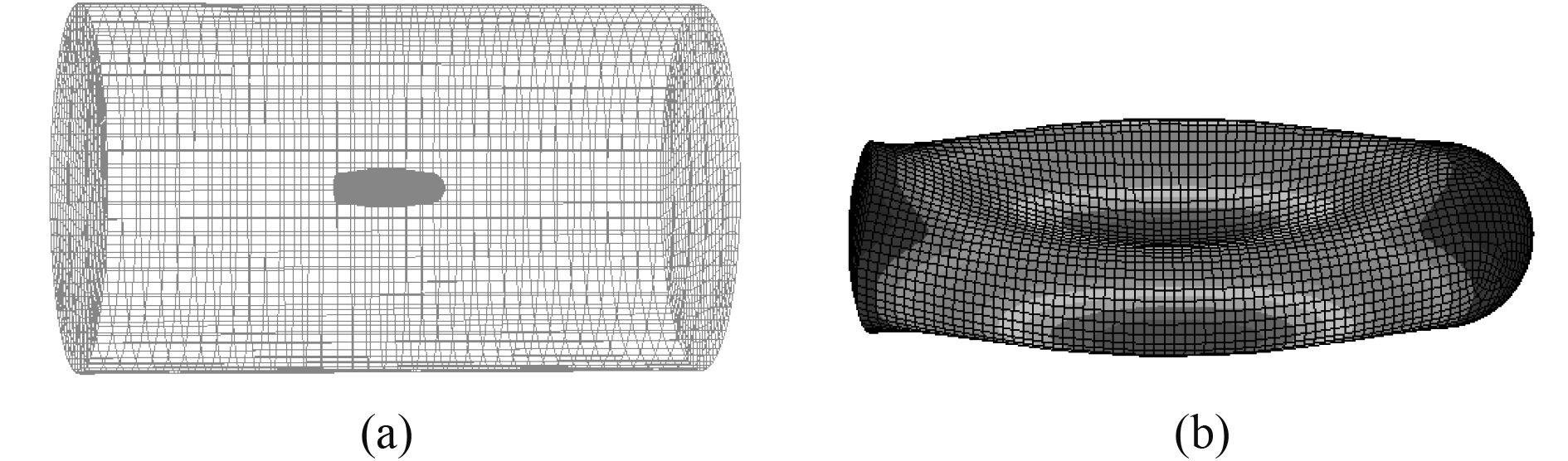
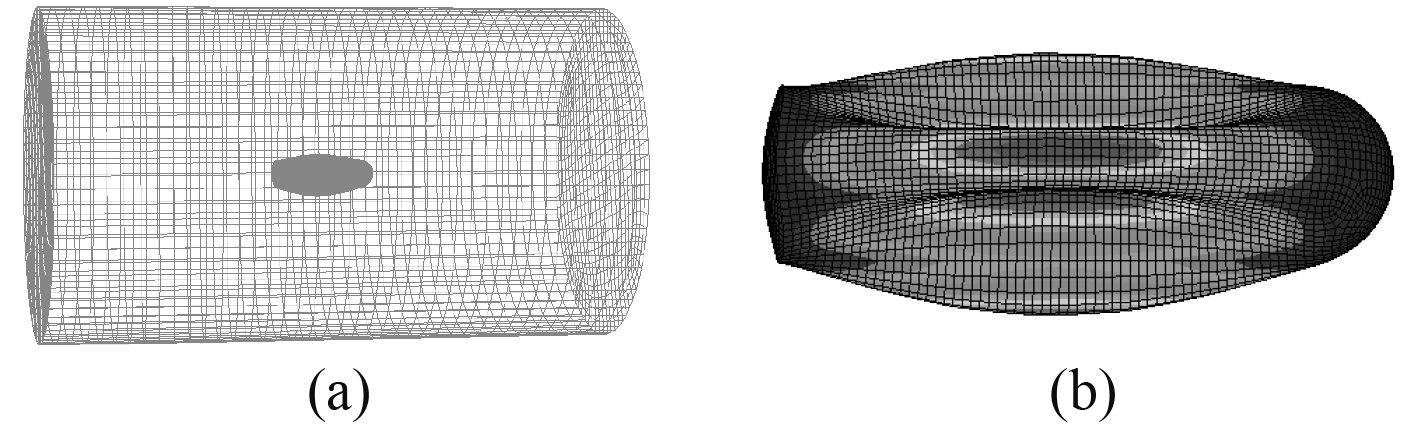
使用Abaqus声固耦合法计算流固耦合效应下的结构模态,同样提取重点关注的结构前两阶扁涨振型频率。流固耦合效应下壳结构1阶扁涨模态频率约为51.5 Hz,声固模型振型如图7(a)所示,内部结构振型如图7(b)。2阶扁涨振型模态频率为66.8 Hz,声固模型振型如图8(a)所示,内部结构振型如图8(b)。
|
图 7 壳体湿模态 1 阶扁涨(51.5 Hz) Fig. 7 One order flat of shell wet mode (51.5 Hz) |
|
图 8 壳体湿模态 2 阶扁涨(66.8 Hz) Fig. 8 Two order flat of shell wet mode (66.8 Hz) |
将壳结构敢模态和流固耦合效应下的湿模态进行对比列为表2。可以看出,在流固耦合效应下,结构的频率大幅下降,其下降程度可达到40%左右,因此,水下结构模态分析和动力学设计必须要考虑到流固耦合效应对结构固有频率的影响。
|
|
表 2 壳结构干、湿模态频率对比 Tab.2 Comparison of the mode and wet mode frequencies of the shell structure |
本文研究了预应力效应和流固耦合效应对水下壳结构模态频率的影响。依据计算结果和对比分析得出如下结论:
1)结构受到的静水外压产生的预应力效应和振动时的流固耦合效应均会使得结构固有频率下降,且结构振动时的流固耦合效应占主导作用。
2)随着壳体预应力的增大,预应力效应对结构固有频率的影响逐渐增大,并达到了不可忽略的地步。
3)当水下结构一直在低应力状态下工作时,可以重点考虑流固耦合效应的影响。但若结构存在高应力工况,预应力效应也会显著降低结构固有频率,此时结构动力学设计必须要考虑预应力效应对结构固有频率的影响。
| [1] | 朱晓芳, 杜志鹏, 金咸定. 浸入水中的船舶尾轴架固有频率的计算方法探[J]. 振动与冲击, 2005, 24 (2): 111–115. |
| [2] | 黄玉盈, 刘忠族. 求附连水质量的一种直接方法[J]. 力学实践, 1996, 18 (5): 19–21. |
| [3] | 李明, 尹云玉. 水下航行体动态响应计算的附加质量探讨[J]. 导弹与航天运载技术, 2008 (4): 16–18. |
| [4] | 傅慧萍, 李杰. 附加质量CFD计算方法研究[J]. 哈尔滨工程大学学报, 2011 (2): 148–152. |
| [5] | 蔡继峰, 方新, 梁乃刚. 有限长圆柱横向附加质量的计算与工程应用方法[J]. 科学技术与工程, 2011 (17): 3886–3892. DOI: 10.3969/j.issn.1671-1815.2011.17.007 |
| [6] | 苏海东, 黄玉盈, 陈琴. 片状域流场中三维结构的湿频率和湿模态[J]. 华中科技大学学报, 2007, 35 (1): 121–124. |
| [7] | 李小彭, 赵光辉, 杨皓天. 考虑结合面影响的组合梁非线性预应力模态分析[J]. 振动与冲击, 2014 (4): 17–21. |
| [8] | 汪勇, 兰波. 液体静水压力对圆柱形储液容器自振频率的影响[J]. 重庆交通学院学报, 1997 (2): 77–81. |
| [9] | 田红莉, 刘志峰, 张乃龙, 等. 箱体结构的声固耦合有限元分析[J]. 机械设计与制造, 2007 (7): 24–26. |
| [10] | 姚熊亮, 杨树涛, 张阿漫, 等. 水下爆炸载荷作用下鱼雷结构优化设计[J]. 舰船科学技术, 2009 (4): 75–80. |
| [11] | 郑治国, 孙大成, 刘宪亮. 用湿模态法进行流固耦合分析时一个问题的探讨[J]. 华北水利水电学院学报, 1998 (2): 22–25. |
| [12] | 杨鸣, 王光军, 段玉康, 等. 基于声固耦合法的储液容器湿模态分析[J]. 四川兵工学报, 2015 (5): 152–154. |
 2017, Vol. 39
2017, Vol. 39
