船用螺旋桨工作时,螺旋桨承受自身重力、离心力和水动力载荷等多力作用,受力情况复杂[1],导致螺旋桨的穴蚀、疲劳断裂等问题,需要从水动力和螺旋桨强度方面研究螺旋桨的破坏原因。通过流固耦合方法将螺旋桨的CFD水动力计算结果与有限元求解耦合起来,来分析螺旋桨水动力和强度性能。螺旋桨水动力研究是建立在势流理论基础之上,如升力线方法和面元法等,以往的研究未能充分考虑水粘性、旋度和计算模型的影响,因而不能准确预测桨叶边界层、尾流场结构及桨叶梢涡的形成等流动特性[2]。随着CFD技术仿真螺旋桨水动力性能方法的发展,该技术能够用于探索螺旋桨水动力性能中的水粘性问题,其计算原理主要基于RANS方法,对螺旋桨周围流场进行数值计算,计算精度得到提高,一些研究者在该方面做了探索性研究。RHEE等[3]以非结构化网格为基础,结合RANS方程和k-ε湍流模型对五叶螺旋桨的敞水性能进行计算,所得推力和转矩系数与试验值之间的误差在10%以内。龚吕等[4]采用非结构化网格和标准k-ε湍流模型对六叶侧斜反弯扭桨进行计算,所得推力和转矩系数与试验值相比,误差在8%以内。在螺旋桨的强度研究方面,流固耦合分析理论应用较为准确,该理论主要研究固体在流场运动的过程中固体和流体在交界面及其周围产生的相互作用,目前流固耦合经常用于船舶与海洋工程、流体结构工程等领域,Khalid等[5]基于Ansys-CFX,采用双向流固耦合法,对垂直轴风机转子进行瞬态流固耦合响应模拟,李果[6]在分析均匀来流情况下,结合计算流体力学方法和有限元发,提出了一种计算复合材料螺旋桨流固耦合问题的数值方法。
本文结合计算流体力学方法与结构有限元法,利用Workbench平台的CFX和Static Structural模块,分别进行螺旋桨流体与结构两方面的数值计算,同时将2个模块连接起来进行数据传递,得到不同进速下螺旋桨弦向压力分布,以及等效应力和总变形随进速的变化,完成螺旋桨的水动力及强度分析,之后改变螺旋桨纵倾角与螺距,并将水动力及强度分析结果与原桨进行对比,确定合适的结构参数。
1 螺旋桨模型的建立 1.1 建立实体模型根据螺旋桨设计参数,利用三维坐标值在Solidworks中建立螺旋桨的三维模型,最终螺旋桨实体模型如图1所示。

|
图 1 螺旋桨三维模型 Fig. 1 3D propeller model |
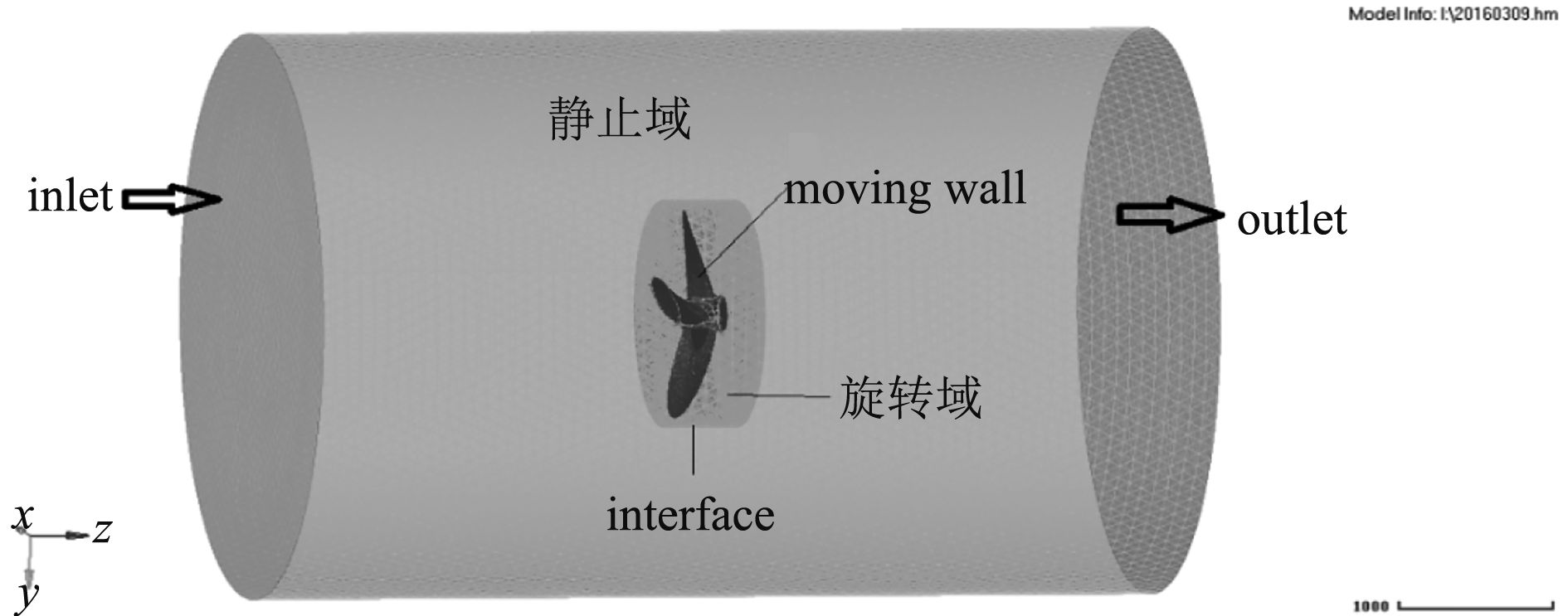
对螺旋桨周围流场进行模拟时,设置多参考系模型(MRF),整个流场被划分为2个圆柱体计算域,外圆柱体区域作为静止域用来模拟静止流场,内圆柱体区域作为旋转域用来模拟螺旋桨旋转[7]。外部静止区域为直径5 D(D为螺旋桨直径)、长度10 D的圆柱体,靠近叶背的面设为进口,另一端设为出口;内部旋转区域为直径1.2 D、长度0.8 D的圆柱体,2个区域中心轴均为桨模型的Z轴。应用Hypemesh对内部旋转域进行非结构化网格划分,网格密度大,对外部静止流场采用结构化网格划分,网格密度低。网格划分如图2所示。在螺旋桨流场仿真模型边界条件设置时,设流场进口为速度进口,设流场出口为自由出口,设静止域外部边界为固定不动的Wall[8]。
|
图 2 螺旋桨流场仿真模型示意图 Fig. 2 Schematic diagram of propeller flow field simulation model |
在hypemesh中对模型进行网格划分,网格选用三角形单元,并且对叶根和叶梢部分进行加密,螺旋桨网格划分如图3所示。

|
图 3 螺旋桨网格划分图 Fig. 3 Meshing diagram of propeller |
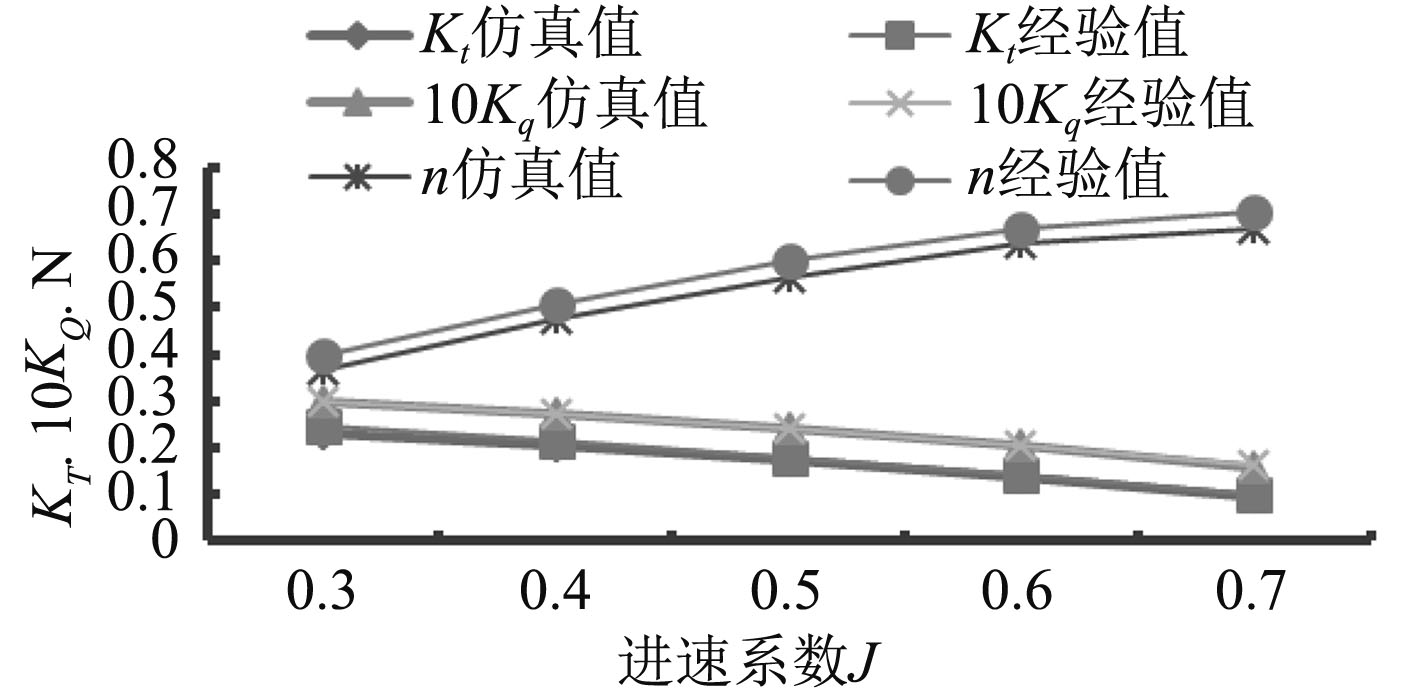
以RNG k-ε模型作为初始场计算螺旋桨的敞水性能,进速系数J依次取0.3,0.4,0.5,0.6,0.7,分别得到推力系数Kt 、扭矩系数Kq和敞水效率η。并与经验值进行对比,结果如图4所示。
|
图 4 螺旋桨敞水特性对比图 Fig. 4 Comparison of characteristics of propeller in open wate |
比较与分析图4所显示的螺旋桨敞水特性曲线随进速变化趋势可得:
1)推力系数分析。在不同进速系数下,CFX计算的仿真结果和经验公式计算结果变化趋势一致,仿真计算的推力系数小于公式计算值,当进速系数为0.6时,两者误差最小,约为4%,推力系数平均误差在7.2%以内
2)力矩系数分析。在不同进速的情况下,力矩系数仿真结果值和公式结果非常接近,变化趋势也一致,力矩系数平均误差在1.86%以内,进速系数大于0.7后可以预测两者差值有增大的趋势。
3)敞水效率分析。在不同进速情况下,螺旋桨敞水效率仿真值小于公式计算值,并且变化趋势与推力系数误差情况基本一致,敞水效率平均误差在7.11%以内,随着进速系数的增大,两者差值有增大的趋势。
总体来讲在考察的进速系数0.3 ~ 0.7范围内,敞水性能仿真结果与经验结果误差较小,吻合较好。
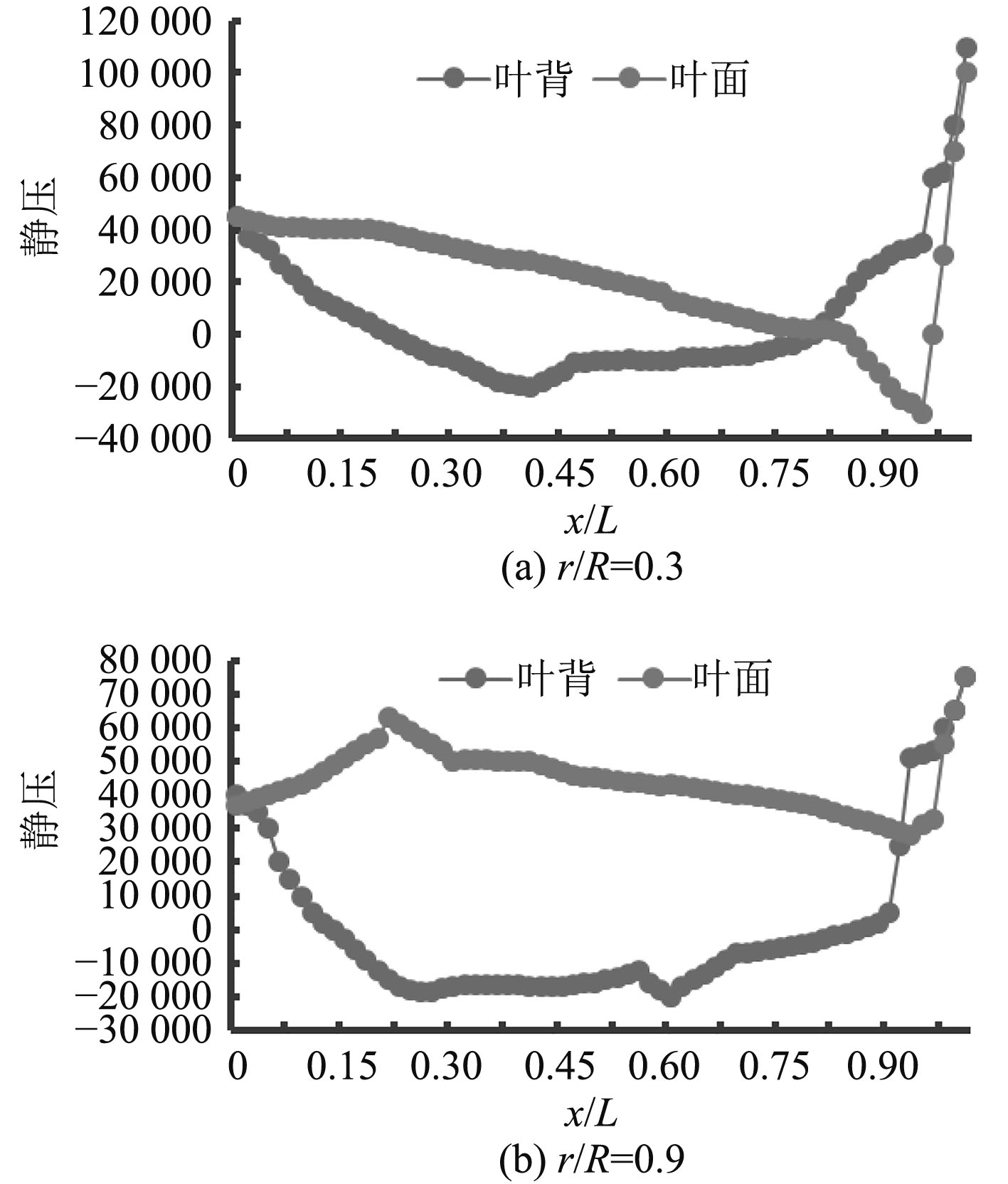
2.2 桨叶压力分布情况分析在保持螺旋桨转速不变,当进速系数为0.4时,得到四叶桨0.3 R半径与0.9 R半径处叶切面的弦向压力分布图,如图5所示,其中x/L=0为随边,x/L=1为导边。并且给出进速系数为0.4时的压力分布云图,如图6所示。
|
图 5 不同半径弦向压力分布图 Fig. 5 Distribution of chord pressure at different radius |

|
图 6 螺旋桨表面压力分布图 Fig. 6 Surface pressure distribution of propeller |
通过图5和图6可以观测到桨叶压力分布情况,叶面压力总体为正,叶背压力总体为负,在某一固定进速下,叶面压力分布由导边向随边逐渐减小,在r=0.5 R处导边边缘出现压力最高值,叶面的压力先从叶根到叶稍逐渐增加,达到一定值后,再逐渐减小,在叶稍处达到最小值[10]。四叶桨叶背压力分布由导边向随边逐渐增加,并且压力值从叶根到叶稍逐渐减小,在r=0.8 R周围的叶稍区域出现最低压力值,随边压力为正值。
随着进速的增加,最大压力从1.786×105 Pa减小到1.151×105 Pa,叶面上的高压区域面积开始缩小,叶面压力变小,叶背上的低压区域面积开始变大,叶面压力变化量小于叶背压力变化量,叶面与叶背之间的压力差开始变小,从而可以预见随着进速的增加,螺旋桨产生的推力会随之减小。
2.3 螺旋桨的强度分析1)水动力对螺旋桨的强度影响
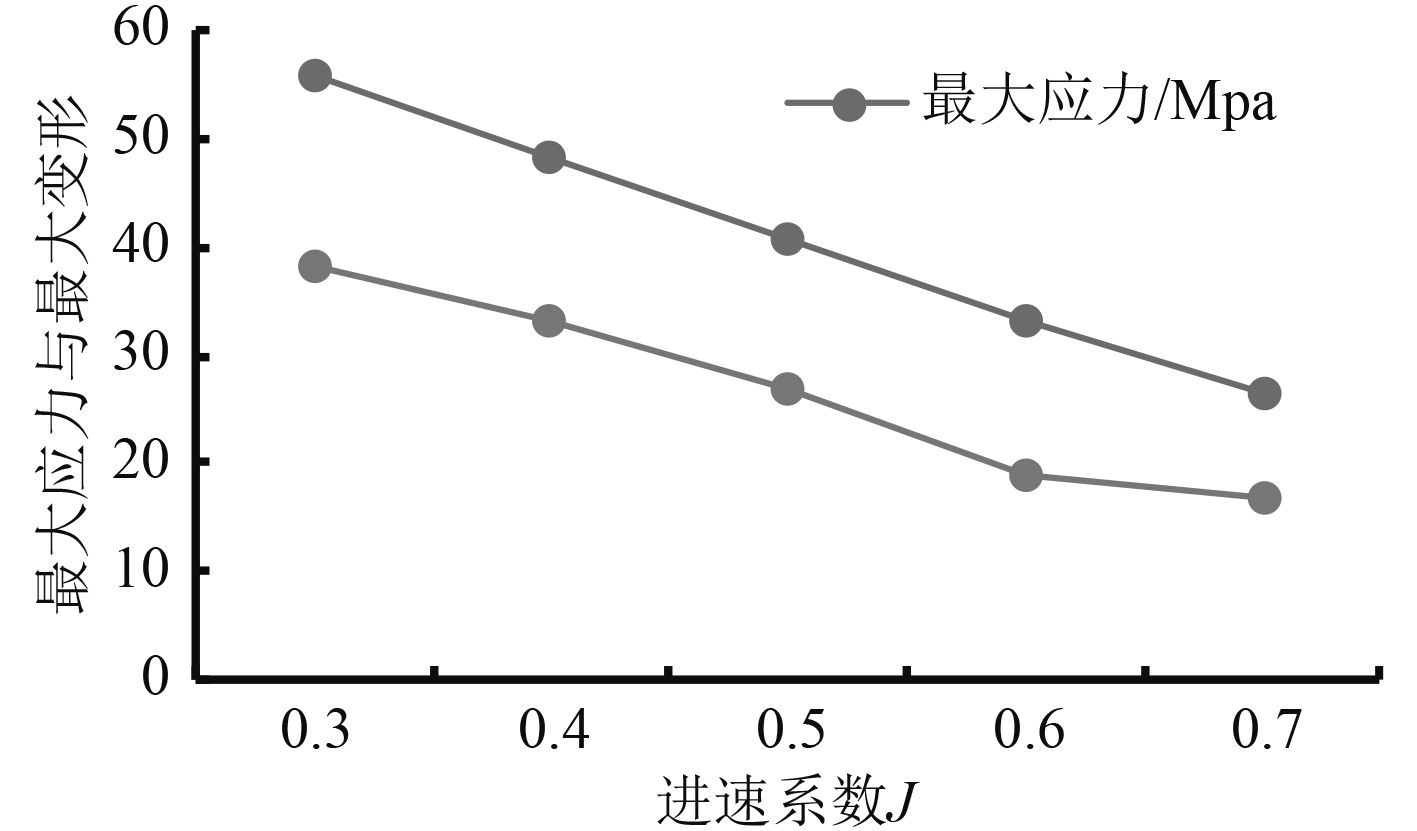
通过Workbench平台将流场中得到的螺旋桨表面压力加载到桨叶实体上,用流固耦合方法分析锰黄铜材料螺旋桨的强度。分析中将桨毂大端面固定,加载离心力载荷,保持螺旋桨转速不变,设定进速系数分别为0.3,0.4,0.5,0.6,0.7时,得到四叶桨最大应力、最大变形曲线图,如图7所示,并且给出J=0.4时的应力、变形分布云图,如图8所示。
|
图 7 螺旋桨最大应力与最大变形曲线图 Fig. 7 Maximum stress and maximum deformation curve of propeller |

|
图 8 螺旋桨应力、变形云图 Fig. 8 Stress and deformation nephogram of propeller |
由图7和图8可以观察到桨叶的应力与变形分布情况,在一定进速范围内,随着进速的增加,最大应力与最大变形大致成线性递减趋势,这与低进速时重载、高进速时轻载相一致。最大应力分布在叶根附近,最小应力分布在叶梢区域,应力值沿径向逐渐减小,这说明螺旋桨工作时叶根处极易发生断裂,在设计和制造螺旋桨时应进行去应力处理保证叶根处有足够的强度。桨叶最小变形处在叶根区域,变形量沿径向逐渐增加,在叶稍处产生最大变形,随着进速的增加,桨叶的应力与变形都逐渐减小。桨叶最大变形处在叶稍位置,而不是最大应力所在的叶根位置,其原因是螺旋桨叶稍区域厚度较薄,较小的压力也会产生较大变形[10]。
3 螺旋桨结构参数优化 3.1 不同纵倾角下螺旋桨性能对比分析1)不同纵倾角下螺旋桨水动力性能对比分析
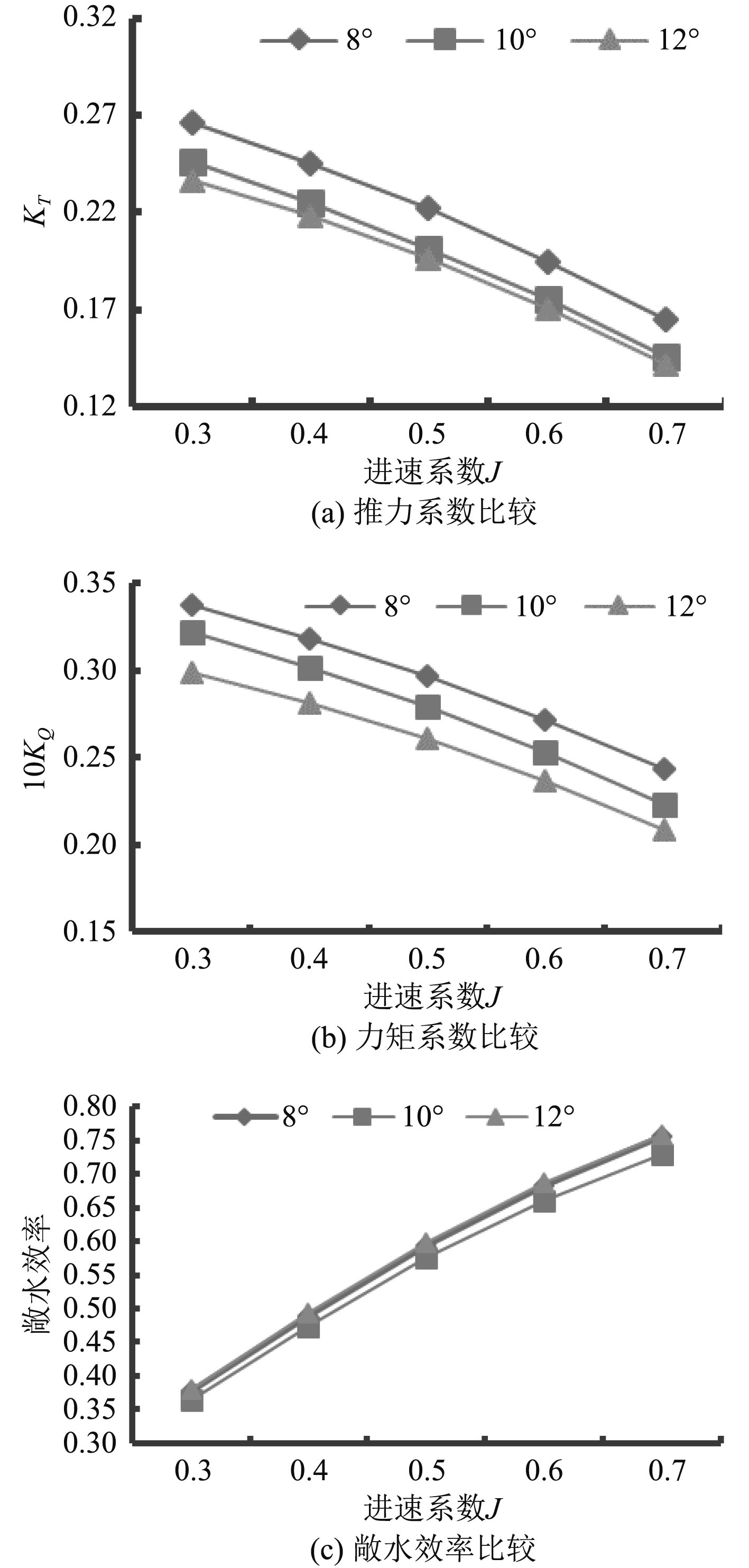
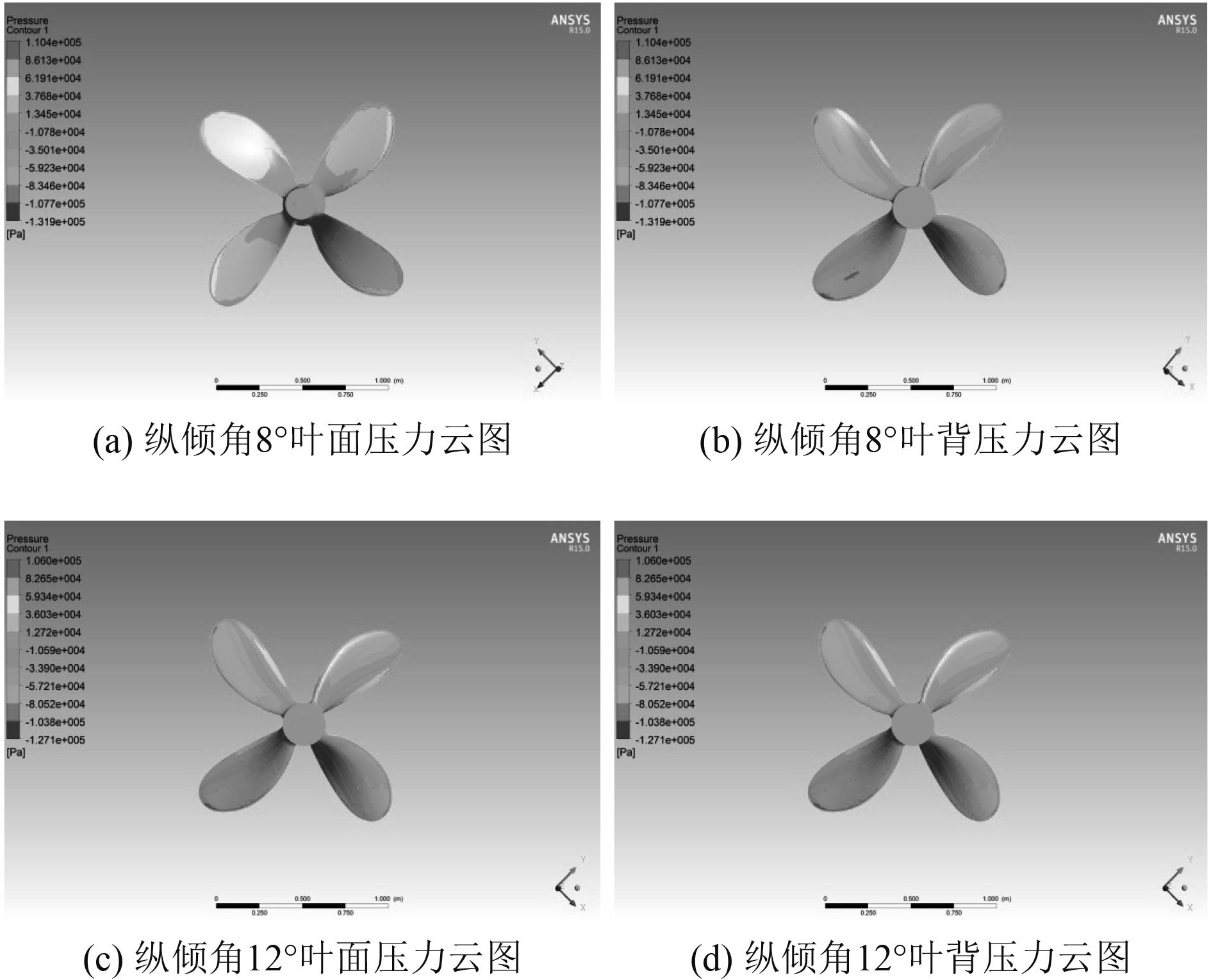
考虑到强度问题,螺旋桨的纵倾角一般不能太大,原始桨的纵倾角为10°,因此分别取纵倾角变化为8°和12°进行研究。保持螺旋桨转速不变,设定进速系数分别为0.3,0.4,0.5,0.6,0.7时,得到新螺旋桨敞水性能曲线,如图9所示。并且给出J=0.4时,纵倾角为8°和12°螺旋桨表面压力分布云图,如图10所示。
|
图 9 不同纵倾角下螺旋桨敞水性能比较 Fig. 9 Comparison of open water performance of propellers at different vertical angles |
|
图 10 螺旋桨压力分布云图 Fig. 10 Nephogram of propeller pressure distribution |
图9可以观察到纵倾角度变换后,螺旋桨推力系数、转矩系数和敞水效率在进速系数0.3 ~ 0.7范围内的计算结果;图10给出的云图为进速系数J=0.4时不同纵倾角下桨叶的压力分布。从敞水性能曲线和桨叶压力分布云图可以看出,随着纵倾角的增大,螺旋桨的推力系数、转矩系数和桨叶压力随着减小,敞水效率会略有增大,但是从另外一个角度来说,由于增大螺旋桨的纵倾角,即增大螺旋桨叶梢与船体尾框架的间隙,能改善螺旋桨诱导的船舶尾部振动,所以在不影响螺旋桨敞水效率前提下,可以适当增大纵倾角来减小船尾的振动[11]。
2)不同纵倾角下螺旋桨强度对比分析
通过上述对比分析可以看出适当增大纵倾角较为有利,选择纵倾角为12°的螺旋桨作为研究对象,并就结构性能仿真结果与原桨进行对比。设定进速系数为0.4。
|
|
表 1 结构性能对比 Tab.1 Structural performance comparison |
由表1可以得到:在同一进速系数J=0.4下,纵倾角为12°的螺旋桨和原桨的最大等效应力分别为48.265 MPa和50.935 MPa,最小等效应力分别为0.03 MPa和0.04 MPa;最大变形分别为1.613 2 mm和3.159 9 mm。从表上可以看出,螺旋桨纵倾角的改变对螺旋桨桨叶的等效应力、变形影响很大,叶根处最大等效应力和叶稍处最大变形都比原桨小,因此适当增大纵倾角也可以增强螺旋桨强度改善结构性能。
3.2 不同螺距下螺旋桨性能对比分析1)不同螺距下螺旋桨水动力性能分析
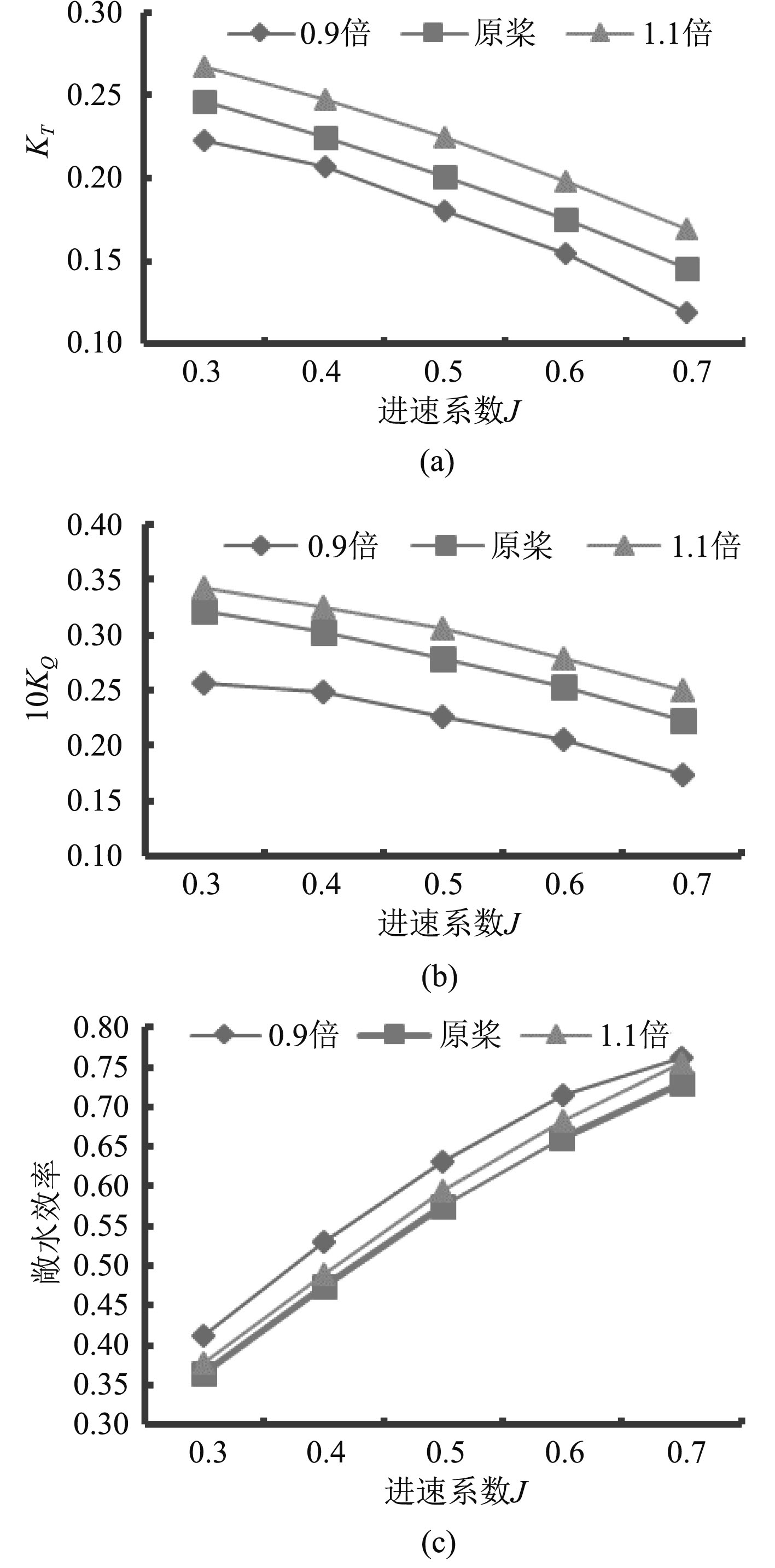
设定进速系数分别为0.3,0.4,0.5,0.6,0.7,对1.1倍和0.9倍螺距的螺旋桨进行敞水性能计算并与原桨对比分析,如图11所示。并且给出J=0.4时,0.9倍螺距与1.1倍螺距下螺旋桨表面压力分布云图,如图12所示。
|
图 11 不同螺距下螺旋桨敞水性能比较 Fig. 11 Comparison of open water performance of propeller under different pitch |
从图11可以观察到不同螺距下螺旋桨推力系数、转矩系数和敞水效率在进速系数0.3~0.7范围内的计算结果。从上述计算结果可以看出,增大螺距使得螺旋桨的推力系数和转矩系数均上升,上升的幅值随着进速系数的增大而逐渐增大,且增幅非常明显;对于敞水效率而言在进速系数0.3~0.7范围内螺距减少使得敞水效率大幅度增大,而且从敞水效率图形的走势可以预测,最佳效率的工况点向进速系数减少的方向移动,同时最佳效率值随着螺距的增大有微小的增大。因此在原桨基础上稍微减少一定量的螺距有利于提高船舶的效率。

|
图 12 不同螺距下螺旋桨敞水性能比较 Fig. 12 Nephogram of pressure distribution |
从图12可以观察到螺旋桨在不同螺距下桨叶的压力分布,可以清楚地看到螺距的改变带来的螺旋桨桨叶上压力特性的变化。其中最明显的是螺距的变化带来的螺旋桨桨叶上压力梯度的变化,螺距增大使得压力梯度迅速增大;同时,螺距的增大使得桨叶上的最小压力区域扩大,其吸力面更易达到水的汽化压力,从而导致叶背区域更早且更大范围的出现空泡现象。综上所述,该桨的螺距减小更为有利,虽然推力系数和转矩系数有所减小,但敞水效率和抗空泡性能有所提升。
2)不同螺距下螺旋桨强度分析
通过对比分析可以看出适当减小螺距有利于船舶螺旋桨的水动力性能,所以选择0.9倍母型桨螺距的螺旋桨作为研究对象,并就结构性能仿真结果与原桨进行对比。设定进速系数为0.4。
|
|
表 2 结构性能对比 Tab.2 Structural performance comparison |
从表2可以观测到在同一进速系数下,0.9倍螺距螺旋桨和原桨叶根处的最大等效应力分别为43.612 MPa和50.935 MPa,最小等效应力分别为0.048 MPa和0.041 MPa;叶稍最大变形量分别为2.7 mm和3.1 mm。通过比较可以看出,0.9倍螺距的螺旋桨桨叶的最大等效应力和最大位移比原桨小,从图上可以看出,螺旋桨螺距的改变对螺旋桨桨叶的等效应力、变形影响很大,叶根处最大等效应力和叶稍处最大变形都比原桨小,因此适当减小螺距可以增大螺旋桨强度改善结构性能。
4 结 语通过仿真分析,得到如下结论:
1)螺旋桨模型复杂,因此对螺旋桨进行精确建模,通过合适的方式对螺旋桨周围流场和结构模型进行网格化分对提高螺旋桨性能仿真精度有较大影响。
2)通过CFD方法仿真AU型螺旋桨的性能,选择RNG k-ε湍流模型,得到不同进速情况下螺旋桨的性能参数,与公式计算值之间相比,仿真值误差小,计算精度满足要求。
3)通过对比研究发现适当增大螺旋桨纵倾角能提高桨叶强度,改善螺旋桨结构性能;适当降低螺距能提高螺旋桨敞水效率、提高抗空泡性能并且有助于提高桨叶强度,改善螺旋桨结构性能。
| [1] | 任弘, 李范春, 杜玲. 流固耦合作用对螺旋桨强度影响的数值计算[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39 (1): 144–147. |
| [2] | 张帅, 朱锡, 侯海量. 船舶螺旋桨流固耦合稳态求解算法[J]. 哈尔滨工程大学学报, 2012, 33 (5): 615–621. |
| [3] | RHEE S H, JOSHI S. CFD validation for a marine propeller using an unstructured mesh based RANS method[C]// Asme/jsme 2003, Joint Fluids Summer Engineering Conference. 2003: 1157–1163. |
| [4] | 龚吕, 姚征, 吴曼. 船舶反弯扭螺旋桨水力特性的数值模拟与分析[J]. 上海理工大学学报, 2007, 29 (1): 65–69. |
| [5] | KHALID S S, ZHANG L, ZHANG X W, et al. Three-dimensional numerical simulation of a vertical axis tidal turbine using the two-way fluid structure interaction approach[J]. Journal of Zhejiang University-SCIENCE A, 2013, 14 (8): 574–582. DOI: 10.1631/jzus.A1300082 |
| [6] | 李果, 李巍, 尤云祥. 复合材料螺旋桨流固耦合特性研究[C]// 船舶水动力学学术会议. 2013. |
| [7] | 曹峰. 复合材料螺旋桨—流固耦合[D]. 上海: 上海交通大学, 2013. |
| [8] | 薛侠峰, 严天宏, 何波. MAU型螺旋桨建模与水动力性能分析[J]. 船舶工程, 2016 (1): 38–42. |
| [9] | 李广. 两种血管通路中血流特性及其对管壁影响的数值模拟研究[D]. 天津大学, 2014. |
| [10] | 黄璐, 陈立, 邱辽原, 等. 螺旋桨水动力性能及流固耦合数值模拟[J]. 舰船科学技术, 2014 (11): 33–37. DOI: 10.3404/j.issn.1672-7649.2014.11.007 |
| [11] | 王亮. 船舶螺旋桨变参数水动力性能研究[D]. 大连: 大连理工大学, 2012. |
 2017, Vol. 39
2017, Vol. 39
