螺旋桨是船舶推进中的最重要部件。在螺旋桨论证、设计阶段经常要获得三维几何造型并对其水动力性能进行数值预报。随着船舶推进技术的不断发展,结构复杂、性能优良的螺旋桨的种类也越来越多,对于这些螺旋桨,将其三维建模过程程序化、通用化,有利于提高螺旋桨的设计效率。本文经过对螺旋桨几何造型的分析,以VC++6.0和OpenGL为工具,建立了螺旋桨三维几何造型程序,对于任意种类的螺旋桨,设计参数确定以后,即可利用该程序对其三维几何造型以及尾涡面进行三维图形化显示,并对其进行人机交互仿真。
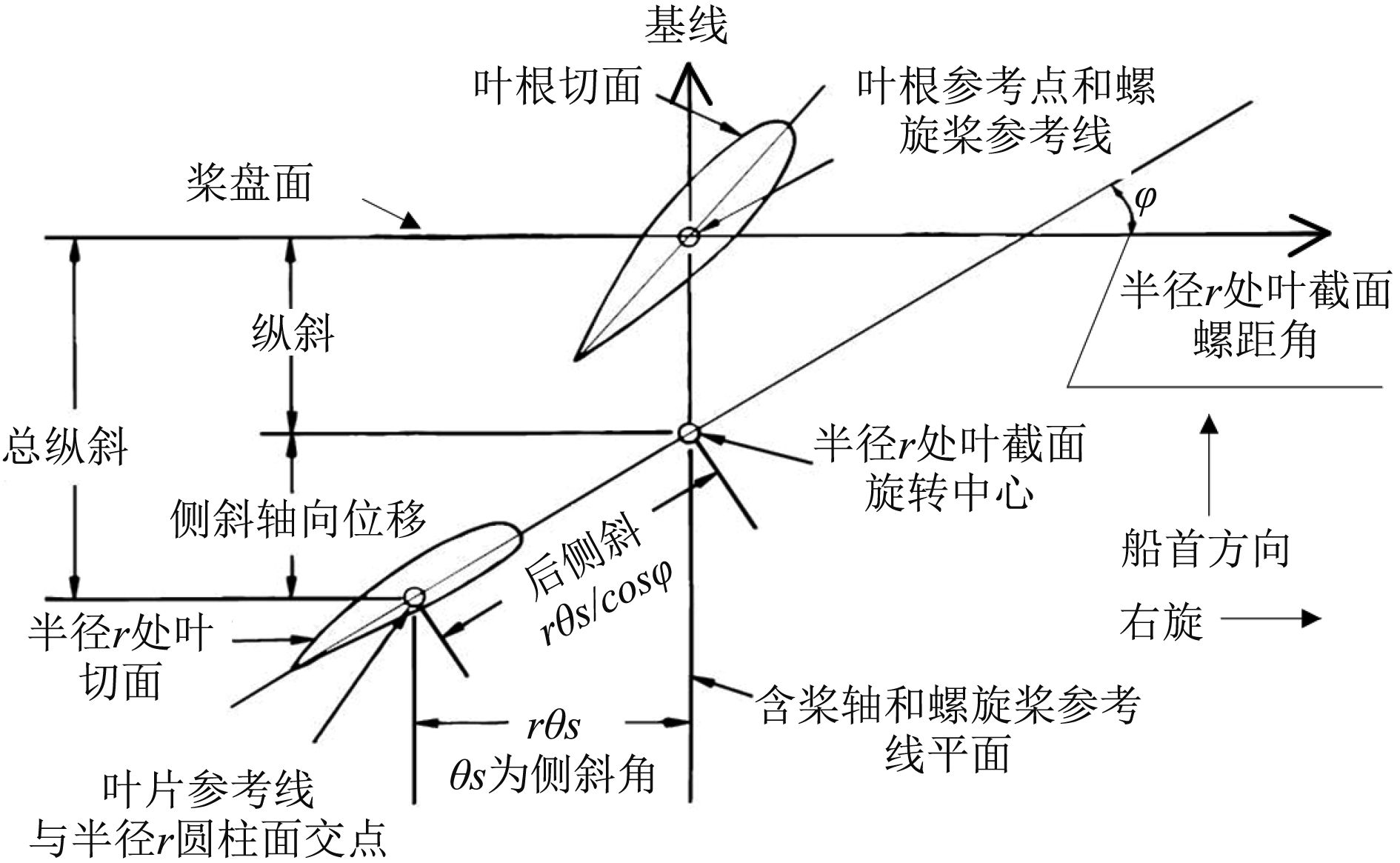
1 螺旋桨几何参数数据库设计根据螺旋桨构造原理可知,决定螺旋桨几何造型的主要参数是:桨盘面直径、叶切面的直径、叶切面的型值(包括压力面的型值和吸力面的型值)、叶切面的螺距和螺旋桨的旋向。对于侧斜桨还应包括各个叶切面的侧斜、纵斜相关参数。在螺旋桨设计图纸中,各个叶切面的数据以二维形式给出。叶切面数据由二维至三维的转换过程如图1所示[1]。
|
图 1 螺旋桨叶切面转换 Fig. 1 The blade surface transform of propeller |
可见,螺旋桨叶切面的变化经历了旋转螺距角、移侧斜、移纵斜以及包覆等过程。包覆是将旋转螺距角、移侧斜和纵斜后的叶切面“包覆”在与该叶切面等直径的圆柱体上。螺旋桨二维叶切面数据换算为三维叶切面数据的计算公式如下:
| $\begin{array}{l}X = r\sin (((x - {x_0})\cos \theta - y\sin \theta )/r)\text{,}\\Y = - r\cos (((x - {x_0})\cos \theta - y\sin \theta )/r)\text{,}\\Z = (x - {x_0})\sin \theta + y\cos \theta - {y_0}\text{。}\end{array}$ | (1) |
式中
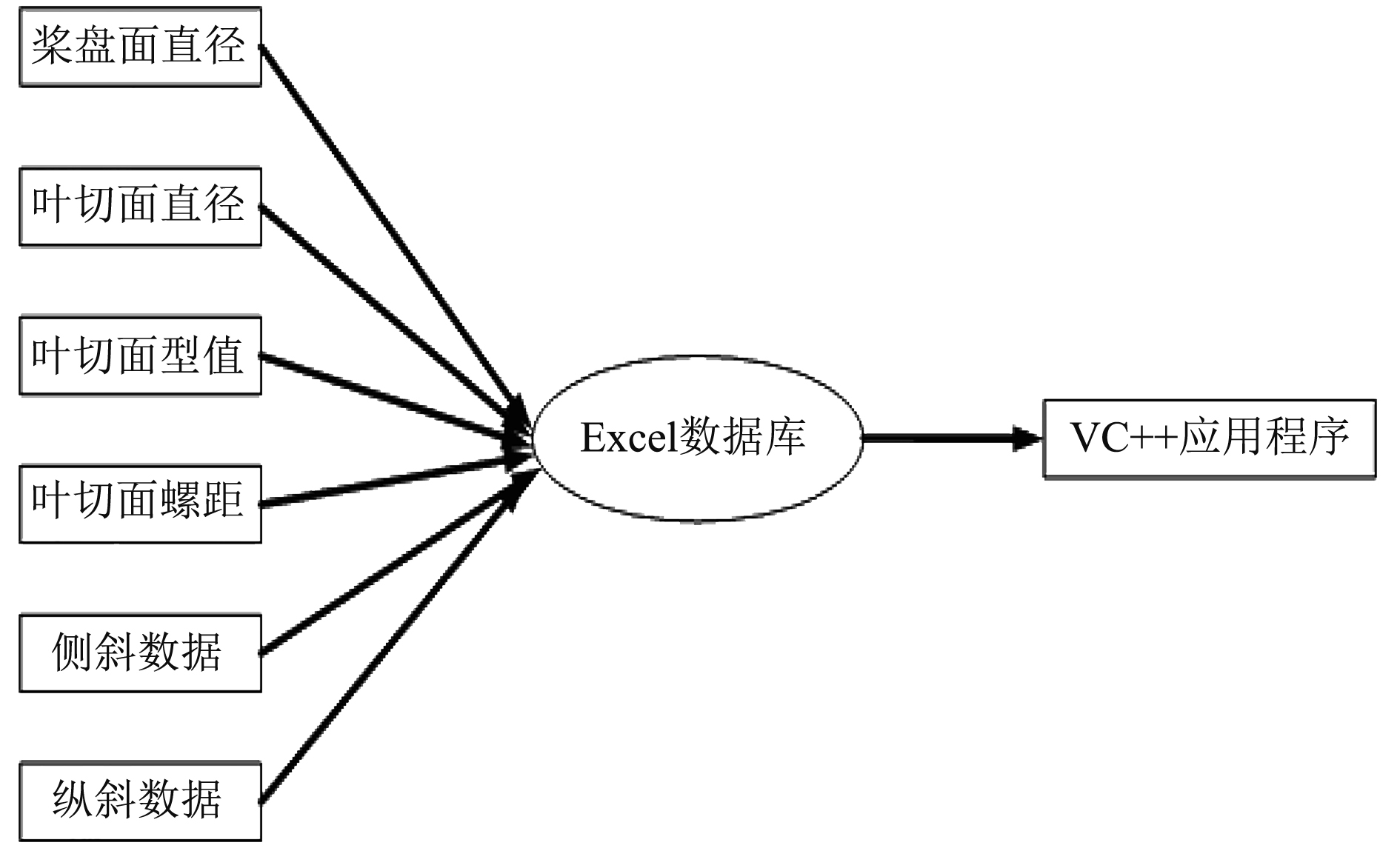
为了实现螺旋桨三维建模程序化,需要建立数据库来储存螺旋桨设计参数。本文选择用Excel存储螺旋桨数据文件,当然还可以选择Access等软件进行数据存储,通过VC++编程实现数据的读取。存储数据时,在数据文件中对每个参数项目加上标识以进行分类存储。为了使程序达到通用的目的,在数据库中建立测斜和纵斜参数数据项目,对于无侧斜和纵斜的螺旋桨,该数据项目的数据为0。这样,数据库可以适用于所有类型的螺旋桨。数据库的存储如图2所示。
|
图 2 螺旋桨几何参数的存储 Fig. 2 Data storing of geometrical parameters of propeller |
螺旋桨三维数据的计算包括桨叶面数据的计算、尾涡面数据的计算以及桨毂数据的计算。
2.1 桨叶数据计算桨叶三维坐标计算实际上是二维数据到三维数据的换算问题。螺旋桨设计图纸提供的叶切面参数较少,一般是10~20个叶切面。为了三维建模时图形更逼近真实形状,利用B样条函数对桨参数进行插值扩充。增加桨叶的叶切面,每个叶切面上吸力面和压力面也分别利用B样条函数进行插值增加数据。利用VC++编程实现叶切面旋转螺距角、移侧斜、移纵斜以及包覆的过程。得到三维的叶片表面数据。桨叶数据处理中的几个关键问题如下:
1)螺旋桨设计图纸提供的叶切面的数据分布方式有2种:一种是由随边开始至导边结束;另一种是由导边开始至随边结束。在程序中桨叶切面数据结构统一转化为第一种分布方式,即由随边开始至导边结束,而且压力面朝下、吸力面朝上。即转化后的叶切面在坐标中的位置是:随边在原点处,如图3所示。这可以简化后续的三维数据计算。在程序运行过程中,由用户指定螺旋桨设计图纸提供的叶切面的数据分布。

|
图 3 转换后的叶切面位置 Fig. 3 The blade position after transform |
2)螺旋桨依旋转方向可分为左旋桨和右旋桨,由于桨叶切面已经转化为图3所示的数据分布,经过简单分析可知,该数据分布表示的是右旋桨。若原螺旋桨为左旋桨,则只需要将经过移侧斜、转螺距角后的叶切面沿图3所示的y轴进行镜像变换即可。在程序运行过程中,由用户指定螺旋桨的旋向。
3)对于调距桨来说,螺距的值可以变化。调距桨设计图纸中给出的螺距数据一般是设计螺距下每个叶切面的螺距。因此,在计算时需要根据用户指定的螺距值来对每个叶切面的螺距值进行计算。根据螺旋桨理论,一般取0.7倍桨半径处叶切面的螺距为整个桨的螺距[1]。因此,设初始螺距值和用户设定螺距值分别为
| $\Delta \theta = \arctan ({P_{{r_{0.7}}}}/2\pi {r_{0.7}}) - \arctan ({P_{0{r_{0.7}}}}/2\pi {r_{0.7}}),$ | (2) |
则各叶切面的螺距P为:
| $P = 2\pi r\tan (\Delta \theta + \arctan ({P_0}/2\pi r))\text{。}$ | (3) |
式中:r为叶切面半径,P0为叶切面初始螺距。
2.2 尾涡面数据处理由螺旋桨理论可知,理想状态下,螺旋桨的尾涡面由无穷多条螺旋线组成,由随边开始,延伸至船后无穷远处。每条螺旋线的螺距与对应叶切面的螺距相等,而且经过该叶切面的2个端点,由以上2个条件可以唯一确定与叶切面对应的螺旋线。螺旋线的方程为:
| $\begin{array}{l}x = a\cos (\omega t + {\phi _0})\text{,}\\y = a\sin (\omega t + {\phi _0})\text{,}\\z = vt\text{。}\end{array}$ | (4) |
式中:a为螺旋线所在圆柱的半径,ω为螺旋线绕圆柱旋转的角速度,v为螺旋线沿圆柱径向的速度,φ0为初始相位角。根据式(4),只要确定v/ω,就可以唯一确定一族等螺距的螺旋线,螺距为v/aω,然后根据叶切面的2个端点确定初始相位φ0,即可唯一确定对应于叶切面的螺旋线。各个叶切面对应的螺旋线就构成了螺旋桨的尾涡面。本文利用VC++编程计算对应于每个叶切面的螺旋线的三维坐标。
2.3 桨毂数据计算桨毂由与叶根剖面所在圆柱体近似表示,桨毂的长度取为桨叶轴向最大宽度的1.5倍。桨毂表面根据相邻叶片的叶根剖面分隔为N个单元,N为螺旋桨叶片数。最后对每个单元进行数据离散。
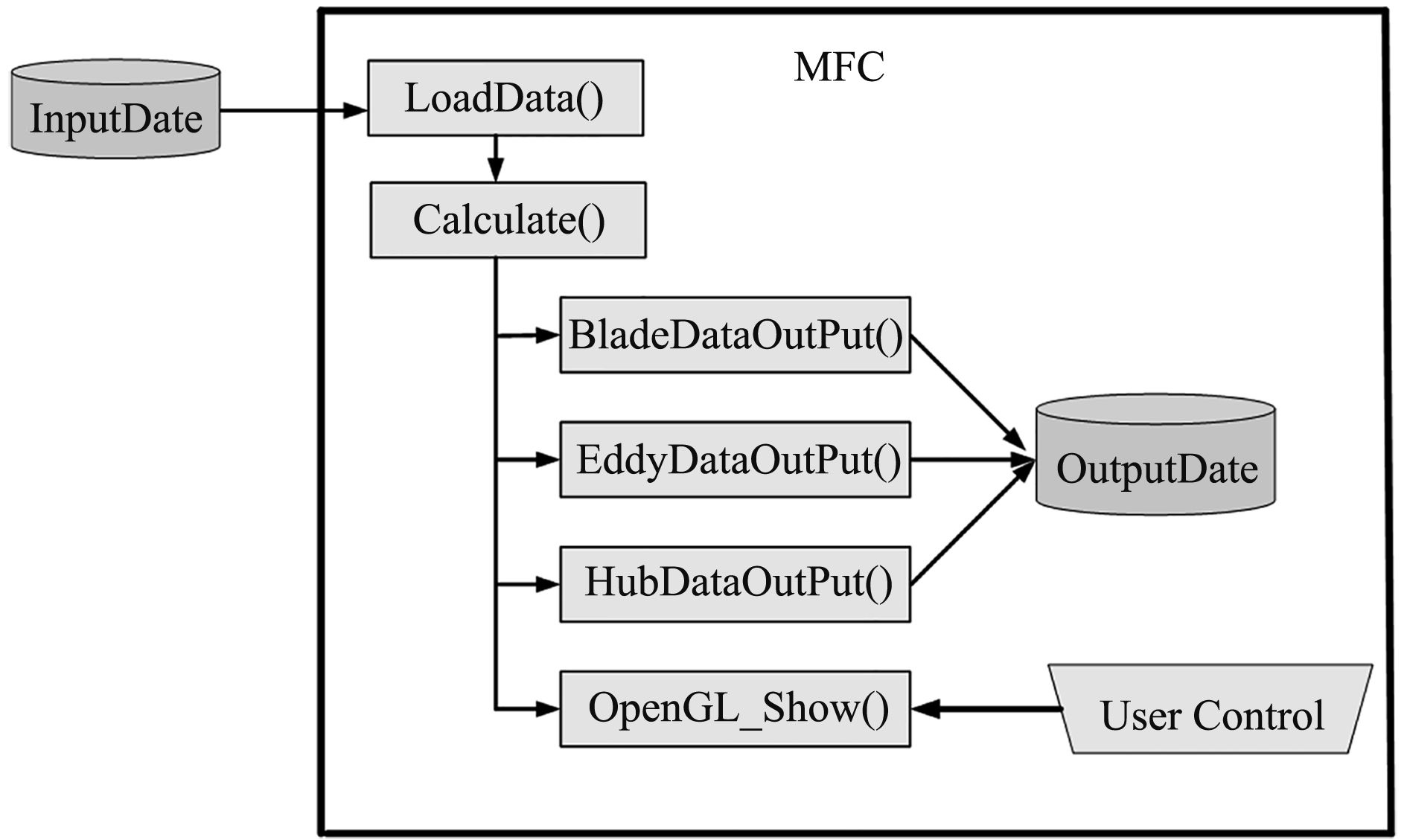
3 基于MFC和OpenGL的螺旋桨几何建模程序MFC(Microsoft Fundation Class)是集成于VC++软件内的程序开发工具,在开发Windows应用程序方面功能强大。本文选择VC++6.0/MFC为工具,开发基于对话框的螺旋桨几何建模应用程序。程序的基本结构如图4所示。
|
图 4 螺旋桨三维仿真程序主要函数 Fig. 4 Main function of 3D programme of propeller |
在图4所示的程序结构中,LoadData()为数据载入函数,该函数实现MFC与EXCEL的数据传输;通过Calculate()函数,对桨叶、尾涡面和桨毂的数据进行计算;由3个OutPut()函数实现数据的输出;由OpenGL_Show()函数实现螺旋桨三维的显示,用户可通过键盘与应用程序进行人机交互。
在三维模型显示过程中用到的OpenGL关键技术如下[4, 5]:
1)利用glBegin(GL_LINE_STRIP)和glBegin_(GL_POLYGON)实现曲线和曲面的绘制。
2)利用glOrtho()指定裁剪区域,避免在窗口形状发生改变时,螺旋桨的形状发生扭曲。
3)在OpenGL绘图程序的初始化函数中加入glutInitDisplayMode(GLUT_DEPTH)和glEnable_(GL_DEPTH_TEST),在显示回调函数中加入glDepthFunc(GL_LESS)、glClearDepth(1)和glClear_(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT)来设置深度缓存,实现三维图形在视角变换过程中图形相互遮挡与消隐的效果。
4)通过glutIdleFunc()和glutKeyboardFunc()函数来实现动画效果和人机交互功能。
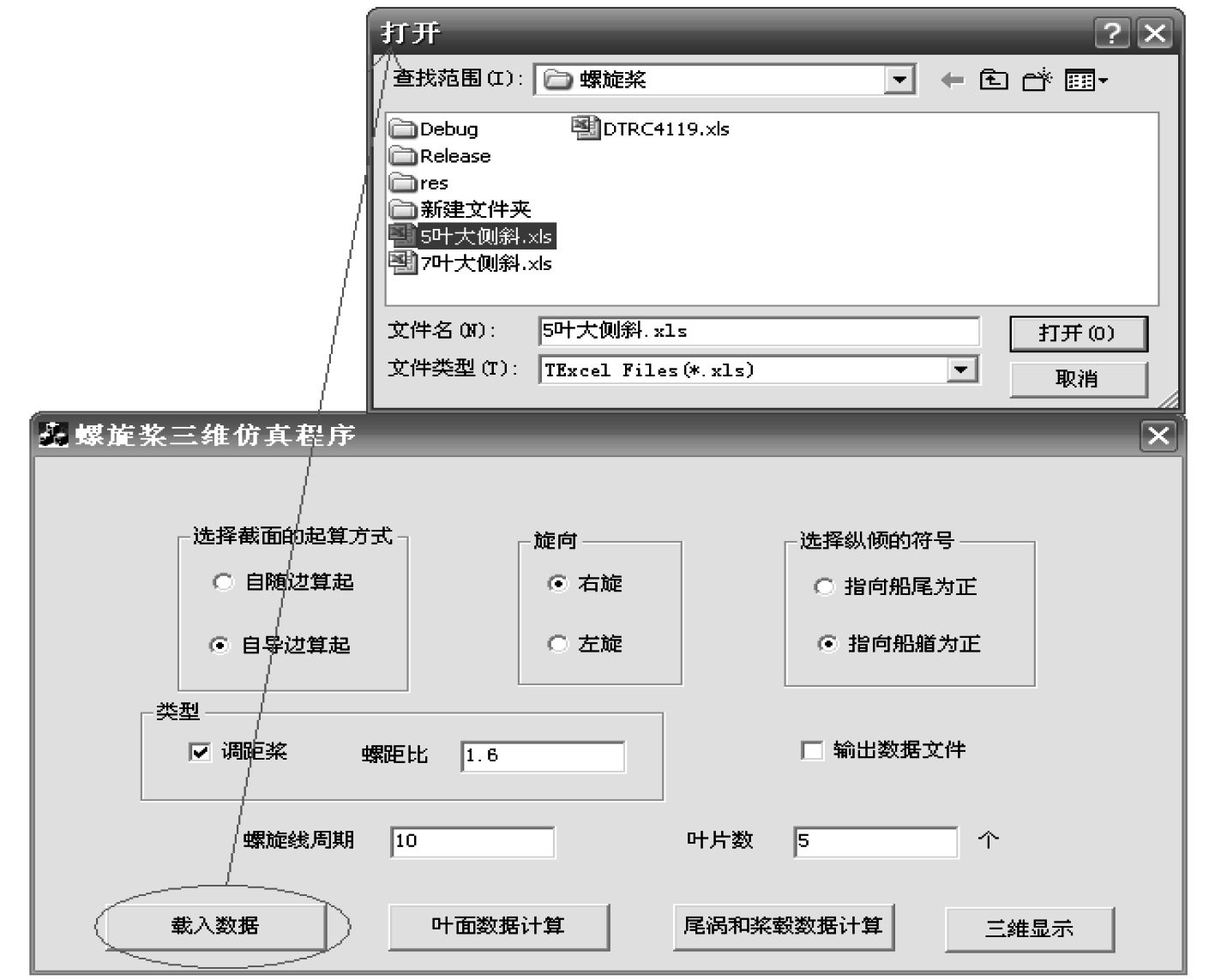
4 仿真实例与应用利用仿真程序对某船5叶大测斜调距桨三维模型进行仿真。在开始仿真前需要设定一些基本参数,初始参数设定完毕后,通过调用Excel数据库来载入该螺旋桨的几何设计参数,见图5。
|
图 5 螺旋桨仿真程序对话框 Fig. 5 Dialog of simulation programme of propeller |
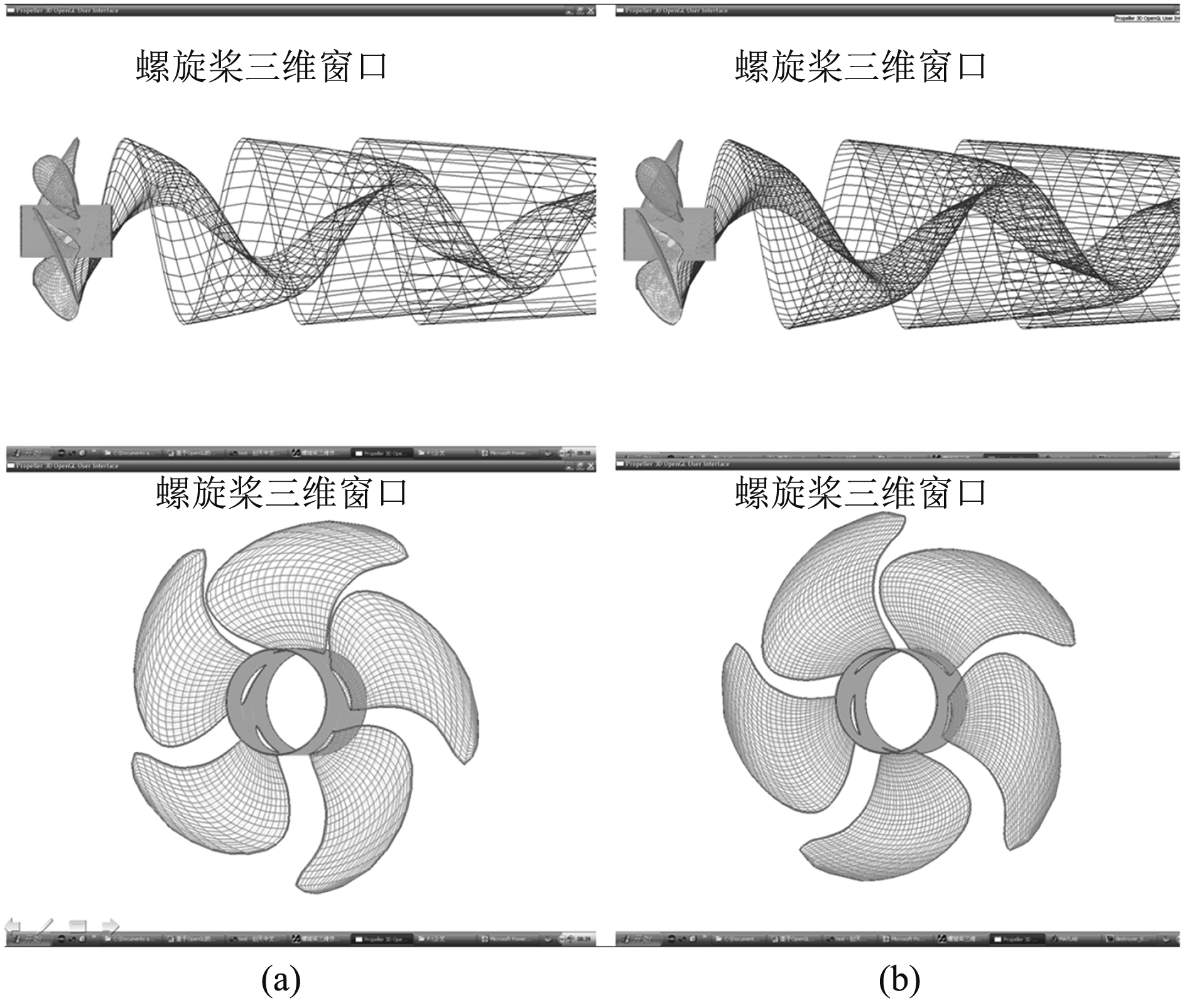
在依次点击了图5所示的“页面数据计算”和“尾涡和桨毂数据计算”功能键后点击“三维显示”,则该5叶大测斜调距桨的三维仿真窗口如图6所示(为了比较的需要,图6是4个三维仿真窗口组合而成)。图6(a)所示的调距桨螺距值为1.6,叶片上的面元数为20×20个,尾涡面上每个周期的面元数为20×30个。图6(b)所示的是相同螺距下,调距桨叶片上的面元数增加为为30×30个,尾涡面上每个周期的面元数增加为30×50个时的仿真结果。由图可见,面元数越多,螺旋桨及其尾涡面的三维造型越逼真,而且调距桨转动过程中尾涡面向后发展的动态过程一目了然。
|
图 6 某5叶大测斜螺旋桨三维仿真 Fig. 6 3D simulation of a five-blade propeller |
该调距桨螺距由1.6变化为–1.5的过程中(中间过程取螺距为1.0和0),桨叶与尾涡面的的变化如图7所示。由仿真结果可见,随着螺距的减小直至负螺距,调距桨的尾涡面逐渐由船尾方向发展到船首方向。即随着螺距的减小,调距桨由推进船舶前进逐渐过渡为拉着船舶后退。

|
图 7 某5叶大测斜调距桨调距过程仿真 Fig. 7 3D simulation of a five-blade propeller when pitch changing |
由以上仿真结果可见,在已知螺旋桨设计图纸提供的基本型值后,该方法可以便捷、快速地显示出该螺旋桨叶片、尾涡面以及桨毂的三维造型,并通过键盘实现该桨三位运动仿真。另一方面,该方法可提供用于螺旋桨水动力预报的面元网格,网格的精度和网格密度分布函数可以根据实际需要进行调整,图8所示的是根据余弦分布函数计算出的面元网格,越接近导边、随边以及叶稍数网格密度越大。

|
图 8 某5叶大测斜调距桨余弦分布面元网格 Fig. 8 Cosine distribution of panel grid of a five-blade propeller |
本文在分析螺旋桨的三维几何结构的基础上,研究了由螺旋桨设计图纸提供的型值数据到螺旋桨三维几何数据计算的全过程。利用VC++6.0实现了适合于各种类型螺旋桨的三维建模程序,并借助OpenGL实现了三维螺旋桨造型及其尾涡面的显示与人机交互功能,提高了螺旋桨三维建模的效率。本文对螺旋桨桨叶、尾涡面以及桨毂的网格计算也为后续的螺旋桨水动力学数值预报提供了基础。
| [1] | 王国强, 董世汤. 船舶螺旋桨理论与应用[M]. 哈尔滨工程大学出版社, 2005. |
| [2] | 董世汤, 唐登海, 周伟新. CSSRC的螺旋桨定常面元法[J]. 船舶力学, 2005, 10 (5): 46–60. |
| [3] | 侯俊杰. 深入浅出MFC [M]. 华中科技大学出版社, 2001. |
| [4] | EDWARD Angel, 段菲. OpenGL编程基础[M]. 清华大学出版社, 2008. |
| [5] | 刘慧杰, 靳海亮. 基于VC_的OpenGL三维图形开发设计[J]. 计算机与数字工程, 2009, 7 : 122–124. DOI: 10.3969/j.issn.1672-9722.2009.04.036 |
 2017, Vol. 39
2017, Vol. 39
