对于大型滚装船、特种军辅船、航母等大型通舱船,为了方便车辆、特种可移动装备的通行,其舱内通常不设支柱。另外,对于大型客船,随着内部美观性和空间视觉效果需求逐渐增加,取消客舱内的支柱而采用无支柱大跨度甲板板架的设计也愈加为人们所喜爱[1]。这些通舱设计长度可达100 m,宽度在20 m以上[2],使得通舱顶部的甲板在横向成为大跨度单层甲板。
大跨度单层甲板由于其横向跨度大,其结构型式一般设计为横骨架式,也可设计成纵骨架式。为了满足大跨度单层甲板的横向刚度、强度和稳定性的要求,则需要设计较大尺寸的横梁或强横梁,这样不仅会导致结构重量增加,而且也会占用有限舱室的空间。故而,大跨度甲板存在刚度和强度不足的问题,有待采用新的结构布置形式给予解决。
目前,针对大跨度单层甲板的布置形式有较多研究[1 – 3],大多针对单层甲板构件进行设计优化。田雷[3]基于强度考虑,认为横骨架式要在应力和变形方面要优于纵骨架式。万琪等[1, 3]基于甲板强度和稳定性条件对大跨度甲板构件进行优化设计,对大跨度甲板强构件和纵骨的结构型式和截面尺寸提出了优化设计方法。另外,针对围壁加筋板设计,国内外学者通过理论解析法、有限元法、实验法等多种方法分析加筋板格的强度、屈曲和极限强度[4 – 6]。LR规范[7]和船舶结构强度设计[9]中以保证横骨架式板架整体稳定性为前提,提出对面内受压的横骨架式板架上次要加强构件的必须弯曲刚度。对于大跨度单层甲板结构的弯曲刚度和强度偏弱的问题,如何在大跨度单层甲板之间设置适当的横向围壁及采用新的结构型式,以提高其横向弯曲刚度和弯曲强度,目前研究尚少。
为提高大跨度横向板架弯曲刚度,目前考虑采用新的结构布置形式,在大型通舱顶部以上的单层甲板间设置若干横向围壁,使其形成大跨度箱形双层甲板,并采用纵桁支撑横梁的结构型式,使得大跨度横向构件变成小跨度构件,以提高大跨度双层甲板整体结构和局部甲板板架弯曲刚度和弯曲强度。
本文基于大跨度双层甲板这一新的结构型式,采用结构有限元数值分析方法对其进行计算,给出横向围壁间距与大跨度双层甲板变形和应力大小关系曲线,分析得到较优的横向围壁设计间距,同时引入用于横向围壁结构初步设计的横向围壁载荷与其间距关系的有效承载系数。研究结果表明:设置横向围壁的大跨度双层甲板,可解决大跨度单层甲板横向弯曲刚度偏弱的难题。
为了便于比较,下面首先对大跨度单层甲板的横向弯曲特性进行计算分析。
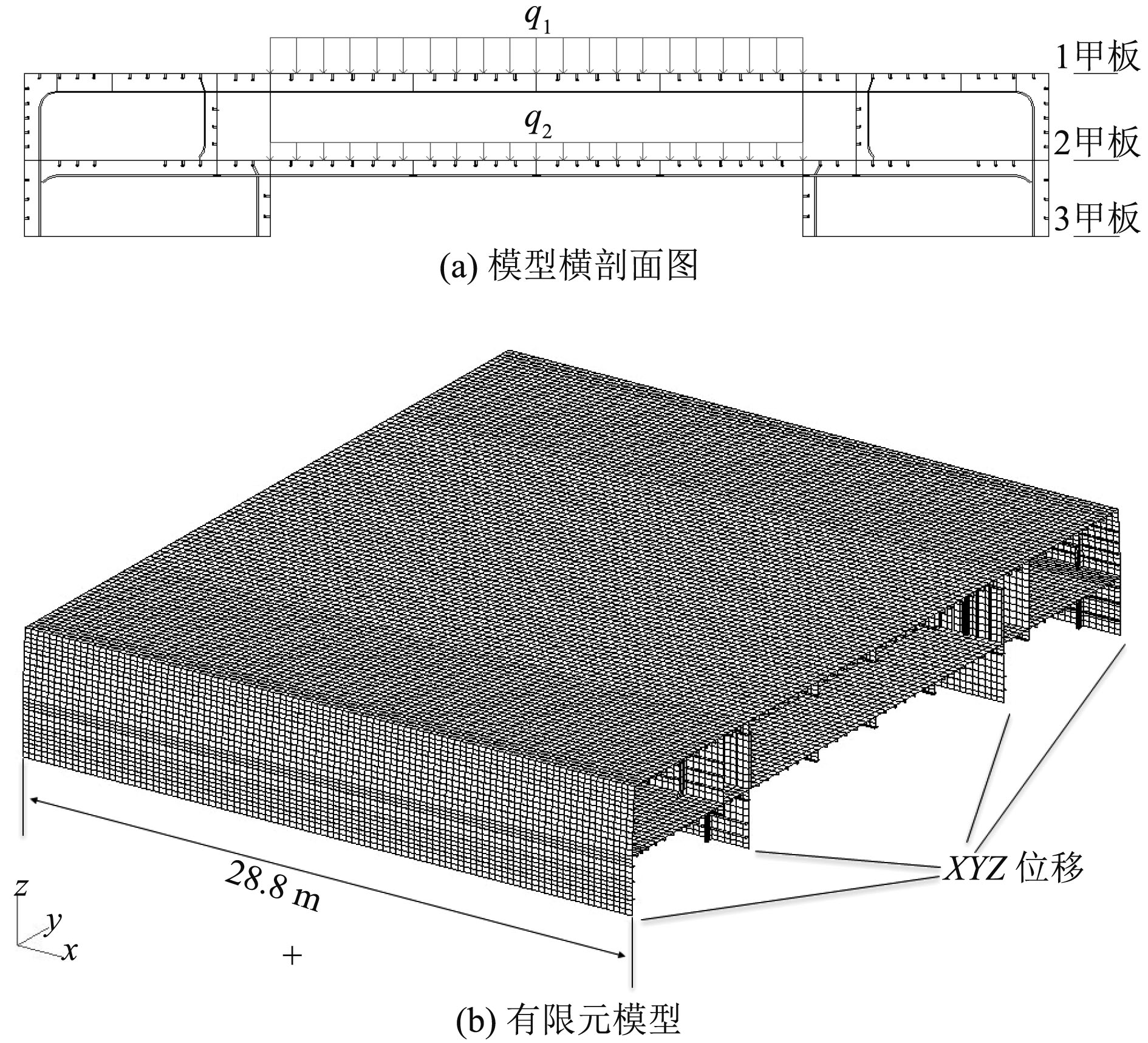
1 大跨度单层甲板横向弯曲特性分析为分析大跨度单层甲板的强度和刚度特性,以某船大型通舱的舱段为研究对象进行计算分析。通舱舱段的选取范围:沿船长方向长28.8 m,船宽方向至两舷,高度方向为1甲板~3甲板。大跨度单层甲板结构型式为纵骨架式,1, 2甲板之间层高3 m,横向大跨度无支撑区域宽b=20 m,肋距0.6 m,其横剖面如图1(a)所示。大跨度单层甲板的主要构件尺寸见表1。
|
|
表 1 大跨度单层甲板构件尺寸 Tab.1 Structural dimension of large-span single deck |
|
图 1 模型横剖面图以及计算有限元模型 Fig. 1 Midship transverse cross-section plan and FE model |
大跨度单层甲板的结构有限元模型采用MSC/PATRAN有限元分析软件建立板梁混合模型,甲板板和主要构件腹板采用板单元,主要构件面板和纵骨采用梁单元,建立的有限元模型如图1(b)所示。
模型材料:选用Q355钢,其材料密度γ=7.80 t/m3,屈服强度σs=355 MPa,弹性模量E=2.1×105 MPa,泊松比υ=0.3。
模型边界条件:为减小边界条件对单层甲板计算结果的影响,在3甲板与纵舱壁和舷侧板相交处约束X,Y,Z方向线位移,如图1(b)所示;
模型施加载荷:在模型1甲板上施加均布载荷q1=20 kPa,在模型四甲板上施加均布载荷q2=10 kPa,施加区域如图1(a)所示。
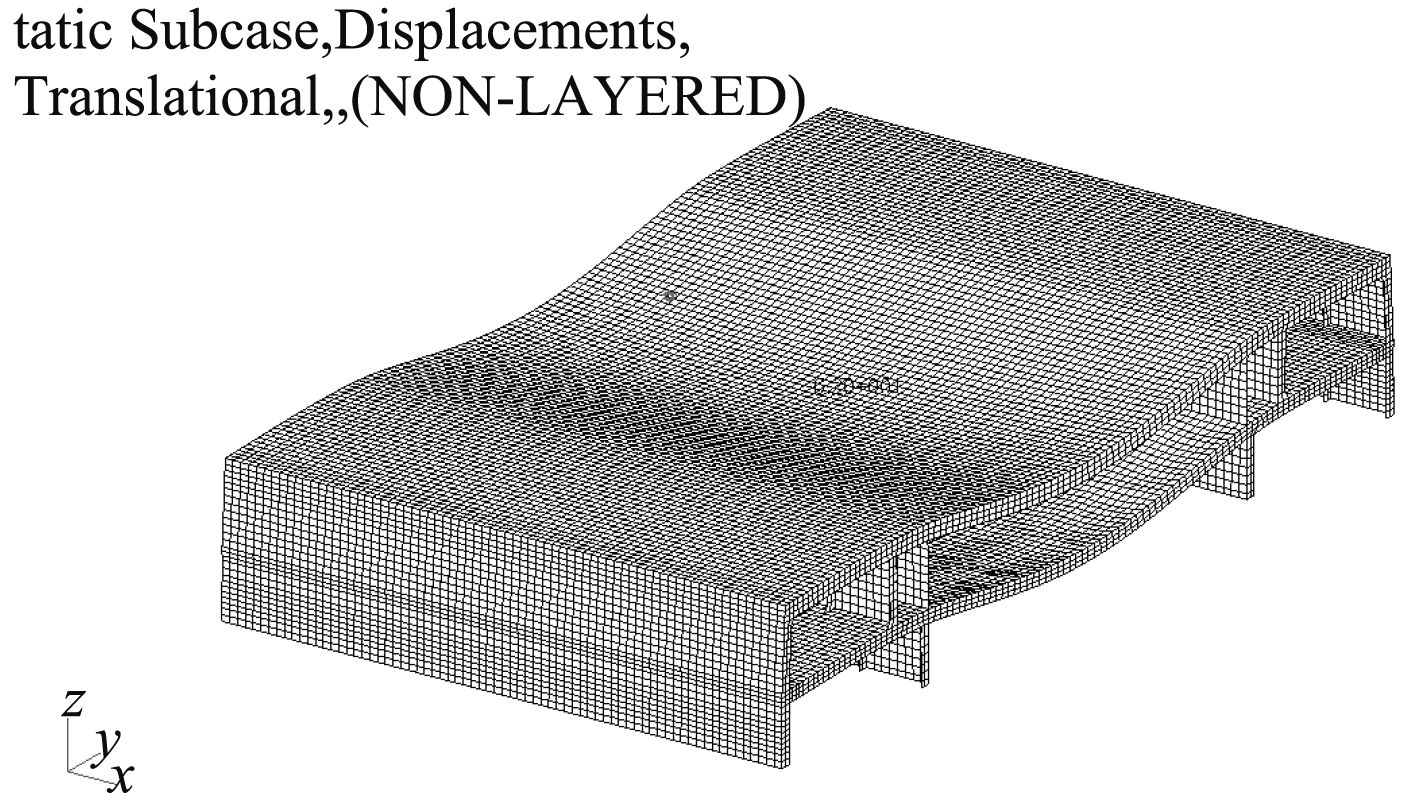
1.2 计算结果根据大跨度单层甲板结构有限元模型的计算结果,大跨度单层甲板变形如图2所示,从图中可以看出,大跨度1,2单层甲板最大位移发生甲板上船中y=0的位置处,整体横向变形都呈现筒形弯曲状态的特征。
|
图 2 大跨度单层甲板变形图 Fig. 2 Deformation of large-span single deck |
1,2甲板强横梁最大变形和应力见表2,从表2中可以看出,1,2甲板强横梁最大变形vmax 均远大于设计衡准[v],1甲板强横梁最大应力σmax也大于设计衡准[σ]。
|
|
表 2 1,2甲板强横梁最大变形和应力 Tab.2 vmax and σmax of web beam |
由于大跨度单层甲板横向弯曲刚度较弱,可采用增大强横梁腹板高度提高其弯曲刚度。经计算,若要满足设计衡准[v]=20 mm,则甲板强横梁腹板高度将达到h腹板=1.4 m左右。而1,2甲板之间层高仅h1-2=3 m,这样的构件尺寸会严重影响1甲板与2甲板之间的有效层高,同时也大大增加船体重量,明显不可行。
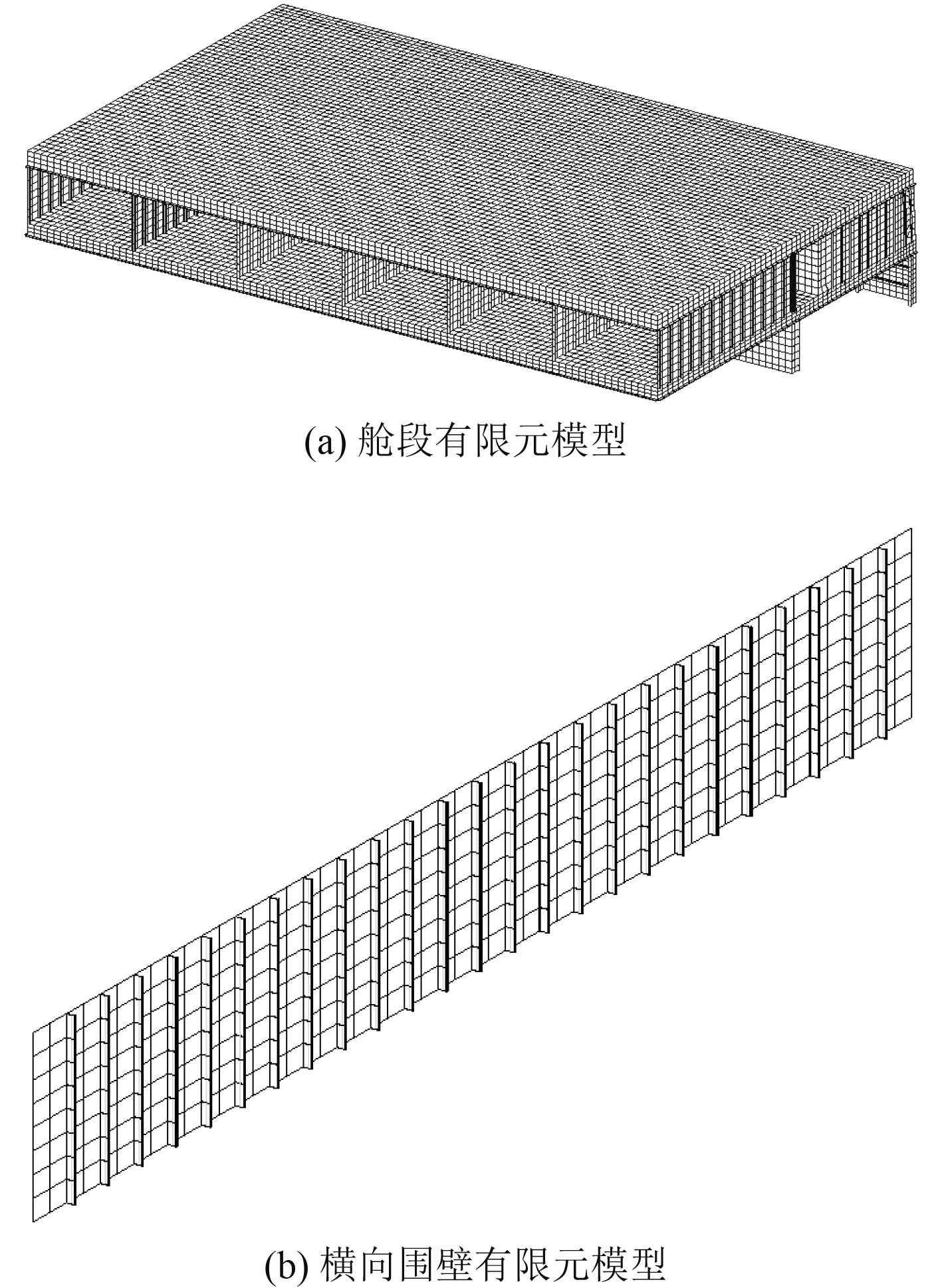
2 大跨度双层甲板结构设计根据新的结构布置形式,某船在通舱顶部的1,2甲板之间设置横向围壁,横向围壁结构尺寸:板厚t=7 mm、垂直扶强材HP120×6,甲板结构型式采用纵骨架式。为了分析大跨度双层甲板的弯曲特性与横向围壁间距S之间变化关系,在兼顾了1,2甲板之间舱室布置的需求基础上,选取4个横向围壁间距S=4.8 m,9.6 m,14.4 m,28.8 m进行舱段结构有限元计算。这里仅给出了横向围壁间距S=4.8 m的舱段有限元模型,如图3所示。
|
图 3 横向围壁间距S=4.8 m的舱段有限元模型图 Fig. 3 Part-cabin FE model when S=4.8 m |
根据舱段有限元模型的计算结果,表3列出了大跨度双层甲板横向围壁和强横梁对应不同横向围壁间距S的最大变形和最大应力。
|
|
表 3 大跨度双层甲板上的最大变形和最大应力 Tab.3 Stress and deformation of large-span double deck |
不同横向围壁间距S下大跨度双层箱型甲板的变形如图4所示,从图4中可以看出:

|
图 4 不同间距横向围壁布置下模型变形图 Fig. 4 Deformation of model in different spacings |
1)大跨度双层箱型甲板的整体变形呈筒形弯曲形状,图4(a)最为明显。
2)横向围壁之间的变形为甲板的局部变形,随着横向围壁间距逐渐增大,甲板的变形逐渐呈锅底状,图4(d)模型中部范围变形与单甲板变形一样呈筒形弯曲。
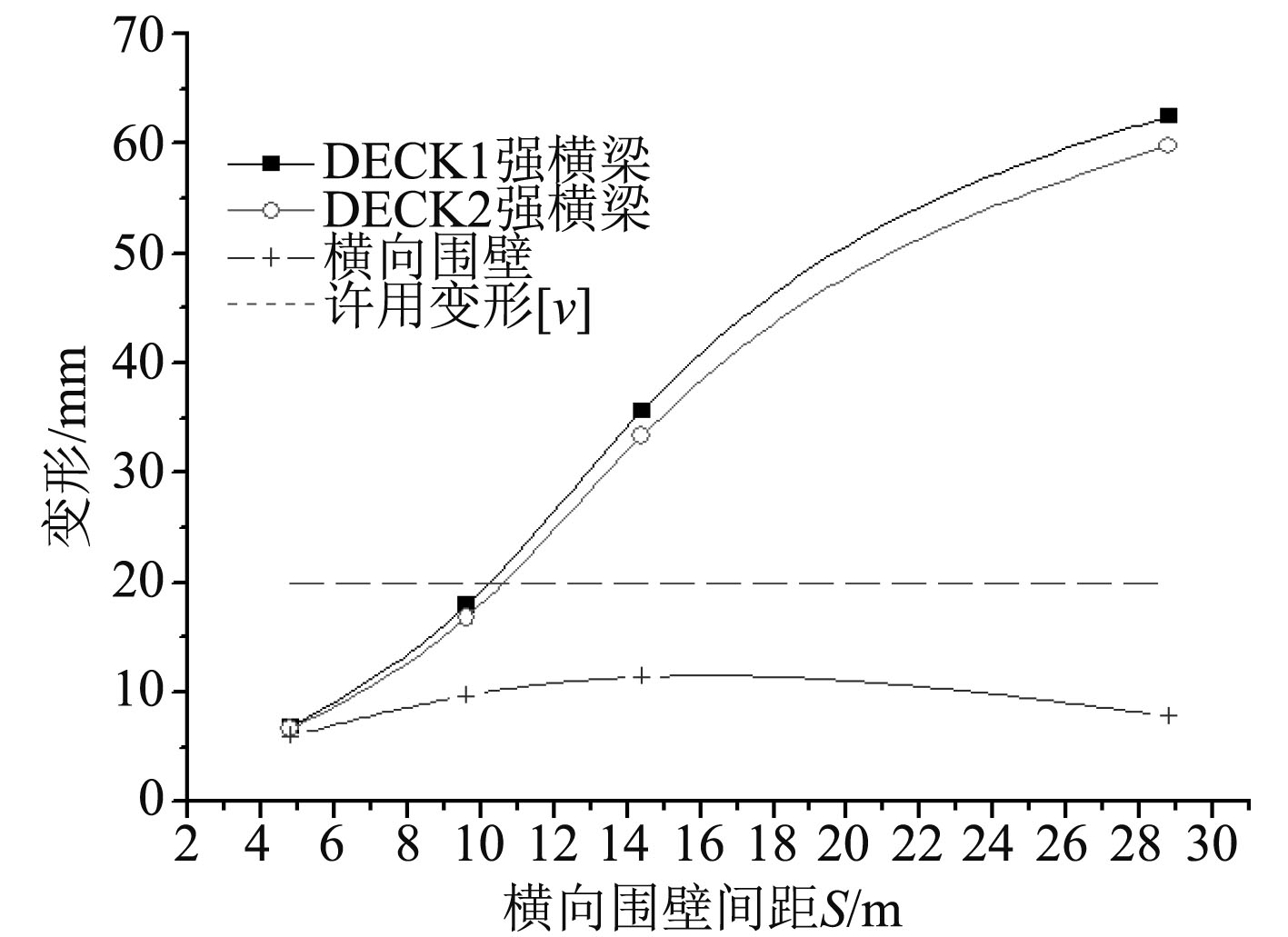
为分析不同横向围壁间距S对于横向围壁和强横梁变形变化的影响,图5给出了横向围壁和强横梁变形v与横向围壁间距S的关系曲线。
|
图 5 横向围壁、强横梁的垂向变形随横向围壁间距S变化的曲线 Fig. 5 v of transverse bulkhead and web beam versus S |
从图5曲线可以看出:
1)横向围壁的变形v随着横向围壁间距S的变化而变化,曲线形状类似抛物线。最大变形出现在横向围壁间距S=14.4 m附近;当S<14.4 m时,变形v随间距S增大而变大;当S>14.4 m时,变形v随间距S增大而变小。
2)强横梁的变形v随着横向围壁间距S的增大而变大。
3)横向围壁的最大变形vmax=11.4 mm<<[v]。
4)当S>9.6 m时,强横梁的变形v>[v];若强横梁满足许用变形[v]的要求,则横向围壁间距S≤9.6 m。
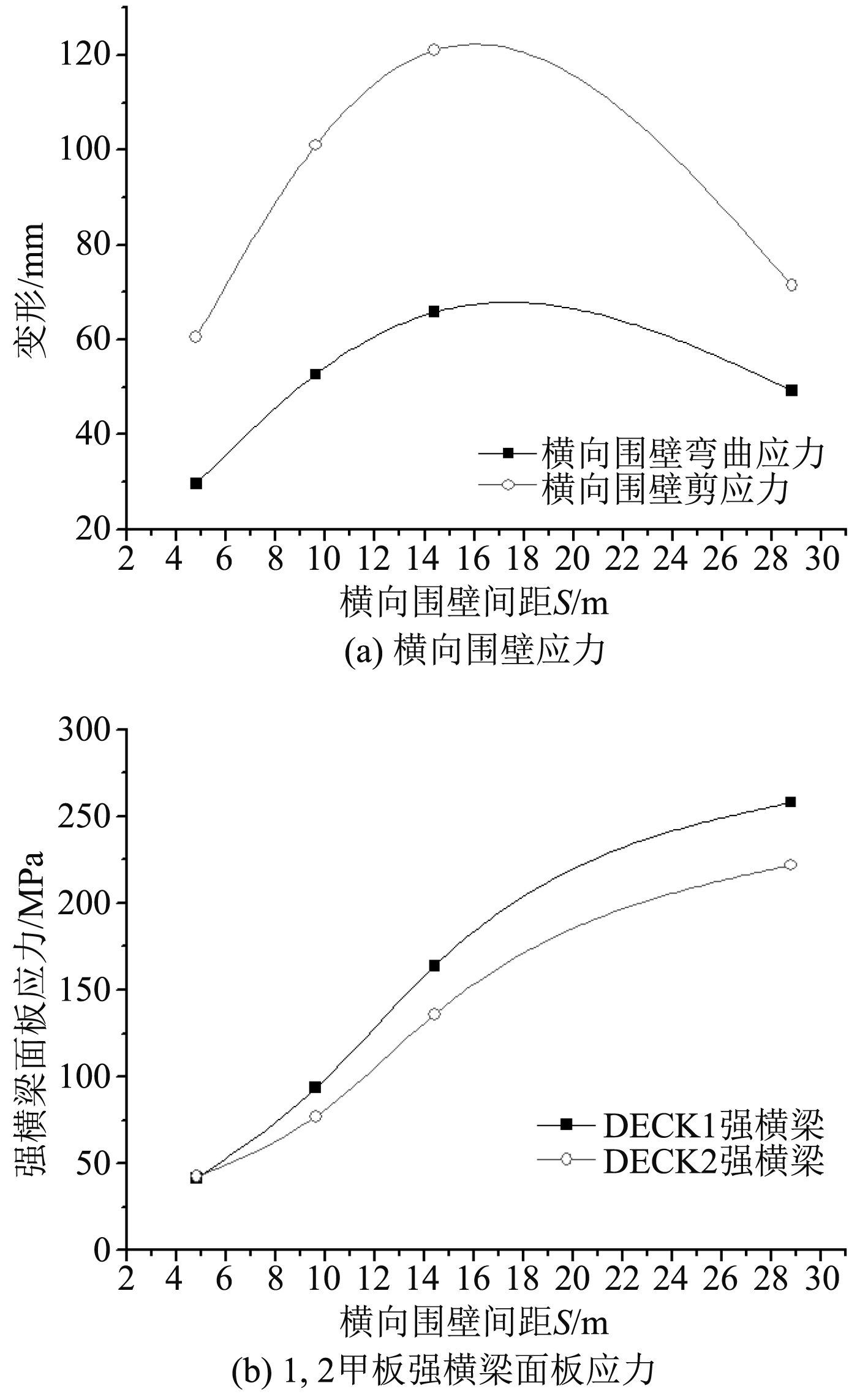
2.1.2 横向围壁、强横梁弯曲应力特征同样为分析横向围壁间距S对横向围壁和强横梁应力变化的影响,图6给出了横向围壁应力(σb、τ)和强横梁弯曲应力σb随横向围壁间距S的变化曲线。从图6曲线中可以看出:
|
图 6 横向围壁、强横梁应力随横向围壁间距S变化的曲线 Fig. 6 Stress of transverse bulkhead and web beam versus S |
1)横向围壁的弯曲应力σb和剪应力τ随横向围壁间距S的变化趋势与横向围壁变形的变化趋势基本相同(见图5),在间距S=14.4 m附近应力出现峰值。其中,剪应力τ 随间距S的变化梯度较大。
2)强横梁的应力σb随着横向围壁间距S的增大而变大,变化趋势也与其变形的变化趋势一样(见图5)。
2.2 横向围壁有效承载系数根据常规的设计方法,如果甲板结构型式为纵骨架式,纵骨由强横梁支撑,强横梁由纵桁支撑,纵桁由横围壁支撑,那么横向围壁上的设计载荷Q=qbS(其中,q为甲板均布荷重)。实际上,强横梁上载荷不完全由纵桁承受,与它们之间的相对弯曲刚度大小有关,在大跨度双层甲板计算中得到的横向围壁实际承受载荷可以说明这一点(见表4)。
|
|
表 4 横向围壁设计载荷和实际承载 Tab.4 Q and Q0 of transverse bulkhead |
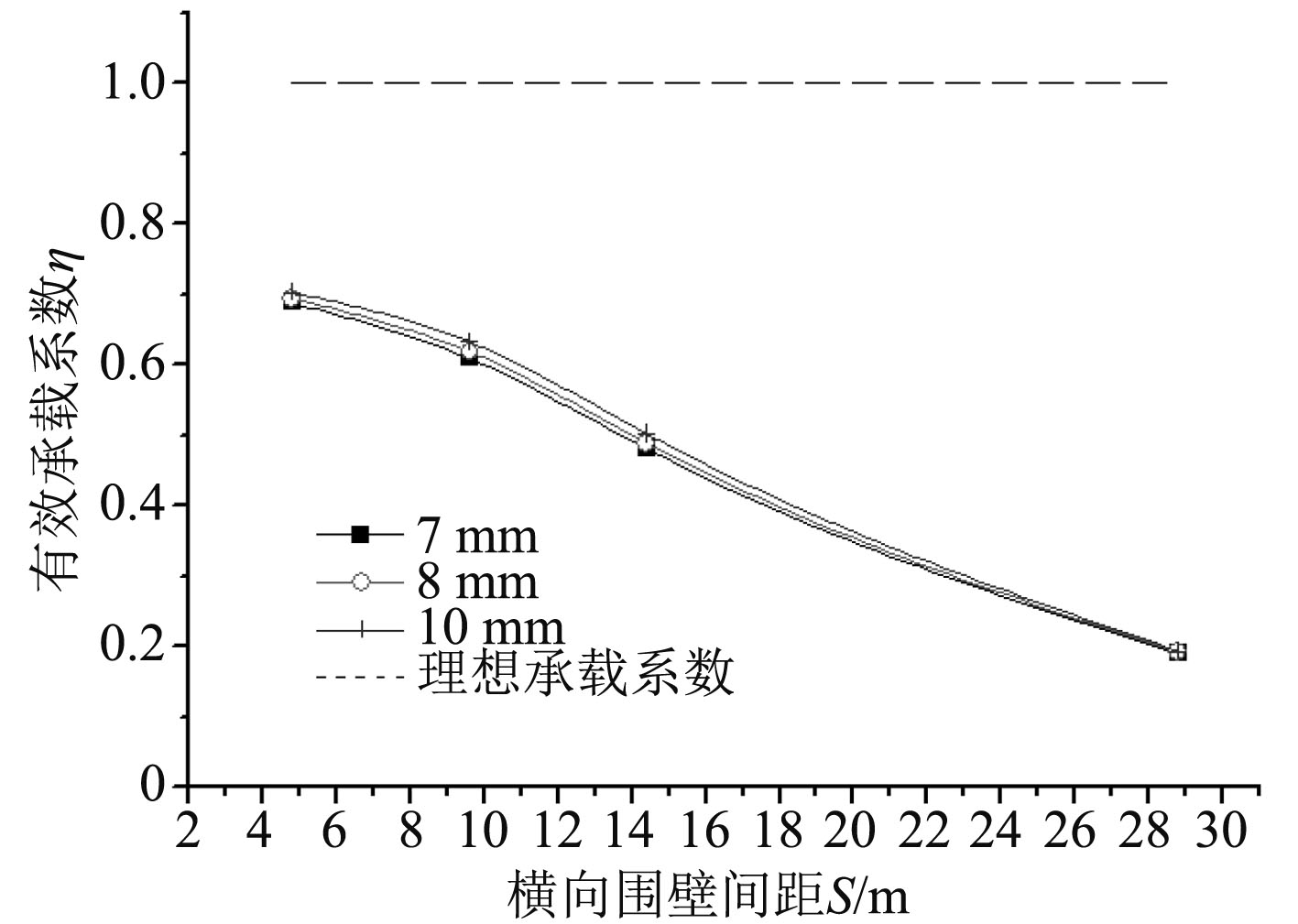
为了分析横向围壁间距S对有效承载系数 η 的影响趋势,图7和图8分别给出了有效承载系数 η 和实际承受载荷Q随横向围壁间距S的变化曲线。
|
图 7 横向围壁有效承载系数η随间距的变化曲线 Fig. 7 η versus S |

|
图 8 横向围壁实际承受载荷Q随间距的变化曲线 Fig. 8 Q versus S |
1)当S≥4.8 m时,横向围壁上的最大有效承担载荷只占70%以下,常规方法设计载荷Q0明显偏于保守,因此可考虑有效承载系数 η 以优化结构尺寸。
2)有效承载系数 η 随横向围壁间距S增大而减小,在S=14.4 m附近,横向围壁实际承受的载荷存在最大值Qmax。其原因主要是:随着横向围壁间距S的增大,纵桁弯曲刚度逐渐减弱,其对强横梁的支撑作用逐渐降低,当间距S过大时,强横梁弯曲刚度大于纵桁弯曲刚度,其承受载荷大部分将由两侧纵舱壁承受。因此,大跨度双层甲板的横向围壁结构采用常规设计载荷进行设计不合理。
3)横向围壁实际承受载荷Q随横向围壁间距S的变化曲线形状也呈抛物线,横向围壁的弯曲特性的变化与其载荷变化趋势相一致(见图5和图6(a)),这符合结构的外力与响应关系。
2.3 大跨度单、双层甲板弯曲特性比较根据有限元计算结果,大跨度单、双层甲板弯曲变形和应力的计算和比较结果如表5所示。
|
|
表 5 大跨度单、双层甲板弯曲变形和应力表 Tab.5 Deformation and stress of single deck and double deck |
从表5中可以看出:
1)在给定的甲板构件尺寸条件下,当横向围壁间距S≤9.6 m,大跨度双层甲板的最大变形v为单层甲板的30%或更小,远小于大跨度单层甲板的变形,满足变形衡准[v]。
2)当横向围壁间距S>9.6 m时,虽然可便于舱室布置,但是大跨度双层甲板变形超出衡准。特别当横向围壁间距S过大或S=28.8 m左右时,横向围壁的作用已丧失,因为此时的大跨度双层甲板的最大变形与大跨度单层甲板基本一样。
3 结 语通过基于大跨度双层甲板这一新的结构型式弯曲特性的计算与分析,结论如下:
1)设置横向围壁的大跨度双层甲板可解决大跨度单层甲板横向弯曲刚度偏弱的问题。
2)常规设计载荷方法不太适合大跨度双层甲板的横向围壁结构设计。
| [1] |
彭勇刚. 基于Workbench平台的大跨度甲板板架结构优化分析[J]. 中国水运, 2014, 14 (3): 11–14.
PENG Yong-gang. Optimization Analysis of Large-span Deck Based on ANSYS-Workbench[J]. China Water Transport, 2014, 14 (3): 11–14. |
| [2] |
万琪, 王福花. 大跨度无支撑甲板纵向稳定性分析和优化设计[J]. 中国造船, 2011, 52 (1): 17–25.
WAN Qi, WANG Fuhua. Longitudinal Stability Analysis and Optimum Desing of Supportless Long-span Deck Structure[J]. Shipbuilding of China, 2011, 52 (1): 17–25. |
| [3] |
田雷. 大跨度无支撑甲板室的两种骨架形式比较[J]. 中国水运, 2014, 14 (3): 15–20.
TIAN Lei. Comparison of Two Framing Structure Forms for Supportless Long-span Deck[J]. China Water Transport, 2014, 14 (3): 15–20. |
| [4] |
黎顺生. 加筋板极限强度计算与分析[D]. 武汉: 武汉理工大学, 2005. 8–22.
LI Shun-sheng. Ultimate strength calculation and analysis of stiffened plate[D]. Wuhan: Wuhan University of Technology, 2005. 8–22. |
| [5] |
刘春香, 李陈峰, 任慧龙, 李晓宇. 大跨度板架屈曲分析的非线性有限元法[J]. 舰船科学技术, 2013, 35 (1): 46–50.
LIU Xiang-chun, LI Chen-feng, REN Hui-long, LI Xiao-yu. The NFEM for buckling anlysis of large-span Grillage[J]. Ship Science and Technology, 2013, 35 (1): 46–50. |
| [6] |
乔迟, 张世联. 大跨度加筋板架优化设计研究[J]. 舰船科学技术, 2015, 37 (8): 23–26.
QIAO Chi, ZHANG Shi-lian. Optimization Design of Large-span Stiffened Panel[J]. Ship Science and Technology, 2015, 37 (8): 23–26. |
| [7] | Lloyd’s Register of shipping. Rules and regulations for the classification of naval ships[M]. Lloyd’s Register of shipping, 2014. |
| [8] | 中国船级社. 钢质海船入级与建造规范[M]. 人民交通出版社, 2012. |
| [9] | 杨代盛. 船体强度与结构设计[M]. 北京: 国防工业出版社, 1982. |
 2017, Vol. 39
2017, Vol. 39
