2. 上海交通大学 海洋工程国家重点实验室,上海 200240
2. State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China
随着船舶的大型化,海峡通道、运河航道等船舶航行的水域宽度相对变窄,岸壁效应随之产生,船舶的水动力性能相较于在无限宽水域中航行时会发生显著变化,这也造成限制水域中船舶操纵运动的控制愈加困难。限宽水域船舶操纵运动中,船舶横荡与首摇运动之间具有较强的耦合性,这需要寻求多输入多输出(MIMO)方法来控制船舶运动。船舶控制的主要方法有PID控制、鲁棒控制和模糊控制[1 – 3]。但在MIMO控制领域,上述方法控制效果一般且算法复杂。Mucha P 与Thomas[4 – 5]则利用LQR控制方法实现对限宽水域中船舶操纵运动的较好控制,展现了LQR控制方法在MIMO控制领域较好的兼容性,为复杂状况下船舶操纵运动的控制提出了一个新的思路。
LQR(Linear Quadratic Regulater)即线性二次型调节器,其控制对象是以状态空间形式给出的线性系统,而目标函数为对象状态和控制输入的二次型函数。LQR的最优解具有标准的解析式,可以形成简单的线性状态反馈控制规律,容易构成最优反馈控制,较好地兼顾了系统的鲁棒稳定性和快速性,在工程中便于实现。
本文以超大型油轮KVLCC2为研究对象,基于LQR控制方法对限宽水域中KVLCC2操纵运动控制问题进行研究。本文采用线性状态空间形式的操纵运动方程,基于数值模拟获取的相应线性水动力系数,计算出使目标函数值最小的增益矩阵K,从而得到满足最优控制规律的时域舵角变化,实现对不同宽度水域中船舶运动的最优控制,并与极点配置控制方法作比较,结果验证了LQR控制器的有效性和优越性。
1 数学模型 1.1 线性船舶操纵运动方程设船舶排水量为∆,z轴惯性矩为Iz,X,Y分别为船舶在纵向与横向所受外力,N为船舶所受竖向力矩。u为船舶前进速度,v为船舶横移速度,r为船舶转首角速度,xg为船舶重心纵向坐标,ψ为船舶航向角,δR为转舵角度。
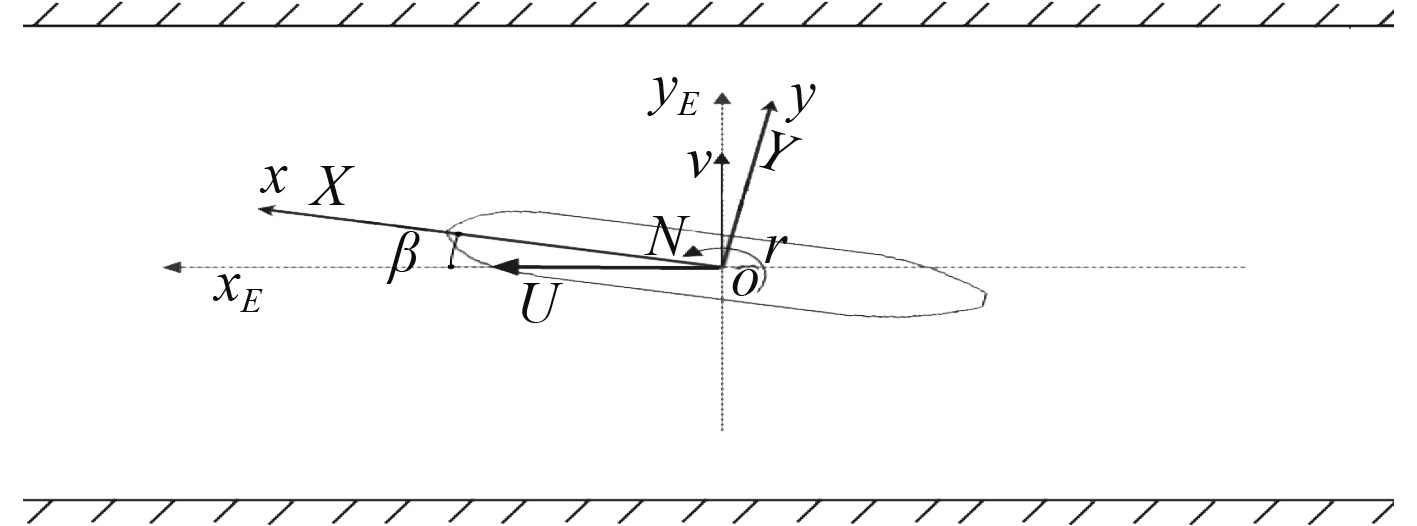
|
图 1 船舶的运动状态与坐标系 Fig. 1 Coordinate systems for ship maneuvering |
基于LQR控制器的控制对象是以状态空间形式给出的线性系统,本文采用首揺-横荡二自由度船舶线性操纵运动方程。非限制水域下线性船舶操纵运动方程为:
| $\begin{split}& \left[ {\begin{array}{*{20}{l}}{ - {Y_{\dot v}} + \Delta }\\{ - {N_{\dot v}} + \Delta {x_g}}\end{array}} \right.\left. {\begin{array}{*{20}{l}}{ - {Y_{\dot r}} + \Delta {x_g}}\\{ - {N_{\dot r}} + {I_z}}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}{\dot v}\\{\dot r}\end{array}} \right] + \\& \left[ {\begin{array}{*{20}{l}}{ - {Y_v}}\\{ - {N_v} - {Y_{\dot v}}}\end{array}} \right.\left. {\begin{array}{*{20}{l}}{ - {Y_r} + \Delta }\\{ - {N_r} + (\Delta - {Y_{\dot r}})}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}v\\r\end{array}} \right] = \\& \left[ {\begin{array}{*{20}{l}}{ - {Y_{{\delta _R}}}}\\{ - {N_{{\delta _R}}}}\end{array}} \right.\left. {\begin{array}{*{20}{l}}{{Y_{{\delta _u}}}}\\{{N_{{\delta _u}}}}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}{{\delta _R}}\\{{\delta _u}}\end{array}} \right]\text{。}\end{split}$ | (1) |
在限宽水域中,由于岸壁效应的影响,船舶将受到岸吸力与力矩的作用。这些岸吸力与力矩主要取决于岸壁距离与前进速度的大小。Thomas[5]岸吸力与力矩的计算公式为:
| ${Y_S} = \frac{1}{2}{C_S}(d)\rho BT{U^2},{N_{\rm{S}}} = \frac{1}{2}{C_M}(d)\rho BTL{U^2}\text{,}$ | (2) |
其中L,B和T分别为船长、船宽与吃水。
在式(1)的右端分别迭加岸吸力YS与岸吸力矩NS,可得修正后的船舶线性操纵运动方程
| $\begin{split}& \left[ {\begin{array}{*{20}{l}}{ - {Y_{\dot v}} + \Delta }\\{ - {N_{\dot v}} + \Delta {x_g}}\end{array}} \right.\left. {\begin{array}{*{20}{l}}{ - {Y_{\dot r}} + \Delta {x_g}}\\{ - {N_{\dot r}} + {I_z}}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}{\dot v}\\{\dot r}\end{array}} \right] + \\& \left[ {\begin{array}{*{20}{l}}{ - {Y_v}}\\{ - {N_v} - {Y_{\dot v}}}\end{array}} \right.\left. {\begin{array}{*{20}{l}}{ - {Y_r} + \Delta }\\{ - {N_r} + (\Delta - {Y_{\dot r}})}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}v\\r\end{array}} \right] = \\& \left[ {\begin{array}{*{20}{l}}{ - {Y_{{\delta _R}}}}\\{ - {N_{{\delta _R}}}}\end{array}} \right.\left. {\begin{array}{*{20}{l}}{{Y_{{\delta _u}}}}\\{{N_{{\delta _u}}}}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}{{\delta _R}}\\{{\delta _u}}\end{array}} \right] + \left[ {\begin{array}{*{20}{l}}{{Y_S}}\\{{N_S}}\end{array}} \right]\text{。}\end{split}$ | (3) |
线性二次型最优设计旨在寻求最优控制u(t),使二次型目标函数J取得最小值。
考虑系统的状态方程为:
| ${ {\dot x }}={ Ax} + { Bu} + { D}\text{,}$ | (4) |
式中:x为系统的状态向量;u为控制向量;D为系统的干扰矩阵;A为由系统运动方程推导而得的控制对象矩阵;B为控制矩阵,用来表示控制向量u对状态向量x的线性作用。
而系统的二次型性能指标为:
| $J = \frac{1}{2}\int_0^{\rm T} {({x^{\rm{T}}}{{Q}x} + {u^{\rm{T}}}{{R}u}){\rm{d}}t} \text{。}$ | (5) |
式中:Q为对状态向量的加权矩阵,是半正定对称矩阵;R为对控制向量的加权矩阵,是正定对称矩阵。这 2 个量决定了系统误差与控制能量消耗之间的相对重要性。
现需寻求一状态反馈控制律:
为使J最小,由最小值原理得到最优控制为:
| $u(t) = - {R^{{\rm{ - 1}}}}BPx(t),$ | (6) |
其中P为代数矩阵Riccati方程的解。
| ${\rm{0}} = PA + {A^{\rm T}}P - PB{R^{ - 1}}{B^{\rm T}}P + Q\text{,}$ | (7) |
综上,最优反馈系数矩阵K为:
| ${{K}} = {{{R}}^{ - 1}}{{BP}}\text{。}$ | (8) |
在控制器设计之前,选取合适的状态加权矩阵Q与控制加权矩阵R至关重要。一般来说,把Q中某个加权系数增大,则对应的状态变量会收敛得更快一些,R中某个加权系数增大则对应的控制量会小一些。Bryson[6]提出了一种对角加权矩阵的选取方法,即,如果每一个状态与控制变量都有对应的预期最大量
| ${Q_{ii}} = \frac{1}{{{x_i}{\rm{ma}}{{\rm{x}}^{\rm{2}}}}}\;\;{R_{ii}} = \frac{1}{{{u_i}{{\max }^2}}}\text{。}$ | (9) |
极点配置[7 – 8]控制法是通过比例环节的反馈把定常线性系统的极点移置到预定位置的一种控制方法。极点配置的实质是用比例反馈去改变原系统的运动模式,以满足设计规定的性能要求。
对于状态方程
| $u(t) = - Kx(t)\text{。}$ | (10) |
为了获取船舶的水动力导数,本文基于计算流体力学(CFD)技术并开发了混合动网格技术,对限宽水域中的平面运动机构(PMM)试验进行数值模拟,从而获取不同岸壁距离下KVLCC2的水动力导数。刘晗等[9 – 10]将上述数值计算结果与循环水槽PMM试验结果进行对比,两者相似程度较高,表明本文所用数值计算水动力系数具有较好的精度。
本文选用 4 种岸壁距离下KVLCC2的水动力导数,岸壁距离分别为:d/L=0.25,d/L=0.35,d/L=0.50,d/L=1.20。图2给出了岸吸力与矩随岸壁距离变化的试验结果。可以看到,随着岸壁距离的增加,岸吸力与力矩快速下降。

|
图 2 岸吸力与岸吸力矩 Fig. 2 Bank suction force and moment |
设系统的状态向量为
| $\begin{split}\left[ {\begin{array}{*{20}{l}}{\dot v}\\{\dot r}\\{\dot \psi }\\{\dot y}\end{array}} \right] = & \left[ {\begin{array}{*{20}{c}}{ - {{{M}}^{ - 1}}{{N}}}&{\begin{array}{*{20}{c}}\;\;0&\;0\\\;\;0&\;0\end{array}}\\{\begin{array}{*{20}{c}}{\rm{0}}&{\rm{1}}\\{\rm{1}}&{\rm{0}}\end{array}}&{\begin{array}{*{20}{c}}0&0\\{{U_1}}&0\end{array}}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}v\\r\\\psi \\y\end{array}} \right] +\\[3pt] & {{{M}}^{ - 1}} {{{{F}}_R}{{{F}}_S}} \left[ {\begin{array}{*{20}{l}}{{\delta _R}}\\{{\delta _u}}\end{array}} \right] + {{{M}}^{ - 1}} {{{\rm{F}}_S}} \text{,}\end{split}$ | (13) |
其中:
| ${{M}} = \left[ \begin{array}{l} - {Y_{\dot v}} + \Delta \\ - {N_{\dot v}} + \Delta {x_g}\end{array} \right.\left. \begin{array}{l} - {Y_{\dot r}} + \Delta {x_g}\\ - {N_{\dot r}} + {I_z}\end{array} \right]\text{,}$ | (14) |
| ${{N}} = \left[ \begin{array}{l} - {Y_v}\\ - {N_v} - {Y_{\dot v}}\end{array} \right.\left. \begin{array}{l} - {Y_r} + \Delta \\ - {N_r} + (\Delta - {Y_{\dot r}})\end{array} \right]\text{,}$ | (15) |
| ${{{F}}_R} = \left[ \begin{array}{l} - {Y_{{\delta _R}}}\\ - {N_{{\delta _R}}}\end{array} \right]\text{,}$ | (16) |
| ${{{F}}_{\rm{S}}} = \left[ \begin{array}{l}{Y_S}\\{N_S}\end{array} \right]\text{。}$ | (17) |
当船舶航行于限制水域中,LQR控制器将产生一个稳定的舵角来抵消岸吸力与岸吸力矩。但当船舶达到稳定状态时,船舶已经与原始航迹产生了偏移。为了消除这一稳态漂移偏差,将在状态空间方程中加入一个状态变量yi,
| ${y_i} = \int_0^t {{\rm{y(}}\tau {\rm{)d}}\tau }\text{,} $ | (18) |
则状态空间方程为:
| $\begin{split}\left[ {\begin{array}{*{20}{l}}{\dot v}\\{\dot r}\\{\dot \psi }\\{\dot y}\\{{{\dot y}_i}}\end{array}} \right] = & \left[ {\begin{array}{*{20}{c}}{ - {{{M}}^{ - 1}}{{N}}}&{\begin{array}{*{20}{c}}\;\;{\rm{0}}\;\,\,&{\rm{0}}\;&{\rm{0}}\\\;\;{\rm{0}}\;\,\,&0&0\end{array}}\\{\begin{array}{*{20}{c}}0&1\\1&0\\0&0\end{array}}&{\begin{array}{*{20}{c}}0&0&0\\{{{\rm{U}}_{\rm{1}}}}&{\rm{0}}&{\rm{0}}\\{\rm{0}}&{\rm{1}}&{\rm{0}}\end{array}}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}v\\r\\\psi \\y\\{{y_i}}\end{array}} \right] + \\[5pt] & {{{M}}^{ - 1}} {{{{F}}_R}{{{F}}_S}} \left[ {\begin{array}{*{20}{l}}{{\delta _R}}\\{{\delta _{{u}}}}\end{array}} \right] + {{{M}}^{ - 1}} {{{{F}}_S}} \text{。}\end{split}$ |
为了展现积分反馈对于控制效果的影响,本文对有稳态误差项方程和无稳态误差项方程分别进行了LQR控制仿真模拟,结果如图3所示。可以看出,无积分反馈项的方程只能保证航向控制,而有积分反馈项的方程可以同时保证航向与航迹的控制。

|
图 3 关于积分反馈的控制对比(d/L=0.25) Fig. 3 Integral feedback control history comparison(d/L=0.25) |
本文分别对不同岸壁距离下船舶控制进行了模拟,岸壁距离分别选取了 4 种情况:d/L=0.25,d/L=0.35,d/L=0.50,d/L=1.20。
|
|
表 1 状态变量与控制变量最大期望值 Tab.1 Maximum desired state and control variables |
为了验证LQR控制较极点配置控制的优越性,本文分别利用这2种控制方法对岸壁距离d/L=0.25工况下的船舶运动控制进行了仿真。对于极点配置控制,主导极点的选取对控制效果的影响至关重要,它将决定系统的阻尼特性与稳定性,本文最终选定的极点为–1.1,–0.85,–0.35,–0.08+0.096*j,–0.08–0.096*j。
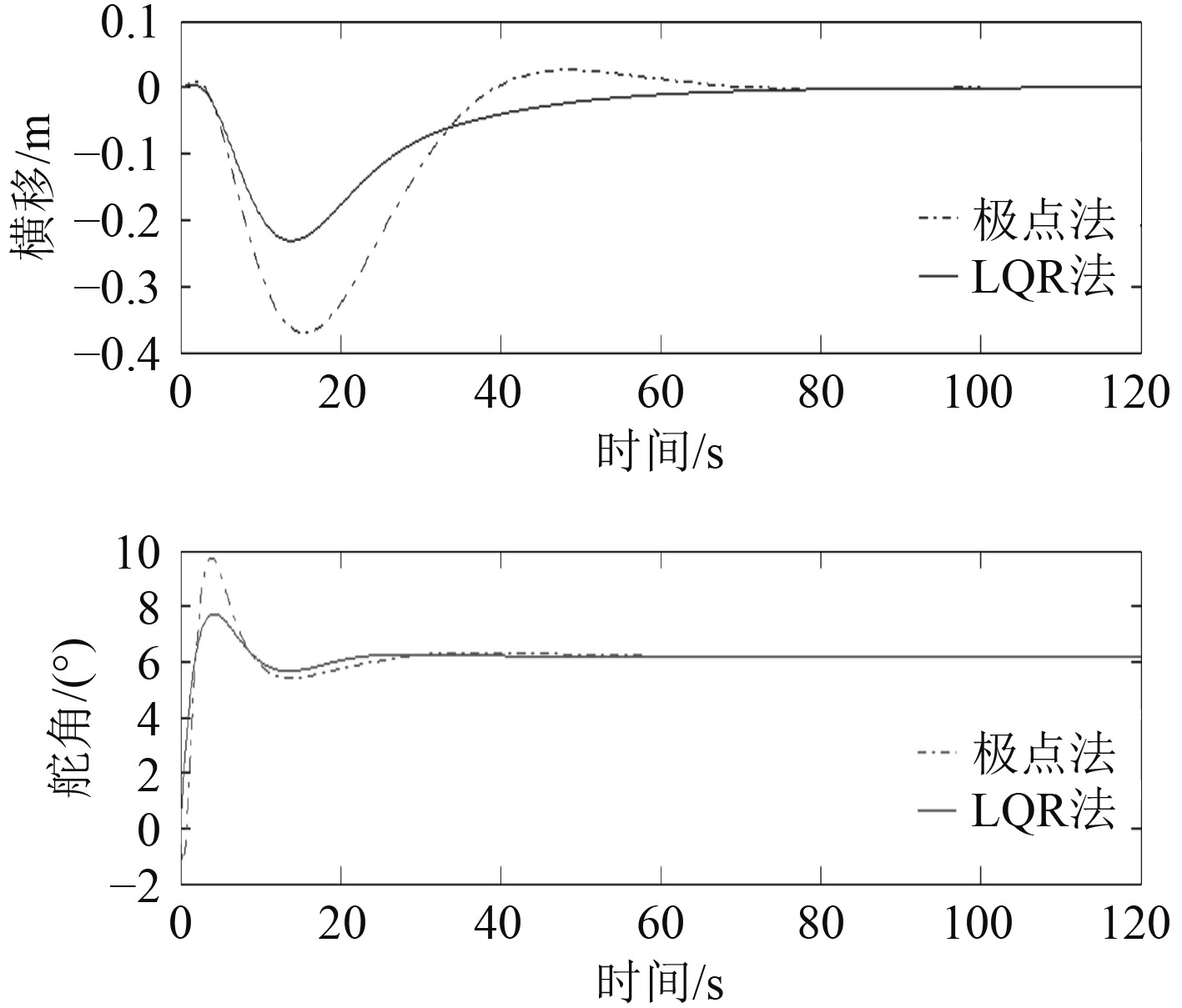
|
图 4 不同控制方法的比较(d/L=0.25) Fig. 4 Comparison of different control designs |
由图4仿真结果可看出,对于船舶横移的控制,LQR控制器相较于极点配置输出明显较小的最大横移偏差,且回复至原有航迹更趋平缓;对于输入舵角,均符合物理现实,但极点配置控制的舵角显示了较大的振荡,而LQR控制器的舵角输入更趋平缓,操舵的执行性更好。综上,相较极点配置控制,LQR控制器具有较好的鲁棒稳定性,显现了LQR控制器的的有效性和优越性。
5.2 LQR控制结果分析图5展现了不同岸壁距离下LQR控制仿真结果。结果表明,当岸壁距离d/L>1.2时,船舶趋于稳定时,基本没有发生横移,且舵角基本上保持为 0,船舶基本不受岸壁效应的影响,控制幅度极小;随着岸壁距离的逐渐减小,船舶最后的稳定舵角与降速也越来越大,当岸壁距离d/L=0.25时,舵角将超过6°,速度下降幅度超过前进速度的10%,岸壁效应明显。
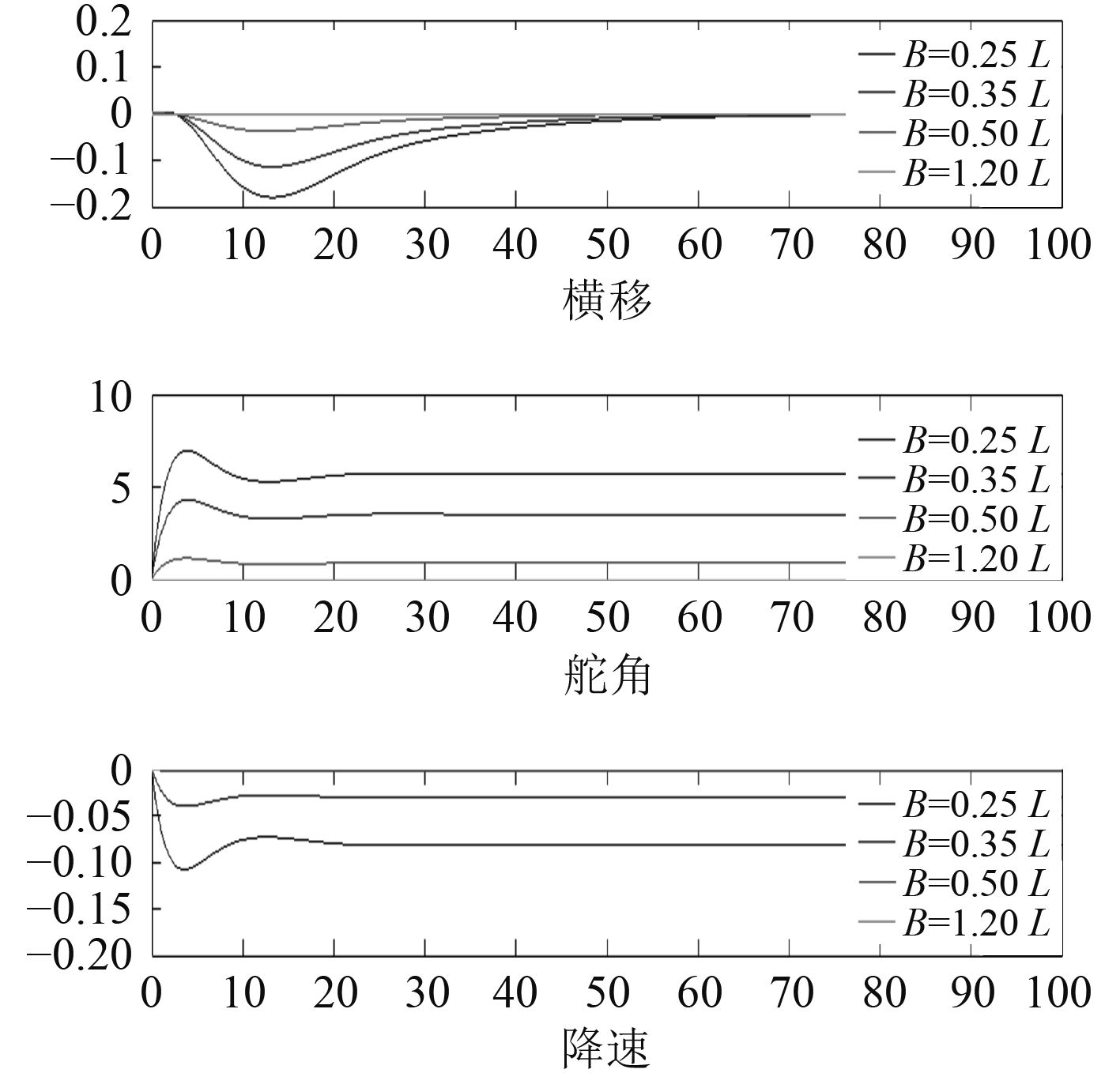
|
图 5 不同岸壁距离下LQR的控制 Fig. 5 LQR Control Histories For Various d/L |
本文基于线性状态空间形式的船舶操纵运动方程,根据最优控制理论,设计了LQR控制器并对不同宽度水域中船舶运动进行了控制模拟,并与极点配置控制法作比较,结果验证了LQR控制器的有效性和优越性。研究结果表明,随着船舶逐渐靠近岸壁,船舶所受横向力与首摇力矩将变大,使用本文设计的LQR控制器通过摆舵与降速可有效矫正与控制船舶运动轨迹,达到最优控制的目的。
| [1] | 张显库. 船舶运动控制[M]. 北京: 国防工业出版社, 2006. |
| [2] | 王先洲. 船舶及潜艇操纵中的鲁棒控制研究[D]. 武汉: 华中科技大学, 2006. |
| [3] | 李铁山, 杨盐生, 洪碧光, 等. 船舶航迹控制鲁棒自适应模糊设计[J]. 控制理论与应用, 2007, 24 (03): 445–448. |
| [4] | MUCHA P, MOCTAR O E. Ship-bank interaction of a large tanker and related control problems[C]// ASME 2013, International Conference on Ocean, Offshore and Arctic Engineering. 2013: V005T06A072. |
| [5] | THOMAS B S, SCLAVOUNOS P D. Optimal-control theory applied to ship maneuvering in restricted waters[J]. Journal of Engineering Mathematics, 2007, 58 (1-4): 301–315. DOI: 10.1007/s10665-006-9130-6 |
| [6] | BRYSON A E, HO Y C, SIOURIS G M. Applied optimal control: optimization, estimation, and control[M]. distributed by Halsted Press, 1975. |
| [7] | CHILALI M, GAHINET P, APKARIAN P. Robust Pole Placement in LMI Regions[J]. IEEE Transactions on Automatic Control, 2000, 2 (12): 2257–2270. |
| [8] | KAUTSKY J, NICHOLS N K, DOOREN P V. Robust Pole Assignment in Linear State Feedback[J]. International Journal of Control, 1985, 41 (5): 1129–1155. DOI: 10.1080/0020718508961188 |
| [9] | LIU H, MA N, GU X. Maneuvering prediction of a VLCC model based on CFD simulation for PMM tests by using a circulating water channel[C]// ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, 2015. |
| [10] | LIU H, MA N, SHAO Chuang. Numerical Simulation of Planar Motion Mechanism Test and Hydrodynamic Derivatives of a ship in Laterally Restricted Water[J]. Journal of Shanghai Jiao Tong University, 2016, 50 (01): 115–122. |
 2017, Vol. 39
2017, Vol. 39
