2. 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 中国船舶及海洋工程设计研究院,上海 200001
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
3. Marine Design and Research Institute of China, Shanghai 200001, China
众所周知,对结构物振动声辐射的研究有着重要的现实意义。具体到船舶行业而言,在军用领域,降低舰船及潜艇的结构振动辐射噪声,特别是远场噪声能够显著地提高其隐蔽性;在民用领域,出于保护海洋生态环境的考虑,国际海事组织海洋环境保护委员会也开始使用非强制性的“减少商船水下辐射噪声导则”,以减少船舶水下辐射噪声对海洋生物的不利影响。可见,对于船舶外部噪声的研究有相当的必要性。
船舶在水下的辐射声场有近场和远场之分,其中,远场声场因作用范围广,具有更加重要的研究意义。在文献[1]中,对于远场声场的标准有着明确的定义:1)声压按照球面波的规律衰减,即与距离成反比关系;2)在以声源为球心的球面上,声压和角度不相关;3)声特性阻抗等于平面波的特性阻抗,即流体密度和流体中声速的乘积。由这一定义可见,对于船舶这样表面速度相位关系复杂的结构,其声学远场只能存在距离声源足够远处。
对于舰艇外壳表面远场声辐射热区的识别有助于为后续的降噪工作指明方向。传统上,常使用有功声强作为振动结构声辐射热区的标识,声强大的地方意味着对辐射声功率的贡献也大。但是,当结构处于吻合频率之下时,由声强标示的能量流并不能真正地把声能量带到远处,而是在振动结构表面进出循环[2],此时,这一部分能量流对结构声辐射热区的定位造成干扰。特别是,对于舰船外壳这类处于水下的薄壳结构,其吻合频率比处于空气中更高,这意味着在更宽的频段内,循环于振动结构表面的能量流一直存在,此时使用常规的有功声强方法进行远场声辐射热区的识别不准确。
振动结构表面附近的声能量传播途径非常复杂,这种复杂性源于声学量之间的相位关系[3],更根本地说是来源自于振动结构本身阻尼导致的表面不同位置之间速度的相位差。在文献[3-5]中,姜哲等对近场声强进行了详细分析研究并明确指出近场中局部声源表面会吸收声场中的能量,这是出现负声强的原因之一,另外,产生负声强的振源为有功声强的有旋分量。鉴于近场声强的复杂性,在对振动结构表面的远场声辐射热区进行定位时,必须使用一定的方法过滤掉循环于振动结构表面的能量流。为实现这一目标,Earl G.Williams最早提出超声速声强的概念[6],通过在波数域中对声场中的倏逝波成分进行过滤得到只包含传播波成分的声场信息(声压和质点速度),进而得到超声速声强。在空间域中,通过把声场直接和某一过滤函数做卷积的方式也可以得到超声速声强[7]。这2种方法,前者因为使用到空间傅里叶变换,必须要求振动结构的几何形状在某一坐标系下可分离,而后者需要进行一次二维卷积计算,计算量远大于进行空间傅里叶变换,对于大型问题并不适用。总而言之,这2种方法在工程应用中存在不足。针对第1种方法的不足,可获得任意形状结构的超声速声强的方法被提出来[8, 9]。该方法基于在振动结构表面离散赫姆霍兹积分方程得到的声辐射阻抗矩阵,对其进行奇异值分解,小的奇异值所对应的振动结构表面速度分布模式对辐射声功率的贡献也小[10]。在实际操作中可以认为这部分速度分布模式产生的是倏逝波,而其他速度分布模式产生的是传播波[11],使用其他速度分布模式就可以计算振动结构的超声速声强,但是,这种方法存在一个 “小”的标准选定问题,即多小的奇异值才算小。并且,即使是最小的奇异值,其所对应的振动结构表面速度分布模式所产生的声场也不完全是倏逝波。Steffen Marburg和Eric Losche等在2013年提出声辐射表面贡献方法[12]。该方法首先设定一个在振动结构表面恒为正的值,之后通过声辐射阻抗和振动结构表面节点法向速度等已知量构造出该值的表达形式,从而完美地避开了奇异值分解方法中筛除较小奇异值的问题。本文将使用这一方法,对一双层环肋耐压壳的远场声辐射进行分析。
1 基本理论本文是基于表面贡献方法进行远场声辐射热区识别,其推导过程利用了边界元方法计算过程产生的声辐射阻抗矩阵。
1.1 任意形状结构外辐射问题的声功率计算[12]结构的辐射声功率W可由结构表面声压p和表面法向振速vn表示为:
| $W = \frac{1}{2}\int_s {{\rm{Re}}\left( {pv_n^{\rm{*}}} \right){\rm{d}}S} ,$ | (1) |
式中:S为结构表面;
| ${Hp} = {G}{{v}_n},$ | (2) |
式中:H和G为系数矩阵,其元素只和结构表面的形状、声音频率及传声介质的属性有关,和结构自身属性无关。p和vn为节点声压和法向速度向量。
把结构表面进行离散之后,每一个单元上的声压值和法向速度值可通过单元插值函数和单元节点值表示为
| $W = \frac{1}{2}{\rm{Re}}\left( {{v}_n^H{Zv}_n^{\rm{*}}} \right) = \frac{1}{2}{v}_n^H{{Z}_R}{v}_n^{\rm{*}},$ | (3) |
式中:
| ${A} = \int_S {{\varPhi ^{\rm{T}}}\varPhi {\rm{d}}S} ,$ | (4) |
声功率表面贡献是一个正值,设为η,通过对其在结构表面进行积分可以得到辐射声功率,即
| $W = \frac{1}{2}\mathop \int_S^{} {\rm{\eta }}\left( {x,y,z} \right){\rm{d}}S\left( {x,y,z} \right)\text{。}$ | (5) |
η的单位是W/m2,假设可以把
| ${\rm{\eta }}\left( {{x_{{k}}},{y_{{k}}},{z_{{k}}}} \right) = {\rm{\beta }}\left( {{x_{{k}}},{y_{{k}}},{z_{{k}}}} \right){{\rm{\beta }}^{\rm{*}}}\left( {{x_{{k}}},{y_{{k}}},{z_{{k}}}} \right), $ | (6) |
| $W = \frac{1}{2}\mathop \int_S^{} {\rm{\beta }}\left( {{x_{{k}}},{y_{{k}}},{z_{{k}}}} \right){{\rm{\beta }}^{\rm{*}}}\left( {{x_{{k}}},{y_{{k}}},{z_{{k}}}} \right){\rm{d}}S\left( {x,y,z} \right)\text{。}$ | (7) |
对上式在边界面上进行离散并把
| $W = \frac{1}{2}\mathop \int_S^{} {{\beta }^{\rm{T}}}{{\varPhi }^{\rm{T}}}{\varPhi }{{\beta }^{\rm{*}}}{\rm{d}}S = \frac{1}{2}{{\beta }^{\rm{T}}}{A}{{\beta }^{\rm{*}}}\text{。}$ | (8) |
对于任意的复数
| ${ {Z_R}\varPsi} = \lambda { A{\bf \varPsi}} \text{。}$ | (9) |
记特征值矩阵和特征向量矩阵分别为Λ和Ψ,则
| ${{\varPsi }^{\rm{T}}}{A\varPsi } = {I}, $ | (10) |
| ${{ \varPsi }^{\rm{T}}}{ {Z_R}\varPsi} = { \varLambda },$ | (11) |
式中,I为单位阵。
结构表面的速度分布模式可以用声辐射模态叠加得到:
| ${ {v}_n} = { {\varPsi \xi }}$ | (12) |
ξ为声辐射模态贡献因子向量。式(12)左乘ΨA并由式(10)进行化简得到
| ${\xi } = {{\varPsi }^{\rm{T}}}{A}{{v}_n}\text{。}$ | (13) |
将式(12)代入式(3)并由式(11)得到
| ${ W} = \frac{1}{2}{{{\xi }} ^{\rm{T}}}{ \varLambda} {{\xi } ^{\rm{*}}} = \frac{1}{2}{{\xi } ^{\rm{T}}}\sqrt{ \varLambda} \sqrt { \varLambda} {{\xi } ^{\rm{*}}},$ | (14) |
再次应用到式(10),式(14)可以表示为:
| ${ W} = \frac{1}{2}{{\xi } ^{\rm{T}}}{ \varLambda} {{\xi } ^{\rm{*}}} = \frac{1}{2}{{\xi } ^{\rm{T}}}\sqrt { \varLambda} {{ \varPsi} ^{\rm{T}}}A{ \varPsi} \sqrt { \varLambda} {{\xi } ^{\rm{*}}}\text{。}$ | (15) |
与式(8)对比可知
| $\beta = { \varPsi} \sqrt { \varLambda} {\rm{ }}{\xi } = {\rm{ }}{ \varPsi} \sqrt { \varLambda} {{ \varPsi} ^{\rm{T}}}{ A{{ v_n}}}\text{。}$ | (16) |
这时通过式(16)和式(6)就可以计算出声功率的表面贡献值向量η。
2 数值计算 2.1 程序验证本文首先从开源边界元程序中提取出声辐射阻抗矩阵,即是式(2)中的H和G矩阵,然后按照声辐射表面贡献方法使用Matlab语言编写程序,为了验算程序的正确性,以下分别以脉动球源模型和处于无限障板中的平板模型进行验证。对于脉动球源,其辐射声功率存在理论解,通过把式(5)的数值结果同理论解作比较就可验证声辐射表面贡献方法计算声功率的准确度。此处使用的脉动球源的半径是1 m,表面法向振速为1 m/s,球面分成2 400个四边形单元和2 402个节点。辐射声功率的计算结果如表1所示,可见程序计算的结果和理论解非常接近,可以证明程序的正确性。
|
|
表 1 脉动球源辐射声功率的理论解和数值解 Tab.1 The theoretical solution and numerical solution of radiated sound power of a pulsating ball |
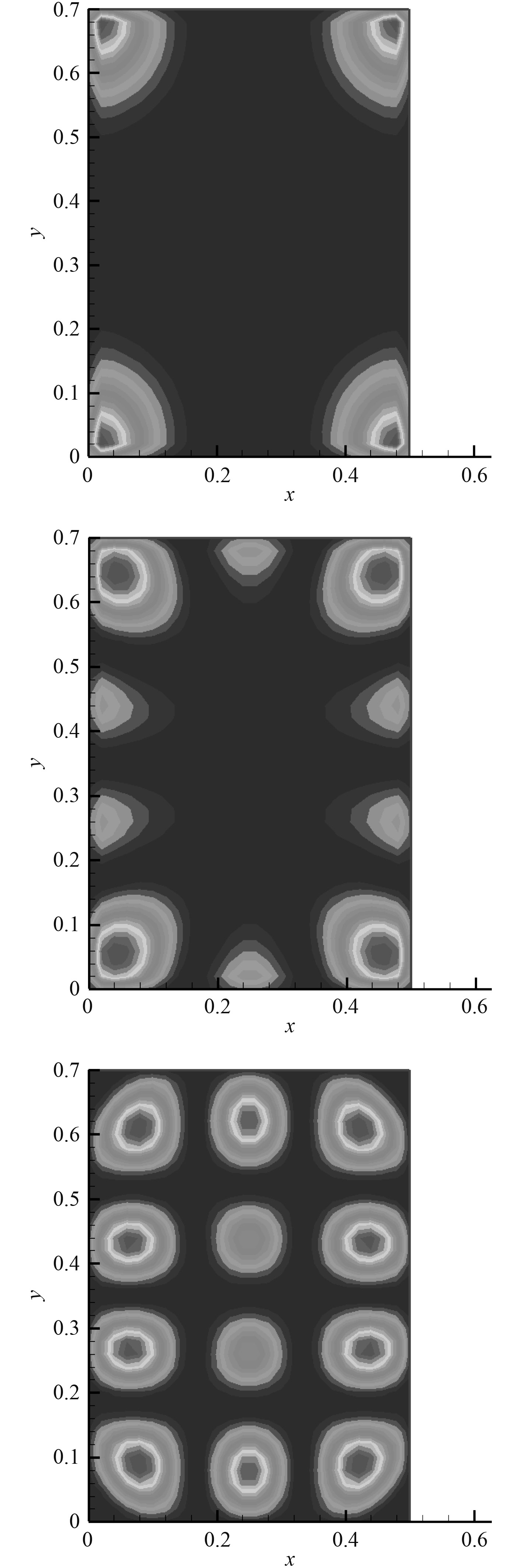
平板的远场声辐射图像和平板的振动频率有关,假设平板的表面以某一速度分布模式进行振动,那么,平板的远场声辐射图像将随着平板振动频率的增加呈现从角辐射模式到边辐射模式到面辐射模式的转化[13],以下是一块边长为0.7 m×0.5 m的平板的2×2阶速度分布模式在80 Hz、200 Hz、500 Hz时的远场声辐射表面贡献图像,可见符合预期。
|
图 1 由表面贡献方法标示的平板声辐射热区 Fig. 1 Sound radiation hot spot of a flat plate marked by surface contribution method |
本文计算的模型是1艘300 t巡逻艇,其主要尺寸和有限元模型分别如表2和图2所示。整船有限元模型在Nastran软件中建造完成,共有使用CQUAR4和CTRIA3单元29 710个,这是考虑了面内拉伸和弯曲刚度的等参板单元,每个节点有3个转动自由度和3个平动自由度。使用CBEAM单元22 103个,该类单元考虑了梁中的弯矩、剪力、轴向力及扭矩。
|
|
表 2 300 t巡逻艇主尺寸表 Tab.2 The main size chart of the 300 ton patrol ship |

|
图 2 整船有限元模型 Fig. 2 Finite element model of whole ship |
这一部分首先计算整船在主机激振力作用下的振动响应,从而得到船壳表面的响应速度,进而使用边界元方法求取船壳表面的声强。对于船壳在远场的声辐射热区,则使用声能量表面贡献方法进行求取。

|
图 3 10 Hz频率处船壳表面声强和远场声辐射热区 Fig. 3 Surface sound intensity and far field sound radiation hot spot at 10 Hz |

|
图 4 46 Hz频率处船壳表面声强和远场声辐射热区 Fig. 4 Surface sound intensity and far field sound radiation hot spot at 46 Hz |
|
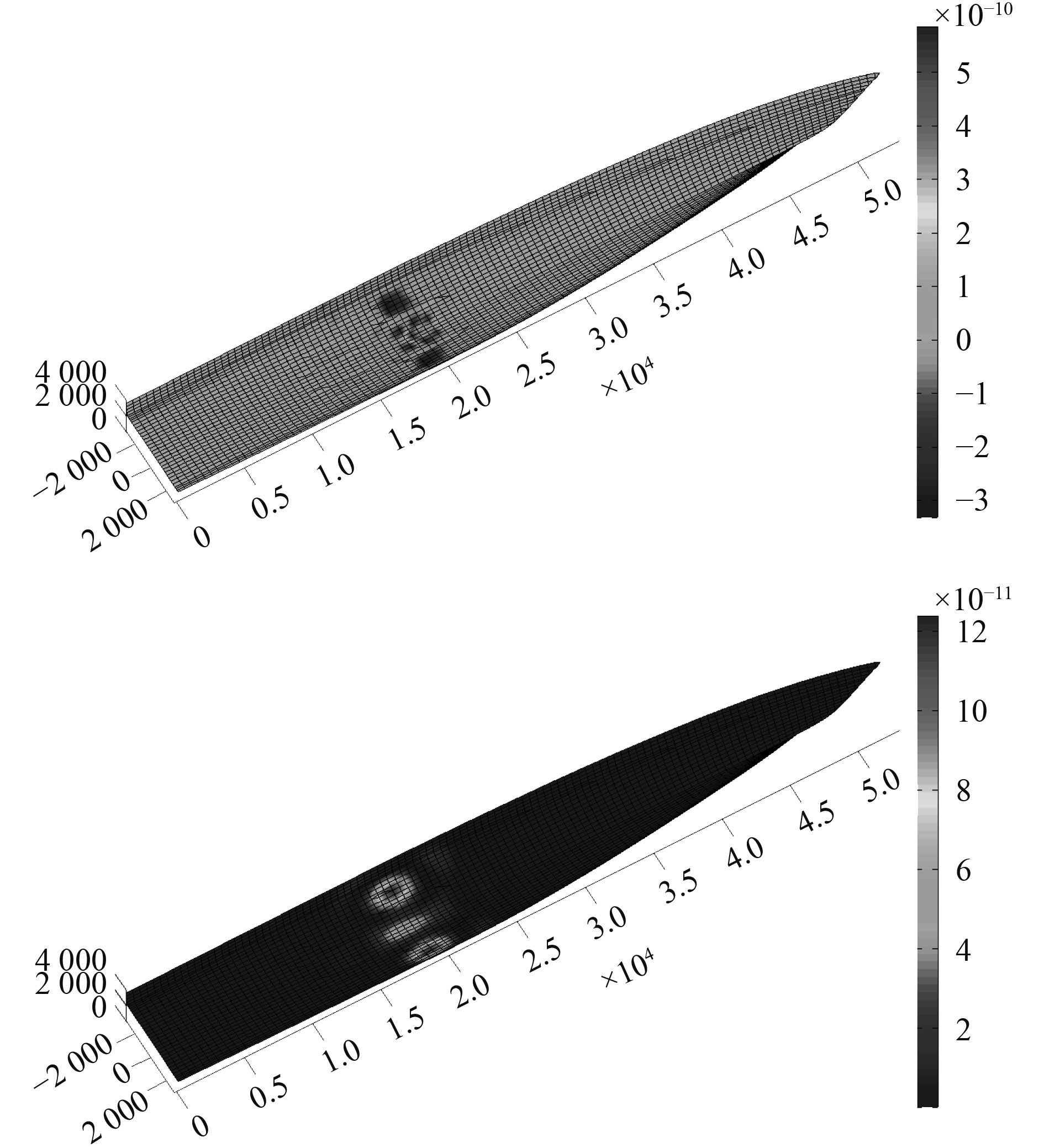
图 5 300 Hz频率处船壳表面声强和远场声辐射热区 Fig. 5 Surface sound intensity and far field sound radiation hot spot at 300 Hz |
图3,图4和图5是分别在10 Hz、46 Hz和300 Hz处表面贡献方法标示的船壳表面声辐射热区,由这些图可见声能量表面贡献方法都准确地把机舱下部标示为声辐射热区。由图4的表面声强图还可以看到,表面声强有正有负,代表了近场声场和结构的能量交换,由包含这一能量流的表面声强所标示的声辐射也弥散于船壳首部至尾部多个区域。而表面贡献图则是统一的正值,数值大小表示了对应面积对声能量的贡献量。这一方法将正负声强进行抵消,只留下对声能量的净贡献,标示的声辐射热区也更为集中。
3 结 语本文使用声能量的表面贡献方法对300 t巡逻艇的远场声辐射热区进行识别,识别结果表明这一方法可以对振动结构表面的正负声强进行抵消,只留下结构表面对声能量的净贡献,并能对这一净贡献进行量化。相比于表面声强,声能量的表面贡献方法能够标示振动结构表面对远场声场有贡献的区域,为后续的降噪工作提供帮助。
| [1] | JUNGER M C, FEIT D. Sound, structures, and their interaction (2nd edition)[M]. Cambridge Ma Mit Press P, 1986, -1(4). |
| [2] | WILLIAMS E G. Supersonic acoustic intensity on planar sources[J]. Acoustical Society of America Journal, 1998, 104 (5): 2845–2850. DOI: 10.1121/1.423868 |
| [3] | 姜哲, 郭骅. 声强的有旋性与表面声强[J]. 声学学报, 1991 (5): 330–337. |
| [4] | 姜哲, 郭骅. 声场中负声强探讨[J]. 声学学报, 1992 (2): 122–128. |
| [5] | 姜哲. 声场中声能量与传递[J]. 振动工程学报, 1999 (1): 126–132. |
| [6] | WILLIAMS E G. Supersonic acoustic intensity[J]. Journal of the Acoustical Society of America, 1995, 97 (1): 121–127. DOI: 10.1121/1.412991 |
| [7] | FERNANDEZGRANDE E, JACOBSEN F, LECLÈRE Q. Direct formulation of the supersonic acoustic intensity in space domain[J]. Journal of the Acoustical Society of America, 2012, 131 (1): 186–93. DOI: 10.1121/1.3662052 |
| [8] | MAGALHÃES M B S, TENENBAUM R A. Supersonic Acoustic Intensity for Arbitrarily Shaped Sources[J]. Acta Acustica United with Acustica, 2006, 92 (2): 189–201. |
| [9] | JUNIOR C A C, TENENBAUM R A. Useful intensity: A technique to identify radiating region on arbitrarily shaped surfaces[J]. Journal of Sound & Vibration, 2013, 332 (6): 1567–1584. |
| [10] | BORGIOTTI G V. The power radiated by a vibrating body in an acoustic fluid and its determination from boundary measurements[J]. Journal of the Acoustical Society of America, 1990, 88 (4): 1884–1893. DOI: 10.1121/1.400211 |
| [11] | PHOTIADIS D M. The relationship of singular value decomposition to wave‐vector filtering in sound radiation problems[J]. Journal of the Acoustical Society of America, 1990, 88 (88): 1152–1159. |
| [12] | MARBURG S, LÖSCHE E, PETERS H, et al. Surface contributions to radiated sound power[J]. Journal of the Acoustical Society of America, 2013, 133 (6): 3700–3705. DOI: 10.1121/1.4802741 |
| [13] | MAIDANIK G. Response of Ribbed Panels to Reverberant Acoustic Fields[J]. Journal of the Acoustical Society of America, 1962, 34 (6): 809–826. DOI: 10.1121/1.1918200 |
 2017, Vol. 39
2017, Vol. 39
