0 引　言

小水线面双体船（small waterplane area twin hull，SWATH）是一种综合性能优良的船型，其应用前景广阔。由于小水线面双体船设计变量较多，变量间交互影响较为敏感，在其设计过程中需要采用仿真方法以缩短设计周期、提高效率。然而，采用计算流体力学或有限元分析等方法，通过计算机代码实现对真实系统仿真模型的求解和优化设计，需要付出昂贵的计算代价^[1]。为了解决这个问题，工程设计人员经常使用近似模型来代替仿真模型^[2]。宋磊等^[3]使用拉丁方实验设计选取样本点并建立Kriging模型用于型线优化设计，有效降低了潜器阻力。常海超等^[4]将Kriging模型应用于船型优化，并验证其实用性和有效性。苟鹏等^[5]将Kriging模型应用于深潜器多球交接耐压壳的结构优化中。

以上学者研究了单一近似模型在船舶工程中的应用，针对不同优化问题或不同性质的响应，各种近似模型的预测能力表现各异，为避免在数据样本点不足的情况下，选择不恰当的近似模型，组合近似模型的核心思想是通过一定的方式组合单一近似模型以充分利用各种模型的优点^[6]。本文提出构建SWATH阻力组合近似模型实现对小水线面双体船因受海浪冲击产生的最大结构应力的预测。

1 单一近似模型技术 1.1 Kriging模型

本文采用Kriging模型构建全局近似模型。在Kriging模型中，一个确定的输出y（x）看作一个随机过程Y（x）的实现^{[7, 8]}：

$Y(x) = \mu + z(x),$

(4)

式中：μ为一个常量；z（x）被假设为一个0平均值的随机过程。Lewis等^[7]和许辉等^[8]详细介绍了Kriging模型。

1.2 径向基函数模型

给定n个样本点 ${{X}_{D1}},{{X}_{D2}},...,{{X}_{Dn}}$ 及其响应y_d= $ [{y_{D1}},{y_{D2}},...,{y_{Dn}}]$ ，径向基函数（RBF）插值可以表示为：

$\hat y({x}) = p({x}) + \sum\limits_{i = 1}^n {{\lambda _i}} \phi (d({x},{{x}_{Di}})),$

(5)

其中p（x）为一个多项式模型；d为欧式距离；φ为一个有多种选择的基函数，如线性函数、立方函数、薄板样条函数、multiquadric函数、高斯函数等。Powell等^[9]对RBF模型进行了详细的介绍。

1.3 支持向量回归

支持向量回归（SVR）是支持向量机（SVM）在拟合黑箱问题时的应用。常用的SVR是ε-SVR，其目标为寻找一个函数与训练输入的样本有ε的偏差。对于线性回归的情况ε-SVR可以表示为：

$\hat f({x}) = \left\langle {{w} \cdot {x}} \right\rangle + b,$

(6)

其中 $\left\langle {{w} \cdot {x}} \right\rangle $ 是w和x间的点积，SVR的另一个目标是使得 $\hat f$ 尽可能平滑，这意味着上式中w的值需要很小，这通过解决下式中的优化问题实现：

$\begin{array}{l}\min \;\;\;\frac{1}{2}{\left| {w} \right|^2},\\s.t.\;\;\;\;{y_i} - \left\langle {{w} \cdot {{x}_i}} \right\rangle - b \leqslant \varepsilon, \\\;\;\;\;\;\;\;{\kern 1pt} \left\langle {{w} \cdot {{x}_i}} \right\rangle + b - {y_i} \leqslant \varepsilon {\text{。}}\end{array}$

(7)

Zhou等^[10]详细介绍了SVR模型的构建。

2 组合近似模型理论

针对不同优化问题或不同性质的响应，各种近似模型的预测能力表现各异，为避免在数据样本点不足的情况下，选择不恰当的近似模型，组合近似模型的核心思想是通过一定的方式组合单一近似模型以充分利用各个模型的优点。组合元模型中的关键环节是权系数的计算方法，目前文献中组合元模型中权系数的选择方法主要分成以下几种：1）通过预估方差选择权系数。如Zerpa等^[11]提出一种用PRS，Kriging和RBF的权重和的组合模型，该模型的权系数由每个模型方差的倒数分别求得。2）通过最小化组合后模型的交叉验误差选择权系数，通常选用交叉验证均方差（GMSE）或预估误差平方和（PRESS）这2个指标进行计算。如Goel等^[12]对反比例平均化法（EI法）进行修正，提出启发式计算方法（EG法），使用不同变量分别控制GMSE的均值和各模型的GMSE重要程度。3）通过最小化均方误差（MSE）（或均方根误差（RMSE））来选择权系数。Acar等^[13]提出通过最小化验证点处RMSE计算权系数。

最常用的构建组合近似模型的方法是由多重近似模型加权线性叠加构成。本文研究由Kriging模型、RBF模型和支持向量回归模型构成的组合近似模型，其可以表示为：

${\hat f_{en}}({x}) = \sum\limits_{j = 1}^3 {{w_j}{{\hat f}_j}({x})}, $

(8)

式中： ${\hat f_{en}}({x})$ 为组合近似模型的响应值；w_j和 ${\hat f_j}({x})$ 分别为第j个模型的权重系数和相应预测值，且 $\sum\limits_{j = 1}^3 {{w_j} = 1} $ 。这类组和近似模型的关键是权重系数的计算。本文采用最小化留一法（LOO）交叉验证均方差（GMSE_LOO）的方法，GMSE_LOO可通过下式计算：

$GMS{E_{LOO}} = \sum\limits_{i = 1}^m {{{\left( {{{\widehat f}_{en, - i}}({x_i}) - f({x_i})} \right)}^2}} /m,$

(9)

其中f（x_i）为点x_i处的真实值， ${\widehat f_{en, - i}}({x_i})$ 为x_i处组合近似模型的预测值。m是样本点数量。则权重系数的求解可以转换为以下优化问题：

$\begin{array}{l}find\;\;{w_j},\\\min \;\; GMS{E_{LOO}}({w_j}) = {\kern 1pt} \\\sum\limits_{i = 1}^m {{{(\sum\limits_{j = 1}^3 {{w_j}{{\widehat f}_j}({x_i})} - f({x_i}))}\!\,^2}} /m, \\{\rm s.t.}\;\;\;\sum\limits_{i = 1}^3 {{w_j}} = 1{\text{。}}\end{array}$

(10)

3 小水线面双体船应力预测 3.1 问题描述

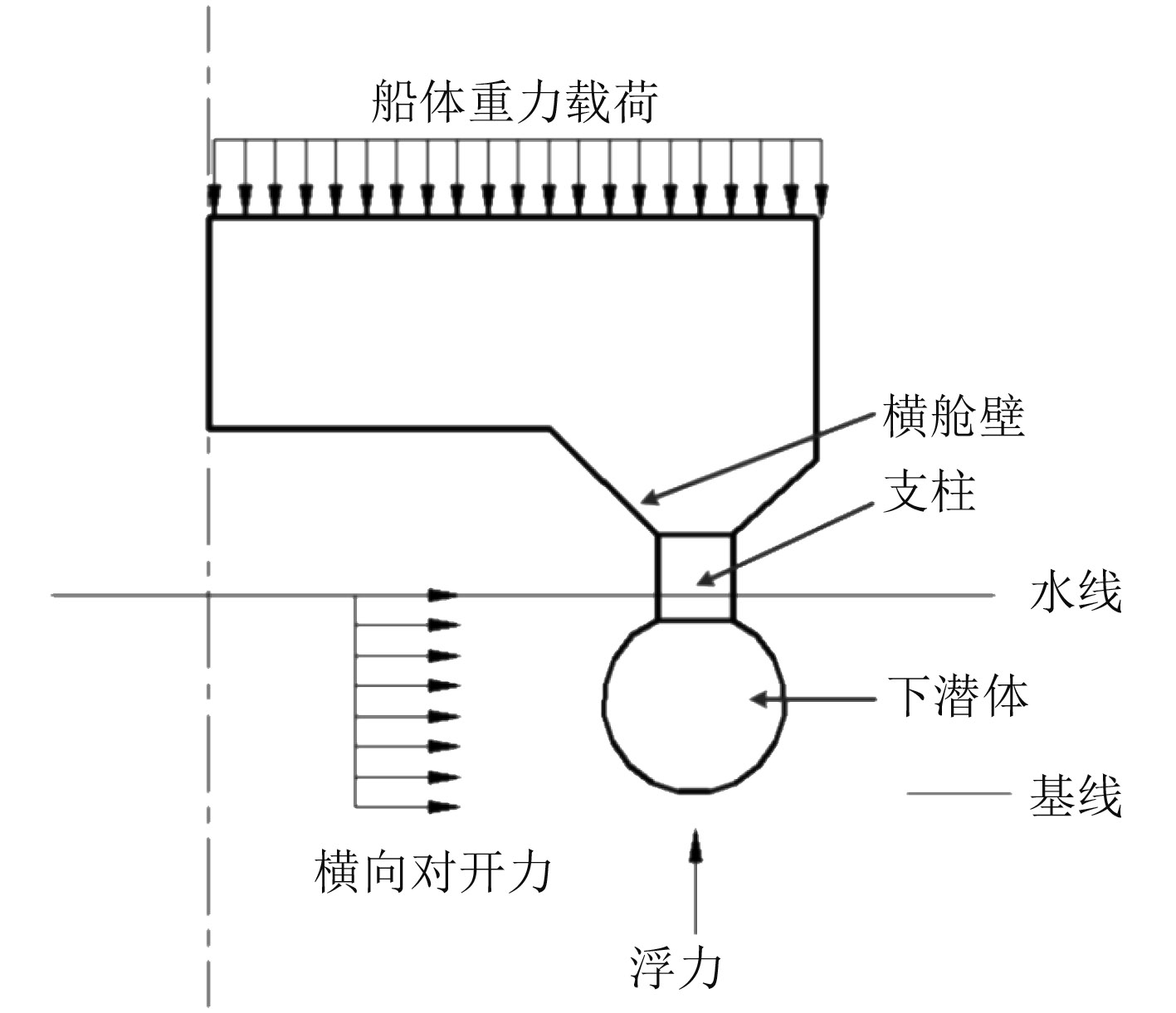
船舶会因遭受海浪冲击产生应力，应力过大时会影响到船舶航行安全。SWATH所受到的外载荷主要是波浪中受到的横向载荷，如果SWATH的结构强度不足，较大冲击会导致船体结构失效，导致安全事故。SWATH所受到的外载荷主要是波浪中所受到的横向载荷。当船体仅受横向波浪力单独作用时结构应力最大，准确预测最大应力受设计参数的影响对后续设计有重要意义。本文研究SWATH在0航速横浪情况下支柱厚度、支柱壳体厚度以及横舱壁厚度对最大应力的影响。此时SWATH受到横向对开力、浮力及船体重力载荷的作用，如图1所示。

参考中国船级社的《小水线面双体船指南》，SWATH横向波浪力设计值计算公式如下：

${F_S} = 9.81DTL\Delta, $

(11)

其中F_S为横向波浪力，∆为排水量，D与T按下式计算：

$D = 3.2376 - 0.5452\log \Delta, $

(12)

$T{\rm{ = }}1.754 \times d/{\Delta ^{1/3}}{\text{。}}$

(13)

式中d为设计吃水深度。L按下式计算：

$L = 0.75 + 0.35th(0.5{L_{sd}} - 6.0){\text{。}}$

(14)

其中 ${L_{sd}} = 3.2984 \times {I_S}/{(\Delta )^{1/3}}$ ，I_S为水线处支柱长度。本文所研究的小水线面双体船的基本参数如表1所示。

3.2 EMs在小水线面双体船应力预测中的应用

本文选取支柱厚度、支柱壳体厚度及横舱壁厚度作为设计变量，用优化拉丁设计^[14]选取15个高精度样本点分别建立3种单一近似模型和组和近似模型。设计变量范围如表2所示。

由于小水线面双体船的对称性，取其水下部分一半进行分析。仿真模型的网格数量为7 000，使用Ansys 14.0软件进行仿真运算，仿真模型及应力分布如图2所示。

为了比较单一近似模型与组合近似模型，随机选取40个高精度样本点验证模型精度，并与单精度近似建模方法进行比较。采用最大绝对误差（MAE），均方根误差（RMSE）^[15]评价近似模型精度。根据式（5）~式（7）求得的3种近似模型的权重系数如表3所示，单一近似模型与组合模型精度如表4所示。

从表3可以看出，组合近似模型的预测精度最高，表明其阻力预测与仿真情况最为接近。

4 结　语

SWATH在遭受海浪冲击时所受最大应力对其安全性能有重大影响。为了减少计算代价，避免选择不适当的近似模型对预测精度的影响，本文提出构建组合近似模型预测船体仅受横向波浪力单独作用时的最大结构应力受设计变量的影响。结果表明，组和近似模型与单一近似模型相比精度最高，能够准确预测最大结构应力，为后续设计提供了指导，具有较大的工程应用价值。