舰船科学技术  2017, Vol. 39 Issue (6): 146-149   PDF    
引用本文
蒋惠芳. 船舶保密系统的设计与实现. 舰船科学技术, 2017, 39(6): 146-149  
JIANG Hui-fang. Design and implementation of ship security system. Ship Science and Technology, 2017, 39(6): 146-149  
船舶保密系统的设计与实现
蒋惠芳    
武汉数字工程研究所，湖北 武汉 430205
收稿日期: 2017-03-08, 修回日期: 2017-03-13.
作者简介: 蒋惠芳(1967 – )，女，工程师，研究方向为计算机科学技术
摘要: 为了提高船舶通信中的信息安全性，进行船舶保密信息系统设计。提出一种基于椭圆曲线密码通信的船舶保密系统设计方法，采用二进制比特序列调制方法进行船舶保密信息传输的信息编码，根据Turbo码构造加密和解密密钥，运用椭圆曲线密码体制构造船舶保密通信的传输协议。在嵌入式Linux内核下进行加密算法加载，实现船舶保密系统优化设计。仿真测试结果表明，采用该方法进行船舶保密通信，数据的加密性较好，抗攻击和干扰能力较强，数据信息安全性得到提高。
关键词: 船舶     保密系统     加密     编码     嵌入式Linux    
Design and implementation of ship security system
JIANG Hui-fang    
Wuhan Digital Engineering Institute, Wuhan 430205, China
Abstract: In order to improve the information security of ship communication, the design of ship security information system. This paper puts forward a design method of ship security system based on elliptic curve cryptography, information encoding using binary bit sequence modulation method for ship secret information transmission, according to the structure of Turbo code encryption and decryption keys, the use of elliptic curve cryptosystem constructed for secure communication protocol. Under the embedded Linux kernel, the encryption algorithm is used to realize the optimal design of ship security system. The simulation results show that the method can be used to secure the ship communication, the data encryption is better, the ability of resisting attack and interference is strong, and the security of data information is improved.
Key words: ship     security system     encryption     encoding     embedded Linux    
0 引　言

船舶航行中需要远程通信和船舶内部之间进行通信，在船舶通信和信息交互过程中，信息安全十分重要，特别是对于军用舰船来讲，船舶的信息安全成为赢得战争的关键。研究船舶保密通信系统，对预防船舶信息泄露，提高信息安全性具有重要意义。由于船舶通信数据的开放性和自组织性，导致在船舶信息传输中容易导致信息丢失，因此船舶保密通信系统设计问题受到人们的重视[1]。

对船舶保密系统设计的核心在于加密算法的设计，典型船舶通信数据加密方法主要有混沌加密方案、线性加密方案、柯西加密方案等[2 – 3]。通过构造船舶信息传输的加密密钥和解码公钥，结合线性码、循环码、卷积码等编码方案进行密钥设计和加密协议设计，实现保密系统设计，取得了一定的加密效果。文献[4]中提出一种基于新型忆阻器混沌加密技术，应用在船舶海事图像的加密传输中。文献[5]中采用一种单向链式网络的激光混沌加密方法进行船舶信息通信保密设计，通过对应的船舶信息传输的双线性映射机制来构建船舶保密通信系统数据加密模型，在嵌入式系统中进行加密电路设计，具有较好的保密安全性能。但上述加密方法存在开销过大、抗强辐射攻击性不好的问题。

针对上述问题，本文提出一种基于椭圆曲线密码通信的船舶保密系统设计方法，采用二进制比特序列调制方法进行船舶保密信息传输的信息编码，根据Turbo码构造加密和解密密钥，实现保密系统优化设计，最后进行仿真测试分析，展示了本文方法在提高加密性能方面的优越性。

1 船舶加密算法设计1.1 船舶通信的算术编码

为了实现对船舶保密系统的优化设计，采用二进制比特序列调制方法进行船舶保密信息传输的信息编码，进行保密算法设计，构造船舶信息加密的椭圆函数描述为：

$\begin{split}\\[-12pt]& Decrypt(sk,{c^ * }){{ A}^{ - 1}}{ A} = \\[5pt]& \left( {\begin{array}{*{20}{c}}{{t_{1,1}}} & \cdots & {{t_{1,m}}}\\ \vdots & \ddots & \vdots \\{{t_{m,1}}} & \cdots & {{t_{m,m}}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{a_{1,1}}} & \cdots & {{a_{1,m}}}\\ \vdots & \ddots & \vdots \\{{a_{m,1}}} & \cdots & {{a_{m,m}}}\end{array}} \right){\text{，}}\end{split}$ (1)

设G1，G2是阶为p的船舶保密通信传输的码元频数，在链路层中的加密数据IDj特征为 $(mk,param,I{D_i})$ ，保密系统的信息输出比特序列为：

$up{k_i} = (up{k_{i1}},up{k_{i2}}) = ({g^{{x_i}}},{({g_1}^{{H_1}(g,{g_1},{g_2},{g_3},h)}h)^{{x_i}}}){\text{，}}$ (2)

式中：u为随机数；g表示阶为p的船舶保密通信反传输的码元频数；h为链路层中通信加密数据所处位置高度。

对于给定保密信息传输过程，给出2个假设为： ${H_1}:{\{ 0,1\} ^*} \to Z_q^*$ ， ${H_0}:{\{ 0,1\} ^*} \to Z_q^*$ ，船舶保密系统的输出密钥参数： $param = \{ {G_1},{G_2},e,g,{g_2},{g_3},h,{H_1},{H_2}\} $ ，密钥生成中心选择一个随机数 ${u_i} \in Z_q^*$ ，由式（2）可得二进制编码组合为：

$ds{k_{I{D_i}}} = (s{k_{i1}},s{k_{i2}}){\text{，}}$ (3)

式中： ${k_{I{D_i}}}$ 为链路层中加密数据的常数比；s为线性码广播系数，利用该系数，结合SSL/TLS的链路层传输协议[6]，根据式（3）得到船舶保密通信输出的代理密钥 $rs{k_{I{D_i}}}$ ，令 ${t_i} = {H_1}(I{D_i},up{k_i})$ ，数据在链路层中的差异性相关函数为：

$ds{k_{I{D_i}}} = (s{k_{i1}},s{k_{i2}}) = ({g_2}^a{({g_1}^{{t_i}}h)^{{u_i}}},{g^{{u_i}}}){\text{，}}$ (4)

代理密钥为：

$rs{k_{I{D_i}}} = (s{r_i} = g_1^{{u_i}}){\text{。}}$ (5)

其中a为常数，该常数的值是根据二进制编码组合所得值决定的。为提高保密系统的运行效率，在链路层中构造编码协议： $ \bullet {\bf{RkeyGen}}(param,rs{k_{I{D_i}}},I{D_i}{\rm{,I}}{{\rm{D}}_j})$ ，根据分组编码方案，在参量满足 ${k_i},{l_i} \in Z_q^*$ 下，计算链路层重加密钥rkij，采用二进制比特序列调制方法进密钥识别，加密信息采样时间序列 ${t_0} = {H_1}(g,{g_1},{g_2},{g_3},h)$ ，结合式（4）和式（5），得到输出编码为：

$\begin{array}{l}(r{k_{1ij}},r{k_{2ij}},r{k_{3ij}},r{k_{4ij}},r{k_{5ij}},r{k_{6ij}}) = \\[5pt]({g^{{x_i}{k_i}}},{({g^{{t_0}}}h)^{{x_i}{k_i}}},\displaystyle\frac{{{x_j}}}{{{x_i}}},sr_i^{x_i^{ - 1}({t_0} - {t_i})}sr_j^{x_i^{ - 1}({t_j} - {t_0})},k,{g^{{k_i}}}){\text{，}}\end{array}$ (6)

其中：

$k \!\!=\!\! e\left( {{g^{{k_i}}},g_1^{{u_i}\left( {{t_0} - {t_i}} \right)}g_1^{{u_j}\left( {{t_j} - {t_0}} \right)}} \right)\frac{{e\left( {{g^{{k_i}}},s{k_{i1}}g_1^{{l_i}}} \right)}}{{e\left( {{{\left( {{g^{{t_0}}}h} \right)}^{{k_i}}},{g^{{u_i}}}} \right)}}e{\left( {g,{g_1}} \right)^{ - {k_i}{l_i}}}{\text{。}}\!\!$ (7)
1.2 加密和解密密钥构造

在进行船舶保密系统的算术编码设计的基础上，根据Turbo码构造加密和解密密钥，在船舶通信信息传输的SSL/TLS链路层，采用Turbo码方法把比特序列输入到加密系统的内频块中，利用单向链式结构，构建Turbo码模型：

$\!\!\!\!\begin{array}{l} C{T_{I{D_i}}} = ({C_1} = up{k_{i1}}^r,\\{C_2} = up{k_{i2}}^r,\\{C_3} = me{({g_1},{g_2})^r}e{({g_1},{g^{{u_i}}}^{({H_1}(I{D_i},up{k_i}) - {H_1}(g,{g_1},{g_2},{g_3},h))})^r},\\{C_4} = Te{({g_1},{g_2})^r}e{({g_1},{g^{{u_i}}}^{({H_1}(I{D_i},up{k_i}) - {H_1}(g,{g_1},{g_2},{g_3},h))})^r},\\\quad \;\;\;\;\;\;{C_5} = 1){\text{。}}\end{array}$

由此，定义加密密钥 $ \bullet {\bf{ReEnc}}(param,CT_i^{},r{k_{ij}})$

$\begin{split} & Decrypt(sk,{c^ * }){({{A}^{ - 1}})^{{{(\alpha _1^{ - 1}, \cdots ,\alpha _m^{ - 1})}^{\rm T}}}}{{A}^{({\alpha _1}, \cdots ,{\alpha _m})}}=\\[5pt] & \left(\!\!\!\!\! {\begin{array}{*{20}{c}}{{\alpha _1}^{ - 1}{t_{1,1}}} & \!\!\!\! \cdots\!\!\!\! & {{\alpha _1}^{ - 1}{t_{1,m}}}\\ \!\! \vdots \!\! & \!\!\!\! \ddots \!\!\!\! & \!\! \vdots \!\! \\{{\alpha _m}^{ - 1}{t_{m,1}}} & \! \! \cdots \!\! & {{\alpha _m}^{ - 1}{t_{m,m}}}\end{array}}\!\! \!\!\right)\left(\!\!\!\!\!{\begin{array}{*{20}{c}}{{\alpha _1}{a_{1,1}}} & \!\!\!\! \!\!\!\! \cdots \!\!\!\! \!\!\!\! & {{\alpha _m}{a_{1,m}}}\\ \vdots & \!\!\!\! \ddots \!\!\!\! & \!\! \vdots \!\! \\{{\alpha _1}{a_{m,1}}} & \!\!\!\! \!\!\!\! \cdots \!\!\!\!\!\!\!\! & {{\alpha _m}{a_{m,m}}}\end{array}}\!\!\!\! \right) \! = {E},\end{split}$ (9)

以M为分块长度，得到船舶保密通信输出链路层的调制帧为：

$\begin{split}{C_3}{k^{'}} & = e({g^{{x_i}r}},g_1^{x_i^{ - 1}{u_i}({t_0} - {t_i})}g_1^{x_i^{ - 1}{u_j}({t_j} - {t_0})})\times \\[5pt] & \displaystyle\frac{{e({g^{{k_i}}},s{k_{i1}}{g_1}^{{l_i}})}}{{e({{({g^{{t_0}}}h)}^{{k_i}}},{g^{{u_i}}})}}e{(g,{g_1})^{ - {k_i}{l_i}}}=\\[5pt]\quad \;\;\; & {C_3}e({g^r},g_1^{{u_i}({t_0} - {t_i})})\displaystyle\frac{{e({g^{{k_i}}},s{k_{i1}})}}{{e({{({g^{{t_0}}}h)}^{{k_i}}},{g^{{u_i}}})}}e({g^{{k_i}}},g_1^{{u_i}({t_0} - {t_i})})=\\[5pt]\quad \;\;\; & me{({g_1},{g_2})^r}e{({g_1},{g^{{u_i}}}^{({t_i} - {t_0})})^r}\times \\[5pt] & e({g^r},g_1^{{u_i}({t_0} - {t_i})})e({g^{r + {k_i}}},g_1^{{u_j}({t_j} - {t_0})})e{({g_1},{g_2})^{{k_i}}}=\\\;\quad \;\; & me{({g_1},{g_2})^{r + {k_i}}}e{(g,g_1^{{u_j}({t_j} - {t_0})})^{r + {k_i}}}{\text{，}}\end{split}$ (10)

在TD-SCDMA上行链路中得到1组公钥码，在式（10）的基础上构造解密密钥输出：

$Decrypt(sk,{c^ * }){A}{{A}^{ - 1}} = \left( {\begin{array}{*{20}{c}}{{t_{1,1}}} & \cdots & {{t_{1,m}}}\\ \vdots & \ddots & \vdots \\{{t_{m,1}}} & \cdots & {{t_{m,m}}}\end{array}} \right) = {E}{\text{，}}$ (11)

对链路层加密数据进行同态稀疏性重组[7]，得到公钥加密后的明文输出序列为：

$\begin{array}{l}Decrypt(sk,{c^ * }){{A}^{({\alpha _1}, \cdots ,{\alpha _m})}}Decrypt(sk,{c^ * }){({{A}^{ - 1}})^{{{(\alpha _1^{ - 1}, \cdots ,\alpha _m^{ - 1})}^{\rm T}}}}\!\!\!=\\[5pt] \left(\!\!\! {\begin{array}{*{20}{c}}{{\alpha _1}{a_{1,1}}} & \!\!\!\!\!\! \cdots \!\!\!\!\!\! & {{\alpha _m}{a_{1,m}}}\\ \vdots & \!\!\!\!\!\! \ddots \!\!\!\!\!\! & \vdots \\{{\alpha _1}{a_{m,1}}} & \!\!\!\!\!\! \cdots \!\!\!\!\!\! & {{\alpha _m}{a_{m,m}}}\end{array}} \!\!\!\right)\left( \!\!\! {\begin{array}{*{20}{c}}{{\alpha _1}^{ - 1}{t_{1,1}}} & \!\!\!\!\!\! \cdots \!\!\!\!\!\! & {{\alpha _1}^{ - 1}{t_{1,m}}}\\ \vdots & \!\!\!\!\!\! \ddots \!\!\!\!\!\! & \vdots \\{{\alpha _m}^{ - 1}{t_{m,1}}} & \!\!\!\!\!\! \cdots \!\!\!\!\!\! & {{\alpha _m}^{ - 1}{t_{m,m}}}\end{array}} \!\!\!\right) = {E}, \ \ \end{array}$ (12)

计算消息的散列值e=h（m），取属于E的疏采样点G，得到船舶保密通信系统解密密钥的Hash函数为：

$\begin{split}\\[-12pt] & Decrypt(sk,{c^ {*} }){({{ {A}}^{({\alpha _1}, \cdots ,{\alpha _m})}})^{ - 1}}=\\ & \left( {\begin{array}{*{20}{c}}{{\alpha _1}^{ - 1}{t_{1,1}}} & \cdots & {{\alpha _1}^{ - 1}{t_{1,m}}}\\ \vdots & \ddots & \vdots \\{{\alpha _m}^{ - 1}{t_{m,1}}} & \cdots & {{\alpha _m}^{ - 1}{t_{m,m}}}\end{array}} \right) = {({{ A}^{ - 1}})^{{{(\alpha _1^{ - 1}, \cdots ,\alpha _m^{ - 1})}^{\rm T}}}}{\text{。}}\end{split}$ (13)

通过上述设计，实现了船舶保密系统的密钥构造，根据公钥机制选择加密算法，进行加密算法设计。

2 加密算法及软件实现2.1 加密算法

本文提出一种基于椭圆曲线密码通信的船舶保密系统设计方法，根据椭圆曲线密码体制构造船舶保密通信的传输协议[8]，描述如下：

1） $K \leftarrow Gen({1^k})$ ：输入船舶通信数据加密的稀疏属性集合与密钥参数k，输出链路层密钥K，进而给定公钥的信源特征，进行算术编码，在a1，a2内进行证书签密；

2） $S \leftarrow Enc(K,d,L)$ ：输入椭圆曲线加密密钥K，设干扰区间 $\left[ { - {2^\rho },{2^\rho }} \right]$ 内的攻击强度为 $W = \{ {w_1}, \ldots ,{w_p}\} $ ，对于数字标签 $L = \{ {L_1}, \ldots ,{L_n}\} $ ，输出解码密文S，根据密钥方案进行对称加密。

3） $(t,i) \leftarrow Token(K,w,o,i)$ ：输入公钥码元频数，查询的数字w、输出bj的二值码，运行 $Gen({1^k})$ 生成船舶保密通信密钥K，算法由用户执行，t与i发送对应稀疏属性集合标签L={a}。

4） $b \leftarrow Search(d,S,t,i)$ ：输入挑战密文Bx和数字标签 $L = \{ {L_1}, \ldots ,{L_n}\} $ ，计算加密密文的信息上S，根据查询令牌 ${T^ * } = \{ t_1^*, \ldots ,t_p^*\} $ ，得到标签选择b=1，计算消息密文 $t \leftarrow f(K,w)$ ，加密比特序列的位置 ${y_1}, \ldots ,{y_r}$ 置为1，获得加密后的密文序列。

2.2 加密系统的软件实现

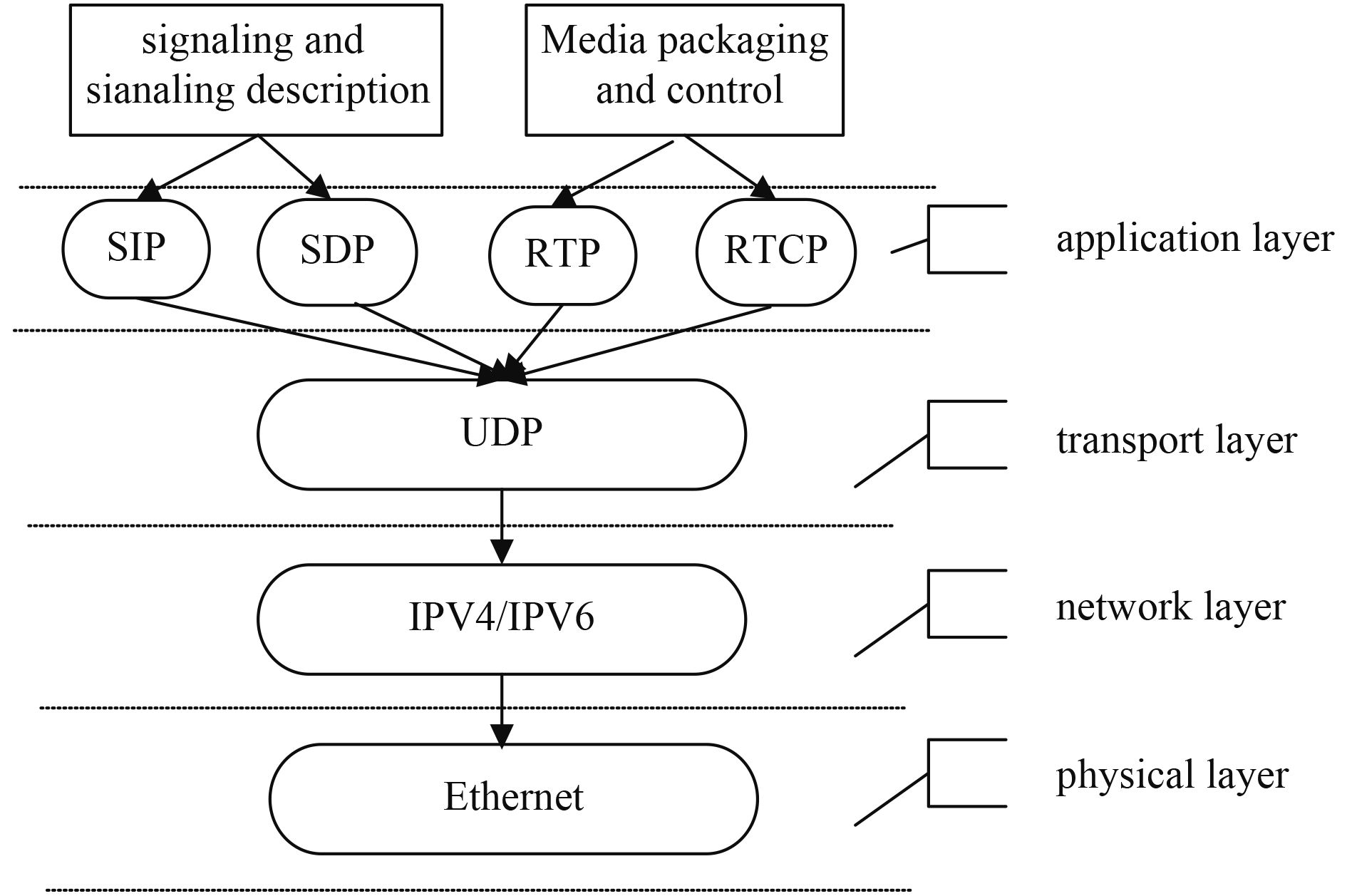
在进行了加密算法设计的基础上，在嵌入式Linux内核下进行船舶保密系统的软件开发设计，用SIP用户代理（User Agent，UA）和SIP用户服务器（User Server，US）分别作为船舶保密系统的客户端和服务器端。采用集中式拓扑和分布式拓扑相结合的方式进行船舶保密通信的信令拓扑控制，在感知控制层进行船舶保密通信信息封装和加密密文信息传输。在云存储模型下构建船舶保密通信的信息存储单元，采用实时传输协议（Real Time Protocol，RTP） 进行船舶保密通信的多点控制，在SIP客户端发送OPTION请求，采用无线自组网技术实现船舶保密通信信息的分布式协同处理和UDP协议控制，根据上述设计原理，构造船舶保密系统的软件层次开发结构如图1所示。

图 1 船舶保密系统的软件层次结构 Fig. 1 Software hierarchy of ship security system

通过图1给出的开发流程图，进行保密通信系统程序设计，将加密算法加载到系统中，执行保密信息传输。

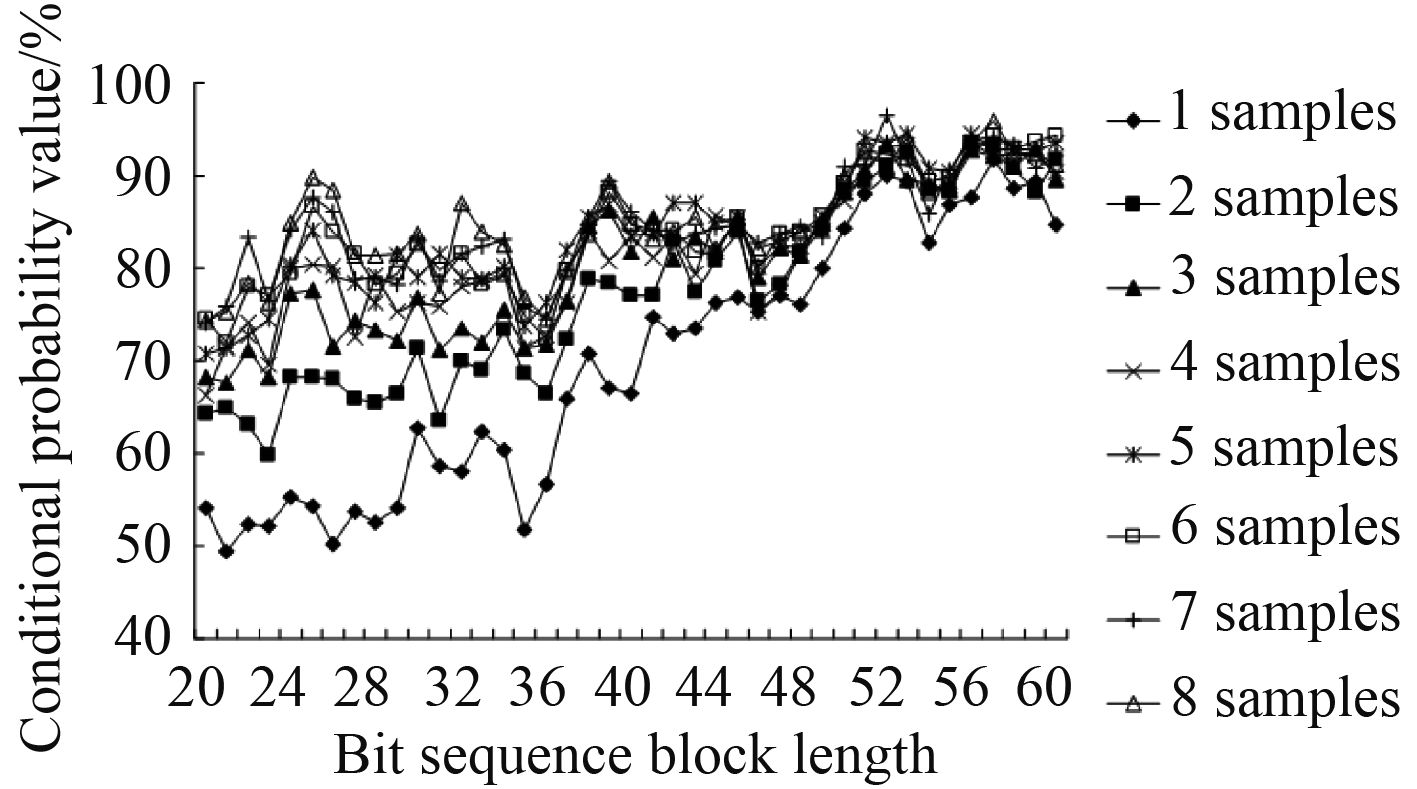
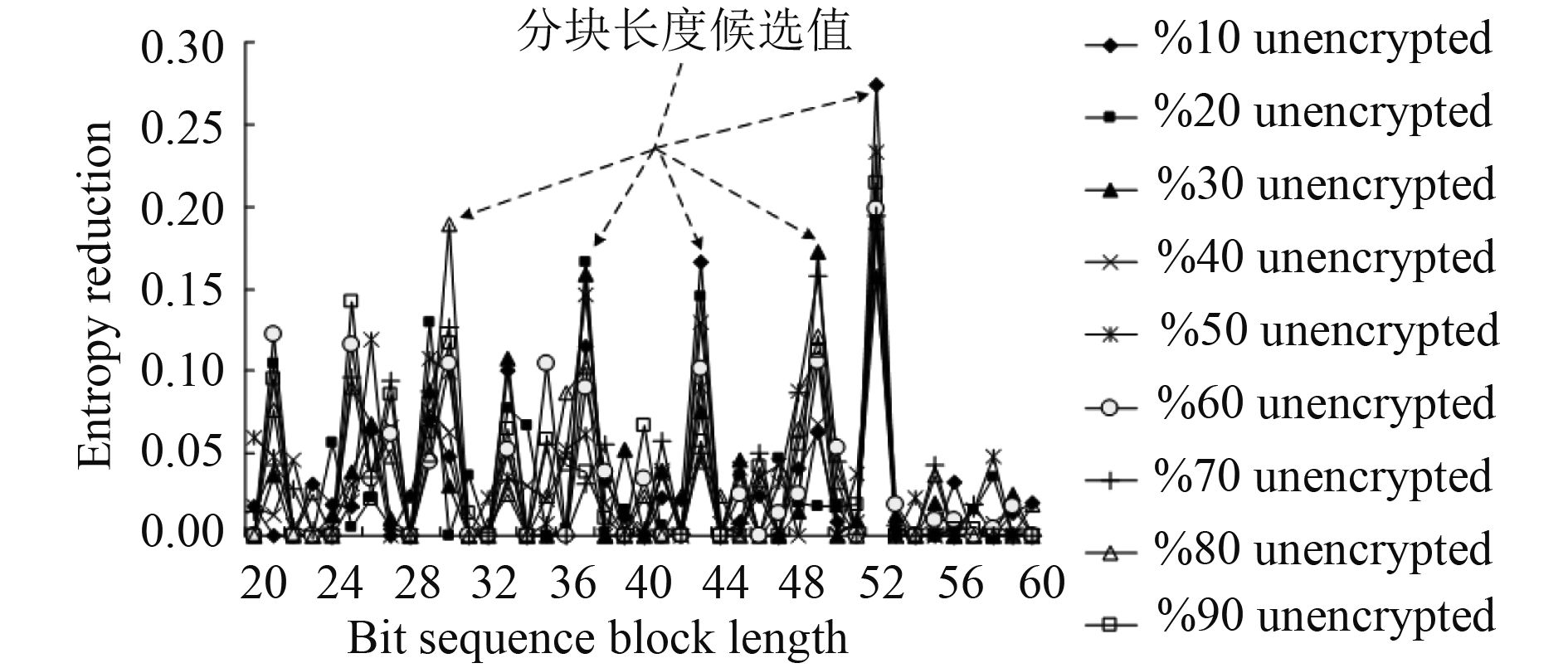
3 仿真实验

为了测试本文设计的保密系统的应用性能，进行仿真实验。实验建立在Matlab 7仿真环境中，船舶保密通信的采样间隔设定为24 ms，信息传输的采样数据包大小为1 024×1 043 bit，采用本文设计系统进行船舶保密通信传输，测试输出样本序列满足保密通信要求的概率值和信息熵统计结果如图2和图3所示。

图 2 满足保密通信要求的样本分布概率值 Fig. 2 Probability distribution of sample distribution to meet the requirements of secure communication

图 3 信息熵统计结果 Fig. 3 Statistical results of information entropy

分析图2和图3结果得知，采用本文方法进行船舶保密通信，数据的加密性较好，抗攻击和干扰能力较强，提高数据信息安全性。

4 结　语

本文提出一种基于椭圆曲线密码通信的船舶保密系统设计方法，采用二进制比特序列调制方法进行船舶保密信息传输的信息编码，根据Turbo码构造加密和解密密钥，根据椭圆曲线密码体制构造船舶保密通信的传输协议。在嵌入式Linux内核下进行加密算法加载，实现船舶保密系统优化设计。实验证明，本文设计的船舶保密系统能提高船舶传输的信息安全性。

参考文献
[1] 白恩健, 朱俊杰. TinySBSec-新型轻量级WSN链路层加密算法[J].哈尔滨工程大学学报, 2014, 35(2): 1–6.
BAI En-jian, ZHU Jun-jie. TinySBSec-the new lightweight WSN link-layer encryption algorithm[J].Journal of Harbin Engineering University, 2014, 35(2): 1–6.
[2] 汤殿华, 祝世雄, 曹云飞. 一个较快速的整数上的全同态加密方案[J].计算机工程与应用, 2012, 48(28): 117–122.
TANG Dian-hua, ZHU Shi-xiong, CAO Yun-fei. Faster fully homomorphic encryption scheme over integer[J].Computer Engineering and Applications, 2012, 48(28): 117–122. DOI: 10.3778/j.issn.1002-8331.2012.28.023
[3] 林如磊, 王箭, 杜贺. 整数上的全同态加密方案的改进[J].计算机应用研究, 2013, 30(5): 1515–1519.
LIN Ru-lei, WANG Jian, DU He. Improved fully homomorphic encryption over integers[J].Application Research of Computers, 2013, 30(5): 1515–1519.
[4] 闵富红, 王珠林, 王恩荣, 等. 新型忆阻器混沌电路及其在图像加密中的应用[J].电子与信息学报, 2016, 38(10): 2681–2688.
MIN Fu-hong, WANG Zhu-lin, WANG En-rong, et al. New memristor chaotic circuit and its application to image encryption[J].Journal of Electronics & Information Technology, 2016, 38(10): 2681–2688.
[5] 刘刚, 任飞, 彭元志. 一种基于Linux容器机制的系统级双域隔离方案[J].信息安全与通信保密, 2016(3): 126–128.
LIU Gang, REN Fei, PENG Yuan-zhi. A system-level dual-domain isolation based on linux container mechanism[J].Information Security And Communications Privacy, 2016(3): 126–128.
[6] 徐甫, 马静谨. 基于中国剩余定理的门限RSA签名方案的改进[J].电子与信息学报, 2015, 37(10): 2495–2500.
XU Fu, MA Jing-jin. Improvement of threshold RSA signature scheme based on chinese remainder theorem[J].Journal of Electronics & Information Technology, 2015, 37(10): 2495–2500.
[7] 赵太飞, 王文科, 刘龙. WDM光网络中一种优先共享通路保护算法[J].激光技术, 2012, 36(3): 408–412.
ZHAO Tai-fei, WANG Wen-ke, LIU Long. A preferential shared path protection algorithm for WDM optical network[J].Laser Technology, 2012, 36(3): 408–412.
[8] 张元天, 刘福强, 陈泱. 基于等级保护体系的信息安全风险评估方法研究[J].信息安全与通信保密, 2016(8): 78–81.
ZHANG Yuan-tian, LIU Fu-qiang, CHEN Yang. Evaluation method of infosec risk based on classified protection system[J].Information Security and Communications Privacy, 2016(8): 78–81.