收稿日期: 2016-10-13.
作者简介: 李艳华(1984 – ),男,博士研究生,工程师,研究方向为船舶装置振动噪声控制
Method of impedance calculation of three-way pipe with arbitrary supports and branch angles considering fluid-structure interaction
China Ship Development and Design Center, Wuhan 430064, China
0 引 言为了满足管路系统的不同功能,船舶上布置有大量的三通分支结构,并处在长期的振动噪声环境下,三通分支管路的振动噪声会通过支撑以及流体等直接或间接向水中辐射噪声,影响隐身性。另外三通也是管路系统中重要的结构,并且其机理和特性比简单直管或弯管等管段结构都要复杂很多,对其进行声学分析和研究是管路系统声学预报和声学优化的关键环节。
近些年来,国内外大量研究者对管路振动噪声的研究都考虑了流固耦合效应,研究结论也充分说明考虑流固耦合的动力学模型是管道振动特性预测精度的前提条件[1 – 5]。在目前研究中,管路流固耦合振动噪声主要是考虑简单的管段结构,只有少量对分支管道开展了研究工作[6 – 9],其中分析的分支管道也以简单、固定形状为主,而且支撑也设置成了自由、固定等形式。但实船三通管路形状各异,例如有T型、Y型等,支撑有固支、简支以及大量的弹性支撑(减振器、弹性支吊架等)等,而不同形状和支撑对管路的振动噪声特性影响比较大。所以对考虑流固耦合的任意支撑和分支角度的三通管道声学研究具有重要的意义。
由于阻抗分析是振动噪声控制领域广泛采用的一种分析方法,一方面通过管道阻抗的研究可以建立管路系统的振动噪声特性预报方法,另外通过对阻抗的分析可以了解和掌握振动噪声能量的传递,进而对设备进行声学优化设计。目前国内外对管道的阻抗研究中管道和支撑是分开考虑的,只能单独考虑管段或支撑的阻抗特性,而支撑对管道振动噪声影响比较大,并且相互影响,很有必要把支撑和管段集成一个独立单元考虑,计算分析其阻抗特性。因此,本文从阻抗的角度入手,建立考虑流固耦合的任意支撑和分支角度三通管道阻抗的计算方法,通过编制计算程序,改变参数可以计算任意支撑、不同形状分支角度的三通管道的阻抗,方便快捷,为实船分支管路阻抗的分析以及声学优化设计提供技术支撑。
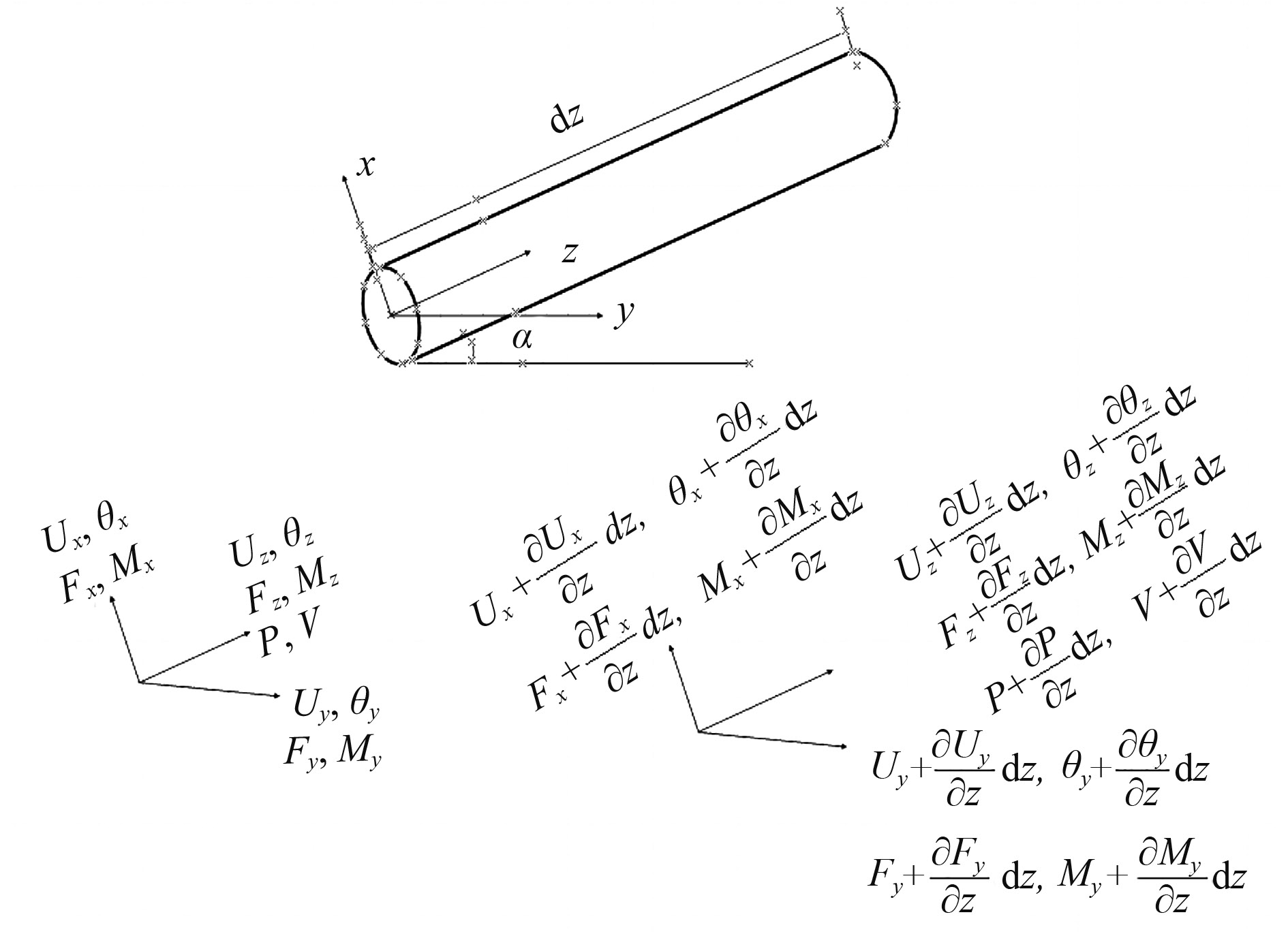
1 直管流固耦合理论模型及求解1.1 直管流固耦合模型因为实船上管道的激励来自各个方向,如图1所示,例如泵、阀门声源激励,主要是影响管道轴线方向振动和噪声(z方向线性振动),基础的振动传递到管道等影响管道横向方向振动和噪声(x,y方向线性振动和弯曲振动),并且管道由于不同角度的空间连接,前一管道的横向振动可能还会产生连接管道的扭转振动(z方向),因此管道的振动包括了轴向、横向以及扭转振动,所以要全面分析管道的振动噪声特性,对其模型的建立和阻抗的计算和分析也应该涵盖这些方向。
管路模型如图1所示,利用流体力学、理论力学等基本理论,建立直管的流固耦合计算模型,包括4个轴向振动方程、8个横向振动方程以及2个扭转方程。具体如下[10]:
轴向振动方程
|
$\frac{{\partial {F_z}}}{{\partial z}} + {\rho _t}{A_t}g\sin \alpha + {\rho _t}{A_t}\frac{{\partial {{\dot U}_z}}}{{\partial t}} = 0\text{,}$
|
(1) |
|
$\frac{{\partial P}}{{\partial z}} + {\rho _l}\frac{{\partial V}}{{\partial t}} + {\rho _l}g\sin \alpha = 0\text{,}$
|
(2) |
|
$\frac{{\partial {{\dot U}_z}}}{{\partial z}} + \frac{1}{{E{A_t}}}\frac{{\partial {F_z}}}{{\partial t}} + \frac{\upsilon }{E}\frac{R}{e}\frac{{R - \frac{1}{2}e}}{{R + \frac{1}{2}e}}\frac{{\partial P}}{{\partial t}} = 0\text{,}$
|
(3) |
|
$[\frac{1}{K} + \frac{2}{E}(\frac{R}{e} + \frac{R}{{R + \frac{1}{2}e}}\upsilon )]\frac{{\partial P}}{{\partial t}} + \frac{{2\upsilon }}{{E{A_t}}}\frac{{\partial {F_z}}}{{\partial t}} + \frac{{\partial V}}{{\partial z}} = 0\text{;}$
|
(4) |
x-z平面振动方程
|
$\frac{{\partial {{\dot U}_x}}}{{\partial z}} - {\dot \theta _y} + \frac{1}{{kG{A_t}}}\frac{{\partial {F_x}}}{{\partial t}} = 0\text{,}$
|
(5) |
|
$\frac{{\partial {{\dot \theta }_y}}}{{\partial z}} + \frac{1}{{E{I_t}}}\frac{{\partial {M_y}}}{{\partial t}} = 0\text{,}$
|
(6) |
|
$\frac{{\partial {F_x}}}{{\partial z}} + ({\rho _t}{A_t} + {\rho _l}{A_l})g\cos \alpha + ({\rho _t}{A_t} + {\rho _l}{A_l})\frac{{\partial {{\dot U}_x}}}{{\partial t}} = 0\text{,}$
|
(7) |
|
$\frac{{\partial {M_y}}}{{\partial z}} + {F_x} + ({\rho _t}{I_t} + {\rho _l}{I_l})\frac{{\partial {{\dot \theta }_y}}}{{\partial t}} = 0\text{;}$
|
(8) |
y-z平面振动方程
|
$\frac{{\partial {{\dot U}_y}}}{{\partial z}} + {\dot \theta _x} + \frac{1}{{kG{A_t}}}\frac{{\partial {F_y}}}{{\partial t}} = 0\text{,}$
|
(9) |
|
$\frac{{\partial {{\dot \theta }_x}}}{{\partial z}} + \frac{1}{{E{I_t}}}\frac{{\partial {M_x}}}{{\partial t}} = 0\text{,}$
|
(10) |
|
$\frac{{\partial {F_y}}}{{\partial z}} + ({\rho _l}{A_l} + {\rho _t}{A_t})\frac{{\partial {{\dot U}_y}}}{{\partial t}} = 0\text{,}$
|
(11) |
|
$\frac{{\partial {M_x}}}{{\partial z}} - {F_y} + ({\rho _t}{I_t} + {\rho _l}{I_l})\frac{{\partial {{\dot \theta }_x}}}{{\partial t}} = 0\text{;}$
|
(12) |
扭转振动方程
|
$\frac{{\partial {M_z}}}{{\partial z}} + {\rho _t}J\frac{{\partial {{\dot \theta }_z}}}{{\partial t}} = 0\text{,}$
|
(13) |
|
$\frac{{\partial {{\dot \theta }_z}}}{{\partial z}} + \frac{1}{{GJ}}\frac{{\partial {M_z}}}{{\partial t}} = 0\text{。}$
|
(14) |
式中:角标x,y,z为方向;l为管内流体;t为管道;U为流体管路的位移;θ为角度;F为管壁内力;M为弯矩;P为流体压力;V为流体振速;At为管壁截面积;Al为流体截面积;k为剪切分布系数;G为剪切模量;K为流体体积模量;υ为泊松比;ρ为密度;e为管壁厚度;R为管道内半径;I为截面惯性矩;J为截面极惯性矩。
1.2 流固耦合模型频域求解利用Laplace变换把流固耦合14个方程化为频域常微分方程,通过中间推导消元的思想,把多元一阶偏微分化为如下一元高阶常微分方程。
|
$\frac{{{d^4}{{\varPhi}_1}}}{{{\rm d}{z^4}}} + a\frac{{{d^2}{{\varPhi}_1}}}{{{\rm d}{z^2}}} + b{{\varPhi}_1} + { X}{{\bf{\varphi }}_1}(z,0) + { Y} = {\bf{0}}\text{,}$
|
(15) |
|
$\frac{{{d^4}{{\varPhi}_2}}}{{{\rm d}{z^4}}} + c\frac{{{d^2}{{\varPhi}_2}}}{{{\rm d}{z^2}}} + d{{\varPhi}_2} + { W}{{\bf{\varphi }}_2}(z,0) + { Q} = {\bf{0}}\text{,}$
|
(16) |
|
$\frac{{{d^2}{{\varPhi}_3}}}{{{\rm d}{z^2}}} + h{{\varPhi}_3} + { Z}{{\bf{\varphi }}_3}(z,0) = {\bf{0}}\text{。}$
|
(17) |
式中:a,b,c,d和h为实常数;X,W,Y,Q,Z为常数矩阵;φ(z,0)为初始值。
对(15)~式(17)求解,得到流固耦合方程的解为
|
${\varPhi}(z) = { TE}(z){\bf{\xi }} + {{ TT}\varphi}(z,0) + { U}$
|
(18) |
其中:
|
$\begin{array}{l}{ T} = diag{\left[ {{{\left[ {{T_1}} \right]}_{4 \times 4}},{{\left[ {{T_2}} \right]}_{4 \times 4}},{{\left[ {{T_3}} \right]}_{4 \times 4}},{{\left[ {{T_4}} \right]}_{2 \times 2}}} \right]_{14 \times 14}}\text{,}\\[6pt]{ E} = diag{\left[ {{e^{{r_1}z}},{e^{{r_2}z}}, \ldots ,{e^{{r_{14}}z}}} \right]_{14 \times 14}}\text{,}\\[6pt]{ TT} = diag{\left[ {{{\left[ {{ T}{{ T}_1}} \right]}_{4 \times 4}},{{\left[ {{ T}{{ T}_2}} \right]}_{4 \times 4}},{{\left[ {{ T}{{ T}_3}} \right]}_{4 \times 4}},{{\left[ {{ T}{{ T}_4}} \right]}_{2 \times 2}}} \right]_{14 \times 14}}\text{,}\end{array}$
|
矩阵
${{ T}_i}{ T}{{ T}_i}(i = 1,2,3,4),U$
为常数矩阵,与初始参数和拉氏变量s有关,E矩阵与初始参量和坐标值有关。
$\xi $
是14个未知常数组成的列向量,由边界条件确定。
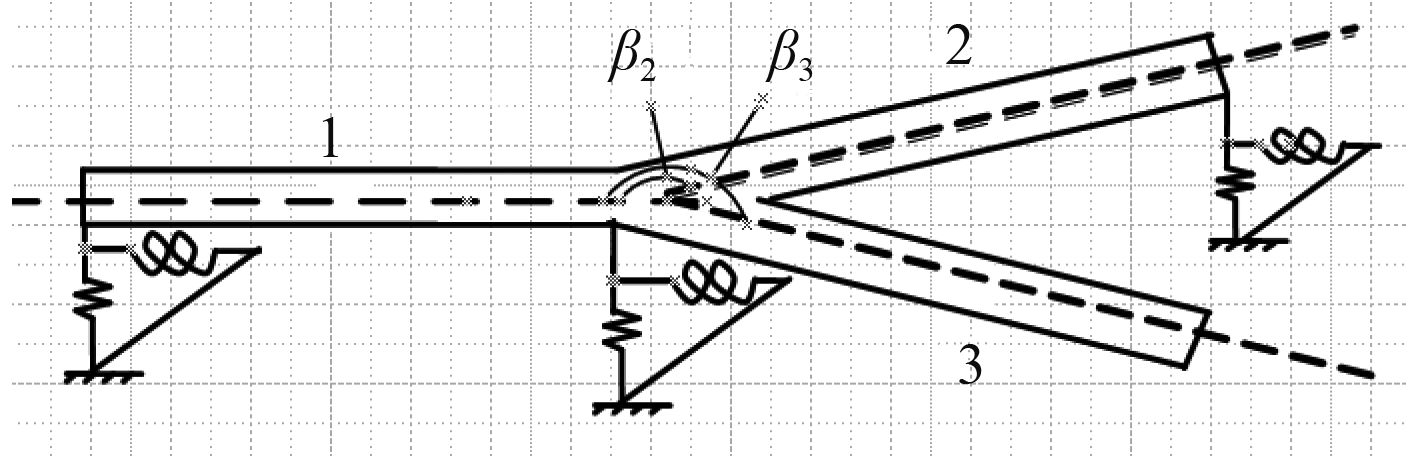
2 任意支撑三通管道传递矩阵建立和求解2.1 分支管传递矩阵建立任意形状的三通分支管道如图2所示,图中管道的线弹簧和扭转弹簧都是 3 个方向的(分别为kx,ktx,ky,kty,kz,ktz)。虚线表示管道的中心线。
在分支点处建立力和位移的平衡条件,得到分支管处的传递矩阵:
|
$\left\{ {\begin{array}{*{20}{c}}{\!\!\!{{\left\{ {{{\varPhi}_1}({L_1})} \right\}}_{14 \times 1}}}\\{{{\left\{ 0 \right\}}_{7 \times 1}}}\end{array}}\!\!\! \right\} \!= \!{\left[ \varGamma \right]_{21 \times 28}}{\left\{\!\!\! {\begin{array}{*{20}{c}}{{{\left\{ {{\varPhi _2}(0)} \right\}}_{14 \times 1}}\!\!\!}\\{{{\left\{ {{\varPhi _3}(0)} \right\}}_{14 \times 1}}\!}\!\end{array}}\!\!\! \right\}_{28 \times 1}}\! + \!{ X}\text{,}$
|
(19) |
式中X为与分支角度、支撑以及管道初始状态相关的向量。
其中:
|
$\varGamma {\rm{ = }}{\left[ {\begin{array}{*{20}{c}}{{A_{1,1}}}&{{A_{1,2}}}\\{{A_{2,1}}}&{{A_{2,2}}}\end{array}} \right]_{21 \times 28}}\text{。}$
|
令
$\kappa = \sin {\beta _2}$
,
$\gamma = \cos {\beta _2}$
,分块矩阵的具体形式如下:
|
${{ A}_{1,1}} = \left[ {\begin{array}{*{20}{c}}1&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&{\frac{{{A_{l2}}}}{{{A_{l1}}}}}&0&{ - (\gamma + \frac{{{A_{l2}}}}{{{A_{l1}}}})}&0&0&0&0&0&\kappa &0&0&0&0\\{ - ({A_{l2}}\gamma + {A_{l1}})}&0&{ - \gamma }&{ - \frac{{{k_z}}}{s}\gamma }&0&0&0&0&\kappa &{\frac{{{k_z}}}{s}\kappa }&0&0&0&0\\0&0&0&{ - \gamma }&0&0&0&0&0&\kappa &0&0&0&0\\0&0&0&0&1&{\frac{{{k_x}}}{s}}&0&0&0&0&0&0&0&0\\0&0&0&0&0&1&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&{ - \gamma }&{ - \frac{{{k_{ty}}}}{s}\gamma }&0&0&0&0&{ - \frac{{{k_{ty}}}}{s}\kappa }&{ - \kappa }\\0&0&0&0&0&0&0&{ - \gamma }&0&0&0&0&{ - \kappa }&0\\{ - {A_{l2}}\kappa }&0&{ - \kappa }&{ - \frac{{{k_y}}}{s}\kappa }&0&0&0&0&{ - \gamma }&{ - \frac{{{k_y}}}{s}\gamma }&0&0&0&0\\0&0&0&{ - \kappa }&0&0&0&0&0&{ - \gamma }&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&1&{\frac{{{k_{tx}}}}{s}}&0&0\\0&0&0&0&0&0&0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&\kappa &0&0&0&0&{ - \gamma }&0\\0&0&0&0&0&0&\kappa &{\frac{{{k_{tz}}}}{s}\kappa }&0&0&0&0&{ - \frac{{{k_{tz}}}}{s}\gamma }&{ - \gamma }\end{array}} \right]\text{,}$
|
|
${{ A}_{12}} = \left[ {\begin{array}{*{20}{c}}0&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&{\frac{{{A_{l3}}}}{{{A_{l1}}}}}&0&{ - \frac{{{A_{l3}}}}{{{A_{l1}}}}}&0&0&0&0&0&0&0&0&0&0\\{ - {A_{l3}}\cos {\beta _3}}&0&{ - \cos {\beta _3}}&0&0&0&0&0&{\sin {\beta _3}}&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&0&1&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&{ - \cos {\beta _3}}&0&0&0&0&0&0&{ - \sin {\beta _3}}\\0&0&0&0&0&0&0&0&0&0&0&0&0&0\\{ - {A_{l3}}\sin {\beta _3}}&0&{ - \sin {\beta _3}}&0&0&0&0&0&{ - \cos {\beta _3}}&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&1&0&0&0\\0&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&{\sin {\beta _3}}&0&0&0&0&0&0&{ - \cos {\beta _3}}\end{array}} \right]\text{,}$
|
|
${{ A}_{2,1}} = \left[ {\begin{array}{*{20}{c}}1&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&{ - \cos {\beta _2}}&0&0&0&0&0&{\sin {\beta _2}}&0&0&0&0\\0&0&0&{\sin {\beta _2}}&0&0&0&0&0&{\cos {\beta _2}}&0&0&0&0\\0&0&0&0&0&1&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&{\sin {\beta _2}}&0&0&0&0&{ - \cos {\beta _2}}&0\\0&0&0&0&0&0&0&{\cos {\beta _2}}&0&0&0&0&{\sin {\beta _2}}&0\\0&0&0&0&0&0&0&0&0&0&0&1&0&0\end{array}} \right]\text{,}$
|
|
${{ A}_{2,2}} = \left[ {\begin{array}{*{20}{c}}{ - 1}&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&{\cos {\beta _3}}&0&0&0&0&0&{ - \sin {\beta _3}}&0&0&0&0\\0&0&0&{ - \sin {\beta _3}}&0&0&0&0&0&{ - \cos {\beta _3}}&0&0&0&0\\0&0&0&0&0&{ - 1}&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&{ - \sin {\beta _3}}&0&0&0&0&{\cos {\beta _3}}&0\\0&0&0&0&0&0&0&{ - \cos {\beta _3}}&0&0&0&0&{ - \sin {\beta _3}}&0\\0&0&0&0&0&0&0&0&0&0&0&{ - 1}&0&0\end{array}} \right]\text{。}$
|
2.2 边界条件边界条件如图2所示。为了得到方程的最终解,还需要结合管道的边界条件。边界条件由位移和力的平衡条件推导得到。忽略中间管段结构,z=0表示管道的初始端,z=L表示管道的末端。支撑简化为6个自由度方向的弹性刚度,分别为kx0,ktx0,ky0,kty0,kz0,ktz0以及kxL,ktxL,kyL,ktyL,kzL,ktzL。角标代表弹性刚度的方向和位置,例如kx0表示z=0端x方向的线弹性刚度,ktx0表示z=0端x方向的弯曲弹性刚度,其余弹性刚度意义相同。通过对边界条件的简化,可以设定不同的弹性系数,表征任意的管道支撑。如:1)6个自由度弹性刚度都为0时,为自由管道;2)6个自由度弹性刚度都为无穷大时,为固定支撑;3)扭转刚度为0,线刚度为无穷大时,为简支管道;4)所有弹性刚度均为非 0,有限刚度时为弹性支撑。
由于本文建立的模型是14方程模型,求解时也是对14个变量一起求解,所以边界条件也应写成矩阵形式。如式(20)~式(22)所示。
|
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! 1\text{\text{号管}}:{\left[ {{{{H}}_{01}}} \right]_{7 \times 14}}{\left\{ {{{{\varPhi }}_1}(0)} \right\}_{14 \times 1}} = {\left[ {{{{F}}_{01}}} \right]_{7 \times 1}}\text{,}$
|
(20) |
|
$2\text{\text{号管}}:{\left[ {{{{H}}_{L2}}} \right]_{7 \times 14}}{\left\{ {{{{\varPhi }}_2}({L_2})} \right\}_{14 \times 1}} = {\left[ {{{{F}}_{L2}}} \right]_{7 \times 1}}\text{,}$
|
(21) |
|
$3\text{\text{号管}}:{\left[ {{{{H}}_{L3}}} \right]_{7 \times 14}}{\left\{ {{{{\varPhi }}_3}({L_3})} \right\}_{14 \times 1}} = {\left[ {{{{F}}_{L3}}} \right]_{7 \times 1}}\text{。}$
|
(22) |
将任意支撑边界条件式(20)~式(22)与频域解(18)联合,就可以得到管路任意位置的参数最终解。
2.3 任意支撑和分支角度三通管道求解结合边界条件,就可以求得一点分支管道的最终解。结合式(19)~式(22),可得求解方程:
|
$\begin{split}\\[-12pt] & {\left[ {\begin{array}{*{20}{c}}{{{\left[ {\begin{array}{*{20}{c}}{{{ T}_1}{{ E}_1}({L_1})}\\{{{\bf{0}}_{7 \times 14}}}\end{array}} \right]}_{21 \times 14}}}&{ - {{{\varGamma }}_{21 \times 28}}{{\left[ {\begin{array}{*{20}{c}}{{{ T}_2}{{ E}_2}(0)}\\{{{\bf{0}}_{14 \times 14}}}\end{array}} \right]}_{_{28 \times 14}}}}&{ - {{{\varGamma }}_{21 \times 28}}{{\left[ {\begin{array}{*{20}{c}}{{{\bf{0}}_{14 \times 14}}}\\{{{ T}_3}{{ E}_3}(0)}\end{array}} \right]}_{_{28 \times 14}}}}\\{{{\left[ {{{ H}_{01}}} \right]}_{7 \times 14}}{{\left[ {{{ T}_1}{{ E}_1}(0)} \right]}_{14 \times 14}}}&{{0_{7 \times 14}}}&{{0_{7 \times 14}}}\\{{0_{7 \times 14}}}&{{{\left[ {{{ H}_{L2}}} \right]}_{7 \times 14}}{{\left[ {{{ T}_2}{{ E}_2}({L_2})} \right]}_{14 \times 14}}}&{{0_{7 \times 14}}}\\{{0_{7 \times 14}}}&{{0_{7 \times 14}}}&{{{\left[ {{{ H}_{L3}}} \right]}_{7 \times 14}}{{\left[ {{{ T}_3}{{ E}_3}({L_3})} \right]}_{14 \times 14}}}\end{array}} \right]_{42 \times 42}}{\left\{ {\begin{array}{*{20}{c}}{\left\{ {{\xi _1}} \right\}}\\{\left\{ {{\xi _2}} \right\}}\\{\left\{ {{\xi _{_3}}} \right\}}\end{array}} \right\}_{42 \times 1}}=\\[5pt] & \quad\quad\quad \quad\quad {\left\{ {\begin{array}{*{20}{c}}{{{{\varGamma }}_{21 \times 28}}{{\left\{ {\begin{array}{*{20}{c}}{{ T}{{ T}_2}{{\bf{\varphi }}_2}\left( {0,0} \right) + {{ U}_2}}\\{{ T}{{ T}_3}{{\bf{\varphi }}_3}\left( {0,0} \right) + {{ U}_3}}\end{array}} \right\}}_{28 \times 1}} + { X} - {{\left\{ {\begin{array}{*{20}{c}}{{ T}{{ T}_1}{{\bf{\varphi }}_1}\left( {{L_1},0} \right) + {{ U}_1}}\\{{{\bf{0}}_{7 \times 1}}}\end{array}} \right\}}_{21 \times 1}}}\\{{{ F}_{01}} - {{ H}_{01}}[{ T}{{ T}_1}{{\bf{\varphi }}_1}(0,0) + {{ U}_1}]}\\{{{ F}_{L2}} - {{ H}_{L2}}[{ T}{{ T}_2}{{\bf{\varphi }}_2}({L_2},0) + {{ U}_2}]}\\{{{ F}_{L3}} - {{ H}_{L3}}[{ T}{{ T}_3}{{\bf{\varphi }}_3}({L_3},0) + {{ U}_3}]}\end{array}} \right\}_{42 \times 1}}{\text{。}}\end{split}$
|
(23) |
通过式(23),可求解得到ξi(i=1,2,3),然后把ξi代入式(18),便可得到任一分支的频域解析解。
3 任意支撑和角度三通分支管阻抗计算通过上面模型的建立以及求解,可以得到管道任意点的流体压力以及管道力等各种参数,包括流体的压力和振速,管道在x,y,z三个方向的应力、速度以及弯矩、角速度,利用阻抗公式就可以得到管道的声阻抗和机械阻抗。
声阻抗和机械阻抗[11-12](力阻抗和弯曲阻抗)公式为:
|
${Z_{P,ij}} = \frac{{{P_i}}}{{{Q_j}}}\left( {\text{\text{声阻抗}}} \right)\text{,}$
|
(24) |
|
${Z_{ij}} = \frac{{{F_i}}}{{{V_j}}}\left( {\text{\text{机械阻抗}}} \right)\text{。}$
|
(25) |
式中:声阻抗中Pi为i点处的压力激励;Qj为在j点处的体积振速响应;机械阻抗中Fi为在i点处的力或弯矩激励;Vj为在j点的速度或角速度响应。当i=j,为输入阻抗,也叫原点阻抗;当i≠j,为传递阻抗。根据此定义,可以得到考虑流固耦合的任意支撑管道不同坐标方向阻抗计算,为了区分,x,y,z的阻抗计算公式分别定义如下:
声阻抗
|
${Z_{P,ij}} = \frac{{{P_i}}}{{{Q_j}}} = \frac{{{P_i}}}{{{A_l}{V_i}}}\text{;}$
|
机械阻抗(x,y,z线性振动和弯曲、扭转振动)
|
$\begin{array}{l}{Z_{FX,ij}} = \displaystyle\frac{{{F_{x,i}}}}{{{{\dot U}_{x,j}}}},\,\,\,{Z_{FY,ij}} = \displaystyle\frac{{{F_{y,i}}}}{{{{\dot U}_{y,j}}}},\,\,\,{Z_{FZ,ij}} = \displaystyle\frac{{{F_{z,i}}}}{{{{\dot U}_{z,j}}}}\text{,}\\[10pt]\,\,\,{Z_{MX,ij}} = \displaystyle\frac{{{M_{x,i}}}}{{{{\dot \theta }_{x,j}}}},\,\,\,{Z_{MY,ij}} = \displaystyle\frac{{{M_{y,i}}}}{{{{\dot \theta }_{y,j}}}},\,\,\,{Z_{MZ,ij}} =\displaystyle \frac{{{M_{z,i}}}}{{{{\dot \theta }_{z,j}}}}\text{。}\end{array}$
|
因此通过此方法,可以得到流体的声阻抗、管道横向、轴向以及弯曲机械阻抗。可以全面分析任意支撑管道流体噪声特性以及管道在不同平面内的振动特性。
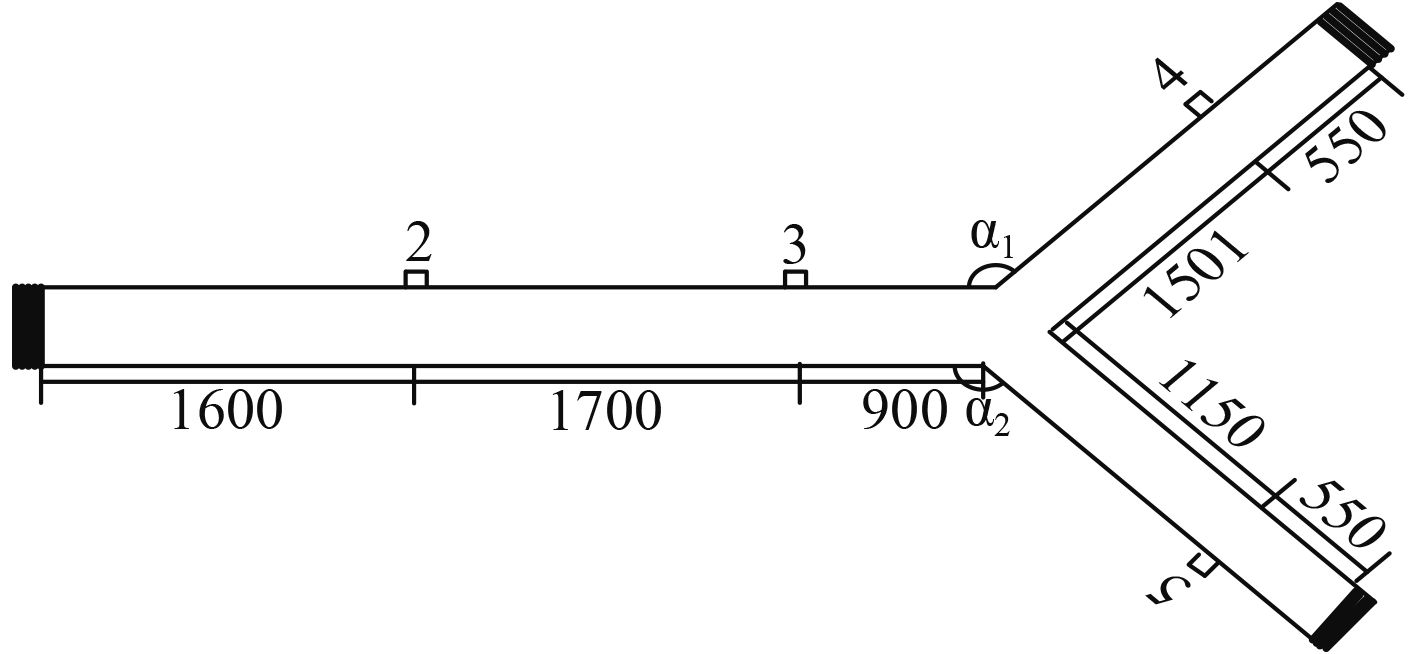
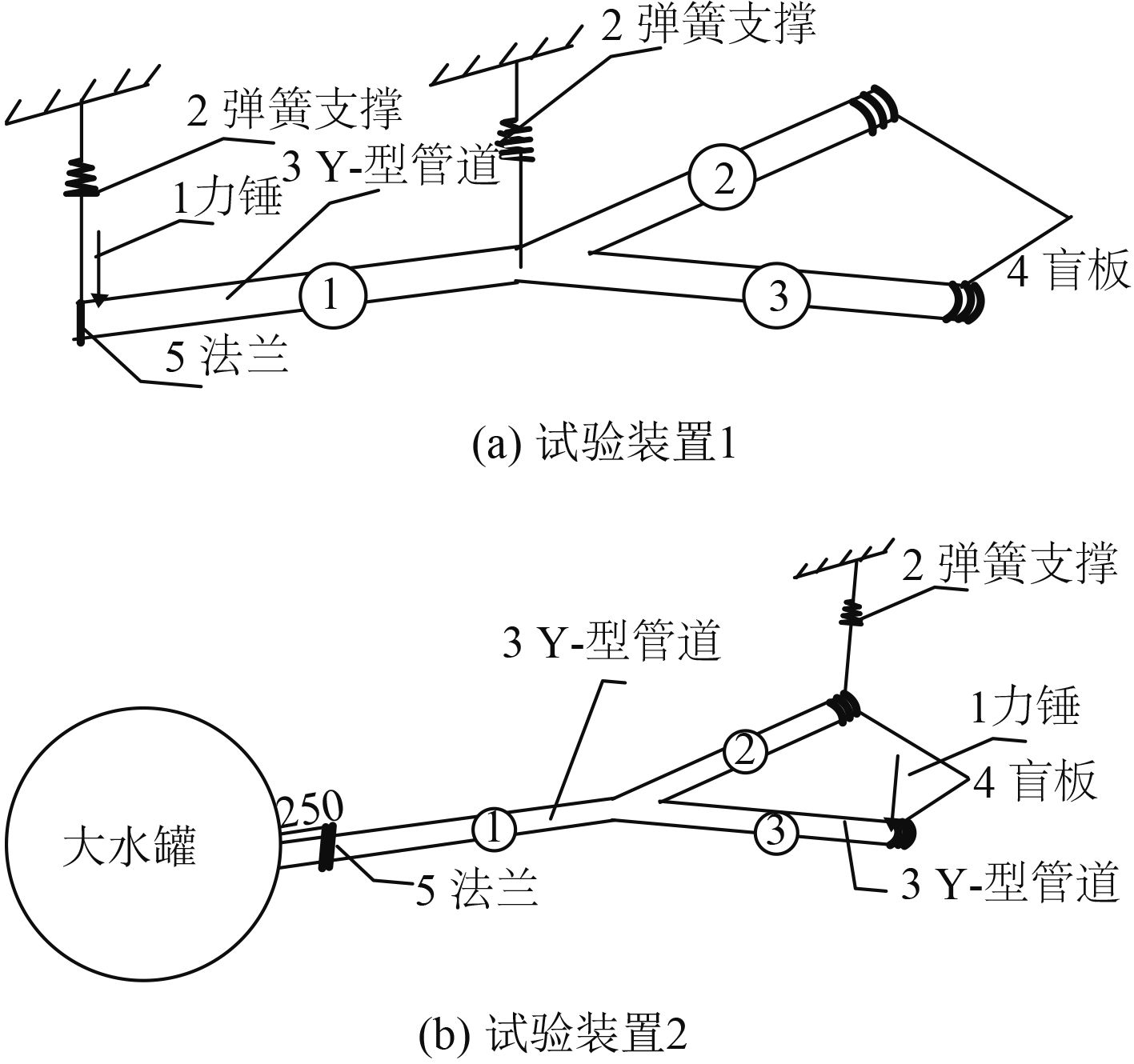
4 试验验证和分析4.1 计算方法试验验证搭建试验台架,利用实测数据验证方法的正确性。为了更好说明三通分支角度的任意性,建立了Y型分支管的试验模型,管道中充满水(见图3),其中α1=α2=3π/4。图4为Y型管道的试验安装图,其中①②③代表三通分支管段编号,为了说明可以考虑任意支撑,试验装置1中在1号管首部和分支点处利用弹性支撑,弹性支撑为横向x方向,其余两管末端为自由支撑,试验装置2中在1号管首部连接大水罐,水罐充满水,质量和体积比三通管要大很多,相当于固定支撑,在2号管端部弹性支撑,为横向x方向,3号管端部自由,Y型管道都是水平安装。试验装置1在1号管首部用力锤分别施加轴向和横向激励,试验装置2在3号管末端用力锤分别施加轴向和横向激励。从前面的方程可看出,各种参量都是相互耦合和关联的,具有非独立性,即某一参量的偏差会带来其他参量的偏差,当然此参量的准确性同样可以佐证其他参量的准确性,同时考虑到部分参数测量的操作性,列出部分参量测量结果与计算结果的对比来验证本文的计算方法。
试验材料参数如表1所示。
表 1(Tab. 1)

表 1 试验材料参数
Tab. 1 Property parameters of measurement pipeline
| 管道 |
水 |
| 内径/ mm |
100 |
体积模量/GPa |
2.14 |
| 壁厚/mm |
4 |
密度/kg·m-3 |
999 |
| 弹性模量/GPa |
206 |
盲板 |
| 泊松比 |
0.3 |
质量(z=0)/kg
|
0.8 |
| 密度/kg·m-3 |
7930 |
质量(z=L)/kg
|
0.8 |
| 剪切系数 |
0.53 |
弹性支撑(弹簧) |
|
|
刚度/N·m-1 |
1.52×105 |
|
表 1 试验材料参数
Tab.1 Property parameters of measurement pipeline
|
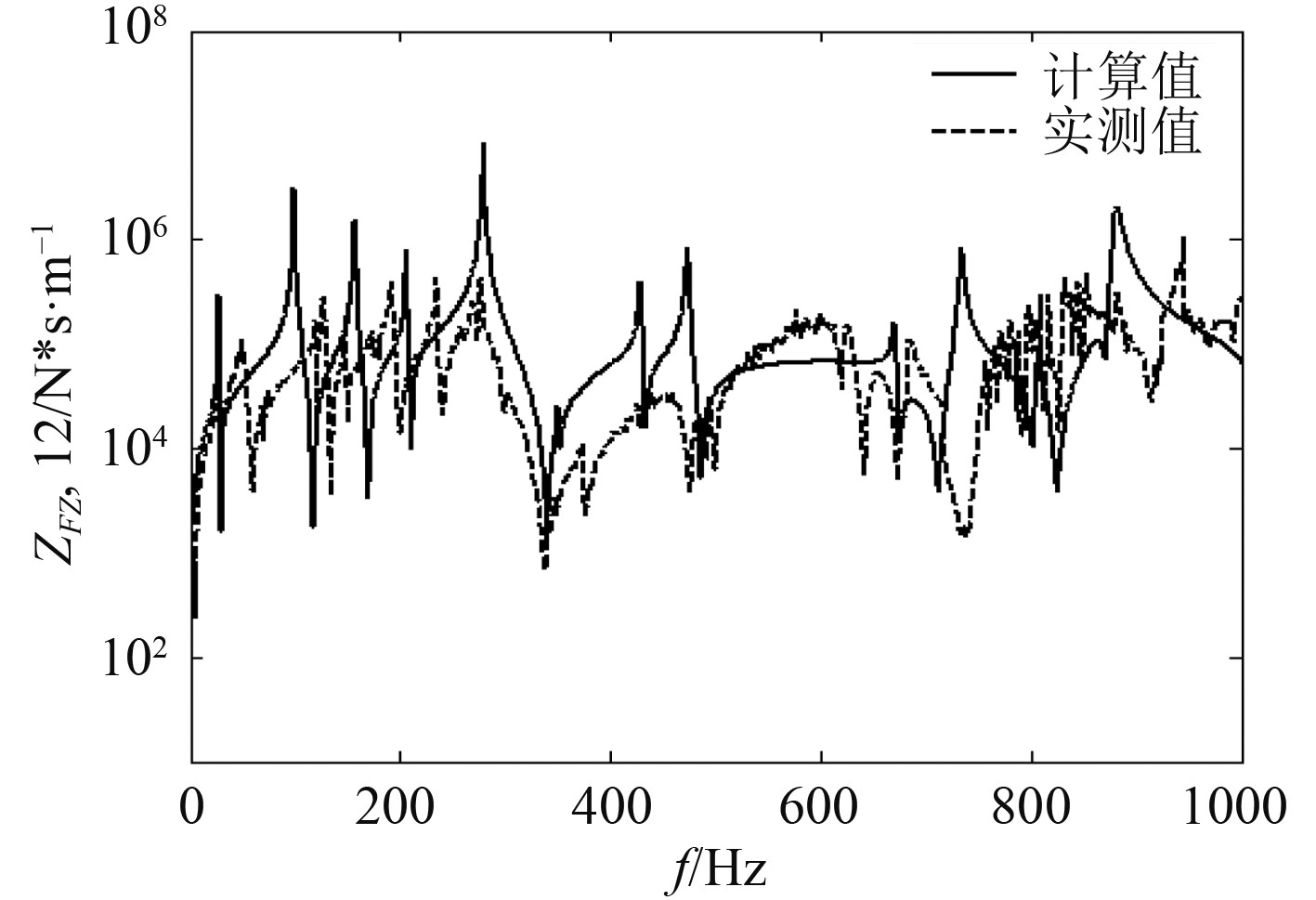
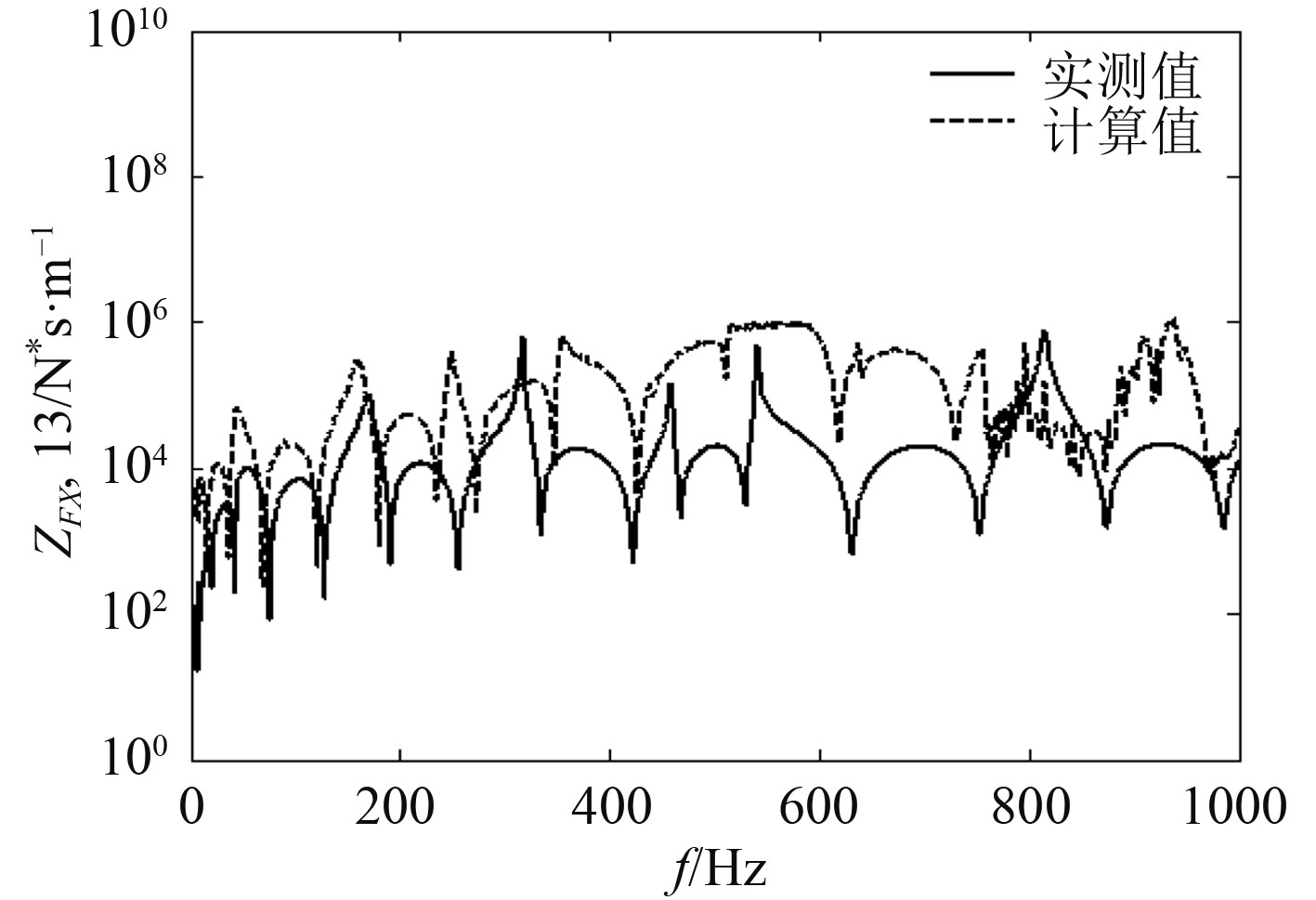
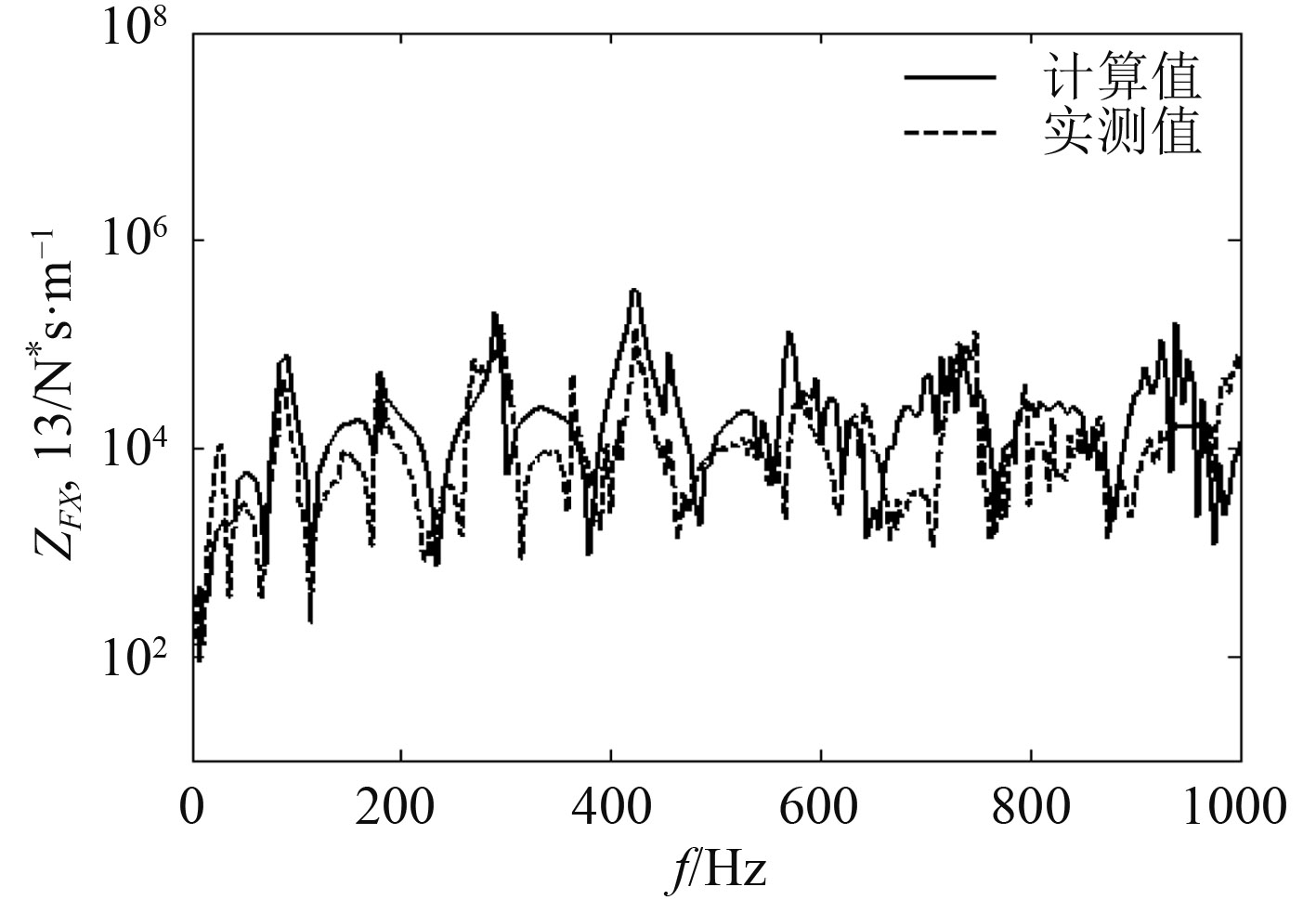
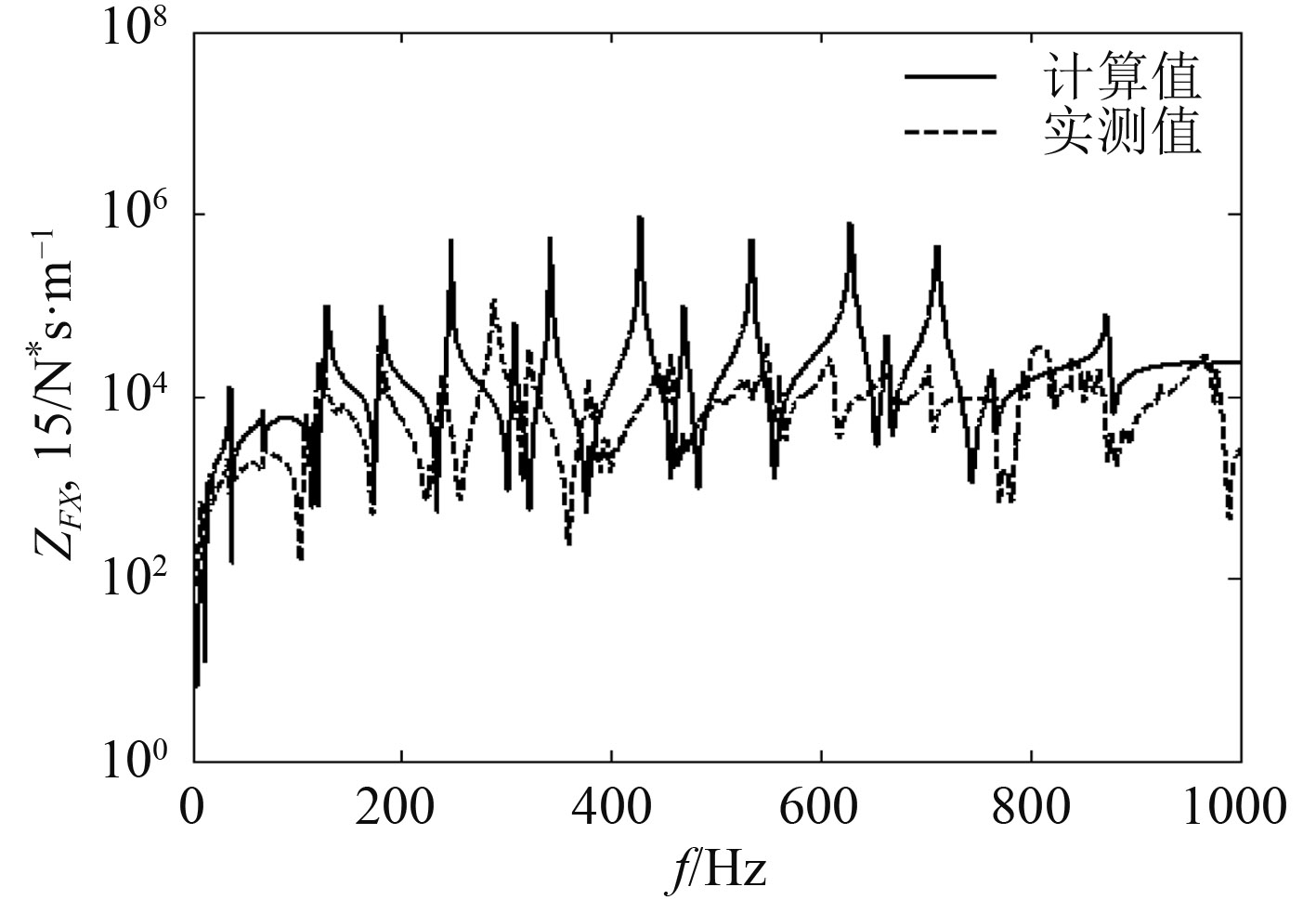
将力锤敲击点设置为1号点,部分阻抗实测值和计算值比较如图5 ~ 图9所示。
从图5~图9可看出,阻抗计算值与实测值量级和趋势都吻合比较好,验证了本文阻抗计算方法的正确性。
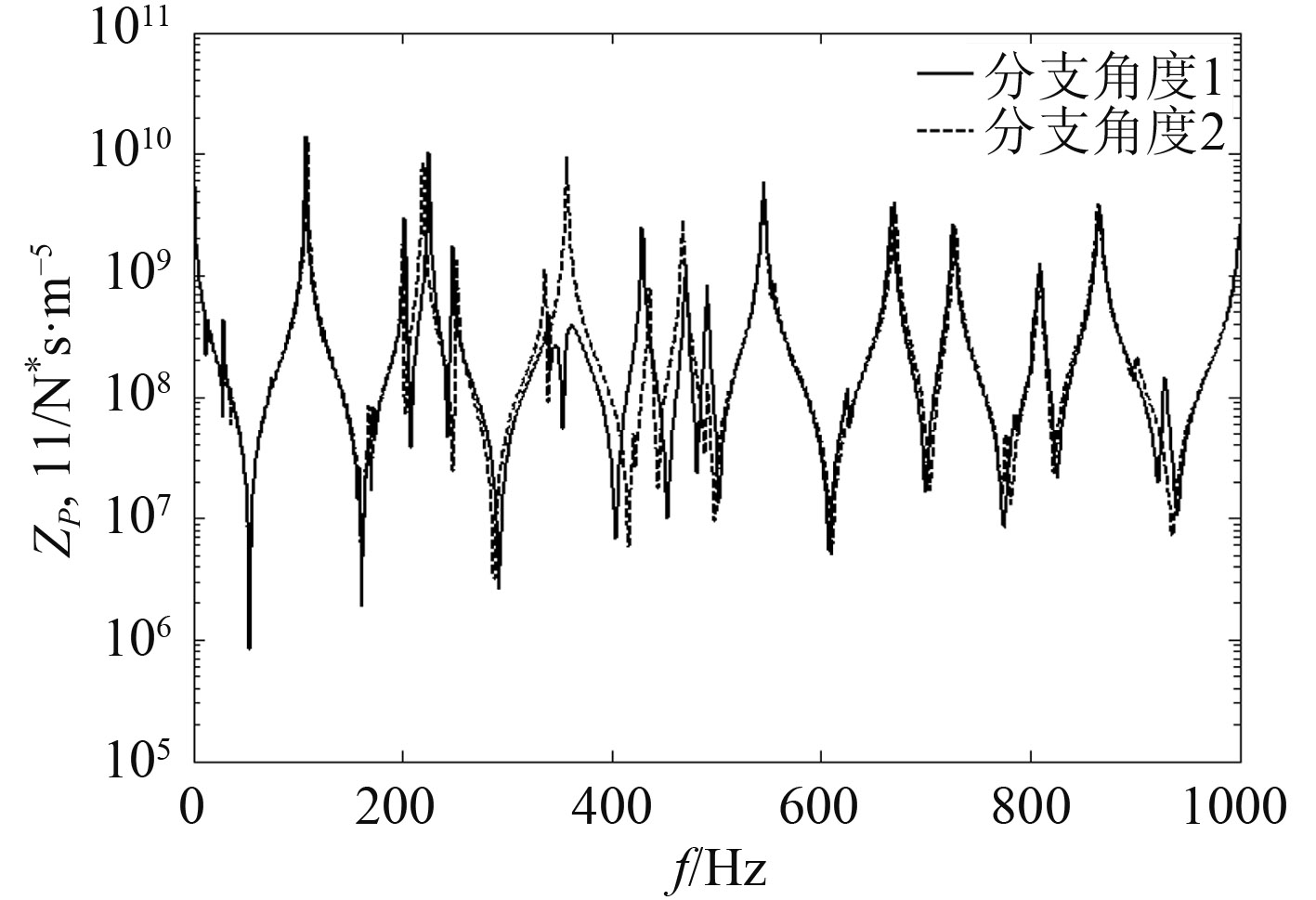
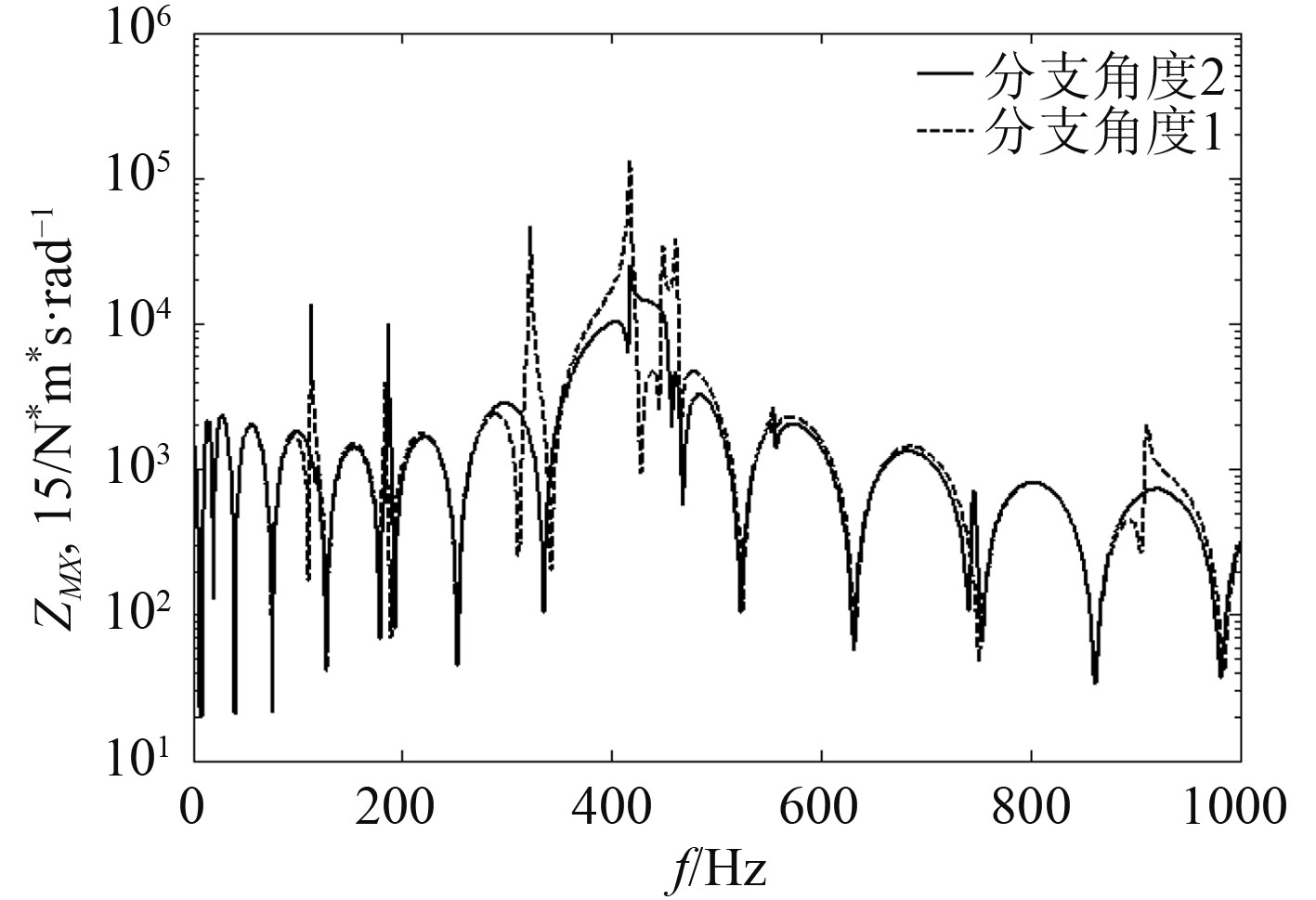
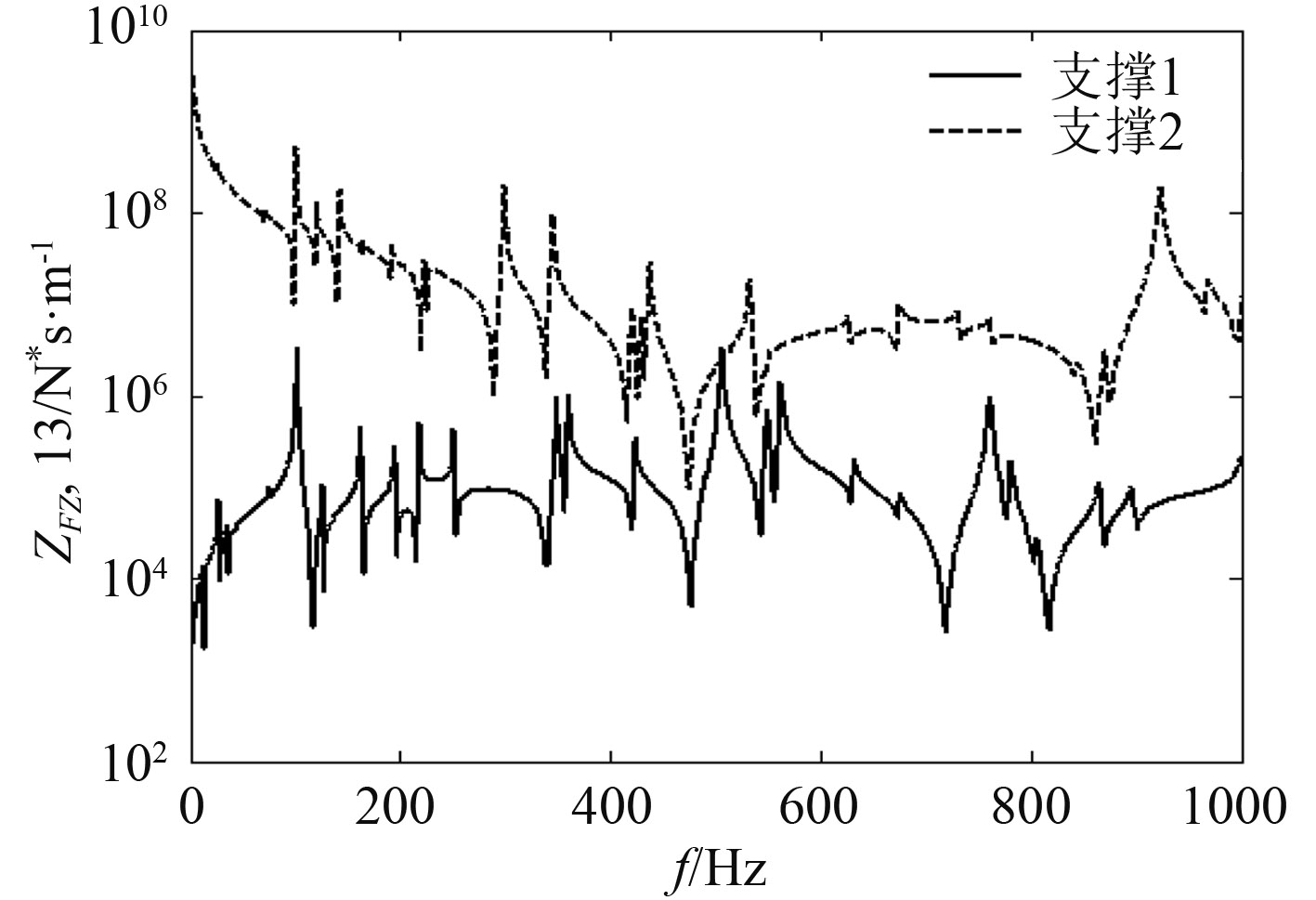
4.2 计算方法分析通过改变不同的分支角度和支撑刚度等参数可以得到不同形状和支撑下的三通分支管的阻抗值,并且计算方法可以计算7个种阻抗值,包括声阻抗以及轴向和横向机械阻抗。以下以试验装置1的基础上改变分支角度和支撑刚度得到的阻抗比较,图10和图11为改变分支角度得到的声阻抗和横向弯曲阻抗比较,分支角度1为α1=π,α2=π/2,分支角度2为α1=π,α2=3π/4。图12为改变支撑刚度得到的阻抗比较,其中支撑1:1号管首部和2,3号管末端kx=ky=kz=ktx=kty=ktz=2×105 N/m。支撑2:1号管首部和2,3号管末端kx=ky=kz=ktx=kty=ktz=2×1010 N/m。
从图10和图11可看出,其中分支角度1为T型三通管,分支角度2为在主干管旁侧产生一个分支,在不同的分支角度下,结构参数和流体参数一定,对阻抗的影响比较小。
从图12可看出,不同的支撑刚度对机械阻抗的影响比较大,支撑2相当于固定支撑,支撑1为弹性支撑,支撑刚度越大,管道传递阻抗越大,根据能量原理,输入激励相同情况下 ,支撑刚度越大,通过管道传递的能力越小,显然通过支撑传递的能量越大,因此实船管路应采用弹性支撑,使通过管道的能量大,而通过支撑传递的能量小,减小管道振动通过支撑传递进而产生声辐射。
从以上可以看出,可通过改变输入参数,很方便地得到不同方向振动对应的阻抗值,计算方法有效便捷,可以为轴向和横向振动的分析提供支撑。
5 结 语1)建立了考虑流固耦合的任意支撑和分支角度的计算方法,并通过试验验证了方法的正确性,可以对不同支撑以及不同形状的三通管阻抗进行计算分析;
2)通过改变支撑、结构等物理参数,利用计算程序可以得到不同方向振动对应的声阻抗和机械阻抗,为三通管道的阻抗分析以及声学优化设计等提供支撑,计算方法方便快捷。

 2017, Vol. 39
2017, Vol. 39
