2. 北京理工大学 宇航学院,北京 100081
2. School of Aerospace Eengineering, Beijing Institute of Technology, Beijing 100081, China
非金属材料如橡胶、聚氨酯发泡材料等制备的减震器由于具有独特的材料属性,以及易加工成型的工艺特点使得其在导弹发射装置减震系统以及其他减震环节中得到了广泛应用。为满足复杂振动环境下的减震要求,这类减震器往往具有复杂的结构特征,其力学性能的研究、模拟和等效一直是国内外研究人员关注的重要内容[1 – 4]。
近年来,张强等[5]为模拟某导弹发射装置减震系统的减震性能,将减震结构简化为非线性弹性单元,研究了弹体遭受冲击后的加速度响应情况,结果表明由外筒、筒间减震块、内筒、适配器组成的两级减震系统具有良好的减震效果,能大幅衰减传递到弹体上的冲击。王平等[6]为提高机载光电吊舱的成像质量和稳定精度,设计了2种能限制一定自由度的小型金属橡胶减振器并将其分别嵌入光电吊舱内、外框架减振系统中,并对其减震性能进行了实验和计算分析仿真结果表明光电吊舱两级减振系统对25Hz以上的角振动有很好的减振效果;Mattias[7]在考虑橡胶减震器的频率与振幅相关特性的基础上,提出了橡胶减震器的一维等效模型,并对其等效效果进行了试验验证;和法家等[8]以研究某飞机发动机橡胶减振器为研究对象,对其进行了一系列实验,得到了振动频率、激励振幅、预载荷与橡胶减震器动刚度的主要关系。可以看出,在复杂减震系统中,有效表征和模拟减震器结构的力学性能、并采用合适的方式进行等效和简化,是进行复杂减震系统分析的关键内容之一。
本文针对复杂减震系统中的非金属减震器结构,利用有限元方法建立其计算分析模型,获得了与实验测试吻合良好的计算结果。在此基础上,提出利用三维实体结构建立等效模型,并通过实物实验或数值实验方法获得等效材料参数的复杂非金属减震结构简化建模方法,为包含大量非金属减震结构的复杂减震系统三维建模和分析提供基础。实例分析表明,文中提出的等效处理方法模型简单、参数明确,在减震器的工作方向上与实际结构的力学性能吻合良好。
1 复杂非金属减震器有限元建模分析1.1 有限元模型复杂非金属减震器的结构形式多种多样,本文以预弯柱体减震器为对象,对其有限元建模分析过程和等效处理方法进行介绍。为便于对照,选取与文献[9]中相同的预弯柱体减振器结构,如图1(a)所示。减震器的外形尺寸为L=105 mm,H=52 mm,W=105 mm,h=32 mm,b=7.5 mm,β=73°,材料为浇注型聚氨酯弹性体。
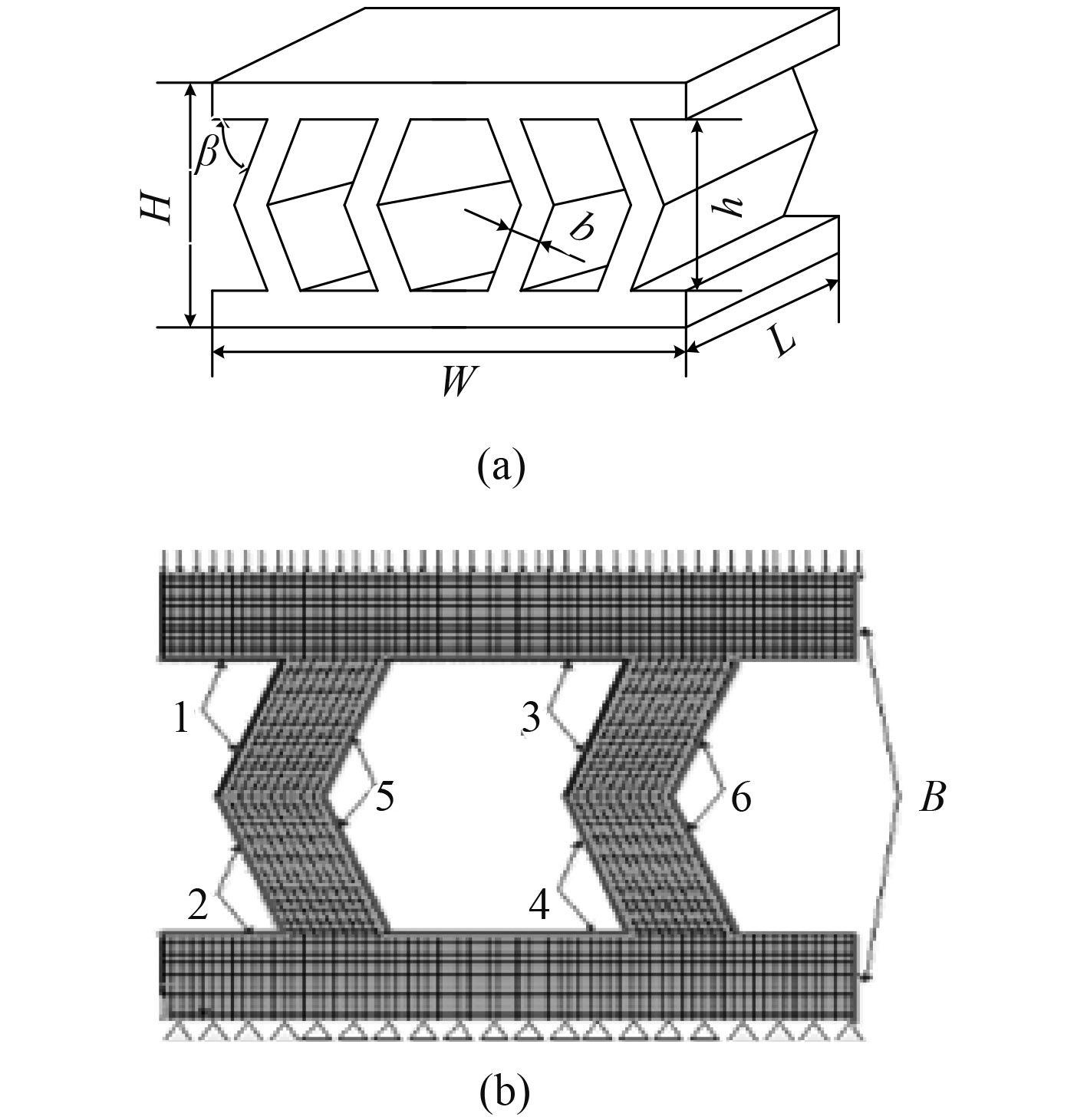
|
图 1 预弯柱体减震器示意图 Fig. 1 Structure of isolator with chevron-shapedstruts |
根据预弯柱体减震器的结构尺寸建立如图1(b)所示的三维有限元模型,在模型上表面施加0~20 mm的位移载荷,在下表面施加固定约束,在图示B处施加对称面约束,在减震器压缩的过程中,1,2,3,4,5,6处会出现接触,因此在这些位置施加对称接触进行处理。接触类型为点面接触,接触过程中不考虑摩擦。考虑到施加的变形尺寸相对原始尺寸较大,在有限元求解计算中采用了大变形模型。
针对聚氨酯材料的超弹特性,这里选用不可压缩的九参数Mooney-Rivlin本构模型对材料属性进行表征,其具体形式为:
| $\begin{split}W \!\!= & {c_{10}}({I_1} \!-\! 3) \!+\! {c_{01}}({I_2} \!-\! 3) \!+\! {c_{20}}{({I_1} \!-\! 3)^2}+\\& \!\!\! {c_{11}}({I_1} \!-\! 3)({I_2} \!-\! 3) \!+\! {c_{02}}{({I_2}\! -\! 3)^2} \!+\! {c_{30}}{({I_1} \!-\! 3)^3}+\\& \!\!\! {c_{21}}{({I_1} \!-\! 3)^2}({I_2} \!- \!3)\! +\! {c_{12}}({I_1} \!-\! 3){({I_2} \!\!-\!\! 3)^2} \!+\! {c_{03}}{({I_2}\! -\! 3)^3}{\text{。}}\end{split}$ | (1) |
式中:I1和I2分别为第一和第二Cauchy-Green应变不变量;cij为与材料相关的参数,其中c10,c01,c20,c30分别为为2 200 000,300 000,–700 000,450 000,其余为0,单位为Pa。
1.2 有限元分析结果利用商用有限元软件Ansys对上述预弯柱体减震器有限元模型进行求解计算,获得随加载位移变化的减震器响应状态。图2给出了加载位移分别为5 mm,20 mm时的结构变形和应力分布。可以看出,在位移载荷为5 mm的情况下,减震器的响应主要为中间柱体的弯曲变形,并在1,2,3,4位置处出现了局部接触状态,而5,6位置处未出现接触,此时减震器的刚度特性主要与减震器中间柱体的抗弯能力有关,应力最大值出现在接触的位置。在位移载荷为20 mm的情况下,中间柱体产生了较大的弯曲变形,1,2,3,4,5,6处均出现了大面积接触,且应力最大值出现在中间柱体的弯曲拉伸部分,此时减震器的刚度特性不仅与聚氨酯材料的特性有关,还与减震器中间柱体的变形以及大面积接触有关。
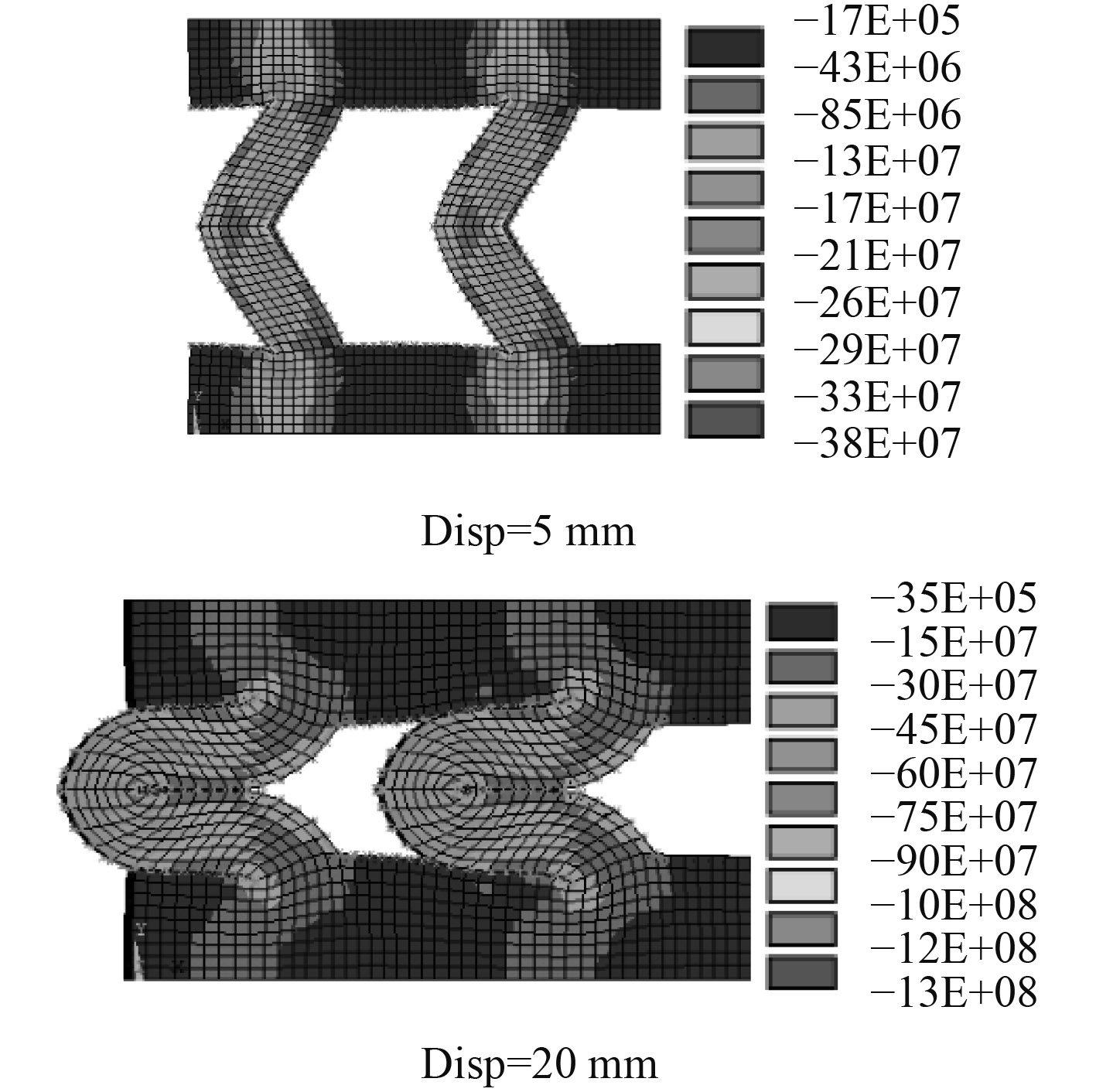
|
图 2 应力分布图 Fig. 2 Stress distribution |
图3给出了计算获得的减震器在位移载荷作用下的变形-受力曲线。图中F为有限元模型下表面节点支反力之和,DISP为减震器在高度方向上的变形量,在很大程度下,该曲线反映了减震器在载荷作用下的刚度特性。从图中可看出,在压缩量较小时(小于8 mm),减震器承受的作用力随压缩量增加而快速增加;压缩量在8~18 mm这一范围内,减震器承受的作用力随压缩量的变化较为缓慢。如前所述,这一阶段减震器中间柱体发生弯曲变形,其整体刚度特性降低。在压缩量超过18 mm后,减震器中间柱体弯曲后产生大面积接触,使其刚度特性快速增加。从这一过程可以看出,对于复杂非金属减震器,其整体刚度特性不但与材料属性有关,也与其内部结构以及工作状态有关,呈现出复杂的非线性状态。在包含多个以至几十个类似复杂减震器的减震系统中,采用完整的减震器结构进行减震性能分析在计算量上存在较大的困难,为此寻求合理的减震器等效模型,并准确反映其在工作方向上的刚度特性,是进行复杂系统分析的关键。
从图3中还可以看出,在整个压缩过程中,计算结果与文献给出的实验数据吻合良好。在压缩量小于18 mm的范围内,结果误差小于5%;在压缩量大于18 mm后,受减震器内部结构产生大面积接触影响,刚度特性快速增加,计算与实验结果间的误差也有所增加,但变化趋势相同。由于数值计算与实物试验具有较好的一致性,因此在本文的研究中,主要采用数值试验的方法获取结构的响应参数,并以此进行等效过程的实例分析。
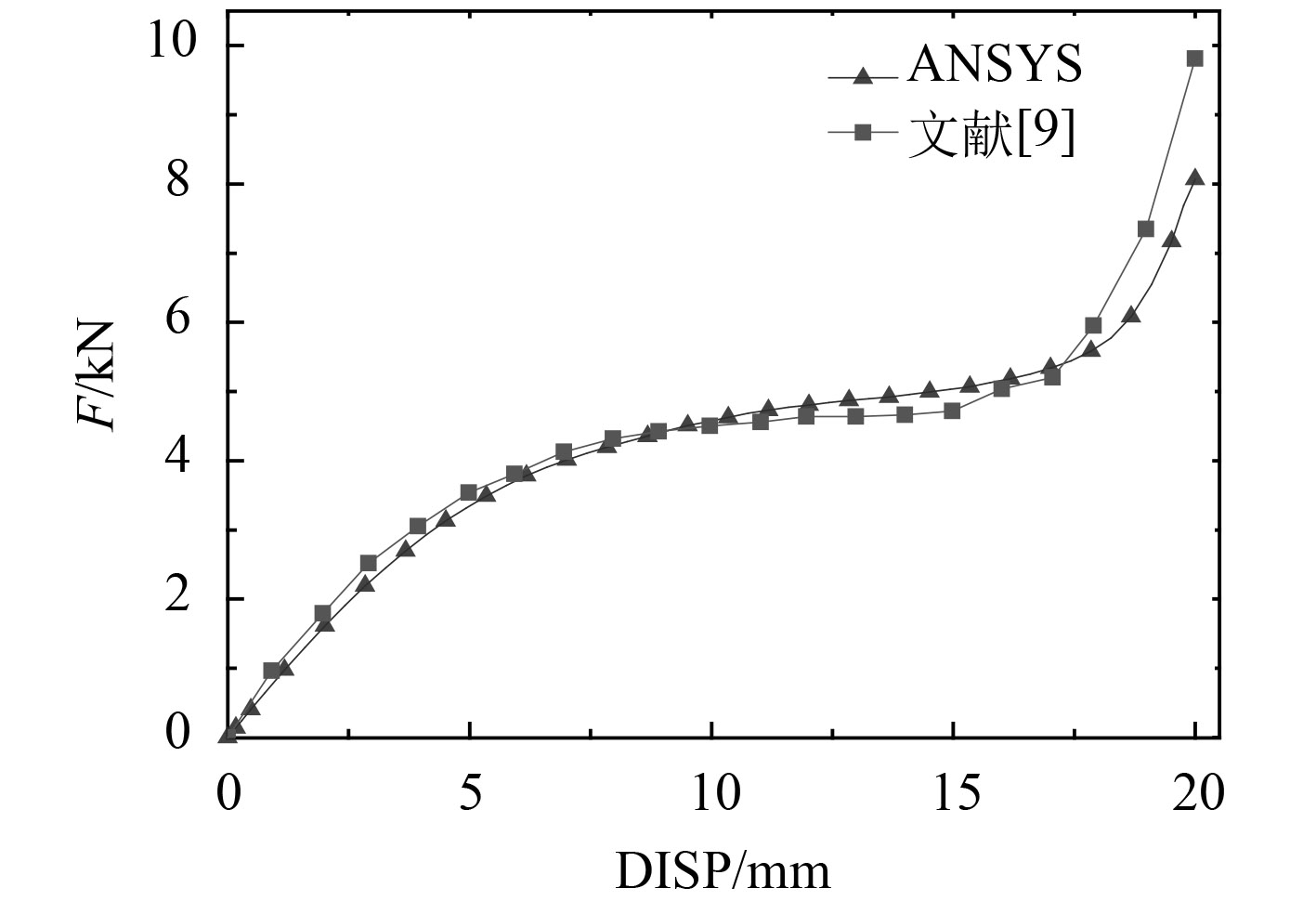
|
图 3 减震器力-位移曲线 Fig. 3 Comparison curves of F-DISP between the tested and the FEA |
在多数情况下,尤其在本文涉及的导弹减震系统中,减震器工作状态通常为压缩变形和吸能,因此在减震器工作时,可将其静态刚度特性考虑为具有超弹本构特性的实心结构在单轴压缩时的响应过程。对于不可压缩的超弹性材料在单轴压缩下的主应力与应变能函数的存在如下关系[10]:
| ${\sigma _{11}}{\rm{ = - }}{p_e} + {\alpha _1}{B_{11}} + {\alpha _2}B_{11}^2{\text{,}}$ | (2) |
| ${\sigma _{22}} = {\sigma _{33}} = - {p_e} + {\alpha _1}B_{11}^{ - 1/2} + {\alpha _2}B_{11}^{ - 1} = 0{\text{,}}$ | (3) |
| ${\alpha _1} = 2(\partial W/\partial {I_1} + {I_1}\partial W/\partial {I_2}){\text{,}}$ | (4) |
| ${\alpha _2} = - 2\partial W/\partial {I_2}{\text{,}}$ | (5) |
| ${{B}} = {{F}} \times {{{F}}^{\rm T}}{\text{,}}$ | (6) |
| ${{F}} = \left[ {\begin{array}{*{20}{c}}\lambda & 0 & 0\\0 & {{\lambda ^{ - 1/2}}} & 0\\0 & 0 & {{\lambda ^{ - 1/2}}}\end{array}} \right]{\text{,}}$ | (7) |
| ${I_1} = tr({{B}}){\text{,}}$ | (8) |
| ${I_2} = \frac{1}{2}\left[ {I_1^2 - tr({{{B}}^2})} \right]{\text{。}}$ | (9) |
式中:pe为静水压力;F为应变梯度张量; B为左Cauchy-Green变形张量;W为应变能函数;I1,I2为B的第一,第二基本不变量;σ11,σ22,σ33为真实应力;λ为单轴压缩方向的拉伸率。
将σ11-λ的关系转化为工程应力应变的关系式为:
| $\sigma _{11}^e = {\sigma _{11}}/\lambda{\text{,}} $ | (10) |
| $\lambda = 1 + \varepsilon {\text{。}}$ | (11) |
式中:
可以看出,σ11-λ的关系、
复杂非金属减震器除具有静态刚度非线性外,通常还具有与应变率相关的刚度特性,通常通过prony级数[11]定义材料的粘弹特性,无量纲后的应力松弛模量可表示为:
| $e(t) = 1 - \sum\limits_{i = 1}^N {{e_i}} \left[ {1 - exp(\frac{{ - t}}{{{l_i}}})} \right]{\text{。}}$ | (12) |
式中:
通过复杂非金属减震器的应力松弛实验,可获得时变工程应力数据。在等效模型中,通过参数拟合,可确定其粘弹性材料的待定参数ei和li值。
2.2 等效方法在包含多个复杂结构减震器的减震系统中,在考虑减震性能时主要考察其整体在冲击响应过程中的力-位移曲线,而不关心复杂结构减震器内部所发生的变化。因此在对复杂结构减震器进行等效时,主要保证等效的减震器在工作方向上的响应特性与复杂结构减震器整体在冲击响应过程中的力-位移曲线相一致即可。在等效过程中,采用如下假设和方法:
1)等效模型为三维实心均匀材料结构,材料各向同性;
2)利用超弹性材料参数表征由实际结构材料以及结构变形、接触等因素引起的位移-载荷非线性变化过程;
3)利用prony级数形式的粘弹性材料参数表征实际结构应变率相关的刚度特性。
具体模型等效的思路和处理过程如图4所示。
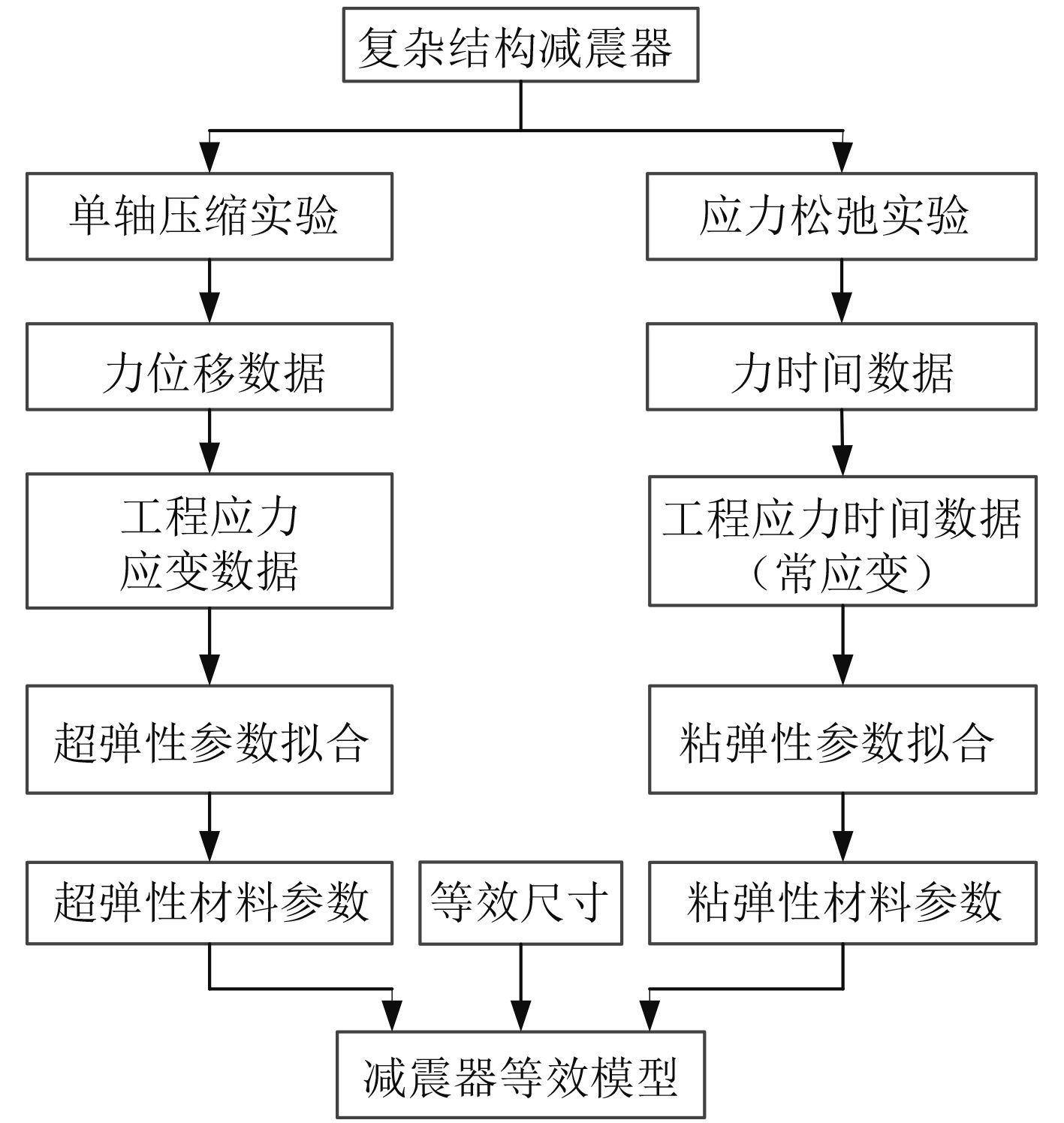
|
图 4 等效流程 Fig. 4 Flow chart for equivalence |
为了使等效模型最大程度地真实反映减震器在工作过程中所起的作用,等效模型的外形尺寸应与减震器尽可能一致。在应用过程中,可取等效模型在工作方向上的高度与减震器相同;在支撑平面上取面积与实际减震器支撑平面面积相同,并参考实际减震器外廓形式设置支撑平面形状。
在通过单轴压缩实验获得实际减震器的力-位移响应后,可通过如下公式直接计算其工程应力和工程应变:
| ${\sigma _{\rm{c}}}{\rm{ = }}N/A{\text{,}}$ | (13) |
| ${\varepsilon _c} = \Delta L/L{\text{。}}$ | (14) |
式中:σc为复杂结构减震器压缩过程中的虚拟工程应力;N为复杂结构减震器的下表面支反力的和;A为等效实心结构支撑面的面积;εc为复杂结构减震器压缩过程中的虚拟工程应变;∆L为复杂结构减震器的压缩位移;L为复杂结构减震器的高度。
在实际应用中,为通过实验数据获得超弹性材料的本构模型,通常需要将单轴压缩数据转变为等双轴拉伸数据,二者在理论上存在如下关系[12]:
| ${\sigma _{{c}}} = {\sigma _b}{(1 + {\varepsilon _b})^3}{\text{,}}$ | (15) |
| ${\varepsilon _{{c}}} = 1/{(1 + {\varepsilon _b})^2} - 1{\text{。}}$ | (16) |
式中:εb为等双轴拉伸工程应变;εc单轴压缩工程应变;σb为等双轴拉伸工程应力;σc为单轴压缩工程应力。
利用等双轴拉伸实验数据,可通过参数拟合方式获得常见超弹性材料本构模型如多项式模型、Mooney-Rivlin模型的待定参数,即获得等效模型的超弹性材料本构参数。对于反应率相关属性的粘弹性模型,同样可通过由实验获得的时变应力数据拟合出prony级数表征的粘弹性材料参数。
3 减震器的等效实例与分析3.1 非线性弹性等效实例在有限元建模分析中参考的减震器结构在工作过程中主要表现为非线性弹性特征。为建立其等效模型,选择其等效模型与实际减震器具有同样的外廓尺寸,如图5所示;设置反映非线性弹性属性的本构模型为5参数的Mooney-Rivlin本构模型。

|
图 5 实际结构与等效实心结构示意 Fig. 5 Comparison between the equivalent structure and the actual structure |
利用图3所示的数值实验数据,通过工程应力和工程应变计算、单轴压缩和双轴拉伸应力应变转换以及参数拟合,可获得5参数Mooney-Rivlin超弹性本构模型的系数如表1所示。
|
|
表 1 等效材料参数表 Tab.1 Material parameters for the equivalent |
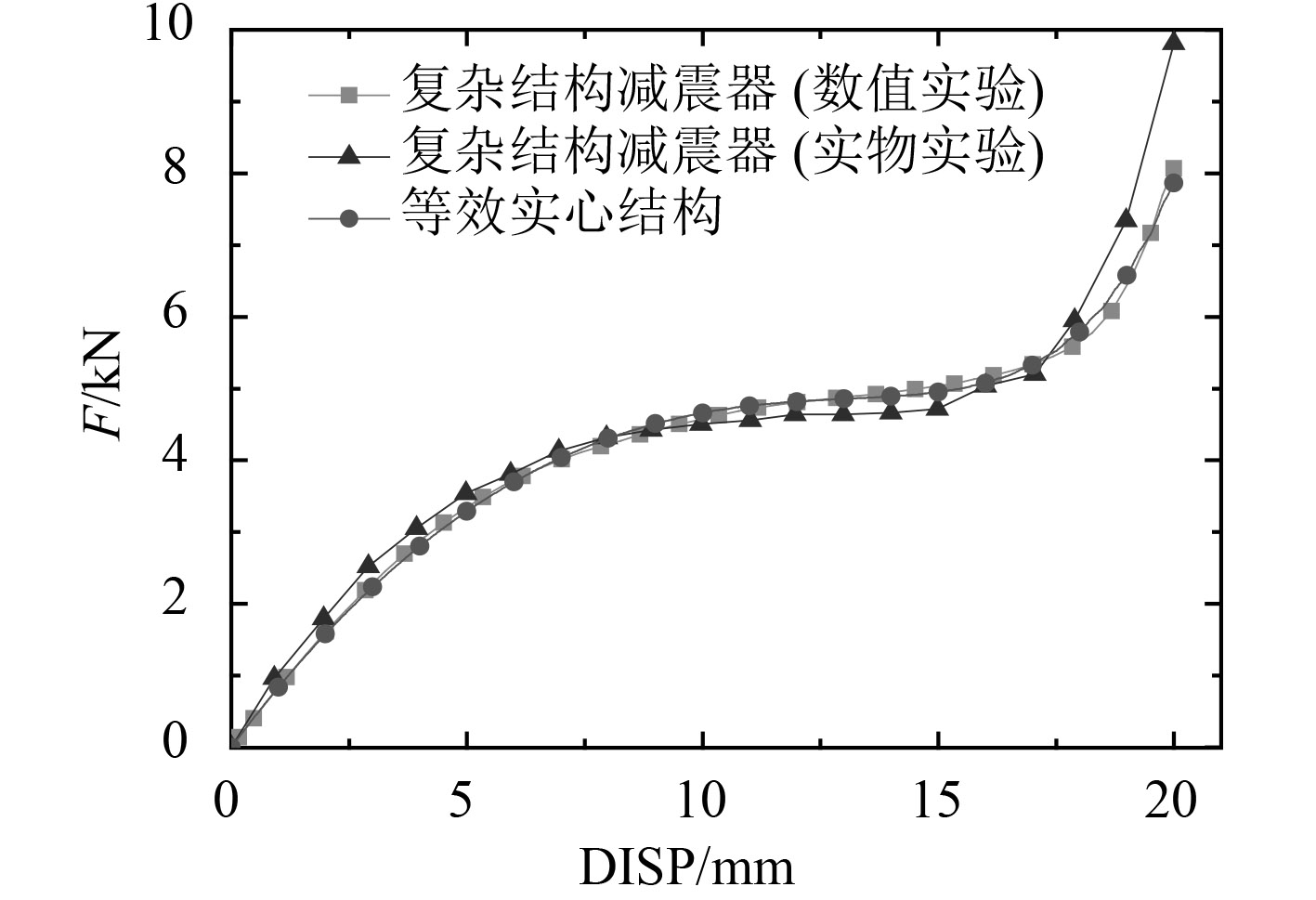
为校验等效模型,同样利用有限元方法建立其计算模型,在其下表面施加固定约束,在其上表面施加0~20 mm位移载荷,获得力-位移曲线如图6所示。从图中可看出,等效模型在压缩过程中的力-位移曲线与实际减震器在压缩过程中的力-位移曲线吻合良好。实际减震器在压缩过程中的力-位移曲线的平台效应主要是由其内部的复杂结构引起;等效模型没有复杂内部结构,但通过等效后的超弹性材料属性,使其力-位移曲线仍然有平台效应,且与复杂结构减震器的力-位移曲线相一致,说明等效实心结构与复杂结构减震器具有相同的静态刚度特性。
|
图 6 等效实心结构与实际结构结果对比 Fig. 6 Comparison of curves between the equivalent structure and the actualstructure |
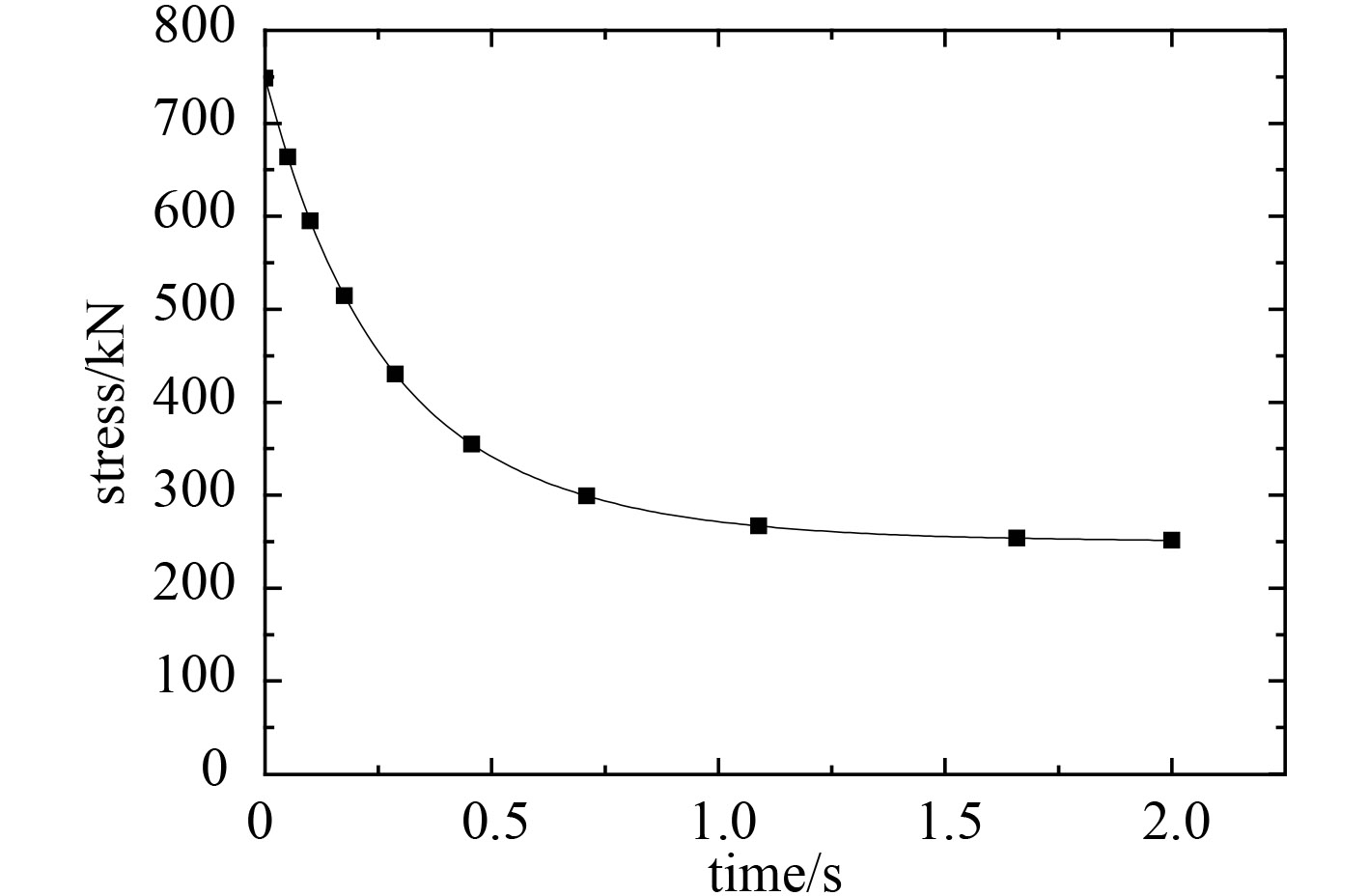
以前述复杂非金属减震器为例,为考虑相关粘弹特性及其等效过程,假定该减震器材料具有粘弹属性,并可通过2参数prony模型进行表示,模型参数[13]设置为a1=0.333 33,t1=0.4,a2=0.333 33,t2=0.2。同样选择其等效模型与实际减震器具有相同的外廓尺寸,并利用2参数prony模型表示其率相关的等效粘弹属性。通过对复杂非金属减震器施加20 mm的常位移载荷进行数值实验并进行转换,获得工程应力随时间变化曲线如图7所示。利用参数拟合,获得prony模型参数与假定的减震器粘弹性材料参数相同,表明该减震器在结构上的阻尼特性并不显著,其率相关特性主要体现为材料的粘弹特性。
|
图 7 应力松弛曲线 Fig. 7 Stress relaxation curve |
为校验同时具有非线性弹性和率相关粘弹特性的减震器等效模型,利用有限元计算模型,在等效模型下表面施加位移约束,上表面施加的正弦位移载荷为:
| ${\mathop{ Disp}\nolimits} = 10 \times \sin \left( {4 \times \uppi \times t + \uppi /2} \right) - 10({\rm mm}){\text{。}}$ | (17) |
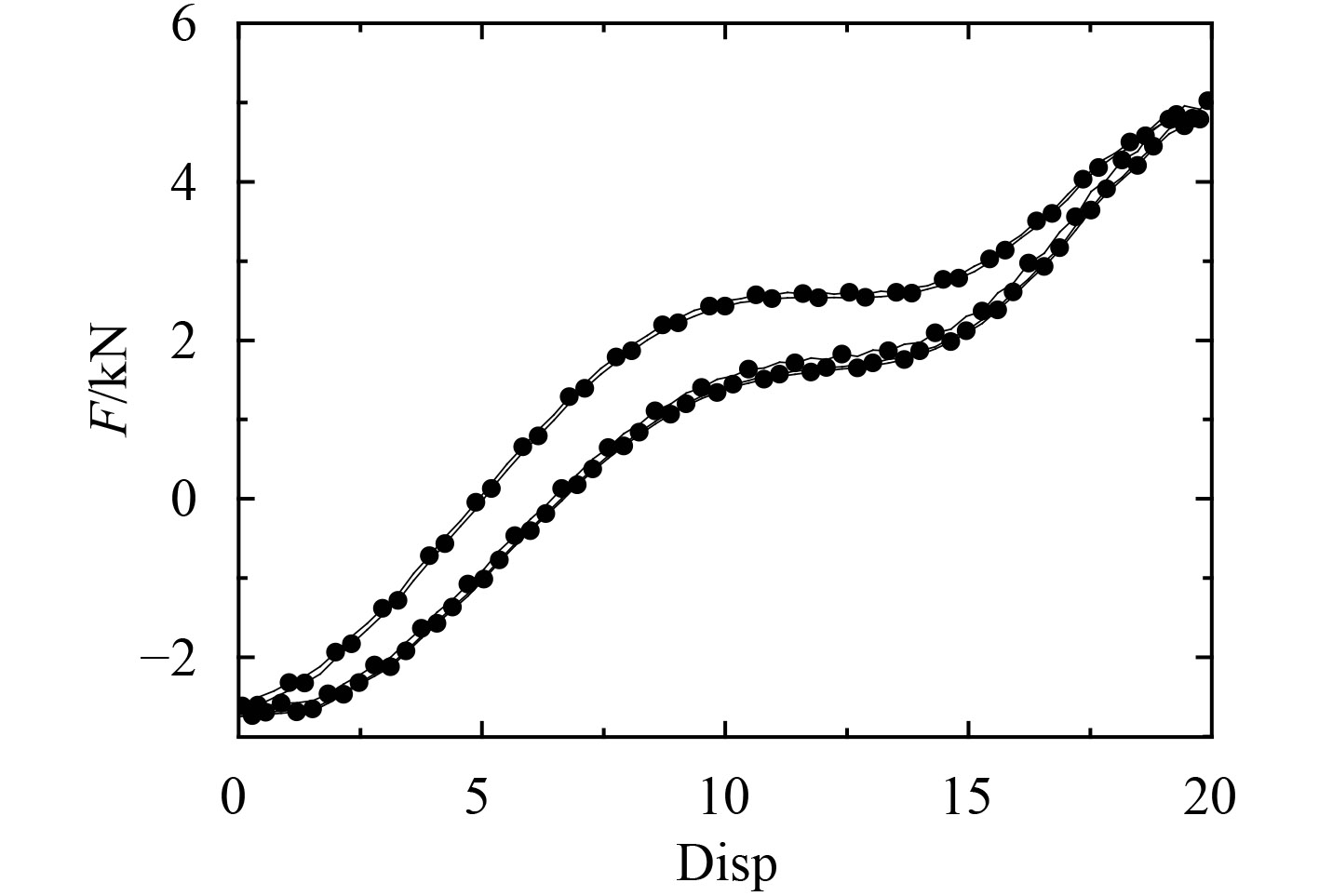
经过4个载荷周期计算,获得等效模型计算稳定后的力-位移曲线如图8所示。可以看出在加、卸载过程中,力-位移曲线经历了不同的过程,呈现出典型的回滞环结构,反映了结构的率相关粘弹特征;在每次独立的加载和卸载过程中,力-位移曲线均出现具有平台效应的非线性弹性状态。值得注意的是,在最大位移20 mm处,由于粘弹性特性的应力松弛效应,同时具有超弹性与粘弹性特性的等效模型的支反力要比只有超弹性材料属性等效结构的支反力小;在位移为0时,由于粘弹性特性的阻尼效应,同时具有超弹性与粘弹性性的等效模型支反力为负值。
|
图 8 力-位移迟滞回线 Fig. 8 Hysteresis loop of F-Disp |
本文针对复杂非金属减震器结构,利用有限元模型进行了计算分析,获得了与实验结果吻合良好的计算数据,表明基于有限元模型的数值实验能够较好的反映非金属减震器的工作过程。
针对复杂大型减震系统简化建模和分析的需求,提出一种利用材料属性等效复杂非金属减震器非线性响应特性的等效建模方法。实例分析表明,等效模型在减震器的主要工作方向上能够有效反映实际减震器结构的非线性弹性和率相关粘弹特性,并能施加减震结构的三维连接和约束关系,能够为复杂减震系统的三维建模和分析提供借鉴和参考。
| [1] | BERG M. A model for rubber springs in the dynamic analysis of rail vehicles[J].Proceedings of the Institution of Mechanical Engin, 1997, 211(2): 95–108. |
| [2] |
隋允康, 彭细荣, 杜家政. 橡胶缓振垫力学性能尺寸效应分析[J].北京工业大学学报, 2004, 30(4): 398–400.
SUI Yun-kang, PENG Xi-rong, DU Jia-zheng. Analysis of size effect on mechanics behavious of the rubber buffer for absorbing vibration[J].Journal of Beijing University of Technology, 2004, 30(4): 398–400. |
| [3] |
王基, 朱石坚. V形橡胶减振器静刚度研究[J].噪声与振动控制, 2003, 23(1): 37–40.
WANG Ji, ZHU Shi-jian. Study on the static stiffness of shape of V rubber Vibration-lsolator[J].Noise and Vibration Control, 2003, 23(1): 37–40. |
| [4] |
周振凯, 徐兵, 胡文军, 等. 橡胶隔振器大变形有限元分析[J].振动与冲击, 2013, 32(5): 171–175.
ZHOU Zhen-kai, XU Bing, HU Wen-jun, et al. Large deformation finite element analysis of rubber isolator[J].Journal of Vibration and Shock, 2013, 32(5): 171–175. |
| [5] |
张强, 吴明晨. 某型发射装置水平减震系统仿真研究[J].舰船电子工程, 2012, 32(2): 73–75.
ZHANG Qiang, WU Ming-chen. Emulation research on lateral shock absorber system of certain launching system[J].Ship Electronic Engineering, 2012, 32(2): 73–75. |
| [6] |
王平, 张国玉, 高玉军, 等. 金属橡胶减振器在机载光电吊舱复合减振系统中的应用[J].振动与冲击, 2014, 33(5): 193–199.
WANG Ping, ZHANG Guo-yu, GAO Yu-jun, et al. Application of metal-rubber dampers in vibration reduction system of an airborne electro-optical pod[J].Journal of Vibration and Shock, 2014, 33(5): 193–199. |
| [7] | SJÖBERG M M, KARI L. Non-linear behavior of a rubber isolator system using fractional derivatives[J].Vehicle System Dynamics, 2002, 37(3): 217–236. DOI: 10.1076/vesd.37.3.217.3532 |
| [8] |
和法家, 卢曦. 某直升机橡胶减震器动刚度特性试验[J].实验室研究与探索, 2014, 33(3): 41–44.
HE Fa-jia, LU Xi. Experimental research on dynamic stiffness characteristics of a Rubber-Shock-Absorber[J].Research and Exploration in Laboratory, 2014, 33(3): 41–44. |
| [9] |
赵华, 王敏杰, 赵书德, 等. 预弯柱体减振器静态特性的尺寸效应[J].兵工学报, 2009, 30(11): 1515–1521.
ZHAO Hua, WANG Min-jie, ZHAO Shu-de, et al. Size effect on static mechanics behaviors of isolator with Chevron-Shaped struts[J].ACTA Armamentarii, 2009, 30(11): 1515–1521. DOI: 10.3321/j.issn:1000-1093.2009.11.021 |
| [10] | YANG L M, SHIM V, LIM C T. A visco-hyperelastic approach to modelling the constitutive behaviour of rubber[J].International Journal of Impact Engineering, 2000, 24(6): 545–560. |
| [11] |
傅志红, 喻坚, 魏灵娇. 聚碳酸酯的应力松弛实验及数据处理分析[J].塑料工业, 2014, 42(6): 89–92.
FU Zhi-hong, YU Jian, WEI Ling-jiao. The stress relaxation experiment and data processing analysis of polycarbonate[J].China Plastics Industry, 2014, 42(6): 89–92. |
| [12] |
李树虎, 贾华敏, 李茂东, 等. 超弹性体本构模型的理论和特种试验方法[J].弹性体, 2011, 21(1): 58–64.
LI Shu-hu, JIA Hua-min, LI Mao-dong, et al. Theory and testing method of hyperelastic material constitutive model[J].China Elastomerics, 2011, 21(1): 58–64. |
| [13] |
刘文武, 翁雪涛, 楼京俊, 等. 基于ANSYS对橡胶制品动态分析的谐响应法研究[J].武汉理工大学学报(交通科学与工程版), 2010, 34(5): 966–968.
LIU Wen-wu, WENG Xue-tao, LOU Jing-jun, et al. Study on the harmonic response method to analyse the dynamic characteristics of rubber products based on ansys[J].Journal of Wuhan University of Technology (Transportation Science & Engineering), 2010, 34(5): 966–968. |
 2017, Vol. 39
2017, Vol. 39
