对于干扰信号,通常使用时域滤波或频域滤波进行抑制,但是对于诸如多基地声呐等混响干扰,这种具有极强的时频耦合干扰[1, 2],很难单纯通过时域或频域滤波进行干扰抑制[3]。分数阶傅里叶变换是最近几年研究比较多的一种时频变换算法,该变换能够对时频耦合进行分离[4],如图1(a)所示的线性调频信号的时频图,目标信号和干扰信号不管在时域还是在频域的投影均相互重叠,无法进行分离。分数阶傅里叶变换作为广义的傅里叶变换能够将信号在时频面内进行任意角度旋转,并且线性调频信号在时频面内表现为一条斜线。因此如果将图1(a)的线性调频信号的时频特性进行一定角度的旋转,可得到如图1(b)所示的效果,这时的干扰信号和目标信号在时域投影上相互分离,就可以通过时域滤波的方式将干扰去除。
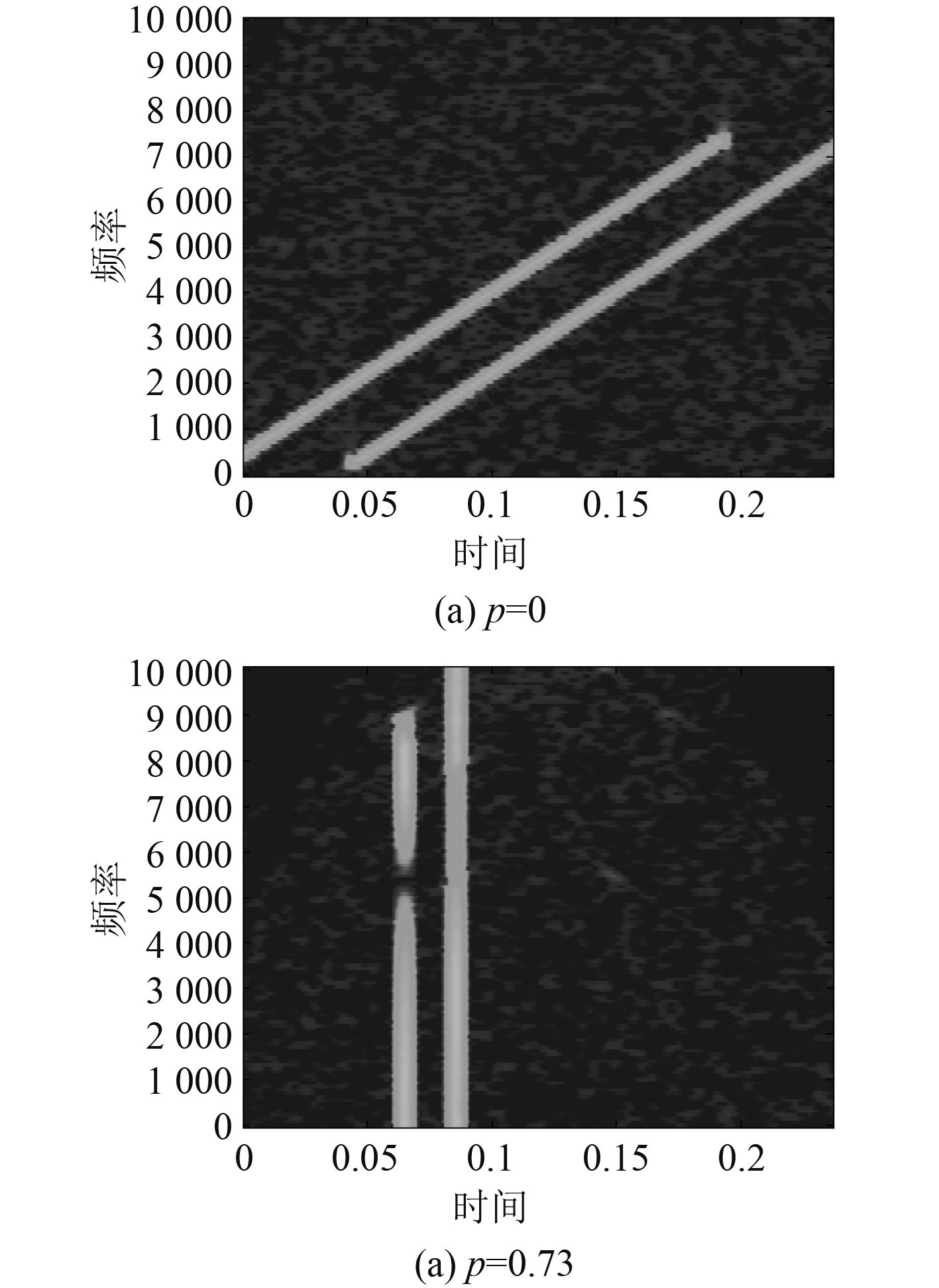
|
图 1 不同分数阶傅里叶变换旋转角度下的时频特性图 Fig. 1 Different fractional Fourier transform under the rotation Angle of the time-frequency characteristics of figure |
本文提出一种基于分数阶傅里叶变换的时频耦合分离特性[5],以及强混响干扰去除方法,并通过数值仿真和水池散射试验对该方法的可行性进行验证。
1 分数阶傅里叶变换的基本原理分数阶傅里叶变换的基本定义如下[5]:
| ${X_p}(u) = {F_p}(x(t)) = \int\nolimits_{ - \infty }^{ + \infty } {x(t){K_p}} (t,u){\rm d}t{\text{,}}$ | (1) |
式中:p为分数阶傅里叶变换的阶次;u为分数阶傅里叶变换域;
| ${K_p}(t,u) \!\!= \!\!\left\{ {\begin{aligned}& \!\!{\sqrt {(1 - j\cot \alpha /2\uppi } }{\text{;}}\\& \,\,\,\, {\exp (j\frac{{{t^2} \!+\! {u^2}}}{2}\cot \alpha \!-\! jut\csc \alpha ), \,\,\, \alpha \! \ne\! n\uppi ;}\\& {\delta (t - u), \quad \quad \quad \quad \quad \quad \quad \quad \alpha \!=\! 2n\uppi ;}\\& {\delta (t + u), \quad \quad \quad \quad \quad \quad \quad \quad \alpha \!\!=\!\! (2n \!\pm\! 1)\uppi }{\text{。}}\end{aligned}} \right.$ | (2) |
其中α为变换角度,
| ${X_{ - p}}(u) = {F_{ - p}}({X_p}(u)) = \int\nolimits_{ - \infty }^{ + \infty } {{X_p}(u){K_{ - p}}} (t,u){\rm d}u{\text{,}}$ | (3) |
从分数阶傅里叶变换的基本定义可知,分数阶傅里叶变换可理解为对信号在时频域内以α角度进行旋转,其中α可以为所希望的任意角度。同时分数阶傅里叶变换又是线性变换,即
| ${F_\alpha }[ax(t) + bn(t)] = {F_\alpha }(ax(t) + {F_\alpha }(n(t){\text{。}}$ | (4) |
信号和噪声叠加后的分数阶傅里叶变换等于各自分别进行分数阶傅里叶变换的叠加,当信号噪声能够通过分数阶傅里叶变换在时频域内进行区分时,就能够对噪声信号进行去除,从而达到抑制干扰的目的。
线性调频信号在分数阶变换(FRFT)域中表现的能量聚焦特性实质为在变换域中的脉冲压缩,图2为线性调频信号在时域和FRFT变换域中的对应关系。由图2可看出,线性调频信号在FRFT变换域中的最佳变换角度α为:
| $\alpha = {\tan ^{ - 1}}(\frac{B}{T})=\;\;\; {\tan ^{ - 1}}(k){\text{,}}$ | (5) |
式中:B为信号的带宽;T为信号脉冲宽度;k为线性调频信号的调频率。

|
图 2 信号在时域和FRFT变换域中的对应关系示意图 Fig. 2 Signal in time domain and the corresponding relation diagram of FRFT transform domain |
在最佳变换角度(α)条件下,线性调频脉冲信号在时域和分数阶域的脉冲宽度变换关系为:
| $\Delta t = T\cos (\alpha )= T\cos (\frac{T}{{\sqrt {{B^2} + {T^2}} }}){\text{。}}$ | (6) |
式中:
从式(6)可看出,线性调频信号在 FRFT 变换域中的脉冲压缩程度取决于信号的带宽、脉冲宽度和调频信号的调频率 k,从本质上说线性调频信号的调频率越大,相应的在变换域中的压缩能力越小,时间分辨能力越差。
通常从水中目标特性测量的角度考虑,需要获得纯净的声散射信号,这就要求最大限度的保证散射信号中除环境噪声外不能混叠其他干扰信号;而对于水中目标探测的角度,只要求能够区分出目标信号即可。根据式(6),将基于分数阶傅里叶变换的混响干扰抑制方法用于目标散射特性测量时,该方法的适用条件为混响和散射声信号的脉冲中心间隔为
考虑到线性调频信号在时频面内表现为以斜率为k的一条斜线,当双基地声呐的发射信号为线性调频信号时,混响和目标散射声在时频面内表现为斜率相同的2条直线,如果能够利用分数阶变换在时频面内进行任意角度旋转的特性,将混响和目标散射声在时频面内旋转至合适角度,使得2条斜线与时间轴相互垂直,则可将混响和目标散射声进行分离。根据上述原理设计的基于分数阶傅里叶变换的混响干扰抑制算法流程如图3所示。
基于上述算法的具体实现步骤如下:
1) 对接收到的包含混响的散射信号进行分数阶傅里叶变换旋转角度扫描,得出最佳旋转角度α;
2) 对接收信号进行角度为α的分数阶傅里叶变换,并在分数阶变换域中对扫描得到的散射信号进行带阻滤波;
3) 对经过带阻滤波的信号进行旋转角度为α的分数阶傅里叶逆变换,得到时域的混响干扰信号;
4) 采用相减法将混响干扰信号从原始接收信号中去除,得到期望的目标散射信号。
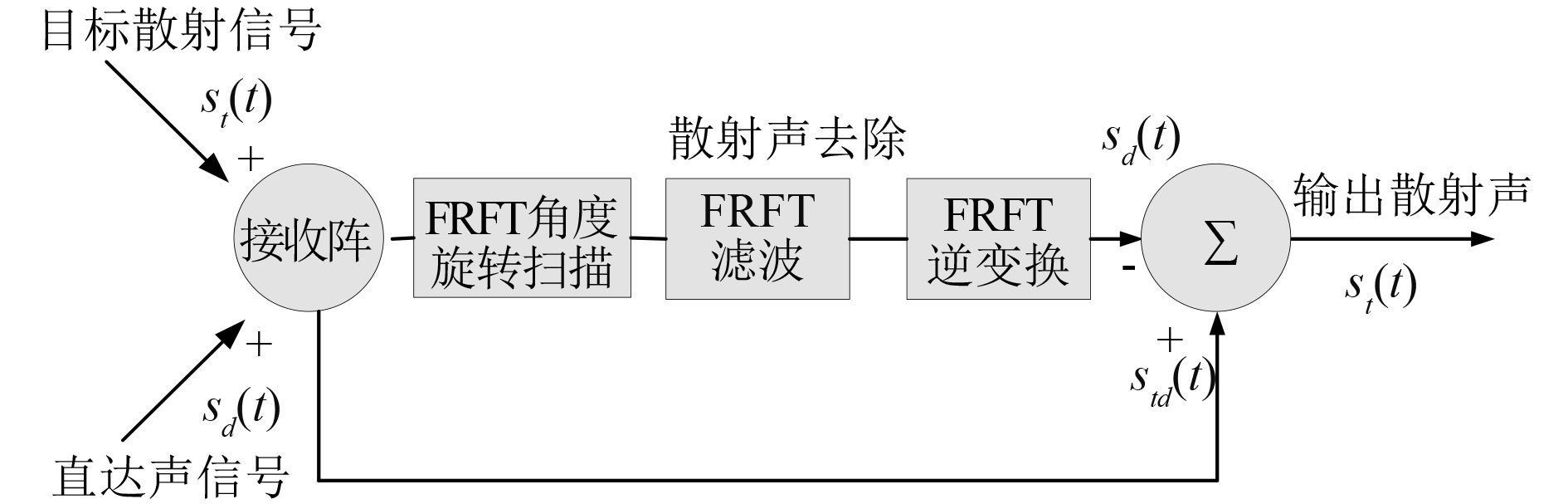
|
图 3 基于分数阶傅里叶变换的混响干扰抑制算法流程 Fig. 3 The reverberation interference suppression algorithm based on fractional Fourier transform process |
为了对基于分数阶傅里叶变换的双基地声呐混响干扰抑制方法的有效性进行验证,本文分别进行了模拟仿真和小目标的水池试验。
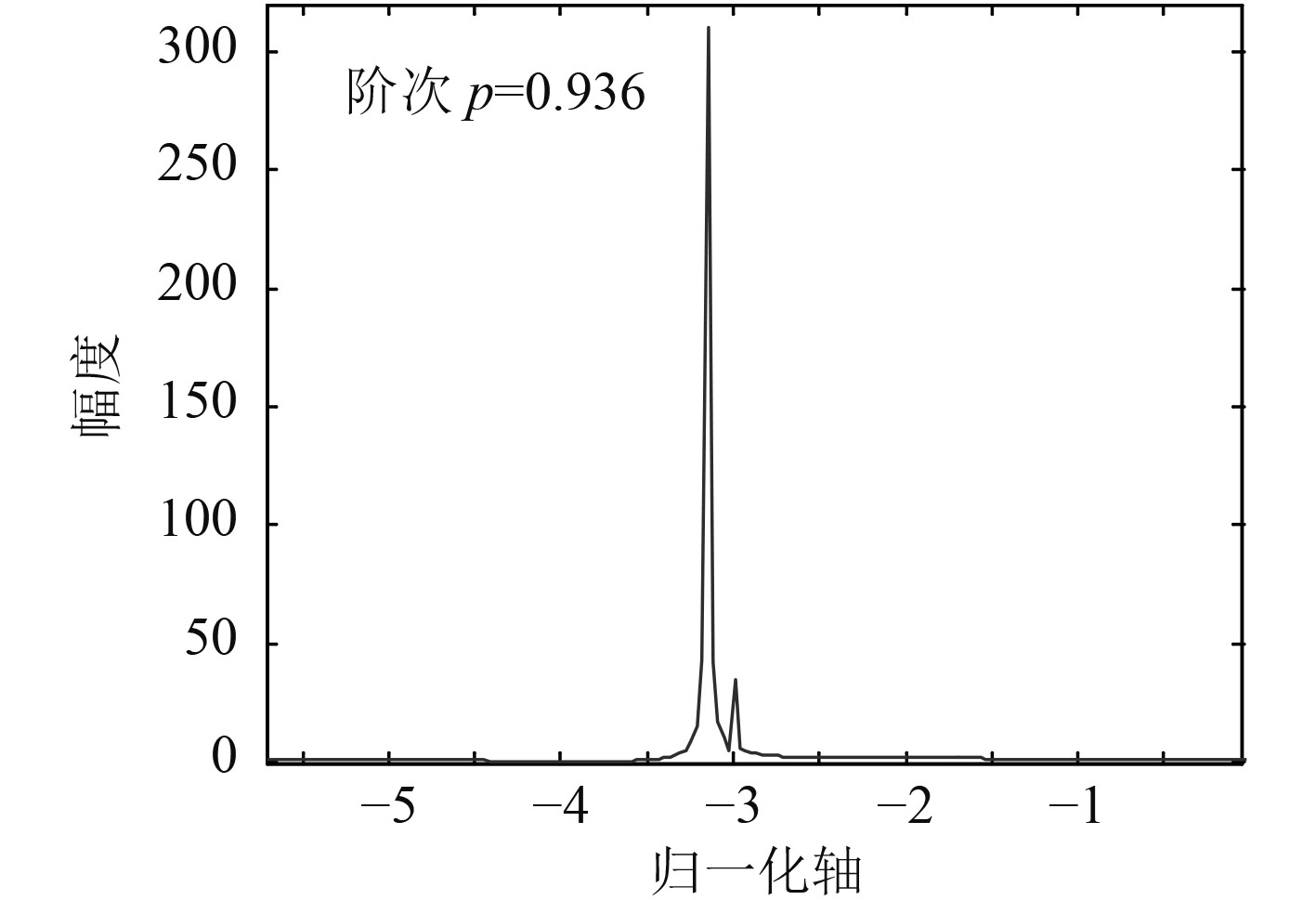
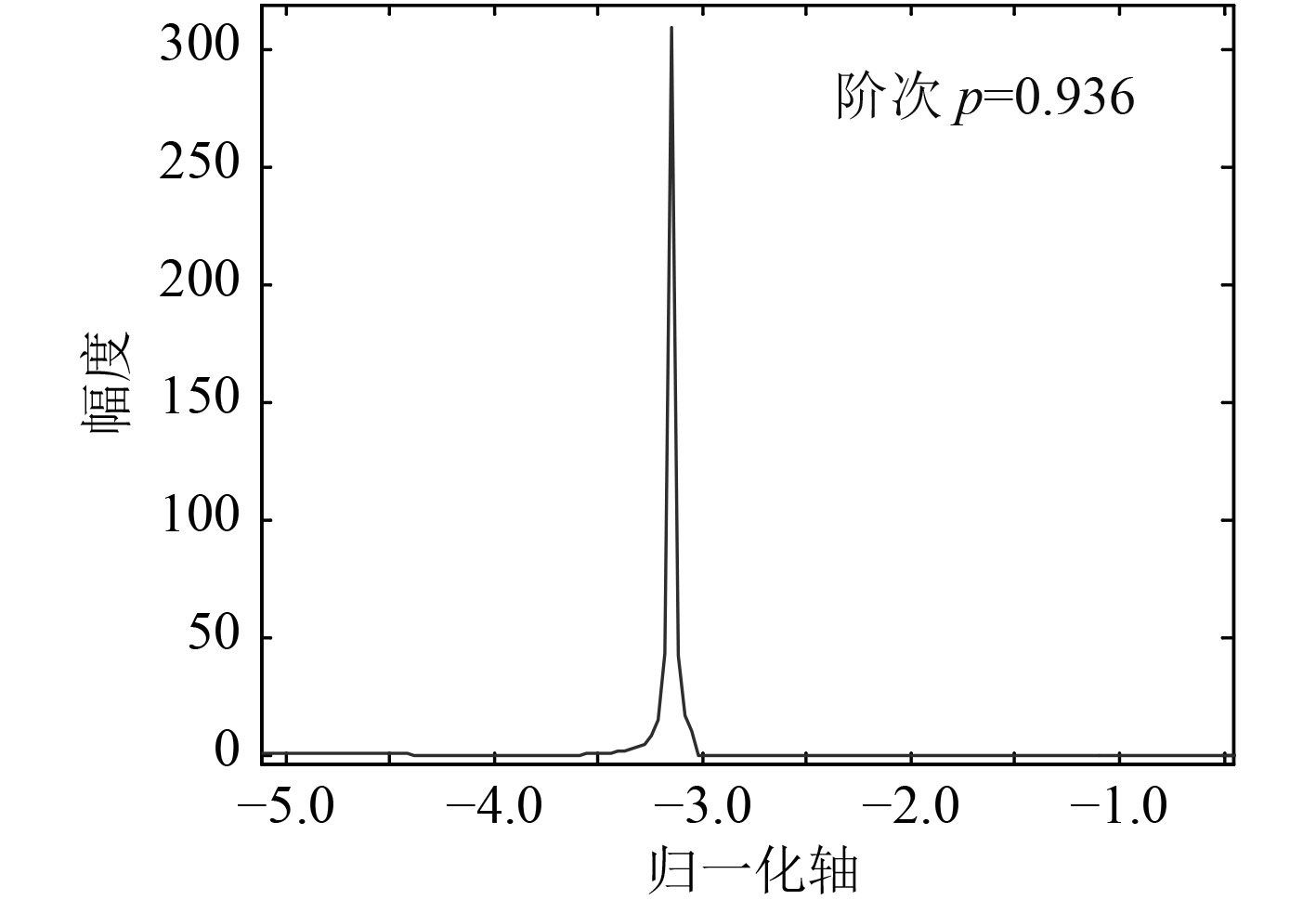
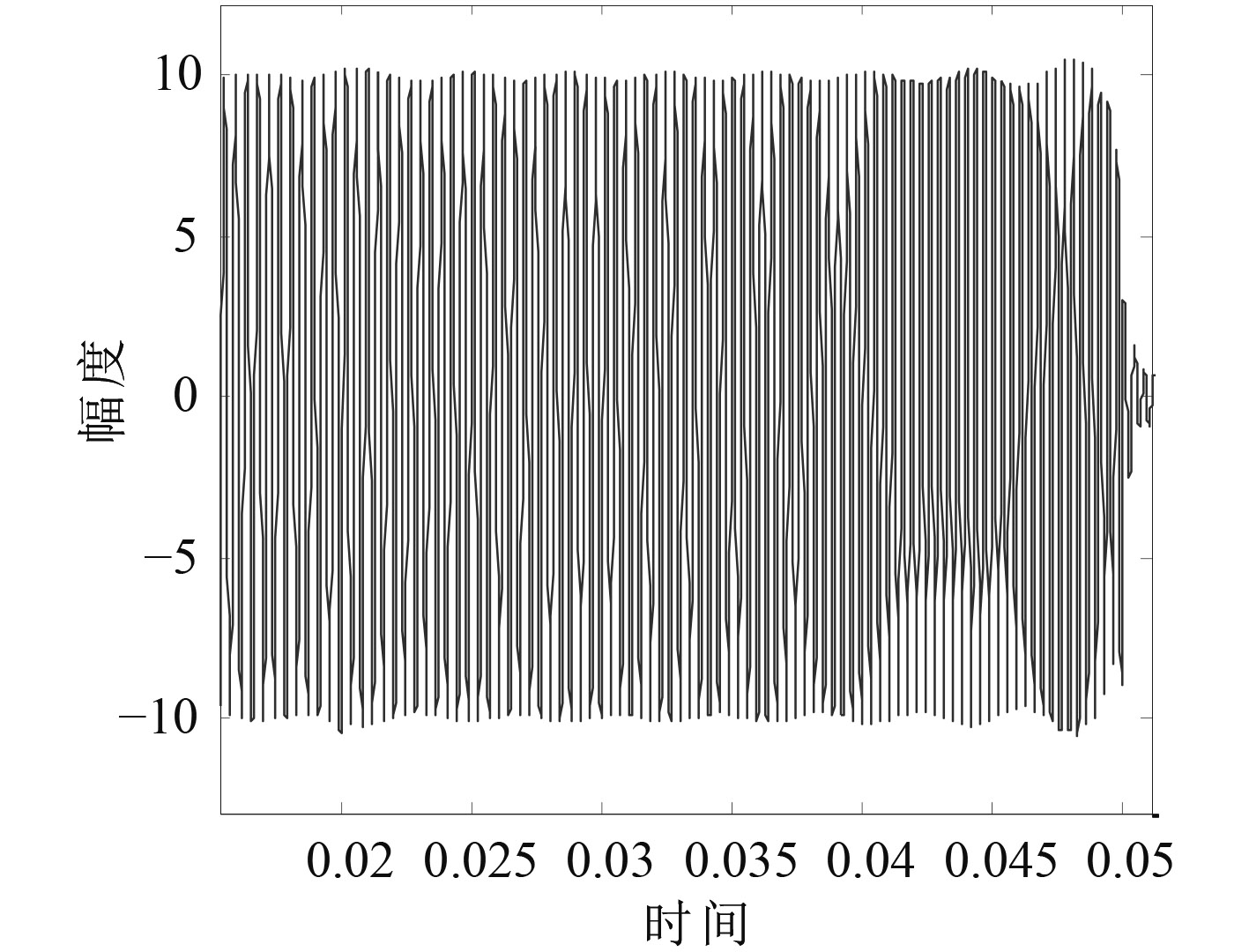
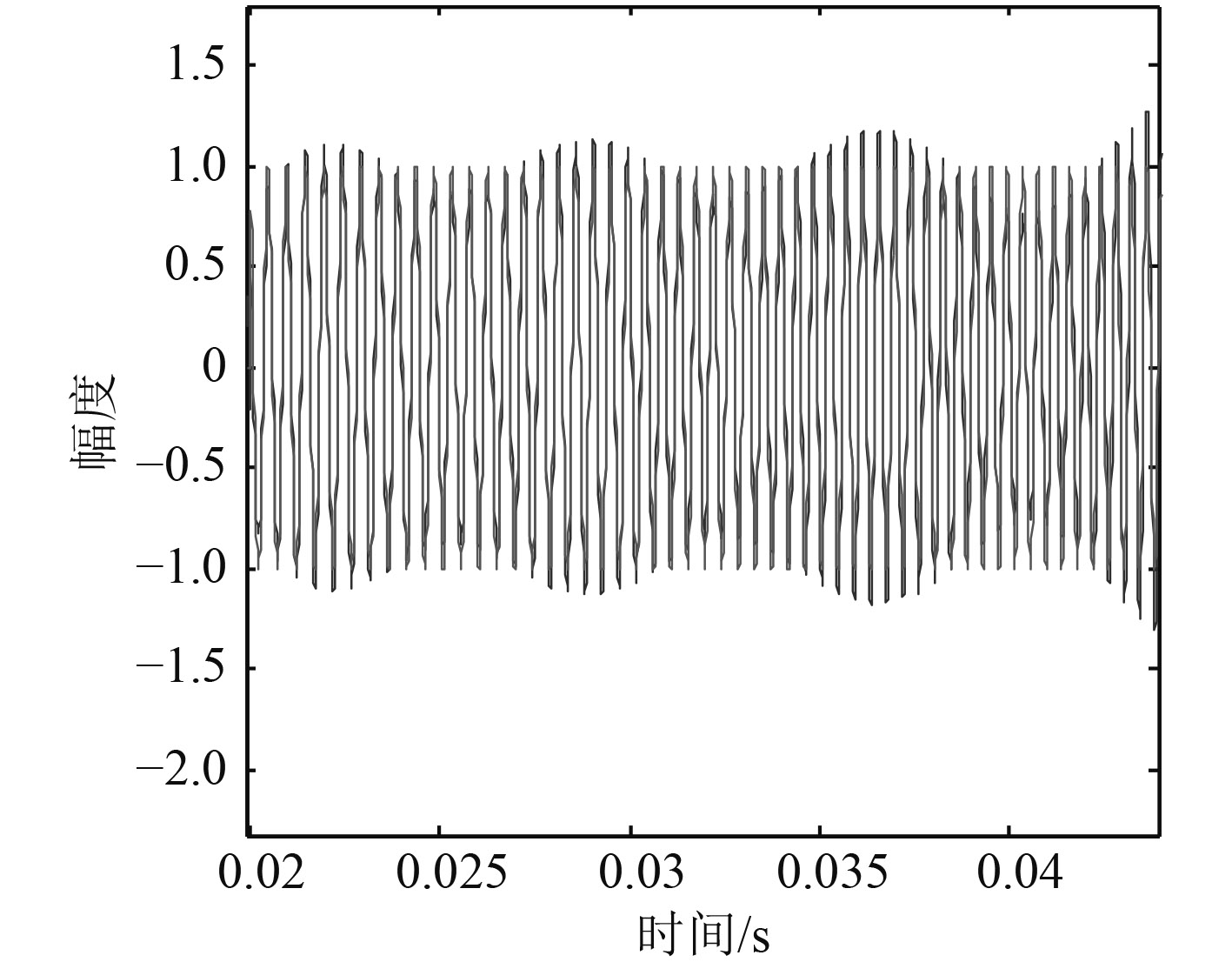
3.1 数值仿真进行数值仿真的线性调频脉冲信号中心频率为3 kHz,带宽1 kHz,仿真的目标散射声信号与混响干扰的信干比为–20 dB,发射信号脉冲宽度为50 ms。图4为仿真的水听器端接收到的混响和目标散射声的叠加信号波形。图5是不同扫描角度的分数阶傅里叶变换结果图,通过扫描可以得出最佳分数阶傅里叶变换的阶次为p=0.936,对应的图6是该旋转角度下的分数阶傅里叶变换结果,对应的2个峰分别为混响和目标散射声,采用加矩形窗的方法进行时频域的带阻滤波如图7所示,图8为经时频域滤波处理后得到的混响干扰信号波形,图9为对应的目标散射声信号波形。仿真研究表明通过基于分数阶傅里叶变换的时频滤波能够很好地去除双基地声呐的直达混响干扰。
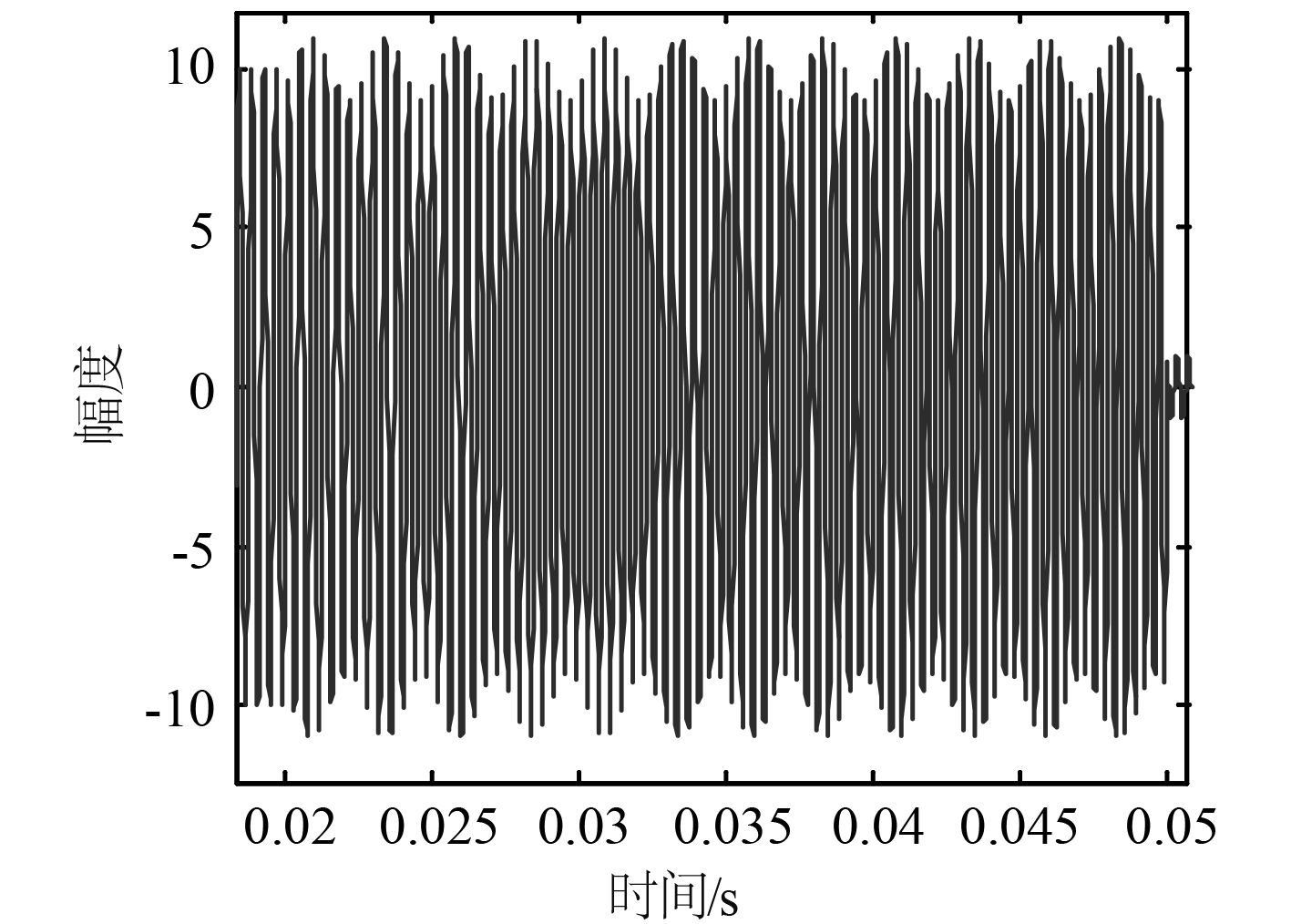
|
图 4 混响信号与目标散射声信号的叠加 Fig. 4 Reverberation sound signal and the target scattering signal superpositon |
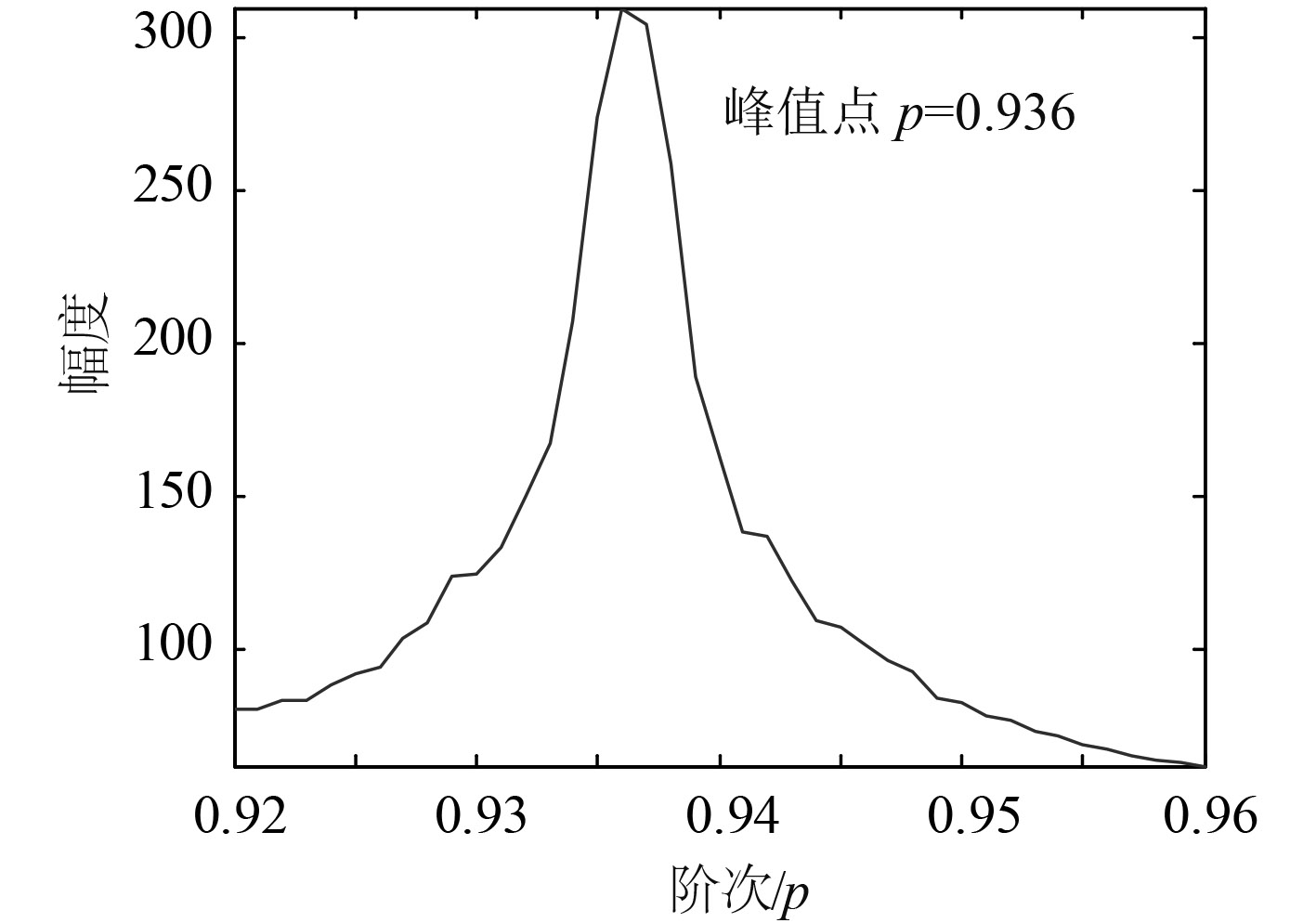
|
图 5 时频域的分数阶傅里叶变换角度扫描 Fig. 5 Time and frequency domain the fractional Fourier transform of scanning Angle |
|
图 6 最佳角度的分数阶傅里叶变换输出 Fig. 6 The best Angle the fractional Fourier transform of the output |
|
图 7 时频域的带阻滤波 Fig. 7 The Time-frequency domain band-stop filter |
|
图 8 经提取的混响信号 Fig. 8 The extraction of reverberation signal |
|
图 9 经混响去除的目标散射声信号 Fig. 9 The acoustic signal by reverberation remove target scattering |
设定目标收发分置散射特性测试的参数为:测试频率4.5~5.5 kHz,发射信号脉冲宽度为50 ms,发射船和接收船的间距为1 000 m。基于参数和仿真研究的结果,可以得出基于分数阶傅里叶变换抗混响干扰的预期性能:使用本方法能够抑制的混响与目标散射声信号的时间间隔为8 ms,对应的收发分置角为162°。
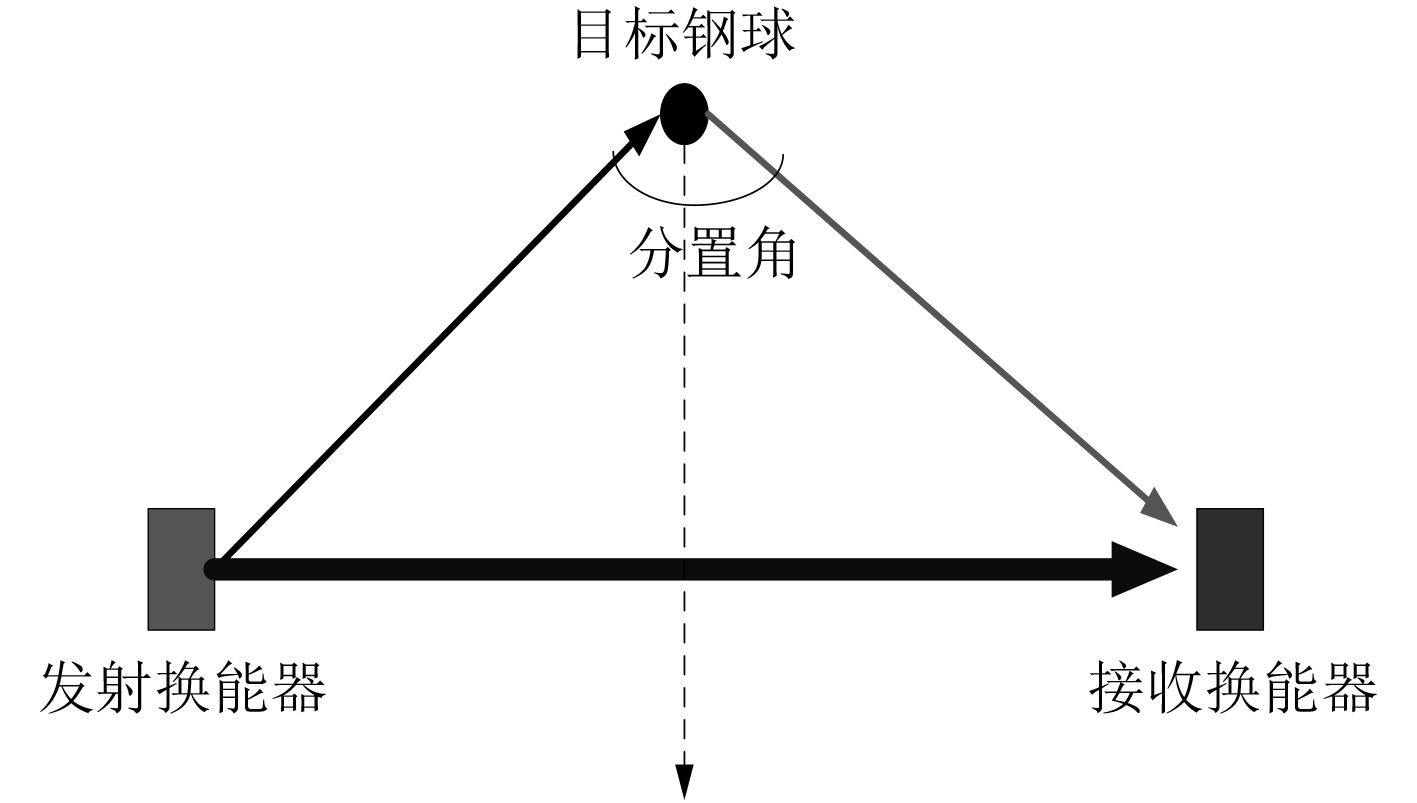
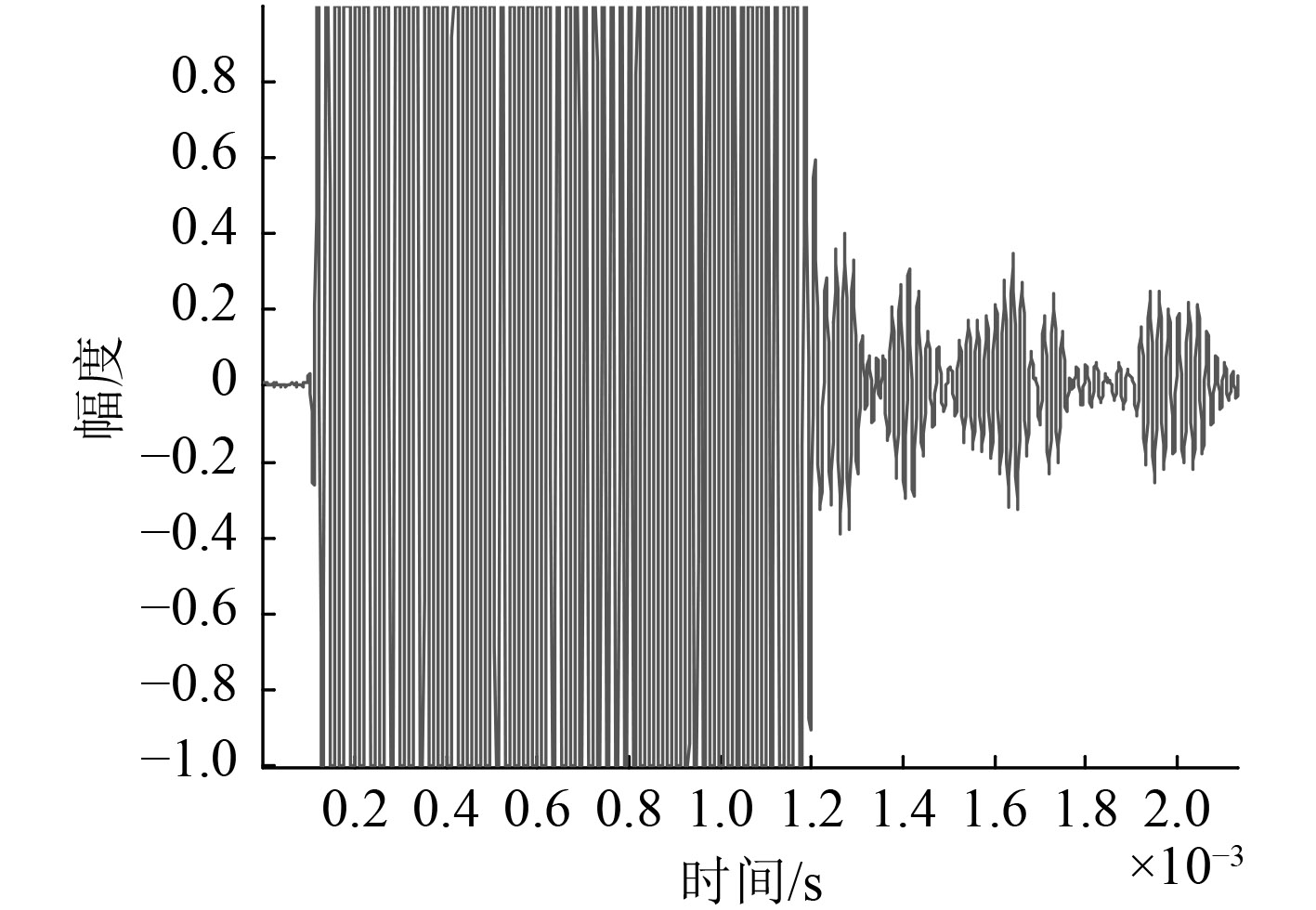
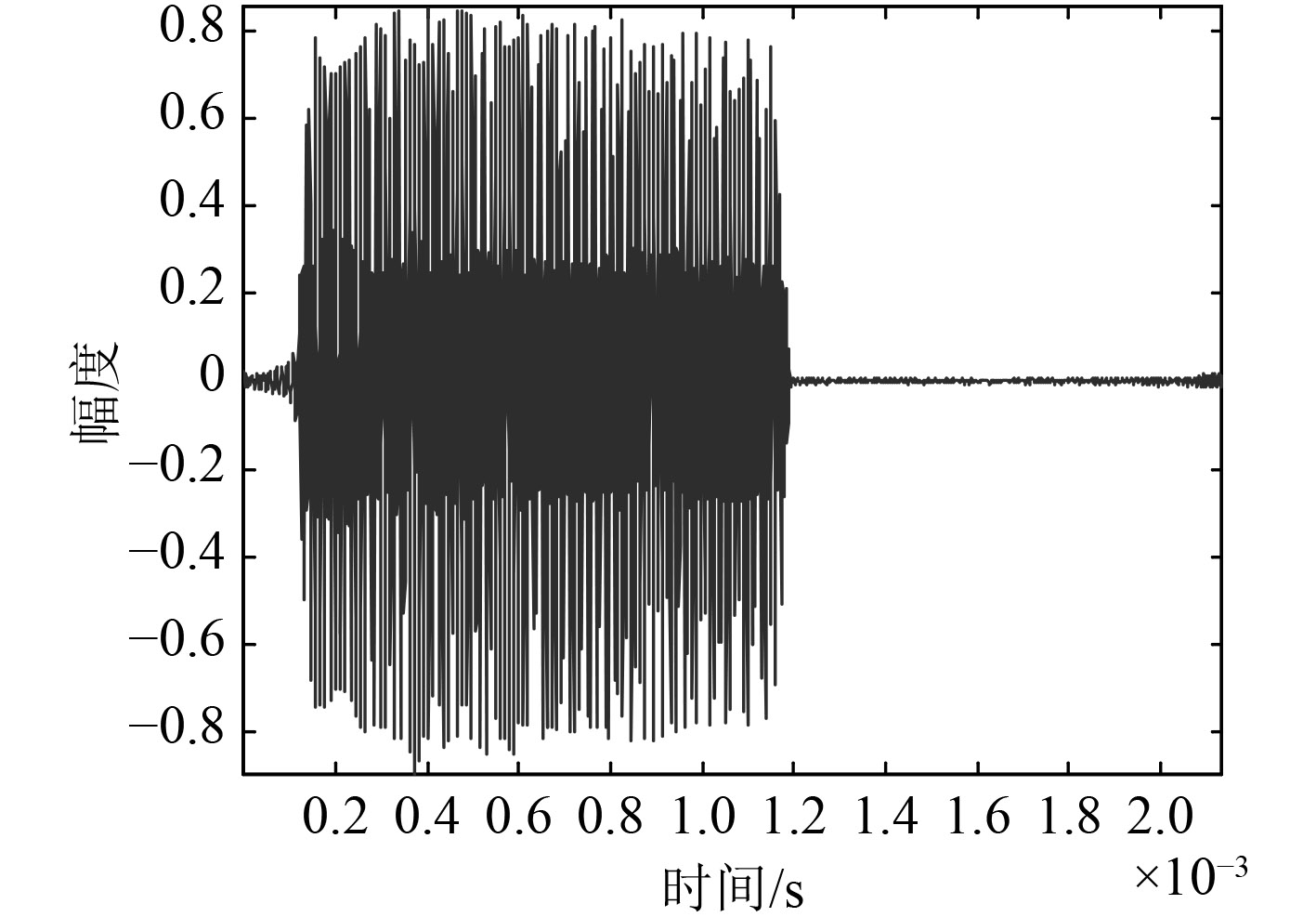
3.2 水池试验水池试验在消声水池进行,其中发射信号为线性调频脉冲,频率范围为45~55 kHz,目标散射体为直径6 cm的实心钢球。目标收发分置散射特性测量试验的试验布局如图10所示,目标球位于发射换能器和接收水听器中间线的位置,并沿着中间线向发射换能器和接收水听器连线的中点移动。根据发射换能器、目标钢球和接收水听器三者之间的位置可对应得到分置角的实际数值。图10~图13分别为分置角175°时的水听器端接收到的信号波形、经混响去除算法处理得到的目标散射声信号和混响信号之间的对比图。
|
图 10 收发分置散射特性测量试验布局图 Fig. 10 Send and receive division scattering measurement test layout |
|
图 11 水听器端接收到的信号波形 Fig. 11 The hydrophone end receives the signal waveform |
|
图 12 经提取的分置角175°目标散射声信号 Fig. 12 By extraction separation Angle of 175o target scattering sound signal |
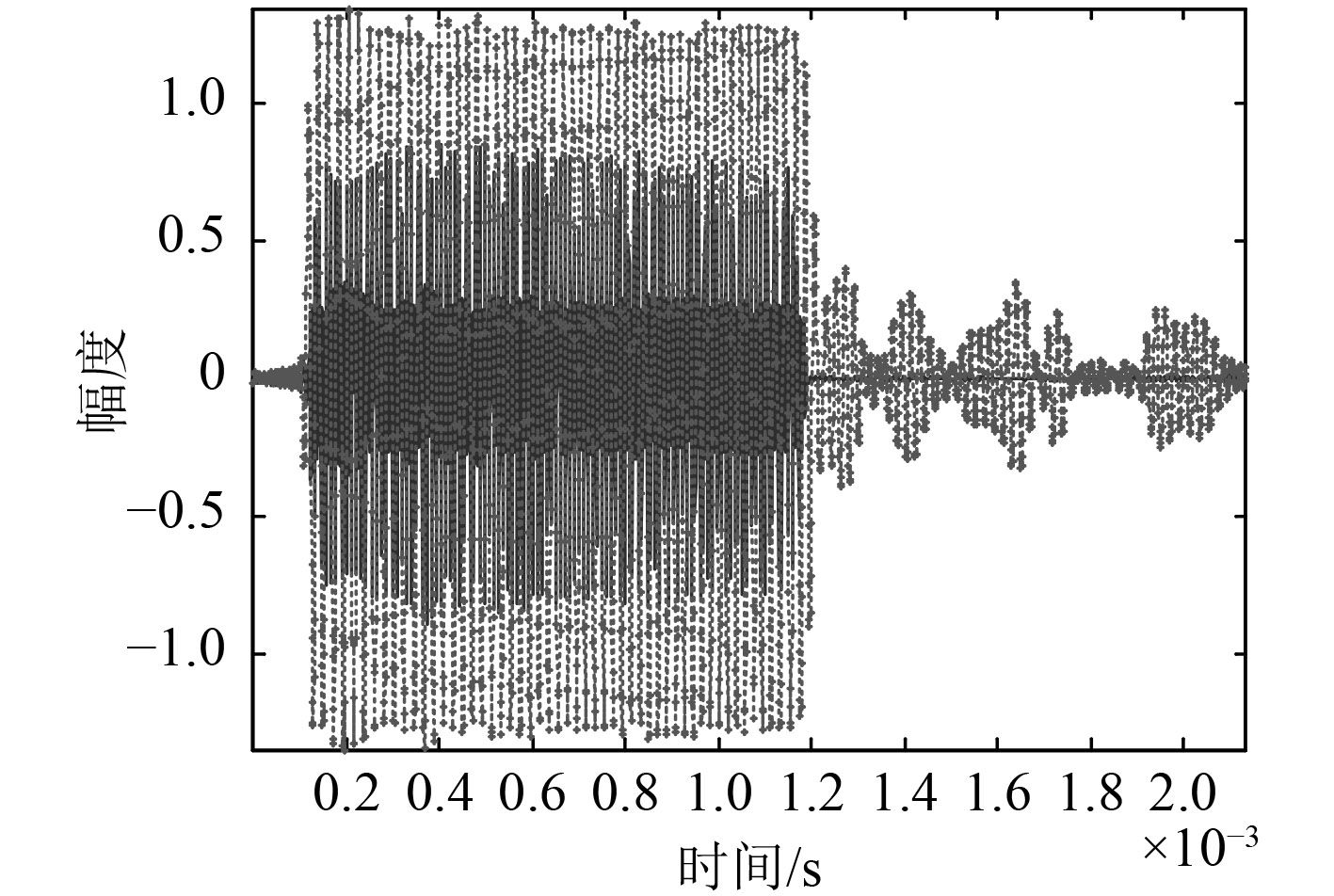
试验结果表明在大分置角情况下,目标散射声信号完全淹没在混响干扰信号中,如图13所示,采用常规的信号处理方法很难将混响干扰去除,而通过本项目研究的基于分数阶傅里叶变换的时频域滤波处理能够有效的将有混响引起的强干扰去除[6 – 8],提取出目标散射声信号。
|
图 13 目标散射信号与混响信号对比 Fig. 13 Compared with reverberation signal target scattering signal |
线性调频信号在分数阶域中表现为冲击响应函数,具有很好的能量聚焦特性,同时线性调频信号是主动声呐的主要工作信号形式之一,基于上述因素,本项目研究了基于分数阶傅里叶变换的混响干扰抑制算法,并通过仿真计算和水池试验证明了该方法用于水中目标收发分置散射特性测量中抗混响干扰的有效性,现将算法使用条件和性能总结如下:
1) 基于分数阶傅里叶变换混响抑制方法只适用于信号形式为线性调频的宽带信号抗混响干扰;
2) 该方法的实质是将脉冲信号在分数阶变换域进行尺度压缩,进而将目标信号和干扰信号在变换域中进行分离。其信号压缩能力与信号的带宽、线性调频信号的调频率以及信号的脉冲宽度有关,信号脉冲压缩能力随信号的带宽增加而增加,但随信号的调频率增加而减小;
3) 将基于分数阶傅里叶变换的混响干扰抑制方法用于目标散射特性测量时,该方法的适用条件为混响和散射声信号的脉冲中心间隔满足式
| [1] | HENRY C. Fundamentals of bistatic active sonar[C]//Underwater acoustic data processing. Klvwer academic publishers, 1989, p3-24. |
| [2] | ALAN A. WINDER[J].leee Transaixions on Sonics and Ultrasonics: p291–332. |
| [3] | |
| [4] | LI Xiu-kun, MENG Xiang-xia, XIA Shi. The characteristics of underwater acoustic scattering echo target geometry in the fractional Fourier transform domain[J].Physics Journal, 2015, 64(6). |
| [5] | OZAKTAS H M, KUTAY M A, ZALEVSKY Z. The fractional fourier transform with applications in optics and signal processing (new york:wiley)[C]//2001:118-122. |
| [6] |
梁红, 李志舜, 王惠刚. 一种变步长自适应格型ⅡR陷波器及其在混响抵消中的应用研究[J].电声技术, 2004(2).
LIANG Hong, LI Zhi-shun, WANG Hui-gang. A variable step-size adaptive ⅡR Notch Filter and its application in reverberation cancellation research[J].Electro-acoustic Technology, 2004(2). |
| [7] | YAO Shuai, FANG Shi-liang, WANG Xiao-yan. Principal component inverse-recursive leastsquare algorithm for direct wave suppression in bistatic sonar[J].Jouurnal of Nanjing University, 2012. |
| [8] |
高勇. 收发分置主动声呐混响特性和抑制方法的研究[D]. 南京:东南大学, 2009
GAO Yong. Study on reverberation characteristics and suppression methods of active sonar[D]. Nanjing:Southeast University. 2009. |
 2017, Vol. 39
2017, Vol. 39
