舰船科学技术  2017, Vol. 39 Issue (6): 72-76   PDF    
引用本文
王旭, 吕俊军. 不同声源深度产生海底地震波仿真分析. 舰船科学技术, 2017, 39(6): 72-76  
WANG Xu, LV Jun-jun. Simulation analysis of seabed seismic wave generated by different depth of sound sources. Ship Science and Technology, 2017, 39(6): 72-76  
不同声源深度产生海底地震波仿真分析
王旭, 吕俊军    
大连测控技术研究所，辽宁 大连 116013
收稿日期: 2016-08-24, 修回日期: 2016-09-22.
基金项目: 国家自然科学基金资助项目(41274051)
作者简介: 王旭(1991 – )，男，硕士研究生，研究方向为舰船地震波仿真建模及数据处理等
摘要: 在浅海环境中，舰船产生的低频水声信号会在海水和海底介质界面处以舰船地震波的形式进行传播[1]，此时海底具有低通滤波的特性。通过理论分析和使用COMSOL Multiphysics软件的声-固耦合模块建立仿真模型，验证其滤波特性的存在，并讨论不同声源深度对海底地震波传播的影响。
关键词: 舰船地震波     有限元仿真     声-固耦合    
Simulation analysis of seabed seismic wave generated by different depth of sound sources
WANG Xu, LV Jun-jun    
Dalian Scientific Test and Control Technology Institute, Dalian 116013, China
Abstract: In shallow sea environment, the low frequency underwater acoustic signal generated by the ship will be transmitted in the form of seismic wave in the interface of the sea water and the seabed medium. At this time, the seabed has the characteristics of low pass filtering. Based on the theoretical analysis and using the sound-solid coupled module of COMSOL Multiphysics software to build the simulation model, the existence of the filtering characteristics is verified. And the influence of different depth of sound source on the seismic wave propagation in the seabed is discussed.
Key words: ship seismic wave     FEM     sound-solid coupled    
0 引　言

舰船地震波场作为一种新兴的舰船物理场，其理论研究以及舰船地震波技术在水中目标探测中应用的重要意义[2]就在于利用舰船地震波独特的频率特性和传播特性来弥补常规声呐在水中目标探测中的不足，提高被动声呐探测舰船目标的能力。舰船地震波信号主要是舰船辐射噪声耦合到海底所产生的沿着海底界面传播的表面波，属于低频微弱振动，具有一般地震波的特点[3]。其最突出的特点是振动连续，没有确定的初至时间，并且随着舰船航行距离的变化而产生弱-强-弱的变化[4]。海底的低通滤波特性，决定了界面波存在一个类似于浅海波动声学中的截止频率，只有低于该频率的信号才会在海水海底界面进行较远距离的传播。随着舰船高频段减震降噪技术的日益成熟，舰船地震波在低频段目标探测领域的潜力应受到足够的重视。资料表明，航行油轮产生的地震波探测距离可达到3 000～5 900 m。本文采用有限元多物理场仿真软件COMSOL Multiphysics，对简单的浅海水平分层海洋环境进行模拟，将低频点声源产生的海底地震波与理论计算结果进行比较，验证其仿真分析的可行性，在此基础上探讨不同深度的点声源产生海底地震波的特性。为以后进一步分析复杂浅海环境舰船地震波场，加强不同类型舰船的目标探测能力提供理论依据。

1 界面地震波传播描述[5]

在地震波动力学中，若上层为半无限流体介质，下层为半无限弹性固体介质，则在界面处存在一种表面波被称为Scholte波。对于Scholte波可由图1的海面-海水-海底模型描述：

图 1 Scholte波理论模型 Fig. 1 The theory model of Scholte wave

设 ${\varphi _L}$ 为声波在海水中的位移势函数， ${\varphi _S}$ 和 ${\psi _S}$ 分别为海底介质中的压缩波位移势函数和剪切波位移势函数，则有：

${\varphi _L} = \mathop \sum \limits_n {A_n}{Q_L}({\kappa _n}){\rm{sin}}({\xi _{Ln}}h){\rm{sin}}({\xi _{Ln}}z)\text{，}$ (1)
${\varphi _S} = \mathop \sum \limits_n {A_n}{Q_S}({\kappa _n}){\rm{sin}}({\xi _{Ln}}h){e^{ - {\xi _{Sn}}(z - H)}}\text{，}$ (2)
${\psi _S} = \mathop \sum \limits_n {A_n}{E_S}({\kappa _n}){\rm{sin}}({\xi _{Ln}}h){e^{ - {\xi _{Sn}}(z - H)}}\text{。}$ (3)

其中：

$\begin{array}{l}{A_n} = \displaystyle\frac{2}{H}\sqrt {\displaystyle\frac{{2\uppi }}{{{\kappa _n}r}}} {e^{{\varphi _n}}}\text{，}\\[5pt]{\varphi _n} = \omega t - {\kappa _n}r - \uppi /4\text{，}\\[5pt]{\xi _{Ln}} = \sqrt {k_{\alpha L}^2 - \kappa _n^2} ,{k_{\alpha L}} = \omega /{\alpha _L}\text{，}\\[5pt]{\xi _{Sn}} = \sqrt {\kappa _n^2 - k_{\alpha S}^2} ,{k_{\alpha S}} = \omega /{\alpha _S}\text{，}\\[5pt]{\zeta _{Sn}} = \sqrt {\kappa _n^2 - k_{\beta S}^2} ,{k_{\beta S}} = \omega /{\beta _S}\text{，}\\[5pt]{Q_L}({\kappa _n}) = - \displaystyle\frac{{{\rho _L}k_{\beta S}^4{\xi _{Sn}}H}}{{{\rho _S}\kappa _n^2\xi _{Ln}^2{M_n}\cos ({\xi _{Ln}}H)}}\text{，}\\[12pt]{Q_S}({\kappa _n}) = - \displaystyle\frac{{{\rho _L}k_{\beta S}^2(\kappa _n^2 + \zeta _{Sn}^2)H}}{{{\rho _{_S}}\kappa _n^2{\xi _{Ln}}{M_n}}}\text{，}\\[10pt]{E_S}({\kappa _n}) = - \displaystyle\frac{{2{\rho _L}k_{\beta S}^2{\xi _{Sn}}H}}{{{\rho _S}\kappa _n^2{\xi _{Ln}}{M_n}}}\text{，}\\[12pt]{M_n} \!\!=\!\! \displaystyle\frac{{{\rho _L}}}{{{\rho _S}}}{\left( {\frac{{{k_{\beta S}}}}{{{\kappa _n}}}} \right)^4}\!\!\left[ {\displaystyle\frac{{\kappa _n^2\sin ({\xi _{Ln}}H)}}{{{\xi _{Ln}}{\xi _{Sn}}}}\left( {1 \!\!+\!\! \frac{{\xi _{Sn}^2}}{{\xi _{Ln}^2}}} \right) \!-\!\! \frac{{{\xi _{Sn}}\kappa _n^2H}}{{\xi _{Ln}^2}}\sec ({\xi _{Ln}}H)} \right] - \\[12pt]\qquad4\left[ {\displaystyle\frac{{{\zeta _{Sn}}}}{{{\xi _{Sn}}}} + \frac{{{\xi _{Sn}}}}{{{\zeta _{Sn}}}} + 2\left( {\frac{{{\xi _{Sn}}{\zeta _{Sn}} - \kappa _n^2 - \zeta _{Sn}^2}}{{\kappa _n^2}}} \right)} \right]\text{。}\end{array}$

式中：ω为波的角速度； ${\alpha _L},{\alpha _S}$ 分别为海水和海底介质中的压缩波波速； ${\beta _S}$ 为海底中的剪切波波速； ${\rho _L},{\rho _S}$ 分别为海水和海底介质的密度；H为海水层的深度；h为声源的深度； $z,r$ 为接收器的圆柱坐标； ${\kappa _n}$ 为n阶简正波的波数，也是下面方程的解：

$\tan \left( {{\xi _{Ln}}H} \right) \!=\! \frac{{{\rho _S}}}{{{\rho _L}}}{\left( {\frac{{{\kappa _n}}}{{{k_{\beta S}}}}} \right)^4}\frac{{{\xi _{Ln}}}}{{{\xi _{Sn}}}}\left[ {4\frac{{{\xi _{Sn}}{\xi _{Sn}}}}{{\kappa _n^2}} \!-\! {{\left( {\frac{{\kappa _n^2 + {\zeta _{Sn}}}}{{\kappa _n^2}}} \right)}^2}} \right]\text{，}$ (4)

此方程解的数目，也是简正波的数目：

$N = \frac{H}{\uppi }\sqrt {k_{\alpha L}^2 - k_{\beta S}^2} + 1\text{。}$ (5)

式中N取整数部分。通过位移势计算质点位移，有下面的形式：

$d = \nabla \varphi + \nabla \times \psi \text{，}$ (6)

在轴对称的条件下，可简化为：

$\begin{split}& {d_{rL}} = \displaystyle\frac{{\partial \varphi }}{{\partial r}}\;\;\;\;{d_{rS}} = \displaystyle\frac{{\partial {\varphi _S}}}{{\partial r}} + \displaystyle\frac{{{\partial ^2}{\psi _S}}}{{\partial r\partial z}}\text{，}\\[8pt]& {d_{zL}} = \displaystyle\frac{{\partial {\varphi _L}}}{{\partial z}}\;\;{d_{zS}} =\displaystyle\frac{{\partial {\varphi _S}}}{{\partial z}} - \displaystyle\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {\psi _S}}}{{\partial r}}} \right)\end{split}\text{。}$ (7)

通过以上势函数衍生的表达式，在边界z=H处可得到：

$\begin{array}{l}{d_{rL}} = - \mathop \sum \limits_n {A_n}\left( {\displaystyle\frac{1}{{2r}} + i{\kappa _n}} \right){Q_L}\left( {{\kappa _n}} \right)\sin \left( {{\xi _{Ln}}h} \right)\sin \left( {{\xi _{Ln}}H} \right)\text{，}\\[10pt]{d_{zL}} = \mathop \sum \limits_n {A_n}{\xi _{Ln}}{Q_L}\left( {{\kappa _n}} \right)\sin \left( {{\xi _{Ln}}h} \right)\sin \left( {{\xi _{Ln}}H} \right)\text{，}\qquad\qquad\;\;(8)\\[5pt]{d_{rS}} = - \mathop \sum \limits_n {A_n}\left( {\displaystyle\frac{1}{{2r}} + i{\kappa _n}} \right)\left[ {{Q_{Sn}}\left( {{\kappa _n}} \right) - {\zeta _{Sn}}{E_{Sn}}\left( {{\kappa _n}} \right)} \right]\sin \left( {{\xi _{Ln}}h} \right)\text{，}\\[5pt]{d_{zS}} = \mathop \sum \limits_n {A_n}\left[ { - {\xi _{Sn}}{Q_{Sn}}\left( {{\kappa _n}} \right) + \left( {\kappa _n^2 - \displaystyle\frac{1}{{4{r^2}}}} \right){E_{Sn}}\left( {{\kappa _n}} \right)} \right]\sin \left( {{\xi _{Ln}}h} \right)\text{。}\end{array}$ (8)

由上式可看出，Scholte表面波沿着海底界面传播时，其位移幅度随信号接收距离呈指数衰减。由于该模型中简正波的解省略了分支线的积分，从而使 ${d_{zL}},{d_{zS}}$ 的表达式不同。但随着r的增加，2个表达式的差异迅速减小，即该理论模型在接收距离较远处满足垂直位移的连续性条件 ${d_{zL}} = {d_{zS}}$ 。

2 仿真模型建立

在波动声学的简正波理论中，存在一个截止频率[6] ${f_1} = \displaystyle\frac{{{c_0}}}{{4H}}$ ，当声源频率 $f < {f_1}$ 时，简正波无法在水层进行无衰减传播，因此低频信号能量耦合进入海底在界面处以地震波形式进行传播，这也是海底具有低通滤波特性的重要原因。截止频率只与海水深度和声速有关，在浅海尤其是本文中所考虑的100 m以下深度的海水，一般认为声速的变化可忽略不计，因此在此仅考虑水深H对滤波特性的影响。

使用COMSOL Multiphysics软件建立如图2所示的三维模型，并进行网格划分：

图 2 仿真模型及其网格划分 Fig. 2 Simulation model and mesh generation

计算区域水平长度400 m，前后宽度100 m。在仿真过程中点声源坐标（0，0，125），即点声源在海面以下25 m，该参数不随水深改变。为了减少边界反射对计算结果的影响，后侧及右侧添加了完美匹配层（PML），即该层介质的波阻抗与相邻介质的波阻抗完全匹配，入射声波会无反射地穿过分界面而进入PML。左侧及前侧采用对称边界条件。在H=50 m时，网格划分共计14 664个单元，其中固体单元7 240个。其余参数为：海水密度1 000 kg/m3，海水声速1 500 m/s，海底介质密度2 500 kg/m3，纵波波速3 000 m/s，横波波速1 800 m/s。

海水深度分别为H=50 m，H=80 m时，得到海水-海面交界处距声源水平距离r=350 m位置点垂直位移的频率特性曲线，如图3所示。

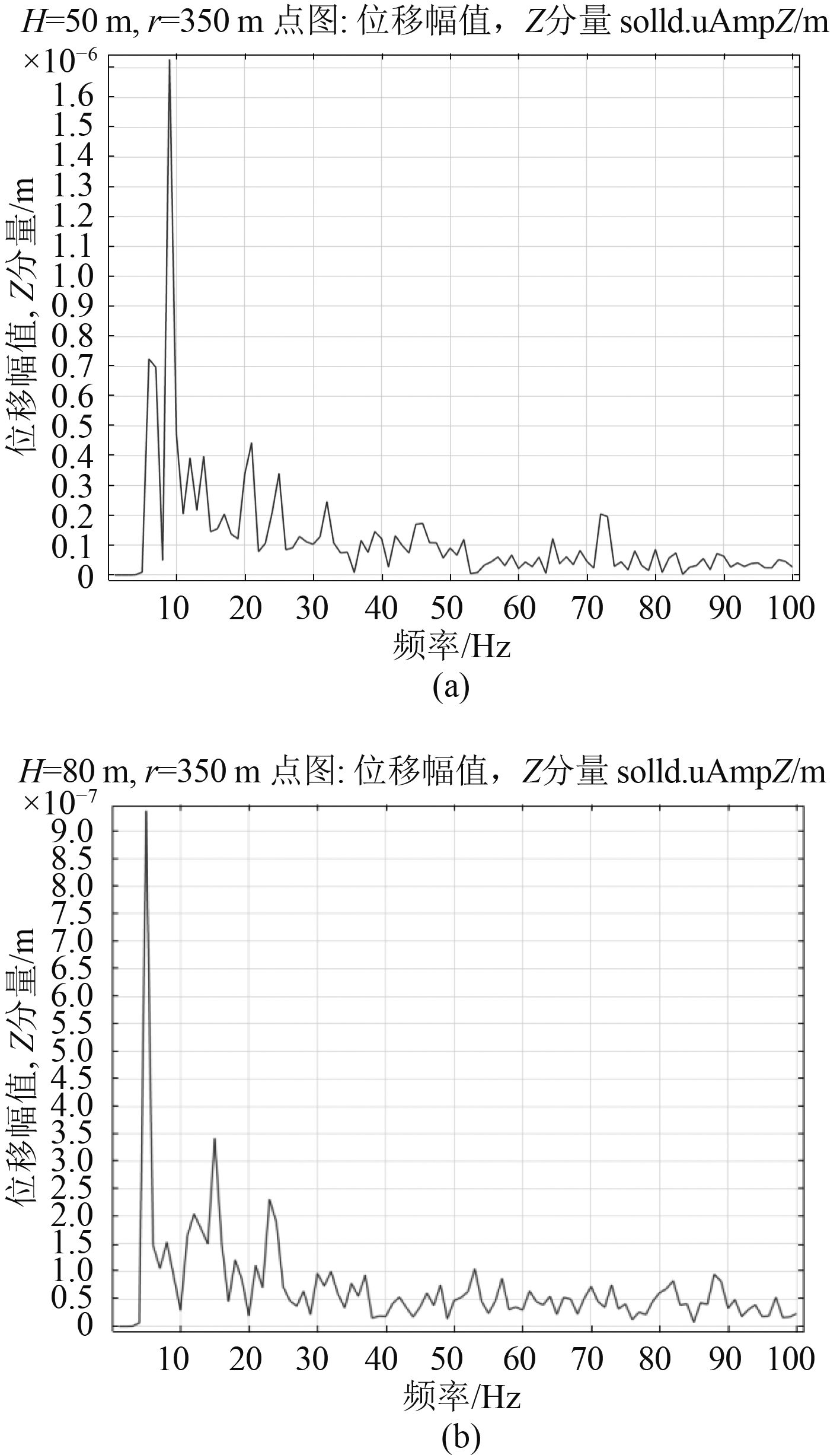
图 3 r=350 m（H=50 m，H=80 m）边界垂直位移频率特性曲线 Fig. 3 r=350 m (H=50 m，H=80 m) Frequency characteristic curve of vertical displacement at boundary

在相同的参数条件下使用理论模型中的边界位移函数 ${d_{zL}}$ 进行验证，得到的分析结果如图4所示。

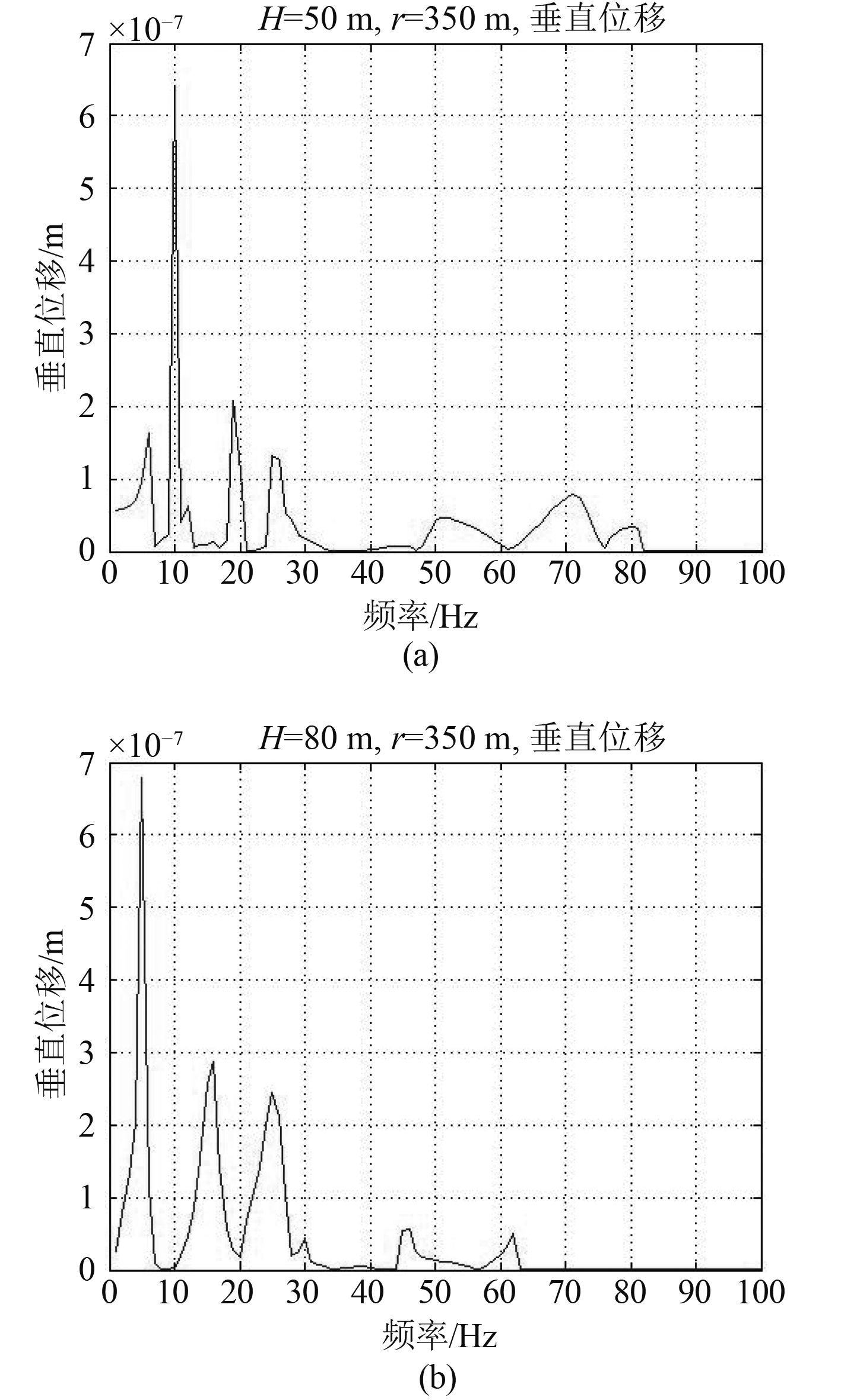
图 4 理论验证结果 Fig. 4 Theoretical verification results

通过对比，使用该模型的仿真结果与理论计算结果具有较好的一致性。

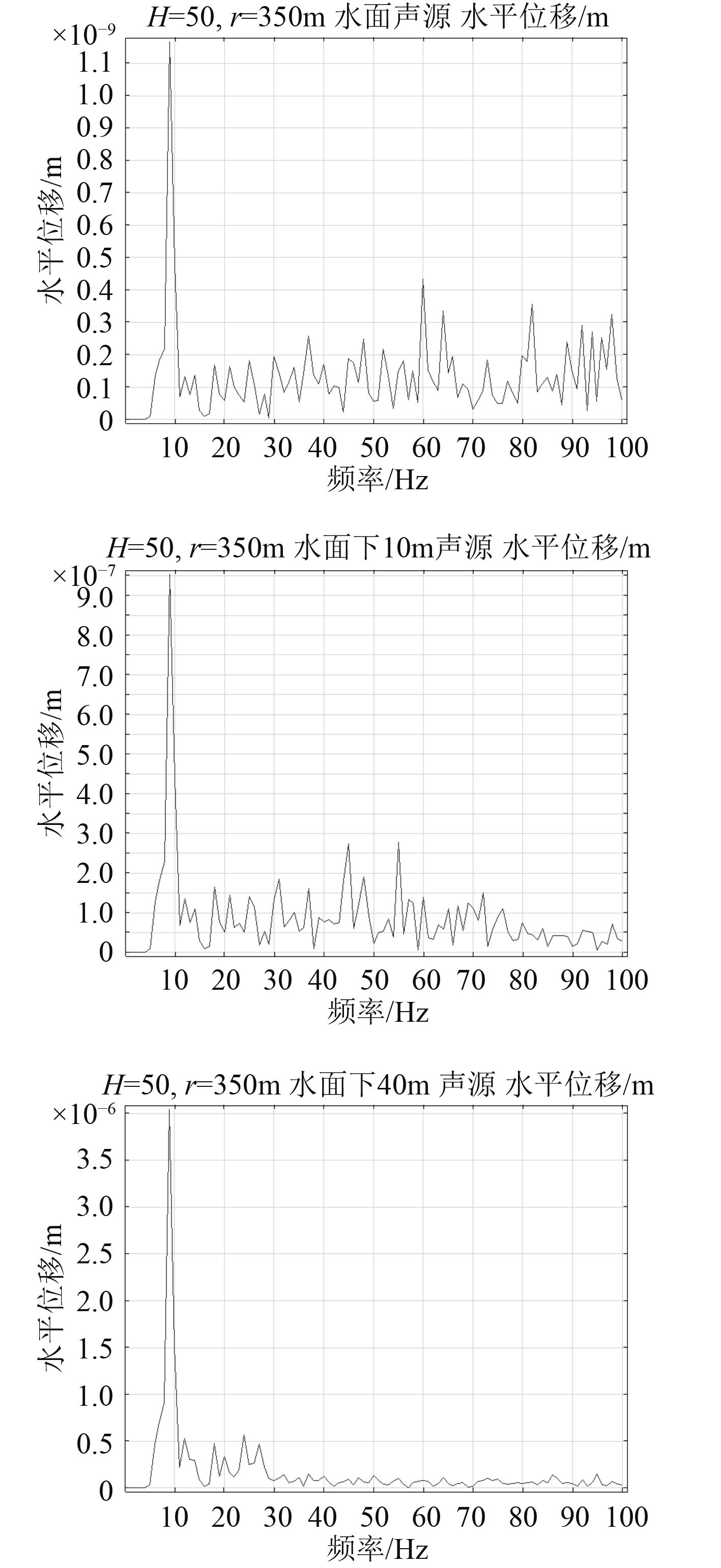
再考虑海水深度为H=50 m的情况下，不同的声源深度对海底地震波传播的影响，在界面处选取相同的接收点r=350。做出水面声源和水下10 m，40 m声源的垂直位移频率特性曲线及水平位移频率特性曲线，如图5~图6所示。

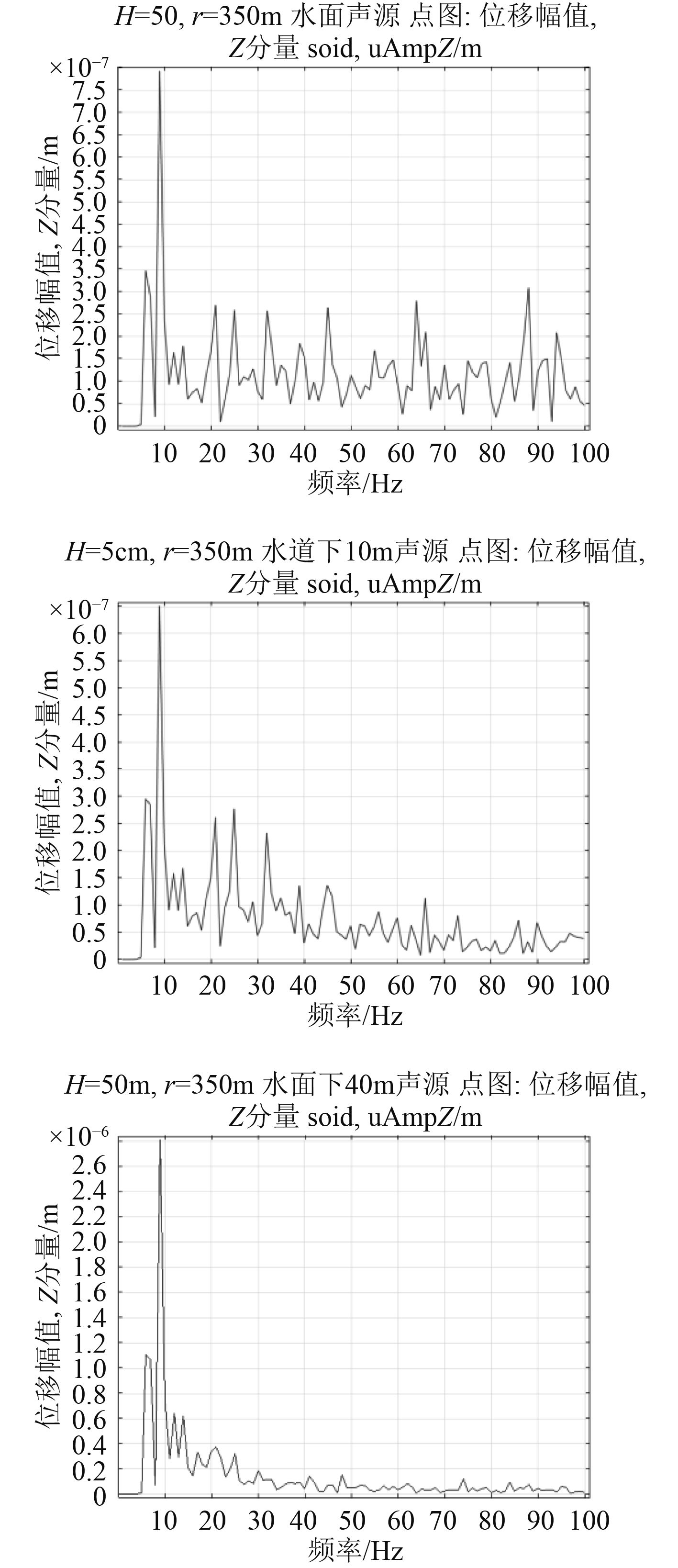
图 5 水面声源、水下10 m，40 m声源垂直位移频率特性曲线 Fig. 5 Frequency characteristic curve of vertical displacement (Sound source of water surface，sound source of underwater 10 m，sound source of underwater 40 m)

图 6 水面声源、水下10 m、40 m声源水平位移频率特性曲线 Fig. 6 Frequency characteristic curve of horizontal displacement (Sound source of water surface，sound source of underwater 10 m，sound source of underwater 40 m)

可以观察到声源深度对地震波传播的频率特性有很大影响。虽然垂直位移和水平位移的峰值频率没有改变，但随着声源深度增加，垂直方向与水平方向地震波信号相类似，能量均越来越向低频段集中。这也是由于理论模型中位移与声源深度有关项 $\sin \left( {{\xi _{Ln}}h} \right)$ ，其中在低频段 ${\xi _{Ln}}$ 为主要作用项，声源深度变化对其影响较小，在30 Hz以上的高频段声源深度h为主要作用项，增大的声源深度使 $\sin \left( {{\xi _{Ln}}h} \right)$ 在递减区间越来越小，因此产生仿真中出现的结果。另一方面，从理论上分析，在海水深度不变的情况下，声源深度越大，声波到达海底界面处的路径越短，能量损耗越小，因此产生的位移幅值就越大，这一点也与仿真结果相符。同时，随着声源深度增加，直达声波在到达相同接收点的入射角逐渐增大，较大的入射角会增加海底介质对低频信号的吸收能力，因此频率特性逐渐向低频段靠拢。

3 结　语

通过有限元软件COMSOL Multiphysics中的声-固耦合模块，使用完美匹配层（PML）边界条件，对简单海洋分层环境下低频点声源产生的海底地震波进行仿真，并与理论计算结果对比，进一步分析不同声源深度对地震波传播频率特性的影响，得到以下结论：

1）仿真结果与理论计算结果在低频段符合较好，高频段有所差异，但大体趋势一致。点声源产生地震波能量大多数集中在低频段。

2）在海底地震波传播过程中，存在所谓的“截止频率”，高于该频率的信号无法以地震波形式进行远距离传播。其大小与海水深度有关，海水深度越大，该频率越小。即浅海环境有利于地震波的形成与传播。

3）地震波传播的频率特性与声源深度有关，通过仿真分析可以明显观察到，无论是垂直位移还是水平位移，当声源在水面处，高频段的信号依然较强，但随着声源深度不断增加，高频段信号逐渐减弱。说明越靠近海面的声源所产生的地震波，频率通过特性越好。由此，针对不同深度、不同类型舰船的探测情况，应该采用不同频率接收范围的传感器。

4）基于PML和对称边界的设定，采用多物理场耦合软件COMSOL Multiphysics中的声-固耦合模块，对低频点声源产生的海底地震波进行仿真模拟是可行的。

由此，可以利用COMSOL Multiphysics软件对一些复杂情况下的地震波传播进行仿真，包括不均匀的海水环境、不同地质特性的海底环境[7]、以及基于Biot理论的多孔介质[8]地震波等。与此同时，可以进一步提高网格划分精度，提高计算准确性，更全面地分析复杂环境下浅海舰船地震波的波动特性，为水面舰船及水下潜艇的探测提供新的思路。

参考文献
[1] 陈云飞, 吕俊军, 于沨. 航行舰船地震波及其在水中目标探测中的应用[J].舰船科学技术, 2005, 27(3): 62–66.
CHEN Yun-fei, LV Jun-jun, YU Feng. The ship induced seismic wave and it's application in the underwater target detection[J].Ship Science and Technology, 2005, 27(3): 62–66.
[2] 李响, 颜冰. 舰船地震波场分析[J].噪声与振动控制, 2007, 8(4): 120–122.
LI Xiang, YAN Bing. Analysis of ship seismic wave field[J].Noise and Vibration Control, 2007, 8(4): 120–122.
[3] 李响, 白正勤, 刘旭东. 基于三轴地震波传感器的舰船被动定位方法[J].探测与控制学报, 2014, 36(4): 36–39.
LI Xiang, BAI Zheng-qin, LIU Xu-dong. Passive localization of ship based on triaxial seismic sensor[J].Journal of Detection & Control, 2014, 36(4): 36–39.
[4] 白春志, 吕俊军, 苏建业. 航行舰船地震波探测理论分析[C]. 大连测控技术研究所, 2005.
BAI Chun-zhi, LV Jun-jun, SU Jian-ye. Theoretical analysis of the seismic wave detection of the ship[C]. Dalian Scientific Test & Control Technology Institute, 2005. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGSU200512001014.htm
[5] EWING W, JARDETSKY W, PRESS F. Elastic waves in layered media[M]. MeGraw-Hill, New York, 1957.
[6] 刘伯胜, 雷家煜. 水声学原理[M]. 哈尔滨:哈尔滨工程大学出版社, 1993.
LIU Bo-sheng, LEI Jia-yu. Principle of underwater acoustics[M]. Harbin:Harbin Engineering University Press, 1993.
[7] 卢再华, 顾建农, 张志宏. 不同浅海环境下点声源海底地震波特征研究[J].声学技术, 2009, 28(5): 596–600.
LU Zai-hua, GU Jian-nong, ZHANG Zhi-hong. Characteristics of seabed seismic wave caused by point sound source in various shallow water circumstances[J].Technical Acoustics, 2009, 28(5): 596–600.
[8] 彭临慧, 赵燕鹏, 郁高坤. 声波在水-多孔介质海底界面上的反射与透射[J].中国海洋大学学报, 2007, 37(4): 671–675.
PENG Lin-hui, ZHAO Yan-peng, YU Gao-kun. Reflection and transmission of acoustic waves at the interface between water and porous media[J].Periodical of Ocean university of China, 2007, 37(4): 671–675.