海上风电运维船用于维护人员及小型零部件的运输,其主要包括海上航行和靠离风机塔基 2 个重要环节。目前,运维船一般采用顶靠方式供维护人员登离风机基础,即船首端顶靠船桩后,人员进行登离[1–2]。所以,在风、浪、流的作用下,运维船的水动力运动响应,尤其是船首端的升沉和纵摇幅值,对维护人员的安全登离塔基有着重大的影响。
为此,考虑船与风机塔基之间也存在风、浪、流的屏蔽效应[3],本文针对某运维船与风机塔基顶靠耦合模型,通过施加不同的浪高和风速,来分析研究风浪不同作用角度时运维船船首端的升沉和纵摇幅值,并依据许可升沉幅值来确定运维船适应风浪的能力,进而为风电场运维船的安全使用提供一定的参考。
1 模型及相关参数的确定1.1 船模及海上风机塔基耦合模型波浪传播过程中与大尺度结构物相遇时,由于结构物的影响,会产生绕射现象,即波浪的一部分能量被结构物阻挡,另一部分能量从结构物侧面绕过,传入结构物后面的水域中。对于大尺度结构物对波浪场的影响以及波浪力的计算等,都需要研究波浪绕射问题。
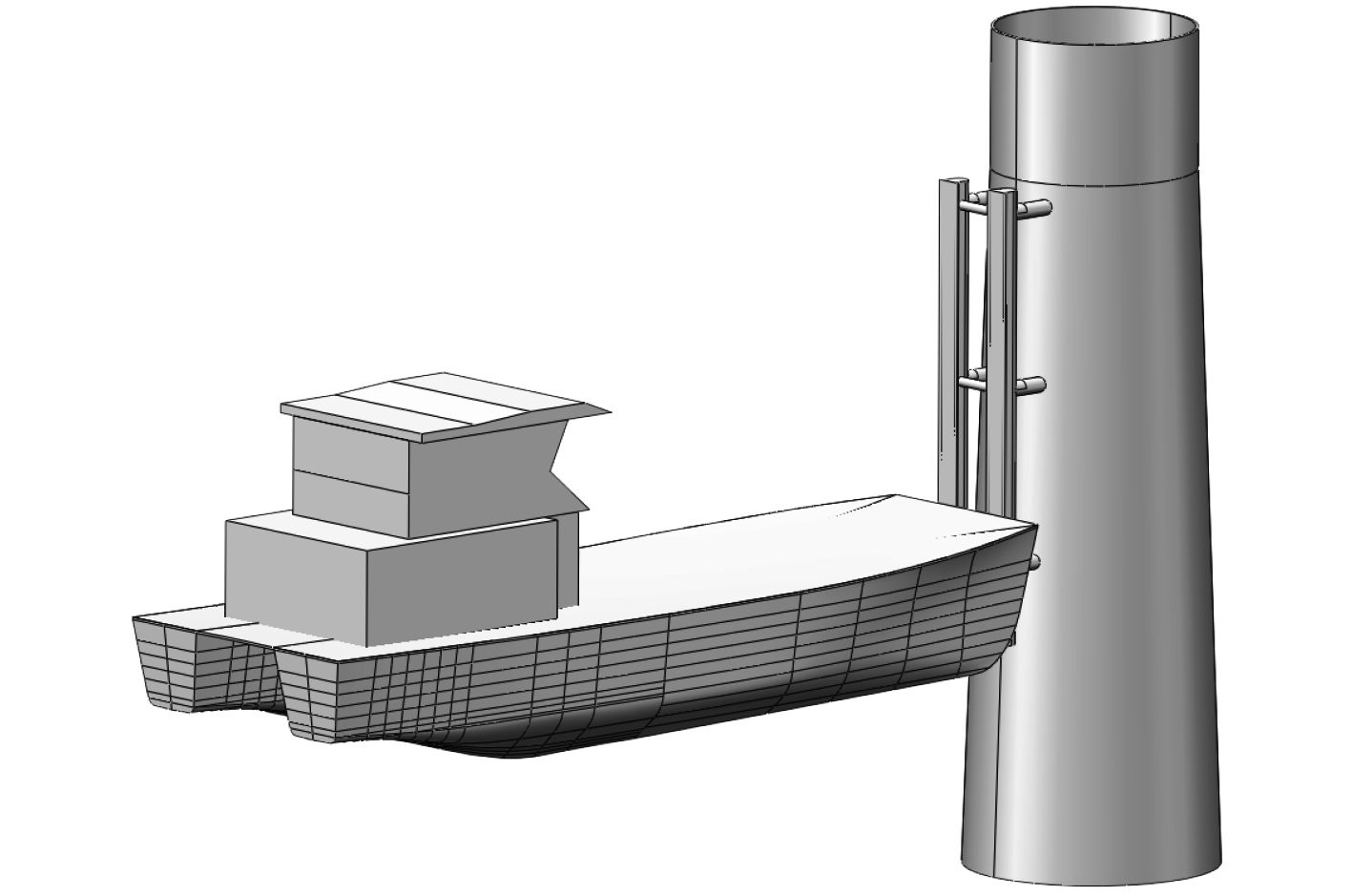
考虑本研究风电塔基(水面处直径5.2 m)相对于运维船尺度(见表1)较大,为此需针对耦合模型(见图1)进行研究。
|
|
表 1 某风电运维船相关参数 Tab.1 Parameters of the maintenance ship |
风机塔基尺寸的直径为5.2 m,其耦合模型如图1所示。
|
图 1 运维船与海上风机塔基耦合模型 Fig. 1 Coupling model of the wind tower and maintenance ship |
本文针对该风电运维船能在 3~4 级海况中工作的使用性能要求,计算有义波高取1.0 m,1.2 m,1.4 m,1.6 m,1.8 m。浪向角取0°,45°,90°(0°为迎浪),风速及流速按表2所取。
|
|
表 2 不同浪向角对应的风速和流速 Tab.2 The speed of wind and wave at different wave angles |
本文采用JONSWAP不规则谱,波浪的计算频率范围取0.3~4.0 rad/s。JONSWAP中形状因子 γ 根据式(1)~式(3)进行计算:
| $\gamma = 5\;\;{\rm{for}}\;\;{T_p}/\sqrt {{H_S}} \leqslant 3.6\text{,}$ | (1) |
| $\gamma = \exp (5.75 - 1.15\frac{{{T_P}}}{{\sqrt {{H_S}} }})\;\;{\rm{for}}\;\;3.6 < {T_p}/\sqrt {{H_S}} < 5\text{,}$ | (2) |
| $\gamma = 1\;\;{\rm{for}}\;\;5 \leqslant {T_p}/\sqrt {{H_S}} \text{。}$ | (3) |
根据ISSC(1979)给出的计算式(4)来参考作为波谱峰周期TP的范围:
| $\sqrt {13{H_S}} \leqslant {T_P} \leqslant \sqrt {30{H_S}} \text{,}$ | (4) |
研究所选定的波谱峰周期为:
| ${T_P} = \frac{{\sqrt {13{H_S}} + \sqrt {30{H_S}} }}{2}\text{,}$ | (5) |
JONSWAP谱的表达式为:
| $\begin{split}{S_\xi }(\omega ) = & 487\left[ {1 - 0.287\ln \gamma } \right]\displaystyle\frac{{H_s^2}}{{T_p^4{\omega ^5}}}\times\\ & \exp \left\{ { - \displaystyle\frac{{1948}}{{{{({T_p}\omega )}^4}}}} \right\}{\gamma ^{\exp \left[ { - \displaystyle\frac{{{{(0.159\omega {T_p} - 1)}^2}}}{{2{\sigma ^2}}}} \right]}}\text{。}\end{split}$ | (6) |
式中σ为峰形参数。当ω≤ωP时,取σ=0.07;当ω>ωP时,取σ=0.09。
由计算可得不同有义波高下的谱峰频率、起始频率、终止频率和Gamma值,如表3所示。
|
|
表 3 不同有义波高下的波谱参数 Tab.3 Parameters of wave spectrum at different significant wave heights |
风机塔基与船首的顶靠处设有橡胶作缓冲之用,其摩擦系数是水动力响应模拟的重要参数之一,根据相关手册,橡胶与钢的摩擦系数约为0.8(超出AQWA设定的上限值0.5),最终计算时橡胶的摩擦系数取为0.5。
此外,顶靠时的推力是另一重要参数。经过计算,本运维船系柱推力为50 kN。
2 风流力系数及粘性阻尼数值仿真本文采用CFD数值仿真软件Fine/Marine进行风流力系数计算,由于AQWA为基于势流理论的水动力分析软件,没有考虑水的粘性阻尼,通常通过CFD或者模型试验方法获得,作为水动力响应分析计算的输入。所以本文同样采用Fine/Marine模拟运维船垂荡及纵摇的自由衰减,从而得到粘性阻尼。
2.1 风流力系数把船与塔基模型导入进Fine/Marine软件进行网格划分,对不同的浪向角(0°,45°,90°)进行计算。由于AQWA计算文件中的风流力系数为力或力矩除以速度的平方,经计算整理得到各工况的风力系数及流力系数如表4所示。
|
|
表 4 某一风速及流速时不同浪向角的风流力系数 Tab.4 Drag coefficients of wind and wave at different wave angles |
浮式结构物的六自由度运动中,横摇、纵摇和垂荡方向有静恢复力或力矩,在平衡位置时,外力作用会使系统偏离平衡位置,当外力停止作用后,由于系统的静恢复力和力矩的作用,系统会绕原来的平衡位置产生单纯的周期性摇荡衰减运动。通过记录摇荡衰减时历曲线,可以得出系统的固有频率和无因次阻尼系数,系统运动方程为[4]:
| ${ M}x'' + { C}x' + { K}x = 0\text{,}$ | (7) |
式中:M为浮式结构物总质量(包括附加质量);C为系统阻尼系数;K为结构刚度矩阵。
确定系统阻尼的一个简单方法是测量系统的衰减率,常用衰减系数的自然对数表示振幅的衰减率:
| $\delta = \frac{1}{N}\ln \frac{{{A_i}}}{{{A_{i + N}}}}\text{,}$ | (8) |
式中:δ 为对数衰减率;Ai和Ai+N为第i个和第i+N个振幅值。
ζ 为阻尼比,可用对数衰减率δ表示为:
| $\zeta \approx \frac{1}{{2\uppi }}\delta \text{,}$ | (9) |
同样,系统的固有周期可由衰减曲线获得:
| $T = \frac{{{t_{k + i}} - {t_k}}}{i}\text{。}$ | (10) |
式中:T为系统固有周期;tk+i和tk为第k+i个和第k个振幅对应的时间。
临界阻尼为CC=2mλ,λ为固有频率,阻尼系数C=CCζ
。回复刚度为:垂荡

|
图 2 纵摇衰减曲线 Fig. 2 The attenuation curve of pitch |
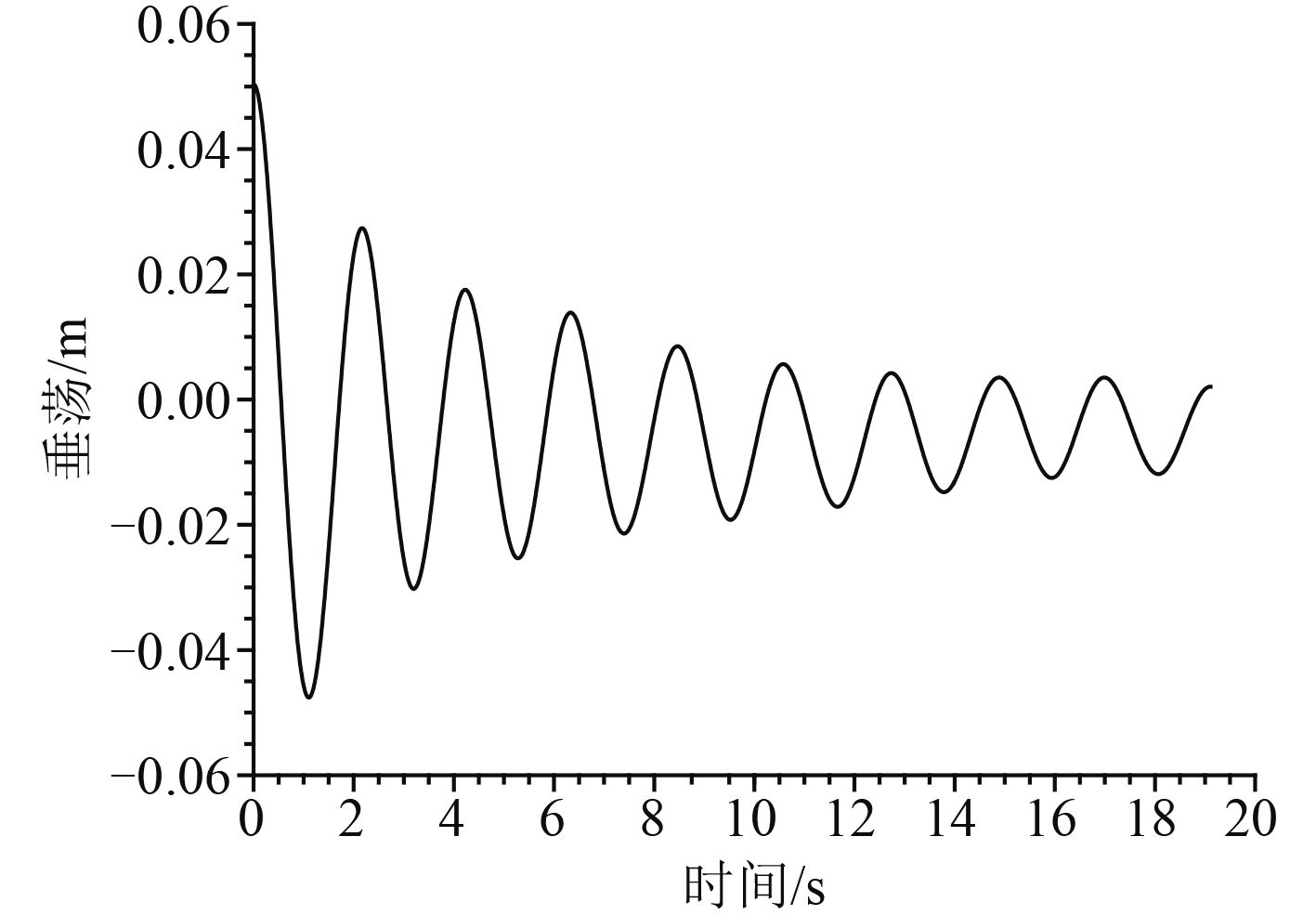
|
图 3 垂荡衰减曲线 Fig. 3 The attenuation curve of heave |
由以上Fine/Marine仿真计算得到的图形,经过换算得到的阻尼如表5所示。
|
|
表 5 阻尼汇总表 Tab.5 The summary sheet of damping |
本文针对不同的波高1.0 m,1.2 m,1.4 m,1.6 m,1.8 m,不同的浪向角0°,45°,90°和不同的风速及风向、流速及流向的组合工况,在考虑一定的螺旋桨推力和船首摩擦阻尼的情况下,利用AQWA软件进行运维船的水动力响应分析计算,利用LINE与DRIFT模块分别计算频域分析与时域分析。
3.1 频域分析根据AQWA-LINE模块计算在计算不同频率不同入射方向的单位波幅规则波作用下双体运维船的动力响应[6],下面给出六自由度方向的随波浪频率变化的响应幅值算子(Response Amplitude Operators,RAO)。
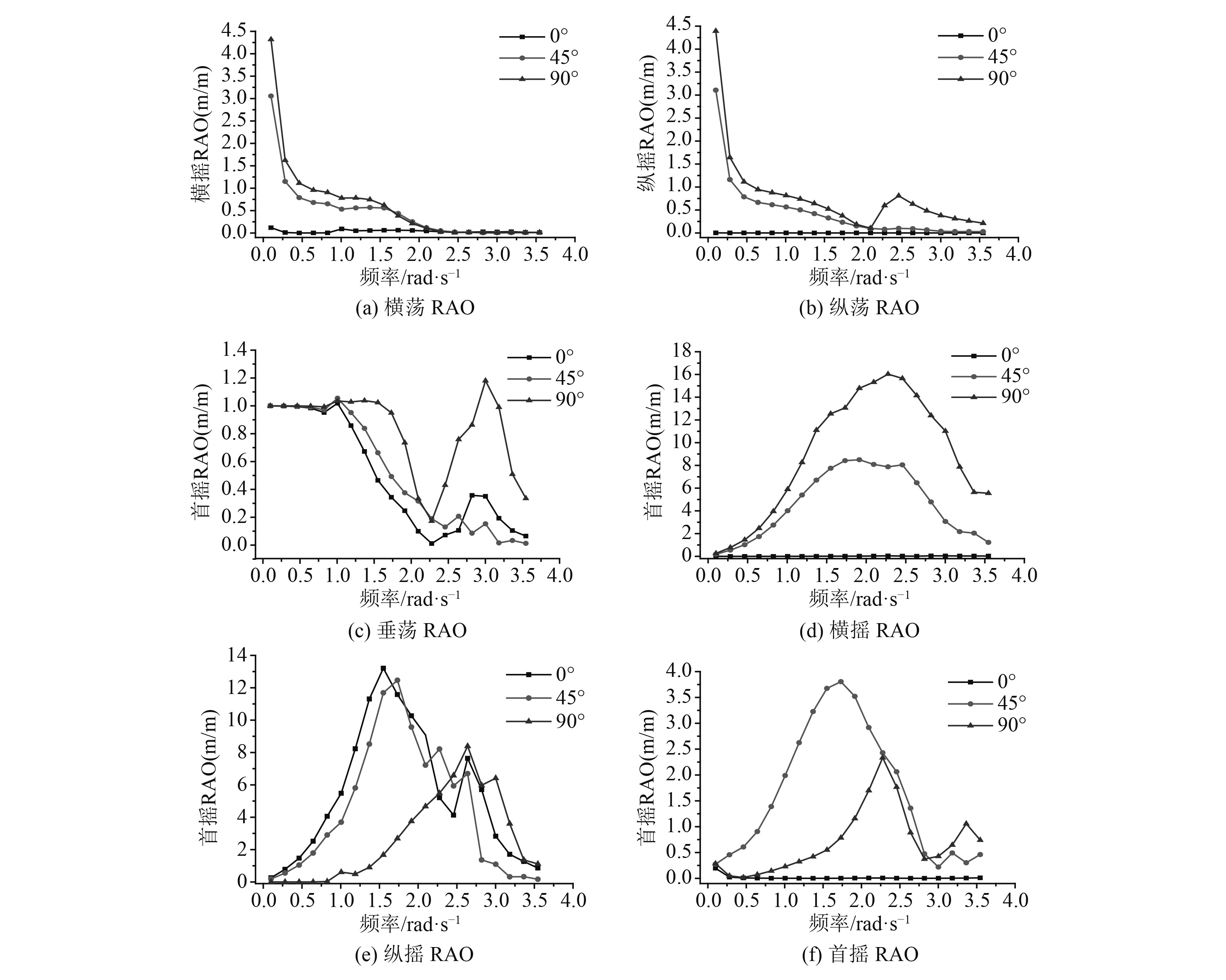
|
图 4 六自由度的RAO随频率变化曲线 Fig. 4 Frequency response curves of RAO with six degrees of freedom |
如图4所示,不同浪向角的横荡与纵荡RAO基本随着频率的增加而下降,其峰值出现在低频。0°和45°时的纵荡RAO也是随着这频率的增加而减小,而90°时的RAO呈波浪状。45°与90°时的横摇与首摇RAO先增大后减小,而0°时的横摇与首摇RAO较小。不同浪向角的纵摇RAO也是先增大后减小,但0°和45°峰值点接近,90°时的峰值频率稍大。
3.2 时域分析海洋中波浪高度是一个具有零均值、各态历经的高斯随机过程,浮体对任意波浪成分的响应是这个成分波波幅的线性函数并且与它对其他波浪成分的响应独立无关[7],因此可以假定浮体对随机波浪的响应等于所有组成风浪的各单元波的响应之和[8]。AQWA-DRIFT模块利用LINE模块计算的不同频率、不同入射方向单位波幅作用下的RAO插值计算得到随机波浪作用下平台的动力响应。
利用DRIFT模块的fender功能对运维船首护舷进行数值模拟,摩擦系数取0.5,fender直径取与某护舷材一致,受力应变关系式取某给定值,并施加航速v=0时的螺旋桨推力作用在船上,以维持顶靠状态。时域分析采用JOHNSWAP谱,具体参数如上文所述。由计算得船首登靠点处z方向的运动如图5所示。

|
图 5 船首登靠点升沉时历曲线 Fig. 5 Time history of heave at the head of the ship |
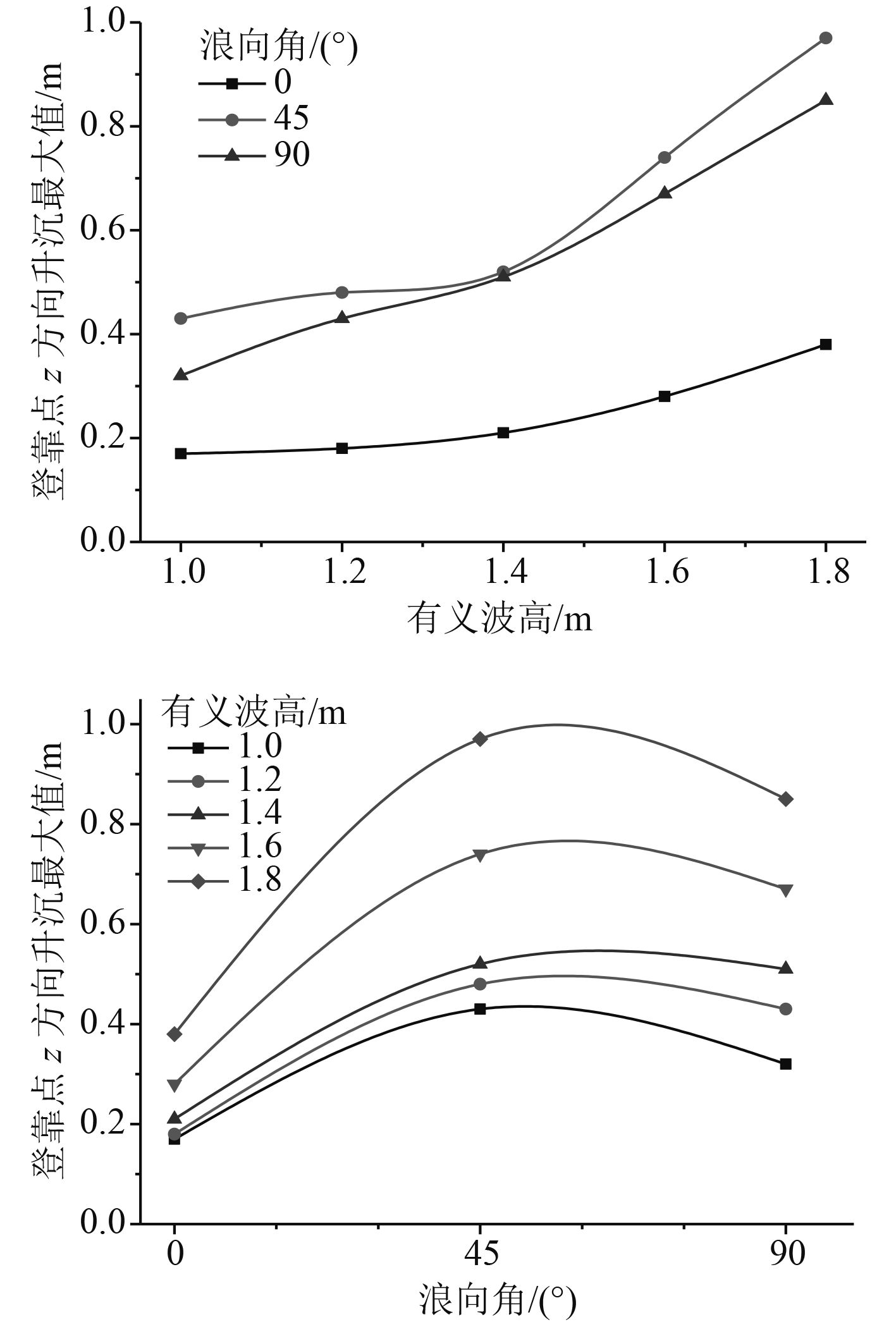
|
图 6 不同有义波高及浪向角下的船首最大升沉值 Fig. 6 Max distances of heave motion at different significant wave heights and angles |
由图6可知,在首部顶靠方式下,浪向角在45°时,船首端船现较大的升沉值(幅度在0.4~0.9 m左右),且浪越高,其值越大;有义波高在1.0 m、1.2 m、1.4 m海况时,其首部升沉最大值基本均在0.6 m以下,符合人员登靠标准。而当有义波高大于1.4 m时,运维船仅在0°首部升沉最大值小于0.4 m;在不同波高时,均出现浪向角在0°首端升沉值最小,45°时的首端升沉值较大,且大于90°时的值。首部升沉最大值基本随着有义波高的增加而变大,当有义波高超过1.4 m时,运动幅值增速变快。
4 结 语本文基于势流理论和波浪的绕射理论,结合计算流体软件FINE/Marine和水动力分析软件AQWA,计算了双体运维船的风流力系数以及粘性阻尼;频域内计算了运维船在单位波幅规则波作用下的运动响应,分析了它的运动响应RAO;基于频域分析结果,对运维双体船行时域耦合动力分析,计算了其在给定不规则波情况下的动力响应,主要结论如下:
1)船在波浪高度不超过1.4 m时,其首端升沉幅值基本小于0.6 m,人员登离较为安全;
2)首部升沉最大值随着有义波高的增加而变大。在一定波高时,浪向角0°时运动幅值较小,45°和90°时的首端登靠点升沉值较大,且45°时的值最大;
3)建议参照风电场风浪流常年方向资料来确定风机塔基靠船桩的安装方位,以避免45°的浪向角,以更好地把控船首升沉幅值,提高维护人员登离时的安全性。
| [1] |
张亮, 朱荣华, 牛福维, 等. 离岸风电运维船设计要点分析[J].国际海上风电, 2014(6): 62–66.
ZHANG Liang, ZHU Rong-hua, NIU Fu-wei, et al. Offshore wind power operational ship design analysis[J].International Offshore Wind, 2014(6): 62–66. |
| [2] |
刘元丹, 熊治国, 刘敬喜. 基于AQWA的旁靠油轮水动力相互作用研究[J].舰船科学技术, 2012, 34(5): 13–22.
LIU Yuan-dan, XIONG Zhi-guo, LIU Jing-xi. Analysis on hydrodynamic interaction between side by side mooring tankers[J].Ship Science and Technology, 2012, 34(5): 13–22. |
| [3] | 李东旭. 高等结构动力学[M]. 北京:科学出版社, 2010. |
| [4] | FALTINSEN O M. Sea loads on ships and offshore structure[M]. Shanghai:Shanghai Jiao Tong University Press, 2013. |
| [5] |
刘震, 黄维平. 基于AQWA的S-Spar平台动力响应分析[J].船舶力学, 2016, 20(1-2): 48–56.
LIU Zhen, HUANG Wei-ping. Dynamic response analysis of S-Spar platform based on AQWA[J].Journal of Ship Mechanics, 2016, 20(1-2): 48–56. |
| [6] |
江红, 赵忠华, 张炎华. 船舶振荡运动仿真[J].上海交通大学学报, 2001, 35(10): 1566–1569.
JIANG Hong, ZHAO Zhong-hua, ZHANG Yan-hua. The simulation of ship's motion[J].Journal of Shanghai Jiao Tong University, 2001, 35(10): 1566–1569. DOI: 10.3321/j.issn:1006-2467.2001.10.029 |
| [7] | 盛振邦, 刘应中. 船舶原理(下册)[M]. 上海:上海交通大学出版社, 2005. |
| [8] |
韩旭亮, 段文洋, 谢彬. 深水浮式结构物系统时域耦合动力方法比较分析[J].中国造船, 2016, 57(01): 149–159.
HAN Xu-liang, DUAN Wen-yang, XIE Bin. Time domain coupling dynamic methods applied to deepwater floating structure system[J].Shipbuilding of China, 2016, 57(01): 149–159. DOI: 10.3969/j.issn.1000-4882.2016.01.016 |
 2017, Vol. 39
2017, Vol. 39
