我国黄渤海水域冬季冰期期间，破冰船需为在此海域通行作业的船舶或海洋装备开辟航道以保障其作业安全性。我国现役的破冰船大多存在服役年限超出、船体结构腐蚀严重等问题。对于老龄破冰船，其推进系统的衰减会导致破冰船的推力降低，使得破冰船的整体破冰能力下降，因此对于较薄厚度的冰层需要采用冲撞式进行破冰。船冰撞击过程中会对船体结构的安全性带来威胁，因此校核冲撞式破冰过程中船体的结构强度有重要的意义。目前国内外学者对破冰船连续式破冰数值仿真方法进行了研究，并取得了较大的进展^{[1 – 5]}，但对于冲撞式破冰的研究相对较少。

本文采用有限元数值仿真的方式对破冰船在撞击海冰过程中的船体结构安全性进行研究。首先探讨模拟海冰脆性破坏方法，建立船体钢材弹塑性模型，提出海冰与船体接触模拟方法和海冰所受浮力模拟方法，在此基础上建立破冰船碰撞式破冰的仿真模型，并以某型破冰船进行结果验证。

海冰的脆性断裂强度需要通过单向拉伸和压缩实验测得^[6]。海冰材料的参数如表1所示。海冰是拉压异性材料，其压缩强度要远远大于拉伸强度^[7]，因此两者的破坏机理不同。

表 1(Tab. 1)

表 1 海冰材料模型的参数 Tab. 1 Material parameters of ice model 密度/kg·m-3 弹性模量/GPa 剪切模量/GPa 泊松比 失效模式 913 Ez=8.2，Ex=6，Ey=6 2.26 0.33 压力10 MPa

表 1 海冰材料模型的参数 Tab.1 Material parameters of ice model

通常为了模拟材料的破坏需要通过实验来确定材料的多轴应力强度^[8]，因此根据材料力学中的第一强度理论来表示海冰破坏的临界状态就可以通过有限元来模拟海冰的失效。总之，对于海冰的失效模拟可采用各向异性的弹性材料模拟海冰失效前的行为，通过定义海冰的最大失效压力作为海冰的临界失效准则。

结构材料的本构关系是碰撞问题中的一项重要研究内容。为了更真实地反映材料的特性，采用线性强化弹塑性模型^[9]。材料的屈服应力为：

式中：σ₀为板材屈服应力，T型材取3.55×10⁸ MPa，球扁钢取2.35×10⁸ MPa；E=2.06×10⁵ MPa为弹性模量；E_h=1.18×10³ MPa为硬化模量。

船冰碰撞是一个动态响应过程，材料的动力特性不能忽略。由于船用低碳钢的塑性对应变率高度敏感，其屈服应力与拉伸强度极限随应变率的增加而增加，故本文在材料模型中引入应变率敏感性的影响。在材料应变率敏感性的众多本构方程中，采用与实验数据符合较好的Cowper-Symonds方程：

式中：σ₀′为塑性应变率ε时的动屈服应力；σ₀为相应的静屈服应力；D=40.4和q=5为钢材的常数。

一般来说，材料的失效过程较为复杂，本文采用MSC.DYTRAN程序中给出的最大塑性应变失效准则。即当结构单元的等效塑性应变达到定义的单元最大塑性失效应变时单元失效，失效单元将不再参与计算。

通过有限元接触面模型可以模拟刚体与刚体、变形体与刚体、变形体与变形体间的相互作用。为模拟撞击须定义相互接触的2个面及其方向，对于破冰过程的模拟定义船首为主面、海冰为从面。此外，碰撞过程中摩擦力也需要考虑。

本文采用罚函数法计算主从接触面间的的接触力。假定接触力与穿透量g_n成正比，穿透量与罚函数K_n相关，则法向的接触力f_n可由下式得到：

在使用罚函数方法计算接触力时，接触面间不允许存在初始穿透，但在计算过程中允许存在穿透，这样通过穿透量与K_n可以求出接触力f_n，在采用罚函数法计算接触力时首先需要选取合适的罚参数值来保证数值求解过程的收敛。在船冰碰撞的计算过程中需要根据多次的试算来确定合适的罚参数K_n。

为计及摩擦力影响，位移偏量u由弹性位移u^e和滑动位移u^s：

在考虑摩擦影响的接触模型中，摩擦力的与法向力f_n成正比：

式中：μ为摩擦系数；f_n可由式（3）求得。当相邻2点发生接触时，摩擦力可由下式计算：

式中：K_t为切向刚度；F_μ为临界摩擦力。

在破冰过程中，海冰由于船首的作用会产生垂向运动，所以需考虑海冰浮力的变化。采用非线性弹簧元模型来计算浮力变化，弹簧单元对海冰的作用模型如图1所示。

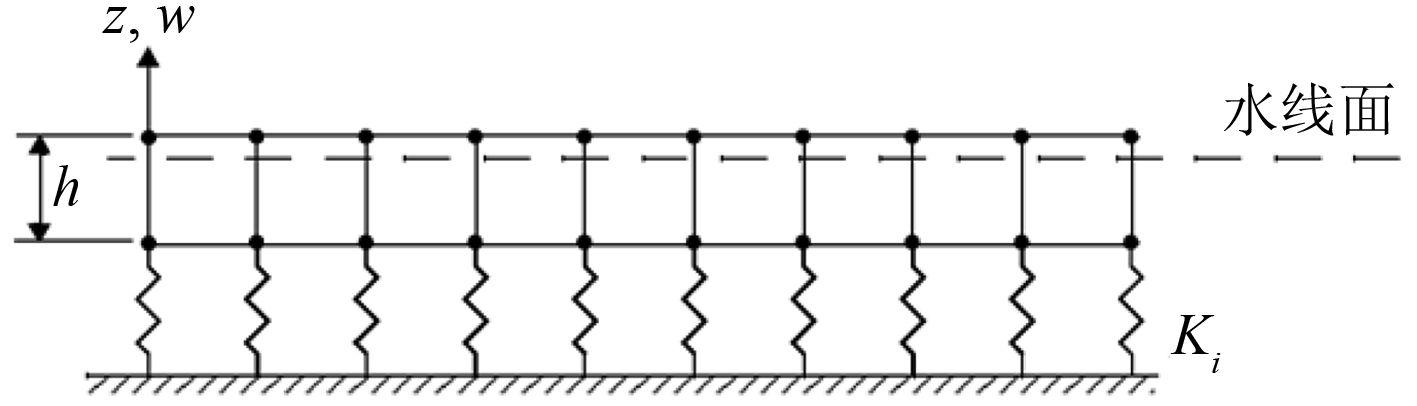
图 1 弹簧单元对浮力的模拟示意图 Fig. 1 Simulation of buoyancy by spring element

连续的非线性弹簧如图2(a)所示，离散弹簧元如图2(b)所示。图中K_f为刚度系数；ρ_i为海冰密度；ρ_w为海水密度；h为冰厚；w为垂向位移；A_i^eff为有效面积。

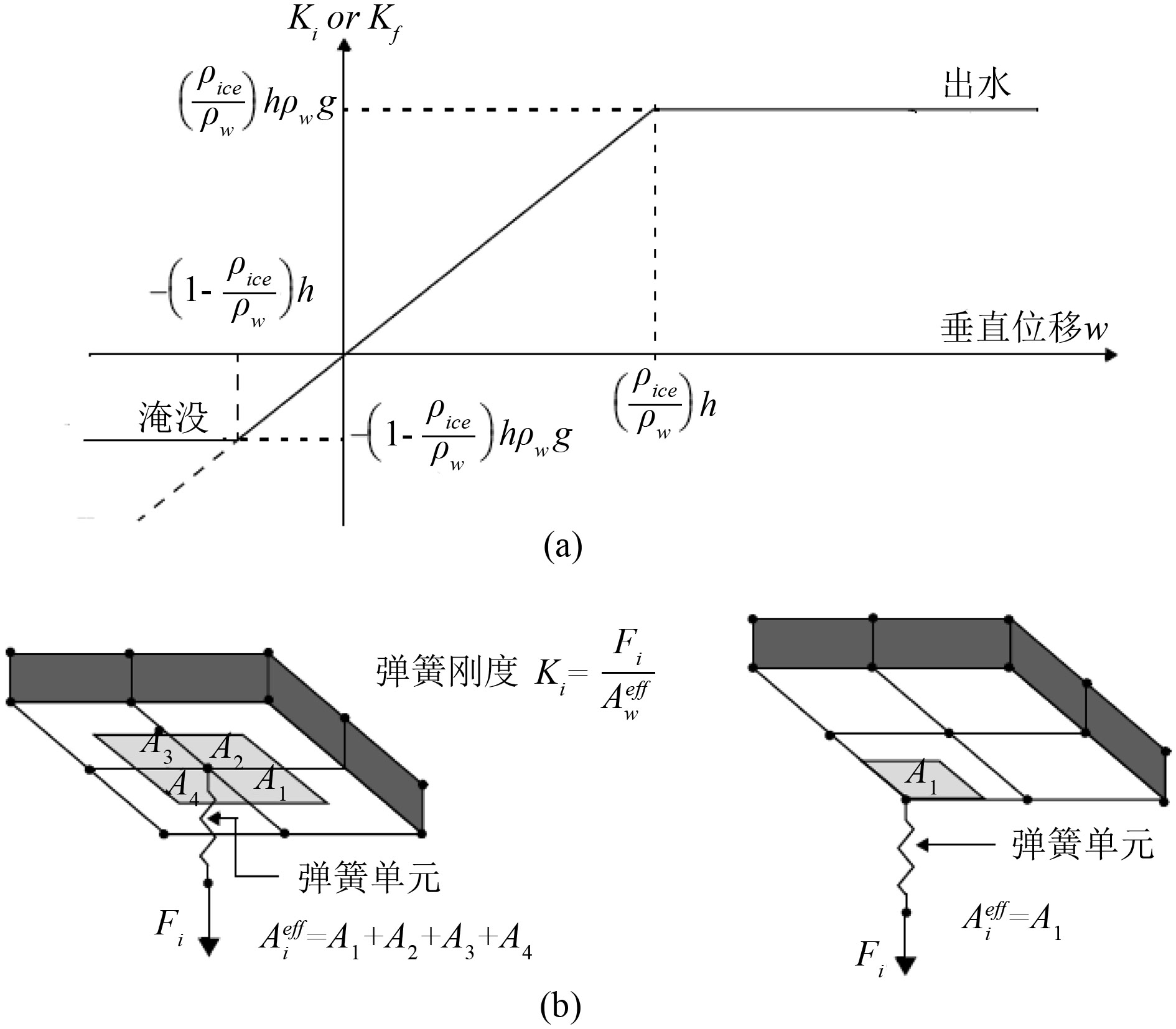
图 2 弹簧单元的刚度示意图 Fig. 2 Spring stiffness settings

设n为当前步数，可以将运动方程写为：

式中： ${F}_n^{\rm ext}$ 为外载荷； ${F}_n^{{\mathop{\rm int}} }$ 为内力， ${F}_n^{{\mathop{\rm int}} } = {C}{v_n} + {K}{d_n}$ 。

加速度可由下式得到：

式中： ${{F}^{\rm residual}} = {F}_n^{\rm ext} - {F}_n^{{\mathop{\rm int}} }$ 为贮备力。M为一集中质量矩阵，通过M可求出节点加速度为

在瞬态动力学分析中，一般采用中心差分法进行时间推进：

在非线性显式求解方法中，时间步长由最小的网格单元决定，以保持计算的稳定：

式中 ${w_{\max }}$ 为有限元最大自然频率。杆单元的最小时间步长可由下式求出：

式中： ${l_{\min }}$ 为最小单元的边长；E为材料弹性模量；ρ为材料密度。

为了验证上述所建立的冲撞式破冰模型的合理性，采用某破冰船进行验证。

本算例中所采用破冰船型的轮廓图如图3所示，相应的主尺度及相关参数如表2所示。计算中的海冰的相关参数如表3所示。

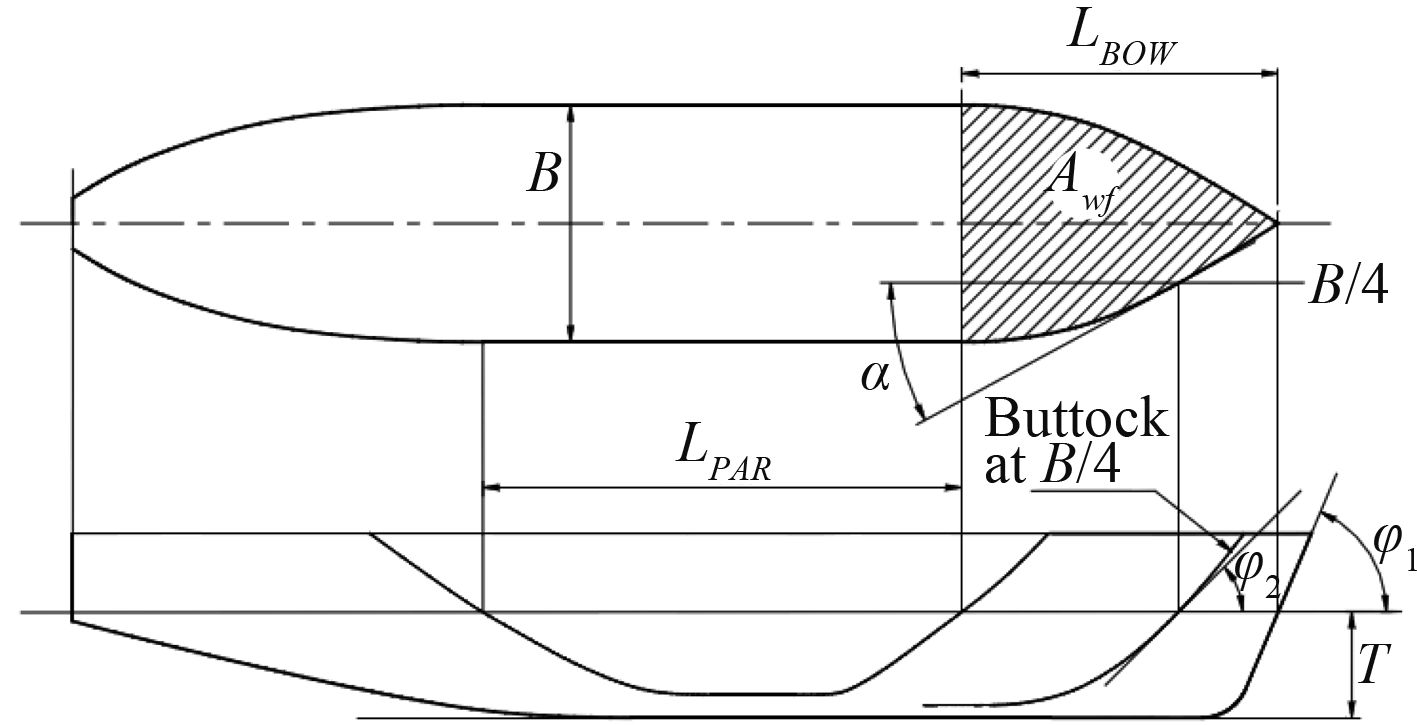
图 3 破冰船轮廓图及参数定义 Fig. 3 The diagram of shape parameter of icebreaker

表 2(Tab. 2)

表 2 破冰船主尺度及相关参数 Tab. 2 Main particulars of the icebreaker 参数 数值 船长 L/m 84.28 船宽 B/m 15 船舶航速 V/m·s-1 5.14 船舶吃水 T/m 5 密度 ρship/kg·m-3 7 850 泊松比 ν 0.3 屈服限 σ/MPa 355 最大塑性应变 ε 0.35

表 2 破冰船主尺度及相关参数 Tab.2 Main particulars of the icebreaker

表 3(Tab. 3)

表 3 海冰相关参数 Tab. 3 Parameters of ice 参数 数值 海冰密度 ρice/kg·m-3 920 海水密度 ρw/kg·m-3 1 025 冰层厚度 H/m 0.6 弯曲强度 σ/MPa 1.10 挤压强度 σ/MPa 10.00 弹性模量 E/MPa 8 900 泊松比 ν 0.30 重力加速度 g/N·m-2 9.81 摩擦系数 μ 0.15

表 3 海冰相关参数 Tab.3 Parameters of ice

在有限元模型建立中，破冰船的结构用板单元建立，海冰用六面体实体单元建立，周围的海水用欧拉网格模拟，海冰所受浮力用非线性弹簧单元模拟。所建立的破冰船、海水、海冰组成的整体模型如图4所示。

图 4 破冰船、海冰与海水相互作用数值模型 Fig. 4 Couple model of ship, ice and water

本文所选取的算例工况中，碰撞过程中破冰船以10 kn的初始速度破冰，设计破冰厚度为0.6 m。破冰船在冲撞式破冰过程中，船体首部会与海冰发生剧烈碰撞^[10]，并产生瞬时的高应力。为了准确模拟这一现象，需将船首结构网格进行细化以保证求解精度，如图5所示，而对于其他位置采用刚体模拟即可。

图 5 首部精细网格模型 Fig. 5 Fine mesh model of the icebreaker

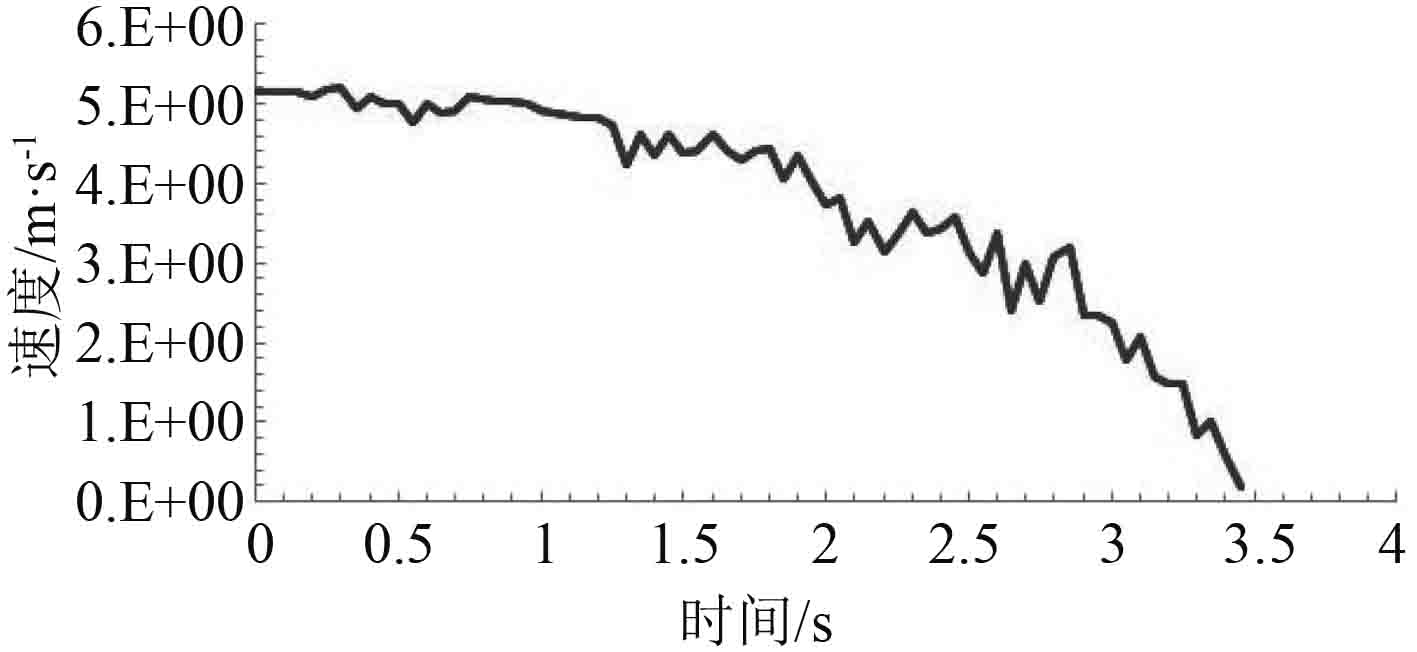
通过软件模拟得到的破冰船以10 kn的速度撞击冰域后的纵向碰撞力和前进速度的变化曲线分别如图6和图7所示，撞击某一瞬时的海冰破碎形状和应力分布如图8所示。

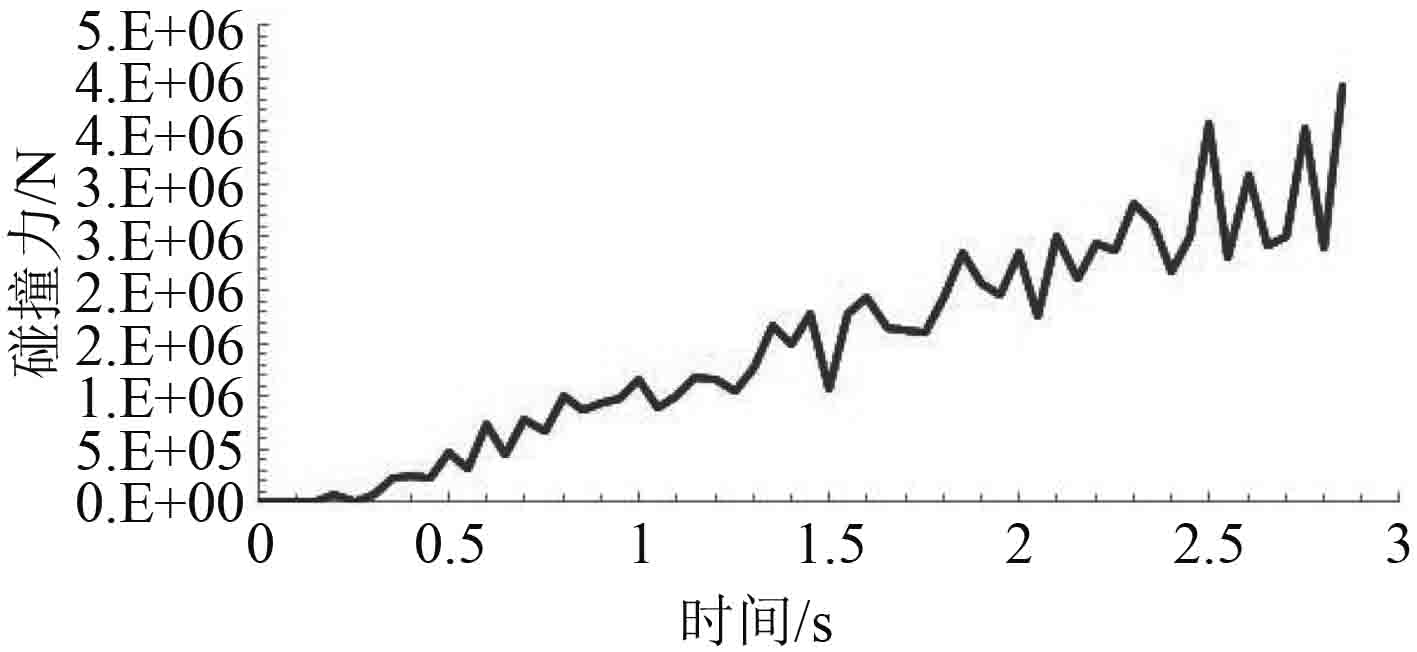
图 6 船冰纵向碰撞力曲线 Fig. 6 Ice force time history in longitudinal direction

图 7 破冰船纵向速度变化曲线 Fig. 7 Speed time history of the icebreaker

图 8 海冰应力分布 Fig. 8 Stress distribution of ice sheet

由模拟结果可看出，船冰在撞击过程中，冲击力随着破冰船进入海冰而逐渐增加，纵向碰撞力的最大值为7.6 MN。碰撞过程中碰撞力会出现瞬间的变化，这是由于海冰单元出现失效导致的碰撞力瞬间下降，直到破冰船再次与海冰单元接触撞击力变大，如此循环反复。在整个碰撞过程中，船体航行方向的加速度逐渐增大，直到速度降为0。

在进行强度校核时，需把船体结构分成若干个构件分别进行强度校核，主要包括甲板、船体外板、横舱壁、横框架、纵舱壁、纵桁等。撞击过程中，各部分构件发生的最大应力情况如表4所示。

表 4(Tab. 4)

表 4 各构件强度校核结果 Tab. 4 Strength assessment results 序号 构件名称 最大等效应力/MPa 屈服极限/MPa 是否满足 1 甲板 53.1 355 是 2 纵桁 72.7 355 是 3 横舱壁 167 355 是 4 纵舱壁 270 355 是 5 外壳板 356 355 否 6 底肋板 324 355 是

表 4 各构件强度校核结果 Tab.4 Strength assessment results

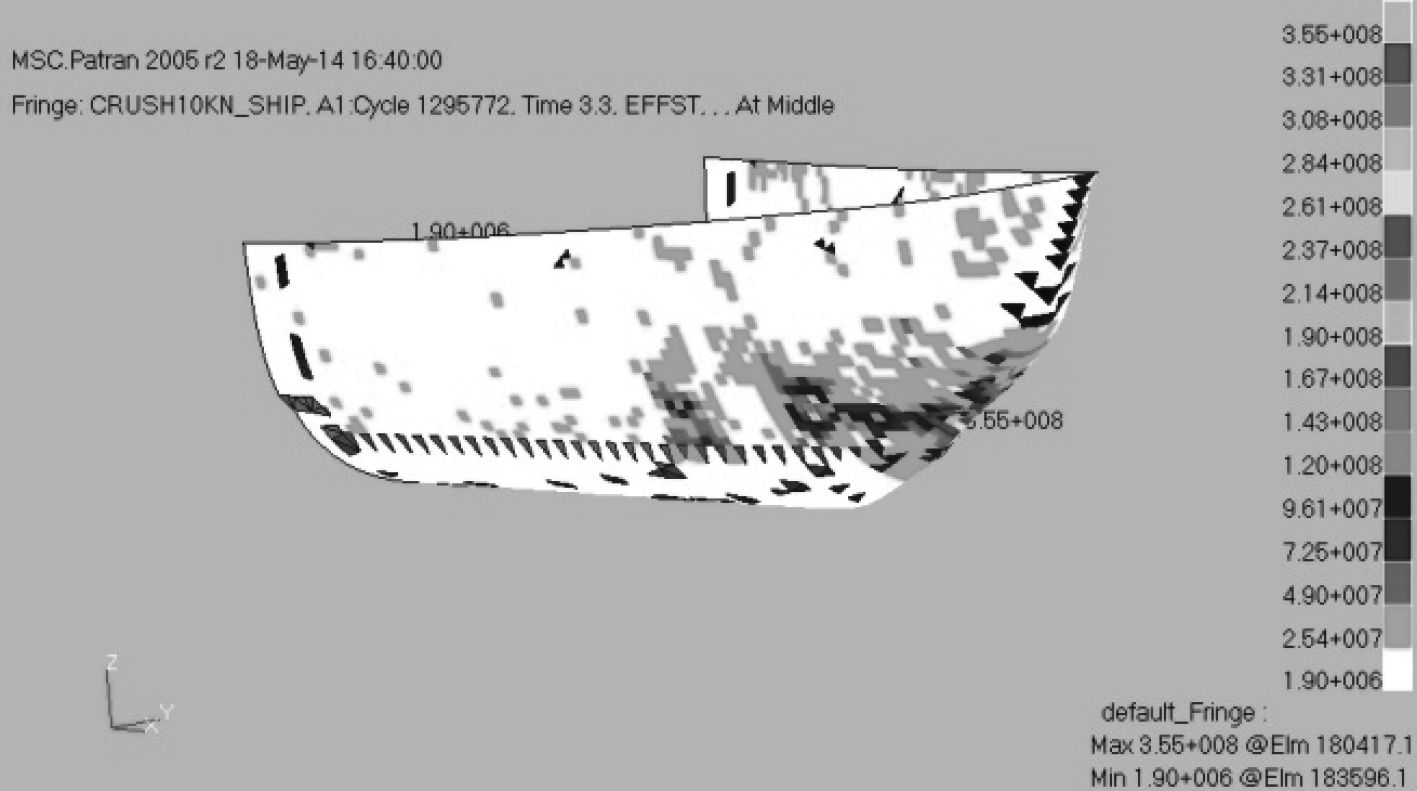
从以上的应力计算结果可知，当破冰船以10 kn 速度冲撞时，部分船体构件出现结构强度问题。船体最大应力发生在外壳板上，其应力分布云图如图9所示，最大应力356 MPa 已超出材料的屈服极限355 MPa。根据其他工况的计算还可以发现，当破冰船以6 kn 和8 kn 初速度撞击海冰时，船体受到的最大应力分别为253 MPa和216 MPa，此时船体结构较为安全。但当初始速度为10 kn 时，船体结构已发生危险。由此可知，出与船体结构安全因素考虑，冲撞式破冰船的破冰速度选取宜适中。

图 9 外板应力分布云图 Fig. 9 The stress distribution of the hull

本文针对冲撞式破冰船提出了结构强度数值分析方法。通过非线性有限元方法进行船冰碰撞的数值模拟，本文对一些关键技术进行研究，其中包括船冰相互接触碰撞算法、接触面间摩擦系数在碰撞力计算中的影响、非线性弹簧元的使用以及显式求解方法等。

根据某破冰船冲撞式破冰过程的算例分析表明，本文所建立的模拟方法可行。并分析得到了撞击过程中船体的应力分布及危险构件强度校核。