舰船噪声主要是由机械噪声、螺旋桨噪声、水动力噪声等部分组成的。近年来,随着机械设计和制造水平的提高,以及新技术的采用,机械噪声已经得到有效的控制,因此作为现阶段舰船主要噪声的螺旋桨噪声,日益引起人们的重视。
对于螺旋桨噪声的预报大致分为 2 种:一种是利用势流理论程序预报;另一种就是利用粘流软件进行数值模拟。Seol H等[1–2]用面元法和噪声分析方法计算了螺旋桨无空泡及空泡噪声;朱锡清等[3–5]结合非定常升力面理论和声类比方法对船舶螺旋桨的频线谱噪声和宽带谱噪声进行研究;杨琼方[6–8]采用流场大涡模拟(large eddy simulation,LES)和声场边界元数值声学的弱耦合方法在频域内进行了螺旋桨噪声分析;王超等[9–10]研究了DTRC4119在均匀流中声压特性;宋晗等[11]通过Kappel桨与传统螺旋桨噪声对比试验,对低噪声螺旋桨的设计进行了探索。
本文选取某一螺旋桨作为计算对象,通过Fluent软件进行了螺旋桨水动力性能计算,采用MRF模型计算螺旋桨定常敞水水动力性能,采用大涡模拟和滑移网格技术得到螺旋桨均匀流流场信息,最终在Actran软件中完成声学仿真。通过试验数据与数值仿真的对比,从定量的角度说明采用基于大涡模拟与Actran耦合的方法能够预报螺旋桨的水动力噪声。
1 数学模型1.1 大涡模拟SGS模型大涡模拟通过滤波函数将紊流中的大、小尺度涡进行分离,并采用不同的方式进行处理,是介于直接模拟(DNS)和RANS之间的一种新型、可行的数值模拟方法。大涡模拟的控制方程由连续性方程和经滤波函数处理而得的非定常N-S方程组成:
| $\frac{\partial }{{\partial t}}\left( {\rho \overline {{u_i}} } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \overline {{u_i}} \overline {{u_j}} } \right) = - \frac{{\partial \overline p }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}}} \right) - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}\text{,}$ | (1) |
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho \overline {{u_i}} }}{{\partial {x_i}}} = 0\text{,}$ | (2) |
其中:
| ${\sigma _{ij}} = \left[ {\mu \left( {\frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} + \frac{{\partial \overline {{u_j}} }}{{\partial {x_i}}}} \right)} \right] - \frac{2}{3}\mu \frac{{\partial {u_i}}}{{\partial {x_j}}}{\delta _{ij}}\text{,}$ | (3) |
| ${\tau _{ij}} = \rho \overline {{u_i}{u_j}} - \rho \overline {{u_i}} \overline {{u_j}} \text{。}$ | (4) |
式中:σij为分子粘性引起的应力张量;τij为亚格子应力(简称SGS应力)。
假设SGS应力为:
| ${\tau _{ij}} = \frac{1}{3}{\tau _{kk}}{\delta _{ij}} - 2{\mu _t}{\overline S _{ij}}\text{,}$ | (5) |
式中:μt为亚格子尺度的涡粘系数。Smagorinsky定义求解公式如下:
| ${\mu _t} = {\left( {{C_S}\Delta } \right)^2}\left| {\overline S } \right|\text{,}$ | (6) |
| ${\overline S _{ij}}\!\! = \!\!\frac{1}{2}\left( {\frac{{\partial {{\overline u }_i}}}{{\partial {x_j}}} \!\!+\!\! \frac{{\partial {{\overline u }_j}}}{{\partial {x_i}}}} \right),\;\left| {\overline S } \right|\!\! = \!\!\sqrt {2{{\overline S }_{ij}}{{\overline S }_{ij}}} ,\;\Delta\!\! =\!\! {\left( {{\Delta _x}{\Delta _y}{\Delta _z}} \right)^{1/3}}\text{。}$ | (7) |
式中:∆i为沿i轴方向的网格尺度;CS为Smagorinsky常数。
1.2 Lighthill声学类比理论Lighthill声学类比理论考虑的模型是:在一个无限大的声场内,介质均匀且为静态,该声场内包含一个有限大的湍流流动区域V,作为声源区。在远离湍流区域V的外部流场中,流体密度的波动与声波相似。
| $\frac{1}{{c_0^2}}\frac{{\partial \rho '}}{{\partial {t^2}}} - {\nabla ^2}\rho ' = 0\text{,}$ | (8) |
Lighthill声类比理论是基于流体力学基本方程N-S方程推导而得的[12]。
| $\frac{{{\partial ^2}\rho }}{{\partial {t^2}}} - c_0^2{\nabla ^2}\rho = \frac{{{\partial ^2}{T_{ij}}}}{{\partial {x_i}\partial {x_j}}}\text{,}$ | (9) |
| $T{'_{ij}} = \rho {u_i}{u_j} + {\delta _{ij}}\left[ {\left( {p - {p_0}} \right) - c_0^2\left( {\rho - {\rho _0}} \right)} \right] - {\sigma _{ij}}\text{。}$ | (10) |
基于声学有限元/无限元技术的Actran软件是20世纪90年代末推出的,它通过对结构和声场建立离散化模型,利用Lighthill声类比方法求解湍流区的流致噪声,通过声学的波动方程模拟噪声的传播。
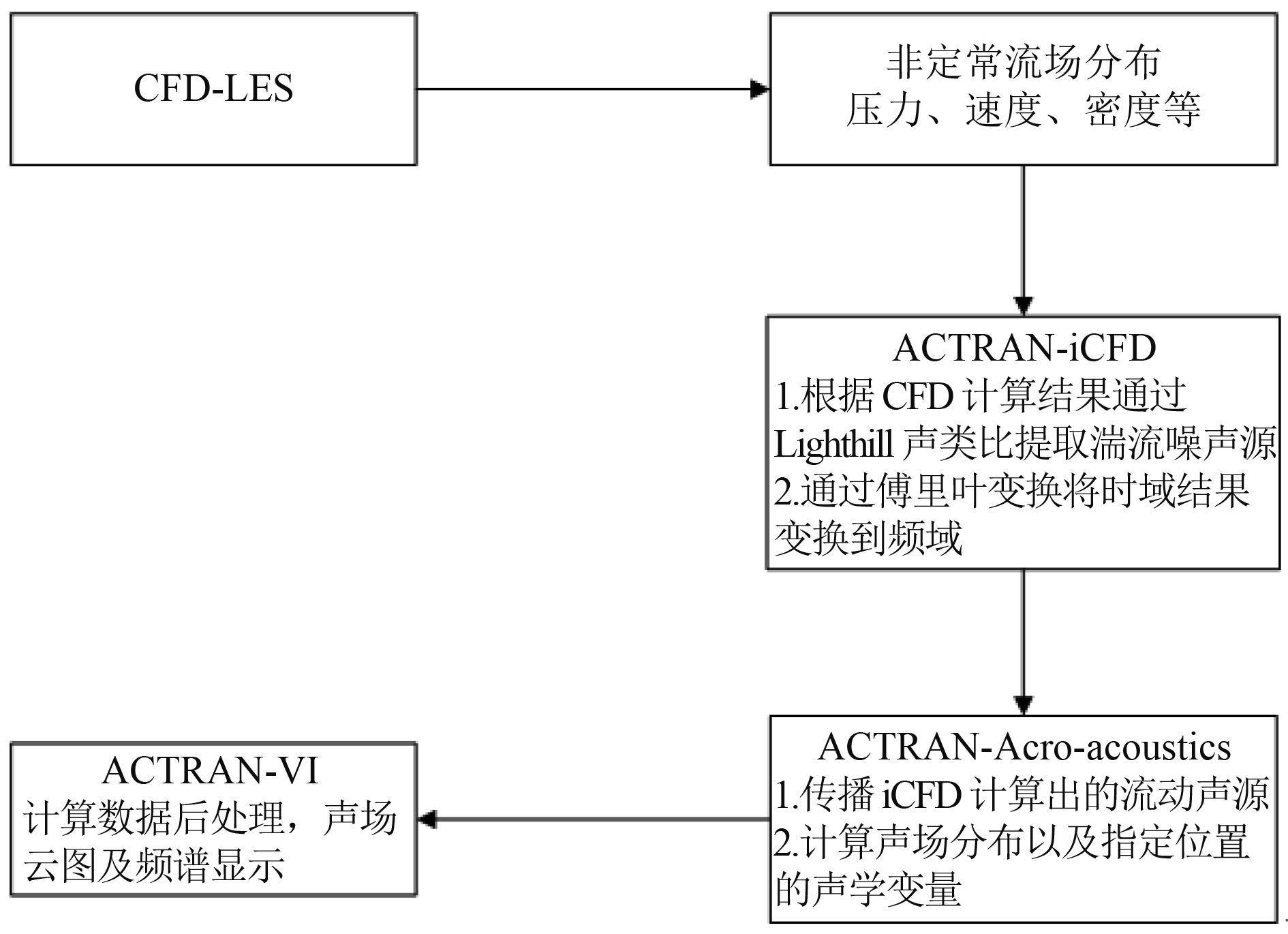
对于噪声分析来说,计算步骤如图1所示。
|
图 1 噪声计算过程 Fig. 1 Noise calculation process |
螺旋桨基本尺寸如表1所示,与空泡水筒试验桨模尺寸一致。首先利用Matlab程序导出桨叶型值点,然后再将其导入ICEM中,把点连成线,由线生成面。螺旋桨模型如图2所示。
|
|
表 1 螺旋桨主要参数 Tab.1 Main parameters of propeller |

|
图 2 螺旋桨模型 Fig. 2 Propeller models |
为了在CFD软件中模拟螺旋桨敞水实验,还需建立虚拟的桨外流域,根据滑移网格技术的特点,将螺旋桨计算域分为静止的部分(即大域)和绕桨轴旋转的部分(即小域),取外流域入口距桨中心3D,尾流出口距离桨中心5D,径向为螺旋桨直径的6倍。外流场计算域与螺旋桨分开建立模型,二者之间通过interface进行数据传递,外部大域模型如图3所示。

|
图 3 外域模型 Fig. 3 Extracellular domain model |
由于螺旋桨和大域几何形状较规整,在划分网格时采用全结构化网格。根据螺旋桨周期性特点,首先划分单个桨叶的网格,然后进行旋转,得到小域整体网格如图4所示。为了适应桨叶形状的变化,适当进行C网划分,保证网格质量,并且此种方式还可以达到在桨叶表面进行局部加密,控制网格数量的作用。

|
图 4 螺旋桨网格结构 Fig. 4 Mesh topology of propeller |
对于该计算桨在靠近桨叶导边随边及叶面的地方,均进行加密,控制桨叶表面第 1 层网格厚度约在0.3 mm左右,网格厚度以1.1倍速率递增,以满足LES对网格的要求如图5所示,整体计算域网格约为280万。

|
图 5 网格加密 Fig. 5 Mesh refinement |
在螺旋桨的敞水计算中,入口和出口边界分别设为速度入口和压力出口;圆柱体表面设为对称面;小域绕桨轴以900 r/min的角速度绕桨轴旋转,通过改变进流速度来实现不同的进速系数;首先采用SST湍流模型进行定常运算,待获得稳定流场后,改用LES湍流模型进行非定常运算。定常计算过程中选用(MRF)模型,非定常水动力性能计算过程选用滑移网格(Moving Mesh)模型。
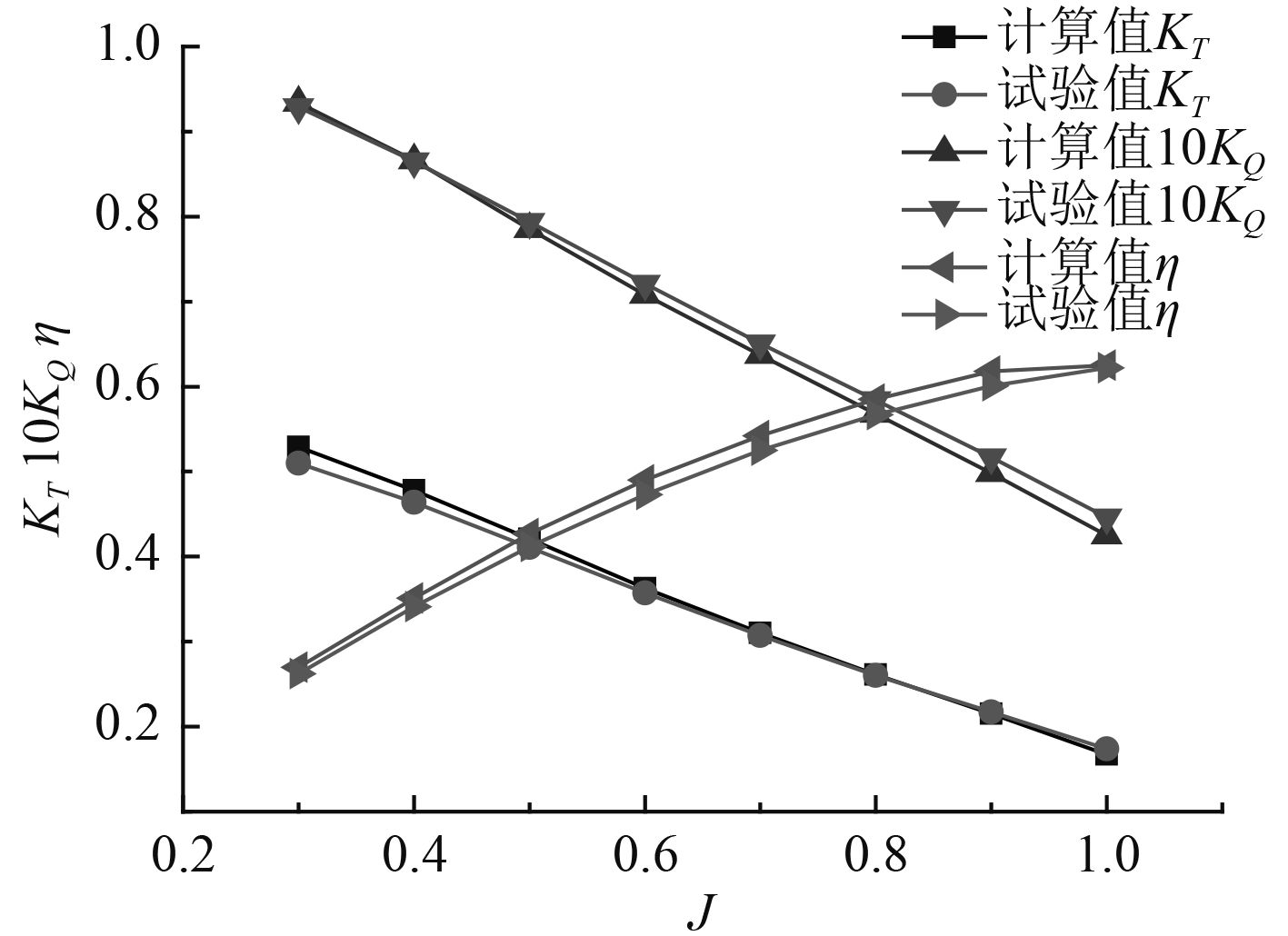
3 螺旋桨水动力性能计算3.1 敞水性能计算验证首先对敞水中的螺旋桨水动力性能进行大涡模拟计算。通过改变来流速度改变螺旋桨的进速系数,图6所示为螺旋桨的水动力性能计算值与试验值的对比。
|
图 6 螺旋桨敞水性能曲线 Fig. 6 Open water performance of propeller |
从图6可看出,转矩系数随着进速系数的增大出现相对较大的误差,是由于在高进速系数时产生的转矩相对较小,受到小的扰动就会产生较大的影响;计算所得数据与实验数据吻合较好,误差控制在5%以下。
总的来说,所采用的计算模型及方法能够有效地预报螺旋桨的水动力性能。
3.2 设计工况计算验证螺旋桨在均匀流场中进行噪声试验工况如表2所示。良好的CFD采样对于Actran噪声计算至关重要,螺旋桨转速n=15,旋转 1 周的时间约为0.067 s,为保证采样的准确性,采样总时间最好是 2 个周期以上,即大于0.134 s。
|
|
表 2 设计工况 Tab.2 Design condition |
|
|
表 3 计算值与试验值对比 Tab.3 Comparison between theoretical value and experimental value |
由表3中的数据可知,推力和转矩计算值和试验值高度吻合,表明了在设计工况处水动力性能预报的准确性,为后续的声学计算提供了保障。
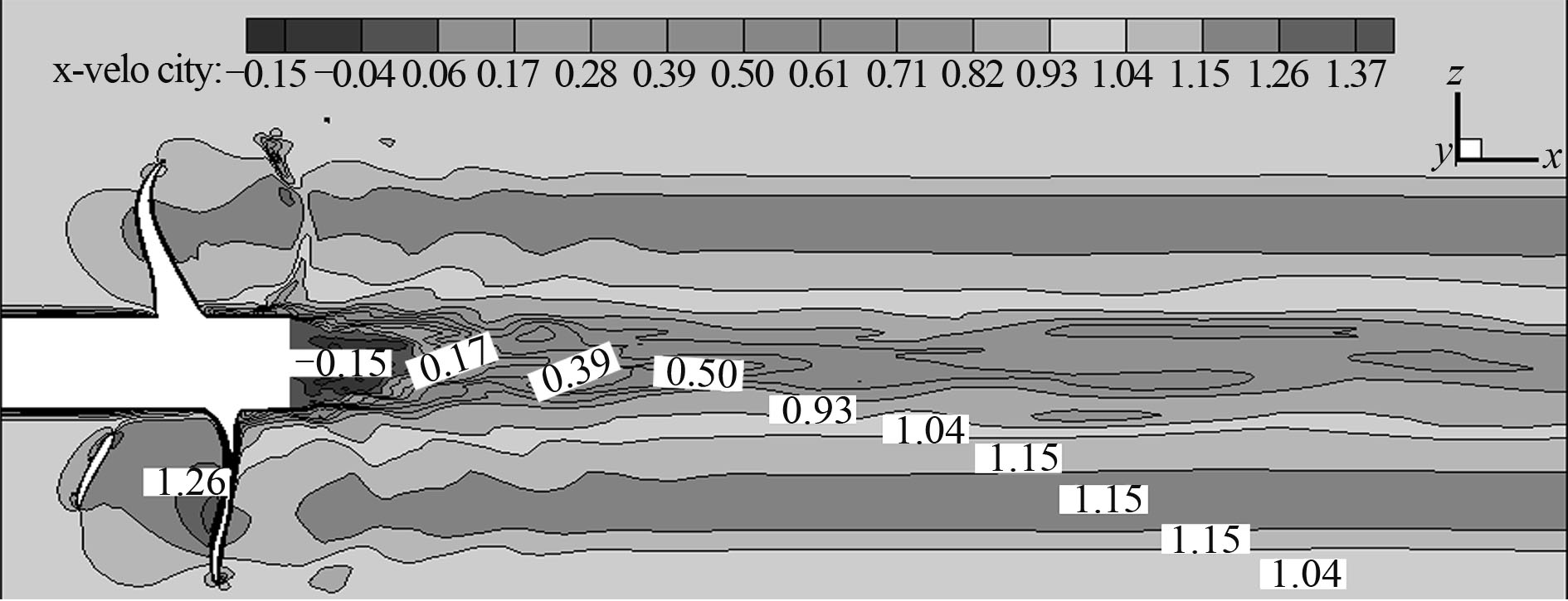
螺旋桨在敞水均匀流场中工作,以轴向速度分量为最大,径向和周向分量相对较小。图7所示为Y=0处XZ平面的无量纲轴向速度。
|
图 7 XZ平面无量纲轴向速度云图 Fig. 7 XZ plane dimensionless axial velocity contours |
观察发现该切面处速度云图显示出在桨毂紧后方的位置里流速减小明显,形成一条低速区,而在桨叶后方形成了 2 条狭长高速区。在低速带内流场较高速带复杂,桨后流场较桨前复杂。
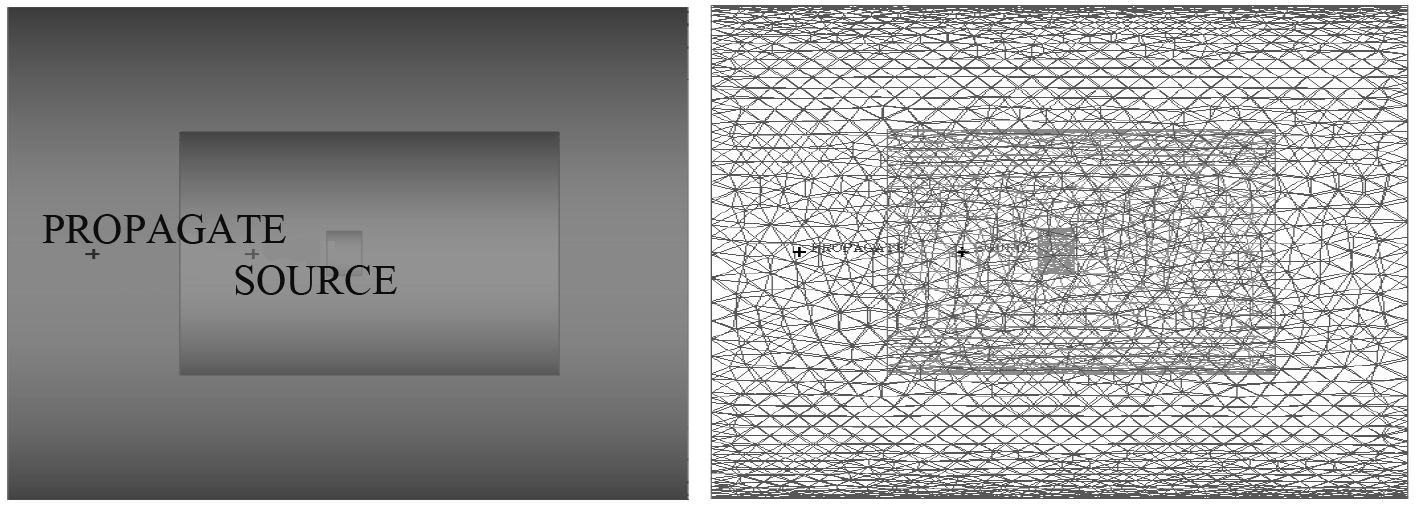
4 螺旋桨噪声数值预报4.1 声学模型与网格划分通过大涡模拟获得稳定的非定常流场后,需要创建声学网格,包括声源区和声传播区,其中声源区取自CFD计算区域,略小于CFD计算区域,以消除边界影响,声传播区则根据需要设置,如图8所示。
|
图 8 声学模型与网格 Fig. 8 Acoustic model and the mesh |
与水听器位置相对应,在距桨中心径向0.6 m处设置特征点监测,同时在通过螺旋桨盘面垂直的平面上距离桨中心0.44 m,0.88 m处,分别各取24个测点平均分布于螺旋桨周围,然后计算各点处总声压级来分析螺旋桨声指向性;同时从桨中心X=0 m到X=1.1 m,Y=0 m到Y=1.1 m均匀布置5个测点,然后计算各点处的总声压级来分析螺旋桨的衰减特性。
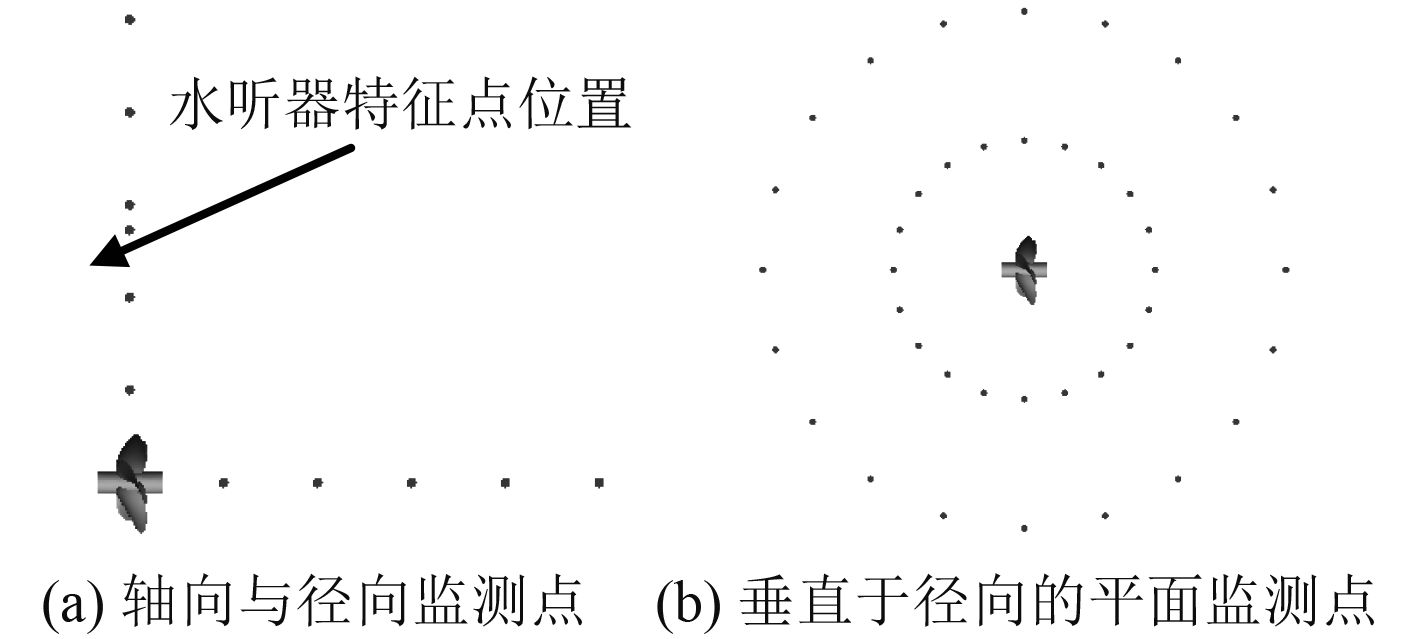
|
图 9 监测点布置 Fig. 9 Monitoring point arrangement |
声场计算支持的最大频率fmax与流场计算时间步长∆t有关,可按下式进行计算:
| ${f_{\max }}{\rm{ = }}\frac{1}{{2\Delta t}}\text{。}$ | (11) |
由于时间步长设置为0.000 25 s,故对应有效频率上限为2 000 Hz,参考声压为1 μPa。
一般水听器的频响范围为0.1~120 000 Hz,普通模型试验中实际测量范围可达0.1~80 000 Hz,但是对于数值计算高频曲线将消耗大量的时间,且螺旋桨噪声主要集中在中低频,所以在此选取试验值0.1~2 000 Hz与数值模拟对比。
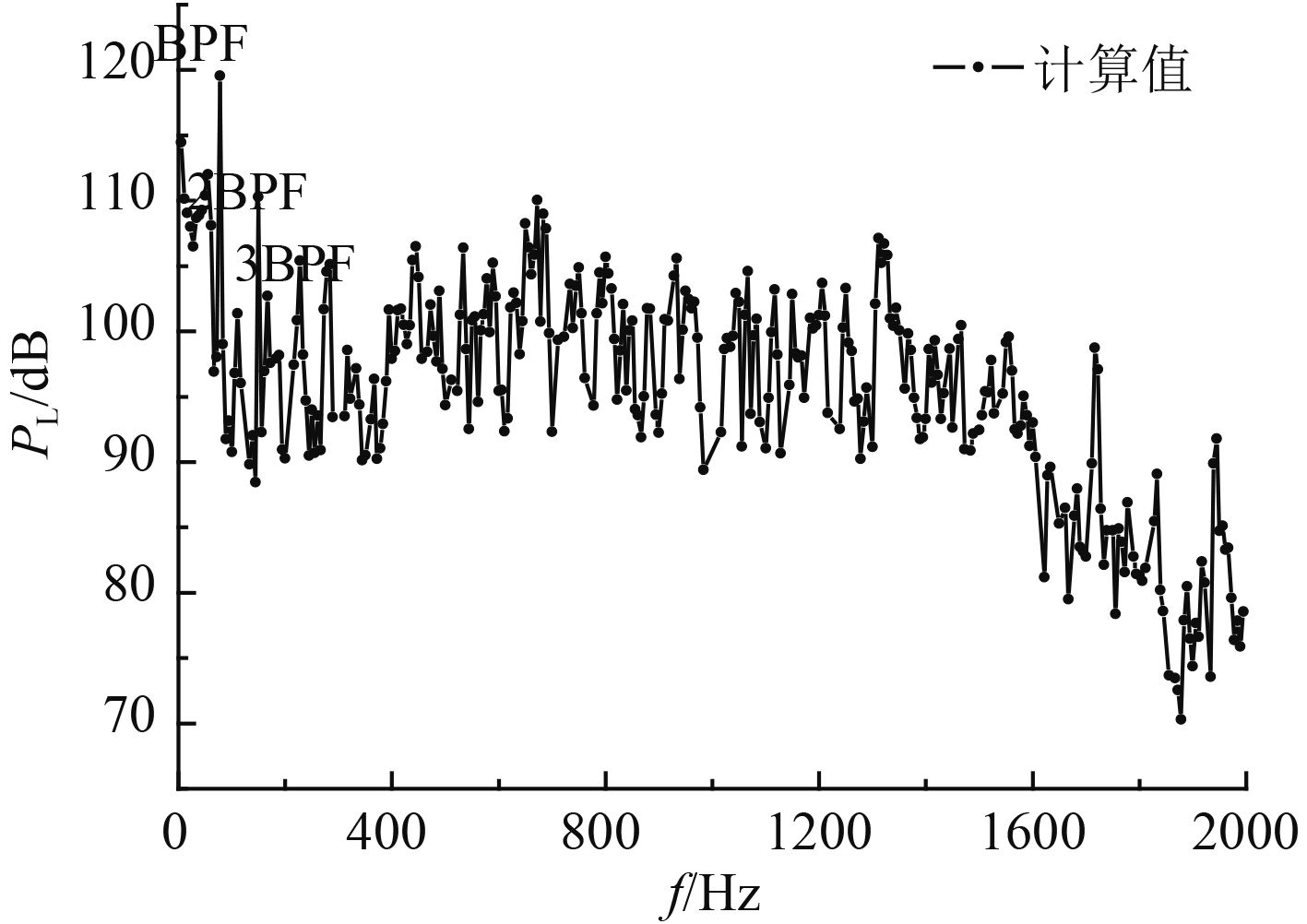
|
图 10 声压频谱曲线 Fig. 10 Sound pressure spectrum |
由图10可看出,数值计算所得的频谱曲线中可观测到较为明显的叶频BPF信息,但随着频率的增大叶频信息无法清晰地观测。
图11为不同频率时通过螺旋桨轴向剖面声压云图。
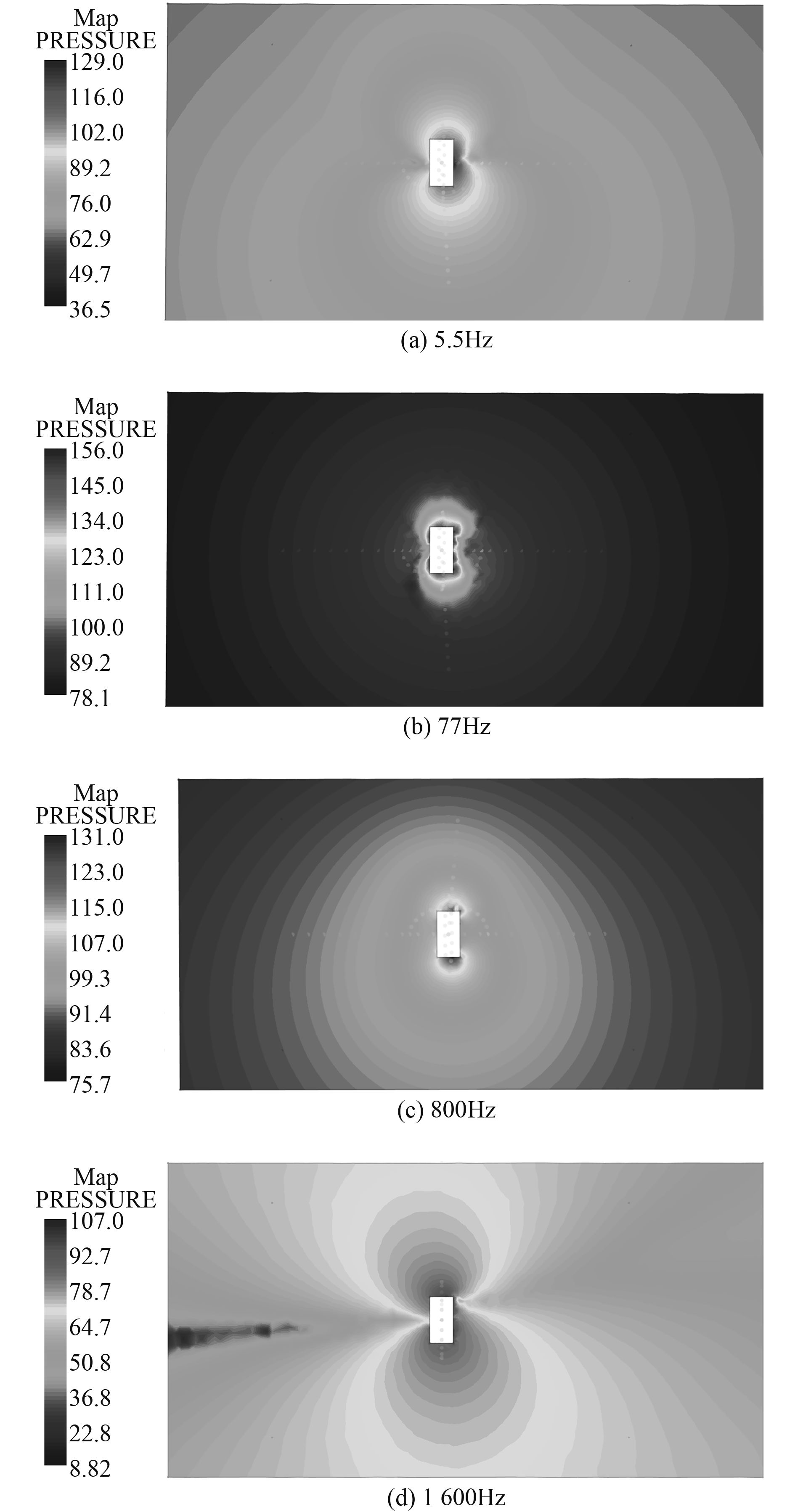
|
图 11 声压云图 Fig. 11 Sound pressure contours |
频率不同时,声压分布云图也存在着很大的差异,在以上云图中均体现出均匀流单极子噪声特性,并且在接近一阶叶频的77 Hz云图中其最大值大于其他频率下的最大值,与频谱曲线趋势相一致。
4.2.2 声指向性及衰减特性螺旋桨周围R=0.44 m处与R=0.88 m总声压指向性分布如图11所示,各点声压级大小相近,但径向位置声压级要略大于轴向位置,另外螺旋桨的旋转推水作用导致桨后位置声压级要略大于桨前位置,声指向性呈向桨后倾斜的“8”字形分布,符合单极子噪声特性。
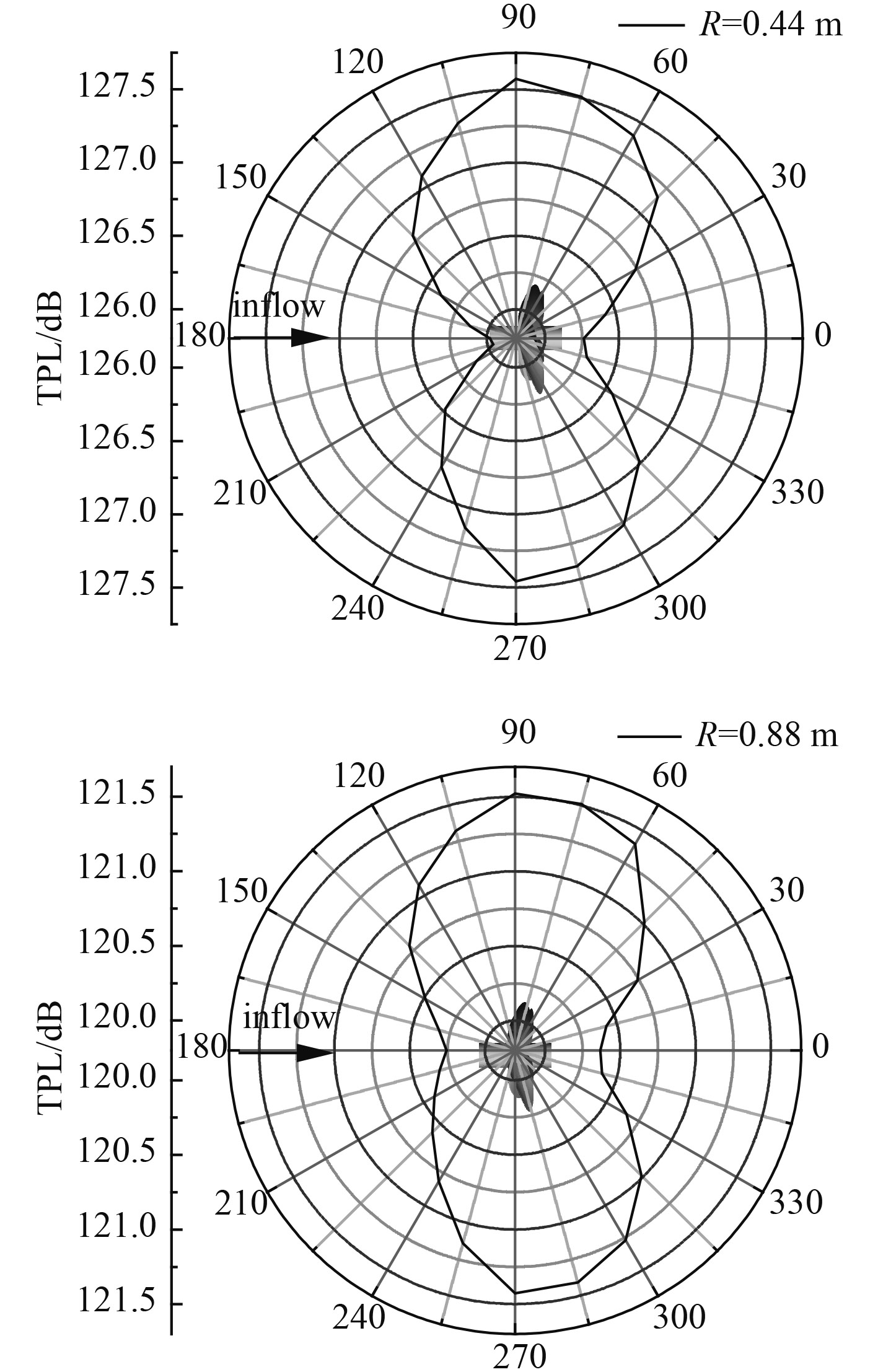
|
图 12 声指向性 Fig. 12 The sound directivity |
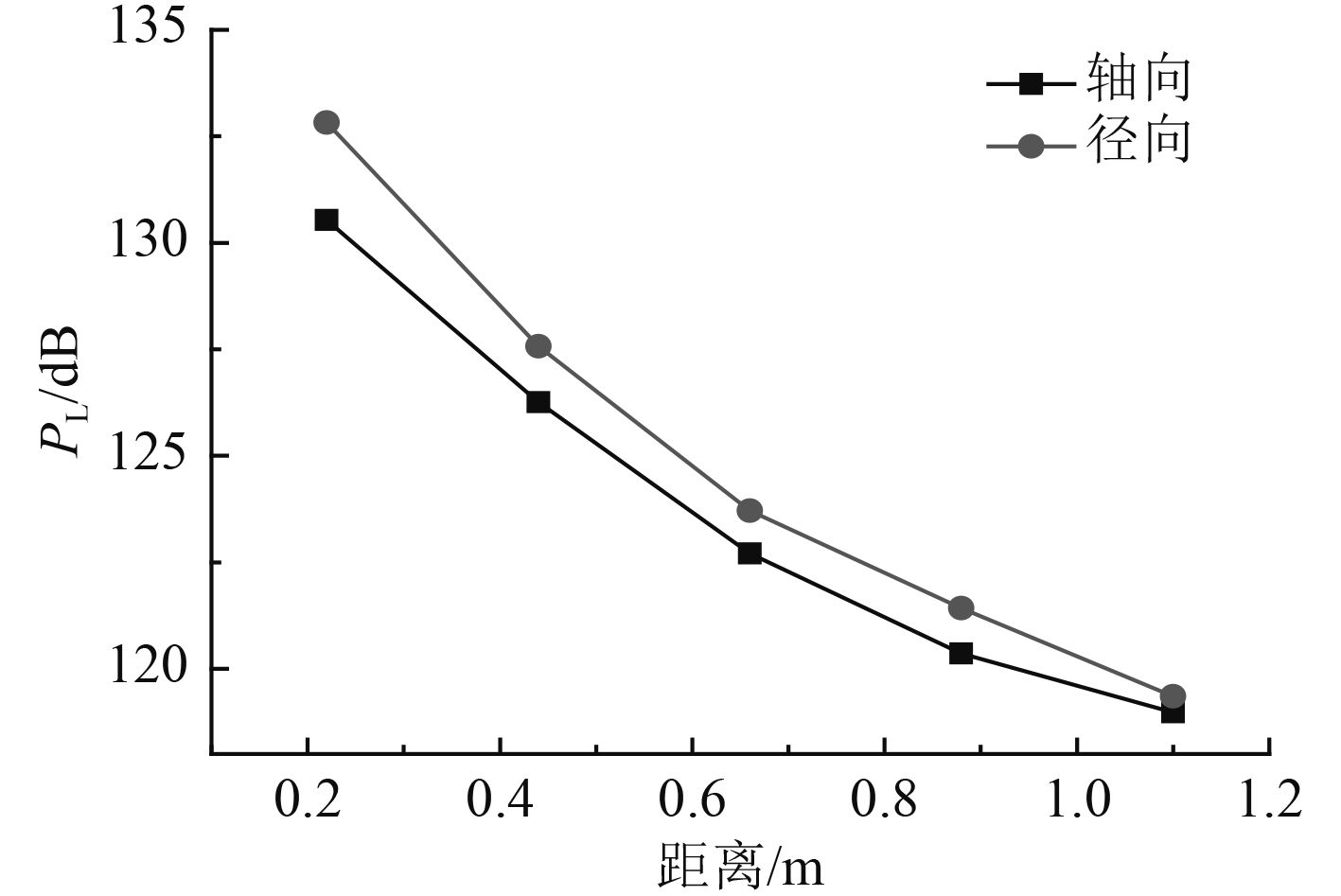
从桨中心X=0 m到X=1.1 m,Y=0 m到Y=1.1 m均匀布置5个测点,然后计算各点处的总声压级所得的螺旋桨的衰减特性曲线如图13所示。
|
图 13 轴向与径向声压级衰减曲线 Fig. 13 The axial and radial attenuation curve |
在相同进速下,远离螺旋桨桨轴中心,无论在轴向上还是在径向上,螺旋桨无空泡噪声随着距离的增大而减小,这是由于螺旋桨旋转与湍流流场相互作用,存在大量涡脱落,随着距离的增加,涡会逐渐耗散消失;离螺旋桨桨轴中心相同距离的监测点,径向上的总声压级要高于轴向上的总声压级,但随着距离的增加,两者之间的差距逐渐减小。
5 结 语本文针对低噪声螺旋桨进行了数值模拟,研究分析了其敞水水动力性能与声学性能,通过与试验对比,从定量的角度验证了大涡模拟与声学软件Actran相结合计算螺旋桨噪声可行,为进一步预报舰船乃至船桨一体噪声性能打下了基础。
| [1] | SEOL H, JUNG B, SUH J C, et al. Prediction of non-cavitation underwater propeller noise[J].Journal of Sound and Vibration, 2002, 257(1): 131–156. |
| [2] | SEOL H, SUH J C, LEE S. Development of hybrid method for the prediction of underwater propeller noise[J].Journal of Sound and Vibration, 2005, 288: 345–360. |
| [3] |
朱锡清, 李亚, 孙红星. 船舶螺旋桨叶片与艉部湍流场互作用噪声的预报研究[J].声学技术, 2006, 25(4): 361–364.
ZHU Xi-qing, LI Ya, SUN Hong-xing. Ship propeller blades and stern turbulence field interaction noise prediction research[J].Journal of Acoustic Technology, 2006, 25(4): 361–364. |
| [4] |
朱锡清, 唐登海, 孙红星, 等. 船舶螺旋桨低频噪声研究[J].水动力学研究与进展(A辑), 2000(1): 78–81.
ZHU Xi-qing, TANG Deng-hai, SUN Hong-xing, et al. Shiplow-requency noise of propeller study[J].Water Dynamics Research and Progress (A), 2000(1): 78–81. |
| [5] |
熊紫英, 朱锡清, 刘小龙, 等. 船尾伴流场-导管-螺旋桨互作用噪声预报研究[J].声学学报, 2009(11): 117–123.
XIONG Zi-ying, ZHU Xi-qing, LIU Xiao-long, et al. ternwake field-catheter-interac;tion noise prediction research[J].Aota Aoustioa, 2009(11): 117–123. |
| [6] |
杨琼方, 王永生, 曾文德, 等. 大侧斜螺旋桨负载噪声的边界元数值声学方法频域内计算分析[J].兵工学报, 2011(9): 1118–1125.
YANG Qiong-fang, WANG Yong-sheng, ZENG Wen-de, et al. Big side of the noise of the propeller load boundary element numerical acoustic method in the frequency domain analysis[J].Acta Armamentarii, 2011(9): 1118–1125. |
| [7] | 杨琼方, 王永生, 魏应三, 等. 基于URANS模拟的伴流场中大侧斜桨无空化噪声的时域和频域预报[C]//第十三届船舶水下噪声学术讨论会论文集, 北京, 2011:325-338. |
| [8] | 杨琼方, 王永生, 张明敏. 舰艇螺旋桨水噪声预测[J].船舶力学, 2011, 5(4): 435–442. |
| [9] | 王超, 张立新, 郑小龙, 等. LES和无限元耦合方法预报螺旋桨均匀流噪声[J].哈尔滨工程大学学报, 2015(36): 91–97. |
| [10] | 王超, 郑小龙, 黄胜, 等. 基于无限元方法预报非均匀流中螺旋桨流噪声[J].中国造船, 2015(56): 142–149. |
| [11] | 宋晗, 王睿, 熊鹰. Kappel桨与传统螺旋桨噪声对比试验[J].中国舰船研究, 2015(10): 92–98. |
| [12] | ESCOBAR M. Finite element simulation of flow-induced noise using Lighthill's acoustic analogy[D]. Bayen:University Erlangen Nurnberg, 2007:36-57. |
 2017, Vol. 39
2017, Vol. 39
