船舶螺旋桨一旦空化，其辐射噪声就会成为船舶航行时最主要的噪声，螺旋桨在船尾非均匀尾流中旋转并产生空化的过程中，空化噪声能量又会被周期性调制，表现为在空化调制谱中有明显的具有倍数关系的多根线谱，利用这些调制线谱可以判断出物理意义明确的螺旋桨转速和桨叶数等特征，是目前船舶噪声识别中非常重要的识别特征^{[1 – 3]}。

螺旋桨空化噪声在不同频带上的调制程度不均匀，但这种非均匀调制特性的规律如何，调制强弱随频带分布关系，乃至这种非均匀调制特性的利用等问题，目前已公开发表的文献中未见有详细研究和结论。本文将从螺旋桨空化噪声谱统计模型出发，将螺旋桨空化噪声非均匀调制特性的机理和规律作为研究重点并进一步考虑其运用。

螺旋桨在非均匀尾流中转动，每个时刻都有大量随机产生和崩溃的空化气泡。对于螺旋桨空化噪声谱，本文综合采用文献[4]中的群空泡崩溃统计模型和文献[3]中假设空泡群平均最大半径服从正态分布的特点，进行推导^{[5 – 7]}，得到螺旋桨空化噪声能量谱的表达式为^[4]：

式中：C为一比例常数；t为时间；ω为频率；K_R为一取决于气体含量和环境压力等因素的常数因子，海况和目标航行深度等的变化会引起其变化；N为某一时刻发生崩溃的空泡个数；R_max为气泡崩溃开始时最大半径；ρ为水的密度；P_∞为无穷远处水的压力（静压力）； $\bar R$ _max为同一时刻大量空泡崩溃最大半径R_max的均值；σ为方差。

螺旋桨在非均匀尾流中转动，N（t）， $\bar R$ _max（t），K_R及σ 随时间t一般不会恒定不变，因此螺旋桨空化噪声能量谱G（ω, t）随时间t一般也不可能保持恒定，表现为幅度随时间产生起伏，即幅度被调制；同时在式（1）中，由于参数ω的作用，G（ω, t）随频率ω变化，即在不同频率处幅度调制会呈现出非均匀性^[8]。

为了表征能量谱幅度被调制的程度，定义m_p为能量谱在一个时间周期T内，能量谱幅值变化的深度，即幅度调制深度。螺旋桨空化噪声可近似视为周期性局部平稳随机过程，短时间内（几个螺旋桨转动周期内）螺旋桨转速、海洋环境、尾流等相对稳定，m_p可视为随时间稳定不变，因此m_p可仅看作是频率ω的函数，记为m_p（ω）；在任一时间周期T内，中心时刻为t，能量谱的时间平均值可视为相对稳定，记为 $\bar G(\omega ,t){\kern 1pt} $ ，能量谱最大值和最小值分别出现在t₁和t₂时刻，则

根据信号调制理论，能量谱被周期性幅度调制，可表示为：

式中f₀为调制频率。则

联立以上两式得：

推得能量谱幅度调制深度为：

从式（8）可看出，能量谱幅度调制深度完全可以由能量谱最大值与最小值之比（最大相对起伏） $\displaystyle\frac{{G(\omega ,{t_1}){\kern 1pt} {\kern 1pt} }}{{G(\omega ,{t_2}){\kern 1pt} }}$ 来表示，用分贝数表示并记为:

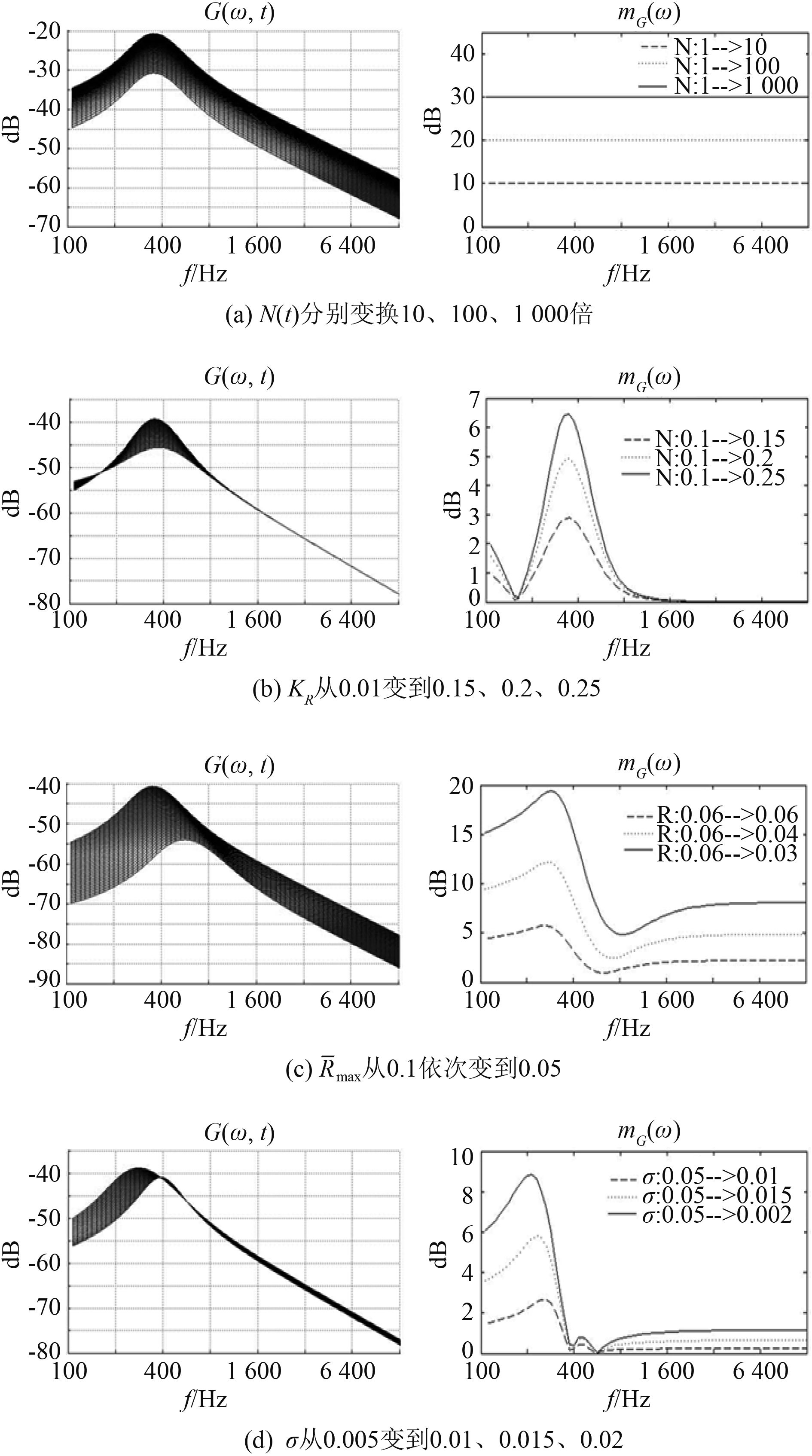
根据式（1）可知，G（ω, t）完全由参数N（t）， $\bar R$ _max（t），K_R及σ 决定，分别变换其中 1 个参数，另外 3 个参数保持不变，4 个参数的默认值分别为1，0.06，0.2，0.01，得到 4 组G（ω, t）和m_G（ω）的仿真计算结果，如图1所示。该图直观地反映了 4 个参数变化前后，能量谱在不同频带ω的幅度调制情况。

图 1 N（t）， $\bar R$ max（t），KR、σ 的变化引起螺旋桨空泡崩溃辐射能量谱在不同频带的幅度调制深度 Fig. 1 The modulation degree of cavitation noise spectrum in different frequency with different N（t）, $\bar R$ max（t）, KR and σ

通过计算，结合图1容易得出：

1）4 个参数中，仅N（t）变化时，m_G（ω）在不同频率ω处为常数，即空泡个数的变化引起了能量谱在不同频带间的均匀调制；而其他 3 个参数 $\bar R$ _max（t），K_R，σ的变化均会引起能量谱在不同频带间的非均匀调制；

2）引起能量谱的调制深度m_G（ω）较大主要因素为N（t）， $\bar R$ _max（t），而K_R，σ的变化引起的调制深度相对较小，尤其是在能量谱峰值频率以上的中高频段上更是如此；

3）空泡平均最大半径 $\bar R$ _max（t）的变化是引起螺旋桨空化非均匀调制的主要因素，中低频段的调制深度值明显大于高频段的调制深度，在能量谱峰值频率前沿，调制深度m_G（ω）最大，峰值频率后沿的m_G（ω）最低，之后会略微增大，高频段的m_G（ω）近似平稳。

从以上分析可知，螺旋桨空化在不同频带的非均匀调制特性主要是受空泡平均最大半径的影响，而影响空泡平均最大半径的因素是螺旋桨桨叶和海水之间的相对来流速度^{[4, 9-10]}，因此，最根本的原因是由船尾形状、螺旋桨结构以及船舶航行工况共同决定的尾流分布所导致的^[3]。由于不同型号船舶的船尾形状、螺旋桨结构具有个体性，因此其也具有特有的螺旋桨空化噪声非均匀调制特性。

此外，据图1的仿真分析还可得出，从螺旋桨空化辐射噪声能量谱看，调制的非均匀特性，主要受能量谱峰值频率的影响。在峰值频率的左侧低频段，调制深度最高，在峰值频率的右侧一小段频带内，调制深度最低，在高频段调制深度基本保持不变，略高于最低调制深度。分析这种现象的原因：一是螺旋桨空化噪声能量谱本身受空泡半径的影响最大，其次是当空泡半径变大时，不仅空化噪声谱线整体上升，而且峰值频率还要向低频移动，势必造成在空化噪声能量谱在低频段调制深度高于高频段，并在紧靠峰值频率而又高于峰值频率一侧具有最低的调制深度^[1]。

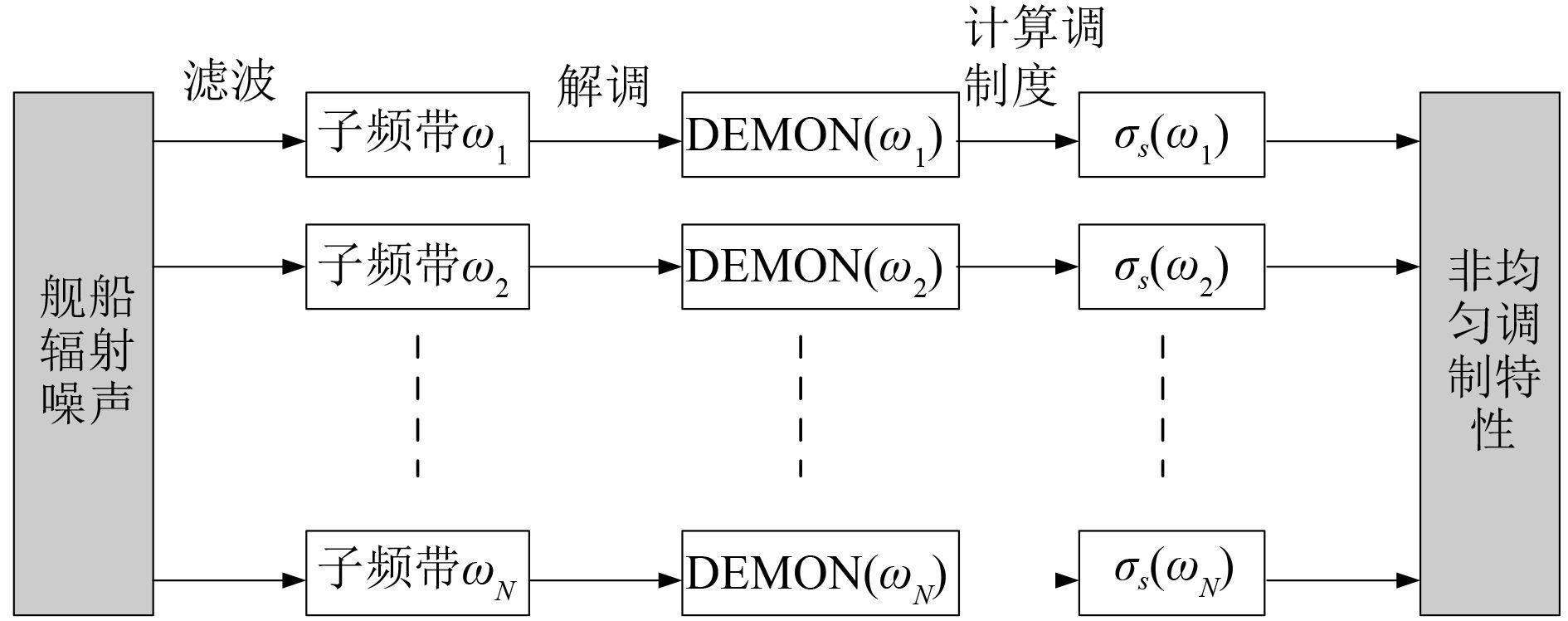
下面通过海上实录的船舶噪声信号进行调制谱分析，验证以上理论是否符合实际情况。为了定量描述噪声调制度大小，采用文献[4]提出的噪声调制度σ_s计算方法。虽然螺旋桨空化噪声不是船舶辐射噪声的全部，但一旦螺旋桨发生空化，就将成为船舶辐射噪声的最主要部分，因此可以用海上实录的高工况航行船舶噪声近似研究螺旋桨空化噪声的调制特性。对船舶噪声进行DEMON分析，通过分析计算轴频及其谐波线谱、叶频及其谐波线谱、干扰线谱之间的大小关系，判定噪声的调制度大小^[11]。在分析噪声不同频带的非均匀调制特性时，首先分频段解调，然后对各频段解调获得的DEMON谱分别计算调制度大小，最后组成调制度矢量，得到非均匀调制特性，计算过程如图2所示。

图 2 舰船噪声非均匀调制特性计算示意图 Fig. 2 Calculation process of non-uniform modulation feature

从实录船舶噪声库中随机选取工况较高的目标513个，每个目标噪声长度40 s～3 min不等，对每个目标按照图2所示步骤分别计算得到一个非均匀调制特性矢量图，从统计结果看，本文认为船舶噪声的非均匀调制特性虽然看似无章可循，但其实是有一定规律的，大多数噪声基本满足本文上节所述的“从螺旋桨空化辐射噪声能量谱看…在峰值频率的左侧低频段，调制深度最高，在峰值频率的右侧一小段频带内，调制深度最低”的特点。

图3为某大型船舶噪声非均匀调制特性图。图中：①为目标功率谱图纵坐标为信号频率0～10 kHz；②为目标全频带噪声DEMON谱图，横坐标为调制频率，范围为0～50 Hz；③为目标DEMON谱历程图，横坐标为调制频率，纵坐标为信号频率；④为目标非均匀调制度矢量图，纵坐标为信号频率，横坐标为各频率子带的调制度大小，dB。

图 3 某大型船舶噪声非均匀调制特性图 Fig. 3 The non-uniform modulation feature picture of a large ship’s radiated noise

该信号的功率谱图较好满足标准船舶噪声功率谱特点：峰值频率很低，在峰值频率以下的频段，由于传感器滤波的原因，看不到幅值的衰减，在峰值频率以上的中高频段大约以–6 dB/倍频程的速率下降；其非均匀性调制度矢量图基本符合上节分析的结论特点，因信号频率基本位于峰值频率以上，其非均匀调制特点则只具有峰值以上频率的调制特性，在整个信号频率范围内，噪声调制度逐渐递增，在高频部分递增的幅度较小，而在靠近且低于1 kHz的信号频段，由于恰巧处于峰值频率的后沿，调制度最弱。

传统DEMON谱分析，一般是依据噪声接收的工作频段，设置一个固定的较为通用的解调频段，所有噪声信号均在该频段内滤波、检波、DEMON谱分析，并据此进行线谱提取和特征分析。而根据本文第1节结论，船舶噪声的调制特性在不同频带上是非均匀的，那么在DEMON谱分析中，如果仅仅在调制度高的信号频段进行解调，获得的DEMON谱线谱清晰度是否会更高呢，这是本节要研究的问题。

根据第1节的分析，对舰船辐射噪声的解调，实际上为对某个频段ω₁噪声能量G_i（t）的频谱分析，即DEMON为：

则全频段的DEMON谱可以近似表示为N个子频带DEMON的谱值积累：

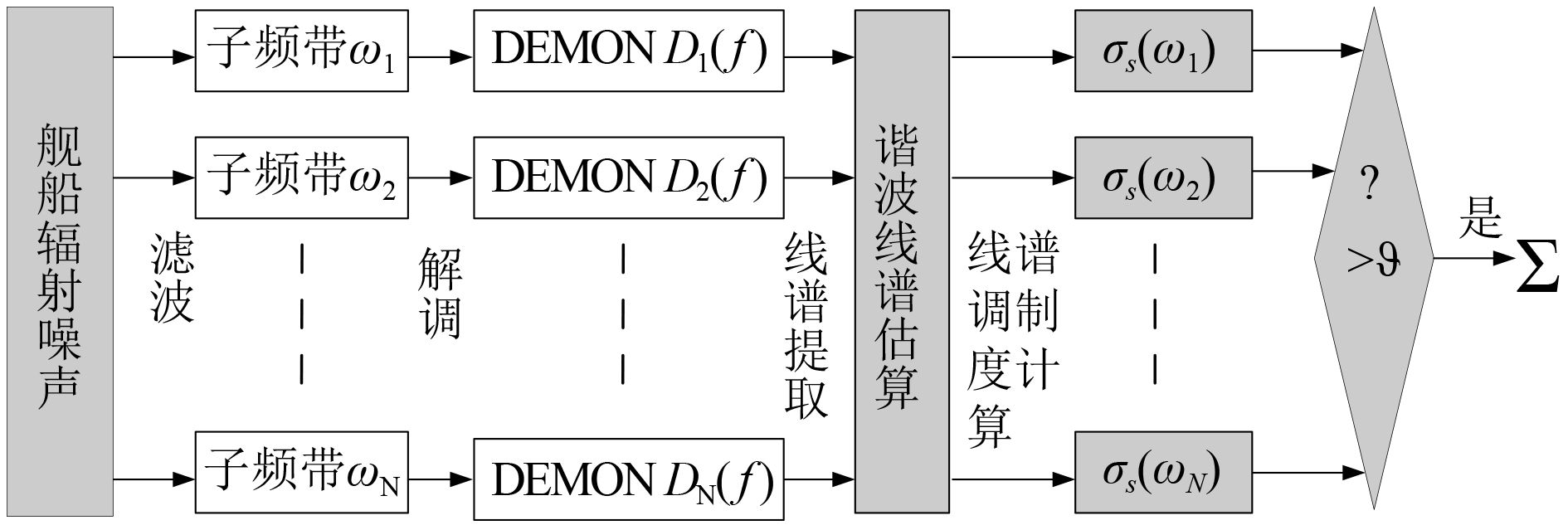
考虑到将调制度大小差异较大的子带DEMON谱值积累一起，与仅将调制度高的子带DEMON谱值积累一起相比，调制特性应该会有所减弱，因此本文在自动计算各子带调制度的基础上，仅将调制度高的子带DEMON谱积累作为最终的DEMON谱，如图4所示。根据大量数据统计结果给定一个调制度可用门限ϑ，若某个子带的调制度σ_s（ω_i）大于门限ϑ，则判定该子带权值为1，否则为0，最终DEMON谱D（f）为：

其中β_i为权值。

图 4 基于多子带自适应加权的DEMON增强算法 Fig. 4 Thecalculation process of DEMON line spectrum strength based on multi sub-band adaptive weighted

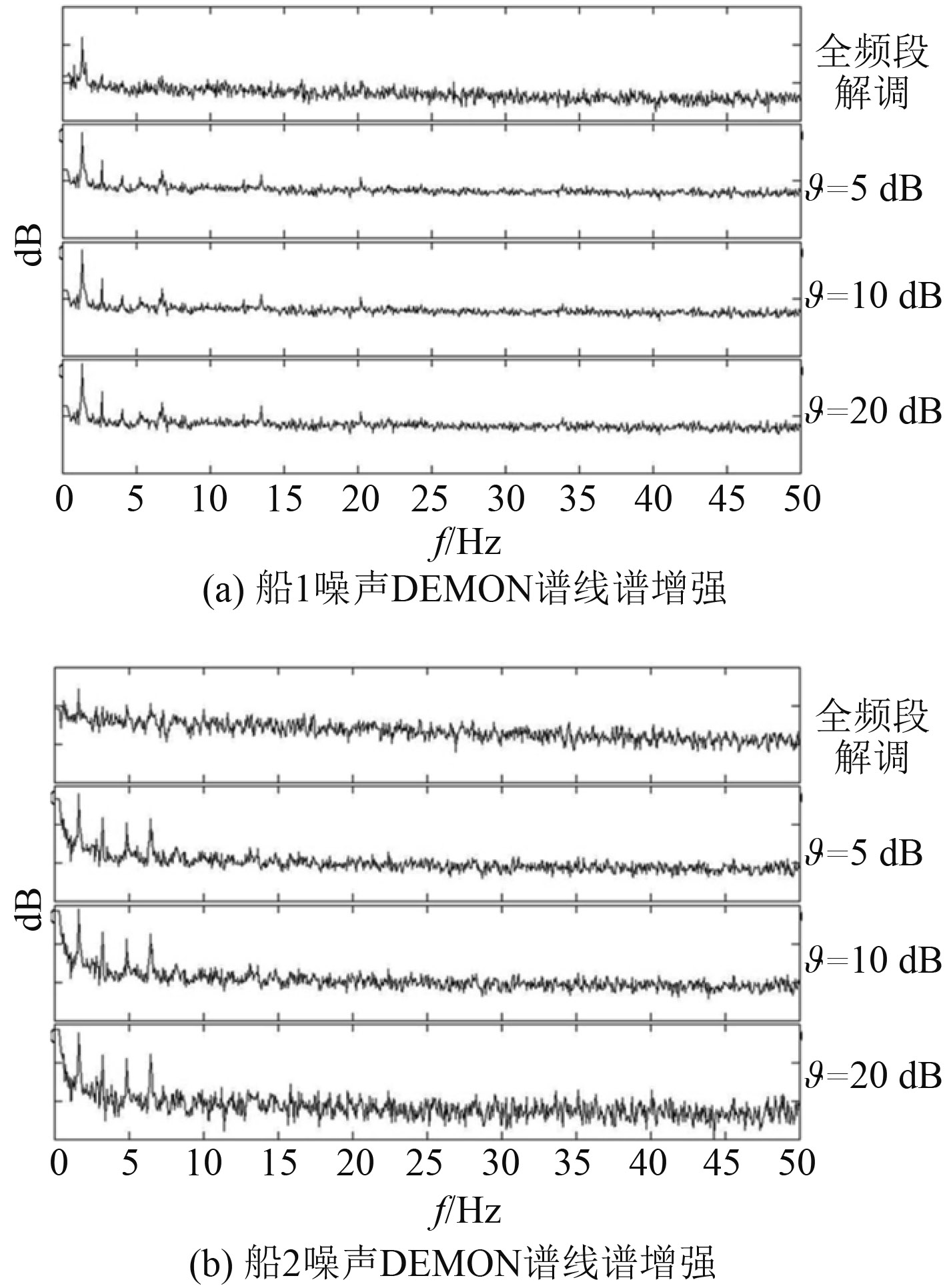
仍然采用第2节使用的513个海上实录船舶噪声数据进行分析计算，分别进行全频段解调和采用不同加权门限ϑ时的多子带自适应加权解调。统计513个目标的平均调制度和线谱平均增强幅度，如表1所示。2 个典型目标噪声的DEMON谱线谱增强前后对比如图5所示。

表 1(Tab. 1)

表 1 多子带自适应加权的DEMON谱线谱增强效果 Tab. 1 The effect of DEMON line spectrum strength based onmulti sub-band adaptive weighted 平均调制度/dB 平均增强幅度/% 全频段解调 7.40 多子带自适应加权 ϑ=5 dB 10.75 45.2 ϑ=10 dB 11.25 52.0 ϑ=20 dB 11.70 58.0

表 1 多子带自适应加权的DEMON谱线谱增强效果 Tab.1 The effect of DEMON line spectrum strength based onmulti sub-band adaptive weighted

图 5 两个典型目标DEMON谱线谱增强前后对比效果 Fig. 5 The effect of DEMON line spectrum strength of two typical targets

从实际噪声数据的分析结果看，频带的非均匀调制特性对DEMON谱线谱幅值的计算结果影响还是比较明显的，尤其是当噪声的调制特性仅分布在比较窄的频带内，影响更甚。通过多子带自适应加权，可以获得较优的DEMON谱线谱清晰度。另外，权限ϑ取较低值（5 dB）时就已经取得的较好的增强效果，而继续把权限值ϑ升高，增强的幅度减缓，这是因为权限ϑ给定一个较低值时，已经将没有调制的频带滤掉，基本上消除了无调制频带对调制特性的影响。

本文主要研究了螺旋桨空化非均匀调制特性的机理、规律和应用。首先从船舶螺旋桨空化噪声谱模型出发，仿真分析了螺旋桨空化非均匀调制特性；然后利用大量海上实录船舶噪声，统计了实际船舶噪声非均匀调制特性，验证了以上结论的合理性；最后基于船舶噪声的非均匀调制特性，提出了一种基于多子带自适应加权的DEMON增强算法，试验表明其效果良好。主要形成以下结论：

1）从形成机理看，螺旋桨空化在不同频带的非均匀调制特性主要是由船尾形状、螺旋桨结构以及船舶航行工况共同决定的尾流分布所导致的，不同型号船舶的非均匀调制特性具有个体性。

2）从舰船噪声信号能量谱看，调制的非均匀特性，主要受能量谱峰值频率的影响。在峰值频率的前沿低频段，调制深度最高，在峰值频率的后沿一小段频带内，调制深度最低，在高频段调制深度基本保持不变，略高于最低调制深度。

3）船舶噪声的非均匀调制特性对DEMON谱线谱幅值影响明显，尤其是当噪声的调制特性仅分布在比较窄的频带内时，影响更甚。通过多子带自适应加权，对DEMON谱线谱增强有明显效果，可以获得更优的线谱清晰度与谱图结构特征。