目标运动分析(Target Motion Analysis,TMA)是利用带噪的阵元域数据估计出目标的运动要素[1]。实际环境中,可观测的目标特征数据极其有限,目标的方位几乎成了唯一可靠的参数,故纯方位目标运动分析(Bearings-Only target motion analysis,BO-TMA)引起了人们极大的关注[2–4]。
BO-TMA方法主要分为递推类算法以及批处理方法两类。绝大多数递推类算法均以卡尔曼滤波(Kalman Filter,KF)为基础,常见方法有伪线性滤波法[5] (Pseudolinear Estimator,PLE)、扩展卡尔曼滤波法[6] (Extended Kalman Filter,EKF)及粒子滤波法[7] (Particle Filter,PF)等。PLE法具有线性结构,稳定性强,但其估计结果有偏,PF方法在非线性非高斯情形下性能优越,但其需要大量的样本来近似系统后验概率分布,计算量巨大,不利于实时处理,EKF法基于泰勒展开对非线性系统线性近似,通常能达到较高精度,且与PF法相比,其计算量显著降低。批处理法则是同时处理一批数据而得目标运动状态,处理过程中需利用数值最优化方法来迭代寻优,MLE法[8]是典型的批处理法,绝大多数情形下,观测数据足够多时,其性能最优。
基于Steven C.Nardone等的研究可知[9],目标匀速直线运动时,单阵BO-TMA需要基阵所在平台进行至少一次机动。复杂多变的实际海战环境中,往往不允许平台执行机动,故单阵BO-TMA通常不适于水下目标运动分析,通常需基于多维信息进行目标运动要素的解算。
本文利用EKF和MLE方法进行双阵纯方位水下目标运动分析,并从航向、位置等方面评价算法性能。关于水下目标BO-TMA的相关文献多是基于数值仿真来进行算法的研究,本文在仿真的基础上,通过对海试数据的处理,从试验层面验证算法的有效性。
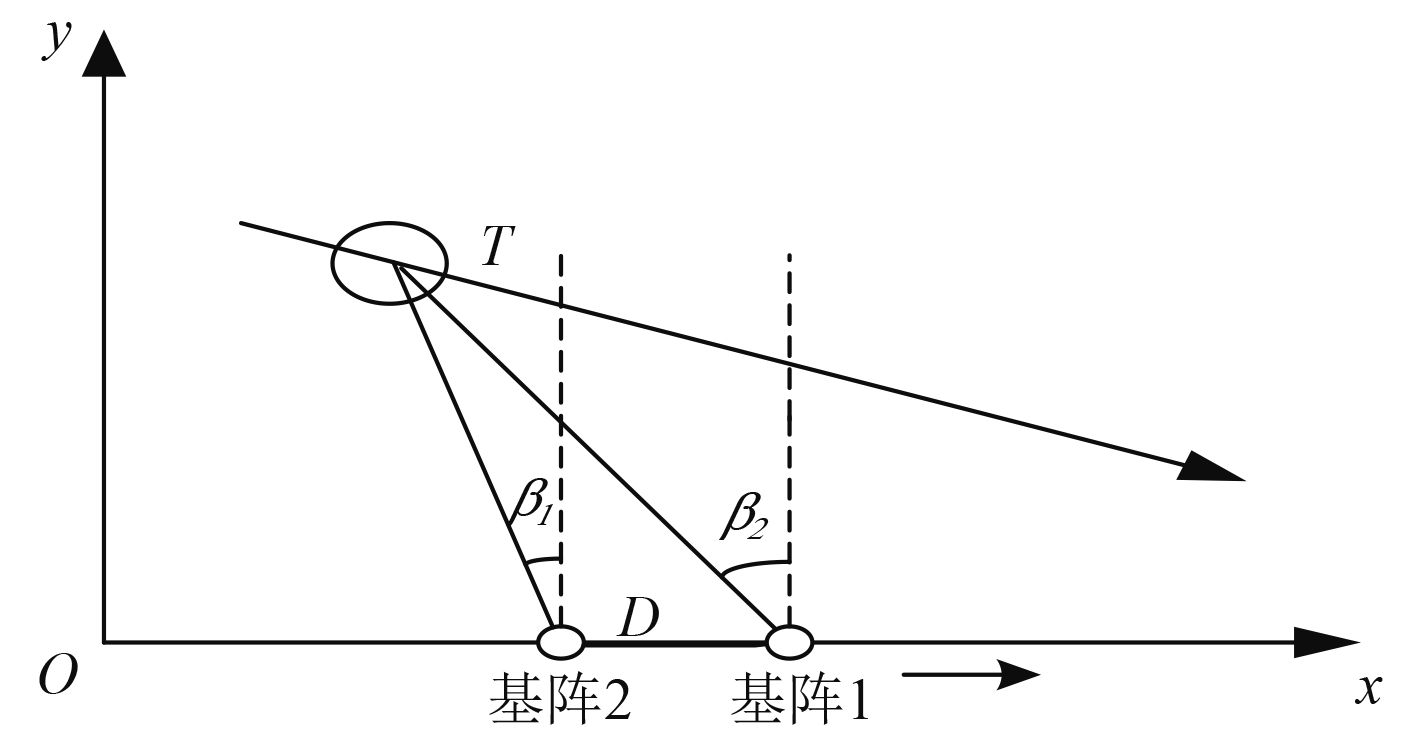
1 双阵纯方位TMA原理考虑如图1所示的基阵与目标间的几何关系,假定二维平面情形,两基阵均随本舰匀速直线运动,阵间距离D可预先测量并能实时修正,目标作匀速直线运动。
|
图 1 目标与观测平台间几何态势 Fig. 1 Target-observer geometry |
以阵1为参考阵,所得状态方程如下:
| ${{{X}}_1}\left( {{t_k}} \right) = {{{\varPhi}} _{{t_k}\left| {{t_{k - 1}}} \right.}}{{{X}}_1}\left( {{t_{k - 1}}} \right) + {{G}}v\left( {{t_{k - 1}}} \right)\text{,}$ | (1) |
其中:
| $\begin{array}{l}{{G}} = {\left[ \begin{array}{l}\displaystyle\frac{{{T^2}}}{2}\;\;\;0\;\;\;T\;\;\;0\\0\;\;\;\displaystyle\frac{{{T^2}}}{2}\;\;\;0\;\;\;T\end{array} \right]^{\rm{T}}}\text{,}\\{{{\varPhi}} _{{t_k}\left| {{t_{k - 1}}} \right.}} = \left[ {\begin{array}{*{20}{c}}1 & 0 & T & 0\\0 & 1 & 0 & T\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{array}} \right] \text{。}\end{array}$ |
式中:t
k
为时刻;
测量方程如下:
| ${{{Z}}_k} = \left[ {\begin{array}{*{20}{c}}{{\beta _1}({t_k})}\\{{\beta _2}({t_k})}\end{array}} \right] = {h_k}({X_1}_k) + {n_k}\text{,}$ | (2) |
式中:n k 为t k 时刻的方位量测噪声; R k 为自相关矩阵,下标表示时间。且有:
| ${{{h}}_k}({{{X}}_1}_k) = \left[ \begin{array}{l}{\tan ^{ - 1}}[{r_{x1}}({t_k})/{r_{y1}}({t_k})]\\{\tan ^{ - 1}}[{r_{x2}}({t_k})/{r_{y2}}({t_k})]\end{array} \right]\text{。}$ |
测量方程为非线性方程,本文分别采用EKF算法和MLE算法进行处理。
1.1 扩展卡尔曼滤波(EKF)[6]EKF算法是典型的卡尔曼滤波(KF)类算法。该法基于泰勒展开对非线性系统线性化近似,然后利用线性KF算法进行处理。其步骤如下:
1)状态以及状态误差协方差矩阵预测
| $\begin{array}{l}\mathop {{{{X}}_1}}\limits^ \wedge ({t_k}\left| {{t_{k - 1}}} \right.) = {{{\varPhi}} _{{t_k}\left| {{t_{k - 1}}} \right.}} \cdot \mathop {{{{X}}_1}}\limits^ \wedge ({t_{k - 1}}\left| {{t_{k - 1}}} \right.)\\{{P}}({t_k}\left| {{t_{k - 1}}} \right.) = {{{\varPhi}} _{{t_k}\left| {{t_{k - 1}}} \right.}} \cdot {{P}}({t_{k - 1}}\left| {{t_{k - 1}}} \right.) \cdot {\left( {{{{\varPhi}} _{{t_k}\left| {{t_{k - 1}}} \right.}}} \right)^{\rm{T}}} \!+\! {{G}} \cdot {{{Q}}_{k - 1}} \cdot {{{G}}^{\rm{T}}}\end{array}$ |
式中 P 为状态误差协方差矩阵;
2)非线性系统的线性化近似
| ${{{H}}_k} = \frac{{\partial {h_k}\left( {{{{X}}_{1k}}} \right)}}{{{{{X}}_{1k}}}}\left| {_{{X_{1k}} = \mathop {{X_1}}\limits^ \wedge ({t_k}\left| {{t_{k - 1}}} \right.)}} \right.\text{;}$ |
3)卡尔曼增益矩阵求解
| ${{{K}}_k} ={{P}} ({t_k}\left| {{t_{k - 1}}} \right.) \cdot {{{H}}_k}^{\rm{T}}{\left( {{{{H}}_k} \cdot {{P}}({t_k}\left| {{t_{k - 1}}} \right.) \cdot {{{H}}_k}^{\rm{T}} + {{{R}}_k}} \right)^{{\rm{ - }}1}}\text{;}$ |
4)状态更新
| $\mathop {{{{X}}_1}}\limits^ \wedge ({t_k}\left| {{t_k}} \right.) = \mathop {{{{X}}_1}}\limits^ \wedge ({t_k}\left| {{t_{k - 1}}} \right.) + {{{K}}_k} \cdot \left[ {{{{Z}}_k} - {h_k}(\mathop {{{{X}}_1}}\limits^ \wedge ({t_k}\left| {{t_{k - 1}}} \right.))} \right]\text{;}$ |
5)状态误差协方差矩阵更新
| ${{P}}({t_k}\left| {{t_k}} \right.) = ({{I}} - {{{K}}_k} \cdot {{{H}}_k}) \cdot {{P}}({t_k}\left| {{t_{k - 1}}} \right.)\text{。}$ |
MLE法是典型的批处理方法,该方法将使得似然函数最大的状态量来作为估计量。
| ${\mathop {{X}}\limits^ \wedge _{j + 1}} = {\mathop {{X}}\limits^ \wedge _j} + {\partial _j} \cdot {{B}}_j^{ - 1} \cdot {{{G}}_j}\text{,}$ | (3) |
式中:∂
j
为迭代步长;
B
j
为正定矩阵;
G
j
为代价函数在
高斯-牛顿(Gauss-Newton,G-N)法[10]常被用于处理此类问题,此时:
| $\begin{array}{l}{{{B}}_j} = {{J}}{({\mathop {{X}}\limits^ \wedge _j})^{\rm{T}}} \cdot {\Sigma ^{ - 1}} \cdot {{J}}({\mathop X\limits^ \wedge _j})\text{,}\\{{{G}}_j} = {{J}}{({\mathop {{X}}\limits^ \wedge _j})^{\rm{T}}} \cdot {\Sigma ^{ - 1}} \cdot {{R}}\left( {{{\mathop X\limits^ \wedge }_j}} \right)\text{,}\end{array}$ |
其中
| ${{{B}}_{j + 1}} = ({{I}} - {\rho _j}{y_j}s_j^{\rm{T}}){{{B}}_j}({{I}} - {\rho _j}{s_j}y_j^{\rm{T}}) + {\rho _j}{y_j}y_j^{\rm{T}}\text{。}$ | (4) |
其中:
本文将BFGS方法与G-N方法结合起来进行求解,既没有较大程度增加求解的复杂性,又保证了算法的收敛速率,较单一的G-N方法有效。
2 仿真结果与分析仿真态势如图1所示,以基阵1为参考阵,方位量测间隔为1 s。对双阵间距D为600 m和1 000 m两种不同情况进行计算;双阵方位测量误差服从高斯分布,标准差均为1.5°,对方位测量误差均值μ为0°和5°两种不同情况进行计算。假定二维平面,本舰航向正东,航速18 kn,基阵1初始位于坐标原点,目标初始位于(–6 000 m,6 000 m),航向120°,航速 40 kn。
利用EKF和MLE算法求解不同情形下目标相对基阵1的航向及位置要素,其中航向是基于解算出的运动要素中的航速分量而求得。
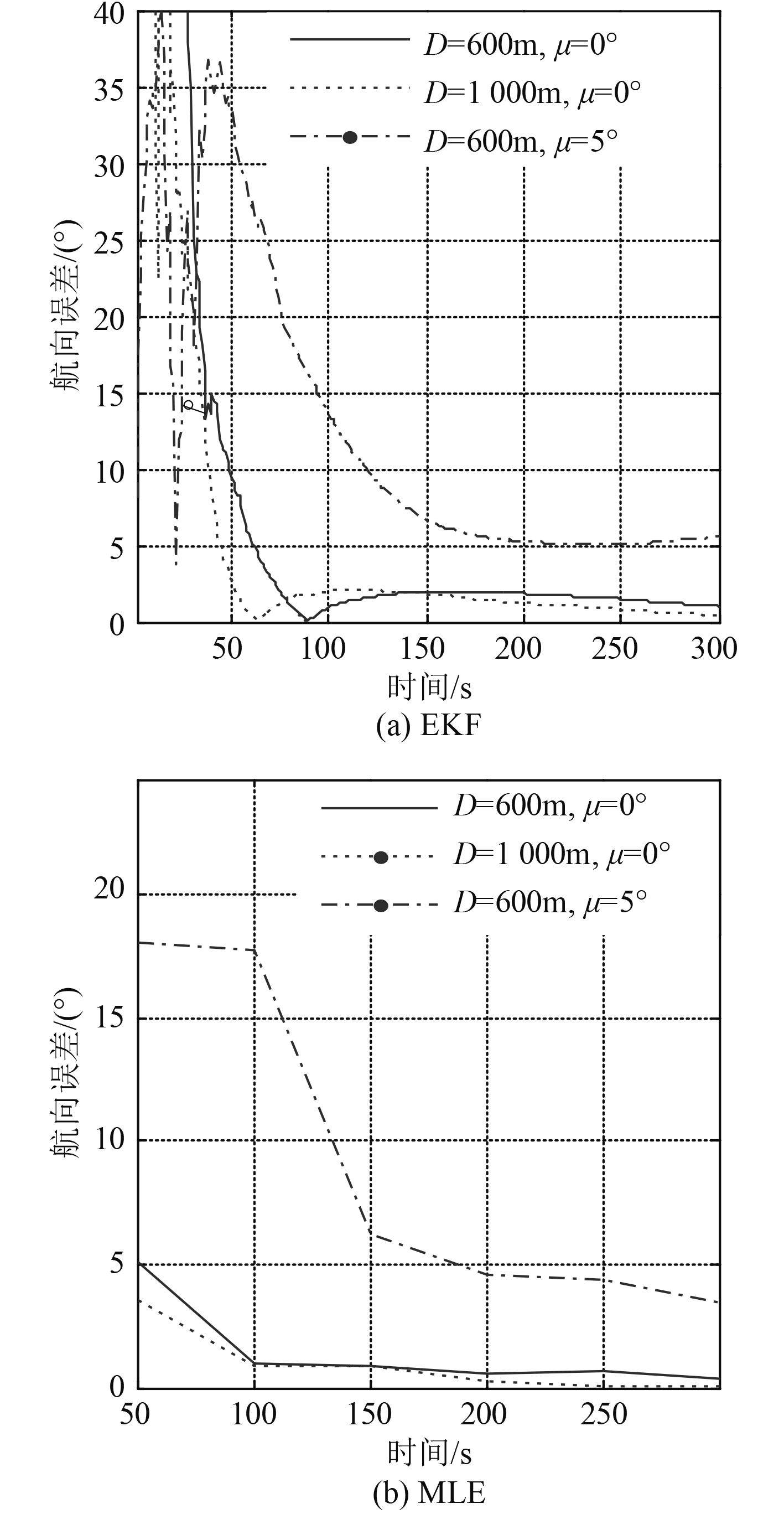
不同间距以及不同方位量测精度情形下,分别基于EKF算法和MLE算法对目标相对基阵1的航向进行求解,结果如图2所示,图2(a)对应EKF算法,图2(b)对应MLE算法,其中纵坐标为航向解算值与真值的绝对差值,采用MLE算法分别对50 s,100 s,150 s,200 s,250 s以及300 s时航向进行求解。
|
图 2 EKF和MLE的航向估计误差 Fig. 2 Course estimation error of EKF and MLE |
由图2可知,2 种算法的航向估算精度均受方位测量精度以及双阵间距的影响,一般而言,航向解算精度与方位测量精度及双阵间距成正相关关系,方位测量越准、双阵间距越大,航向解算值越接近真值。
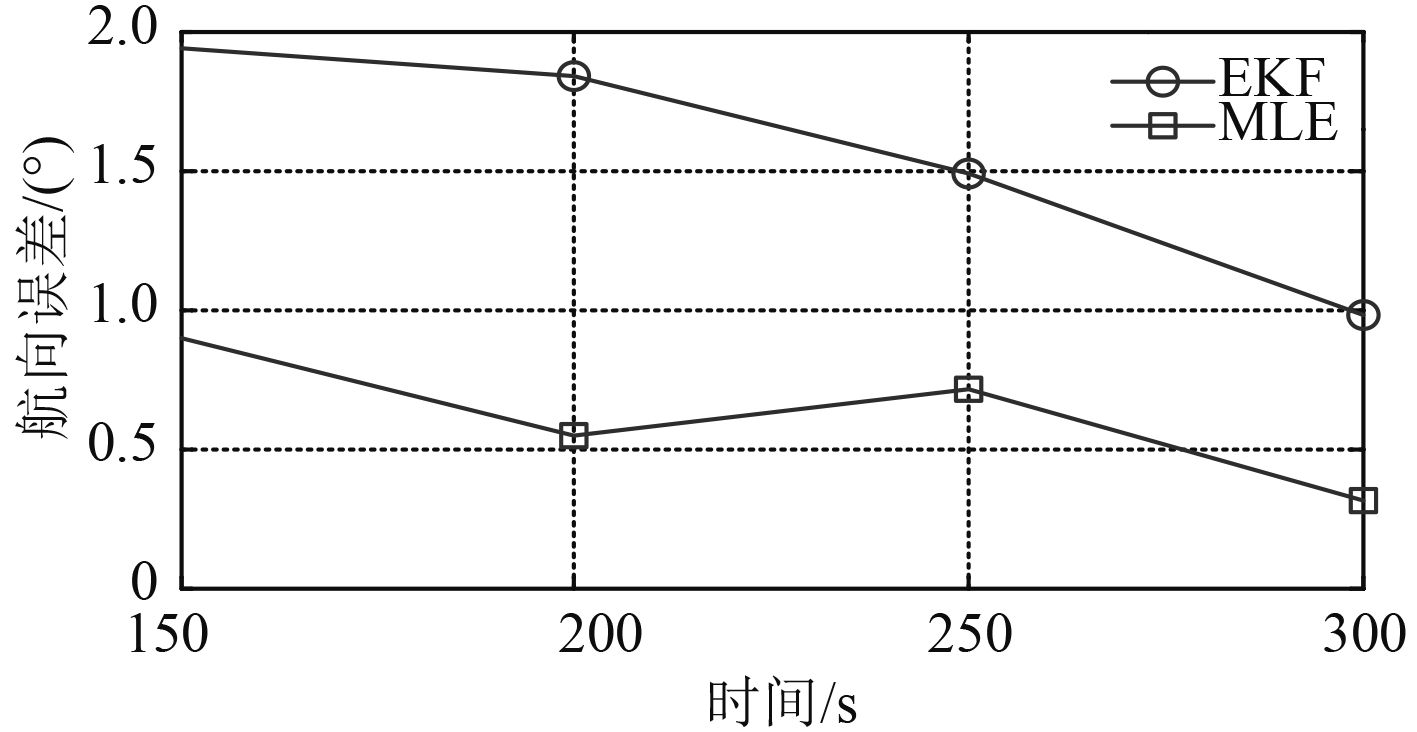
|
图 3 EKF和MLE的航向估计结果比较 Fig. 3 Compare of course results solved by EKF and MLE |
D=600 m,μ=0°情形下,利用EKF和MLE算法分别对150 s,200 s,250 s以及300 s时航向进行求解,结果如图3所示。由图 3 可知,与EKF相比,MLE性能较优,该结果符合MLE的最优性质。
横向分析图2与图3可知,算法性能亦受观测时长影响。总体而言,基于MLE和EKF算法的航向解算精度均随观测时间的增加而变高。
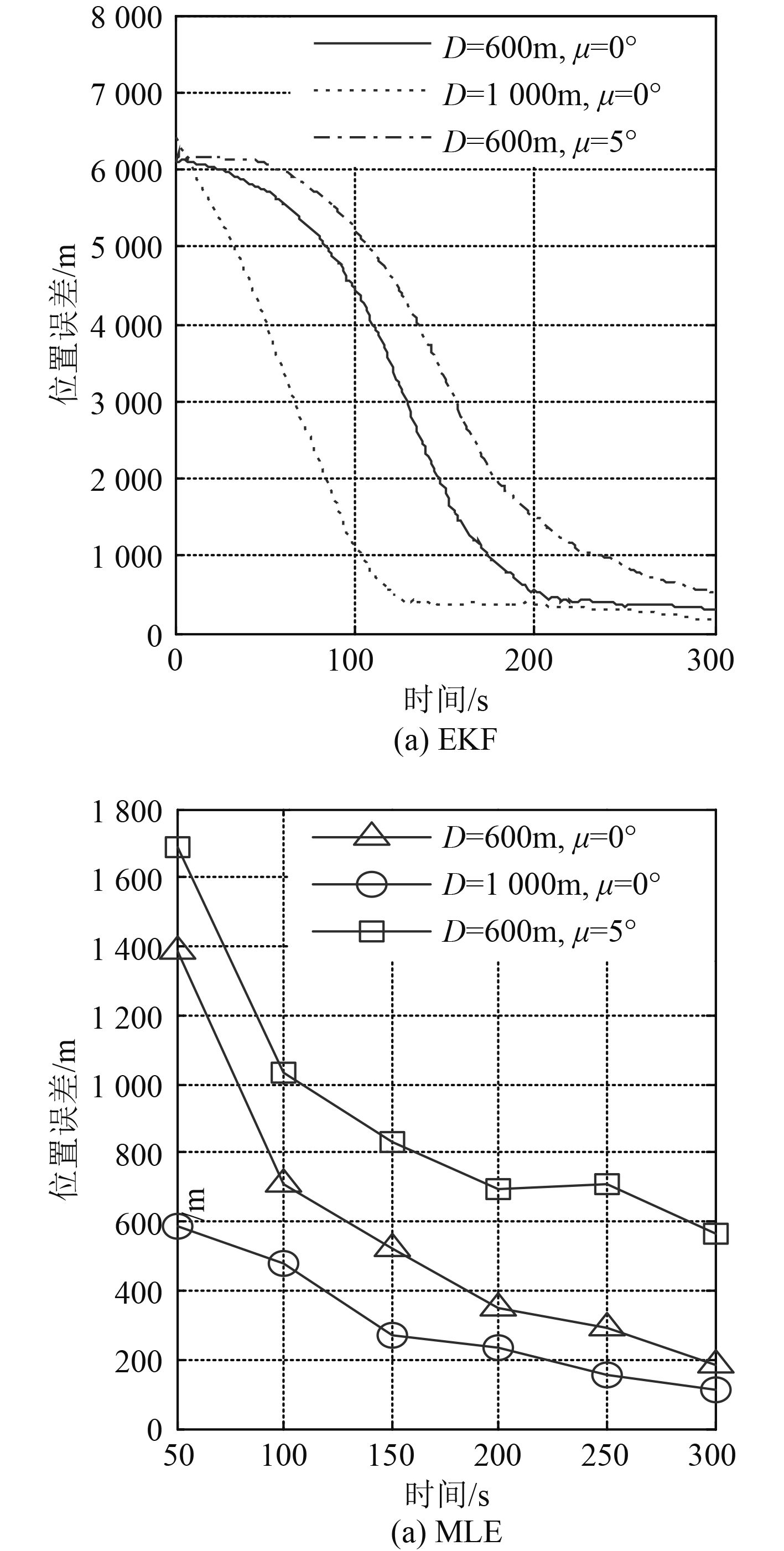
不同间距以及不同方位量测精度情形下,分别基于EKF和MLE算法对目标相对基阵1的位置进行求解,结果如图4所示,图4(a)对应EKF算法,图4(b)为MLE算法结果,纵坐标为位置估计误差,该误差定义为目标位置(相对基阵1)解算值与真值之间的空间距离,分别在50 s,100 s,150 s,200 s,250 s及300 s时基于MLE算法进行求解。
|
图 4 EKF和MLE的位置估计误差 Fig. 4 Position estimation error of EKF and MLE |
由图4可知,2 种算法的位置估计精度均受双阵间距以及方位量测精度的影响。一般而言,位置解算精度与双阵间距以及方位量测精度呈正相关关系,方位测量误差均值越小、双阵间距越大,解算结果越准。
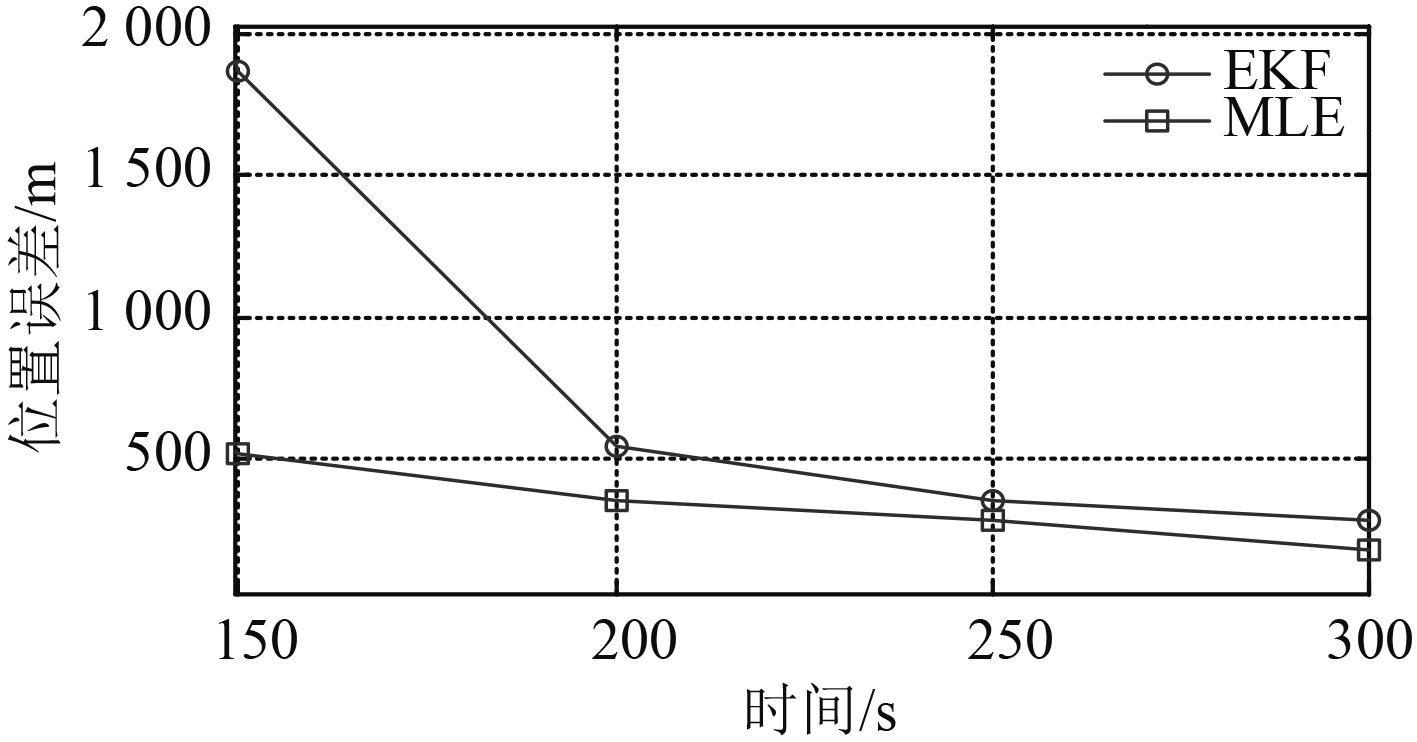
D=600 m,μ=0°情形下,分别于150 s,200 s,250 s以及300 s时基于EKF和MLE算法进行目标位置求解,结果如图5所示。由图可知,与EKF相比,MLE性能较优,该结果符合MLE的最优性质。
|
图 5 EKF和MLE的位置估计结果比较 Fig. 5 Compare of position results solved by EKF and MLE |
横向分析比较图4和图5可知,与航向解算相同,位置估计精度亦受观测时长的影响,总体而言,观测时间越长,2 种算法的性能越好。
通过仿真分析,可知对于双阵纯方位TMA,MLE和EKF算法性能均受双阵间距、方位量测精度以及观测时间的影响,双阵间距越大、方位测量误差均值越小、观测时间越长,解算结果越准。仿真结果表明:在方位测量精度、双阵间距以及观测时长均足够的情形下,一定条件下理论上可以实现对目标的航向及位置要素的较高精度求解。
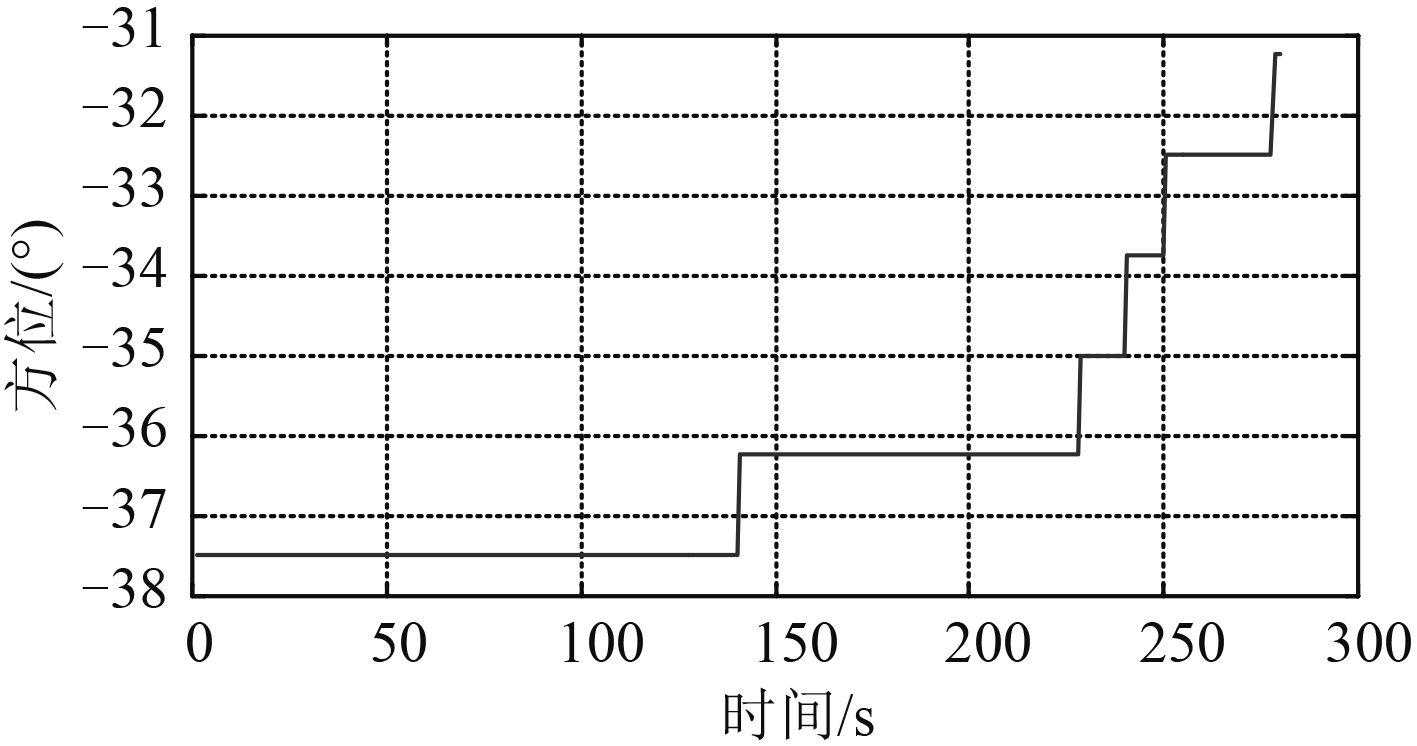
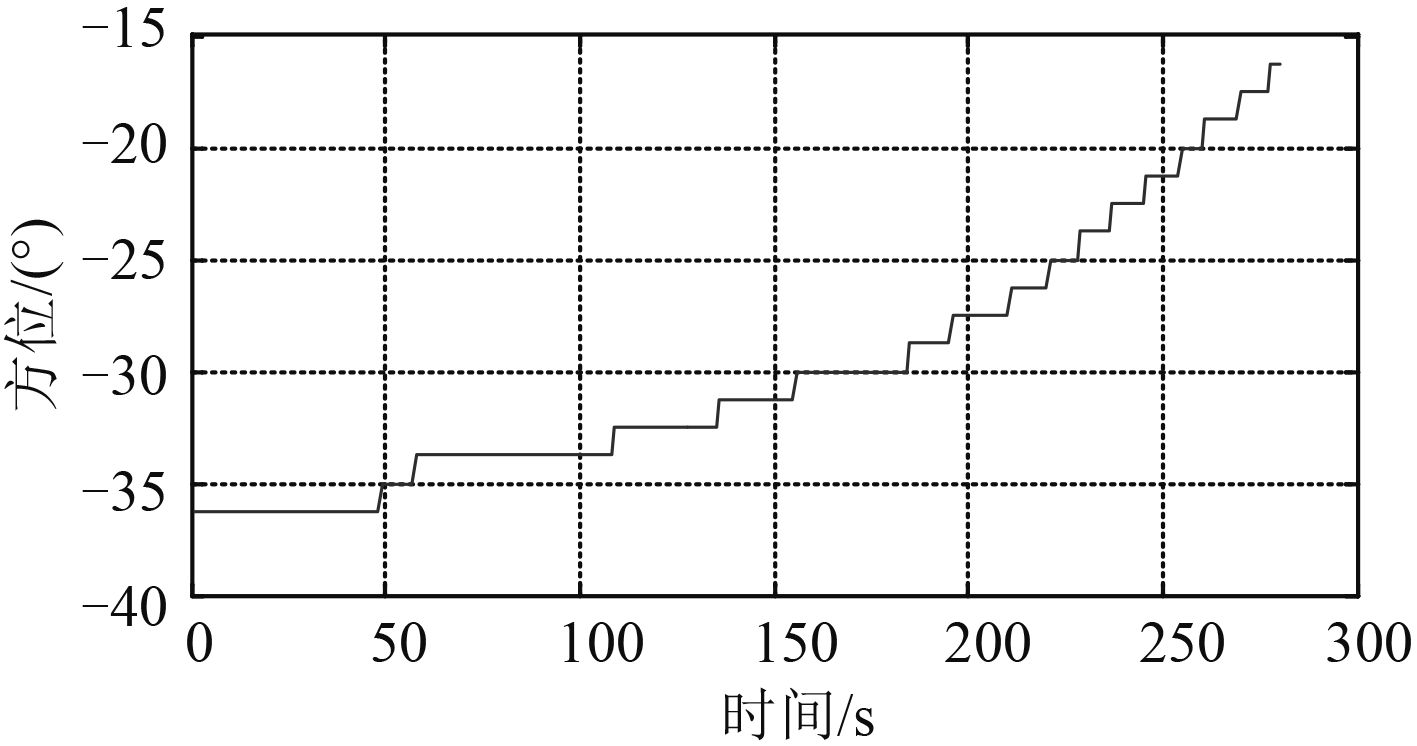
3 海试数据处理试验使用母船球鼻首安装的平面阵和尾部拖曳线列阵,双阵同时记录水下目标辐射噪声信号,采用分裂波束测向方法获取双阵方位信息,如图6~图 7 所示。
|
图 6 基于平面阵观测的目标方位 Fig. 6 Target bearings measured by planar array |
|
图 7 基于拖线阵观测的目标方位 Fig. 7 Target bearings measured by towed array |
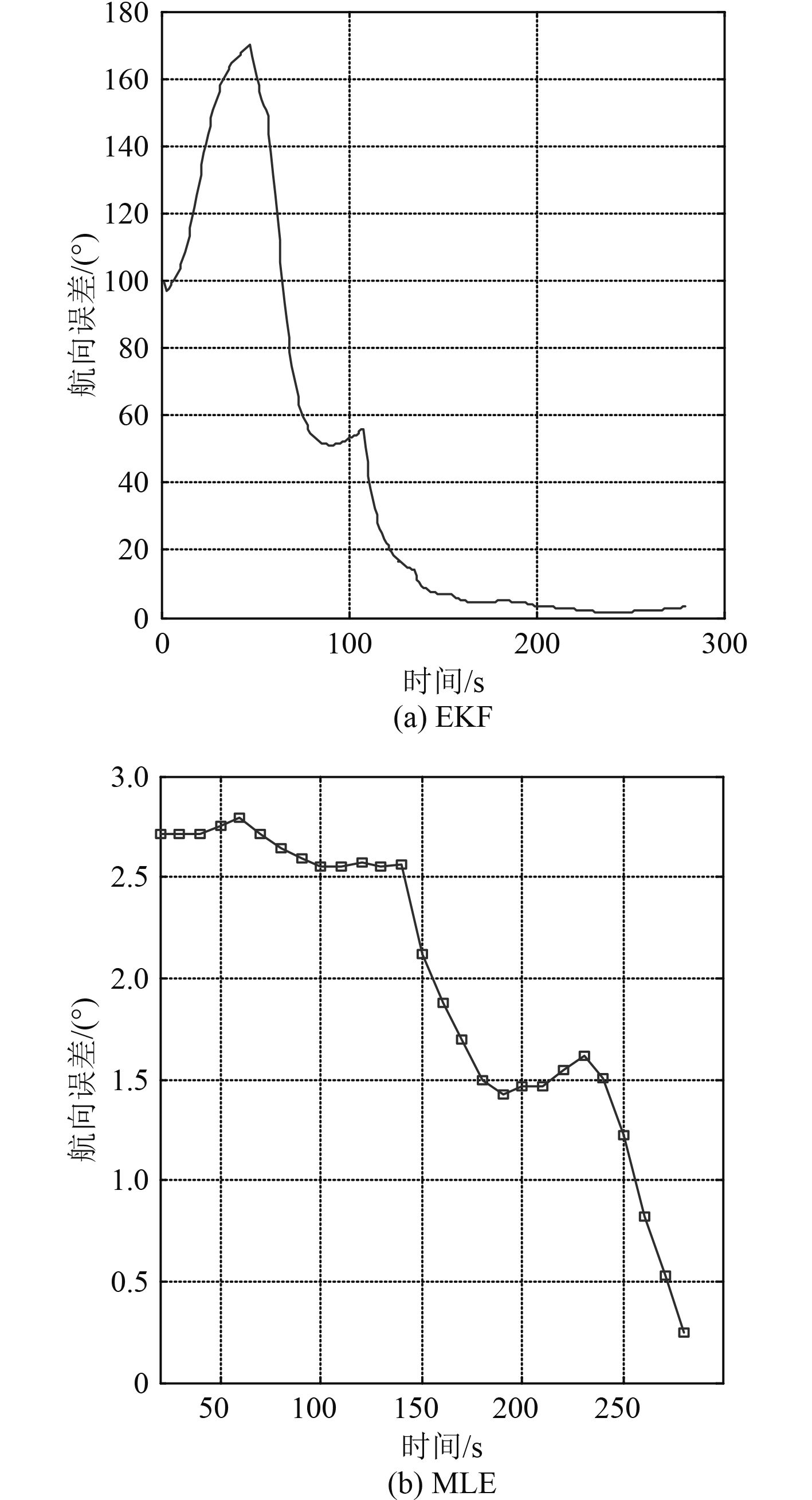
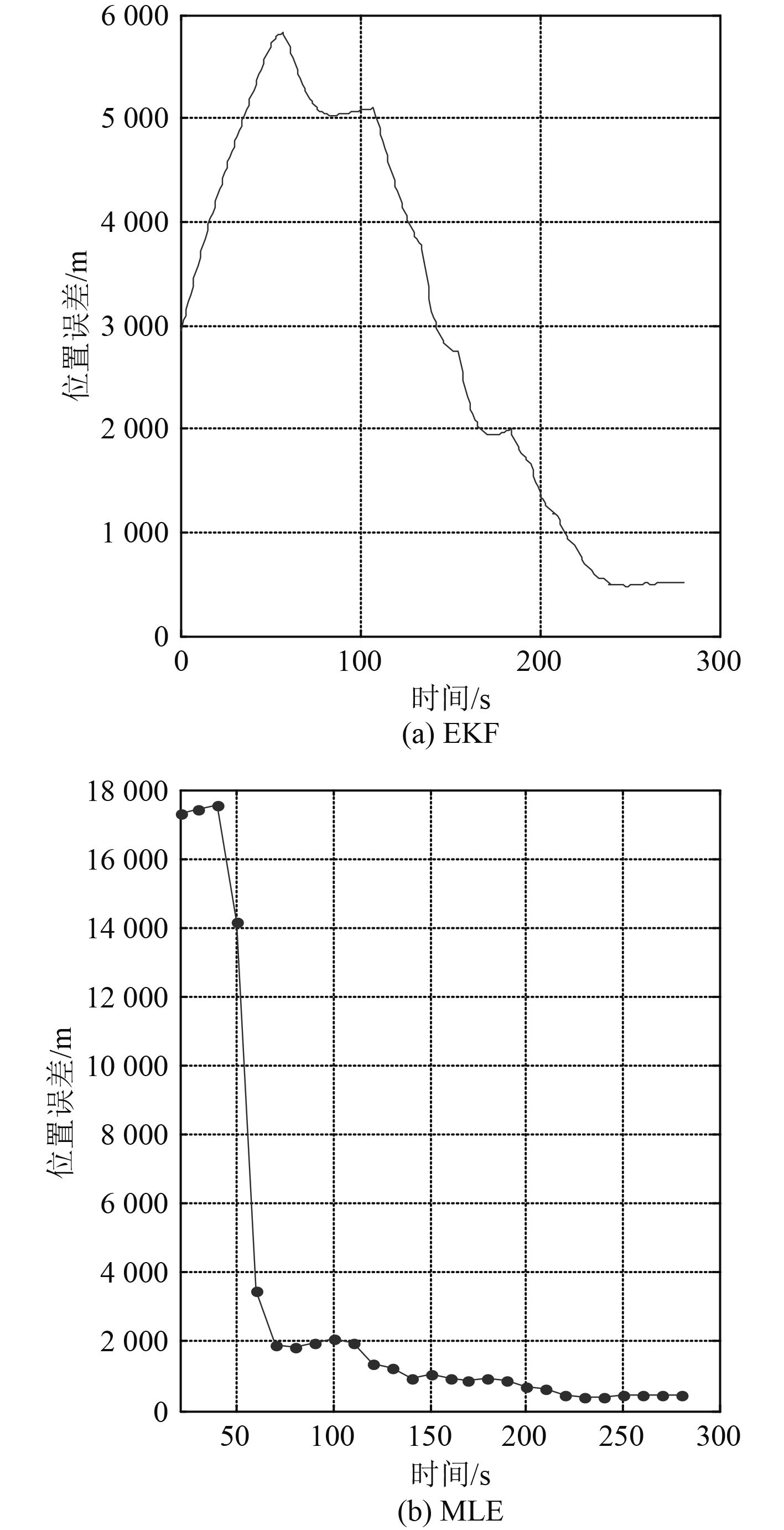
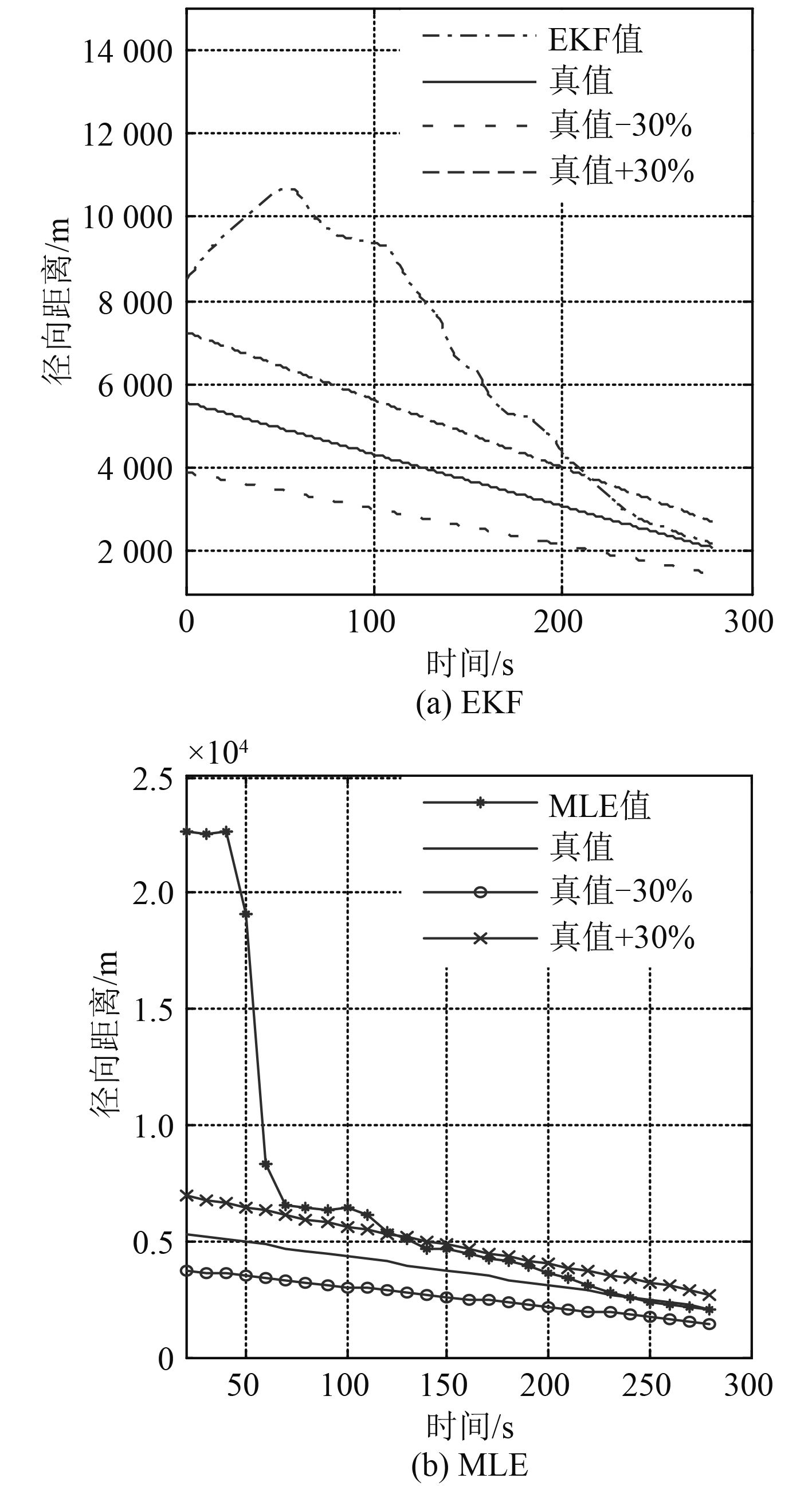
选取平面阵为参考基阵,观测总时长为280 s。基于MLE和EKF方法对目标相对参考阵的航向、位置以及径向距离进行求解,结果分别对应如图8~图 10 所示,左侧子图对应EKF算法,右侧子图则对应于MLE算法,其中纵坐标分别为航向估计误差、位置估计误差以及径向距离估计值。其中,MLE算法对应的批处理时长分别为20 s,30 s,…,280 s。
|
图 8 EKF和MLE的航向估计误差 Fig. 8 Course estimation error of EKF and MLE |
|
图 9 EKF和MLE的位置估计误差 Fig. 9 Position estimation error of EKF and MLE |
|
图 10 EKF和MLE的径向距离估计 Fig. 10 Radial distance estimation result of EKF and MLE |
横向分析比较图8~图 10 可知,在观测时长一定时,2 种算法估计结果均能达到较高精度,总体而言,观测时间越长,估计值越精确,算法性能越好。
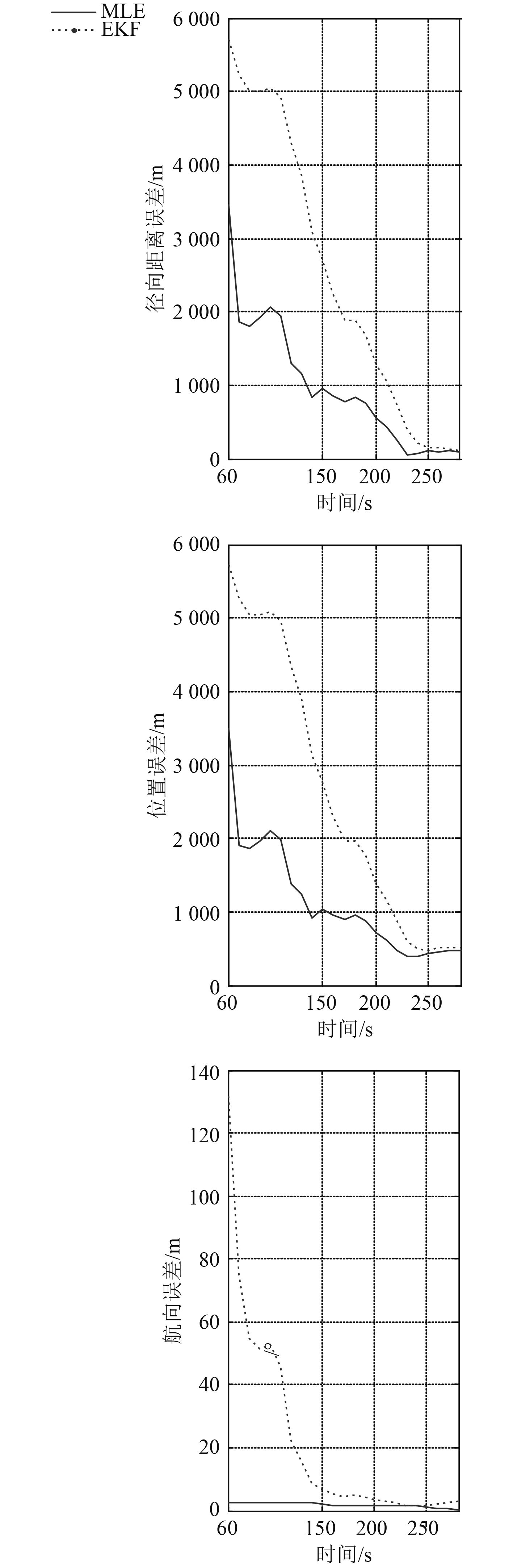
EKF法是典型的卡尔曼滤波类算法,这类算法在观测时长较短时,性能受初值等因素影响较大,其估计值起伏剧烈,图8~图 10 的图(a)验证了这一说法,故在观测时长分别为60 s,70 s,……,280 s时比较EKF和MLE算法的性能,其结果如图11所示,从右至左,3 幅子图的纵坐标分别为航向估计误差、位置估计误差以及径向距离估计误差。
|
图 11 EKF和MLE的性能比较 Fig. 11 Compare of performance of EKF and MLE |
由图11可知,与EKF算法相比,MLE估计精度更高,二者的性能差异在观测时长较短时尤为明显,随着观测时间的增加,性能差异越小,二者各自估计结果趋于真值。
海试结果表明,一定条件下,MLE与EKF算法均能达到一定估计精度,二者性能均受观测时长影响,一般而言,观测时间越长,二者性能越好,且MLE算法的估计精度优于EKF算法,这一差异在观测时间足够长时会较小。海试结果与仿真结果一致,验证了2种算法在一定条件下的有效性。
4 结 语本文利用MLE和EKF方法对水下运动目标进行双阵纯方位TMA研究,并从航向、位置等方面评价算法性能。目前关于水下目标BO-TMA的相关文献多是基于数值仿真来进行问题的研究,针对这一情况,本文在仿真基础上,通过对海试数据的处理,从试验层次分析算法性能。仿真结果表明:2 种算法性能均受方位量测精度、双阵间距以及观测时长影响,一般而言它们之间呈现正相关的关系,一定条件下,方位量测误差均值较小、双阵间距及观察时长足够长时,EKF和MLE法理论上均能达到较高精度。海试数据的处理结果验证了这一结论,说明了 2 种算法的实际有效性。
| [1] | TREMOIS O, LE CADRE J. Target Motion Analysis with multiple arrays: Performance Analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32 (3): 1030–1046. DOI: 10.1109/7.532262 |
| [2] |
曲毅, 刘忠. 基于UKF的水下目标纯方位跟踪算法[J]. 舰船科学技术, 2009, 31 (7): 133–136.
QU Yi, LIU Zhong. Research of underwater bearings-only target tracking algorithm based on UKF[J]. Ship Science and Technology, 2009, 31 (7): 133–136. |
| [3] |
杜选民, 姚蓝. 多基阵联合的无源纯方位目标运动分析研究[J]. 声学学报, 1999, 24 (6): 604–610.
DU Xuan-min, YAO Lan. Passive bearings-only target motion analysis based on association of multiple arrays[J]. Actc Acustica, 1999, 24 (6): 604–610. |
| [4] |
何友, 关欣, 衣晓. 纯方位二维运动目标的不可观测性问题研究[J]. 系统工程与电子技术, 2003, 25 (1): 12–14.
HE You, GUAN Xin, YI Xiao. Research on the unobservability problem for two dimensional tracking based on bearings only measurments[J]. Systems Engineering and Electronics, 2003, 25 (1): 12–14. |
| [5] | RAMA DEVI B, RAJARAJESWARI K, KOTESWARA RAO S. Underwater Bearings only Passive Target Tracking Using Pseudo Linear Estimator[J]. International Journal of Engineering Research & Technology, 2013, 2 (10): 21–25. |
| [6] | RESHMA A. Bearing Only Tracking Using Extended Kalman Filter[J]. International Journal of Advanced Research in Computer and Communication Engineering, 2013, 2 (2): 1140–1144. |
| [7] | LI Jia-qiang, ZHAO Rong-hua, CHEN Jin-li, et al. Target tracking algorithm based on adaptive strong tracking particle filter[J]. IET Science, Measurement & Technology, 2016, 10 (7): 704–710. |
| [8] | STEVEN C. Fundamental Properties and Performance of Conventional Bearings-Only Target Motion Analysis[J]. IEEE Transactions on automatic control, 1984, 29 (9): 775–787. DOI: 10.1109/TAC.1984.1103664 |
| [9] | STEVEN C. Observabilily criteria for bearings-only target motion analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 1981, 17 (2): 162–166. |
| [10] | JORGE N, STEPHEN J. W. Numerical optimization[M]. Second Edition. Springer. New York, 2006. |
 2017, Vol. 39
2017, Vol. 39
