对船用惯性导航设备的航向与姿态精度检测手段主要有 3 种[1 – 3]:以三轴摇摆台为试验平台的陆上模拟检测、以差分 GPS 为核心的姿态测量和以天文测姿设备作为真值测量设备的海上检测。目前,摇摆台模拟检测存在不能真实反应海上动态和陆上摇摆状态的缺陷;差分 GPS 测姿系统原理简捷,但 GPS 接收天线安装误差、船体变形对姿态测量的影响、如何克服多路径效应等难题是制约该方法在工程上推广应用的重要因素。
船用天文测姿系统具备双通道同步测星实时输出船体姿态和航向功能,实现高精度、连续天文定姿定向,是海上动态条件下姿态传递精度与基准对准精度的重要考核手段之一,可拓展应用于各种导航设备在动态条件下的姿态精度检测。
作为精度检测设备,天文测姿系统的精度指标格外重要,对其测量误差的影响因素进行分析是一项非常重要的工作。天文测姿系统的主要误差源包括轴系误差、时间误差、不同步误差、大气折射修正残差、光电检测误差、测角零位误差、地理位置误差、大气扰动误差等[4 – 7]。
1 主要误差源由轴系误差引起的测角误差表达式为:
| $\begin{array}{l}\Delta {E_V} = V \cdot \cos (A - {A_V}) \text{,}\\[5pt]\Delta {A_V} = V \cdot \sin (A - {A_V}) \cdot {\rm{tg}}E \text{,}\\[3pt]\Delta {E_b} = \displaystyle\frac{{{b^2}}}{{2\xi }} \cdot {\rm{tg}}E \text{,}\\[7pt]\Delta {A_b} = b \cdot {\rm{tg}}E \text{,}\\[3pt]\Delta {E_c} = \displaystyle\frac{{{c^2}}}{{2\xi }} \cdot {\rm{tg}}E \text{,}\\[3pt]\Delta {A_c} = c \cdot \sec E \text{。}\end{array}$ |
式中:V 为垂直轴最大倾角量,(″);A V 为出现 V 方向的方位角,(°);A、E 为被测星体的方位角、高度角;b 为水平轴不垂直度角量,(″);c 为视准轴不垂直度角量,(″);ξ 为弧度转化成方位角秒的变换系数。
时间误差导致天体地方时角计算误差:
| $\Delta {t_{m1}} = 1.002738 \cdot \Delta t \text{,}$ |
不同步误差指脱靶量测量时刻与实时采样时刻不一致造成的脱靶量测量误差。测量数据实时采样时刻是帧同步脉冲前沿,而脱靶量测量时刻是在这一帧的某一时刻,最大误差为一个帧周期,按概率分布考虑,则不同步误差为:
| ${\sigma _\tau } = \dot \theta \cdot {T}\text{,}$ |
式中:
大气折射修正公式如下:
| $\rho = \displaystyle\frac{{60.04}}{{tgE}}\left( {\displaystyle\frac{{{P_A}}}{{760}} - 0.00383T} \right)\text{,}$ |
修正后残差:
| $\Delta \rho = \displaystyle\frac{{60.04}}{{760 \cdot tgE}}\Delta {P_A} - \displaystyle\frac{{60.04 \times 0.00383}}{{tgE}}\Delta T\text{。}$ |
式中:ρ 为大气折射修正量,(″);P A 为气压,mmHg;T 为温度,℃。
光电检测误差包括目标提取误差、焦距误差等,一般结果精确检测后焦距误差可忽略不计。
星光经过大气的折射、散射、吸收后,才能到达光学系统,经过光电转换成数字信号后由计算机进行处理。作为一个光学通道,大气的抖动、湍流、烟雾、上升的热空气、大风等会影响系统的测量精度。大气的不稳定性决定了大气的光学参数的不定性,使得大气的光学参数在围绕某一平均值摆动[9],对测角精度影响分别为 σ ηE ,σ ηA 。大气扰动主要分以下 3 个方面:
1)低频振荡。频率 0.01~2 Hz,振幅为几个角秒;
2)高频振荡。频率从几十赫兹到几百赫兹,振幅 0.3″~1.0″;
3)湍流。频率超过 1 000 Hz,振幅达到 1″。
2 单项误差对总体精度的影响星体赤经、赤纬计算值误差为:
| $\begin{aligned}\Delta \alpha = {\mu _\alpha } \cdot \Delta t \text{,}\\\Delta \delta = {\mu _\delta } \cdot \Delta t \text{。}\end{aligned}$ |
设备测量两颗导航星体在甲板系下的 E 1,E 2,q 1,q 2,并根据载体当地地理位置 λ,φ,星体计算赤经 α 1,α 2,赤纬 δ 1,δ 2 和时间 t 即可计算姿态和航向[11 – 12]。
| $\begin{aligned}& K\!\! =\!\! \arctan \displaystyle\frac{{ - \cos {\delta _0} \cdot \sin {t_0}}}{{\cos \phi \cdot \sin {\delta _0} - \sin \phi \cdot \cos {\delta _0} \cdot \cos {t_0}}} \text{,}\\& P \!\!=\!\! \arcsin (\sin \phi \cdot \sin {\delta _0} + \cos \phi \cdot \cos {\delta _0} \cdot \cos {t_0}) \text{,}\\& R \!\!= \!\!\arcsin (\sin \!K\! \cdot \cos {\phi _0}/\cos {\delta _0}) - \arcsin (\sin K \!\cdot \!\cos \phi /\cos {\delta _0})\text{。}\end{aligned}$ |
根据姿态和航向解算模型,可推导得出各分项误差对姿态和航向的影响函数。
3 仿真计算根据推导的各项误差对天文测姿系统测量精度的影响函数理论公式,对定姿定向的误差影响函数进行仿真计算。
仿真条件:2016 年 4 月 10 日 9 点整(世界时零时的恒星时
根据仿真条件及式(1)~ 式(3),计算各误差项的影响函数,其曲线如图 1 所示。

|
图 1 航向与姿态曲线 Fig. 1 Course and attitude curve |
|
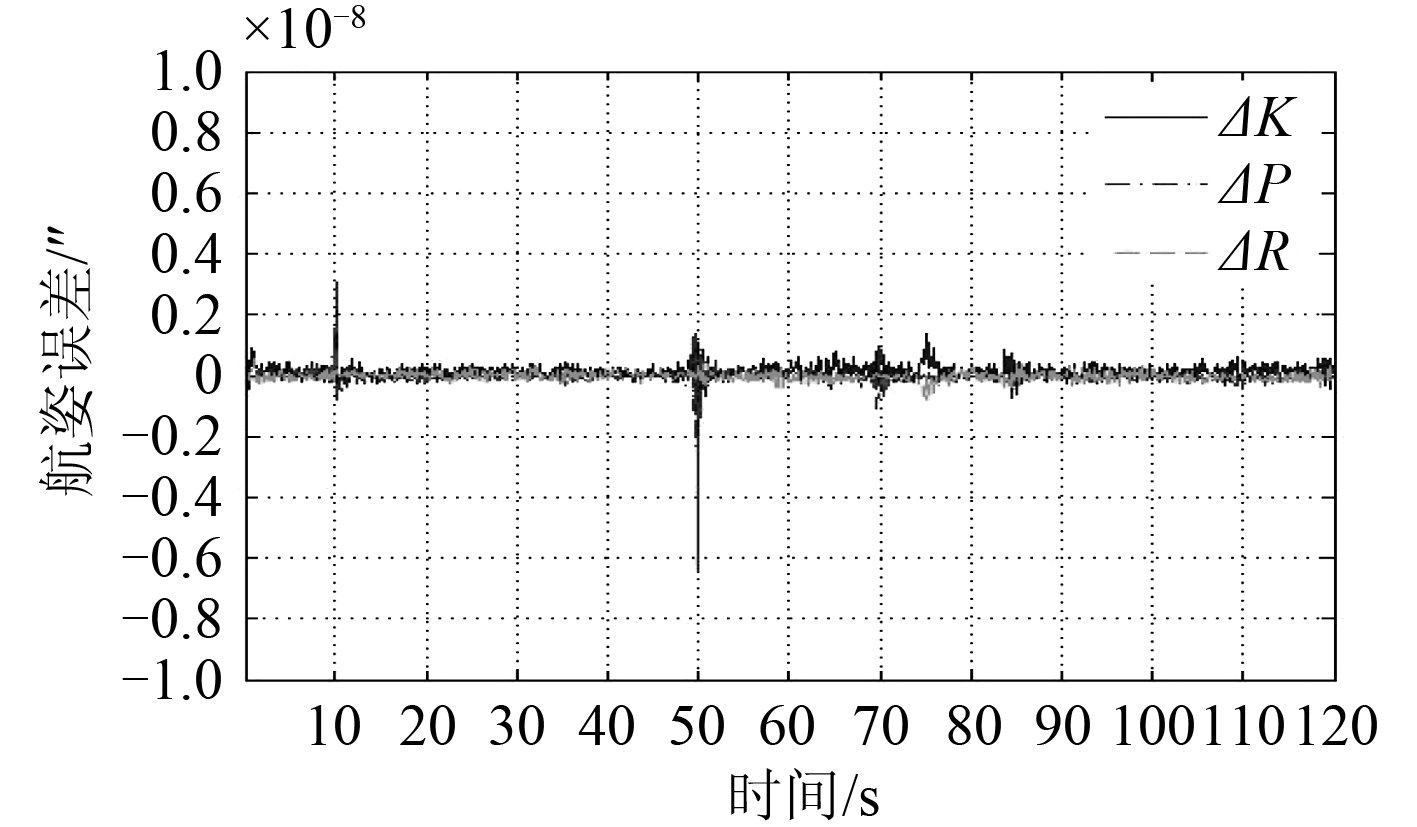
图 2 姿态和航向解算模型误差 Fig. 2 Course and attitude model error |
|
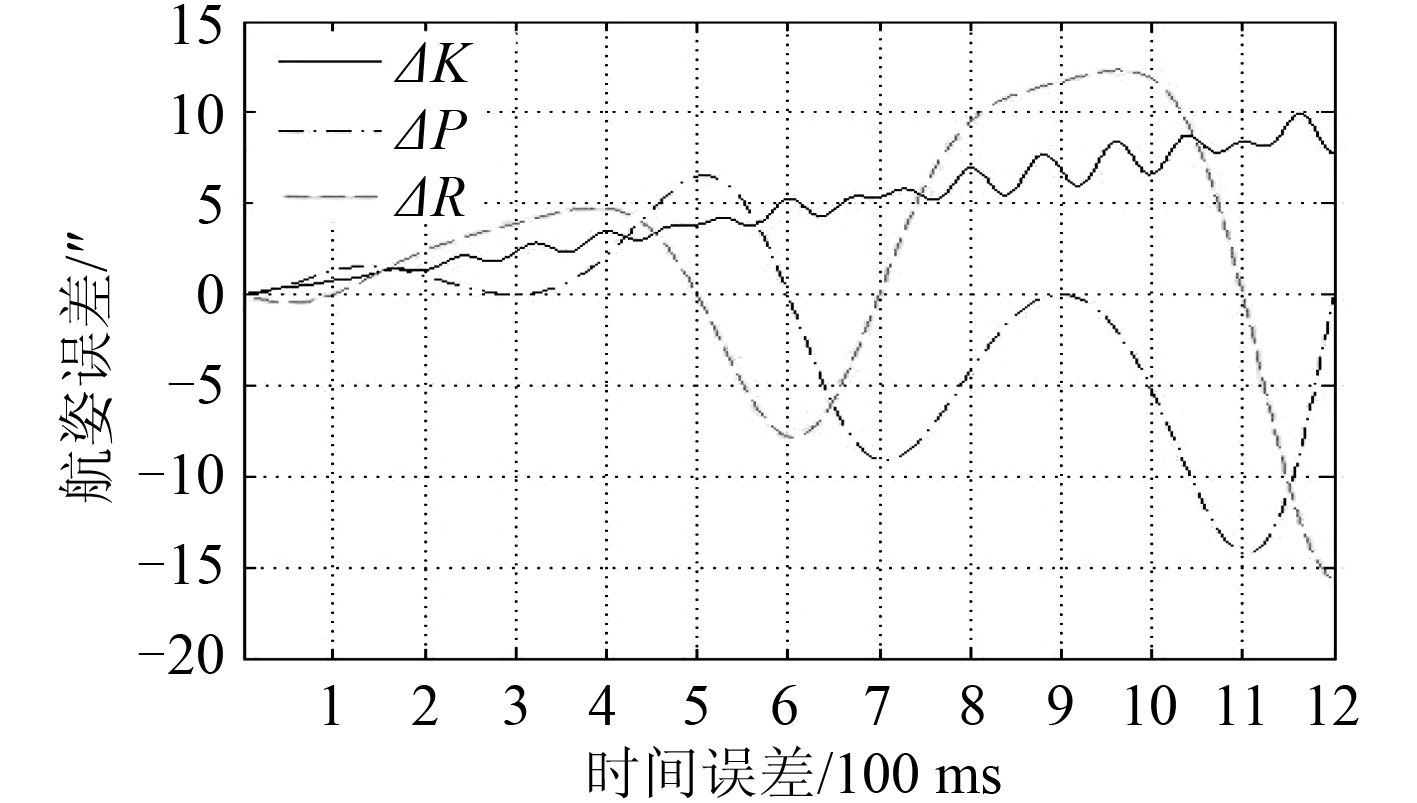
图 3 KPR 变化时,∆t 与测量误差的关系 Fig. 3 Relationship between ∆t and measuring error along KPR change |
|
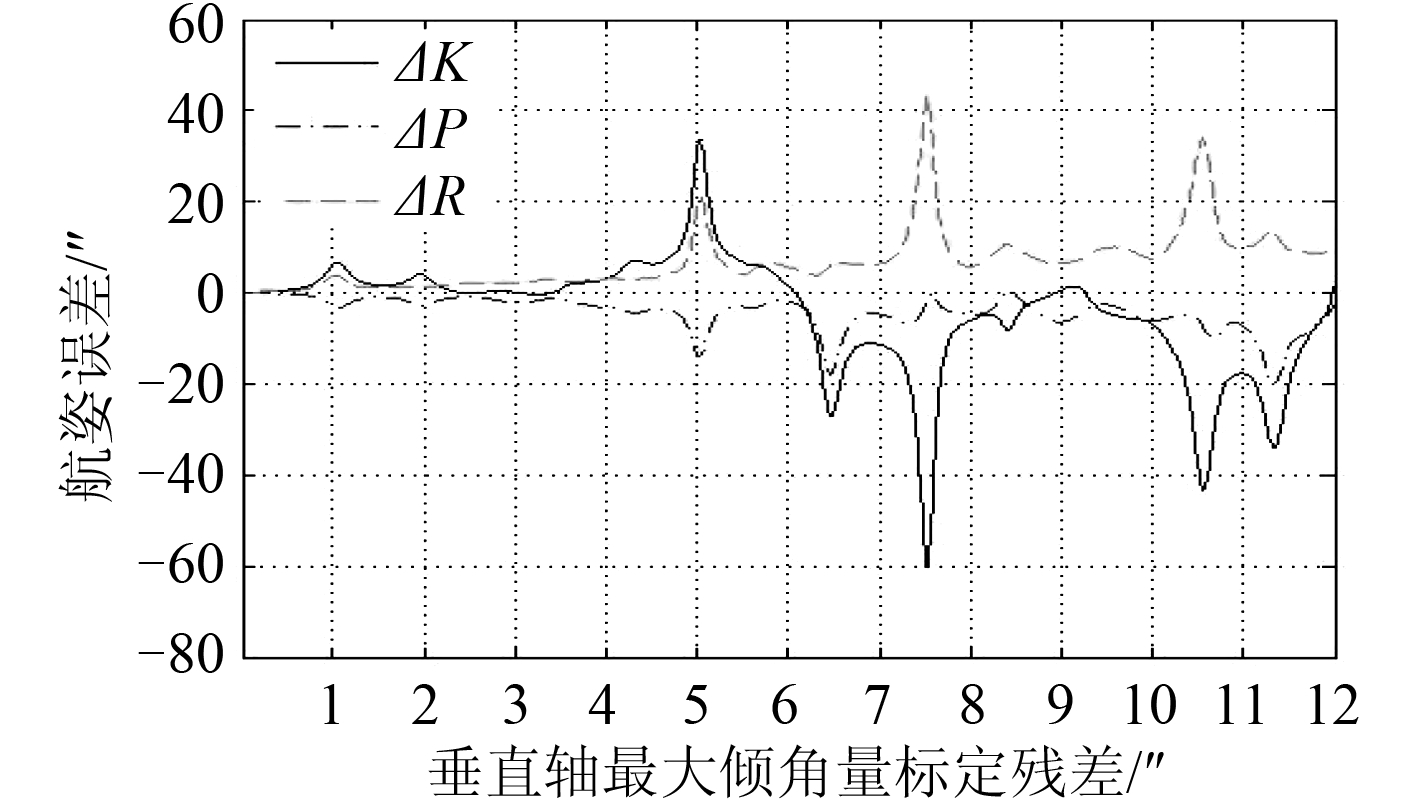
图 4 KPR 变化时,∆V 与测量误差的关系 Fig. 4 Relationship between ∆V and measuring error along KPR change |
|
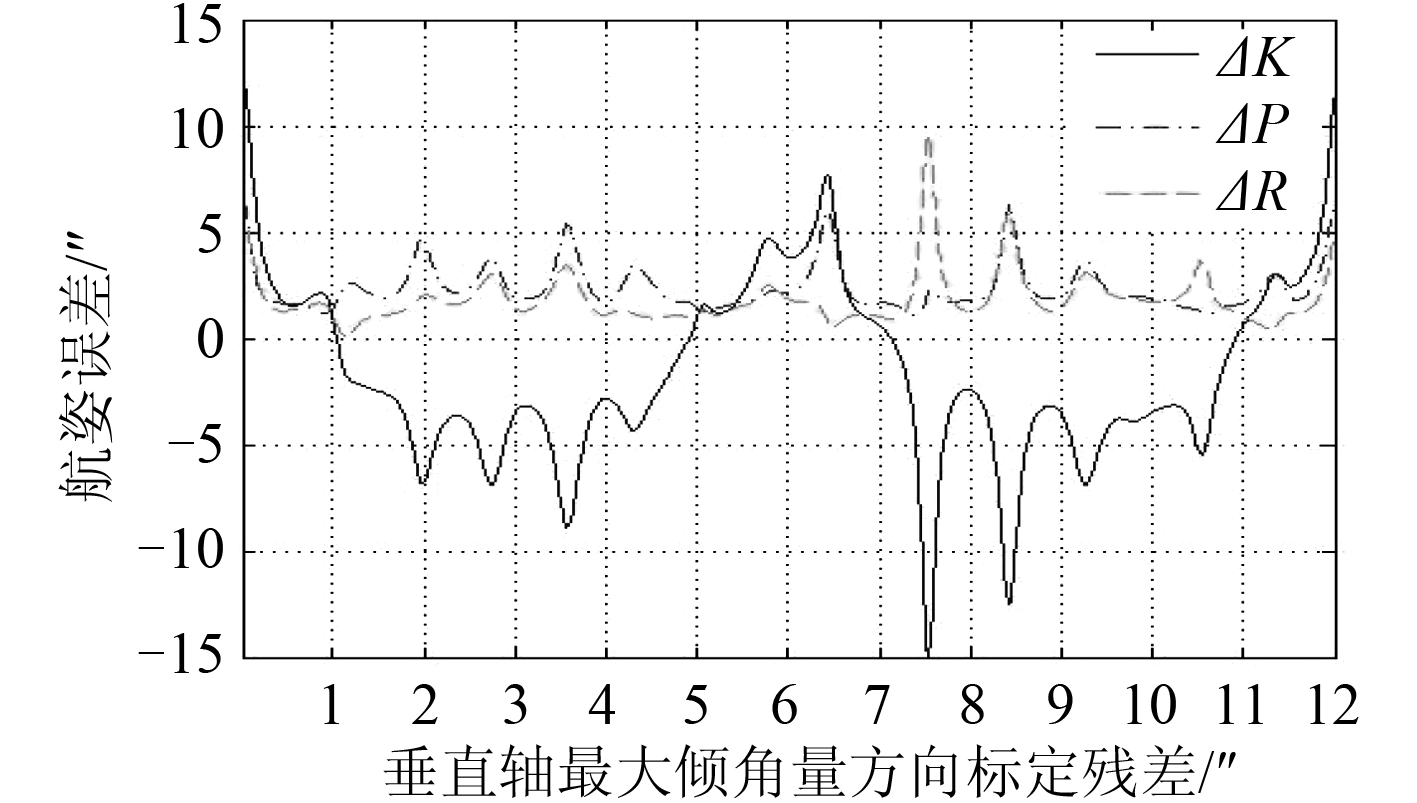
图 5 KPR 变化时,∆A V 与测量误差的关系 Fig. 5 Relationship between ∆A V and measuring error along KPR change |
|
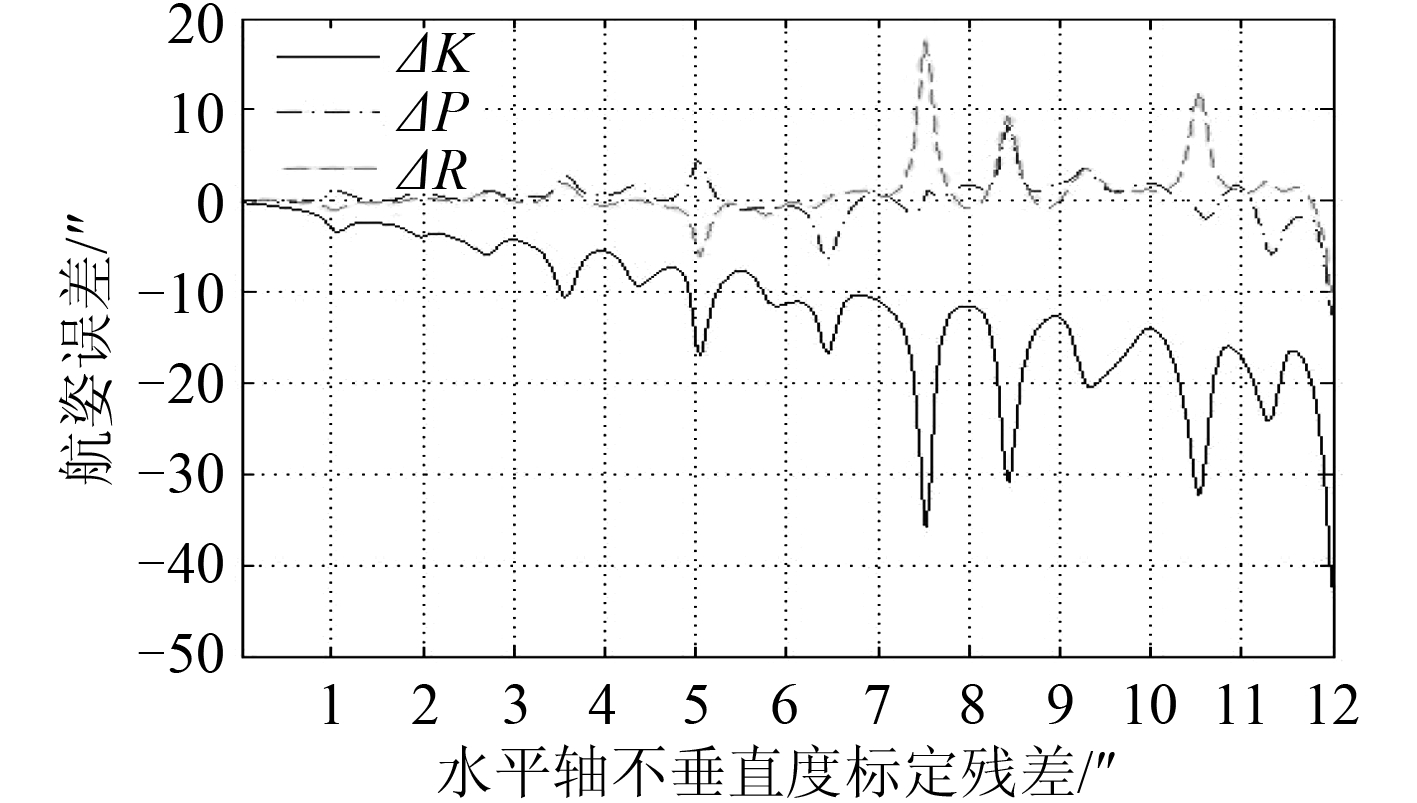
图 6 KPR 变化时,∆b 与测量误差的关系 Fig. 6 Relationship between ∆b and measuring error along KPR change |
|
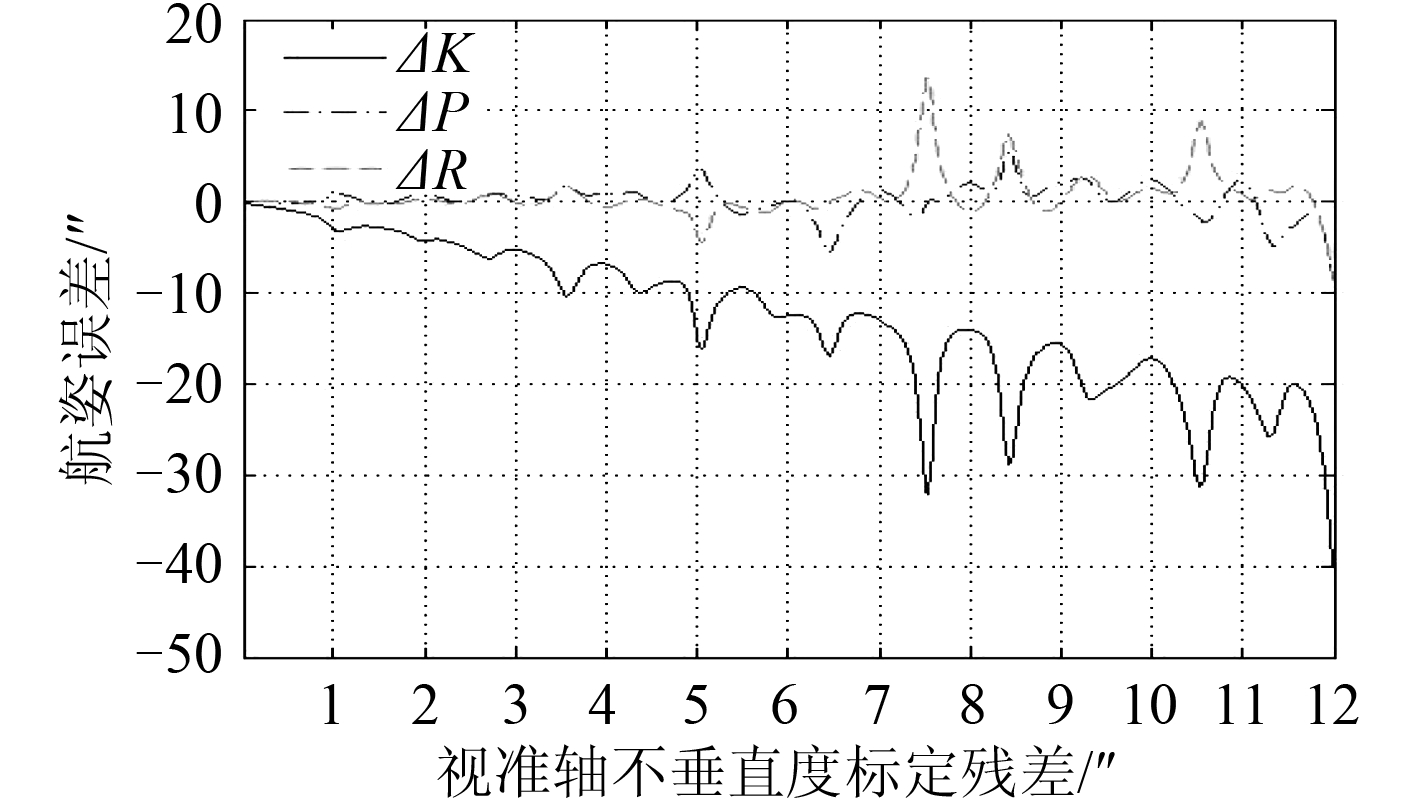
图 7 KPR 变化时,∆c 与测量误差的关系 Fig. 7 Relationship between ∆c and measuring error along KPR change |
|
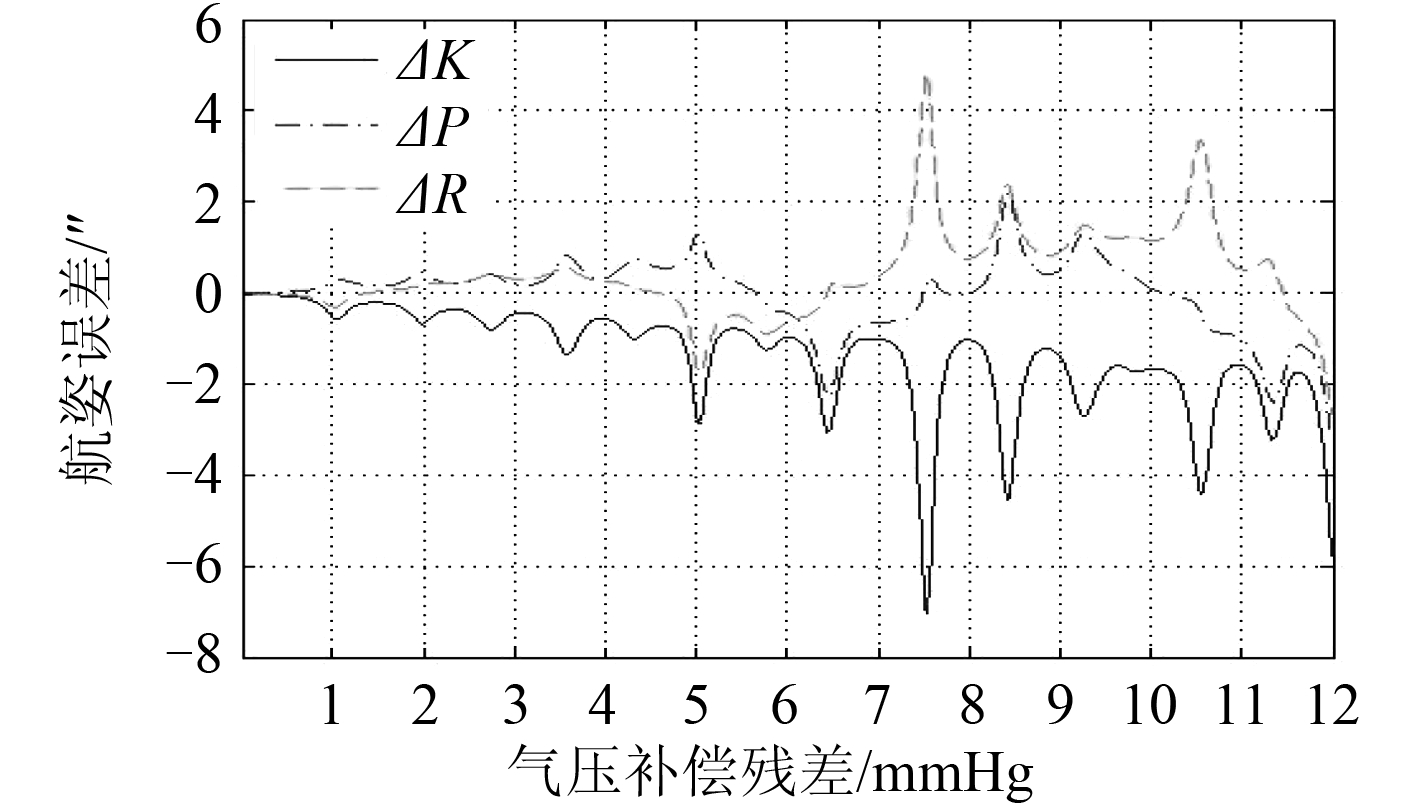
图 8 KPR 变化时,气压误差与测量误差的关系 Fig. 8 Relationship between air pressure error and measuring error along KPR change |
|
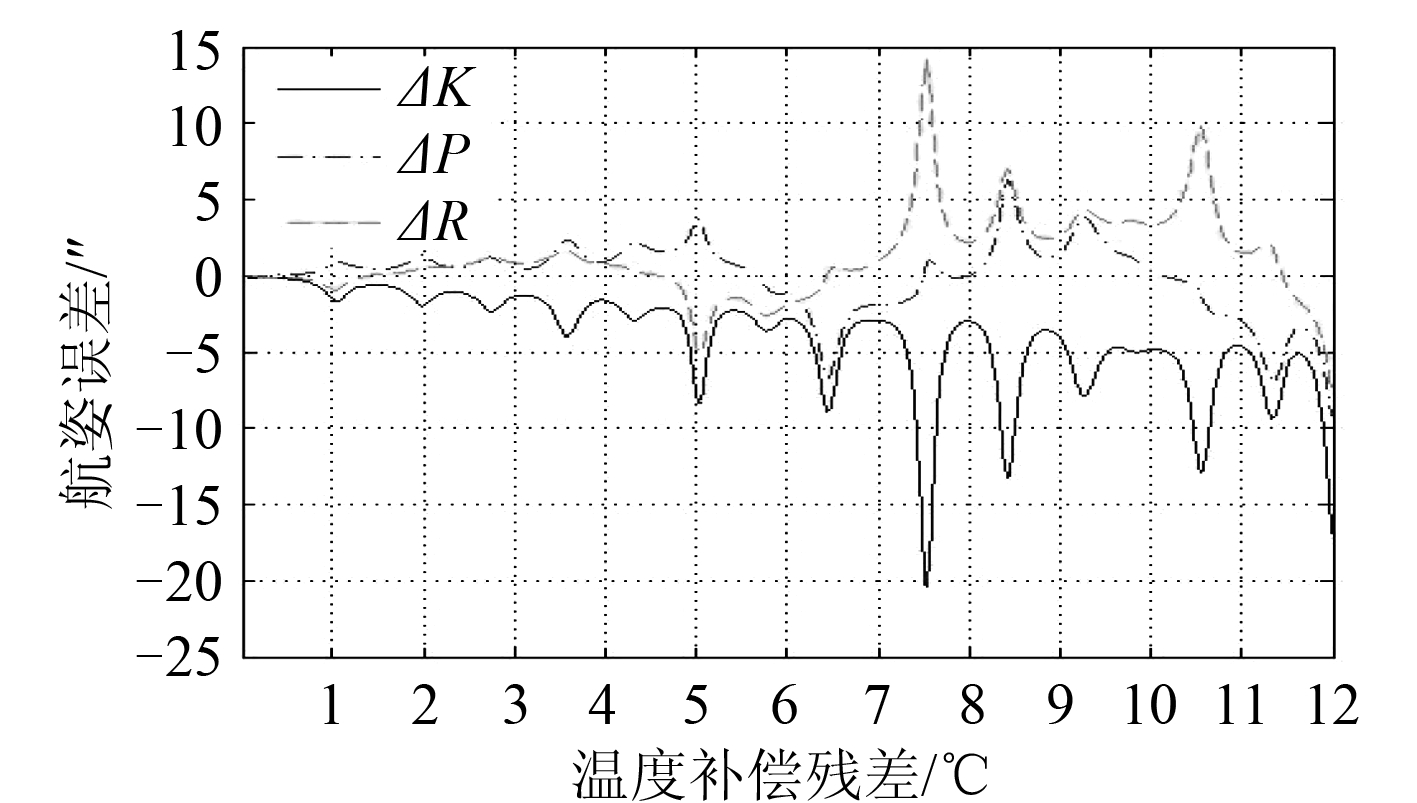
图 9 KPR 变化时,温度误差与测量误差的关系 Fig. 9 Relationship between temperature error and measuring error along KPR change |
|
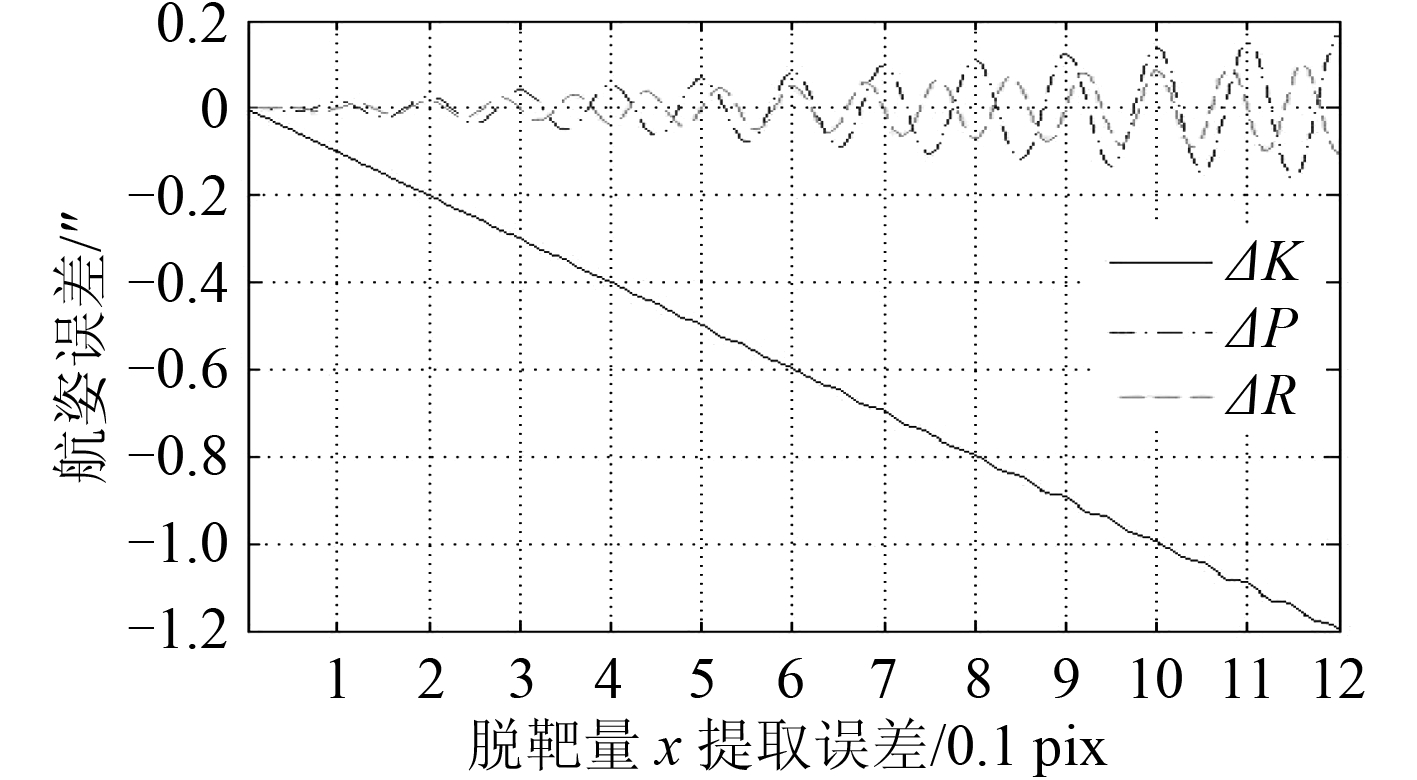
图 10 KPR 变化时,∆x 与测量误差的关系 Fig. 10 Relationship between ∆x and measuring error along KPR change |
|
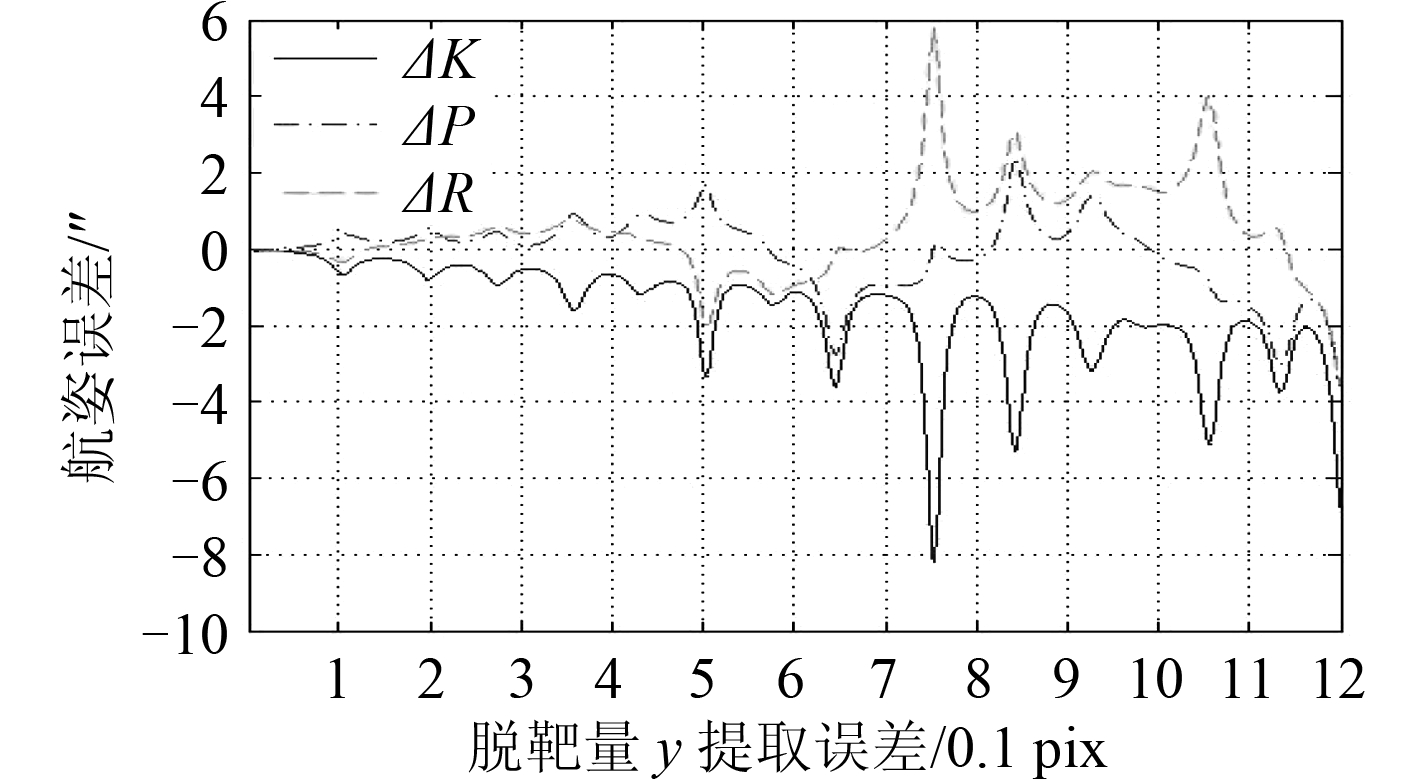
图 11 KPR 变化时,∆y 与测量误差的关系 Fig. 11 Relationship between ∆y and measuring error along KPR change |

|
图 12 KPR 变化时,∆λ 与测量误差的关系 Fig. 12 Relationship between ∆λ and measuring error along KPR change |
|
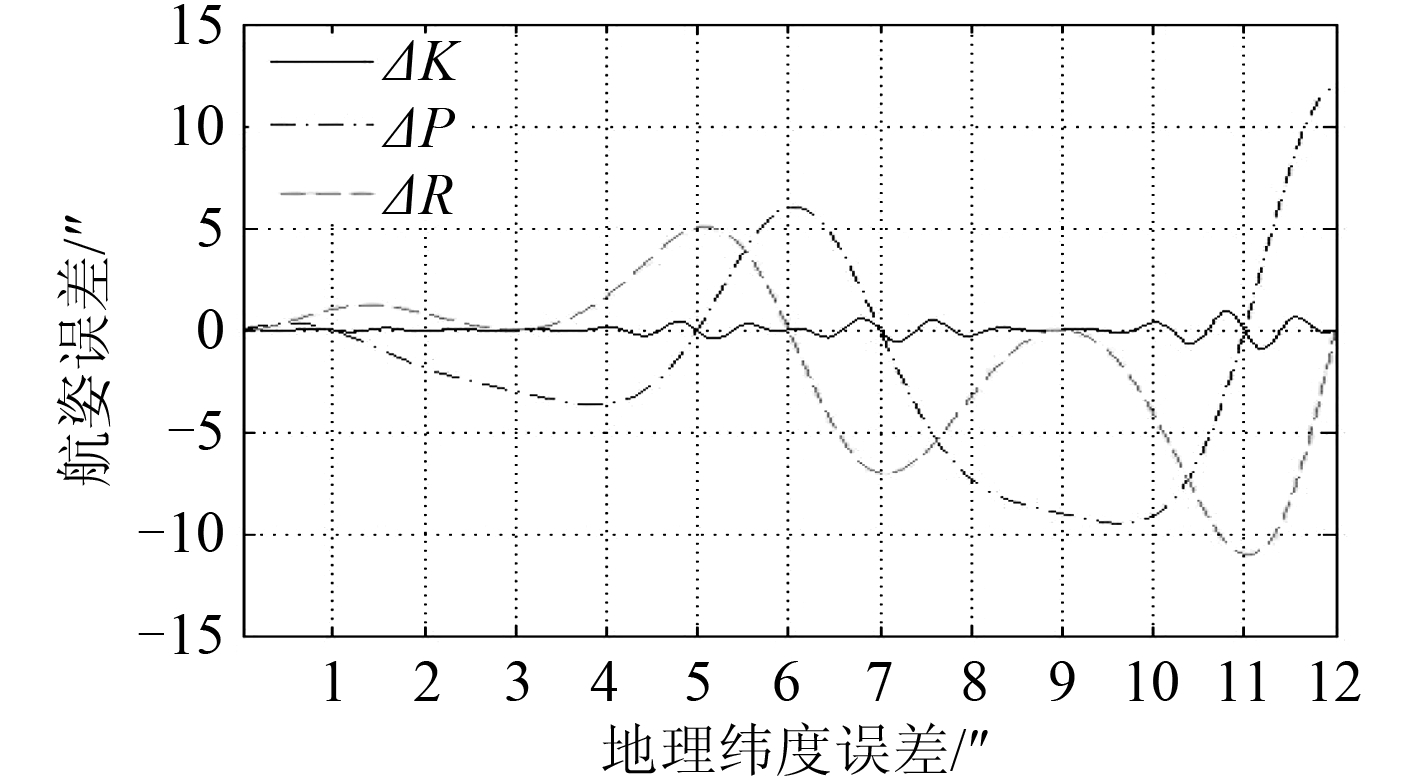
图 13 KPR 变化时,∆φ 与测量误差的关系 Fig. 13 Relationship between ∆φ and measuring error along KPR change |
从图 2 可看出,航向与姿态解算模型的数学模型误差在10-6(″),可忽略不计。
图 3 和图 12 曲线比较接近,表明时间误差和地理经度误差的影响特性较为一致,这完全符合天文导航原理。一般时间误差可控制在 100 ms 以内,而通过差分 GPS 地理经度误差、地理纬度误差均可控制在 0.1″ 以内。
图 4、图 6和图 7 反映了垂直轴最大倾角量标定残差,水平轴不垂直度标定残差,视准轴不垂直度标定残差对航姿测量误差的影响,在兼顾考虑航姿测量误差和设备装调难度 2 个方面的情况下,这 3 项误差可进行合理控制。
从图 5 可看出,航向测量精度主要取决于垂直轴最大倾角量标定残差,而垂直轴最大倾角量方向标定残差对该项测量精度的影响极为有限。
图 8和图 9 分别反映了气压、温度对大气折射修正残差的影响,而图 10和图 11 则反映了脱靶量提取误差对最后解算结果的影响。因为气压误差、温度误差、Y 轴脱靶量提取误差均对星体测量高度角产生影响,因此这3幅有极为相似,其中温度误差对解算结果的影响大于其余两项。
| [1] | 郑梓祯, 刘德耀, 蔡迎波, 等. 船用惯性导航系统海上试验[M]. 北京: 国防工业出版社, 2006. 131–137. |
| [2] |
郑梓祯, 刘德耀, 蔡迎波. 船用惯性导航系统试验方法研究[J]. 中国惯性技术学报, 2004, 12(1): 74–76.
ZHENG Zi-zhen, LIU De-yao, CAI Ying-bo. Maritime test method of marine inertial navigation system[J]. Journal of Chinese Inertial Technology, 2004, 12(1): 74–76. |
| [3] |
李德彪, 刘其富, 郑梓祯, 等. 高精度航向测量系统方案设计[J]. 中国惯性技术学报, 2004, 12(3): 64–69.
LI De-biao, LIU Qi-fu, ZHENG Zi-zhen, et al. Project design of high accuracy course measure system[J]. Journal of Chinese Inertial Technology, 2004, 12(3): 64–69. |
| [4] | 张坤石. 潜艇光电装备技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2007. 551–559. |
| [5] | 刘丙申, 刘春魁, 杜海涛. 靶场外测设备精度鉴定[M]. 北京: 国防工业出版社, 2008. 207–219. |
| [6] | 王敏, 胡绍林, 安振军. 外弹道测量数据误差影响分析技术及应用[M]. 北京: 国防工业出版社, 2008. 50–56. |
| [7] |
邹志, 唐建博. 天文导航系统星图像质分析[J]. 光学与光电技术, 2009, 7(5): 118–121.
ZOU Zhi, TANG Jian-bo. Image analysis of celestial navigation system[J]. Optics & Optoelectronic Technology, 2009, 7(5): 118–121. |
| [8] | 中国科学院紫金山天文台. 2000年中国天文年历[M]. 北京: 科学出版社, 2008. 519–520. |
| [9] |
修吉宏, 翟林培. 影响航空图像质量的主要因素分析[J]. 红外, 2005, Vol. 26, No. 8: 10–16.
XIU Ji-hong, ZHAI Lin-pei. Main factors affecting the quality of aerial images[J]. Infrared, 2005, 26(8): 10–16. |
| [10] |
王敏, 胡绍林, 安振军. 跟踪测量数据系统误差残差的影响分析[J]. 飞行力学, 2004, Vol. 22, No. 1: 74–78.
WANG Min, HU Shao-lin, AN Zhen-jun. Influence analysis of tracking measurement data system residual error[J]. Mechanics of Flight, 2004, 22(1): 74–78. |
| [11] |
季必达. 天文定位的直接解算法[J]. 舰船光学, 2008, 44(4): 1–2.
JI Bi-da. Direct solution arithmetic of astronomical positioning[J]. Ship Optics, 2008, 44(4): 1–2. |
| [12] |
周罡, 唐建博, 邹志. 一种高精度的天文导航姿态与航向解算模型[J]. 舰船科学技术, 2009, 31(5): 72–75.
ZHOU Gang, TANG Jian-bo, ZOU Zhi. An high precision calculation model of attitude and course about celestial navigation[J]. Ship Science and Technology, 2009, 31(5): 72–75. |
 2017, Vol. 39
2017, Vol. 39
