高精度声学多普勒计程仪(Acoustic Doppler Log,ADL)可应用于水面舰船和水下运载器的导航定位,为导航系统提供精确的速度信息,以修正导航系统由于长时间的速度误差累积,满足远程、长时间航行的导航要求,因此提高多普勒计程仪的测速精度非常重要。
目前,评定多普勒计程仪对不同水流层测速精度的常用方法为水槽拖车试验、同步比测试验及自身航行试验[1 – 4]。
水槽拖车试验适用于工作频率大于 300 kHz 的计程仪精度检验,难以模拟真实的多普勒计程仪复杂的使用环境,不适用于高精度 ADL 测流精度考核[2]。
同步比测试验是最为简单理想的精度检验方法[3],但一方面,需要工作频率与被检验多普勒计程仪工作频率不在同一频段的更高精度的计程仪作为检测标准仪器,而国外的高精度大深度多普勒计程仪对我国是全面限制的,这就使得同步比测法无法用于新研制的高精度计程仪;另一方面,实艇条件下,一般不具备同时安装被测和同步比测的计程仪的条件,这进一步限制了同步比测方法的使用。
对于工作频率不大于 300 kHz 的计程仪,且试验船上不具备同时安装被测和同步比测的计程仪时,只有通过自身航行试验来考核计程仪的分层对水相对速度测量精度。
目前,声学多普勒计程仪检测标准给出的自身航行试验法都是以高精度 GPS 作为检测标准仪器,常用的是“顺-逆”合速度标量消流法。
该方法的检测原理为:试验船在同一航线上,通过“顺-逆”或“逆-顺”2个航次消流的方式,由 ADL 对某一深度的水层进行测速,通过与高精度 GPS 测得的对地速度相比较的方法统计 ADL 对水测速偏差。
“顺-逆”合速度消流法的核心思想在于:被检 ADL 在同一航线顺流和逆流航行的直接测量值(海流相对于载体的速度)的合速度标量之和等于载体顺流和逆流航行的对地速度值(GPS 测量值)的合速度标量之和。该思想成立的前提条件是试验船的航向与洋流、风等外界作用力的方向保持同向。当洋流方向、风向、浪涌流向等外界作用力方向与试验船的航向有夹角时,该方法的计算精度会受到影响,即“顺-逆”合速度标量消流法的计算精度与洋流流速、风速及洋流流向和风向与试验船航向夹角大小等因素相关。
“顺-逆”合速度标量消流法虽然可以用于在真实的海洋环境中对 ADL 的流速测量精度进行考核,但为保障考核精度,对试验船的机动、海区海况等试验条件要求苛刻,这就决定了该方法在实际试验中也无法获得很高的考核精度。
为解决以上问题,降低或消除洋流流速流向、风速风向等外界因素对 ADL 测流速度考核精度的影响,本文提出一种新的高精度 ADL 测流速度考核方法——矢量平均法,给出该方法抗洋流流速流向、风速风向等外界因素干扰的特性原理,理论分析该方法相对于标量消流法的精度优势,最后通过试验数据验证该方法相对于“顺-逆”合速度标量消流法具有更高考核精度的特性。
1 矢量平均法原理分析影响“自身航行试验法”对 ADL 测流考核精度的主要因素为各水流层的流速流向和风速风向,下面将从原理上分析考虑风和洋流的影响(有风,各层洋流的流速流向均不相同)下,试验船在同一航线上往返匀速直线航行时,GPS 测得的试验船速度值 VGPS 与 ADL 测得的试验船相对于各洋流层速度值的关系。在以下的分析中,假定:
第一往返匀速直航期间,各洋流层的流速、流向和风速、风向均保持稳定,风速为 V风,风向与航向的夹角为 θ风,第 k 层洋流流速为
第二往返匀速直航的航迹线重合或近距离平行(航迹线下的洋流状态一致);
第三往返匀速直航期间,试验船的主机转速 V 主 保持不变。
1)顺流,航向角为 β 时
ADL 测得的试验船相对于第 k 层洋流的横向速度和纵向速度分别为:
横向速度
| $V_{DPL- {\text{横}}}^{{\text{顺}}- k} = V_{{\text{横}}}^{{\text{风}}} - V_{{\text{流} - \text{横}}}^k\text{,}$ | (1) |
纵向速度
| $V_{DPL- {\text{纵}}}^{{\text{顺}}- k} = {V_{{\text{主}}}} + V_{{\text{纵}}}^{{\text{风}}} - V_{{\text{流} - \text{纵}}}^k\text{;}$ | (2) |
GPS 测得的试验船的对地横向速度和纵向速度分别为:
横向速度
| $V_{\rm{GPS}- {\text{横}}}^{\text{顺}} = V_{{\text{流} - \text{横}}}^0 + V_{{\text{横}}}^{{\text{风}}}\text{,}$ | (3) |
纵向速度
| $V_{\rm{GPS}- {\text{纵}}}^{\text{顺}} = {V_{{\text{主}}}} + V_{{\text{流} - \text{纵}}}^0 + V_{{\text{纵}}}^{{\text{风}}}\text{。}$ | (4) |
2)逆流,航向角为 +180° 时
ADL 测得的试验船相对于第 k 层洋流的横向速度和纵向速度分别为:
横向速度
| $V_{DPL- {\text{横}}}^{{\text{逆}}- k} = -V_{{\text{横}}}^{{\text{风}}} + V_{{\text{流} - \text{横}}}^k\text{,}$ | (5) |
纵向速度
| $V_{DPL- {\text{纵}}}^{{\text{逆}}- k} = {V_{{\text{主}}}} - V_{{\text{纵}}}^{{\text{风}}} + V_{{\text{流} - \text{纵}}}^k\text{;}$ | (6) |
GPS 测得的试验船的对地横向速度和纵向速度分别为:
横向速度
| $V_{\rm{GPS}- {\text{横}}}^{\text{逆}} = -V_{{\text{流} - \text{横}}}^0 - V_{{\text{横}}}^{{\text{风}}}\text{,}$ | (7) |
纵向速度
| $V_{\rm{GPS}- {\text{纵}}}^{\text{逆}} = {V_{{\text{主}}}} - V_{{\text{流} - \text{纵}}}^0 - V_{{\text{纵}}}^{{\text{风}}}\text{。}$ | (8) |
则“顺-逆”2个航程
ADCP 横向速度平均值
| $\bar V_{DPL - {\text{横}}}^k = \frac{{V_{DPL - {\text{横}}}^{{\text{顺}}- k} \;\;\;+ V_{DPL - {\text{横}}}^{{\text{逆}} - k}}}{2}{\rm{ = }}0\text{,}$ |
ADCP 纵向速度平均值
| $\bar V_{DPL - {\text{纵}}}^k = \frac{{V_{DPL - {\text{纵}}}^{{\text{顺}}- k} \;\;\;+ V_{DPL - {\text{纵}}}^{{\text{逆}} - k}}}{2}{\rm{ = }}{V_{{\text{主}}}}\text{,}$ |
GPS 横向速度平均值
| $\bar V_{GPS - {\text{横}}}^k = \frac{{V_{GPS - {\text{横}}}^{{\text{顺}}- k} \;\;\;+ V_{GPS - {\text{横}}}^{{\text{逆}} - k}}}{2}{\rm{ = }}0\text{,}$ |
GPS 纵向速度平均值
| $\bar V_{GPS - {\text{纵}}}^k = \frac{{V_{GPS - {\text{纵}}}^{{\text{顺}}- k} \;\;\;+ V_{GPS - {\text{纵}}}^{{\text{逆}} - k}}}{2}{\rm{ = }}{V_{{\text{主}}}}\text{。}$ |
即有
“顺-逆”或“逆-顺”2个航程的 ADL 速度矢量平均值
由此得到一种高精度的 ADL 测流精度考核方法,命名为“矢量平均法”。该方法不受风速、风向、流速、流向等复杂海洋环境的影响,抗干扰能力强,对各层洋流流速的考核精度具有一致性。影响考核精度的主要因素为航向稳定性。
2 误差分析与比较现有的计程仪对水测速精度考核方法中,应用最多精度最高也最贴近实际的是“顺-逆”合速度标量相消法,下面将详细分析实际海洋环境下“顺-逆”合速度标量相消法与矢量平均法的考核精度高低[5 – 6]。
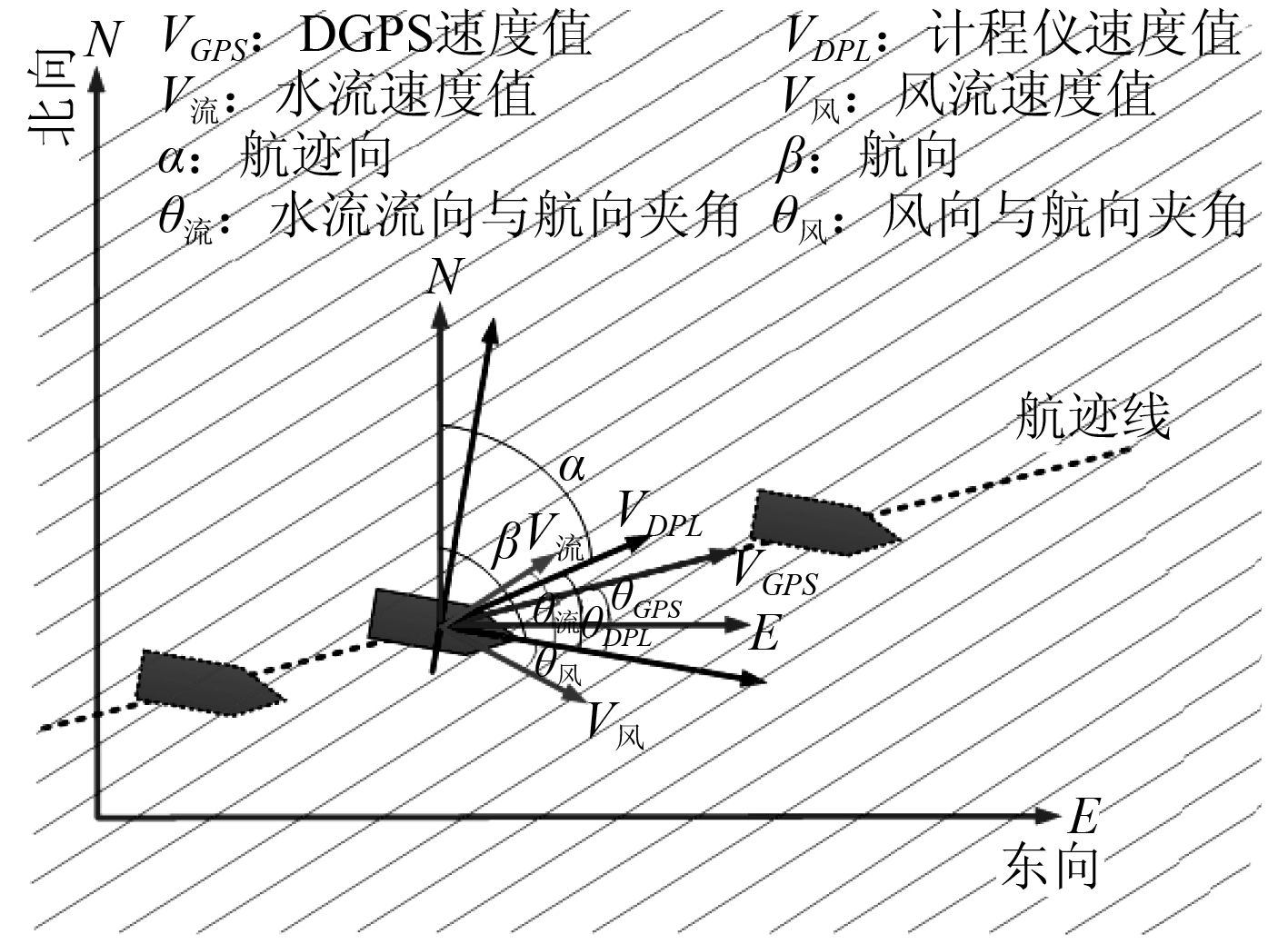
|
图 1 考虑风和水流因素时,计程仪设备载体试验航行的解算示意图 Fig. 1 The diagram of calculating the navigaiton speed for ADL on a ship when considering the influence of wind and current |
在实际的海洋环境中,洋流流向和风向与试验船的航向是有一定的夹角的,各层洋流的流向也不相同,唯一能精确控制的是试验船的主机转速V
主。采用第 1 节的外界干扰分析,假设:船航迹向为 α,航向角为 β,风速为 V风,风向与航向的夹角为 θ风,第 k 层洋流流速为
1)“顺-逆”合速度标量消流法对水测速考核误差分析
当风速、风向和流速、流向稳定,且 ∆β = 0 时,依据合速度标量消流法测得的试验船速度真值为:
| ${\bar V_{GPS}}{\rm{ = }}\frac{{V_{GPS}^{{\text{顺}}} + V_{GPS}^{{\text{逆}}}}}{2}\text{,}$ | (9) |
其中,依据式(1)~式(8)有
| $\begin{split}V_{GPS}^{{\text{顺}}}{\rm{ = }} & \sqrt {{{\left( {V_{GPS{\rm{ - }}{\text{横}}}^{{\text{顺}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {V_{GPS{\rm{ - }}{\text{纵}}}^{{\text{顺}}}} \right)}^{\rm{2}}}}= \\ & \sqrt {{{\left( {V_{{\text{流}}{\rm{ - }}{\text{横}}}^0{\rm{ + }}V_{{\text{横}}}^{{\text{风}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {{V_{{\text{主}}}}{\rm{ + }}V_{{\text{流}}{\rm{ - }}{\text{纵}}}^0{\rm{ + }}V_{{\text{纵}}}^{{\text{风}}}} \right)}^{\rm{2}}}} \text{,}\end{split}$ |
| $\begin{split}V_{GPS}^{{\text{逆}}}{\rm{ = }} & \sqrt {{{\left( {V_{GPS{\rm{ - }}{\text{横}}}^{{\text{逆}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {V_{GPS{\rm{ - }}{\text{纵}}}^{{\text{逆}}}} \right)}^{\rm{2}}}} = \\[5pt] & \sqrt {{{\left( {{\rm{ - }}V_{{\text{流}}{\rm{ - }}{\text{横}}}^0{\rm{ - }}V_{{\text{横}}}^{{\text{风}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {{V_{{\text{主}}}}{\rm{ - }}V_{{\text{流}}{\rm{ - }}{\text{纵}}}^0{\rm{ - }}V_{{\text{纵}}}^{{\text{风}}}} \right)}^{\rm{2}}}} = \\[5pt] & \sqrt {{{\left( {V_{{\text{流}}{\rm{ - }}{\text{横}}}^0{\rm{ + }}V_{{\text{横}}}^{{\text{风}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {{V_{{\text{主}}}}{\rm{ - }}V_{{\text{流}}{\rm{ - }}{\text{纵}}}^0{\rm{ - }}V_{{\text{纵}}}^{{\text{风}}}} \right)}^{\rm{2}}}} \text{,}\end{split}$ |
而计程仪测得的试验船待考核速度值
| ${\bar V_{DPL}}{\rm{ = }}\frac{{V_{DPL}^{{\text{顺}}} + V_{DPL}^{{\text{逆}}}}}{2}\text{。}$ | (10) |
其中,依据式(1)~式(8)有
| $\begin{split}V_{DPL}^{{\text{顺}}}{\rm{ = }} & \sqrt {{{\left( {V_{DPL{\rm{ - }}{\text{横}}}^{{\text{顺}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {V_{DPL{\rm{ - }}{\text{纵}}}^{{\text{顺}}}} \right)}^{\rm{2}}}} = \\ & \sqrt {{{\left( {{\rm{ - }}V_{{\text{流}}{\rm{ - }}{\text{横}}}^k{\rm{ + }}V_{{\text{横}}}^{{\text{风}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {{V_{{\text{主}}}}{\rm{ - }}V_{{\text{流}}{\rm{ - }}{\text{纵}}}^k{\rm{ + }}V_{{\text{纵}}}^{{\text{风}}}} \right)}^{\rm{2}}}} \text{,}\end{split}$ |
| $\begin{split}V_{DPL}^{{\text{逆}}}{\rm{ = }} & \sqrt {{{\left( {V_{DPL{\rm{ - }}{\text{横}}}^{{\text{逆}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {V_{DPL{\rm{ - }}{\text{纵}}}^{{\text{逆}}}} \right)}^{\rm{2}}}} = \\ & \sqrt {{{\left( {V_{{\text{流}}{\rm{ - }}{\text{横}}}^k{\rm{ - }}V_{{\text{横}}}^{{\text{风}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {{V_{{\text{主}}}}{\rm{ + }}V_{{\text{流}}{\rm{ - }}{\text{纵}}}^k{\rm{ - }}V_{{\text{纵}}}^{{\text{风}}}} \right)}^{\rm{2}}}} \text{。}\end{split}$ |
很明显,当
2)矢量平均法对水测速考核误差分析
由第 2 节内容分析可知,当风速、风向和流速、流向稳定,且 ∆β = 0 时,矢量平均法的理论算法误差为 0,即
| $\Delta V{\rm{ = }}\left| {{{\bar V}_{DPL}}{\rm{ - }}{{\bar V}_{GPS}}} \right| = \left| {{V_{{\text{主}}}}{\rm{ - }}{V_{{\text{主}}}}} \right|{\rm{ = }}0\text{。}$ |
故而,从算法理论误差分析上可知,矢量平均法的对水测速考核精度要高于合速度标量消流法。
3 矢量平均法试验原理及步骤为了消除流的随机性,进一步提高考核精度,采用往返航行 3 个航次进行消流计算。
1) 试验原理
以 GPS 作为检测标准仪器,试验船在同一航线上往返航行 3 个航次(如“顺-逆-顺”或“逆-顺-逆”),3 个航次中分别记录 ADCP 测得的试验船相对于各水层的横向分速度和纵向分速度,然后对这 3 个航次记录的各水层横向平均分速度与纵向平均分速度进行消流处理,其结果值的合速度即为样机的待考核速度,通过与 GPS 速度真值(约等于轮机转速)比对统计测量偏差[7]。其中,GPS 速度真值的计算方法为:在“顺-逆-顺”或“逆-顺-逆” 3 个航次中,先将 GPS 速度分解到船的横向和纵向 2 个方向上,分别求出这 2 个方向上 3 个航次的平均速度,再分别求出横向和纵向 2 个方向上 GPS 平均速度的平均值,然后求出航迹向合速度,即为考核真值。在以上测量过程中,为保障测速精度,需要多普勒流速剖面仪设备载体在航行过程中保持轮机转速 V e 不变,航向偏差 ≤ ±1°,具体实现方式如下文所示[8]。
2)试验步骤
分别记录 3 个航次 k(k=1,2,3)的试验数据:
记录时刻:
ADL 横向测速结果:
| $V_{DPL - {\text{横}}}^k(T_1^k)、V_{DPL - {\text{横}}}^k(T_2^k)、 \ldots\ldots 、V_{DPL - {\text{横}}}^k(T_n^k)\text{,}$ |
ADL 纵向测速结果:
| $V_{DPL - {\text{纵}}}^k(T_1^k)、V_{DPL - {\text{纵}}}^k(T_2^k)、 \ldots 、V_{DPL - {\text{纵}}}^k(T_n^k)\text{,}$ |
DGPS 横向测速结果:
| $V_{GPS - {\text{横}}}^k(T_1^k)、V_{GPS - {\text{横}}}^k(T_2^k)、 \ldots 、V_{GPS - {\text{横}}}^k(T_n^k)\text{,}$ |
DGPS 纵向测速结果:
| $V_{GPS - {\text{纵}}}^k(T_1^k)、V_{GPS - {\text{纵}}}^k(T_2^k)、 \ldots 、V_{GPS - {\text{纵}}}^k(T_n^k)\text{。}$ |
每个航次后,分别计算 ADL,DGPS 测得的分速度平均值,分别如下:
ADL 横向速度平均值
| $\bar V_{DPL{\rm{ - }}{\text{横}}}^k = (1/n)\sum\limits_{i = 1}^n {V_{DPL - {\text{横}}}^k(T_i^k)} \text{,}$ | (11) |
ADL 纵向速度平均值
| $\bar V_{DPL{\rm{ - }}{\text{纵}}}^k = (1/n)\sum\limits_{i = 1}^n {V_{DPL - {\text{纵}}}^k(T_i^k)} \text{,}$ | (12) |
DGPS 横向速度平均值
| $\bar V_{GPS{\rm{ - }}{\text{横}}}^k = (1/n)\sum\limits_{i = 1}^n {V_{GPS - {\text{横}}}^k(T_i^k)} \text{,}$ | (13) |
DGPS 纵向速度平均值
| $\bar V_{GPS{\rm{ - }}{\text{纵}}}^k = (1/n)\sum\limits_{i = 1}^n {V_{GPS - {\text{纵}}}^k(T_i^k)} \text{。}$ | (14) |
对以上 3 个航次 ADL 和 DGPS 的横向、纵向速度测量值的平均值进行消流处理:
消流后的 ADL 横向速度平均值
| ${\bar V_{DPL{\rm{ - }}{\text{横}}}} = \frac{{\bar V_{DPL{\rm{ - }}{\text{横}}}^1 + 2\bar V_{DPL{\rm{ - }}{\text{横}}}^2 + \bar V_{DPL{\rm{ - }}{\text{横}}}^3}}{4}\text{,}$ | (15) |
消流后的 ADL 纵向速度平均值
| ${\bar V_{DPL{\rm{ - }}{\text{纵}}}} = \frac{{\bar V_{DPL{\rm{ - }}{\text{纵}}}^1 + 2\bar V_{DPL{\rm{ - }}{\text{纵}}}^2 + \bar V_{DPL{\rm{ - }}{\text{纵}}}^3}}{4}\text{,}$ | (16) |
消流后的 DGPS 横向速度平均值
| ${\bar V_{GPS{\rm{ - }}{\text{横}}}} = \frac{{\bar V_{GPS{\rm{ - }}{\text{横}}}^1 + 2\bar V_{GPS{\rm{ - }}{\text{横}}}^2 + \bar V_{GPS{\rm{ - }}{\text{横}}}^3}}{4}\text{,}$ | (17) |
消流后的 DGPS 纵向速度平均值
| ${\bar V_{GPS{\rm{ - }}{\text{纵}}}} = \frac{{\bar V_{GPS{\rm{ - }}{\text{纵}}}^1 + 2\bar V_{GPS{\rm{ - }}{\text{纵}}}^2 + \bar V_{GPS{\rm{ - }}{\text{纵}}}^3}}{4}\text{。}$ | (18) |
由
① 当以合速度进行考核时
GPS 速度真值为:
| ${\bar V_{{\rm{GPS}}}} = \sqrt {{{\left( {{{\bar V}_{{\rm{GPS - }}{\text{横}}}}} \right)}^2}{\rm{ + }}{{\left( {{{\bar V}_{{\rm{GPS - }}{\text{纵}}}}} \right)}^2}} \text{,}$ | (19) |
流速剖面仪待考核速度值为:
| ${\bar V_{{\rm{DPL}}}} = \sqrt {{{\left( {{{\bar V}_{{\rm{DPL - }}{\text{横}}}}} \right)}^2}{\rm{ + }}{{\left( {{{\bar V}_{{\rm{DPL - }}{\text{纵}}}}} \right)}^2}} \text{,}$ | (20) |
由此可得,流速剖面仪对水测速的精度为:
| $\Delta V{\rm{ = }}\left| {{{\bar V}_{DPL}}{\rm{ - }}{{\bar V}_{GPS}}} \right|\text{。}$ | (21) |
② 当以分速度进行考核时
GPS 横向速度与纵向速度真值分别如式(17)、式(18)所示,流速剖面仪待考核横向速度与纵向速度值分别如式(15)、式(16)所示,流速剖面仪对水横向与纵向测速精度分别为:
| $\left\{ \begin{array}{l}\Delta {V_{{\text{横}}}}{\rm{ = }}\left| {{{\bar V}_{DPL{\rm{ - }}{\text{横}}}}{\rm{ - }}{{\bar V}_{GPS{\rm{ - }}{\text{横}}}}} \right|\\\Delta {V_{{\text{纵}}}}{\rm{ = }}\left| {{{\bar V}_{DPL{\rm{ - }}{\text{纵}}}}{\rm{ - }}{{\bar V}_{GPS{\rm{ - }}{\text{纵}}}}} \right| \text{。}\end{array} \right. $ | (22) |
在某次水上试验中,同时利用合速度标量消流法和矢量平均法对国外多普勒流速剖面仪产品的测流精度进行了考核,按照第 3 节的检测原理、算法及流程,进行了试验,分别检测了 ADL 对 6~10 m,10~14 m,14~18 m 三个不同水层的对水速度,结果如下:
|
|
表 1 第 1 航段数据结果 Tab.1 Data results of the first leg |
|
|
表 2 第 2 航段数据结果 Tab.2 Data results of the second leg |
|
|
表 3 第 3 航段数据结果 Tab.3 Data results of the third leg |
依据合速度标量消流法的原理,可得 3 个水层的 ADL 测速误差分别为:
6~10 m 水层误差值:∆V = 0.231 kn;
10~14 m 水层误差值:∆V = 0.073 kn;
14~18 m 水层误差值:∆V = 0.027 kn。
2)用矢量平均法处理试验数据,结果如下:
|
|
表 4 第 1 航段数据结果 Tab.4 Data results of the first leg |
|
|
表 5 第 2 航段数据结果 Tab.5 Data results of the second leg |
|
|
表 6 第 3 航段数据结果 Tab.6 Data results of the third leg |
依据矢量平均法的原理,可得 3 个水层的 ADL 测速误差(合速度)分别为:
6~10 m 水层误差值:∆V = 0.215 kn;
10~14 m 水层误差值:∆V = 0.014 kn;
14~18 m 水层误差值:∆V = 0.009 kn。
图 2 给出了此次试验在 6~10 m 水层、10~14 m 水层、14~18 m 水层分别用合速度标量消流法和矢量平均法处理试验数据所得的多普勒测速测流仪测流误差结果对比。
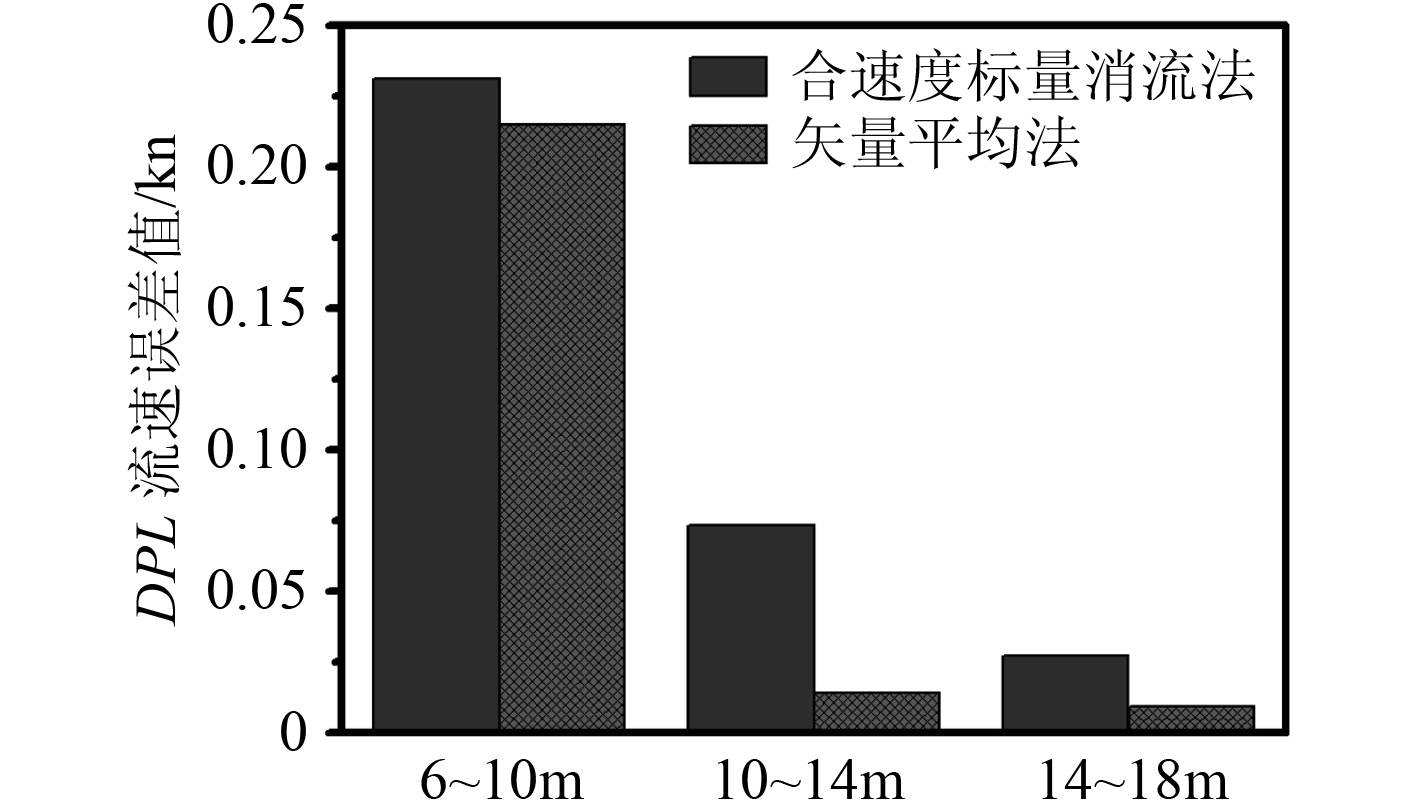
|
图 2 用合速度标量消流法和矢量平均法处理试验数据所得的多普勒测速测流仪测流误差结果对比图 Fig. 2 The experimental results for scalar dissipation method and vector averaging method |
比较 2 种方法的处理结果,3 个不同水层,矢量平均法的误差计算结果均小于标量消流法。
5 结 语本文提出了一种高精度的多普勒计程仪测流精度考核新方法,该方法能适应恶劣的试验环境条件,可有效降低设备精度评估试验过程中,风、洋流等对设备考核精度的影响。文中还理论分析了矢量平均法抗风、洋流影响的算法原理,给出了矢量平均法的试验步骤、试验原理和数据处理方法,并从理论误差计算角度,得到了其优于合速度标量消流法的结论。最后,通过海上试验结果,验证了矢量平均法比标量消流法具有更高的精度和抗外界干扰的能力。
| [1] |
邹洪, 向大威, 宣志芬, 等. 多普勒计程仪测速精度的测定[J]. 声学技术, 2002, 21 (4): 188–191.
ZOU Hong, XIANG Da-wei, XUAN Zhi-feng, et al. Speed-precision measurement for ADL[J]. Technical Acoustics, 2002, 21 (4): 188–191. |
| [2] |
GB/T 24558-2009, 声学多普勒流速剖面仪[S].
GB/T 24558-2009, Acoustic Doppler current profiler [S]. |
| [3] |
HY/T 102-2007, 声学多普勒流速剖面仪检测方法[S].
HY/T 102-2007, Test method of acoustic Doppler current profiler [S]. |
| [4] |
SL 337-2006, 声学多普勒流量测验规范[S].
SL 337-2006, Code for discharge measurement of acoustic Doppler current [S]. |
| [5] |
邹红, 向大威, 许伟杰, 等. 多普勒计程仪速度参照系统的误差分析[J]. 声学技术, 2003, 22 (3): 162–168.
ZOU Hong, XIANG Da-wei, XU Wei-jie, et al. Error analysis of speed reference system for ADL[J]. Technical Acoustics, 2003, 22 (3): 162–168. |
| [6] |
芮震峰, 陆冬青, 石爱国, 等. 一种舰船实际航速的计算方法[J]. 舰船科学技术, 2006, 28 (1): 37–40.
RUI Zhen-feng, LU Dong-qing, SHI Ai-guo, et al. A calculating method of ship’s actual speed[J]. Ship Science and Technology, 2006, 28 (1): 37–40. |
| [7] |
傅菊英, 吴炳昭. 声学多普勒计程仪测速误差分析与补偿[J]. 海洋技术, 2011, 30 (2): 91–93.
FU Ju-ying, WU Bing-zhao. Error analysis and compensation of acoustic Doppler velocity log[J]. Ocean Technology, 2011, 30 (2): 91–93. |
| [8] |
黄雄飞, 周徐昌, 苑秉成. ADCP载体运动参数的控制[J]. 舰船科学技术, 2007, 29 (5): 67–69.
HUANG Xiong-fei, ZHOU Xu-chang, YUAN Bing-cheng. The control of the parameters of shipboard with ADCP[J]. Ship Science and Technology, 2007, 29 (5): 67–69. |
 2017, Vol. 39
2017, Vol. 39
