0 引　言

故障诊断系统是先进船舶控制系统的重要工具^{[1 – 2]}。为保障船舶系统安全运行，当船舶设备发生故障时，需及时准确地识别出现的异常。由于船舶动力系统的故障具有多样性，设备相互关联导致故障机理复杂，且反映故障的各种特征参数也不尽相同，给核动力船舶设备故障诊断带来很大困难。因此需要采用有效的方法进行故障诊断。

目前核动力船舶设备故障诊断的主要方法是依靠运行人员的经验或穷举方法进行诊断排除^[3]。随着人工智能技术的不断应用与发展，神经网络、模糊系统、小波分析等方法逐步开始应用于故障诊断^{[4 – 7]}。但由于核动力船舶系统故障样本故障数据相对于正常数据较少，甚至根本无法获得完整有效的故障样本，上述方法在原理上无法保证诊断结果的正确性，有必要研究一种新的故障诊断方法，为核动力船舶设备故障诊断提供更多的工具和方法。概率因果^{[8 – 9]}诊断模型已基本成功应用于各个领域的故障诊断，能够解决故障样本少的根本问题，其原理是通过 Bayes 定理在已知征兆集前提下，计算后验概率求得故障诊断的最优解。因此，本文利用概率因果模型（Probability Casual Model，PCM）将核动力船舶设备的故障诊断问题转化为最优化求解问题。由于模型的高度非线性特点及传统遗传算法存在的缺陷和不足，采用信息熵免疫遗传算法^[10]（Information Entropy Immune Genetic Algorithm，IEIGA）对模型进行最优化求解避免算法出现“早熟”，提高算法寻优速度，确保快速收敛于全局最优解。

1 数学描述

概率因果理论是在概率论基础上发展起来的因果推理模型，能够实现多故障的综合诊断。定义核动力船舶设备故障诊断问题为一个概率因果网络，表示为：

　　　　　　　 ${\rm{P}}\left( {{{\rm{D}}_0}} \right) = \left\langle {{\rm{D}},\;{\rm{M}},\;{\rm{C}},\;{{\rm{M}}^ + }} \right\rangle $ 。

式中： $D = \left\{ {d_1},\;{d_2},\; \ldots ,\;{d_n} \right\}$ 为有限非空故障集合，代表核动力船舶设备原因事件； $M = \left\{ {{m_1},\;{m_2},\; \ldots ,\;{m_k}} \right\}$ 为有限非空征兆集合，代表核动力船舶设备结果事件； $C \subseteq D \times M$ 为定义在 $D \times M$ 上的关系集，代表故障与征兆之间的因果关系； ${M^ + } \subseteq M$ 是 M 的一个子集，代表已知存在的征兆集合；D ₀ 为问题的解，是通过竞争机制实现最高后验概率的故障集合。

应用概率因果理论进行核动力船舶设备故障诊断需有如下定义及假设：

①定义

${d_i} \in D$ 表示故障 d _i 存在， $\overline {{d_i}} $ 表示故障不存在；

${m_j} \in M$ 表示征兆 m _j 存在， $\overline {{m_j}} $ 表示征兆不存在；

${m_j}:{d_i}$ 表示因果事件：故障 d _i 引起征兆 m _j ；

${C_{ij}} = P\left( {{m_j}:{d_i}{\rm{|}}{d_i}} \right)$ 表示 ${m_j}:{d_i}$ 发生的条件因果概率。

②假设

1）所有先验概率 ${\rm{P}}\left( {{{\rm{d}}_{\rm{i}}}} \right)$ 已知，根据长期经验积累确定；所有条件因果概率 C _ij 已知，根据故障的特征参数归一化确定。

2）一个原因事件的发生独立于其他原因事件。即对任何 $\left( {{d_1},\;{d_2},\; \cdots {d_n}} \right) \in D$ ，式（1）成立。

$P\left( {{d_1} \wedge {d_2} \wedge \cdots \wedge {d_n}} \right) = P\left( {{d_1}} \right) \cdot P\left( {{d_2} \wedge {d_3} \wedge \cdots \wedge {d_n}} \right)\text{。}$

(1)

3）因果事件 ${m_j}:{d_i}$ 的发生独立于任何其它因果事件。

在以上假设基础上，根据 Bayes 概率理论，核动力船舶设备故障诊断问题理解为：已知所有设备故障 ${d_i} \in D$ 的先验概率 $P\left( {{d_i}} \right)$ 和所有因果事件 ${m_j}:{d_i}$ 的条件因果概率 C _ij ，在已知征兆集 M⁺ 的前提下，求最大后验概率的故障集合 D ₀。即

$P({D_0}\left| {{M^ + }} \right.) = \mathop {\max }\limits_{{D_l} \subseteq D} P({D_l}\left| {{M^ + }} \right.)\text{，}$

(2)

根据 Bayes 公式：

$P({D_l}\left| {{M^ + }} \right.) = \frac{{P({M^ + }\left| {{D_l}} \right.) \cdot P({D_l})}}{{P({M^ + })}}\text{，}$

(3)

式中 ${\rm{P}}\left( {{{\rm{M}}^ + }} \right)$ 为常数。

根据假设2：

$\begin{split}P({D_l}) =& P((\mathop \wedge \limits_{{d_i} \in {D_l}} {d_i}) \wedge (\mathop \wedge \limits_{{d_i} \in D - {D_l}} {\overline d _i}))=\\[3pt]& \textstyle\mathop \prod \limits_{{d_i} \in {D_l}} P({d_i}) \cdot \mathop \prod \limits_{{d_i} \in D - {D_l}} (1 - P({d_i}))=\\[3pt]&\textstyle \mathop \prod \limits_{{d_i} \in {D_l}}\frac{{P({d_i})}}{{1 - P({d_i})}} \cdot \mathop \prod \limits_{{d_i} \in D} (1 - P({d_i}))\text{，}\end{split}$

(4)

式中 $\mathop \prod \limits_{{d_i} \in D} (1 - P({d_i}))$ 为常数。

根据假设3：

$\begin{aligned}P({M^ + }\left| {{D_l}} \right.) = \textstyle\mathop \prod \limits_{{m_j} \in {M^ + }} P({m_j}\left| {{D_l}} \right.) \cdot \mathop \prod \limits_{{m_j} \in M - {M^ + }} P({\overline m _j}\left| {{D_l}} \right.)=\\[3pt]\textstyle\mathop \prod \limits_{{m_j} \in {M^ + }} (1 - \mathop \prod \limits_{{d_i} \in {D_l}} (1 - {C_{ij}})) \cdot \mathop \prod \limits_{{m_j} \in M - {M^ + }} \mathop \prod \limits_{{d_i} \in {D_l}} (1 - {C_{ij}})\text{，}\end{aligned}$

(5)

由式（3）～式（5）得到：

$\begin{aligned}P({D_l}\left| {{M^ + }} \right.) = \alpha \cdot \textstyle\mathop \prod \limits_{{m_j} \in {M^ + }} (1 - \mathop \prod \limits_{{d_i} \in {D_l}} (1 - {C_{ij}}))\text{× } \\ \textstyle\prod \limits_{{m_j} \in M - {M^ + }}\mathop \prod \limits_{{d_i} \in {D_l}} (1 - {C_{ij}}) \cdot \mathop \prod \limits_{{d_i} \in {D_l}} \frac{{P({d_i})}}{{1 - P({d_i})}}\text{。}\end{aligned}$

(6)

式中 $\alpha = \frac{1}{{P({M^ + })}}\mathop \prod \limits_{{d_i} \in {D_l}} (1 - P({d_i}))$ 为常数。第 1 项反映了故障集 D ₁ 引起征兆集 M⁺ 发生的程度，第 2 项反映了故障集 D ₁ 引起征兆集（M – M⁺）发生的程度，第 3 项代表由故障集 D ₁ 的先验概率组成的加权。针对该模型的复杂性特点，采用免疫遗传算法最大后验概率的故障集合。

2 基于信息熵的免疫遗传算法

与标准遗传算法相比，免疫遗传算法结合了生物免疫原理与传统遗传算法的优点：视求解核动力设备故障诊断问题的目标函数和约束条件为抗原，视优化的故障可行解为抗体，当抗原首次入侵时，免疫器官和免疫细胞产生大量不同的抗体，从而保证了抗体的多样性；此后保存记忆细胞，记忆细胞分泌抗体，体现了抗体的记忆性；免疫系统的自我调节能力使抗体的浓度越高越抑制，浓度越低越促进，以保持抗体的多样性和均衡性，体现了抗体的抑制性和促进性。抗体多样性提高了免疫遗传算法的全局寻优能力，防止陷入局部解；利用抗体的免疫记忆功能，可以直接从数据库中产生可行解，改善了搜索速度。抗体的抑制和促进作用，有助于消除多余的解并克隆新的可行解，提高了局部搜索能力。本文用信息熵^[11]表示抗体间亲和度和浓度，根据聚合亲和度的概念来实现抗体群的自我调节和多样性保持。

将 IGA 应用于核动力船舶设备故障诊断问题，定义概率因果模型得到的似然值函数 $P\left( {{D_l}{\rm{|}}{M^ + }} \right)$ 最大为抗原，计算过程中故障集合 D _l 中间结果为抗体，求取故障集合 D ₀，使 $P\left( {{D_l}{\rm{|}}{M^ + }} \right)$ 最大。

2.1 基本流程

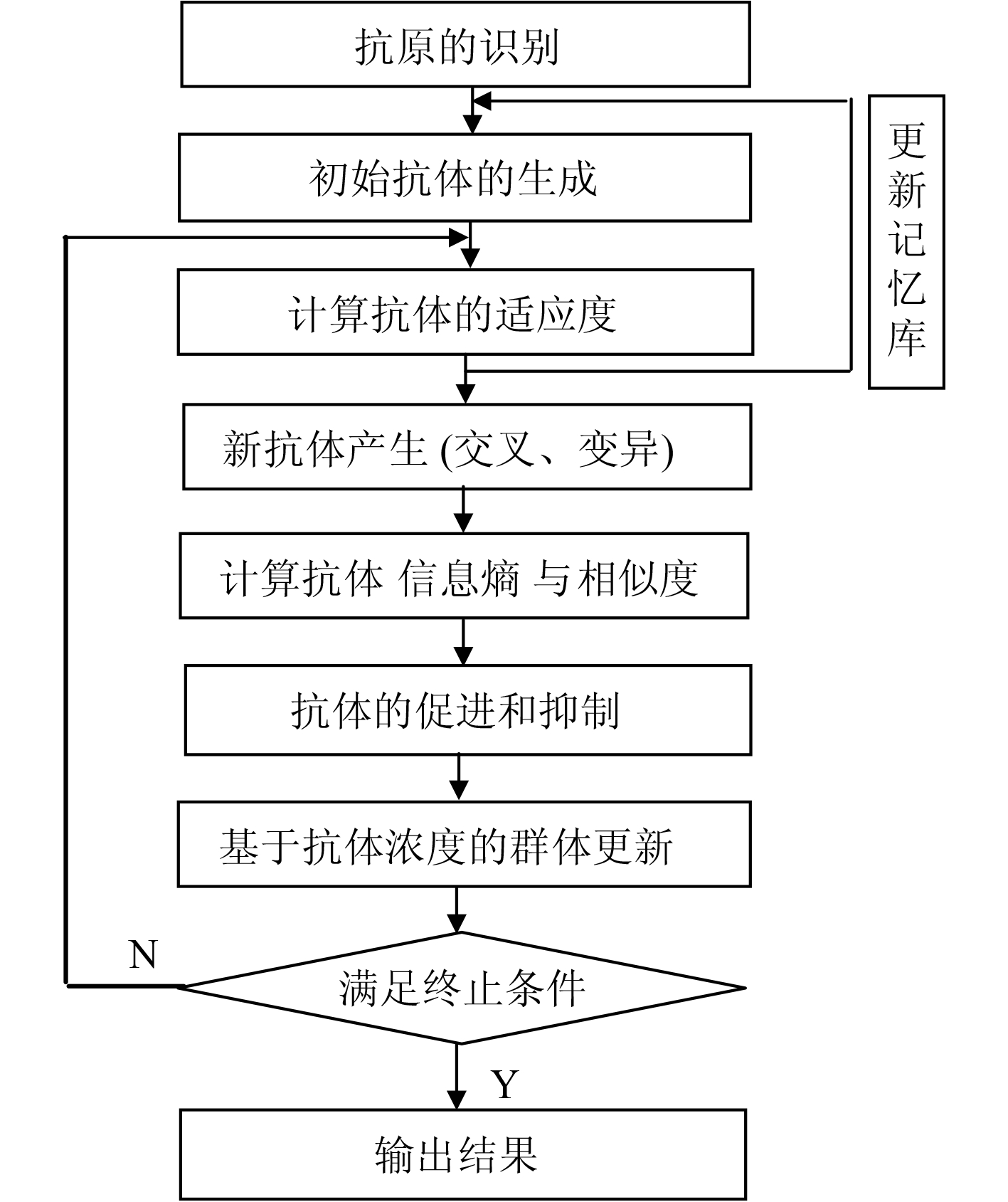
免疫遗传算法的基本流程如图 1 所示。

2.2 初始抗体生成

采用二进制编码方式表示故障集 D，假设每个染色体编码的二进制位数等于故障总数，1 表示设备故障发生，0 表示设备故障未发生，每个染色体中所有值为 1 的故障构成了故障诊断的一个可行解 D ₁。例如染色体编码“010010001”表示故障总数为 9，发生的故障为 {2，5，9}。

2.3 抗体与抗原的亲和度

抗体与抗原的亲和度表示为传统遗传算法的适应度，采用概率因果模型得到的似然值函数 $P\left( {{D_l}{\rm{|}}{M^ + }} \right)$ 代表了适应度大小，用来评价群体中个体的好坏。适应度值 $P\left( {{D_l}{\rm{|}}{M^ + }} \right)$ 越大，表示故障集合的后验概率越大。

2.4 信息熵

假设免疫系统由 E 个抗体组成，每个抗体基因长度为 F，定义 p _k 为基因符号编码出现在基因 k 上的概率， ${H_k}\left( E \right)$ 为第 k 个基因的信息熵：

${H_k}\left( E \right) = - \mathop \sum \limits_{{\rm{h}} = 1}^{\rm{E}} {p_k}\log \left( {{p_k}} \right)\text{，}$

(7)

则 E 个抗体的平均信息熵为：

$H\left( E \right) = \frac{1}{F}\mathop \sum \limits_{{\rm{k}} = 1}^{\rm{F}} {H_k}\left( E \right)\text{。}$

(8)

2.5 抗体与抗体的亲和度

抗体与抗体亲和度体现了抗体间的相似水平，2 个抗体 a 和 b 的亲和度表示为：

${A_{ab}} = \frac{1}{{1 + H\left( 2 \right)}}\text{，}$

(9)

其中 H（2）为抗体 a 和 b 的平均信息熵。

定义 E 个抗体的相似度为 A（E）：

${\rm{A}}\left( {\rm{E}} \right) = \frac{1}{{1 + H\left( E \right)}}\text{。}$

(10)

A（E）越大，群体相似程度越高，多样程度越低。

2.6 抗体浓度

抗体的浓度 J _a 表示为相似抗体所占种群的比例：

${J_a} = \frac{{{A_{ah}}}}{E}\text{，}$

(11)

式中： A _ah 为与抗体 a 亲和度大于 λ 的抗体的总；λ 为自定义常数。

聚合亲和度 A’ _ab 是抗体的亲和度 A _ab 与浓度 J _a 均衡评价的结果，即

${A_{ab}}' = \frac{{{A_{ab}}}}{{1 + \varepsilon \ln \left( {1 + {J_a}} \right)}}\varepsilon > 0\text{。}$

(12)

由式（12）可知，抗体浓度 J _a 一定时，亲和度 A _ab 越大，聚合亲和度 A’ _ab 越大，抗体被选择概率越大；亲和度 A _ab 一定时，抗体浓度 J _a 越大，聚合亲和度 A’ _ab 越小，抗体被选择的概率越小，既有效保留了高亲和度的抗体，又抑制了高浓度的抗体。

3 应用实例

为了验证所提出的模型和方法的可行性，给出以下 2 个诊断实例：

1）实例 1。 表 1 数据来自某船舶核动力装置蒸汽发生器典型故障样本集^[12]，其中 d ₁ ～ d ₇ 代表 7 种不同的蒸汽发生器故障，m ₁ ～ m ₁₃ 为 13 种不同的征兆，P（d _i ）为各个故障发生的先验概率，其他数值为故障 d _i 和征兆 m _j 间的因果强度 C _ij ，为区分征兆集在故障时所处的状态而设置。0.5 代表正常运行，1.0 代表上限关机，0.0 代表下限关机值，0.75 和 0.25 代表上下报警状态。当船舶核动力蒸汽发生器出现征兆 0.5，0.25，0.29，0.75，0.5，0.5，0.5，0.5，0.5，0.5，0.25，0.75，0.75 时，利用上述算法完成对核动力蒸汽发生器的故障诊断。

设置 IGA 种群大小为 40，染色体长度为 7，交叉率为 0.7，变异率为 0.07。经过 5 次迭代，适应度函数取得最大值 3.0 × 10 ^–4，获得染色体编码为 0000001，判断故障 {d ₇} 发生。结果与文献[12]一致。

由图 2 可看出，适应度函数以较快的速度收敛到最优解。图 3 来自文献[12]。将两图进行对比可以发现，对于同一设备同一故障诊断问题，在相同计算精度下，基于信息熵的免疫遗传算法需要更少的迭代次数，更快的收敛速度。

2）实例 2。 表 2 数据来自文献[3]某船用核动力液压泵故障和征兆的样本集，其中d ₁ ～ d ₁₀ 为 10 种不同的液压泵故障，m ₁ ～ m ₉ 为 9 种不同的征兆，P（d _i ）为各个故障发生的先验概率，其他数值为故障 d _i 和征兆 m _j 间的因果强度 C _ij ，是故障状态下振动加速度信号小波包分解后，对特征频段进行归一化的结果。在核动力液压泵出现 m ₁，m ₆，m ₇，m ₈ 4 种征兆时，利用上述算法完成对核动力液压泵的故障诊断。

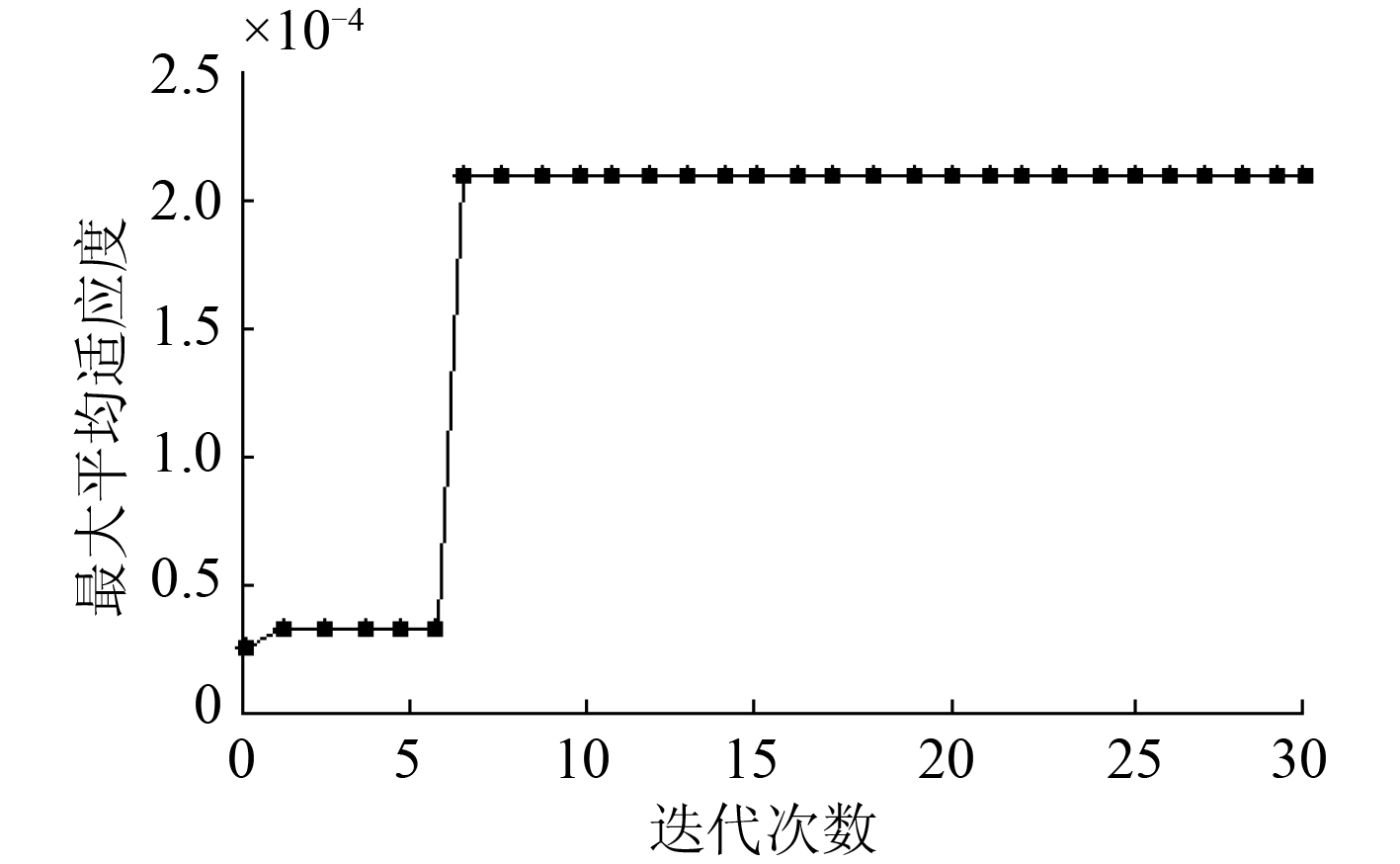
设置 IGA 种群大小为 40，染色体长度为 10，交叉率为 0.7，变异率为 0.07。经过 5 次迭代，适应度函数取得最大值 2.1 × 10 ^–3，获得染色体编码为 1000010000，判断故障 {d ₁，d ₆} 发生，与文献[3]计算结果一致，验证了本算法的准确可行性。

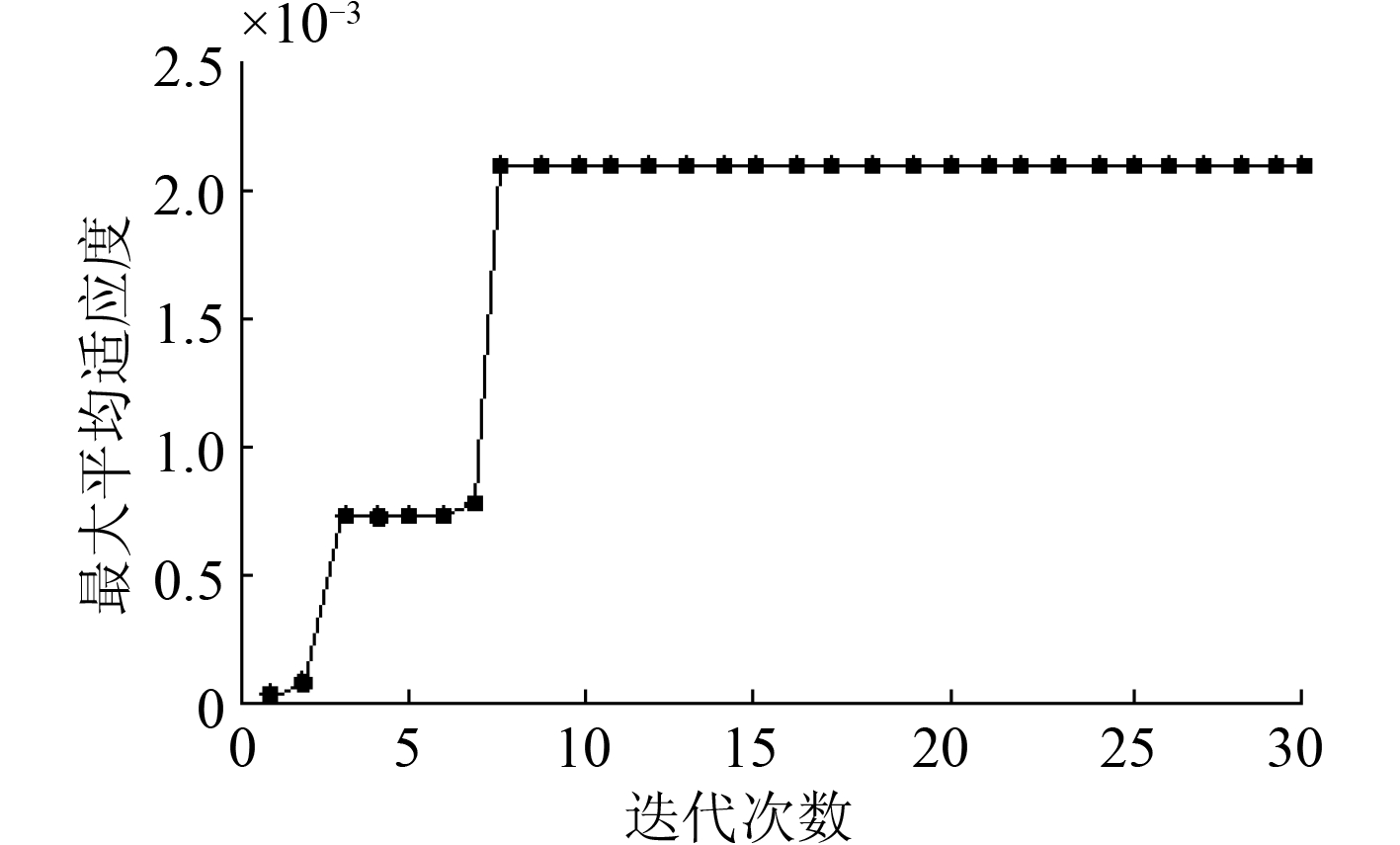
由图 4 可看到，适应度函数的最优解能够以较快的速度收敛到稳态值；图 5 为与文献 3 应用入侵性野草算法的计算结果，将两图进行对比可以发现，对于同一设备同一故障诊断问题，在相同计算精度下，本文提出方法需要更少的迭代次数，更快的收敛速度。

由以上 2 个算例可看出，针对不同的故障诊断实例，基于信息熵免疫遗传算法优化的概率因果模型不受故障样本的限制，具有较好的通用性，且模型故障诊断精度较高、寻优速度快。

4 结　语

1）针对船舶核动力设备故障诊断样本少的问题，应用概率因果模型将故障诊断问题转化为最大后验概率优化求解问题，能够避免运行人员依据经验判断错误及穷举方法导致的典型 NP（Non-deterministic Polynomial）问题。仿真结果表明：该模型不受限于具体的故障样本，适应于其他领域设备的故障诊断问题。

2）应用信息熵免疫遗传算法计算概率因果模型的最优解，视概率因果模型的似然值函数为抗原，视求解的故障为抗体。本方法收敛速度较快，寻优速度优于其他智能优化算法。