2. 江苏科技大学,江苏 镇江 212003
2. Jiangsu University of Science and Technology, Zhenjiang 212003, China
舰艇管路系统的冲击破坏是一个不容忽视的问题,诸多战例和试验情况表明,舰艇管路系统对冲击载荷作用非常敏感,遭受冲击载荷后通常会引起管路系统应力或变形过大而破坏,导致相关的设备基本功能丧失的严重后果[1]。裂纹和腐蚀是大多数结构最为常见的一种损伤缺陷,它的存在可能造成局部应力集中,而使裂纹发生失稳扩展,降低结构的极限承载能力。因此,采用恰当的方法建立合理的剩余极限强度计算模型,以考察冲击载荷作用下,裂纹和腐蚀损伤对舰艇管路结构强度的影响,这对舰艇的安全性和战斗力评估具有重要的意义。
目前国内关管路系统剩余强度研究主要集中在油气管道的剩余强度研究,针对船舶管路的研究比较少。文献[2 – 6] 基于有限元分析腐蚀影响下的管道剩余强度进行了评估,从腐蚀模型、计算方法选择、有限元建模技术等方面对管道剩余强度进行对比分析,为船舶管路时变剩余强度研究提供了理论基础,但是裂纹和腐蚀作为常见结构损伤缺陷,研究中没有考虑腐蚀和裂纹的共同作用;文献[7 – 10] 分别建立了船舶在全寿命期的腐蚀疲劳模型,对结构剩余寿命进行了评估和预测,并推导出船体极限强度分析的简化逐步破坏法流程。研究针对的是船体或局部船体结构,不考虑内部管路系统。而在冲击载荷作用下,腐蚀裂纹损伤下船体管路更容易破坏而失去作战能力。建立合理的船舶管路系统裂纹和腐蚀模型,研究管路系统受到冲击载荷作用下的极限强度是保证作战能力可靠性的重要手段。
因此,针对典型管路系统管路段,建立仿真精度较高的典型管路有限元模型,基于时域分析方法对管路系统三向抗冲击性能进行分析,确定抗冲击薄弱环节(称之为关键节点或关键结构)。在此基础上,给出腐蚀、裂纹2种因素联合作用下,舰艇管路系统关键构件或关键节点剩余强度的计算方法。研究成果可以为船舶管路的设计和优化提供可靠的理论依据,有效预防腐蚀裂纹下结构损伤带来的严重后果,对社会经济发展和军事实力提高有着重要的现实意义;同时,该研究方法对石油、海工、天然气等管道研究有一定借鉴意义。
1 管路抗冲击时变剩余强度分析关键技术 1.1 抗冲击时域分析方法时域分析指控制系统在一定的输入下,根据输出量的时域表达式,分析系统的稳定性、瞬态和稳态性能[7]。与其他分析方法相比,时域分析放在管路系统冲击研究方面更加直观、准确。管路系统抗冲击时域求解方程可表示为:
| $\left[{M} \right]\left\{ {\ddot x\left( t \right)} \right\} + \left[{C}\right]\left\{ {\dot x\left( t \right)} \right\} + \left[{K}\right]\left\{ {x\left( t \right)} \right\} = \left[{E}\right]\left\{ {F(t)} \right\}\text{。}$ | (1) |
式中:
采用中心差分法求解方程(1),得到管路系统速度、加速度、位移响应。在用中心差分法求解时,所取时间步长要足够小,才能满足精度要求。步长越小,求解步骤就越多,那么方程单元矩阵阶数越高,就有可能导致求解结果不收敛的情况。这种情况是不可避免的,因此采用合理单元建立有限元模型,划分网格,有效的边界处理对于计算结果的准确性至关重要。
1.2 管路时变剩余强度预报模型 1.2.1 裂纹扩展 Paris 公式对中船重工澄西船舶修造有限公司船舶管路维修资料进行统计,表明管路系统破环原因之一是由于在外力反复作用下,裂纹沿着其深度方向不断扩展贯穿板厚,导致管路形成穿透裂纹而发生断裂,破环形式以疲劳破坏为主。在船舶受到瞬时冲击载荷时,空间管路系统在交互应力下尤其容易发生疲劳破坏,因此本文根据断裂力学的 Paris 方程[11] 计算裂纹深度随服役年限变化。
| $\frac{{{\rm{d}}a}}{{{\rm{d}}N}} = C\Delta {K^m}\text{,}$ | (2) |
| $\Delta K = \Delta \sigma Y\left( a \right)\sqrt {{\rm{\rm{\pi }}} \cdot a}\text{。}$ | (3) |
式中:ΔK 为应力强度因子;a 为裂纹长度;Δσ 为特定工况下的应力范围;N 为应力循环次数;Y(a) = 1 为几何形状因子保持不变;C 为材料系数呈正态随机分布
对式(2)积分,得到m = 2 时裂纹扩展的 S-N 曲线表达式
| $a\left( N \right) = {a_0}{\rm{exp}}\left( {C\Delta {\sigma ^2}{Y^2}{\rm{\pi }}N} \right)\text{。}$ | (4) |
目前,线性腐蚀模型被广泛应用于油气管路剩余寿命和极限强度研究中,采用线性模型的前提是假设管道处于稳定腐蚀的状态,由于船舶管路在工作时受到压力、温度、外界载荷以及本身结构特点等多重因素影响,腐蚀必定是一个非线性的过程,因此建立管路非线性腐蚀模型能更科学地模拟腐蚀过程。
Caleyo[12] 提出了模拟管道腐蚀的非线性幂函数模型,该模型考虑到管道防护和所处的环境,使用更灵活。幂函数模型表达的最大腐蚀深度为:
| $d\left( T \right) = k{\left( {T - {T_0}} \right)^a}\text{。}$ | (5) |
式中,T 0 腐蚀时间初始点;T 为腐蚀时间;k、a 为待定系数。
1.3 腐蚀裂纹损伤下管路剩余强度分析方法本文采用有限元实体建模、冲击时域分析法、逐步破坏弧长法,对全寿命期内管路系统损伤下的时变剩余强度进行研究,将有限元嵌套技术、裂纹扩展 Paris-Erdogen 方程、腐蚀非线性数学模型理论应用于研究,采用实体建模技术建立精度较高的管路系统整体有限元模型,进行抗冲击非线性分析,确定冲击载荷作用下的管路系统抗冲击薄弱环节。将不同服役年限的腐蚀厚度和疲劳裂纹长度作为剩余极限强度分析的变量,建立管路系统时变剩余强度预报模型。船舶管路系统剩余强度的计算方法和实现流程如图 1 所示。
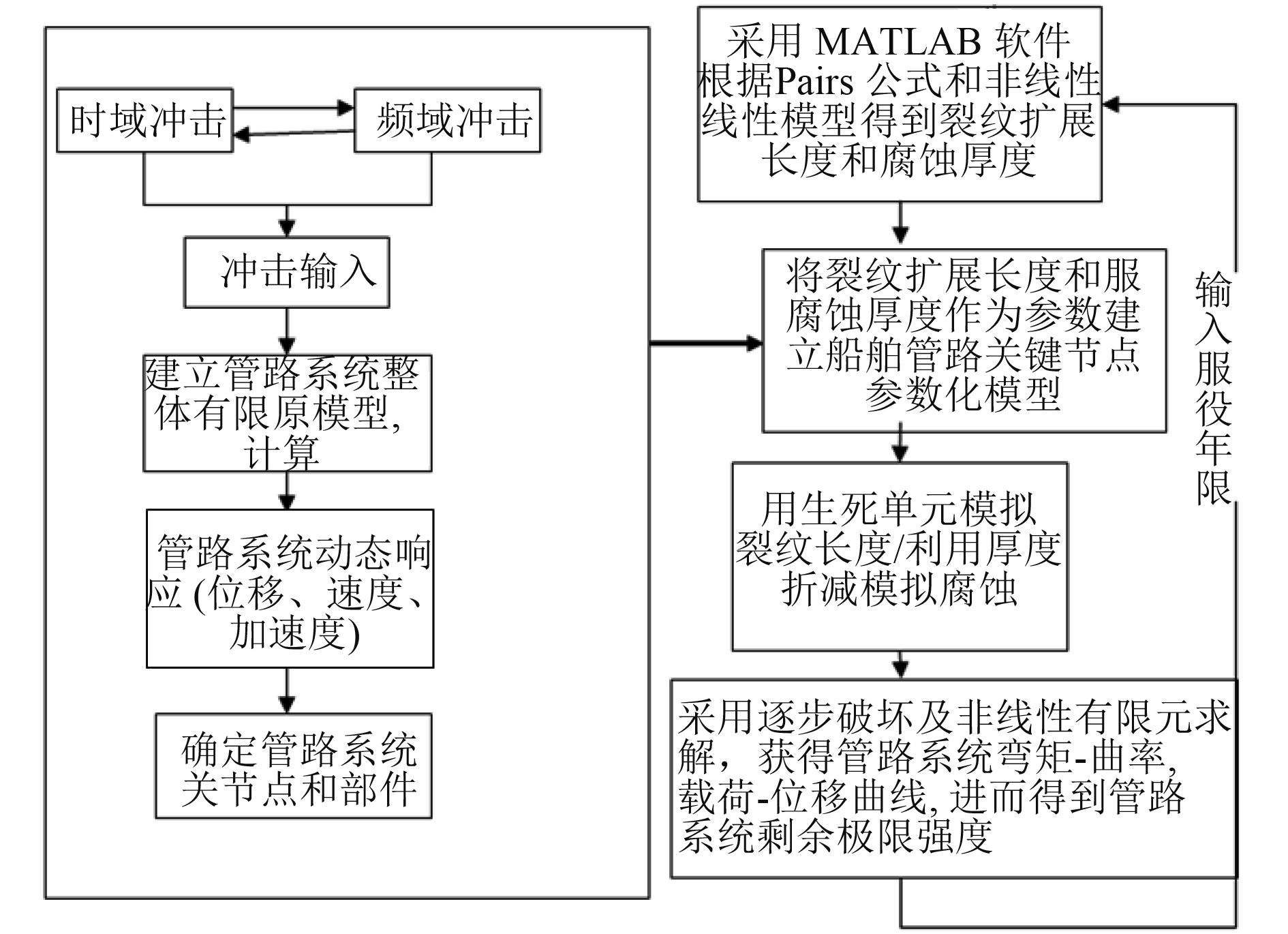
|
图 1 管路系统剩余强度的计算方法 Fig. 1 Calculation method of residual strength of pipeline system |
采用元器件局部模型与整体模型的嵌套技术,建立管路系统的整体有限元模型。选取船舶典型空间管路段,利用实体建模技术,采用四节点壳单元划分管路有限元模型、实体单元划分管路元器件,根据管路实际布设特点,采用 TARGE170,CONTA175 面——面接触单元模拟螺栓、法兰连接、马板、吊架、套管等连接方式,采用弹簧单元简化管路系统与船体弱连接问题,建立整体有限元模型,管路弹性模量 E = 2.06 GPa,泊松比为 0.3,模型共划分 23 891 个单元,38 212 个节点。
根据图 1 所示的管路系统剩余强度的计算方法,利用逆傅里叶公式[1] 将最大谱加速度转化为时域冲击加速度作为冲击输入,在实际工作中,该输入相当于外界的冲击或者爆破载荷。为了研究管路系统三维冲击特性,选择 100 g 垂向、纵向、横向冲击载荷作为初始输入,分别计算 3 种输入工况下的管路系统非线性响应。在结果中提取 3 种工况下位移最大处的加速度、一次应力进行分析。本文给出垂向冲击下最大位移和应力响应如图 2 和图 3 所示,抗冲击仿真结果如表 1 所示。
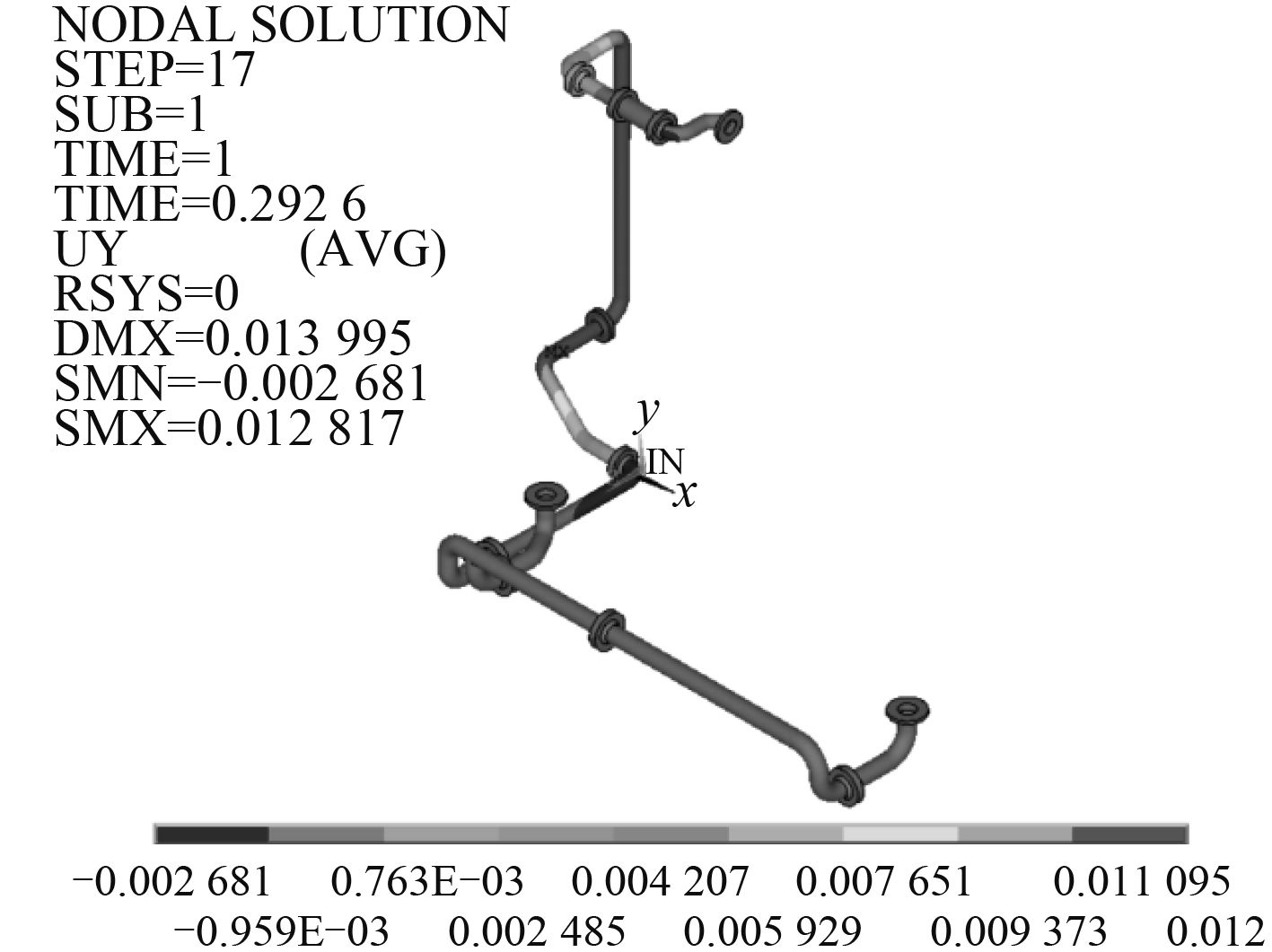
|
图 2 垂向冲击下最大位移响应 Fig. 2 Maximum displacement under vertical impact |

|
图 3 垂向冲击下应力响应 Fig. 3 Stress response under vertical impact |
|
|
表 1 不同冲击载荷下空间管路动力响应 Tab.1 Dynamic response of space pipeline under different impact loads |
根据表 1 计算结果,在管路系统受到垂向冲击时,位移和应力的最大值处于垂直立管的弯管处;受到纵向冲击时,位移和应力的最大值位于法兰处;受到横向向冲击时,应力的最大值处于支管连接处。据此,可以确定 3 种不同冲击工况下管路系统的关键部位,将关键部位应力峰值点作为裂纹扩展的起点,服役年限内裂纹扩展深度和腐蚀厚度作为变量参数,基于 APDL 语言建立船舶管路系统关键部位有限元模型。
2.2 剩余极限强度分析的变量 2.2.1 裂纹扩展长度SH/T3059-2012《石油化工管道设计器材选用通则》明确规定:管道设计寿命宜为 15 年,考虑到管道的安全系数,因此研究设计管路系统服役年限为 20 年。假定初始裂纹深度 a 0 服从极值分布,根据平台抗冲击仿真结果:垂向、横向、纵向冲击载荷作用下管路的应力幅(最大应力-最小应力)分别 215 MPa,134 MPa,257 MPa,采用 Matlab 软件编程计算裂纹深度随管道寿命变化,不同工况下裂纹深度随服役年限的变化曲线如图 4 所示。

|
图 4 裂纹深度随服役年限的变化曲线 Fig. 4 Variation curve of crack depth with service life |
以上研究结果表明:裂纹扩展速率在服役前期比较缓慢,后期扩展速率加快;船舶管路在垂向、纵向、横向冲击载荷作用下的裂纹扩展长度分别为 8 mm、3.3 mm、4.1 mm,裂纹扩展对垂向冲击载荷比较敏感,因此确定垂向冲击载荷为管路系统时变剩余强度研究的主载荷。
2.2.2 腐蚀厚度考虑到管道防护,取腐蚀时间初始点T 0 = 1,根据油气管路腐蚀统计数据[12],取 k = 2.84;a = 0.05,最大腐蚀深度随服役年限的变化规律如表 2 所示。
|
|
表 2 时变腐蚀厚度 Tab.2 Corrosion thickness with service life |
采用 Ansys 生死单元模拟裂纹,厚度折减模拟腐蚀厚度,研究腐蚀裂纹2种因素共同作用下的船舶管路抗冲击时变剩余强度。为了保证能够获得出现拐点的管路系统弯矩-曲率,载荷-位移曲线,选择 200 g 冲击载荷作为初始输入,采用非线性弧长法[13] 求解,在求解过程中,通过合理选择步长、采用四边形网格单元、细化裂纹处网格等方法不断尝试,保证最终结果收敛。纵向、横向冲击载荷作用下的管路系统时变剩余强度计算方法类似。
服役第 6 年,船舶管路在垂向冲击时的弯矩-曲率曲线如图 5 所示,极限弯矩为 3.65 × 10 8N·m。全寿命期内,腐蚀裂纹损伤下船舶管路垂向、纵向、横向抗冲击时变剩余强度用弯矩来表示,如图 6 所示。
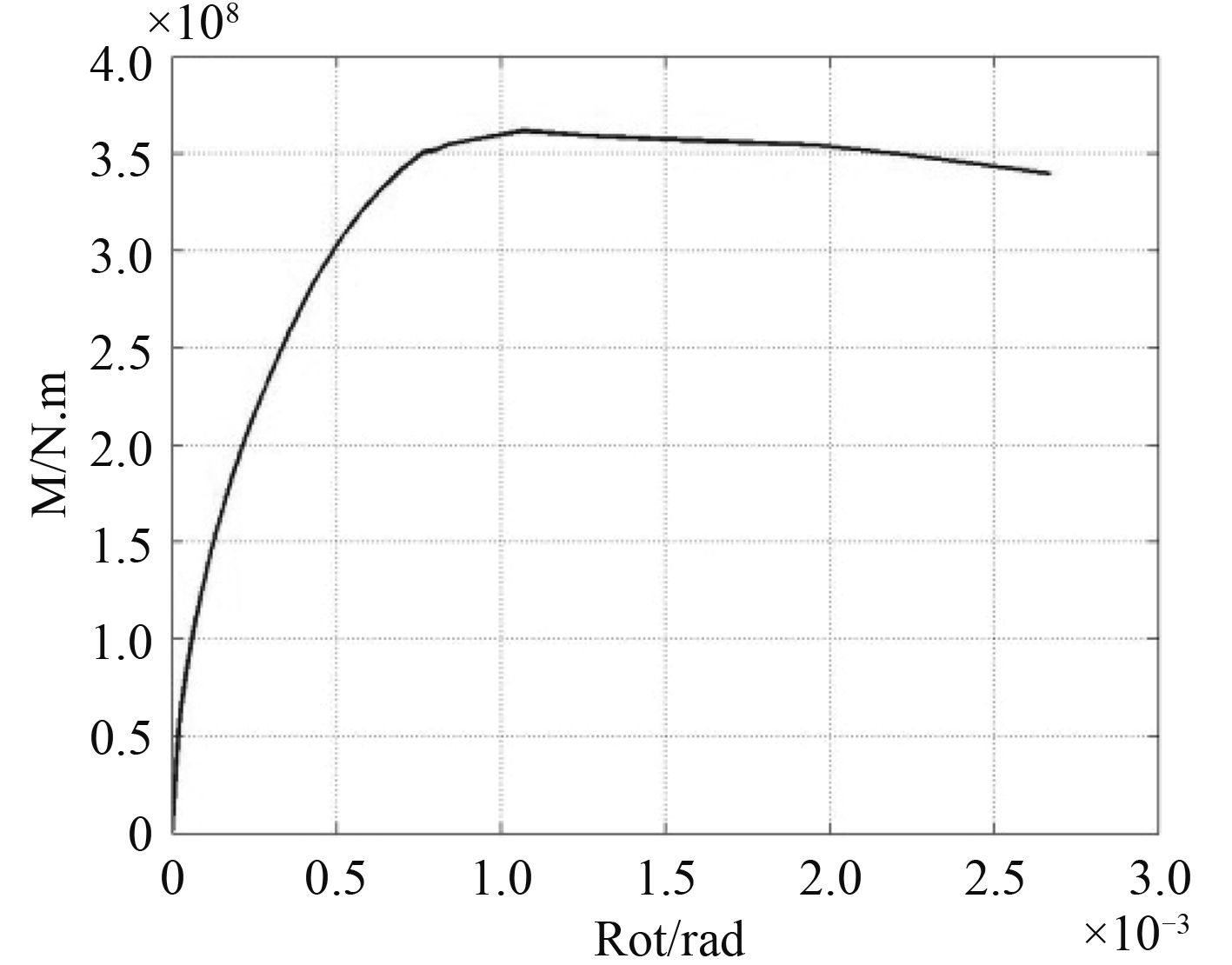
|
图 5 垂向冲击时的弯矩-曲率曲线 Fig. 5 Moment-curvature curve of vertical impact |
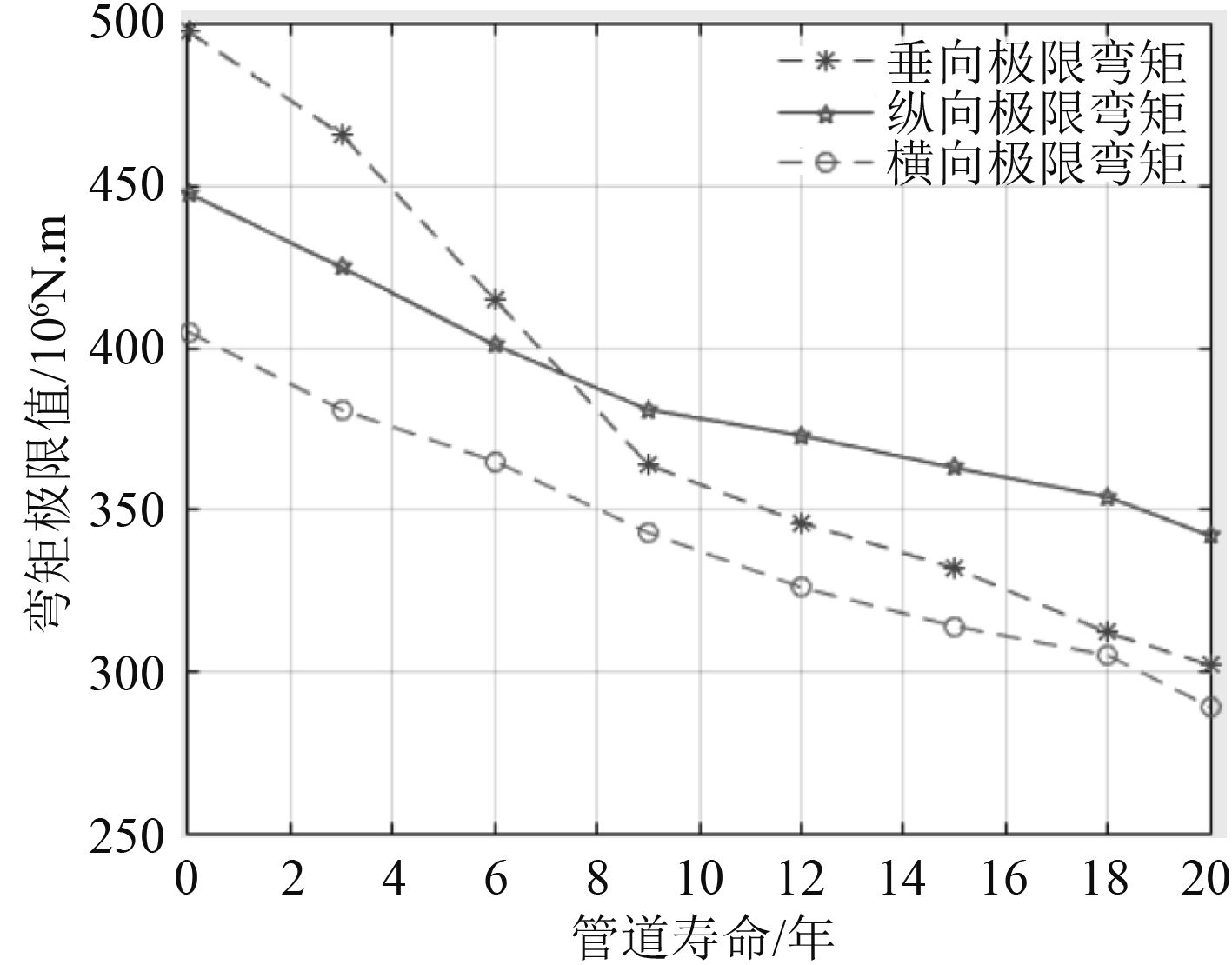
|
图 6 舰船管路时变剩余强度 Fig. 6 Residual strength of marine pipeline |
对腐蚀和裂纹损伤下空间管路系统在不同方向冲击载荷作用下极限承载力计算结果进行分析,得到以下结论:
1)管路系统在无损条件下的垂向、纵向、横向冲击载荷作用下的极限弯矩分别为 4.98 × 10 8N·m、4.48 × 108N·m、4.05 × 108N·m,管路的垂向抗冲击性能最好,其次是纵向抗冲击性能,横向抗冲击性能最差。
2)随着服役年限的增长以及腐蚀裂纹的影响,冲击极限载荷整体呈下降趋势,服役 20 年后,极限弯矩分别下降为 3.02 × 10 8N·m,3.42 × 108N·m,2.89 × 108N·m,下降了 39.3%,23.6%,28.6%,说明腐蚀裂纹损伤对管路的垂向抗冲击性能影响较大,其次是横向抗冲击性能,对纵向抗冲击性能影响不大。
3)由图 6 可知,管路系统在服役前 10 年,极限强度呈线性下降趋势,服役后期极限强度下降趋于平缓,因此要加强管路系统在服役前期的腐蚀裂纹防护。
3 结 语本文采用实体建模技术建立了仿真精度较高的典型管路系统有限元模型,根据典型管路系统抗冲击仿真结果,确定管路结构强度的薄弱节点或分段;基于管路系统腐蚀和裂纹的发展规律建立管路裂纹扩展模型和非线性腐蚀模型;基于有限元计算方法,建立管路系统时变剩余强度预报模型,发展一种分别计及腐蚀、裂纹2种因素作用下,舰艇管路系统在三向冲击载荷作用下的剩余强度的计算方法和实现流程。
通过研究得知:管道的裂纹扩展对垂向冲击载荷比较敏感。无损条件下管路的垂向抗冲击性能最好,其次是纵向抗冲击性能,横向抗冲击性能最差;在舰艇作战时,提高纵向和横向抗冲击性能是保证其战斗力的有效措施。腐蚀裂纹损伤对管路的垂向抗冲击性能影响较大,其次是横向抗冲击性能,对纵向抗冲击性能影响不大,因此服役中的舰艇管路的垂向抗冲击性能要重点评估。管路系统在服役前期,极限强度呈线性下降趋势,服役后期极限强度下降趋于平缓,因此要加强管路系统在服役前期的腐蚀裂纹防护。
在后续研究中,还应考虑管内压力,重力载荷以及温度变化对管路的影响,结合实际情况,针对三维冲击载荷随机作用下的管道冲击性能进行分析。
| [1] |
沈晴晴. 典型管路系统抗冲击性能仿真评估研究[D]. 镇江: 江苏科技大学, 2012.
SHEN Qing-qing. Simulation and evaluation method for shock resistant of typical pipeline system[D]. Zhenjiang: Jiangsu University of Science and Technology, 2012. |
| [2] |
高启荣, 淡勇. 含腐蚀缺陷管道剩余寿命预测方法研究[J]. 石油化工设备, 2014, 42 (1): 15–17.
GAO Qi-rong, DAN Yong. Study of Life-Span Prediction for Oil and Gas Piping Containing Corrosion Defects[J]. Petro-chemical Equipment, 2014, 42 (1): 15–17. |
| [3] |
张旭呁, 韩军. 基于ANSYS有限元的外腐蚀管道剩余强度和剩余寿命的研究[J]. 化工机械, 2014, 40 (5): 639–641.
ZHANG Xu-yun, HAN Jun. Study on Residual Strength and Remaining Life of Externally-corroded Pipelines Based on Finite Element Analysis[J]. Chemical Engineering and Machinery, 2014, 40 (5): 639–641. |
| [4] |
韩文海, 周晶. 海底管道腐蚀模型对比研究[J]. 石油工程建设, 2014, 40 (3): 9–13.
HAN Wen-hai, ZHOU Jing. Comparative Research of Corrosion Models for Corroded Submarine Pipelines[J]. Petroleum Engineering Construction, 2014, 40 (3): 9–13. |
| [5] |
高旭, 曾国英. 螺栓法兰连接结构有限元建模及动力学分析[J]. 润滑与密封, 2010, 35 (4): 68–71.
GAO Xu, ZENG Guo-ying. The Finite Element Modeling and Dynamic Analysis of Bolts-flanges Connecting Structure[J]. Lubrication Engineering, 2010, 35 (4): 68–71. |
| [6] |
施哲雄, 王志文. 基于模拟的腐蚀管道可靠性分析[J]. 中国安全科学学报, 2003, 13 (7): 67–70.
SHI Zhe-xiong, WANG Zhi-wen. Simulation Based Reliability Analysis of Corroded Pipeline[J]. China Safety Science Journal, 2003, 13 (7): 67–70. |
| [7] |
李尧, 李少芬. 腐蚀疲劳作用下的船舶极限强度可靠性分析[J]. 舰船科学技术, 2013, 35 (9): 53–56.
LI Yao, LIN Shao-fen. Ship longitudinal strength reliability analysis of ship hull subjected to corrosion and fatigue[J]. Ship Science and Technology, 2013, 35 (9): 53–56. |
| [8] | 李云龙, 庄传晶. 油气输送管道疲劳寿命分析及预测[J]. 油气储运, 2004, 23 (12): 41–43. DOI: 10.3969/j.issn.1000-8241-D.2004.12.011 |
| [9] | JI Chun-yan, LI Shan-shan, CHENG Ming-lu. A global reliability assessment method on Aging offshore platforms with corrosion and cracks[J]. China Ocean Engineering, 2009, 23 (2): 211–220. |
| [10] | CHEN N, GUEDES SOARES C. Ultimate longitudinal strength of ship hulls of composite materials[J]. Journal of Ship Research, 2008, 52 (3): 184–193. |
| [11] |
郦正能. 应用断裂力学[M]. 北京: 北京航空航天大学出版社, 2012. 1
LI Zheng-neng. The application of fracture mechanics[M]. Beijing: Beijing University of Aeronautics and Astronautics Press. 2012. 1 |
| [12] | CALEYO F, VELAZQUEZ J C, HALLEN J M. Probability distribution of pitting corrosion depth and rate in underground pipelines: amonte Carlo study[J]. Corrosion, 2009, 51 (7): 1925–1934. |
| [13] |
于雯. 半潜式海洋平台结构全寿命期剩余极限强度预报方法研究[D]. 镇江: 江苏科技大学, 2012
YU Wen. Prediction method of the ultimate strength of of semi-submersible platforms in total life cycle[D]. Zhen jiang: Jiangsu University of Science and Technology, 2012. |
 2017, Vol. 39
2017, Vol. 39
