船舶舵机的有效控制是船舶航行的关键,和船舶行驶安全有很大关系[1-2]。当前,随着海运领域的迅猛发展,船舶吨位逐渐上升,航速越来越快,人们对船舶运输安全性的要求越来越高[3 – 5]。所以,研究一种高性能的船舶舵机控制系统具有重要意义,是相关学者研究的重点课题[6-7]。
文献[8]提出一种基于数学模型的船舶舵机控制方法,依据历史数据建立数学模型,通过数学模型实现船舶舵机的控制,该方法实现过程简单,但由于船舶本身运行端机参数相对而言不稳定,且具有非线性,没有办法以此构建较为精确的数学模型;文献[9]提出一种基于以太网和 CAN 技术的船舶舵机控制系统,通过传感器节点、智能设备、控制节点等构成船舶舵机控制系统。该系统可实现对船舶舵机的实时监控,但硬件成本过高,不适于实际应用;文献[10]提出一种离散船舶舵机控制系统,将遗传算法应用于离散系统中,实现对船舶舵机的控制。该方法实现过程简单,但计算复杂程度和计算量较高,也就是有计算量膨胀的弊端。
针对上述方法的弊端,设计一种新的基于神经网络的船舶舵机控制系统,分别介绍系统中 4 项主要模型(参考模型、船舶舵机模型、船舶模型和扰动模型),依据功能要求设计船舶舵机控制系统结构,利用神经网络设计船舶舵机控制器。实验结果表明,所设计系统控制效果好,不易受外界环境的干扰。
1 基于神经网络的船舶舵机控制系统设计 1.1 控制系统中各项模型设计 1.1.1 参考模型参考模型相当于预筛选器,不论要求的参考偏航角如何变化,参考模型和船舶的动力特性都匹配。
本节选用的参考模型为:
| ${T_m}{\ddot \psi _d} + {\dot \psi _d} + {K_m}{\psi _d} = {K_m}{\psi _r},$ | (1) |
其中:T m 为时间常数;K m 为模型增益系数。在实际应用中模型为非线性,即
| ${\dddot \psi _d}{K_m} + a{\ddot \psi _d} + b{\dot \psi _d} + c{\psi _d} = c{\psi _r}\text{。}$ | (2) |
其中:系数 a,b,c 可通过经验获取,本节参数取为 a = 0.934,b = 0.204,c = 0.018 2。
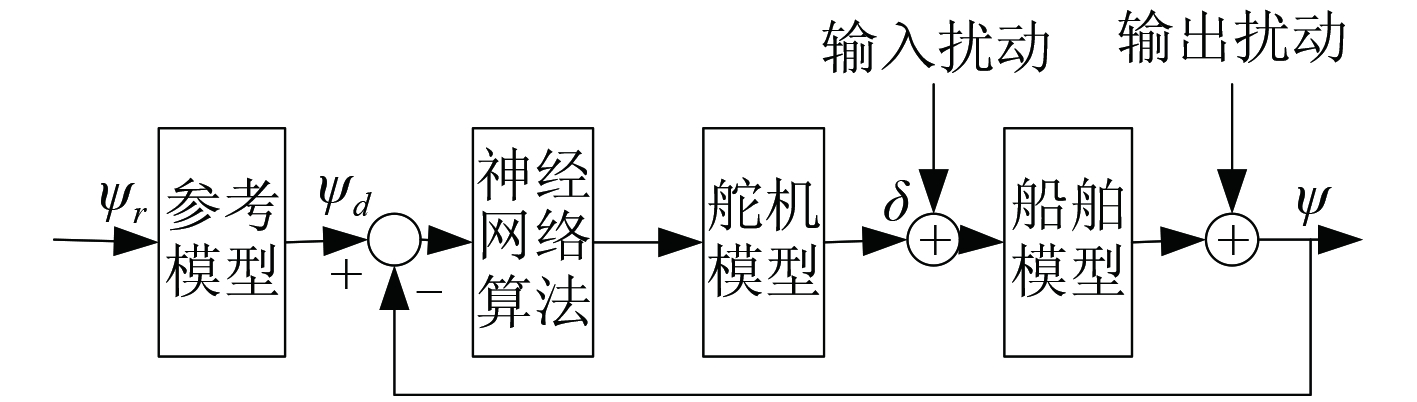
1.1.2 船舶舵机模型船舶舵机主要负责将舵调整至控制系统要求的角,本节选用的船舶舵机模型用图 1 进行描述。
|
图 1 船舶舵机模型 Fig. 1 Model of ship steering gear |
图 1 中,δ c 用于描述命令舵角,对大部分船舶来说,最大操舵角为 ±35°,最大操舵速率为 ±8°/s; ψ r 为船舶参考航向;ψ d 为设计航向;ψ为实际航向;δ 为操舵角。
1.1.3 船舶模型受很多因素的影响,船舶模型是非线性的,本节选用的船舶模型如下:
| $T\ddot \psi + {a_1}\dot \psi + {a_3} + {a_3}\dot \psi {}^3 = K\delta \text{。}$ | (3) |
其中: a 1,a 3 为 Norrbin 系数,本节 a 1 和 a 3 依次取 1 和 5。
1.1.4 扰动模型船舶舵机控制中的扰动问题较为复杂,通常认为是受到风与海浪的干扰,可通过一个典型的二阶低通滤波器形成的海浪波谱模型形成,公式描述如下:
| $x = \frac{{\omega _n^2}}{{{s^2} + 2{\omega _n}\zeta + \omega _n^2}},$ | (4) |
式中:ω n 为自然频率;ζ 为二阶低通滤波器的阻尼比;s 为白噪声带宽。ω n 计算公式如下:
| ${\omega _n} = {\omega _0} + \omega _0^2u\cos \gamma /{\rm g}$ | (5) |
式中:ω 0 为海浪频谱的峰值频率;u 为船速;γ 为船舶航向和海量之间的夹角;g为重力加速度。
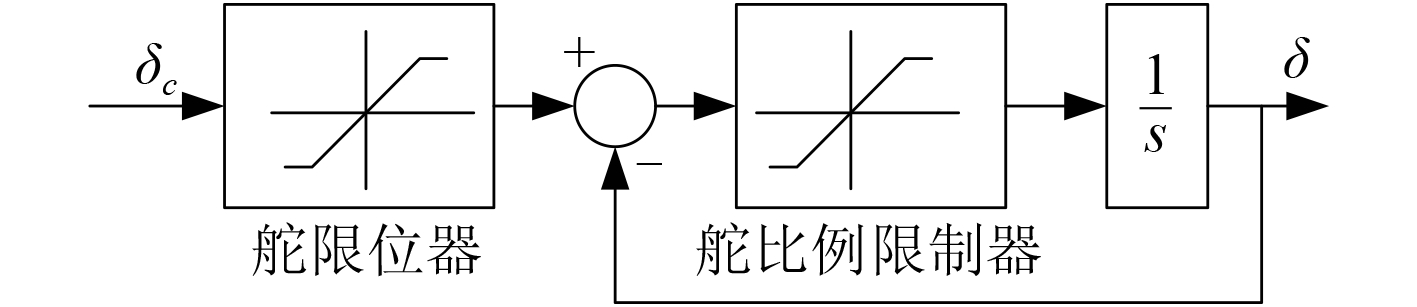
所设计的基于神经网络的船舶舵机控制系统主要包括航向改变功能和航向保持功能 2 个功能,航向改变功能要求系统操纵能力强,航向保持功能要求系统稳定性强,依据上述功能要求设计的船舶舵机控制系统结构如图 2 所示。
|
图 2 船舶舵机控制系统结构 Fig. 2 Structure of ship steering control system |
所设计的神经网络控制器由 4 层前向神经网络组成,依次为输入层、隶属度函数层、规则层和输出层。假设第 i 层的第 j 个节点输入用
第 1 层为输入层。该层中各神经元均代表 1 个输入变量,本节输入向量为航向角偏差 e 和偏差的变化量
| $O_j^{\left( 1 \right)} = f\left( {{x_i}} \right) = {x_i}\text{。}$ | (6) |
第 2 层为隶属度函数层,该层中神经元代表输入变量的一个隶属度函数,本节将高斯函数看作隶属度函数,该层输出可描述成:
| $net_{ij}^{\left( 2 \right)} = - \frac{{{{\left( {x_i^{\left( 2 \right)} - {m_{ij}}} \right)}^2}}}{{{\sigma _{ij}}}}\text{,}$ | (7) |
| $O_{ij}^{\left( 2 \right)} = \exp \left( {net_{ij}^{\left( 2 \right)}} \right)\text{,}$ | (8) |
其中,m ij ,σ ij 分别为第 i 个输入变量第 j 个模糊集合的高斯函数均值与方差。
第 3 层为规则层,其神经元数量即模糊规则数量,其输出可描述成:
| $net_k^{\left( 3 \right)} = x_{1j}^{\left( 3 \right)} \cdot x_{2j}^{\left( 3 \right)} \cdot O_{ij}^{\left( 2 \right)}\text{,}$ | (9) |
| $O_k^{\left( 3 \right)} = {f^{\left( 3 \right)}}\left( {net_k^{\left( 3 \right)}} \right) = net_k^{\left( 3 \right)}\text{,}$ | (10) |
其中,
第 4 层为输出层,该层输出可描述如下:
| $net_i^{\left( 4 \right)} = \sum {w_i^{\left( 4 \right)}} x_i^{\left( 4 \right)} + O_k^{\left( 3 \right)} \cdot {\theta ^{\left( 4 \right)}}\text{,}$ | (11) |
| $y = O_1^{\left( 4 \right)} = {f^{\left( 4 \right)}}\left( {net_1^{\left( 4 \right)}} \right) = net_1^{\left( 4 \right)}\text{。}$ | (12) |
其中
进行上述 4 个分层结构设计后,实现船舶舵机的整体控制。
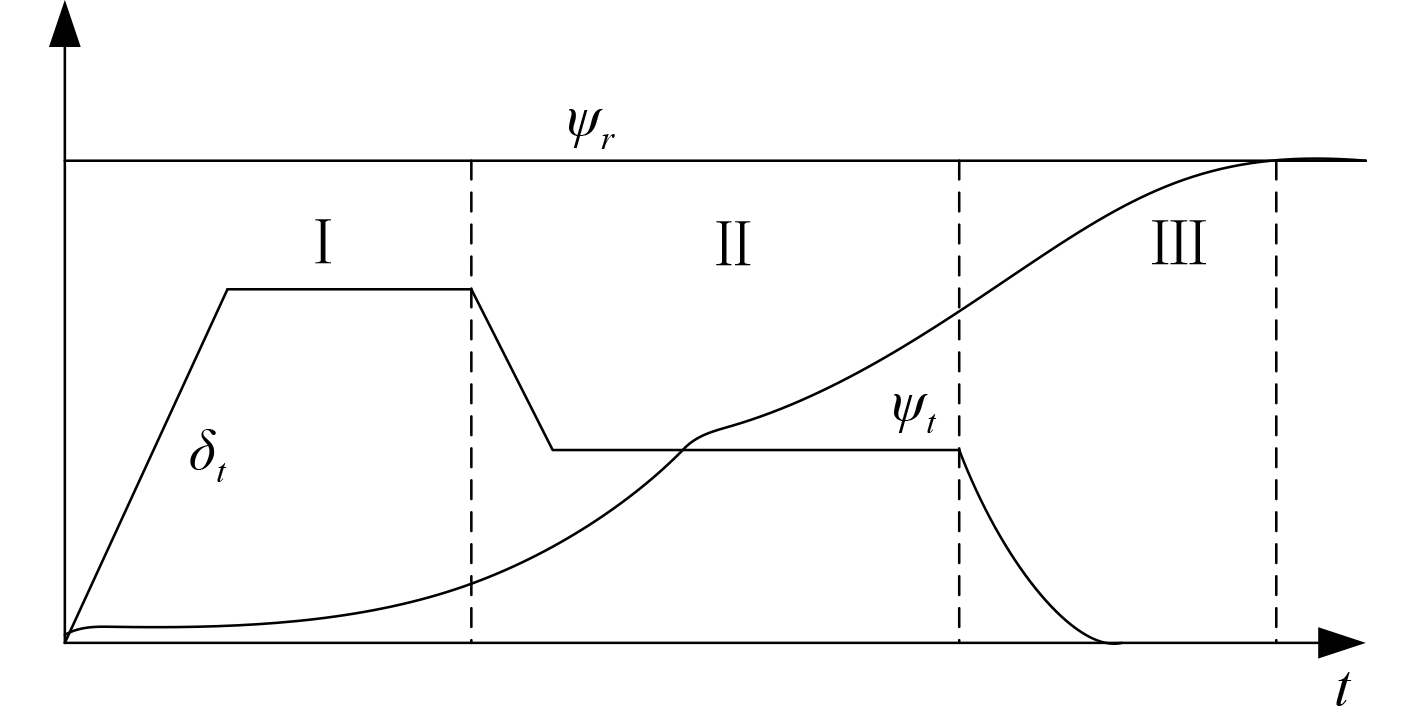
考虑在船舶航向易出现偏差,设计船舶舵机控制过程如图 3 所示。
|
图 3 船舶舵机控制过程 Fig. 3 Control process of ship steering gear |
当控制过程处于阶段Ⅰ时,船舶开始回旋,处于阶段Ⅱ时,船舶不会沿着之前的方向继续前进,新方向的提示会使得船舶调转方向,处于阶段Ⅲ时,舵机需保证船舶的航向角不出现超调现象。
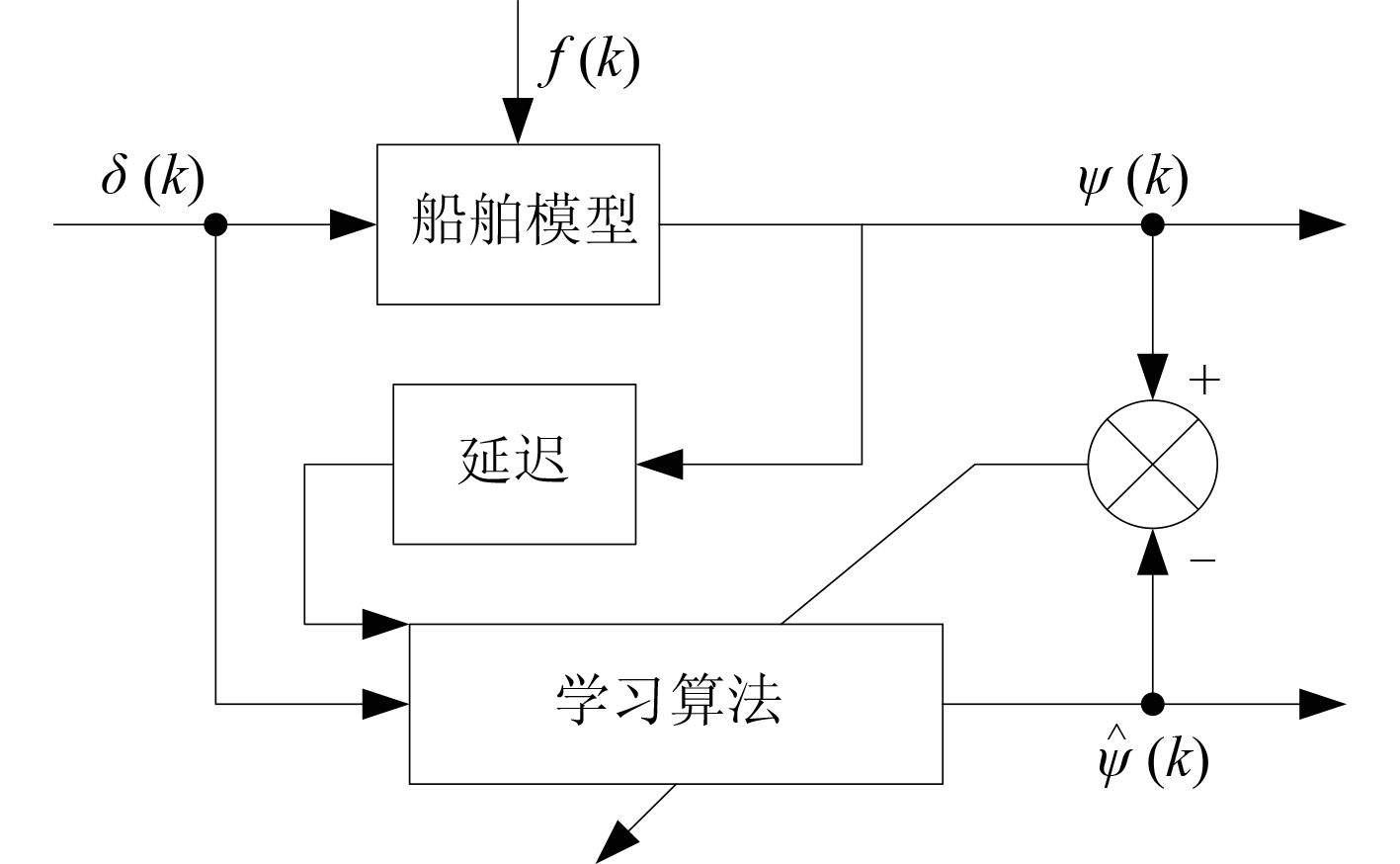
本节通过神经网络对船舶舵机进行控制,采用的神经网络控制器用图 4 进行描述,δ 为操舵角,ψ 为实际航向,将 δ,ψ 看作神经网络的输入,将
|
图 4 控制器整体设计 Fig. 4 Controller design |
利用神经网络算法对其中的参数进行调整,将指标函数 E c 看作参考模型输出 ψ m 与船舶输出 ψ 之间的方差:
| ${E_c} = \frac{1}{2}y{\left( {\psi - \mathop \psi \limits^ \wedge } \right)^2}\text{,}$ | (13) |
定义:
| $\begin{split}\gamma _1^{\left( 4 \right)} = \displaystyle - \frac{{\partial {E_c}}}{{\partial net_1^{\left( 4 \right)}}} = \displaystyle - \frac{{\partial {E_c}}}{{\partial y}}\frac{{\partial y}}{{\partial net_1^{\left( 4 \right)}}} = \\ \displaystyle \qquad\qquad\quad\qquad {e_c}\frac{{\partial \psi }}{{\partial y}} \approx {e_c}\frac{{\partial \mathop \psi \limits^ \wedge }}{{\partial y}},\left( {y = \delta /{K_3}} \right),\end{split}$ | (14) |
| $\gamma _1^{\left( 3 \right)} = - \frac{{\partial {E_c}}}{{\partial net_1^{\left( 3 \right)}}} = \gamma _1^{\left( 4 \right)}{f^{\left( 3 \right)}}\left( {net_j^{\left( 3 \right)}} \right)w_j^{\left( 4 \right)},$ | (15) |
| $\gamma _1^{\left( 2 \right)} = - \frac{{\partial {E_c}}}{{\partial net_1^{\left( 2 \right)}}} = \gamma _1^{\left( 3 \right)}\sum {O_{ki}^{(2)}O_{ij}^{(2)}} ,i \ne k \text{。}$ | (16) |
式中:
则可获取不同可修正参数的学习算法,针对第 n 次学习,学习规则可描述如下:
| $\begin{split}w_i^{\left( 4 \right)}\left( {n + 1} \right) = w_i^{\left( 4 \right)} + {\eta ^{\left( 4 \right)}}\gamma _i^{\left( 4 \right)}x_i^{\left( 4 \right)} + \\{\alpha ^{\left( 4 \right)}}\left[ {w_i^{\left( 4 \right)}\left( n \right) - w_i^{\left( 4 \right)}\left( {n - 1} \right)} \right],\end{split}$ | (17) |
| $\begin{split}{m_{ij}}\left( {n + 1} \right) = {m_{ij}}\left( n \right) + {\eta _m}\frac{{\partial {E_c}}}{{\partial {m_{ij}}}} + \\{\alpha _m}\left[ {{m_{ij}}\left( n \right) - {m_{ij}}\left( {n - 1} \right)} \right],\end{split}$ | (18) |
| $\begin{split}{\sigma _{ij}}\left( {n + 1} \right) = {\sigma _{ij}}\left( n \right) + {\eta _\sigma }\displaystyle\frac{{\partial {E_c}}}{{\partial {\sigma _{ij}}}} + \\{\alpha _\sigma }\left[ {{\sigma _{ij}}\left( n \right) - {\sigma _{ij}}\left( {n - 1} \right)} \right]\text{。}\end{split}$ | (19) |
式中:
学习率 η 选择是否合理对神经网络控制算法收敛性有很大影响,会导致收敛速度慢;如果选择的学习率值过大,则学习过程将出现不稳定现象。在 η 符合条件
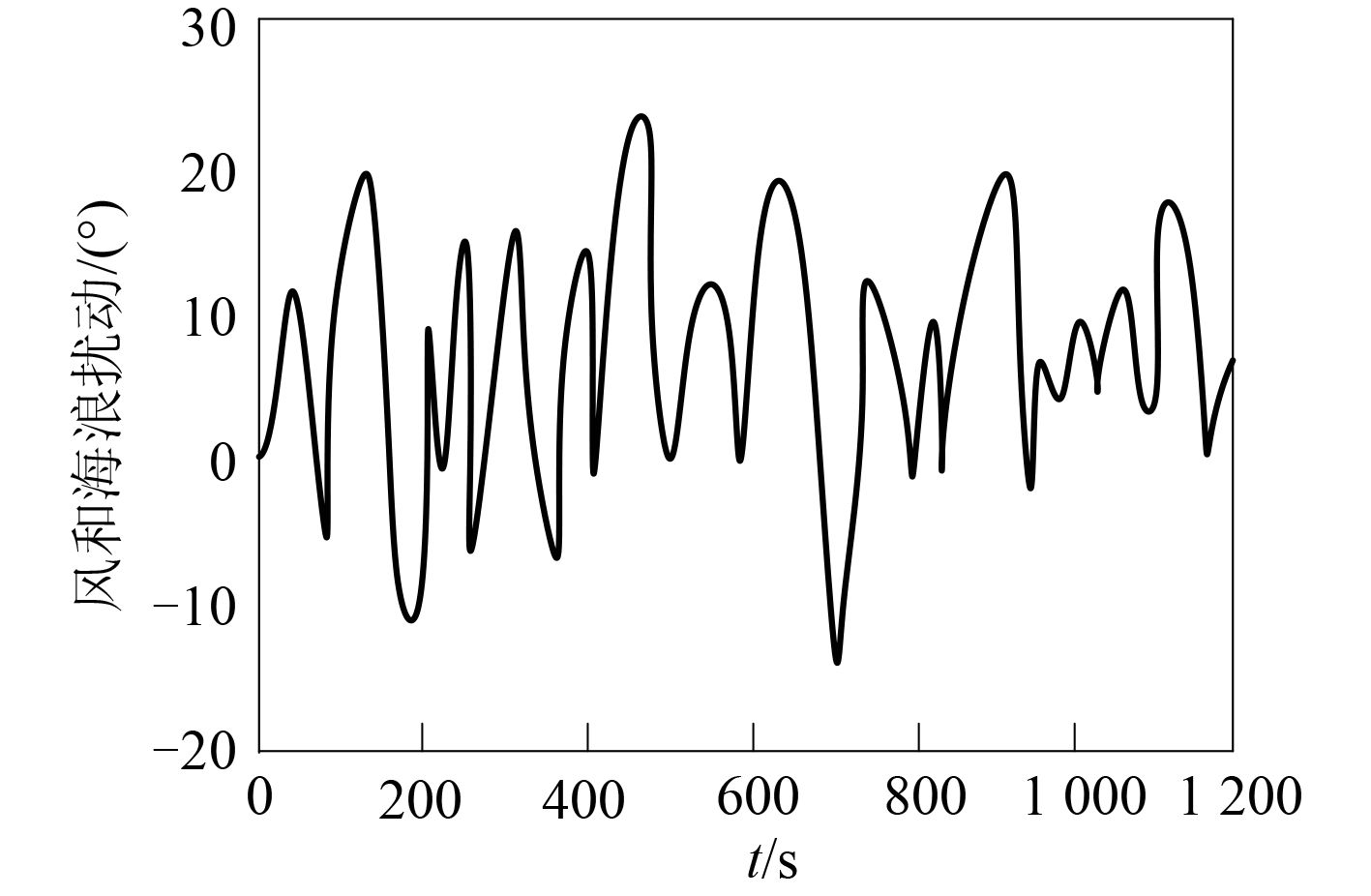
船舶舵机控制系统的设计需采用船舶与舵机的响应数据,上述数据可通过控制对象的计算机仿真获取。为了验证本文设计系统的有效性,将 PID 控制系统和模糊控制系统作为对比,对船舶舵机控制进行仿真研究。将控制周期设置为 2 s,仿真时间为 1 200 s。在进行实验的过程中,作用于船舶舵机的风和海浪扰动由带宽是 1 Hz 的白噪声产生,其部分时间序列用图 5 进行描述。
|
图 5 作用于舵机的风和海浪扰动 Fig. 5 Wind and wave disturbance acting on the steering gear |
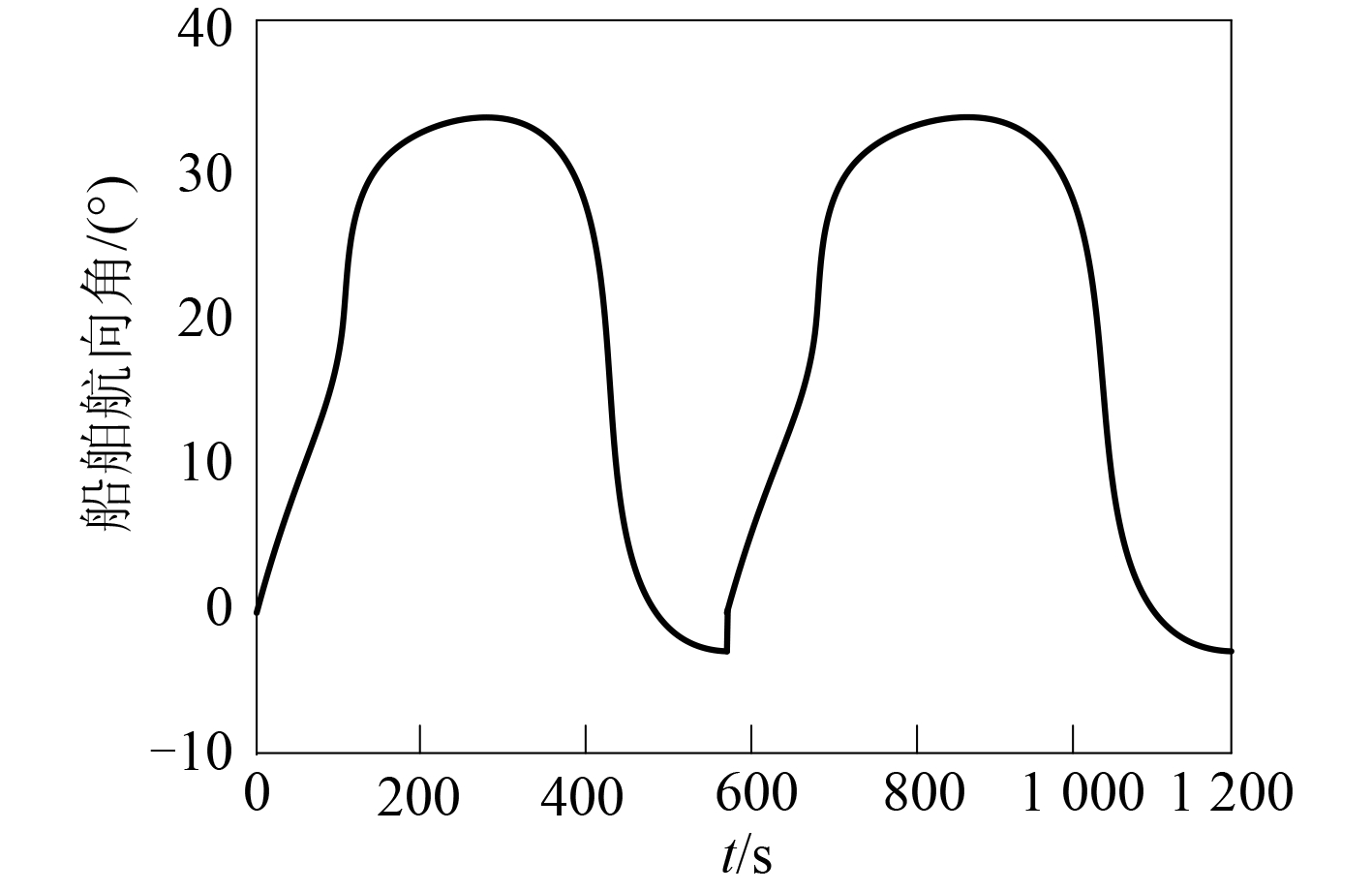
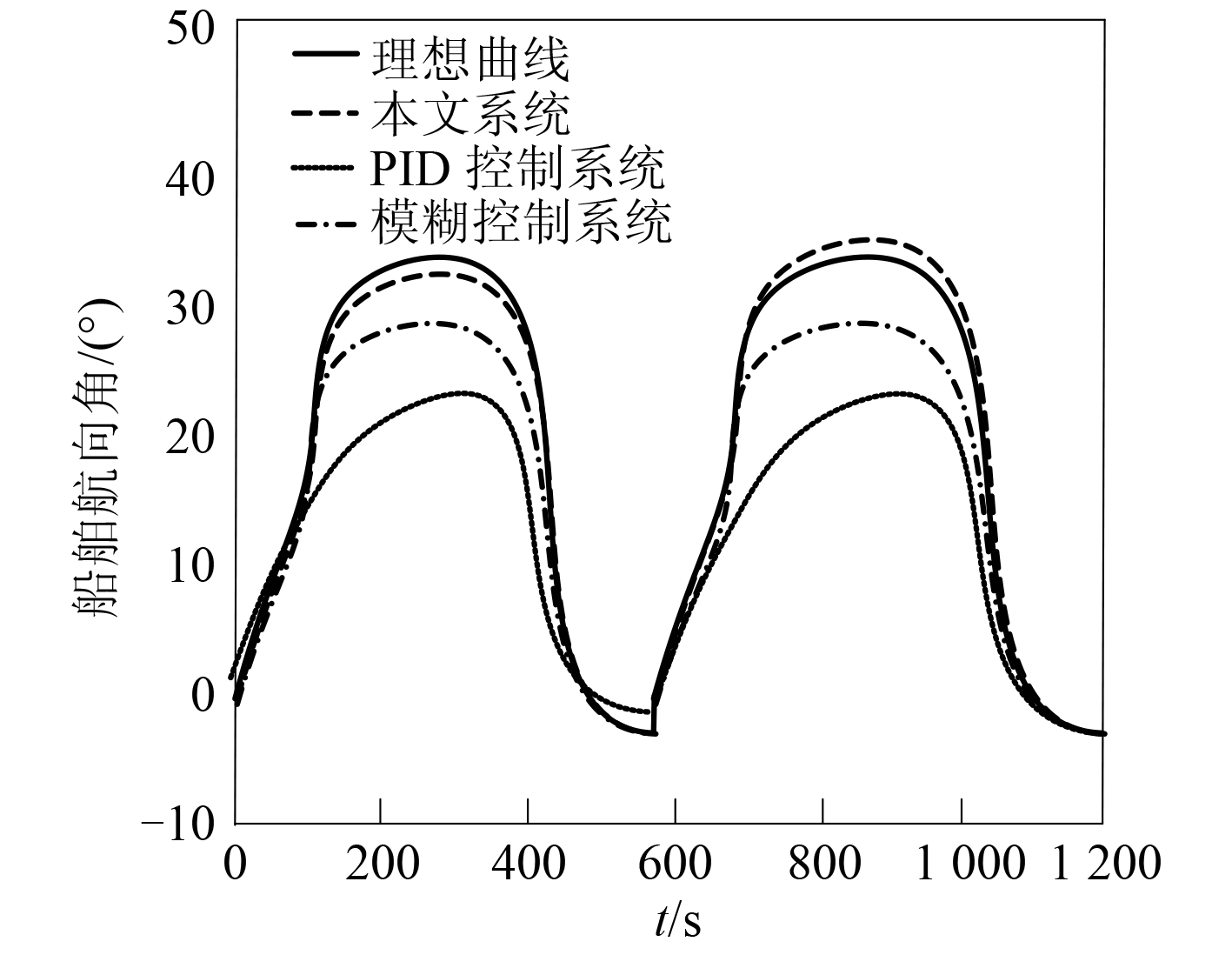
通过理想舵机控制获取船舶航向角变化的理想曲线,结果用图 6 进行描述。通过本文系统、PID 控制系统和模糊控制系统对船舶舵机进行控制,控制航向角变化情况和理想航向变化角比较结果如图 7 所示。
|
图 6 理想航向角控制曲线 Fig. 6 Ideal course angle control curve |
|
图 7 三种系统控制曲线和理想航向曲线比较结果 Fig. 7 Comparison results between the control curves and the ideal course curves of the three systems |
分析图 7 可看出,通过本文系统对船舶舵机进行控制,船舶航向角变化曲线和理想曲线基本吻合,超调量最小,明显优于 PID 控制系统和模糊控制系统,且本文控制系统响应速度最快。
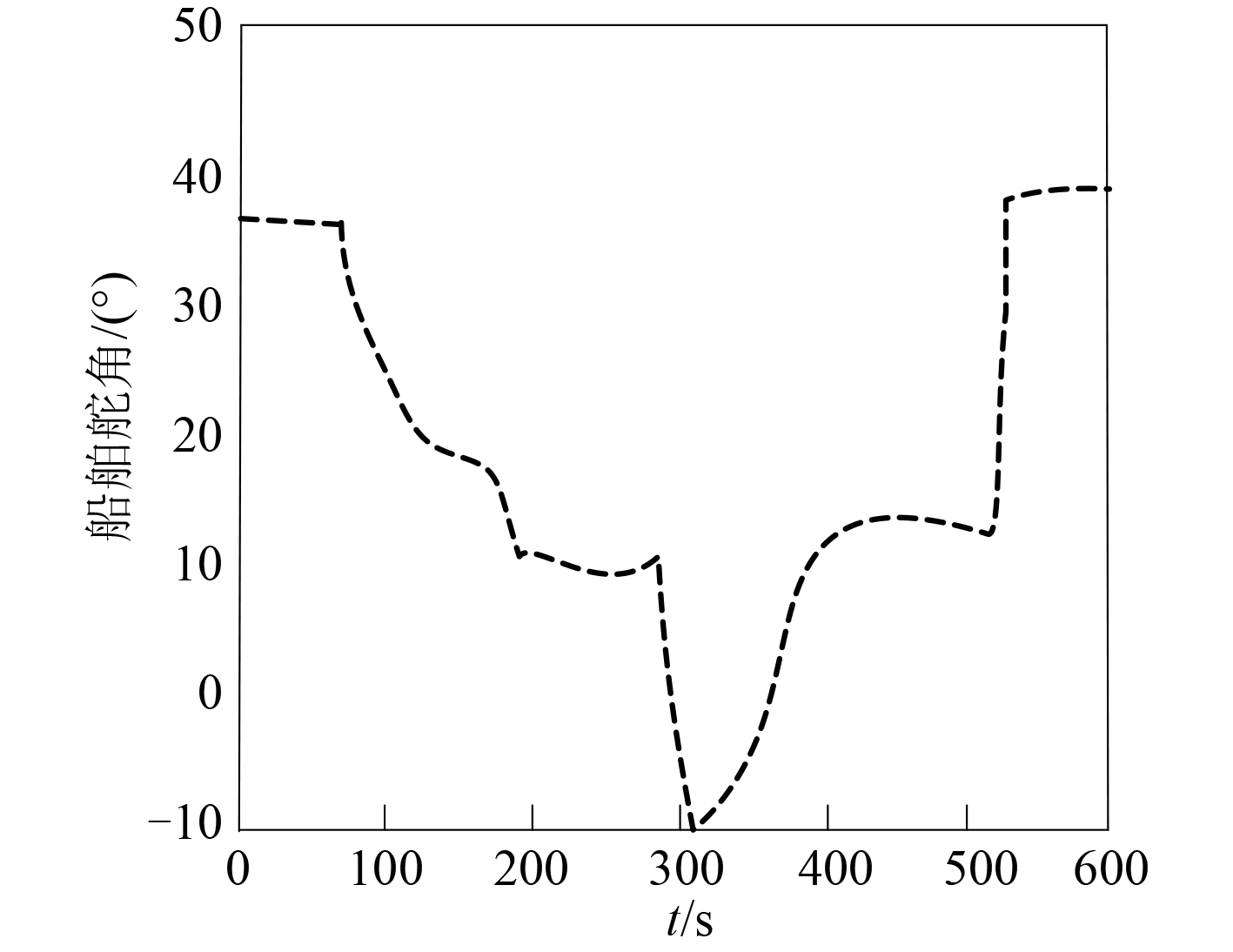
图 8 和图 9 分别为在无干扰和有干扰状态下,本文系统控制下舵角输出曲线。
|
图 8 无干扰下舵角输出曲线 Fig. 8 Output curve of rudder angle without disturbance |
|
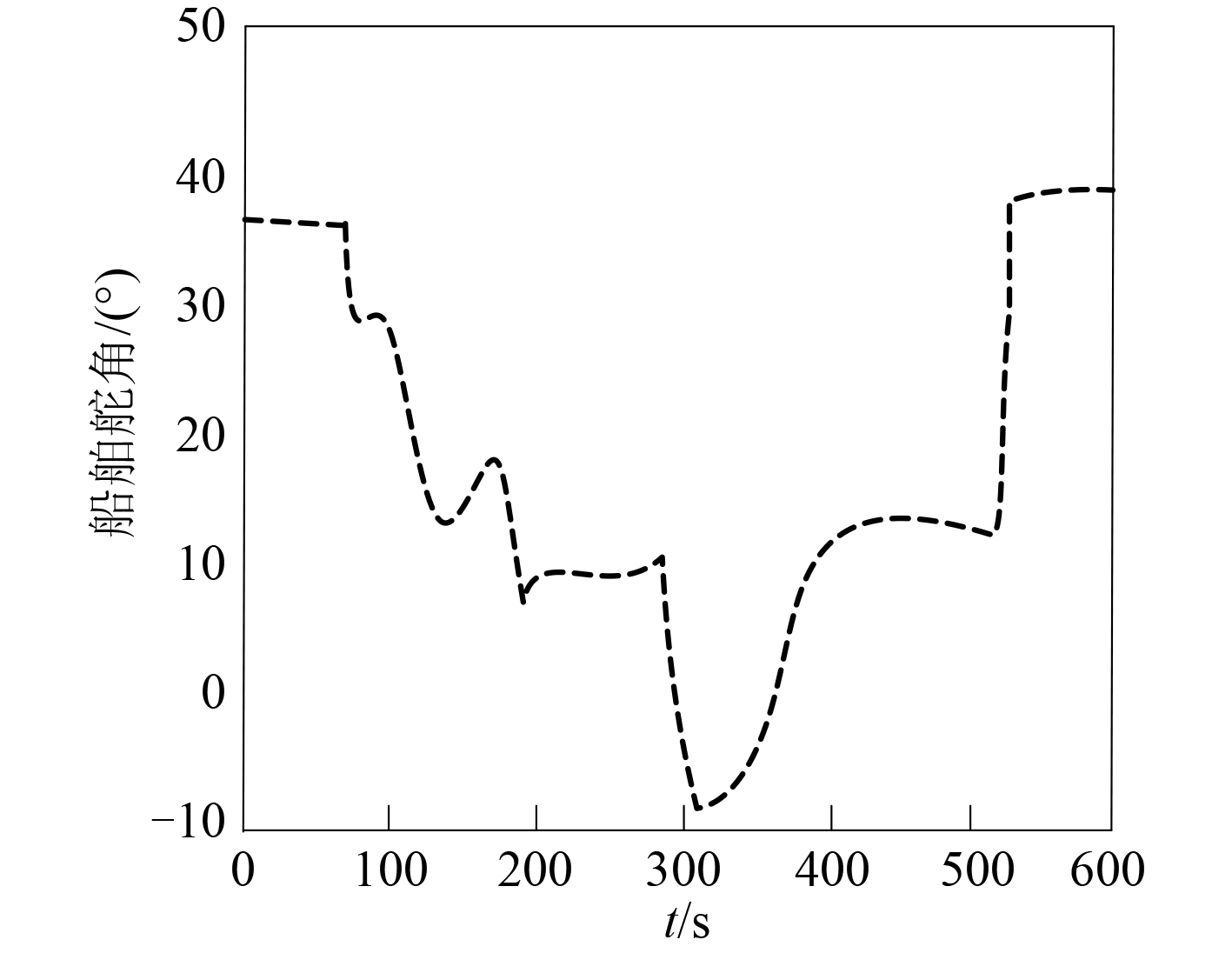
图 9 有干扰下舵角输出曲线 Fig. 9 Output curve of rudder angle under disturbance |
分析图 8 和图 9 可看出,在有干扰情况下,本文系统对舵角的控制结果和无干扰情况下船舶舵角控制结果之间的差异不大,说明本文系统对外界干扰的适应能力很强,能够有效达到系统要求。
3 结 语本文设计了一种新的基于神经网络的船舶舵机控制系统,依据功能要求设计船舶舵机控制系统结构,介绍了参考模型、船舶舵机模型、船舶模型和扰动模型,利用神经网络对船舶舵机进行控制,输出结果即为船舶舵机控制结果。实验结果表明,所设计系统控制效果好,不易受外界环境的干扰。
| [1] | 和江, 文建刚, 侯文. 基于模糊神经网络PID算法的舵机控制与仿真[J]. 中北大学学报自然科学版, 2016, 37 (2): 150–156. |
| [2] | 陈黎, 鲁涛. 液压式船舶舵机控制系统设计与仿真[J]. 舰船科学技术, 2014, 36 (12): 78–81. DOI: 10.3404/j.issn.1672-7649.2014.12.017 |
| [3] | 谭成午, 张桂香, 刘福建. 基于复合控制的飞机舵机伺服系统动态仿真[J]. 计算机仿真, 2016, 33 (1): 77–80. |
| [4] | 刘晓琳, 王春婷, 袁昆. 飞机舵机电液加载系统的多余力抑制方法研究[J]. 计算机测量与控制, 2014, 22 (12): 4166–4169. DOI: 10.3969/j.issn.1671-4598.2014.12.100 |
| [5] | 王修岩, 谷新铭, 李宗帅. 基于单神经元和前馈补偿的电动加载复合控制[J]. 电气传动, 2015, 45 (7): 48–51. |
| [6] | 张艳, 郭凯, 丁茂森. 船舶柴油发电机组转速的模糊RBF神经网络PID控制[J]. 船电技术, 2014, 34 (5): 1–5. |
| [7] | 夏永泉, 李耀斌, 李晨. 基于多神经网络的小麦病害在线诊断系统[J]. 科技通报, 2016, 32 (10): 59–62. DOI: 10.3969/j.issn.1001-7119.2016.10.013 |
| [8] | 康见见, 柴嘉鸿, 孙士杰, 等. 基于BP神经网络的柴油机燃烧特征参数前馈预测模型[J]. 科学技术与工程, 2014, 14 (24): 221–225. DOI: 10.3969/j.issn.1671-1815.2014.24.040 |
| [9] | 郝帆. 基于神经网络的工程结构智能监测系统设计[J]. 电子设计工程, 2016, 24 (23): 112–114. DOI: 10.3969/j.issn.1674-6236.2016.23.034 |
| [10] | 宋文龙, 吕迎春, 秦建敏, 等. 基于MSP430和BP神经网络PID的跑步机控制系统[J]. 现代电子技术, 2016, 39 (22): 150–153. |
 2017, Vol. 39
2017, Vol. 39
