2. 武汉船用电力推进装置研究所,湖北 武汉 430064;
3. 湖南铁道职业技术学院,湖南 株洲 412001
2. Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China;
3. Hunan Railway Professional Technology College, Zhuzhou 412001, China
综合电力推进系统由于具有诸多优点,在舰船推进领域得到广泛应用,是未来舰船动力的主要发展方向之一。变频器作为舰船电力推进系统的核心设备,其可靠性直接影响整个系统性能。现代舰船变频器的发展趋势是中压、大容量、高性能。二极管钳位(NPC)三电平变频器具有开关器件电压应力低,输出电压纹波小等优点,在舰船大功率电力推进、交流电力传动、有源滤波及风力发电等领域得到了广泛应用。
脉冲宽度调制(PWM)技术是 NPC 三电平逆变器的关键技术之一,空间矢量脉冲宽度调制(SVPWM)技术具有直流电压利用率高、谐波含量小、便于实现等优点得到了广泛的研究和应用。在某些特定场合下,需要在有限的直流母线电压下提高输出电压,获得更高的直流电压利用率,过调制技术应运而生。三电平过调制技术与两电平过调制技术原理一样,主要的过调制策略有以下几种[1 – 5]:最小相角误差过调制策略、最小幅值误差过调制策略和此为基础的双模过调制策略、单模过调制策略。单模策略将过调制区当作一个整体,采用统一算法进行控制,双模式策略将过调制区分为 2 部分,2 个部分分别采用不同的过调制算法。双模式过调制输出基波电压较高,谐波含量较少;单模式过调制实现方法简单,但输出基波电压较小,谐波含量较大。
过调制技术应用于 NPC 三电平逆变器中时,在过调制策略中,当参考电压矢量落于六边形之外时,实际输出电压矢量只能由中矢量和其他基本矢量合成。而中矢量会引起中点电压矢量的偏移和波动,并且这种影响是不可控的[6]。文献[4]对这一问题没有尽心分析。为了避免中矢量对中点电压的影响,文献[5、7]不使用中矢量而使用大矢量和小矢量来合成在六边形上的输出矢量,虽然消除了过调制引起的重点电位偏移与波动,但这种方式使输出电压变为两电平。三电平电压源逆变器工作与过调制区时,由于中矢量作用会引起中点电位的偏移与波动,过调制算法必须采用中点电压波动的抑制措施[8 – 10]。文献[11]在借鉴文献[9 – 10]思想的基础上提出一种利用合成矢量三电平过调制技术,用2个大矢量与中矢量来代替中矢量作用,达到降低中点电位偏移与波动的目的。由于大矢量不影响中点电位,中矢量对中点电位影响不受控,虽然该算法减小中点电位作用时间到原来 1/3,但是依然避免不了中点电位偏移与波动。
针对以上问题,本文提出一种新的三电平 SVPWM 过调制算法,采用大矢量、小矢量与中矢量合成矢量来代替中矢量,即降低中矢量作用时间,又可以用小矢量来调节中点电位,真正实现过调制时对中点电位偏移与波动的抑制作用。
1 三电平 SVPWM 调制逆变器输出的空间电压矢量定义为:
| $U = \displaystyle\frac{2}{3}({u_A} + {u_B}{e^{j2\pi /3}} + {u_C}{e^{j4\pi /3}})\text{。}$ | (1) |
式中:u A ,u B ,u C 为逆变器输出的三相对称电压;U 为逆变器输出的空间电压矢量。
三电平逆变器一共可以输出 27 个电压矢量,其中 6 个长度为 2U
dc
/3 的大矢量(U
dc
为直流母线电压),12 个长度为 U
dc
/3 的小矢量,6 个长度为
如图 1 所示,在第1扇区内,根据标准划分方式[12 – 13],将一扇区空间划分为 A、B、C、D 四个小扇区。根据伏秒特性,在一个开关周期 T s 内变频器输出空间矢量 U 的作用效果可以用基本矢量作用来等效。在小扇区A 内,用基本矢量 U 1、U 4 和零矢量去等效参考电压矢量;在小扇区 B 内,用基本矢量 U 1、U 4 和 U 3 去等效参考电压矢量;在小扇区 C 内,用基本矢量 U 1、U 2 和 U 3 去等效参考电压矢量;在小扇区 D 内,用基本矢量 U 3、U 4 和 U 5 去等效参考电压矢量。在每个小扇区内,都用到小矢量 U 1 或 U 4,每个小矢量都有 1 对矢量(100 和 0-1-1、110 和 0-1-1),这 1 对矢量对中点电位影响相反,通过调节这 1 对小矢量作用时间,可以起到调节平衡中点电位作用。
以小扇区 C 为例,用基本矢量 U 1、U 2 和 U 3 的作用去等效参考电压矢量在一个开关周期内作用,基本矢量作用时间分别为 T 1,T 2 和 T 3,则矢量作用时间有如下关系:
| ${T_1} = {T_s}(2 - \displaystyle\frac{{3{u_\alpha } + \sqrt 3 {u_\beta }}}{{{u_{dc}}}})\text{,}$ | (2) |
| ${T_2} = {T_s}(\displaystyle\frac{{3{u_\alpha } - \sqrt 3 {u_\beta }}}{{{u_{dc}}}} - 1)\text{,}$ | (3) |
| ${T_3} = {T_s}\displaystyle\frac{{2\sqrt 3 {u_\beta }}}{{{u_{dc}}}}\text{。}$ | (4) |
式中:u α 、u β 为参考电压矢量在 αβ 轴上分量;T s 为开关周期。

|
图 1 一扇区区域划分及矢量合成 Fig. 1 Area partition & voltage space vector systhesize in No.1 sector |
线性调制下,输出空间矢量最大幅值为
输出电压矢量轨迹从圆形过渡到六阶梯梯形时,控制方式发生很大变化,调制方式从线性调制进入到过调制。线性调制区,输出电压矢量能够跟踪参考电压矢量,轨迹能保持一致;进入到过调制区,参考电压矢量依然保持为圆形轨迹,但是逆变器无法输出如此大幅值圆形轨迹的电压矢量。
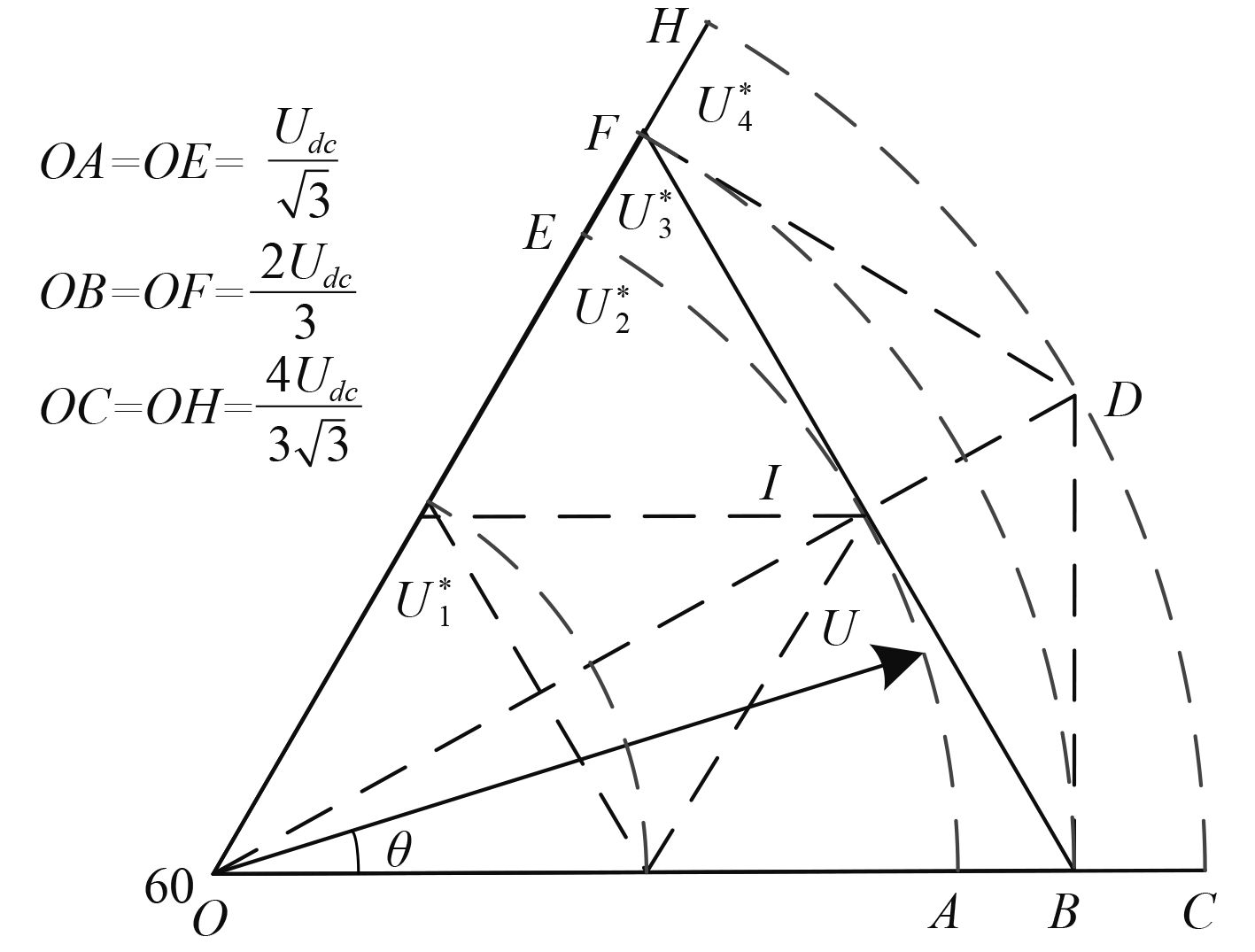
2 过调制控制策略三电平过调制策略与两电平过调制策略无本质区别,参照文献[11,14]过调制思想,如图 2 所示。在圆弧 U 2* 以内,属于线性调制区;在圆弧 U 2* 和 U 3* 之间,处于过调制Ⅰ区;在圆弧 U 3* 和 U 4* 之间,处于过调制Ⅱ区。过调制Ⅰ区内,输出电压矢量的幅值和相位都连续可调;过调制Ⅱ区,输出电压矢量的幅值和相位不连续。
|
图 2 扇区 C 区域划分及矢量合成 Fig. 2 Overmodulation area partition & voltage space vector systhesize in C sector |
由于输出电压波形对称,下面以第一扇区为例对过调制情况进行分析。过调制Ⅰ区,采用最小相角误差过调制方法,将参考电压矢量幅值限制在六边形边 BF 上。过调制Ⅱ区,参考电压矢量位于直线 BD 或 DF 左边,采用最小相角误差过调制策略,参考电压矢量位于直线 BF 或 DF 右侧,则限制输出电压矢量直接输出该区域的大矢量,直接转换为六拍输出模式。
假设参考电压矢量经过小扇区 C,扇区 1 逆变器输出合成矢量由基本矢量 U 1,U 2 和 U 3 合成,基本矢量作用时间分别为 T 1,T 2,T 3,周期为 T s 。如果参考电压矢量位于直线 BD 右侧,则:
| ${u_\alpha } > \frac{2}{3}{U_{dc}}\text{,}$ | (5) |
| $\displaystyle\frac{1}{3}{U_{dc}}{T_1} + \displaystyle\frac{2}{3}{U_{dc}}{T_2} + \displaystyle\frac{1}{2}{U_{dc}}{T_3} = {u_\alpha }{T_s}\text{,}$ | (6) |
由式(5)和式(6)可得:
| $\frac{1}{2}{T_1} + {T_2} + \frac{3}{4}{T_3} > {T_s}\text{。}$ | (7) |
同理,假设参考电压矢量经过小扇区 D,扇区 1 逆变器输出合成矢量由基本矢量 U 3,U 4 和 U 5 合成,基本矢量作用时间分别为 T 1,T 2,T 3,可得:
| ${u_\beta } > - \displaystyle\frac{{\sqrt 3 }}{3}{u_\alpha } + \displaystyle\frac{4}{{3\sqrt 3 }}{U_{dc}}\text{,}$ | (8) |
| $\displaystyle\frac{{\sqrt 3 }}{6}{U_{dc}}{T_1} + \displaystyle\frac{{\sqrt 3 }}{3}{U_{dc}}{T_2} + \displaystyle\frac{{\sqrt 3 }}{6}{U_{dc}}{T_3} = {u_\beta }{T_s}\text{,}$ | (9) |
| $\displaystyle\frac{1}{6}{U_{dc}}{T_1} + \displaystyle\frac{1}{3}{U_{dc}}{T_2} + \displaystyle\frac{1}{2}{U_{dc}}{T_3} = {u_\alpha }{T_s}\text{,}$ | (10) |
| $\displaystyle\frac{1}{2}{T_1} + {T_2} + \displaystyle\frac{3}{4}{T_3} > {T_s}\text{。}$ | (11) |
根据计算出来的矢量作用时间 T 1,T 2,T 3 就可以判断过调制采用何种模式,对过调制策略进行切换。
3 过调制小、中矢量作用时间分析根据以上分析,在小扇区 C、D,小矢量作用时间如式(2)所示。假设参考电压矢量幅值为u,角度为 θ,则式(2)可表示为:
| $v\frac{{{T_1}}}{{{T_s}}} = 2 - \frac{{2\sqrt 3 u}}{{{u_{dc}}}}\sin (\displaystyle\frac{\pi }{3} + \theta )\text{。}$ | (12) |
在圆弧 U 1* 和 U 3* 之间,参考电压矢量的幅值在范围 [1/3,2/3] 之内,参考电压矢量的角度在范围 [0,π/3] 之内。图 3 即为小扇区 C、D 内小矢量作用时间,参考电压矢量幅值增加时,小矢量作用时间减小,当参考电压矢量终点位于正六边形边 BF 上时,小矢量作用时间为零;以直线 OD 为边界,当参考电压矢量角度从 0 增加到 π/6,小矢量作用时间逐渐减小,在直线 OD 达到最小,然后随着角度继续增加到 π/3,小矢量作用逐渐增加到最大。

|
图 3 扇区 C、D 区域小矢量作用时间 Fig. 3 Duration time of small vectors in C sector & D sector |
在小扇区 C,中矢量作用时间为:
| $\displaystyle\frac{{{T_3}}}{{{T_s}}} = \displaystyle\frac{{2\sqrt 3 {u_\beta }}}{{{u_{dc}}}}\text{,}$ | (13) |
在小扇区 D,中矢量作用时间为:
| $\displaystyle\frac{{{T_3}}}{{{T_s}}} = \displaystyle\frac{{3{u_\alpha } - \sqrt 3 {u_\beta }}}{{{u_{dc}}}} = \displaystyle\frac{{2\sqrt 3 u}}{{{u_{dc}}}}\sin (\displaystyle\frac{\pi }{3} - \theta )\text{。}$ | (14) |
由式(13)和式(14)可知,在小扇区 C 内,中矢量作用时间随参考电压矢量 β 轴分量 u β 增加逐渐从 0 增加,当参考电压矢量与中矢量重合时,达到最大值 T s ;同样在小扇区 D 内,随参考电压矢量角度 θ 增加逐渐减小,当角度增加到 π/3 时,中矢量作用时间为0。
三电平 SVPWM 调制,由于中矢量对中点电位影响不可控,在线性调制区内一般采用调节一对小矢量作用时间来调节与减小中点电位波动,当参考电压矢量终点位于正六边形边 BF 上,小矢量作用时间为 0,而中矢量作用时间大于 0,此时中点电位必然发生较大的波动,这也是过调制时中点电位难以控制根本原因。
4 中点平衡过调制算法常规三电平 SVPWM 调制策略中,中矢量是中点电位偏移与波动的主要原因。参考电压矢量位于直线 BD 或 DF 右侧,只使用大矢量,逆变器进入六拍输出模式,无中矢量参与输出;只有在参考电压矢量位于直线 BD 或 DF 左侧,需要考虑中矢量作用,对中点电位波动进行抑制。
如图 2 所示,参考电压矢量位于过调制Ⅰ区,且参考电压矢量位于正六边形边 BF 左侧,则采取最小相角误差过调制策略;如果参考电压矢量位于正六边形 BF 右侧,只使用大矢量,逆变器进入六拍输出模式。
当参考电压矢量位于正六边形 BF 右侧时,根据上述分析,可得小矢量作用时间为:
| ${T_1} < 0\text{,}$ | (15) |
| ${T_2} + {T_3} = (\displaystyle\frac{{3{u_\alpha } + \sqrt 3 {u_\beta }}}{{{u_{dc}}}} - 1){T_s} > {T_s}\text{。}$ | (16) |
根据前一节分析可知,当参考电压矢量位于正六边形BF左侧时,小矢量作用时间 T 1 ≥ 0 且 T 2 + T 3 ≤ T s ,因此可以调节一对小矢量的作用时间来实现对中点电位调整,调整控制方法与线性调制方法一致。
由式(15)和式(16)可知,直接根据小矢量、中大矢量作用时间判断采用何种过调制策略,不再需要额外算法进行判断,方便线性调制、最小相角误差过调制以及六拍输出过调制之间切换。提出的过调制方法虽然使得过调制Ⅰ区内,输出电压矢量连续调节范围变小,但是采用这种算法之后,能够有效降低中点电位波动与偏移。
5 仿真分析直流母线电压设定为 1 000 V,母线电容 10 mF,负载为非平衡负载,其中 A,C两相负载电阻 1 欧,负载电抗为 1 mH,B 相负载电阻 0.1 Ω,负载电抗 1 mH。开关频率取 4 kHz,基波频率为 50 Hz,中点电位平衡因子取值在范围 [0.1,0.9]。
图 4 为传统过调制方法与本文提出新方法参考电压调制比与实际输出电压基波调制比曲线。仿真结果表明,传统过调制方法在过调制区采用最小相角误差调制,使得幅值偏差加大,导致实际输出电压较参考电压低。而本文提出过调制方式在正六边形边外直接采用六拍输出模式,输出电压幅值与给定电压一致。当调制比大于 1.1 之后,2 种过调制方法都进入六拍输出模式,输出电压达到输出极限,基波电压为

|
图 4 参考调制比与实际调制比曲线 Fig. 4 Curve for modulation of conferrence & practice |
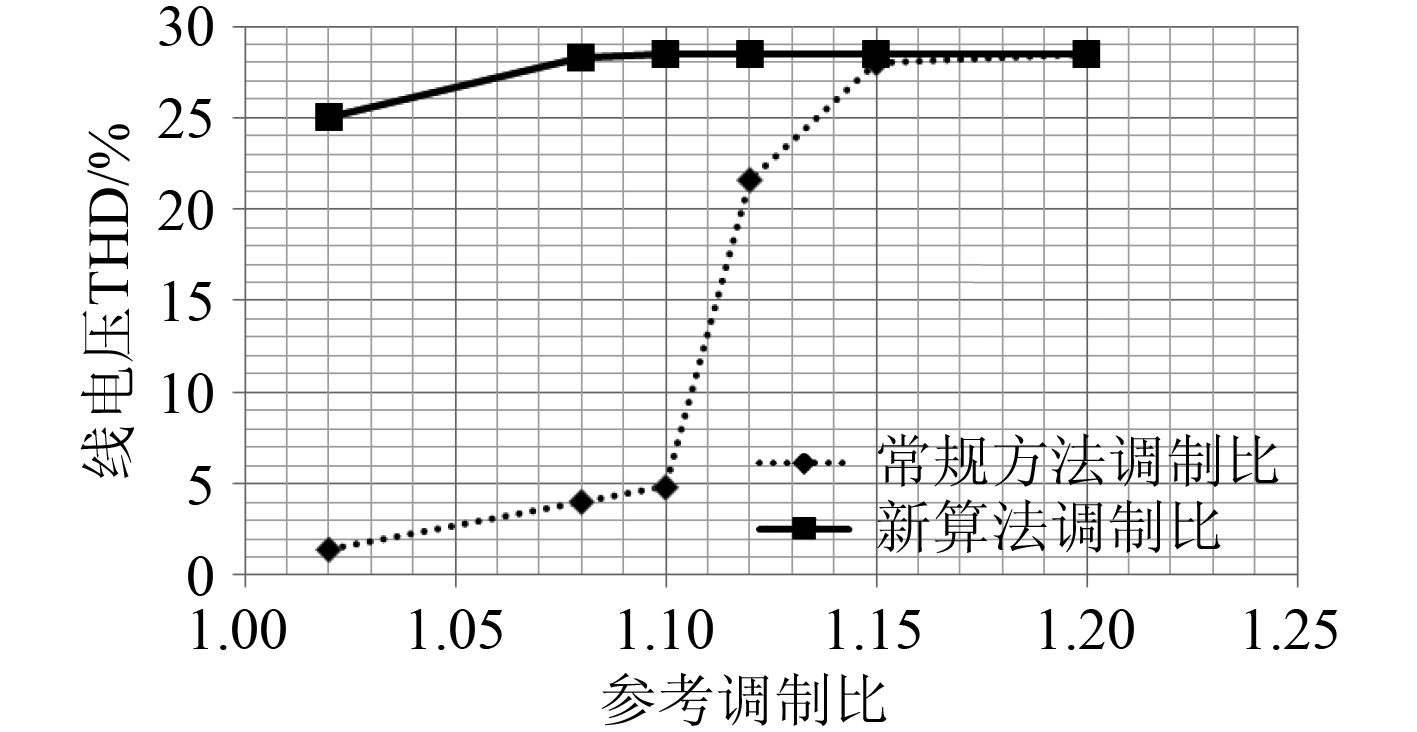
图 5 为传统过调制方法与本文提出新方法线电压 THD 随参考电压调制比变化曲线。由于本文提出方法在正六边形外即采用六拍输出模式,因此导致输出线电压 THD 急剧增加,当调制比增加到 1.1 之后,常规过调制方法也采用六拍输出模式,导致线电压 THD 急剧增加,最后随调制比增加,2 种方法 THD 相同。
|
图 5 线电压 THD Fig. 5 THD of line voltage |
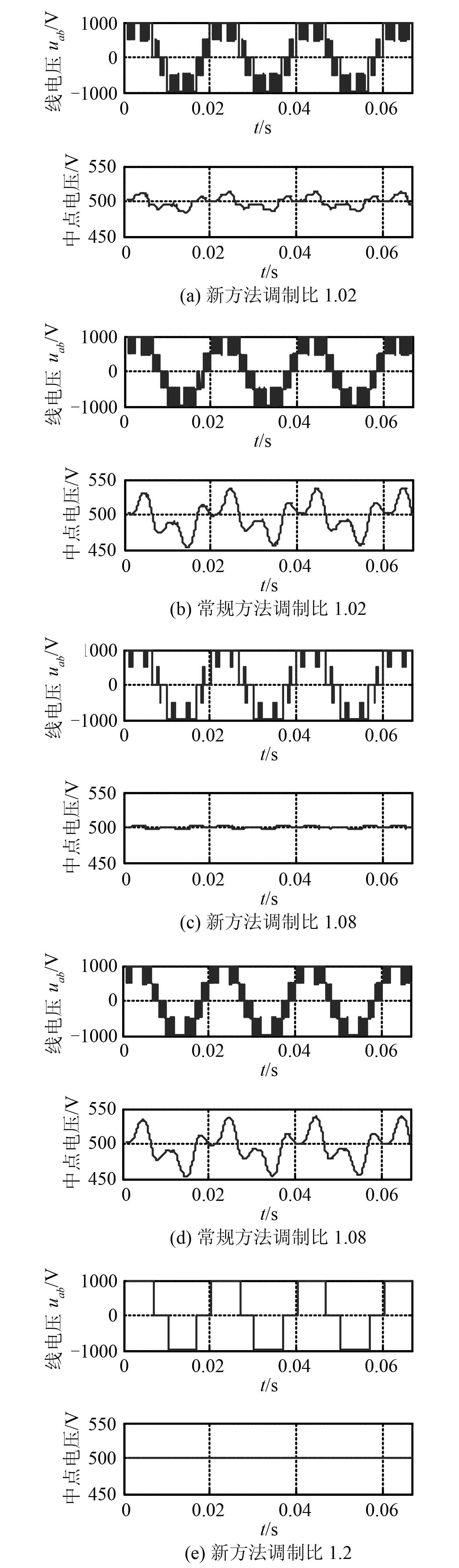
图 6 为不同参考电压调制比下常规方法及新方法输出线电压及中点电压的仿真波形。图 6(a)、图6(b)为调制比为 1.02 时 2 种过调制波形,新方法在过调制Ⅰ区,采用与线性调制相同的中点电位平衡策略,将中点电位的波动范围在 ±10 V 左右,常规方法由于小矢量作用时间为0之后,对中点电位无调节作用,因此中点电位波动范围为 ±40 V。
继续增加参考电压调制比,如图 6(c)、图6(d)所示,参考电压逐渐到正六边形之外,新方法直接采用六拍输出模式,没有使用中矢量参与输出,因此中点电位波动反而降低;常规方法则由于中矢量继续参与输出,因此中点电位波动范围依然在 ±40 V 左右。当参考电压调制比到 1.2 时,如图 6(e)、图6(f)所示,此时常规方法与新方法都处于六拍输出模式,此时只有大矢量输出,因此中点电位能维持恒定。
|
本文对 PWM 过调制进行了分析,提出了一种新的过调制方法,通过理论推导与仿真分析,可以得到如下结论:
1)NPC 三电平电压源逆变器过调制时,由于只有中矢量和大矢量输出,导致中点电位偏移和波动增大;
2)与常用过调制方法在过调制区内存在幅值偏差不同,新方法在过调制区输出电压基波能够跟踪给定电压,不存在幅值偏差;
3)新提出的过调制方法在正六边形边 BF 左侧,采用小矢量对中点电位进行调节;在 BF 右侧,只选用大矢量输出,该方法有效降低中点电位偏移和波动,但是存在 THD 较大问题。
| [1] | 李阳, 戴鹏, 于月森, 等. 三电平逆变器SVPWM过调制策略综述[J]. 电气传动, 2010, 40 (7): 8–12. |
| [2] | HOLTZ J, LOTZKAT W, Ashwin M Khambadkone. On continuous Control of PWM Inverters in the Overmo dulation Range Including the Six-step Mode[J]. IEEE Transactions on Power Electronics, 1993, 8 (4): 546–553. DOI: 10.1109/63.261026 |
| [3] | BOLOGNANI S, ZIGLIOTTO M. Novel Digital Continuous Control of SVM Inverters in the Overmodulation Range[J]. IEEE Transactions on Industry Applications, 1997, 33 (2): 525–530. DOI: 10.1109/28.568019 |
| [4] | 金舜, 钟彦儒, 程为彬. 新颖的SVPWM过调制策略及其在三电平逆变器中的应用[J]. 中国电机工程学报, 2006, 26 (20): 84–9O. DOI: 10.3321/j.issn:0258-8013.2006.20.015 |
| [5] | GUPTA A K, KHAMBADKONE A M. A simple space vector PWM scheme to operate a three level NPC inverter at high modulation index including over modulation region with neutral point balancing[J]. IEEE Transactions on Industry Applications, 2007, 43 (3): 751–760. DOI: 10.1109/TIA.2007.895766 |
| [6] | 李永东, 肖曦, 高跃. 大容量多电平变换器-原理•控制•应用[M]. 北京: 科学出版社, 2005. |
| [7] | 罗永吉, 尹华杰, 周艳青. 三电平NPC逆变器中点电位平衡的软件算法[J]. 电机传动, 2008, 38 (5): 3–7. |
| [8] | 姚文熙, 吕征宇, 费万民, 等. 一种新的三电平中点电位滞环控制法[J]. 中国电机工程学报, 2005, 25 (7): 92–96. |
| [9] | 宋文祥, 陈国呈, 武慧, 等. 一种具有中点电位平衡功能的三电平空间矢量调制方法及其实现[J]. 中国电机工程学报, 2006, 26 (21): 95–100. |
| [10] | 窦真兰, 张同庄. 三电平NPC整流器空间矢量脉宽调制及中点电位平衡控制[J]. 电力自动化设备, 2008, 25 (2): 65–79. |
| [11] | 王颢雄, 马伟明, 张狄林, 等. 利用矢量合成的三电平变流器SVPWM过调制技术[J]. 高电压技术, 2011, 37 (1): 234–240. |
| [12] | MONDAL S K, PINTO J O P, BOSE B K. A neural-network based space-vector controller for a three-level voltage-fed inverter induction motor drive[J]. IEEE Transactions on Industry Applications, 2002, 38 (3): 660–669. DOI: 10.1109/TIA.2002.1003415 |
| [13] | SEO J H, CHOI C H, HYUN D S. A new simplified space-vector PWM method for three-level inverters[J]. IEEE Transactions on Power Electronics, 2001, 16 (4): 545–550. DOI: 10.1109/63.931078 |
| [14] | 吴芳, 万山明, 黄声华. 一种过调制算法及其在永磁同步电动机弱磁控制中的应用[J]. 电工技术学报, 2010, 25 (1): 58–63. |
 2017, Vol. 39
2017, Vol. 39
