永磁同步电动机(PMSM)以其效率高、功率因数高、力矩惯量比大、定子电流和定子电阻损耗小且转子参数可测、控制性能好等优点,成为船舶推进电机的最优选择。作为船舶电力推进的核心,交流电机调速目前有2种比较成熟且应用广泛的控制策略,分别是矢量控制(Vector Control,VC)和直接转矩控制(Direct Torque Control,DTC)[1]。虽然这 2 种控制方法在其它领域已得到广泛应用,但由于船舶推进电机具有大功率、大转动惯量等特点[2],且运行工况较为复杂,所以 VC 和 DTC 两种控制策略能否适用于船舶电力推进系统的永磁同步电动机调速控制以及两种策略的调控效果优劣仍有待深入研究。
本文在船舶永磁同步推进电机模型的基础上分别建立矢量控制和直接转矩控制系统,在 Matlab/Simulink 仿真平台上进行全船电力推进系统建模与仿真分析,对永磁同步电机的矢量控制、直接转矩控制效果进行对比分析。
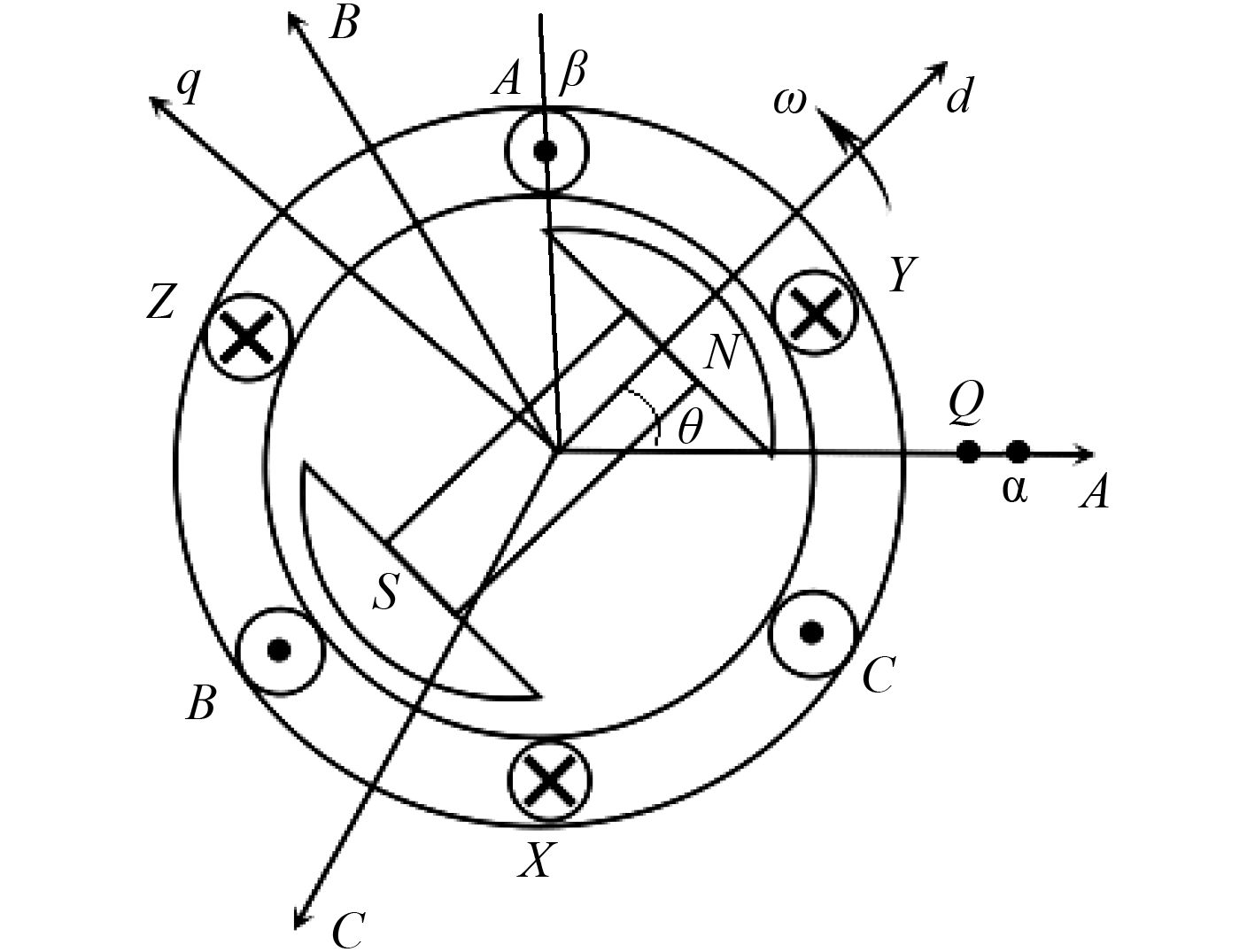
1 推进电机及负载建模 1.1 永磁同步电机模型永磁同步电机(PMSM)的磁场是由永磁体产生,既节约了能耗,又简化了电机结构,提高了电机的质能比。与交流电机相比,永磁同步电机没有激磁损耗,不需要从电网中吸收无功功率,提高了功率因素。PMSM 电机的物理模型如图 1所示。
|
图 1 PMSM 电机的物理模型 Fig. 1 The physical model of permanent magnet synchronous motor |
为了方便分析数学方程,运用坐标变换原理做线性化处理,将图 1 分解成不同坐标系,实现电机解耦控制,通常所用到的坐标有 ABC 三相静止坐标系、αβ 两相静止坐标系和 dq 两相旋转坐标系 3 种,如图 2所示。

|
图 2 不同坐标系及绕组示意图 Fig. 2 Different coordinate system and winding |
通常情况下,在永磁同步电机建立数学模型时一般忽略铁芯饱和,不考虑转子上的阻尼绕组,不计涡流损耗,不考虑谐波且感应电动势为理想正弦波,两相旋转坐标系中的 PMSM 的电压方程,即数学模型为[3]:
| $\left\{ {\begin{aligned}{{u_d} = {R_1}{i_d} + p{\psi _d} - \omega {\psi _q}}\text{,}\\{{u_q} = {R_1}{i_q} + P{\psi _q} - \omega {\psi _d}}\text{,}\end{aligned}} \right.$ | (1) |
式中:u d ,u q 分别为定子在 dq 坐标下直轴电压和交轴电压;i d ,i q 为定子在 dq 坐标系下的电流分量;ω 为转子磁链旋转角速度;ψ d ,ψ q 为定子在 dq 坐标系下的磁链分量。磁链方程为:
| $\left\{ {\begin{aligned}& {{\psi _d} = {\psi _f} + {L_d}{i_d}}\text{,}\\& {{\psi _q} = {L_q}{i_q}}\text{,}\end{aligned}} \right.$ | (2) |
式中:L d ,L q 分别为 PMSM 的直轴电感和交轴电感;ψ f 为永磁体的磁链。
电机转矩方程:
| $\begin{aligned}{T_e} = \displaystyle\frac{3}{2}{p_n}\left( {{\psi _d}{i_q} - {\psi _q}{i_d}} \right) = \displaystyle\frac{3}{2}{p_n}\left[ {{\psi _f}{i_q} + \left( {{L_d} - {L_q}} \right){i_d}{i_q}} \right]\text{,}\!\!\!\!\!\end{aligned}$ | (3) |
电机机械运动方程:
| $\displaystyle\frac{J}{{{p_n}}}\displaystyle\frac{{{\rm{d}}{\omega _e}}}{{{\rm{d}}t}} = {T_e} - F\displaystyle\frac{{{\omega _e}}}{{{p_n}}} - {T_L}\text{。}$ | (4) |
式中:T L 为负载转矩;J 为转动惯量;F 为阻尼系数;p n 为电机磁极对数;ω e 为转子电角度。
1.2 螺旋桨负载模型螺旋桨与船体之间具有强耦合性,一般将二者作为一个整体建模,数学模型如下:
螺旋桨转矩
| $M = K'{_M}\rho {D^3}\left( {{v_p}^2 + {D^2}{n^2}} \right)\text{,}$ | (5) |
螺旋桨推力
| $P = K'{_p}\rho {D^2}\left( {{v_p}^2 + {D^2}{n^2}} \right)\text{,}$ | (6) |
船桨系统运动方程
| $\left( {m + \Delta m} \right)\displaystyle\frac{{{\rm{d}}{v_s}}}{{{\rm{d}}t}} = P\left( {1 - t} \right) - R \text{,}$ | (7) |
船体与螺旋桨间的关系
| ${v_p} = {v_s}\left( {1 - \omega } \right)\text{,}$\text{,} | (8) |
有界形式的进速比
| $J' = \displaystyle\frac{{{v_p}}}{{\sqrt {{v_p}^2 + {D^2}{n^2}} }}\text{。}$ | (9) |
式中:v s 为船速;v p 为螺旋桨前进速度;ω 为伴流系数;ρ 为海水密度;D 为螺旋桨直径;n 为螺旋桨转速;t 为推力减额系数;R 为船舶阻力;m 为船体重量;Δm 为随船一起运动的附着水质量;K’ M 和 K’ p 分别为修正扭矩系数和推力系数,是 J′ 的函数。
2 推进电机调速控制策略 2.1 矢量控制(VC)推进电机的速度调节通常是通过控制电磁转矩来实现,对于表贴式三相永磁同步电机,电磁转矩表达式(3)可变为:
| ${T_e} = \displaystyle\frac{3}{2}{p_n}{\psi _f}{i_q}\text{。}$ | (10) |
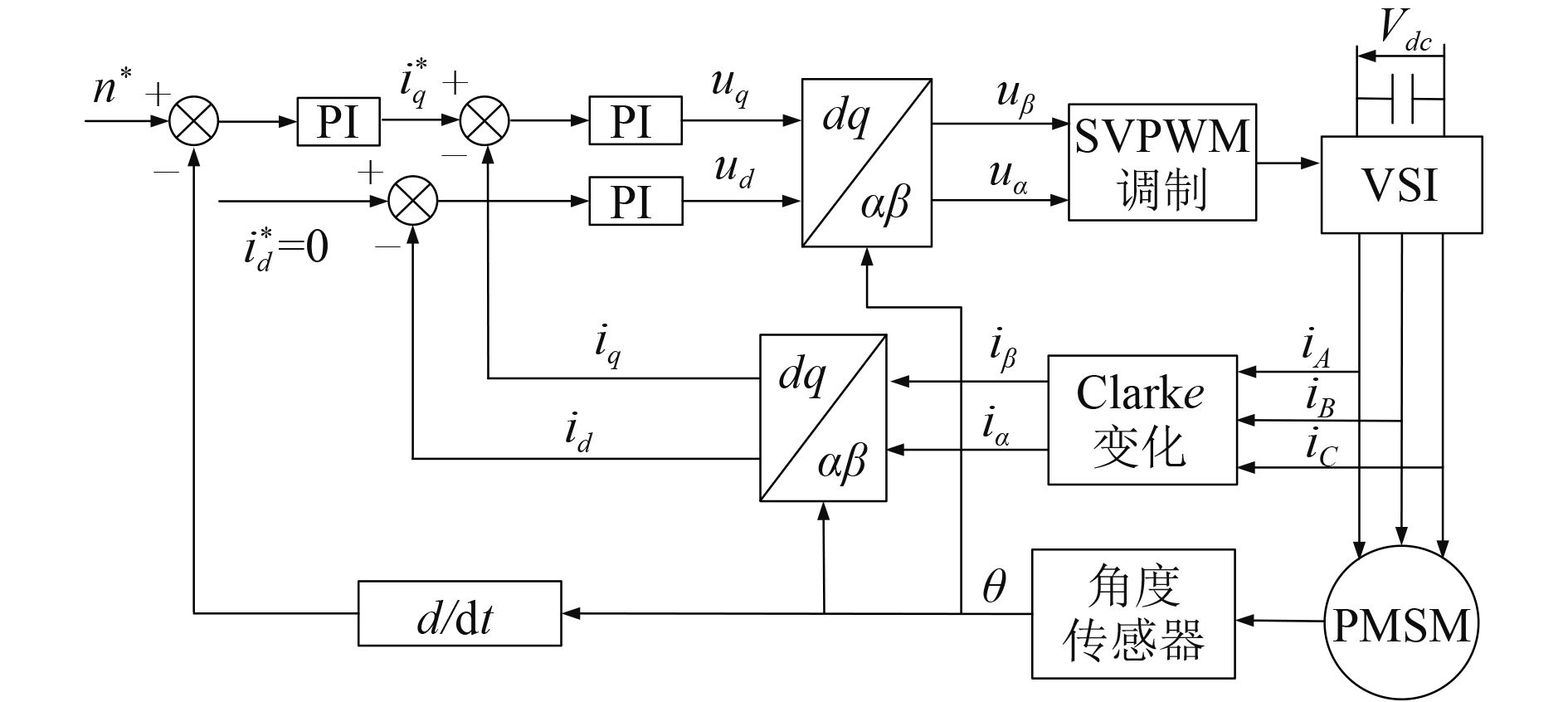
式(10)表明,决定电磁转矩的是定子电流在 q 轴上的分量,即转矩电流 i q 。在 dq 坐标系沿转子磁场定向的前提下,若控制 i d = 0,则在dq 坐标系中定子电流全是转矩电流且 i q 与 ψ f 始终相对静止。此时从转矩生成的角度,可将 PMSM 等效为他励直流电动机,控制 i q 可获得与他励直流电动机同样的转矩控制效果[4]。本文拟用 PMSM 矢量控制系统(VC),如图 3 所示。
图 3 中,PMSM 矢量控制系统为双闭环控制系统,外环为速度环,内环为电流环。系统由 1 个转速调节器、2 个电流调节器、3 个坐标变换模块、1 个空间电压矢量脉宽调制(SVPWM)模块、角度传感器、电压源逆变器和 PMSM[5]组成。系统将检测到的定子三相电流通过坐标变换转化为 dq 坐标系下的 2 个分量,分别与电流励磁分量给定值和转矩分量给定值做差,通过电流调节器生成参考电压,经坐标变换转化为两相静止坐标系下的分量,输入到 SVPWM 模块,然后产生 PWM 信号控制逆变器开关,驱动电机工作。其中定子电流励磁分量给定值设为 0,即 i d * = 0[6];转矩分量给定值由实际转速与给定转速的差值经速度调节器得到。该过程通过转子磁场定向和矢量变换,实现了定子电流励磁分量和转矩分量的解耦,分别控制 2 个分量可获得与直流电动机同样的控制品质。
|
图 3 PMSM 矢量控制系统图 Fig. 3 Permanent magnet synchronous motor vector control system |
电磁转矩的生成可看成是定子磁场和转子磁场相互作用的结果,电磁转矩表达式(3)可变形为
| ${T_e} = \displaystyle\frac{3}{2}{p_n}\displaystyle\frac{{|{\psi _s}|}}{{{L_q}}}{\psi _f}\sin \delta \text{。}$ | (11) |
式中: ψ s 为定子磁链;δ 为定子磁链和转子磁链之间的夹角。转子磁链 ψ f 为常数,若能控制定子磁链的幅值不变,则电磁转矩就只和负载角 δ 有关,通过控制 δ 可控制电磁转矩的大小,这是直接转矩控制的基本原理[7]。
PMSM 定子电压方程为:
| ${u_s} = {R_s}{i_s} + \displaystyle\frac{{{\rm{d}}{\psi _s}}}{{{\rm{d}}t}}\text{,}$ | (12) |
船用永磁同步电机的定子电阻很小,若忽略定子电阻的影响,则有
| ${u_s} = \displaystyle\frac{{{\rm{d}}{\psi _s}}}{{{\rm{d}}t}}\text{。}$ | (13) |
所以可通过外加电压 u s 来控制定子磁链的幅值和转速。在很短时间内依靠 u s 的作用使定子磁链加速旋转,而这期间转子速度来不及变化,由此可加大负载角 δ,若保持定子磁链的幅值不变,就可以使电磁转矩增大;若使定子磁链反向旋转,可使电磁转矩减小[8]。
本文拟用 PMSM 直接转矩控制系统(DTC)如图 4 所示,系统由速度调节器、滞环比较器、电压矢量开关表、Clark 变换、磁链和转矩观测器,角度传感器、电压源逆变器和 PMSM组成。系统将检测的定子三相电流i ABC 经过 Clark 变换后输入磁链和转矩观测器,估算出定子磁链和转矩的大小分别与磁链和转矩给定值做比较,其差值分别经过滞环比较器得到磁链控制信号 D ψ 和转矩控制信号 D T ,然后根据定子磁链位置 θ(N)、转矩控制信号 D T 和磁链控制信号 D ψ ,利用电压矢量开关表选择响应的电压矢量控制逆变器开关的通断,驱动电机运行。其中磁链给定信号为常数,转矩给定信号由实际转速与给定转速的差值经速度调节器得到的。该过程将转矩和磁链作为反馈信号,省去复杂的矢量变换,直接控制电磁转矩,从而达到调速的目的[9]。

|
图 4 PMSM 直接转矩控制系统图 Fig. 4 Permanent magnet synchronous motor direct torque control system |
除了永磁同步推进电机及螺旋桨负载建模和 2 种控制系统模型外,船舶电力推进系统中还有柴油发电机组、高低压负载等模块建模,参见文献[10]。
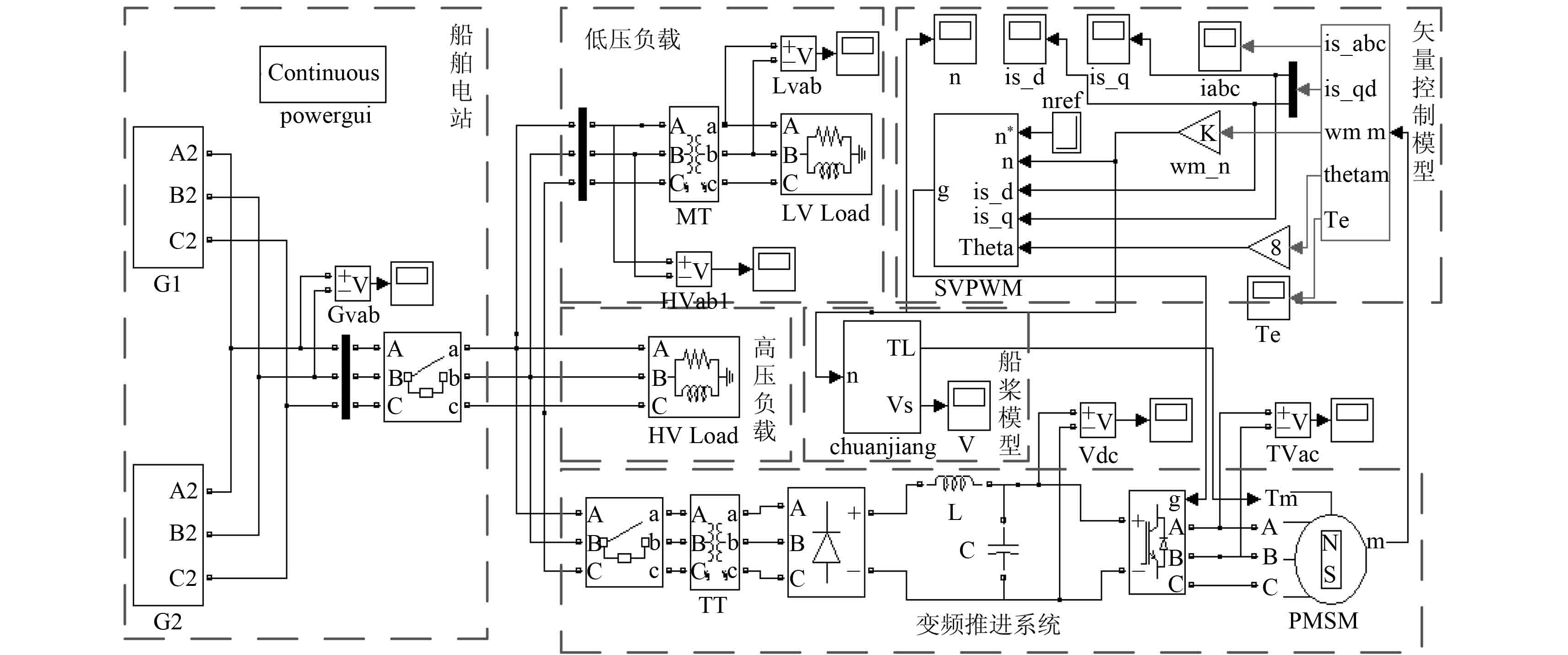
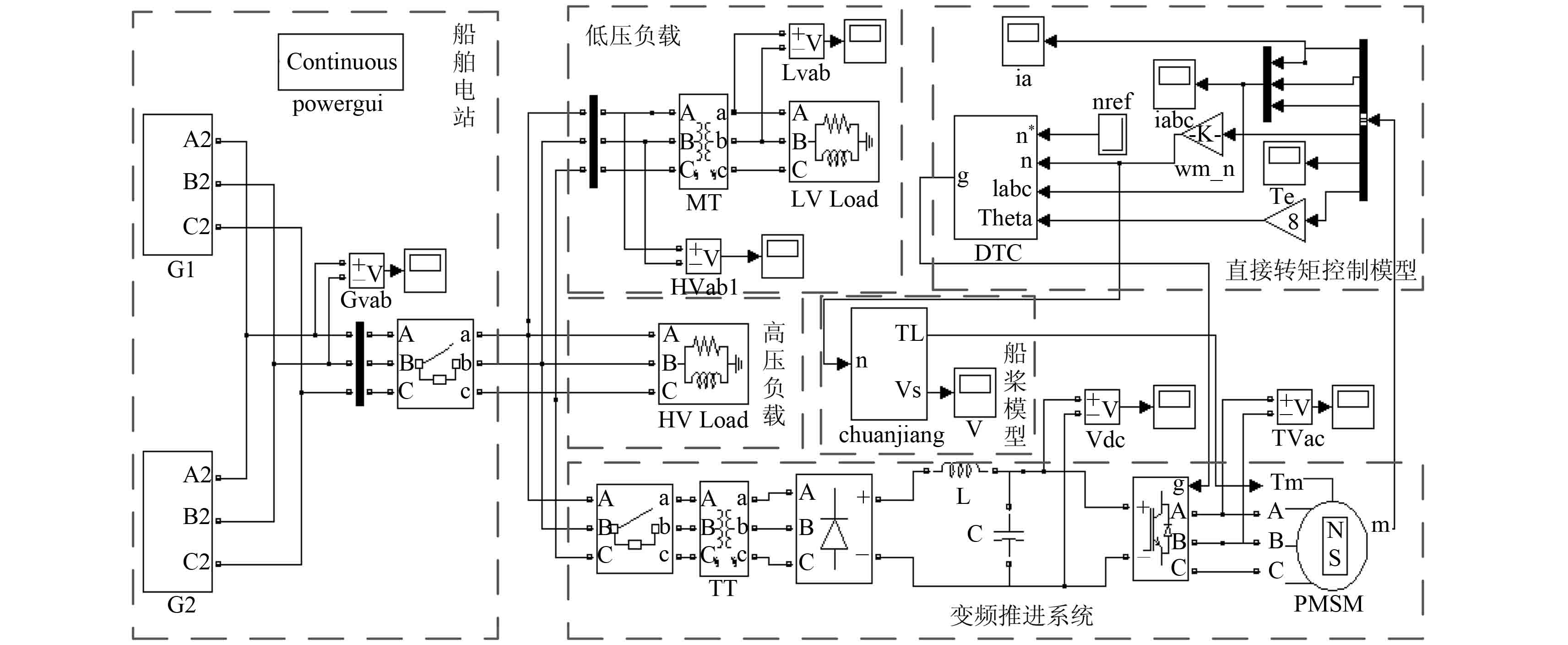
3.1 仿真对象及系统参数以某船为母型船,基于 VC 和 DTC 两种控制策略,在 Matlab/Simulink 仿真平台中建立船舶电力推进系统模型,如图 5 和图 6 所示。该船采用的是 6 600 V、50 Hz 船舶中压电力系统,由 2 个中心电站组成,每个电站有 2 台中压柴油发电机组;2 套推进系统,本文采用 1 个电站和 1 套推进器进行仿真分析。发电机组额定容量 3 388 kVA,额定电压 6 600 V,额定电流 296 A,功率因素 0.85,频率 50 Hz;推进电机的额定功率 4.088 MW,电机额定电压 660 V,额定转速 200 r/min,额定转矩Tn = 195 200 N·m;螺旋桨直径 3.6 m,桨叶数为 4,船体质量 16 229 t。
|
图 5 基于 VC 控制的船舶中压电力推进系统模型 Fig. 5 Based on the vector control of medium voltage electric propulsion system of the ship |
|
图 6 基于 DTC 控制的船舶中压电力推进系统模型 Fig. 6 Based on direct torque control of ship electric propulsion system |
仿真时间长度为 8 s,0 s 时发电机组启动,达到额定电压后接入电网;1 s 时船上其它负载投入运行;3 s 时船舶启动航行,初始转速设定为 100 r/min;4 s 时加速,设定速度变为 150 r/min;5 s 时加入负载转矩 100 kN·m 扰动,6 s 时扰动消失。电力系统中观测的主要参数有发电机有功功率、发电机端电压、励磁电压、频率。推进系统中观测的参数有推进电机转速、电磁转矩、定子三相电流、船速等。
3.3 仿真结果分析 3.3.1 船舶电站特性参数分析船舶电站主要特性参数的系统仿真结果如下:

|
图 7 船舶电站主要特性曲线 Fig. 7 Ship power station main characteristic curve |
2 种控制策略下船舶电站及负载的变化趋势基本相同,船舶电站的参数变化曲线如图 7 所示。取其中一种情况加以说明,1 s 时辅机及日常用电设备投入运行,发电机有功功率增大,经过短暂的过渡时间后进入稳定状态,励磁电压立刻上升然后回落至额定值,使得发电机端电压基本无变化,向电网稳定供电,同时发电机频率经过小范围下降后回到额定值;3 s 时大功率推进系统投入运行,发电机功率增大,励磁电流瞬时大范围增大以调节并补偿大功率负载造成发电机输出电压的压降,发电机输出电压下降 0.5%,对于电力系统影响可以忽略不计;4 s 加速时,发电机组的励磁电压、输出电压和频率与上一秒变化相同,但变化范围减小;5 s 加入负载扰动时,发电机组有功功率继续增大,推进系统的转矩呈现波动状态,此时励磁电压增大,发电机输出电压有少量的波动,电压波动不到 0.7%,频率降低;6 s 负载扰动消失,发电机组有功功率减小,励磁电压降低,发电机输出电压波动逐渐消失并稳定在额定值,频率增大然后稳定在额定值。整个过程中,频率相对保持稳定,最大变化率不超过 0.2%,在允许范围内。由此可见,基于 2 种控制策略的推进系统在运行时对于船舶电力系统的影响不大,都在可调节的范围内,故 2 种控制策略在船舶电力推进系统都有一定的适用性。
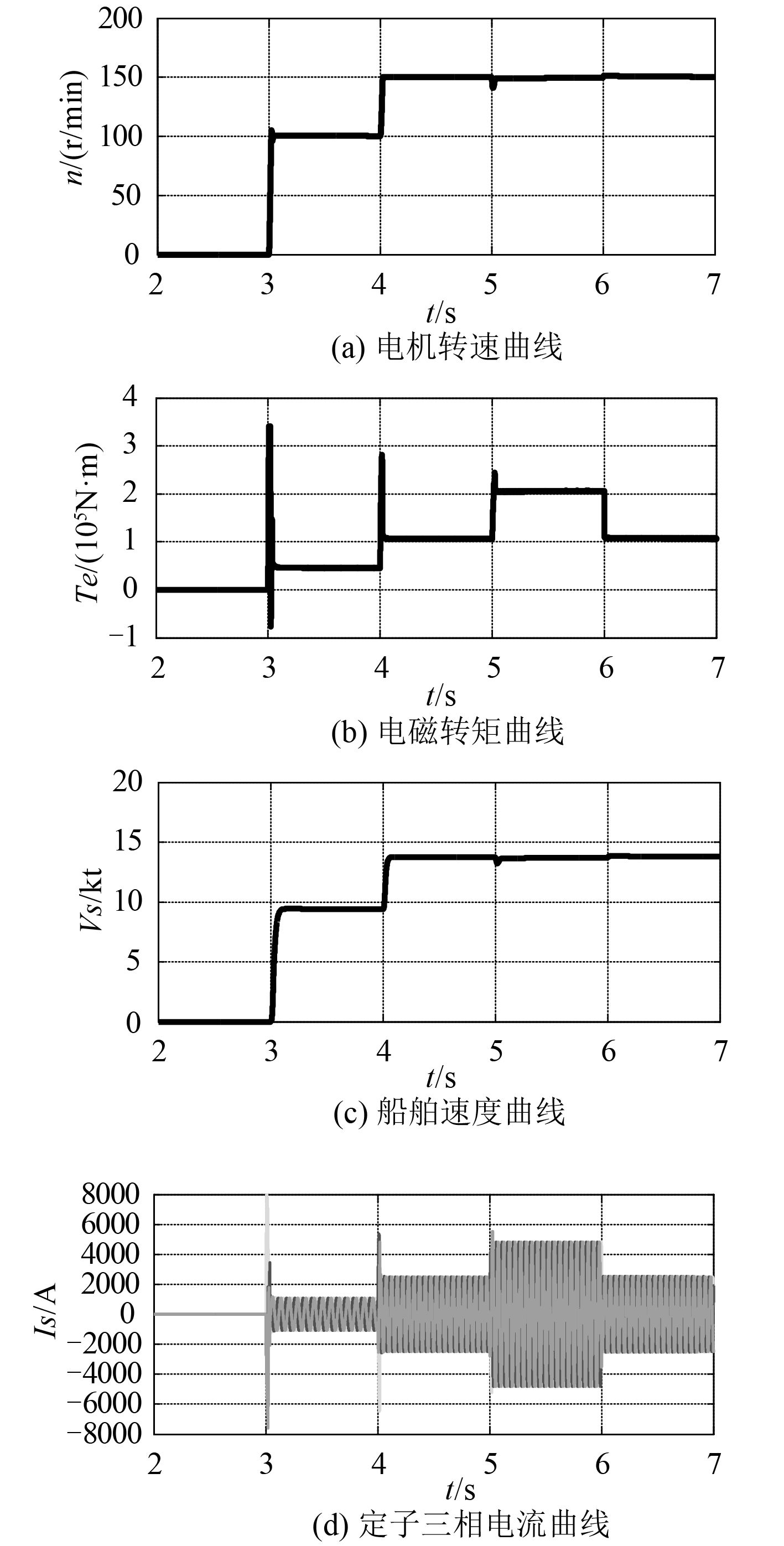
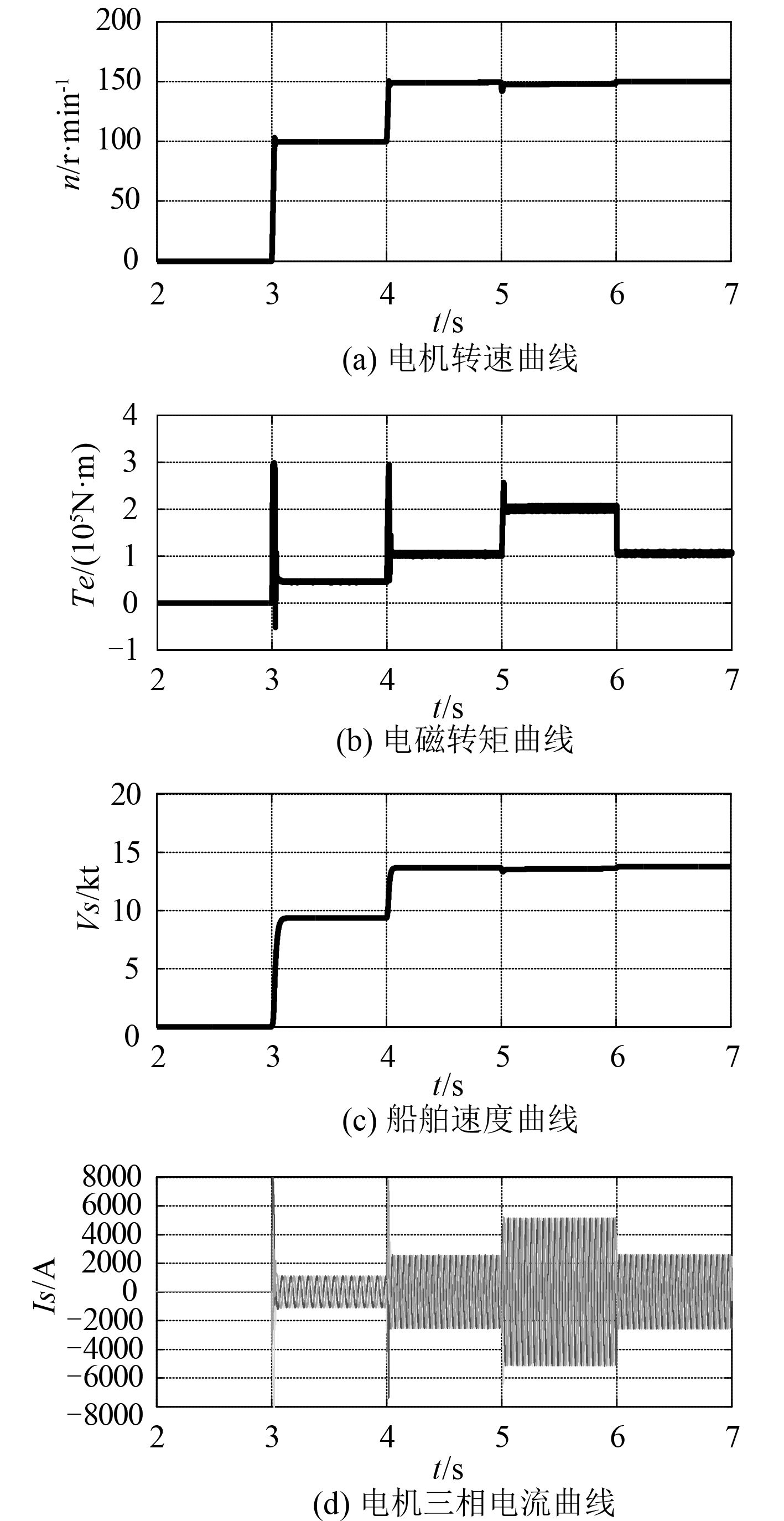
3.3.2 控制策略比较分析推进系统在最后 1 s 时间内稳定运行,性能指标没有变化,所以这里取 2~7 s 的时间段对推进系统性能指标进行观测,VC 和 DTC 控制策略仿真结果分别如图 8 和图 9 所示。
|
图 8 基于 VC 推进系统参数特性曲线 Fig. 8 Based on vector control propulsion system parameter characteristic curve |
|
图 9 基于 DTC 推进系统参数特性曲线 Fig. 9 Based on direct torque control characteristic curve of propulsion system parameters |
图 8 和图 9 分别为矢量控制(VC)和直接转矩控制(DTC)下的推进系统参数变化曲线,仿真结果显示,2种控制算法都有良好的动态响应,二者具体性能比较见表 1。在启动和加速时,2 种控制策略都有快速响应,其中 DTC 响应更快。因为 VC 的输出电压由电流调节器产生,存在时间上的滞后,而 DTC 通过滞环比较器和电压开关选择表输出电压,没有电流控制回路,可获得较大的电压变化率和较快的电流响应,所以 DTC 的转矩响应比 VC 快些。VC 系统的起动转矩比 DTC 系统大,且启动电流相对较小。VC 系统的速度环输出采取了电流限制,而 DTC 系统为防止过电流,速度环输出采取转矩限制措施,因此 DTC 的转矩被限制在一定范围,而起动电流比 VC 大。
系统加入负载扰动时,VC 系统的过渡时间稍长,转速的动态偏差也较大,但系统稳定后无静态偏差;而 DTC 系统转速动态偏差虽小,但系统稳定后存在静态偏差。而且在稳态时 VC 系统的转矩和定子电流变化相对平滑;DTC 系统的转矩波动范围相对较大,较为粗糙,定子电流脉动大,不是标准的正弦电流。在 VC 系统中,对定子电流的励磁和转矩分量进行解耦,并通过 PI 调节器分别对电流励磁分量和转矩分量进行调节,进而对转矩进行控制。该过程通过 PI 调节器实现了电流和转矩的连续控制,使得电流和转矩波形较为平滑,在稳态时由于转矩误差小并与负载转矩达到高度平衡,使得转速几乎没有静态偏差。而 DTC 系统采用滞环比较器,使得转矩和定子磁链总存在误差,稳态时转矩和电流脉动大;由于转矩波动大,与负载转矩之间总存在差值,使得转速难以精确达到期望值,存在静态偏差。
在整个过程中,2 种控制策略下的船舶速度都较为平稳,加速时船速响应快,负载扰动下,船速几乎没有变化,可见两种控制策略下的船舶电力推进系统灵活性好,操纵性强,而且具有很好的鲁棒性。
|
|
表 1 矢量控制与直接转矩控制系统性能比较 Tab.1 Vector control and direct torque control system performance comparison |
本文将永磁同步电机的矢量控制(VC)和直接转矩控制(DTC)策略分别应用于船舶电力推进系统,仿真结果表明:
1)2 种控制策略都有良好的动态响应,在工况变化时可以保证推进电机调速的准确性、快速性和稳定性。
2)矢量控制系统的算法相对复杂,但可以实现转矩的平滑控制,转矩和电流波动小;直接转矩控制算法相对简单,动态响应快,但转矩和电流波动较大。
3)2 种控制策略在船舶电力推进系统中都有一定的适用性,目前矢量控制策略已相对完善,直接转矩控制策略在减小转矩波动等方面仍有改进空间。
| [1] | 池飞飞. 船用永磁同步电机直接转矩控制仿真研究[D]. 武汉: 武汉理工大学, 2013. |
| [2] | 李崇坚. 交流同步电机调速系统[M]. 北京: 科学出版社, 2013: 292–294. |
| [3] | KRISHNAN R. 永磁无刷电机及其驱动技术[M]. 柴凤, 译. 北京: 机械工业出版社, 2013: 182–187. |
| [4] | 王成元, 夏加宽, 孙宜标. 现代电机控制技术[M]. 北京: 机械工业出版社, 2014. |
| [5] | 柯常国, 还芳, 王劲. 电力推进系统控制策略仿真[J]. 船电技术, 2016, 36 (4): 15–18. |
| [6] | JIA G X, ZHAO H C, SHAO H J. Simulation research on PMSM vector control system based on SVPWM[C]//Electrical and Control Engineering (ICECE), IEEE Conference Publications, 2010: 1936–1940. |
| [7] | 杨建飞, 胡育文. 永磁同步电机直接转矩控制转矩调节器设计[J]. 中国电机工程学报, 2013, 31 (9): 76–81. |
| [8] | 徐艳平, 钟彦儒. 扇区细分和占空比控制相结合的永磁同步电机直接转矩控制[J]. 中国电机工程学报, 2009, 29 (3): 102–108. |
| [9] | 郭昊昊, 刘彦呈, 任俊杰. 电力推进船舶中永磁电机直接转矩控制[J]. 电机与控制应用, 2011, 38 (11): 31–33. |
| [10] | 胡淼. 船舶电力推进永磁同步电机控制系统的研究[D]. 大连: 大连海事大学, 2013. |
 2017, Vol. 39
2017, Vol. 39
