随着全球能源供应的紧缺,石油、天然气的开采越来越受到重视。然而,我国对石油和天然气的开采主要停留在浅海区域,开采设备和技术人员的开采能力较弱。在世界各国对深海资源激烈竞争的国际形势和我国在海洋事业的投入力度加大的背景下,对海洋平台技术的研究显得尤为重要。
由于平台在恶劣的环境载荷作用下会产生波频摇荡运动和低频漂移运动,因此半潜平台立柱结构的设计和水动力特性的分析具有重要意义。许多学者针对水动力的各种特性对平台结构的影响做了大量研究。朱航等[1]以“海洋 981”平台进行研究,采用风洞实验研究了 0o~ 90o风载荷与平台表面风压力分布规律,进行了测压实验和测力实验,得到了表面风压系数,从而计算了平台所受的整体风载荷,实验结果与数值模拟结果基本相同。StDenis[2]把船舶的摇荡运动看成一个随机的过程,提出了船舶在不规则波中的运动计算方法。Koevin Kroukovsky[3]首次提出了切片理论,并计算了船舶的纵荡和垂荡运动。张金平等[4]对海洋平台波浪理论和波浪力计算方法的发展情况进行了综述,总结了不同波浪理论的优缺点和适用范围。宋安科[5]对第五半潜式平台进行了水动力分析,得到了水动力时间历程响应曲线。张凤伟[6]运用 AQWA 软件建立了风机安装船的频域计算模型,对安装船的水动力性能进行了系统地分析。吴澜等[7]针对深水半潜式平台,建立了三维水动力模型,使用 AQWA 软件进行数值模拟,研究了水动力系数变化特征并进行了运动响应预报。
本文在现役半潜平台立柱结构的基础上,设计 2 种不同立柱结构的平台,以满足平台在深水作业时的工作要求,运用 AQWE-LINE 模块对 2 种平台进行频域下的水动力分析,并对分析结果进行后处理,为半潜式平台的设计提供理论支撑。
1 两种立柱结构的半潜式海洋平台设计随着时间的推移,海洋石油的开发已经从浅水到深水,使开发深度进一步加大和开采能力进一步提高。由于半潜式海洋平台的优良性能,能够适应复杂的海况,使其最近几年发展迅速,逐步在石油、天然气的开发中占据重要地位,海洋平台正在向着钻井深度超过 12 000 m,工作水深超过 3 000 m的方向发展。
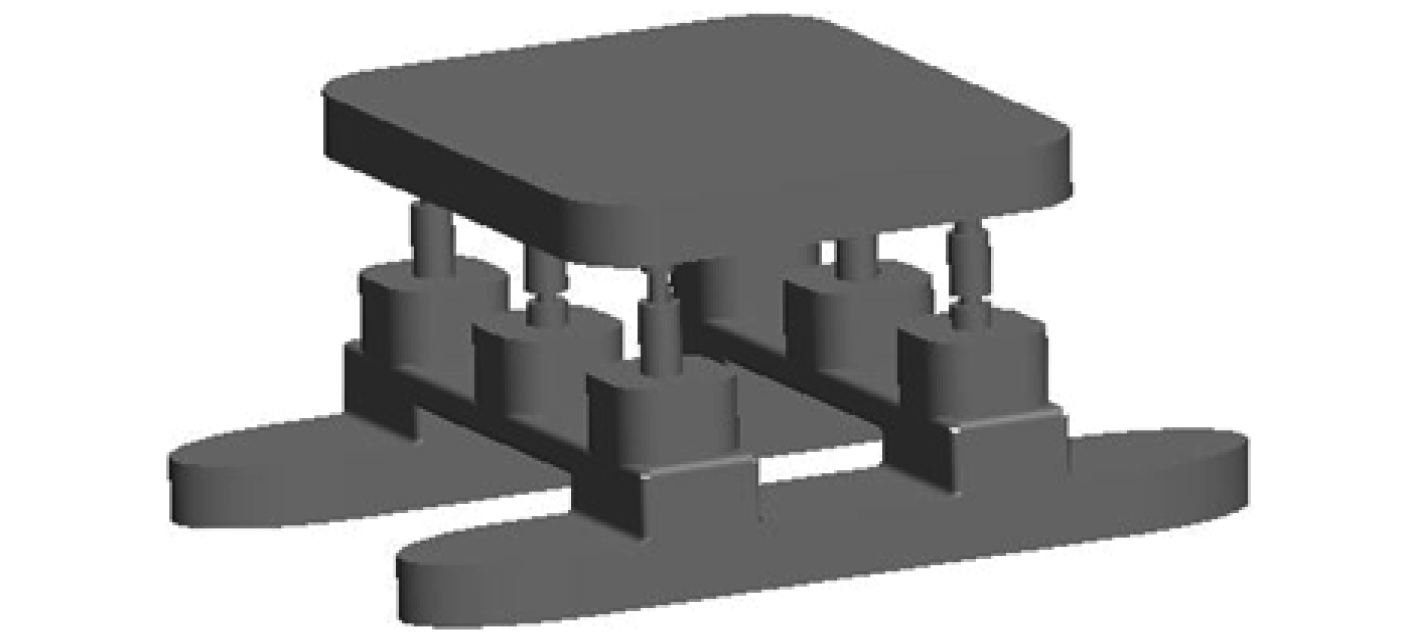
在海洋深水区域,平台所受的环境载荷极其恶劣,特别是波浪载荷对平台立柱影响极大,这就要求有优良的立柱结构来抵挡各种不规则波浪所产生的力对平台的影响,作业人员要时刻监控平台随时间变化的运动响应。根据 API RP 2SK《浮式结构定位系统的设计与分析规范》、CCS2005《海上移动平台规范》等规范,设计了 2 种不同立柱结构的半潜式海洋平台,由双浮体、六立柱,箱型封闭式上平台等组成,结构如图 1 和图 2 所示,尺寸如表 1 和表 2 所示。
|
图 1 A 型立柱结构平台 Fig. 1 The A type column structure platform |
|
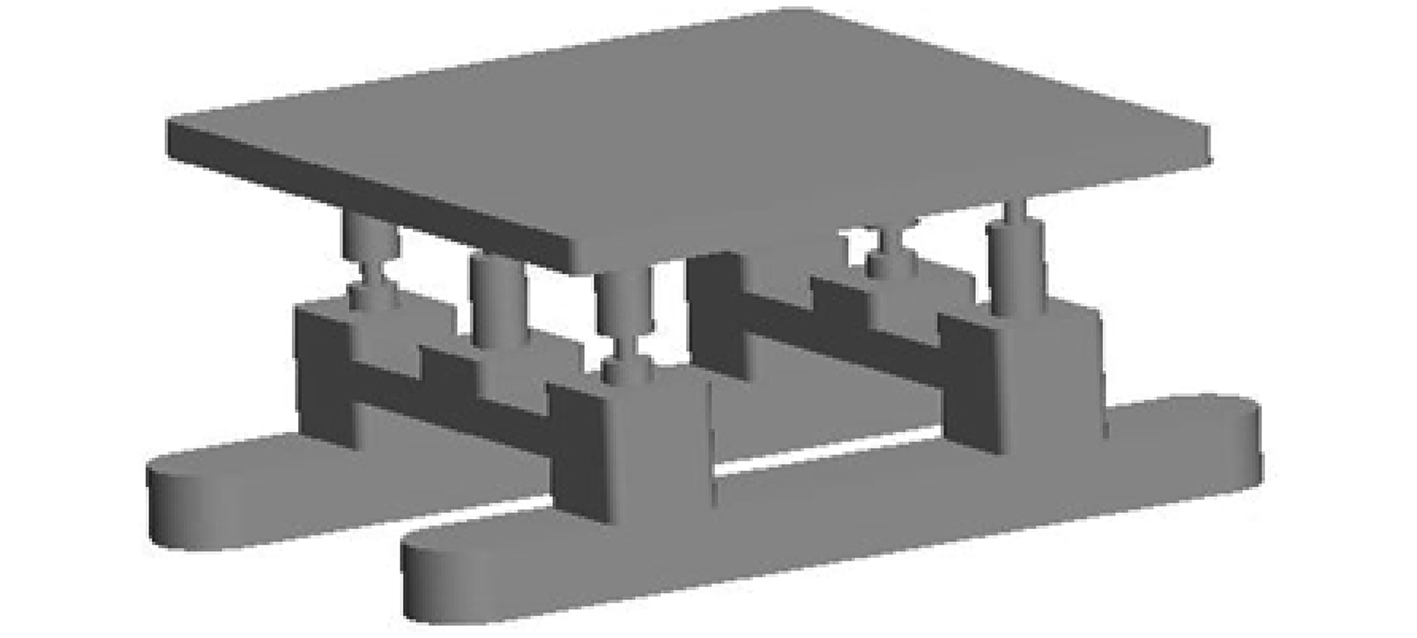
图 2 B 型立柱结构平台 Fig. 2 The B type column structure platform |
|
|
表 1 A 型立柱结构平台尺寸参数 Tab.1 Dimension parameters of A type column structure platform |
|
|
表 2 B 型立柱结构平台尺寸参数 Tab.2 Dimension parameters of A type column structure platform |
深水半潜式海洋平台由于工作环境的恶劣性,导致每时每刻承受环境载荷的影响,并且环境载荷具有随机性,导致平台会产生振动和变形,平台所受载荷主要有风载荷、浪载荷、流载荷,其中波浪载荷对平台的影响最大[8]。
波浪载荷的计算方法有特征波法和谱分析法[9]。特征波法选择单一规则波的有效波高、周期和平台的有关尺寸代入 Morison 公式(小尺寸结构物)或绕射理论公式(大尺寸结构物)计算波浪力。谱分析法认为波浪是许多不同周期和波高的规则波迭加成的不规则波,主要是利用概率论的方法和海浪谱来精确反应波浪力,一般选择不规则波 JONSWAP 谱,更有实际意义。
由北海联合波浪研究计划发展得到的 JONSWAP 谱,适用于欧洲北海地区,其形式为:
| $S\left( f \right) = \frac{{\alpha {g^2}}}{{{{\left( {2\pi } \right)}^4}{f^5}}}\exp \left[ { - \frac{5}{4}{{\left( {\frac{f}{{{f_0}}}} \right)}^{ - 4}}} \right]{\gamma ^4}\text{,}$ |
式中:f 为频率,Hz,
| $\begin{aligned}\alpha = \exp \left[ { - \frac{{{{\left( {f - {f_0}} \right)}^2}}}{{2{\sigma ^2}{f_0}^2}}} \right]{\text{;}}\;\;\;\;\sigma = \left\{ {\begin{array}{*{20}{c}}{{\sigma _a} = 0.07,f \leqslant {f_0}}\\{{\sigma _b} = 0.09,f > {f_0}}\end{array}} \right.\text{。}\end{aligned}$ |
式中:f 0 为 S(f)的极大值所对应的频率值,与风区参数 F 有关,
| ${f_0} = 2.64{\left( {g\frac{F}{{{U^2}}}} \right)^{ - 0.33}},\;\;\;\;\alpha = 0.066{\left( {g\frac{F}{{{U^2}}}} \right)^{ - 0.22}},\;\gamma = 3.3\text{。}$ |
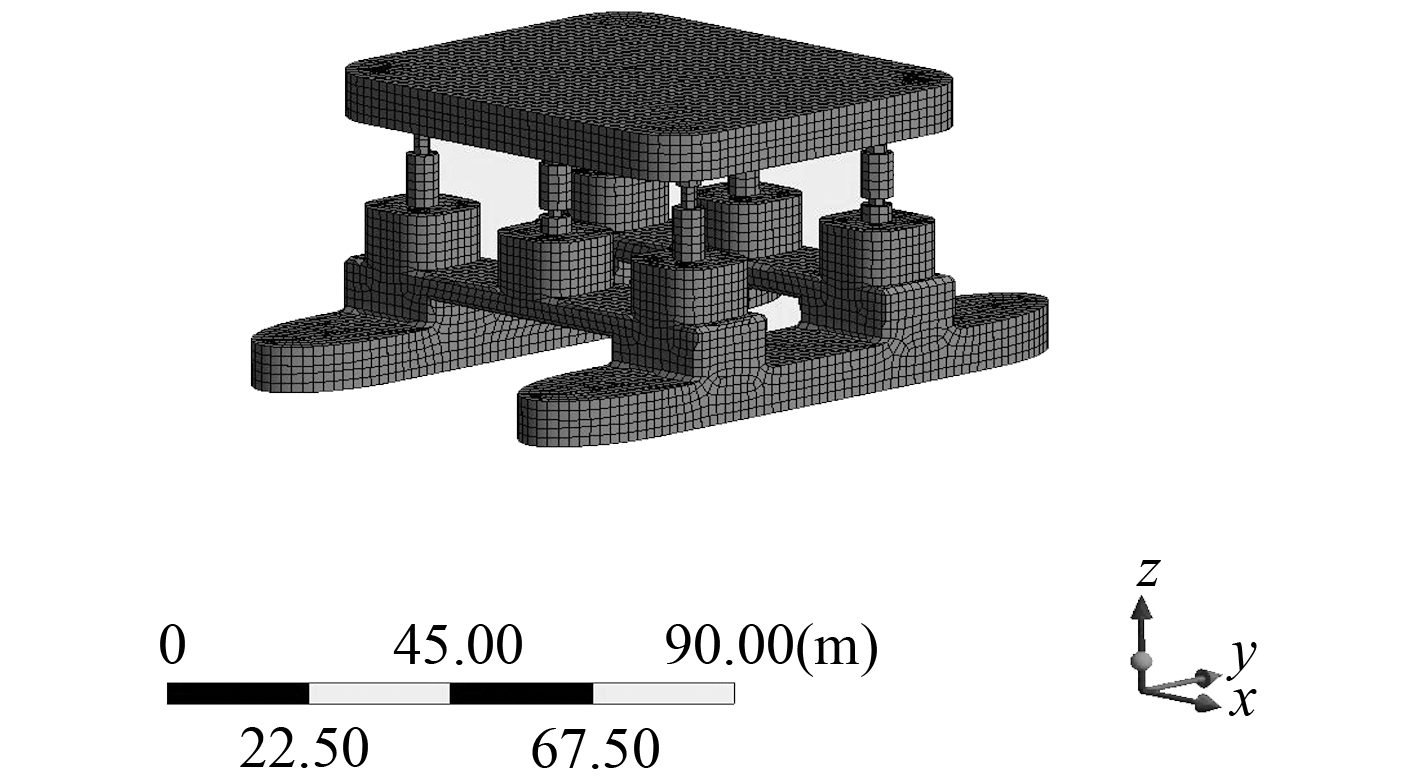
将上述结构简化模型导入 Workbench 中进行网格划分,由于分析海洋平台的水动力响应等数据,因此只要建立其湿表面模型即可。大尺度结构物的模型单元选择如 shell63 等 Panel 单元。首先将简化的模型进行抽壳、冷冻、切片处理,再要对水面在平台的高度进行设定,然后对模型进行重心质量和重心位置的设定,最后进行网格划分,划分网格时要考虑以下事情:1)划分的网格单元一般为四边形,单元尺寸小于入射波的波长;2)单元的横纵比尽量统一且要大于 1/3;3)网格单元要覆盖平台湿表面;4)一个波长要最少覆盖模型的 7 个最大的单元尺寸,网格越细,计算量越大,但可计算的波浪频率也增大。经过调节网格尺寸与大小,选择网格尺度为 3 m,采用均匀方式划分。平台水动力模型如图 3 和图 4 所示。
|
图 3 A 型立柱结构平台水动力模型 Fig. 3 The hydrodynamic model of A type column structure platform |
|
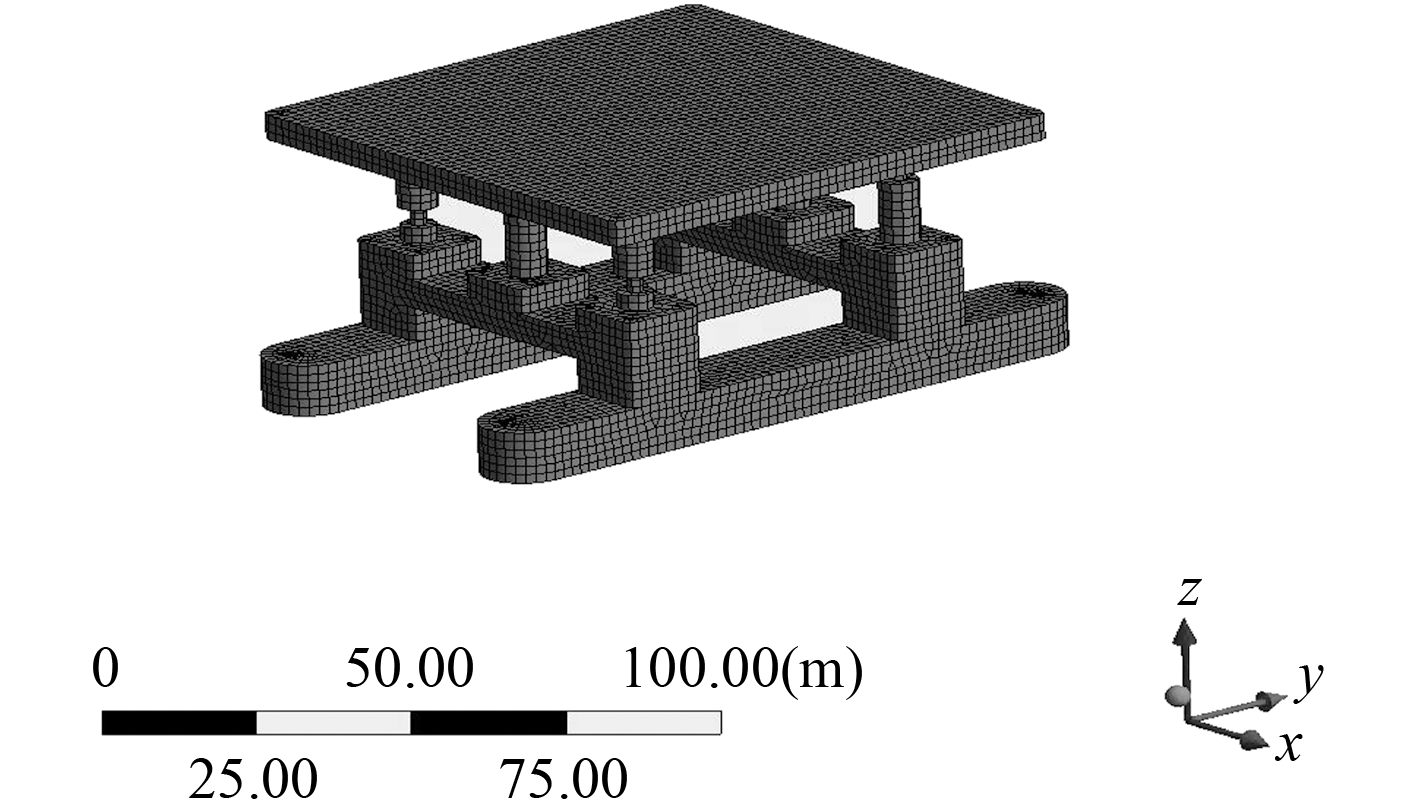
图 4 B 型立柱结构平台水动力模型 Fig. 4 The hydrodynamic model of B type column structure platform |
运用 AQWA-LINE 模块对两种不同立柱结构平台横荡、纵荡、垂荡、横摇、纵摇、首摇 6 个自由度方向的一阶波浪力和平台运动响应进行计算,并对计算结果进行后处理。
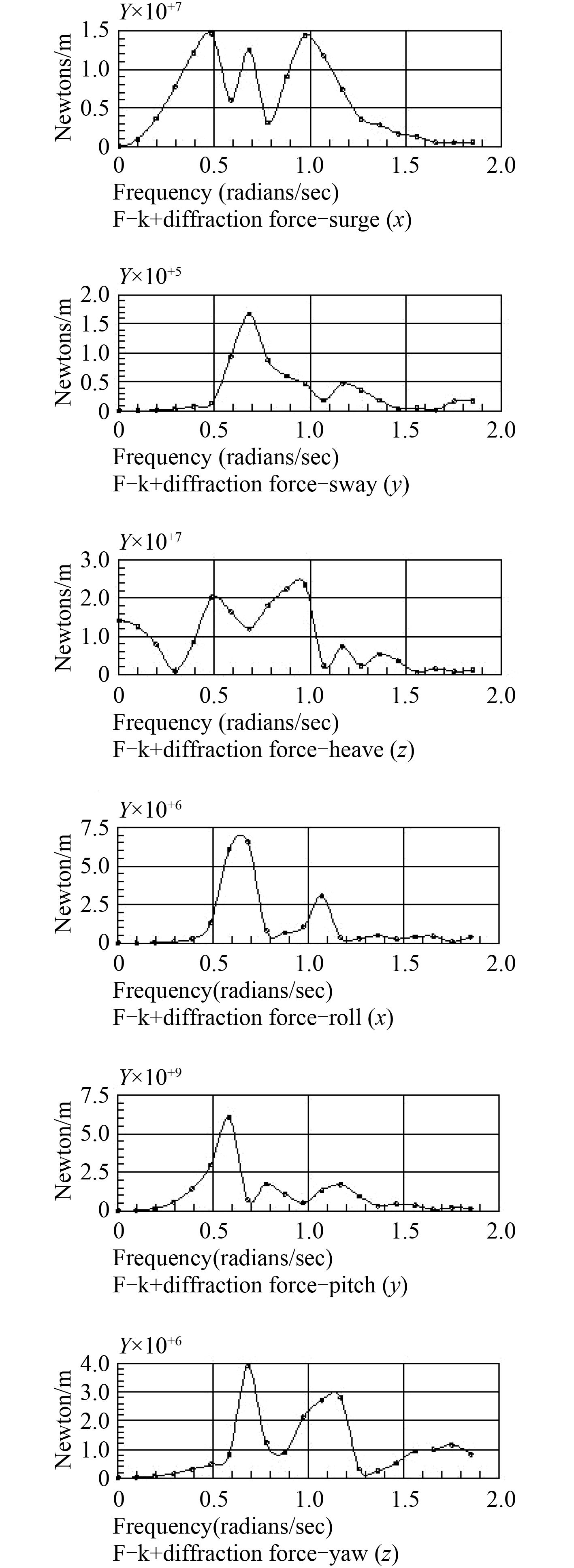
3.1 一阶波浪力一阶波浪力是与波浪频率相等的振荡力,引起低频运动,与波高成线性关系[10]。包括绕射波浪力和入射波浪力。波浪作用下半潜式平台周围波浪的绕射作用非常复杂,在线性理论为基础的假设中,目标平台为一个线性系统,平台在单一频率的入射波作用下,一阶波浪力的大小与入射波的幅值成正比。一阶波浪力通常以频率响应函数的形式来表示,即单位波浪作用下半潜式平台的系统响应。一阶波浪力的幅值响应,如图 5 和图 6 所示。
|
图 5 A 型立柱结构平台一阶波浪力(–180 o ~ +180o ) Fig. 5 The first order wave force of A type column structure platform(–180o to 180o) |

|
图 6 B 型立柱结构平台一阶波浪力(–180o ~ +180o) Fig. 6 The first order wave force of B type column structure platform(–180o to 180o) |
由于波浪载荷对平台垂荡方向运动影响较大,因此分析垂荡方向波浪力的大小尤为重要。A 型立柱平台垂荡方向在低频区域产生的力最大,为 2.4 × 10 7 N;B 型立柱平台垂荡方向在低频区域产生的最大力为 2.2 × 10 7 N;所以,B 型立柱平台在垂荡方向低频区域内较为稳定。
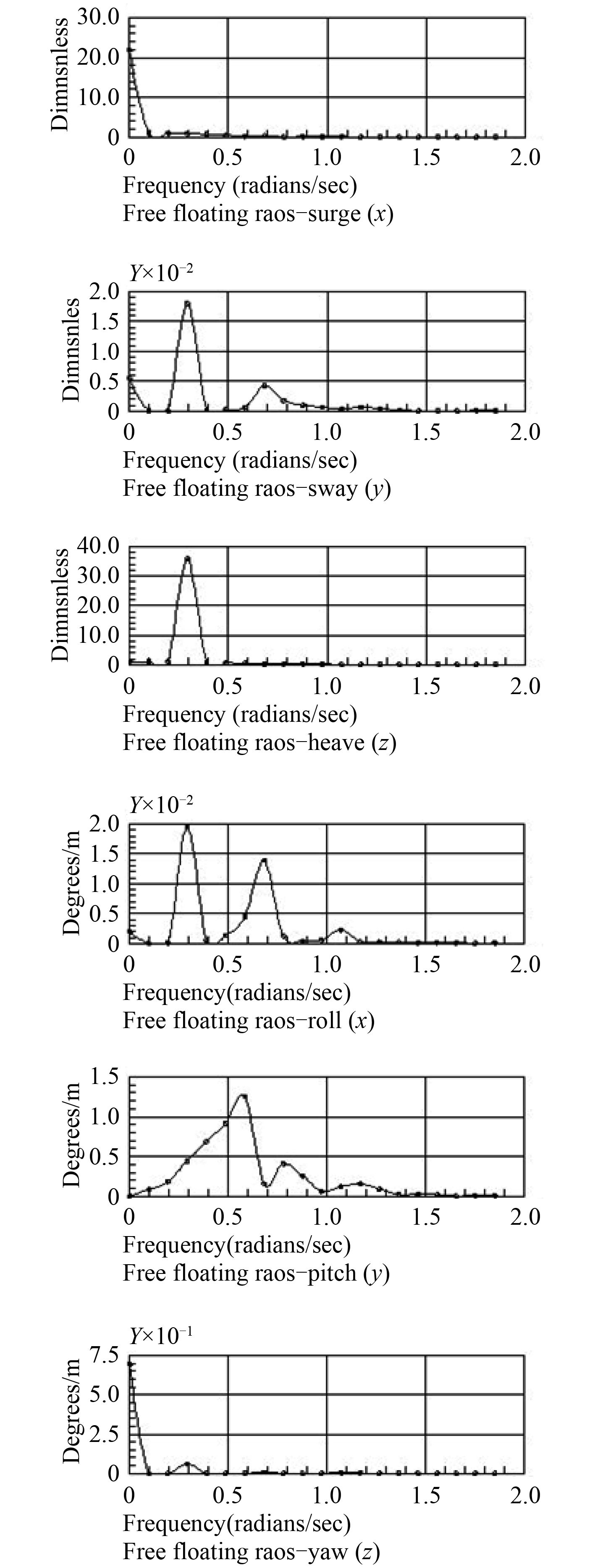
3.2 运动响应(RAO)在频域分析中,半潜式海洋平台在规则波的作用下存在 6 个自由度的运动和响应 6 个方向的波浪力和力矩,由于平台是一个线性系统,通过水动力分析能够得到这些量随时间的响应传递函数 RAO[11],表示单位波高作用下的运动响应。A 型平台与 B 型平台运动响应函数如图 7 和图 8 所示。
|
图 7 A 型平台运动响应函数 Fig. 7 The motion response function of A type platform |

|
图 8 B 型平台运动响应函数 Fig. 8 The motion response function of B type platform |
根据图像可看出,2 种平台的纵荡运动在低频区域明显,在高频区域趋于 0,说明纵荡运动主要呈现低频特性;A 型平台横荡运动在低频区域内高于 B 型平台,并且随着频率的增加而减小,说明横荡运动呈现低频特性和波频特性;同时,2 种平台垂荡运动在 0.4 ~ 1.0 rad/s 时变化剧烈,且 A 型平台垂荡方向变化比 B 型平台剧烈,呈现低频特性;而纵摇、横摇的变化趋势和垂荡一样,主要是波频特性。所以,A 型平台在垂荡方向运动随时间变化的运动响应比 B 型平台更明显,B 型立柱平台更为稳定。
4 两种平台 Ansys/WorkBench 后处理分析通过后处理功能,显示波浪作用方向与平台浮体方向成 90o下 2 种平台运动响应(RAO),并对分析结果进行对比。其中波浪频率设置为 0.233 Hz,波高设置为 2 m。
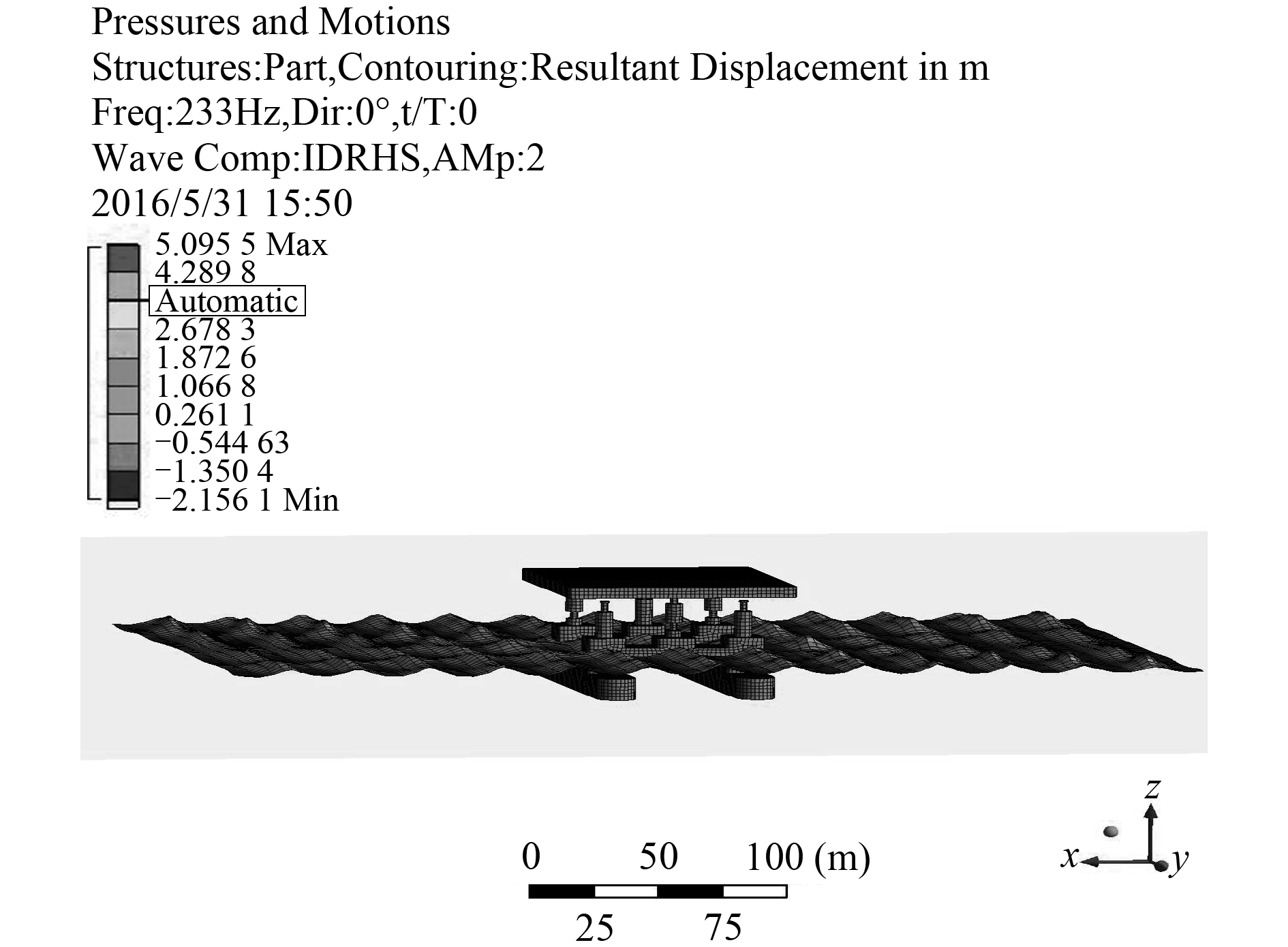
利用平台 6 个自由度的运动响应求出每个波浪频率下的运动响应,再叠加即可得到多个波浪作用下的平台运动。通过 Workbench 的后处理可以得到 2 种平台幅值运动响应(RAO)云图[12],如图 9 和图 10 所示,在频率为 0.233 Hz,幅值为 2 m 时,A 型平台的最大位移为 5.195 9 m,B 型平台的最大位移为 5.095 5 m,均出现在平台迎浪方向的波峰处,B 型平台的位移略小于 A 型平台。

|
图 9 A 型平台运动响应 RAO 云图 Fig. 9 The RAO cloud image of motion response of A type platform |
|
图 10 B 型平台运动响应 RAO 云图 Fig. 10 The RAO cloud image of motion response of B type platform |
本文以现役海洋平台为基础,设计了 2 种不同立柱结构的半潜式海洋平台,并建立水动力数值模型,运用 AQWA 软件进行数值计算,得到不同立柱结构运动响应等数据。结果分析如下:
1)在相同环境载荷作用下,计算得到 2 种平台 6 个自由度方向所受一阶波浪力随时间变化的曲线。由于海洋平台的主要作用是钻井,所以垂荡方向受力的大小决定了平台的稳定性。根据计算结果,B 型平台比 A 型平台在垂荡方向更加稳定。
2)在相同环境载荷作用下,计算得到 2 种平台 6 个自由度方向随时间变化的运动响应,得到函数图像,可以得知平台运动变化趋势,为响应预报做准备。同时,在低频区域内,A 型平台比 B 型平台运动更加剧烈,所以 B 型平台在垂荡方向更加稳定。最后,运用 Workbench 对 2 种立柱平台运动响应(RAO)进行后处理,得到结果与函数曲线相吻合,为平台试验模型建立提供了理论依据。
| [1] | 朱航, 马哲. 梯度风作用下HYSY-981半潜式钻井平台平面风载荷与表面风压分布研究[J]. 航海工程, 2007, 22 (4): 270–274. |
| [2] | St. D enis, M. and Pierson, W. J. Jr. On the motions of ships in confused sesa[J]. Trans, SNAME, 1953, 61, 280–358. |
| [3] | KOEVIN-KROUKOVSKY B V. Investigtion of ship motion[J]. Trans, SNAME, 1955, 63. |
| [4] | 张金平, 段艳丽, 刘学虎. 海洋平台波浪载荷计算方法的分析和建议[J]. 石油矿场机械, 2006 (03): 10–14. DOI: 10.3969/j.issn.1001-3482.2006.03.004 |
| [5] | 宋安科. 深水半潜式钻井平台锚泊系统方案设计与分析[D]. 哈尔滨: 哈尔滨工程大学, 2008. |
| [6] | 张凤伟. 风机安装船海上作业运动及其流体动力分析[D]. 哈尔滨: 哈尔滨工程大学, 2012. |
| [7] | 吴澜. 基于AQWA的半潜式平台水动力特性研究[J]. 中国海洋平台, 2014, 29 (5): 29–30. |
| [8] | 贾德君, 李范春. 深水半潜式海洋平台极限波浪环境载荷计算[J]. 强度与环境, 2016, 43 (1): 41–48. |
| [9] | 黄祥鹿, 陆鑫森. 海洋工程流体力学及结构动力响应[M]. 上海: 上海交通大学出版社, 1992. |
| [10] | 沈庆, 江召兵. 浮体和浮式多体系统流固耦合动力分析[M]. 北京: 科学出版社, 2011. |
| [11] | YANG Min-dong, TENG Bin. Static and Dynamic Analysis of Mooring Lines by Nonlinear Finite Element Method[J]. 中国海洋工程(英文版), 2010, 24 (3): 417–430. |
| [12] | 白雪平. 深水半潜式平台锚泊系统设计研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. |
 2017, Vol. 39
2017, Vol. 39
