船舶及航运行业是工业制造及交通运输中的重要产业,但其能耗及碳排放的增长幅度却远超其他行业水平[1],国际海事组织 IMO 已于 2009 年 MEPC59 次会议上通过了“新船能效设计指数(EEDI)计算方法临时导则”作为绿色船舶设计的关键参考性指标,旨在通过限制船舶 CO 2 排放来进行船型优化,并促进节能环保船型的开发。另一方面,集装箱船作为目前三大主流船型之一,所产生的温室气体排放量在所有船型中占比最高[2],其载重吨位也正逐年快速增加,集装箱船的超大型化已成为近年来的趋势,然而我国目前有超过 57% 集装箱船能效设计水平未达到 IMO 规定的 EEDI 最低要求[3],因此提高超大型集装箱船的能效设计水平为应对全球变暖问题具有十分重要的意义。
EEDI(Energy Efficiency Design Index)是集船舶快速性、耐波性、节能减排技术等于一体的衡量船舶 CO 2 排放量的指标,该指标的制定是为了提高船舶能效和降低二氧化碳的排放。刘飞[4]对 EEDI 公式本身、适用船型、基线公式、折减系数和敏感性因素均做了较为全面的分析;刘亮[5]对关键参数失速系数 f w 进行了深入研究,采用不同计算方法得到波浪增阻并与实验值进行比较,为精确计算失速系数提供了参考依据;在此基础上,封培元等[6]进一步考虑了船机桨之间的匹配问题,提出了一种计算结果较 IMO 推荐方法更为保守的失速系数计算方法;颜林[7]在对国内大量实船进行能效水平评估的基础上,提出了节能百分比计算公式,并进一步讨论了设计航速对 EEDI 的影响;而程红蓉等[8]则直接利用 Friendship-Framework 船型优化软件平台,结合 EEDI,对 1 艘油船进行了主尺度结合型线的多目标优化。
本文针对超大型集装箱船 10 000TEU,维持其服务航速和推进效率不变,在船舶初步设计阶段通过对其型线进行优化、减少航行阻力,以降低该超大型集装箱船对装机功率(主机功率)的需求,从而减少燃油消耗、降低 CO 2 排放量,达到 IMO 对能效设计指数的要求。在对该目标船型优化过程中,利用平移法与径向基函数方法进行船体曲面重构,采用基于 Rankine 源非线性势流理论的 SHIPFLOW 软件计算兴波阻力,考虑到优化过程中船型变化对船体表面边界层的影响,由 SHIPFLOW 边界层动量积分模块计算摩擦阻力,以提高总阻力的预报精度,波浪增阻由 HydroSTAR 计算,最后通过全局优化算法和局部优化算法相结合的方式在设计空间中探索满足排水量约束条件的最优船型。
1 EEDI 设计指数及基线公式EEDI(Energy Efficiency Design Index)作为衡量新造船舶 CO 2 排放量的指标,是当今船舶节能减排领域关注的焦点,最初由巴西在 IMO 环境保护委员会(MEPC)第 58 次会议上提出,其计算公式如下:
| $EEDI = \displaystyle\frac{{{E_{ME}} + {E_{AE}} + {E_{PTI}} - {E_{eff}}}}{{{f_i} \cdot {f_c} \cdot {f_l} \cdot Capacity \cdot {f_w} \cdot {V_{ref}}}}\text{,}$ | (1) |
其中:
| $\begin{split}\left\{ \begin{array}{l}\!\!\!\!{E_{ME}}\! =\! \left( {\displaystyle\prod\limits_{j = 1}^n {{f_j}} } \right)\left( {\displaystyle\sum\limits_{i = 1}^{nME} {{P_{ME(i)}} \cdot {C_{FME(i)}} \cdot SF{C_{ME(i)}}} } \right)\text{,}\\[13pt]\!\!\!\!{E_{AE}}\! = \!{P_{AE}} \cdot {C_{FAE}} \cdot SF{C_{AE}}\text{,}\\[4pt]\!\!\!\!{E_{PTI}}\! = \! \left( {\displaystyle\prod\limits_{j = 1}^n {{f_j}} \! \cdot\!\!\!\! \displaystyle\sum\limits_{i = 1}^{nPTI} {{P_{PTI(i)}}}\!\! - \!\!\sum\limits_{i = 1}^{neff} {{f_{eff(i)}} \!\cdot \!{P_{AEeff(i)}}} } \!\right) \times\\[7pt] \quad\quad{C_{FAE}} \!\cdot \!S\!F{C_{AE}}\text{,}\\[4pt]\!\!\!\!{E_{eff}} \!=\! \displaystyle\sum\limits_{i = 1}^{neff} {{f_{eff(i)}} \cdot {P_{eff(i)}} \cdot {C_{FME}} \cdot SF{C_{ME}}} \text{。}\end{array} \right.\end{split}$ | (2) |
式中各参数的含义文献[5]中已经有详细介绍。本文在 EEDI 计算过程中,考虑了该超大型集装箱船在远东——北美西海岸航线航行时失速系数f w 对 EEDI 的影响(采用 IMO 目前推荐方法),较高精度地估计了该船在该海域航行时 CO 2 的排放量,表 1 给出了主要参数。
|
|
表 1 10 000 TEU 集装箱船能效信息 Tab.1 Energy efficiency information for 10 000 TEU |
在提出能效设计指数概念的基础上,国际海事组织于 2011 年 8 月提出了各船型 EEDI 基线回归公式,并制定了不同阶段相对于该基准线的 EEDI 值的折减率 X,因此新造船舶实际需要满足的 EEDI 值如下式:
| $Baseline = a \cdot Dead{\kern 1pt} {\kern 1pt} Weigh{t^{ - c}}\text{,}$ | (3) |
| $Required{\rm{ }}EEDI = \left( {1 - X/100} \right) \cdot Baseline{\rm{ }}Value\text{。}$ | (4) |
对于集装箱船,经数据库统计回归可得参数 a 和 c 的取值分别为 174.22 和 0.201,现阶段的折减率 X 为 10(施行年限为 2015.1.1 – 2019.12.31)。因此文中该万箱集装箱船的 EEDI 基准值为 17.761 g/t·nm,而目前考虑折减系数后实际需要满足的 EEDI 规定值为 15.985 g/t·nm。
2 船体型线优化虽然降低主机功率和减小服务航速可以有效控制能效设计水平,但降低航速的方式未综合考虑船舶实际营运情况,并不适用于所有船型,且通过该方式降低 EEDI 仅能满足 IMO 设定的基准值,难以达到计及折减系数后的要求[5]。因此本文在维持服务航速和推进效率不变的前提下,以降低对主机功率的需求、减少燃油消耗为出发点,对该超大型集装箱船的阻力性能进行优化。
2.1 优化目标与算法通过对船体型线的优化可以有效减小船舶航行阻力从而降低主机功率、减少温室气体的排放,以满足 IMO 对新造船舶能效设计指数的要求,本文以超大型集装箱船 10 000TEU 在服务航速下(Fn = 0.218)的总阻力为目标函数 ,即
| ${\rm {Min}}imize[f]\text{,}$ | (5) |
式中f 为总阻力系数 C t 。
为了保证优化后船型的合理性,以排水量作为约束条件,优化后的船体排水量(V)与母型船(V
0)相差控制在 ± 0.5%以内,即:
为了找到满足约束条件下的最优船型,文中首先采用非劣分类遗传算法 NSGA-II 对整个设计空间进行探索,并以此得到近似全局最优解,然后通过序列二次规划算法(NLPQL)对其进行反复迭代和更新逐步逼近精确的全局最优解。
2.2 船体曲面重构本文采用基于整体(平移法)与局部(径向基函数法)相结合的几何重构方法对万箱集装箱船进行船体表面的几何变形。
2.2.1 平移法[9](Shifting Method)横截面面积曲线(SAC)目标船型的横截面面积曲线由如下公式进行表达:
| ${f^n}(x) = {f^0}(x) + g(x,{\alpha _1},{\alpha _2})\text{,}$ | (6) |
| $g = \left\{ {\begin{array}{*{20}{c}}\!\!\!\!\!\!{{\alpha _1}{{[\{ 0.5(1 \!-\! {\rm {cos}}2\pi \displaystyle\frac{{x - {x_1}}}{{{\alpha _2} - {x_2}}})\} ]}^{1/2}},{x_1}\! \leqslant\! x\! \leqslant \!{\alpha _2}}\text{,}\\[10pt]\!\!\!\!\!\!{ - {\alpha _1}{{[\{ 0.5(1 \!- \!{\rm {cos}}2\pi \displaystyle\frac{{x - {\alpha _2}}}{{{\alpha _2} - {x_2}}})\} ]}^{1/2}},{\rm{ }}{\alpha_2} \!\leqslant\! x\! \leqslant\! {x _2}}\text{,}\\[10pt]{{\rm{0, \quad \quad \quad\quad \quad \quad \quad \quad \quad \quad \quad\quad \quad\!\!\!\!\!\!\! elsewhere}}}\text{。}\end{array}} \right.$ | (7) |
式中:
若
| $S({{x}}) = \sum\limits_{j = 1}^N {{\lambda _j}\phi (\left\| {{{x}} - {{{x}}_{{j}}}} \right\|)} + p({{x}})\text{,}$ | (8) |
式中:
选用具有二阶连续性的 Wendland[10]方程
| $p({{x}}) = {c_1} + {c_2}x + {c_3}y + {c_4}z\text{,}$ | (9) |
| $\phi (\left\| {{x}} \right\|) = {(1 - \left\| {{x}} \right\|)^4}(4\left\| {{x}} \right\|{\rm{ + }}1)\text{。}$ | (10) |
则系数
| $S({{{x}}_j}) = {{{f}}_j}\;\;; \;\;\sum\limits_{j = 1}^N {{\lambda _j}p({{{x}}_j}) = 0, j = 1,...,N} \text{,}$ | (11) |
| $\left( {\begin{array}{*{20}{c}}{{f}}\\0\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{{M}}&{{P}}\\{{{{P}}^{\rm T}}}&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}{\bf{\lambda }}\\{\bf{c}}\end{array}} \right)\text{,}$ | (12) |
式中:
| $\begin{array}{l}{M_{i,j}} = \phi \;\;\left( {\left\| {{{{x}}_i} - {{{x}}_j}} \right\|} \right)\;\;;{P_{i,j}} = {p_j}({{{x}}_i}), \\[5pt]\;\;\;\;\;\;\;\; \;\;\;i=1\;\;,\;\;...\;\;,N,j = 1\;\;,\;\;...\;\;,4\text{。}\end{array}$ | (13) |
如图 1 所示,数字旁边的黑色控制点表示移动控制点,用于球鼻首和船体进流段处的局部几何重构;深灰色为固定控制点,用于避免因局部曲率变化过大而变换出较为畸形的中间船型,各优化变量的详细信息见表 2。

|
图 1 RBF 固定控制点与移动控制点 Fig. 1 RBF fixed nodes and movable nodes |
|
|
表 2 10 000 TEU优化信息 Tab.2 10 000 TEU optimization information |
船体总阻力由兴波阻力和摩擦阻力相加获得,分别由 Shipflow 软件的势流模块和边界层动量积分模块进行计算。该势流求解器在求解兴波阻力时同时采用船体表面压力积分法和船后波形能量积分法 2 种不同的方法。由于优化过程中船体艏部可能会出现曲率突变或者存在折角的地方、计算网格容易存在缺陷,而采用基于 Rankine 源势流理论的压力积分方法计算兴波阻力时其结果的稳定性往往对船身网格质量的依赖性较大,实际计算过程中容易出现发散或阻力为负的结果,而采用能量法便可以避免这种情况。另外,由于船体表面压力的数值积分精度不足等原因[11],采用能量法计算兴波阻力,在精度上也要优于压力积分法。钱建魁等[12]则通过船模阻力实验对能量法的阻力预报精度进行了验证,结果显示在
整个优化过程分为 2 步:在第 1 步利用遗传算法(NSGA-II)全局寻优阶段,经过 1 280 次优化后得到了阻力值的全局近似最优解;在此基础上,采用序列二次规划法(NLPQL)将上一步得到的近似最优解作为局部寻优的初始设计点,在该点附近运用梯度算法进行优化,直至逼近全局最优解,经过 13 次迭代后计算收敛,优化结束。
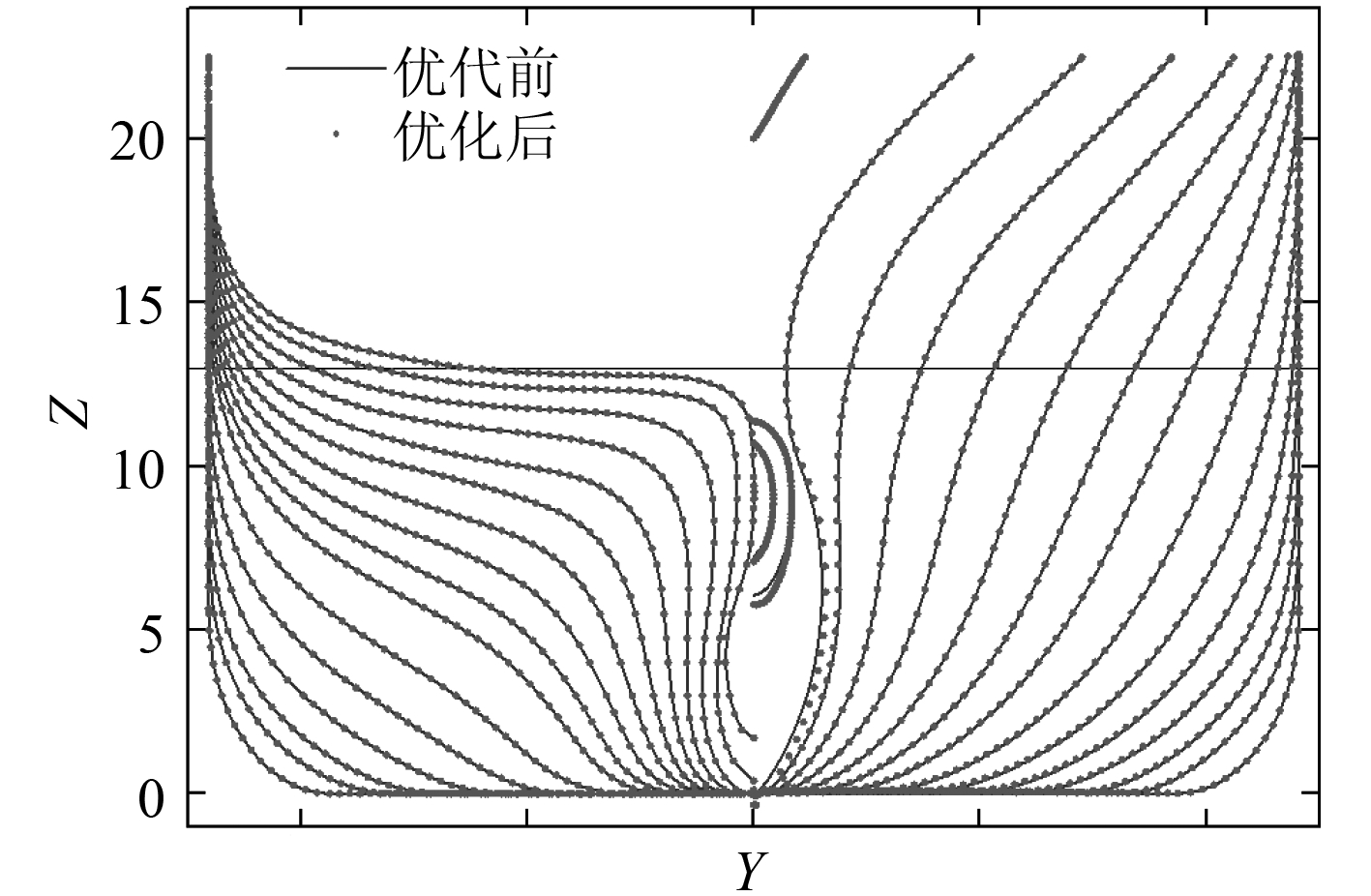
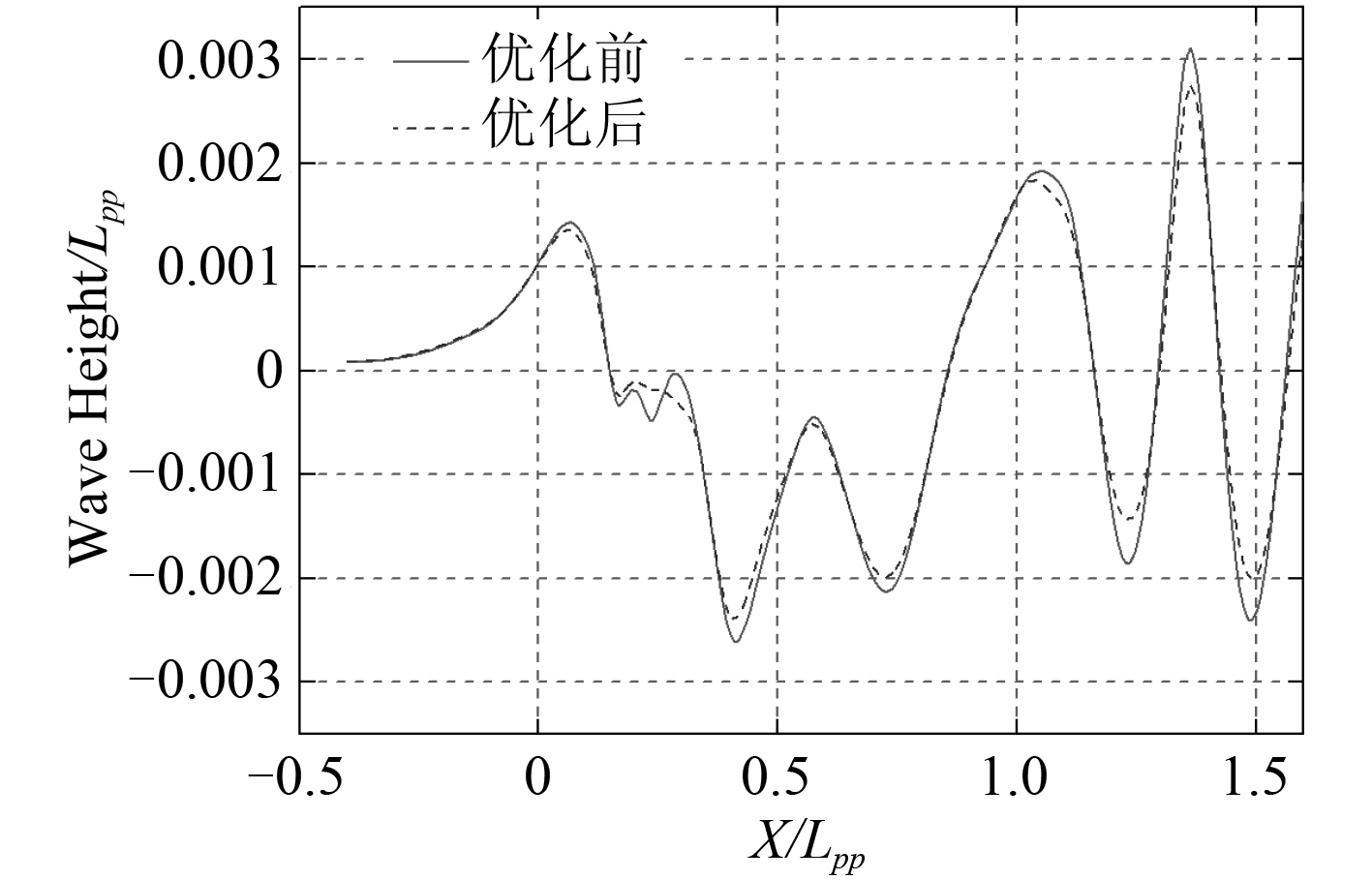
3.1 阻力优化结果表 3给出了采用本文船型优化方法后得到的最优船型与母型船关于排水量 ▽、湿表面积 S wet 、各阻力系数及总阻力 R t 的数据对比;图 2 和图 3 分别为优化前后船型的船体横剖面图以及舷侧纵切波形图。
|
|
表 3 10 000 TEU阻力优化结果 Tab.3 The optimized resistance results of 10 000 TEU |
|
图 2 优化前后船体横剖图对比 Fig. 2 Comparison of body plan between the initial hull |
|
图 3 舷侧纵切波形图对比(y/L pp = 0.1) Fig. 3 Longitudinal wave cut on the y/L pp = 0.1 plane and the optimal hull |
从中可以看出,本文优化后得到的最优船型兴波阻力系数较母型船有较为明显的改善,这一点也可从图 3 纵切波形图中各处的峰值均有所减小反映出;尽管波阻系数在总阻力成分中占比较小以及优化后湿表面积有微幅增加,但最终总阻力依然有近 3% 的优化幅度,且排水量和船体型线与母型船相比变化量都十分微弱。
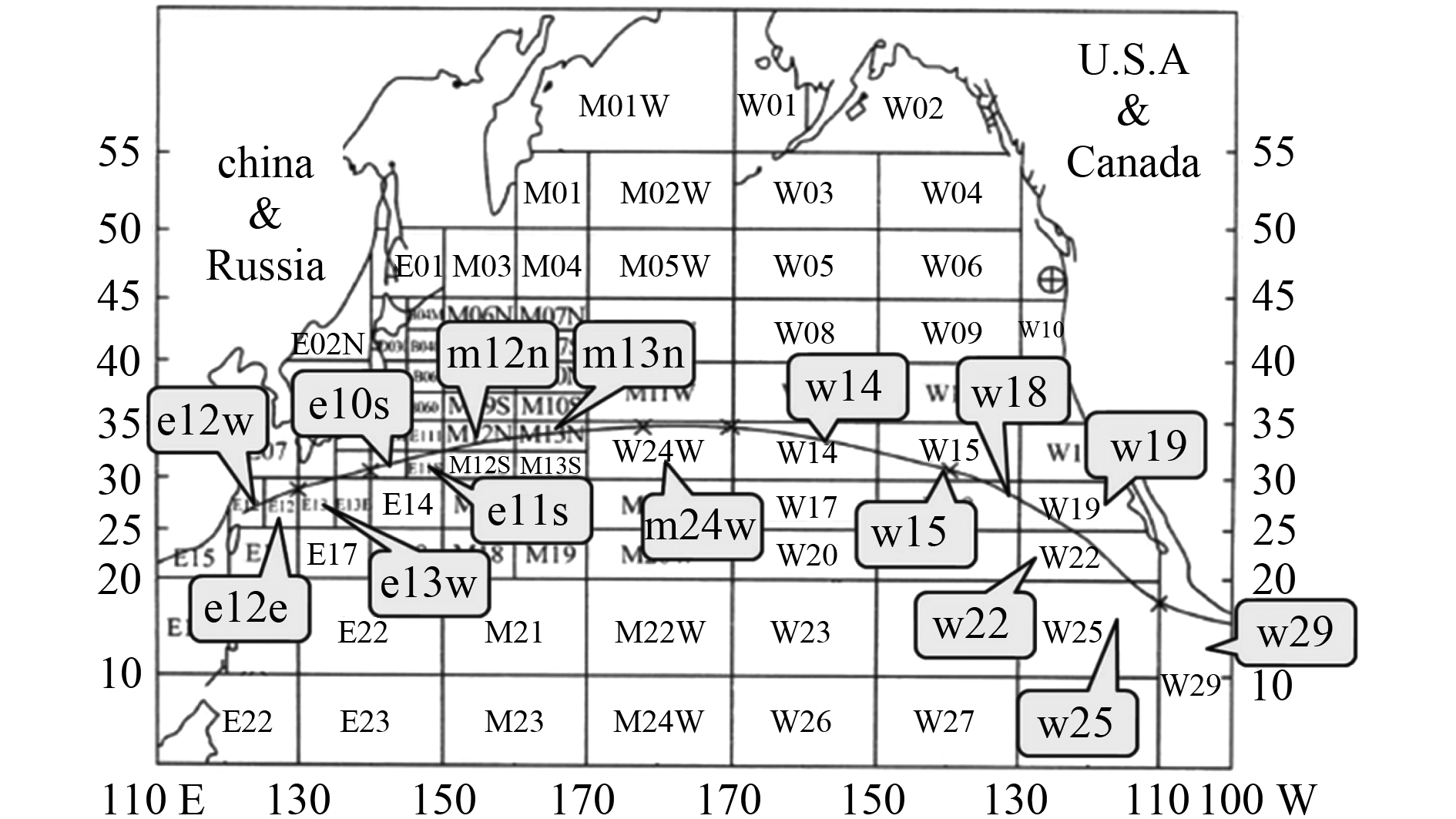
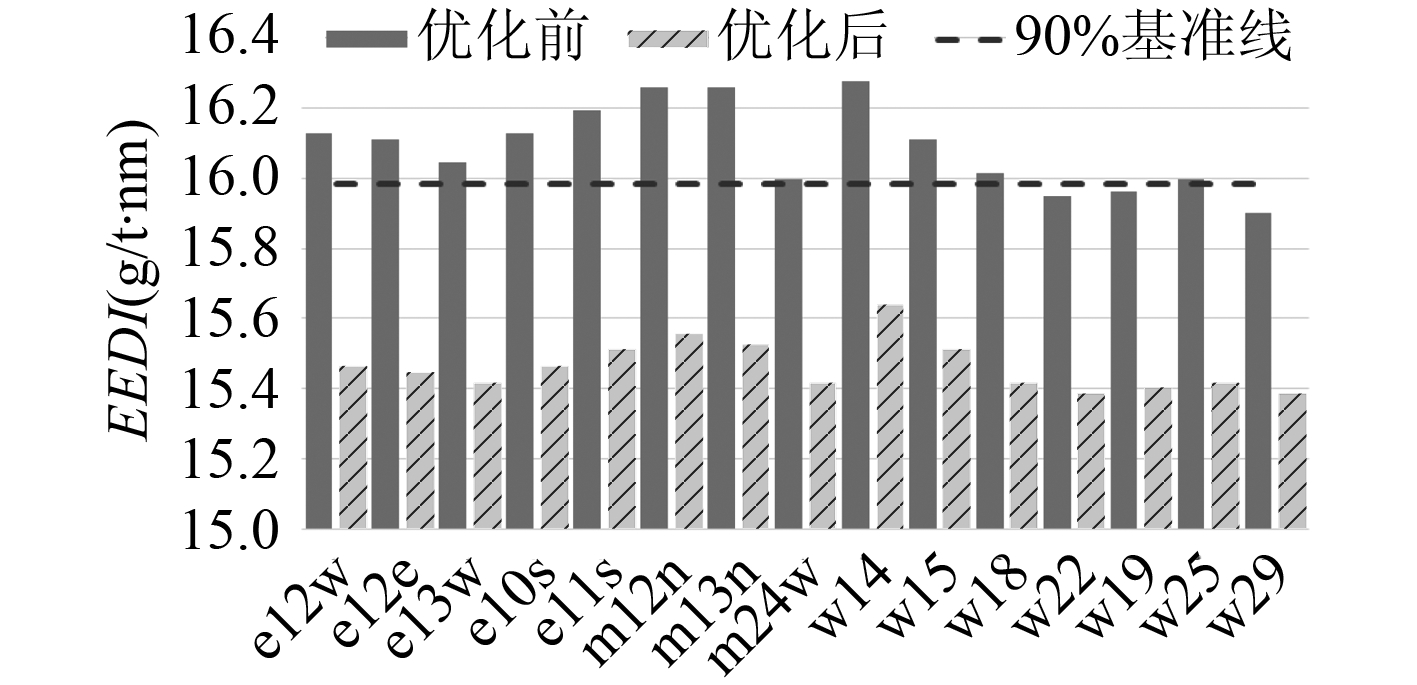
3.2 EEDI 优化结果图 4 描绘了该超大型集装箱船所航行的远东–北美西海岸航线以及该航线所经过的 15 个海区;表 4 为优化船型与母型船在不同海区内关于失速系数 f w 与能效设计指数 EEDI 的对比;图 5给出了优化前后的能效设计指数与 IMO 基准值(17.761 g/t·nm)考虑折减系数(X = 10)后的实际规定值(15.985 g/t·nm)的比较。
|
|
表 4 10 000 TEU 远东–北美航线各海区 EEDI 优化结果 Tab.4 The optimized 10 000 TEU EEDI values in the sea areas of AAN route |
|
图 4 远东–北美航线及航行海区 Fig. 4 ANN route and sea areas |
|
图 5 优化前后各航行海区 EEDI 值对比 Fig. 5 Comparison of the initial and optimized EEDI values |
从中可以看出,经过型线优化后的船型不仅阻力性能有所提高,其在实海域中航行时因波浪增阻(暂不考虑风阻的影响)而造成的失速现象也有所改善;主机所产生的 CO 2 排放量一般在 EEDI 计算时占主要部分(本文不同海区主机部分占比达到 95% 左右),因此阻力性能优化后的万箱集装箱船降低了对主机功率的需求后,使得优化前其未达到 IMO 对能效设计指数 EEDI 要求的海区(高达 12 个)全部满足新造船舶计及折减系数后的控制标准,有效减少了温室气体的排放。
4 结 语本文针对超大型集装箱船 10 000 TEU,在保持其服务航速和推进效率不变的前提下,以降低对主机功率的需求、减少燃油消耗为出发点,对其船体型线进行了优化。文中同时采用平移法与径向基函数方法进行船体曲面重构以获得更多可行的中间船型,并用稳定性更好、计算精度更高的能量积分方法计算兴波阻力,最后通过全局寻优与局部优化 2 种算法相结合的方式在设计空间中探索最优船型。最终,通过该船型优化方法获得的优化船型,其能效设计指数降低程度明显,能够满足现阶段 IMO 对新造集装箱船计及第一阶段折减系数后的控制标准,实现了节能减排的目标。
| [1] |
李碧英. 航运业节能减排现状及其低碳发展的途径[J]. 工程研究: 跨学科视野中的工程, 2012, 4 (3): 260–269.
LI Bi-ying. The Status Quo of Energy Saving and Emission Reduction in Shipping Industry and Its Approach to Low-Carbon Development[J]. Journal of Engineering Studies, 2012, 4 (3): 260–269. |
| [2] | ICCT. The energy efficiency design index (EEDI) for new ships[M]//ICCT. 2011: 1–9. |
| [3] | 张云浩. 基于EEDI的集装箱船技术要素研究[D]. 武汉: 武汉理工大学, 2013. |
| [4] |
刘飞. EEDI对船舶总体设计影响分析研究[D]. 大连: 大连理工大学, 2011.
LIU Fei. The research of EEDI impact on the basic ship design [D]. Dalian: Dalian University of Technology, 2011. |
| [5] | 刘亮. 船舶能效设计中若干耐波性影响因素研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. |
| [6] |
封培元, 马宁, 顾解忡. 基于船机桨匹配和波浪统计的船舶失速系数分析[J]. 上海交通大学学报, 2012, 1248 : 1253.
FENG Pei-yuan, MA Ning, GU Xie-chong. Analysis of the Ship Speed Loss Coefficient Based on Hull-Engine-Propeller Matching and Wave Statistics[J]. Journal of Shanghai Jiao Tong University, 2012, 1248 : 1253. |
| [7] |
颜林. 国内船舶能效指数与CO2排放基线实船研究[D]. 武汉: 武汉理工大学, 2011.
YAN Lin. Energy efficiency design index and CO2 emission baseline based on domestic full-scale ships [D]. Wuhan: Wuhan University of Technology, 2011. |
| [8] |
程红蓉, 刘晓东, 冯佰威. 多目标优化在船型设计中的应用研究[J]. 中国造船, 2014, 01 : 76–82.
CHENG Hong-rong, LIU Xiao-dong, FENG Bai-wei. Study on Multidisciplinary Optimization Method for Hull Forms Design[J]. Shipbuilding of China, 2014, 01 : 76–82. DOI: 10.3969/j.issn.1000-4882.2014.01.009 |
| [9] | KIM H. Multi-objective optimization for ship hull form design[D]. George Mason University, 2009. |
| [10] | DE BOER A, VAN DER SCHOOT M S, Bijl H. Mesh deformation based on radial basis function interpolation[J]. Computers & structures, 2007, 85 (11): 784–795. |
| [11] | 程天柱, 石仲堃. 兴波阻力理论及其在船型设计中的应用[M]. 武汉: 华中工学院出版社, 1987. |
| [12] |
钱建魁, 毛筱菲, 王孝义. 基于CFD和响应面方法的最小阻力船型自动优化[J]. 船舶力学, 2012, 16 (1): 36–43.
QIAN Jian-kui, MAO Xiao-Fei, WANG Xiao-yi. Ship Hull Automated Optimization of Minimum Resistance via CFD and RSM Technique[J]. Journal of Ship Mechanics, 2012, 16 (1): 36–43. |
| [13] | TELSTE J G, REED A M. Calculation of transom stern flows[C]//Proceedings of the Sixth International Conference on Numerical Ship Hydrodynamics, 1994: 78–92. |
 2017, Vol. 39
2017, Vol. 39
