2. 中国人民解放军 91421 部队,山东 青岛 266011;
3. 海军工程大学,湖北 武汉 430033
2. No. 91421 Unit of PLA, Qingdao 266011, China;
3. Naval University of Engineering, Wuhan 430033, China
潜艇外挂武器模块(模块内可为 UUV、导弹、鱼雷等),对提升我海军现在及未来水下作战能力具有重大意义。有关潜艇外外挂武器的应用主要有布雷箱和 UUV[1 – 3],在潜艇外部外挂研究方面,国内主要对潜器携带吊舱的水动力系数进行计算[4]。而在潜艇空间操纵仿真方面,国外已在潜艇水下操纵性、航行的安全性和攻击规避的有效性、陆上操纵仿真训练和综合显示集中控制涉及的相关理论和研究方面达到了一定的研究水平[5 – 7],国内也取得了很多研究成果[8]。本文将在这些成果的基础上,针对潜艇外外挂武器模块后的运动进行建模仿真和初步分析。
1 潜艇运动建模与仿真 1.1 模型的建立与求解
|
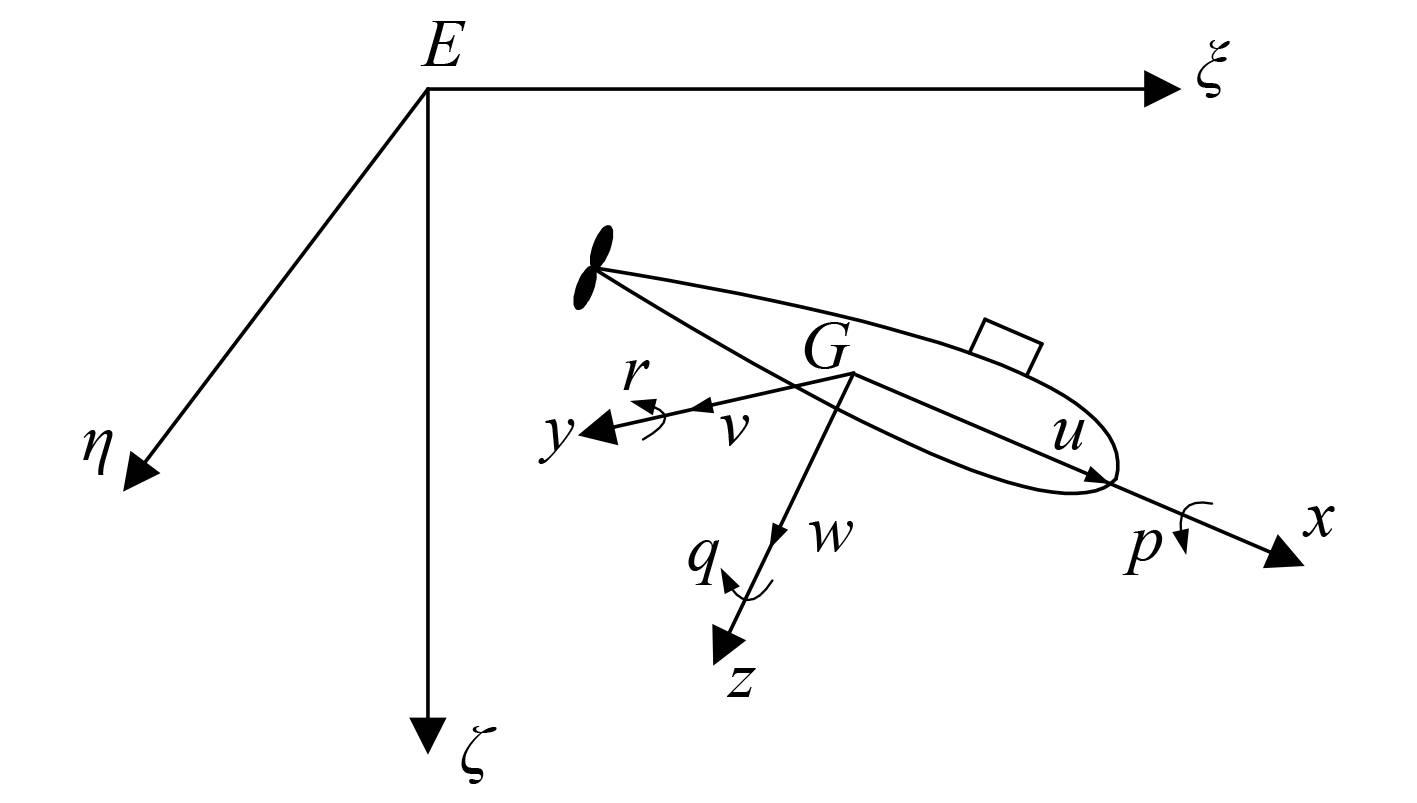
图 1 固定坐标系与运动坐标系 Fig. 1 Fixed coordinate system & moving coordinate system |
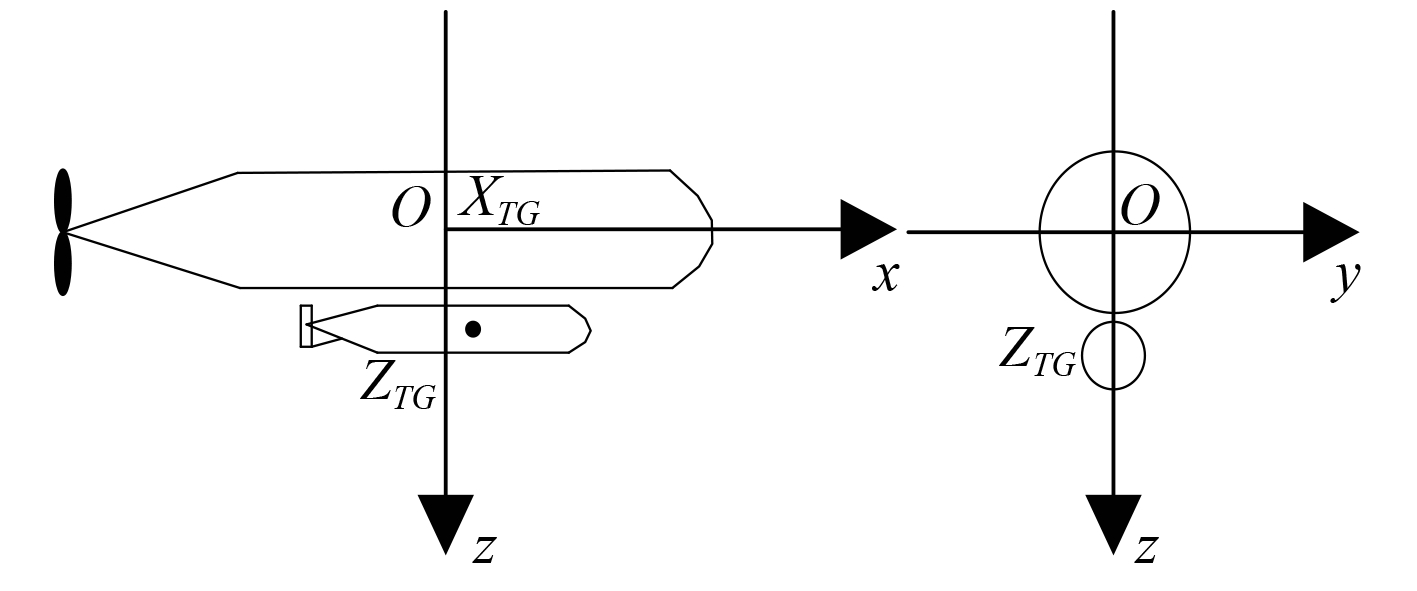
建立如图1所示的固定坐标系 E-ξηζ(简称“定系”)和运动坐标系 G-xyz(简称“动系”)。假设潜艇重心处相对于地球的速度为 V,V 在动系上的投影为 u(纵向速度)、v(横向速度)、w(垂向速度);潜艇以角速度 Ω 转动,Ω 在动系上的投影为 p(横倾角速度)、q(纵倾角速度)、r(偏航角速度)。同时规定:横倾角 φ 向右倾为正,首向角 ψ 向右转为正,纵倾角 θ 向尾倾为正。方向舵角 δ r 右舵为正,首舵角 δ b 和尾舵角 δ s 的正负号按右手定则决定,则有:首舵角 δ b 为正是上浮舵角,尾舵角 δ s 为正是下潜舵角。
在所建立的坐标系基础上,依据葛特勒(Gertler)等提出的“用于潜艇模拟研究的标准运动方程”[9],省略螺旋桨负荷的影响,同时将微分项移到方程的左边,其余项放在方程右边,从而得到六自由度空间运动方程如下:
纵向力方程
| ${a_{11}}\dot u + {a_{15}}\dot q + {a_{16}}\dot r = {f_1},$ | (1) |
横向力方程
| ${a_{22}}\dot v + {a_{24}}\dot p + {a_{26}}\dot r = {f_2},$ | (2) |
竖向力方程
| ${a_{33}}\dot w + {a_{34}}\dot p + {a_{35}}\dot q = {f_3},$ | (3) |
横倾力矩方程
| ${a_{42}}\dot v + {a_{43}}\dot w + {a_{44}}\dot p + {a_{45}}\dot q + {a_{46}}\dot r = {f_4},$ | (4) |
纵倾力矩方程
| ${a_{51}}\dot u + {a_{53}}\dot w + {a_{54}}\dot p + {a_{55}}\dot q + {a_{66}}\dot r = {f_5},$ | (5) |
偏航力矩方程
| ${a_{61}}\dot u + {a_{62}}\dot v + {a_{64}}\dot p + {a_{65}}\dot q + {a_{66}}\dot r = {f_6}\text{。}$ | (6) |
式中:
| $\begin{aligned}{f_1} = & \left[ {m{x_G} + \frac{1}{2}\rho {L^4}{{X'}_{qq}}} \right]{q^2} + \left[ {m{x_G} + \frac{1}{2}\rho {L^4}{{X'}_{rr}}} \right]{r^2} - \\& m{y_G}pq + \left[ {\frac{1}{2}\rho {L^4}{{X'}_{pp}} - m{z_G}} \right]pr + \\& \left[ {\frac{1}{2}\rho {L^3}{{X'}_{vr}} + m} \right]vr + \left[ {\frac{1}{2}\rho {L^3}{{X'}_{wq}} - m} \right]wq +\end{aligned}$ |
| $\begin{aligned}& \frac{1}{2}\rho {L^2}\left[ {{{X'}_{uu}}{u^2} + {{X'}_{vv}}{v^2} + {{X'}_{ww}}{w^2}} \right] + \\& \frac{1}{2}\rho {L^2}{u^2}\left[ {{{X'}_{{\delta _r}{\delta _r}}}{\delta _r}^2 + {{X'}_{{\delta _b}{\delta _b}}}{\delta _b}^2 + {{X'}_{{\delta _s}{\delta _s}}}{\delta _s}^2} \right] + \\& \frac{1}{2}\rho {L^2}\left[ {{a_T}{u^2} + {b_T}u{u_c} + {c_T}{u_c}^2} \right] - \left( {W - B} \right)\sin \theta ;\end{aligned}$ |
| $\begin{aligned}{f_2} = & \left[ {\frac{1}{2}\rho {L^4}{{Y'}_{pq}} - m{x_G}} \right]pq + m{y_G}\left[ {{p^2} + {r^2}} \right] - m{z_G}qr + \\& \left[ {\frac{1}{2}\rho {L^3}{{Y'}_r} - m} \right]ur + \frac{1}{2}\rho {L^3}{{Y'}_p}up + \left[ {\frac{1}{2}\rho {L^3}{{Y'}_{wp}} + m} \right]wp + \\& \frac{1}{2}\rho {L^2}\left[ {{{Y'}_0}{u^2} + {{Y'}_v}uv + {{Y'}_{v\left| v \right|}}v\left| {{{\left( {{v^2} + {w^2}} \right)}^{1/2}}} \right|} \right] + \\& \frac{1}{2}\rho {L^2}\left[ {{{Y'}_{vw}}vw + {{Y'}_{{\delta _r}}}{u^2}{\delta _r}} \right] + \left( {W - B} \right)\cos \theta {\sin ^{ - 1}}\varphi; \end{aligned}$ |
| $\begin{aligned}{f_3} = & m{z_G}\left[ {{p^2} + {q^2}} \right] - m{x_G}rp - m{y_G}rq + \frac{1}{2}\rho {L^4}{{Z'}_{rr}}{r^2} + \\& \left[ {\frac{1}{2}\rho {L^3}{{{\rm{Z'}}}_q} + m} \right]uq - \left[ {m - \frac{1}{2}\rho {L^3}{{Z'}_{vp}}} \right]vp + \frac{1}{2}\rho {L^3}{{Z'}_{vr}}vr + \\& \frac{1}{2}\rho {L^2}\left[ {{{{\rm{Z'}}}_0}{u^2} + {{Z'}_w}uw + {{Z'}_{w\left| w \right|}}w\left| {{{\left( {{v^2} + {w^2}} \right)}^{1/2}}} \right|} \right] + \\& \frac{1}{2}\rho {L^2}\left[ {{{{\rm{Z'}}}_{\left| w \right|}}u\left| w \right| + {{Z'}_{ww}}\left| {w{{\left( {{v^2} + {w^2}} \right)}^{1/2}}} \right|} \right] + \\& \frac{1}{2}\rho {L^2}\left[ {{{{\rm{Z'}}}_{vv}}{v^2} + {{Z'}_{{\delta _b}}}{u^2}{\delta _b} + {{Z'}_{{\delta _s}}}{u^2}{\delta _s}} \right] + \left( {W - B} \right)\cos \theta \cos \varphi ;\end{aligned}$ |
| $\begin{aligned}{f_4} = & \frac{1}{2}\rho {L^5}\left[ {{{K'}_{qr}}qr + {{K'}_{pq}}pq + {{K'}_{p\left| p \right|}}p\left| p \right|} \right] + \\& \frac{1}{2}\rho {L^4}\left[ {{{K'}_p}up + {{K'}_r}ur + {{K'}_{wp}}wp} \right] + \\& \left( {{J_y} - {J_z}} \right)qr - {J_{xy}}pr - {J_{yz}}\left( {{r^2} - {q^2}} \right) + {J_{zx}}pq + \\& \frac{1}{2}\rho {L^3}\left[ {{{K'}_0}{u^2} + {{K'}_v}uv + {{K'}_{v\left| v \right|}}v\left| {{{\left( {{v^2} + {w^2}} \right)}^{1/2}}} \right|} \right] + \\& \frac{1}{2}\rho {L^3}\left[ {{{K'}_{vw}}vw + {{K'}_{{\delta _r}}}{u^2}{\delta _r}} \right] + \left( {{y_G}W - {y_C}B} \right)\cos \theta \cos \varphi - \\& \left( {{z_G}W - {z_C}B} \right)\cos \theta \sin \varphi - {T_N};\end{aligned}$ |
| $\begin{aligned}{f_5} = & \left( {{J_z} - {J_x}} \right)rp + {J_{xy}}qr + \left( {{r^2} - {p^2}} \right){J_{zx}} - {J_{yz}}pq + \\& \frac{1}{2}\rho {L^5}\left[ {{{M'}_{rr}}{r^2} + {{M'}_{rp}}rp + {{M'}_{q\left| q \right|}}q\left| q \right|} \right] + \frac{1}{2}\rho {L^4}{{M'}_q}uq + \\& \frac{1}{2}\rho {L^3}\left[ {{{M'}_0}{u^2} + {{M'}_w}w + {{M'}_{w\left| w \right|}}w\left| {{{\left( {{v^2} + {w^2}} \right)}^{1/2}}} \right|} \right] + \\& \frac{1}{2}\rho {L^3}\left[ {{{M'}_{\left| w \right|}}u\left| w \right| + {{M'}_{ww}}\left| {w{{\left( {{v^2} + {w^2}} \right)}^{1/2}}} \right|} \right] + \\& \frac{1}{2}\rho {L^3}\left[ {{{M'}_{vv}}{v^2} + {{M'}_{{\delta _b}}}{u^2}{\delta _b} + {{M'}_{{\delta _s}}}{u^2}{\delta _s}} \right] - \\& \left( {{x_G}W - {x_C}B} \right)\cos \theta \cos \varphi - \left( {{z_G}W - {z_C}B} \right)\sin \theta ;\end{aligned}$ |
| $\begin{aligned}{f_6} = & \left( {{J_x} - {J_y}} \right)pq + \left( {{p^2} - {q^2}} \right){J_{xy}} + {J_{yz}}rp - {J_{zx}}rq + \\& \frac{1}{2}\rho {L^5}\left[ {{{N'}_{pq}}pq + {{N'}_{\left| r \right|r}}\left| r \right|r} \right] + \frac{1}{2}\rho {L^4}\left[ {{{N'}_p}up + {{N'}_r}ur} \right] + \\& \frac{1}{2}\rho {L^3}\left[ {{{N'}_0}{u^2} + {{N'}_v}uv + {{N'}_{v\left| v \right|}}v\left| {{{\left( {{v^2} + {w^2}} \right)}^{1/2}}} \right|} \right] + \\& \frac{1}{2}\rho {L^3}\left[ {{{N'}_{vw}}vw + {{N'}_{{\delta _r}}}{u^2}{\delta _r}} \right] + \left( {{x_G}W - {x_C}B} \right)\cos \theta \sin \varphi +\\& \left( {{y_G}W - {y_C}B} \right)\sin \theta\text{。}\end{aligned}$ |
上式中各符号意义参见文献[9]。
联立式(1)~ 式(6)求解可以得到加速度矩阵:
| $\left[ \begin{array}{l}{\dot u}\\{\dot v}\\{\dot w}\\{\dot p}\\{\dot q}\\{\dot r}\end{array} \right] = \left[ \begin{array}{l}{f_1}\\{f_2}\\{f_3}\\{f_4}\\{f_5}\\{f_6}\end{array} \right]/\left[ {\begin{array}{*{20}{c}}{{a_{11}}} & \cdots & {{a_{16}}}\\ \vdots & \ddots & \vdots \\{{a_{61}}} & \cdots & {{a_{66}}}\end{array}} \right] \text{。}$ | (7) |
式中未赋值 a ij 的值为 0。
对式(7)矩阵中的加速度进行积分得到速度和角速度,根据定系和动系之间的转换关系再次积分可求得潜艇任意时刻的位置和姿态角。
1.2 模型的验证为了检验所建立的数学模型的准确性,根据数学模型编制仿真程序,对潜艇的 5 种典型运动进行验证。
1)水平面定常回转运动
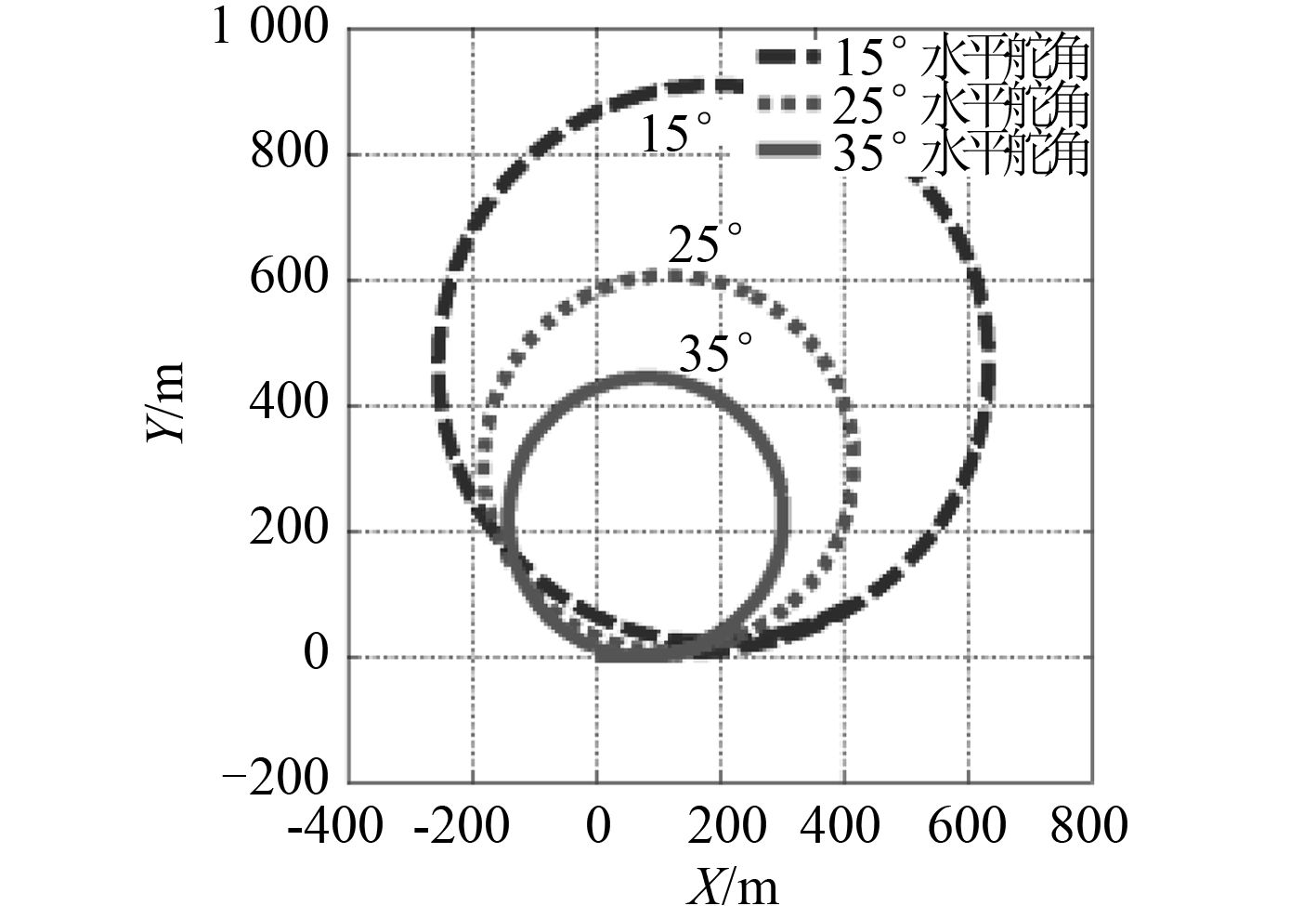
潜艇直航时,当方向舵保持某一固定的舵角,潜艇将作圆周运动,称为水平面定常回转运动。对潜艇操 15°,25°,35° 方向舵时的定常回转运动进行仿真,得到潜艇重心轨迹曲线如图 2 所示。
|
图 2 水平面运动轨迹曲线 Fig. 2 Locus curves of motion in horizontal plane |
2)水平面Z型操舵运动
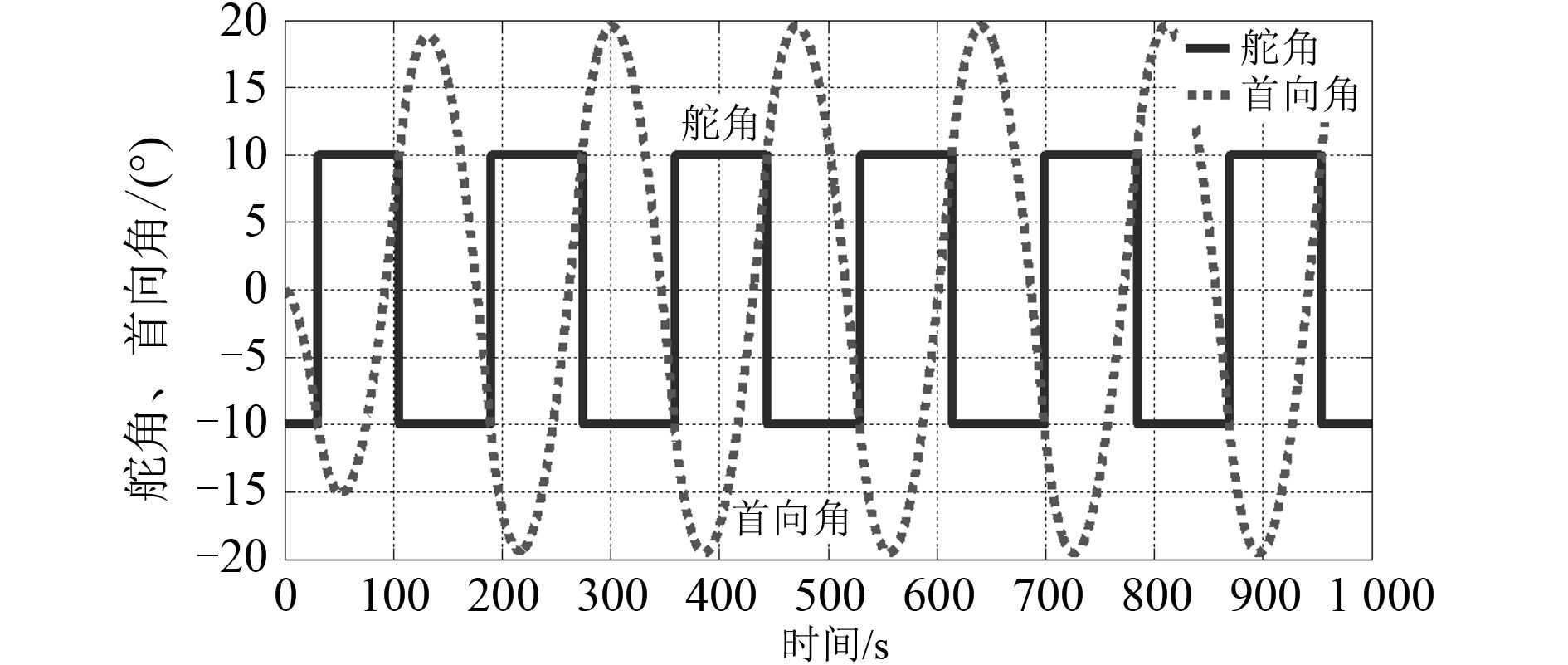
潜艇在实际的航行中,常常是在保持航向的基础上执行操舵机动,这种中等舵角时的机动性可以通过Z型操舵来研究,其重点是潜艇的应舵性。对潜艇在 δ r /ψ = 10°/10° 时的Z型操舵运动仿真,得到的舵角、首向角变化曲线如图 3 所示。
|
图 3 水平面运动舵角、首向角变化曲线 Fig. 3 Variation curves of rudder angle and heading angle of motion in horizontal plane |
3)垂直面定常直线潜浮运动
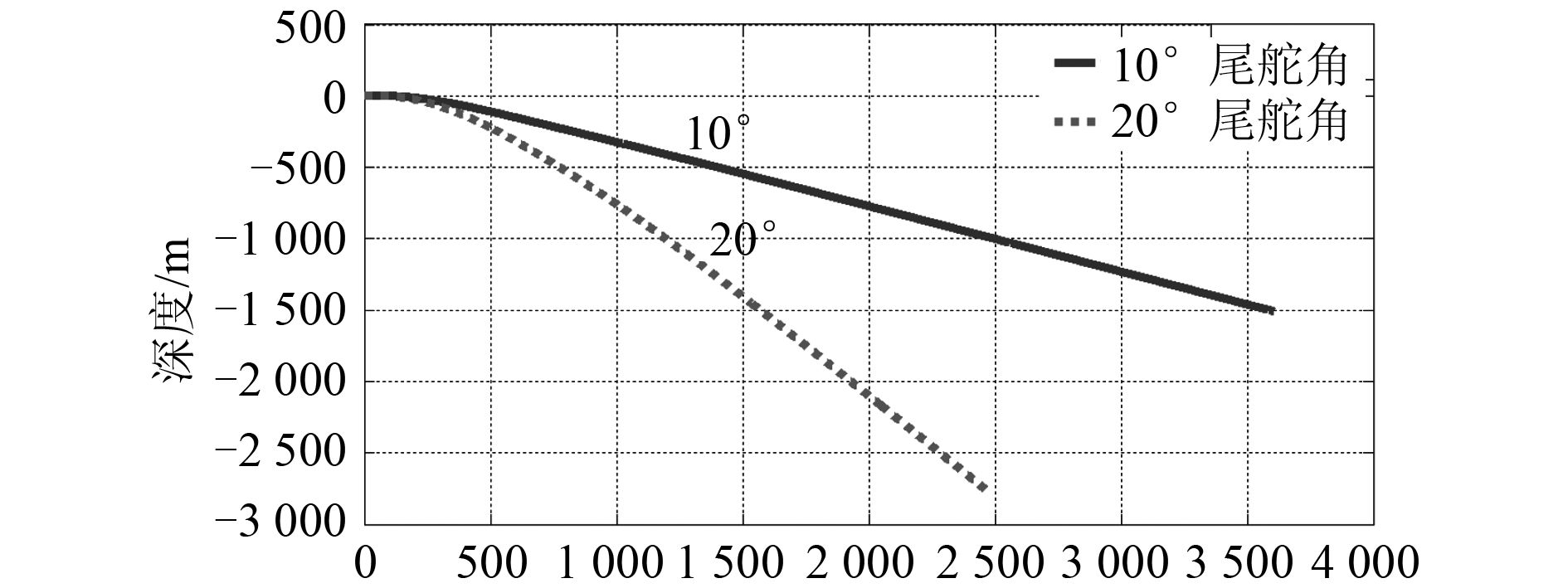
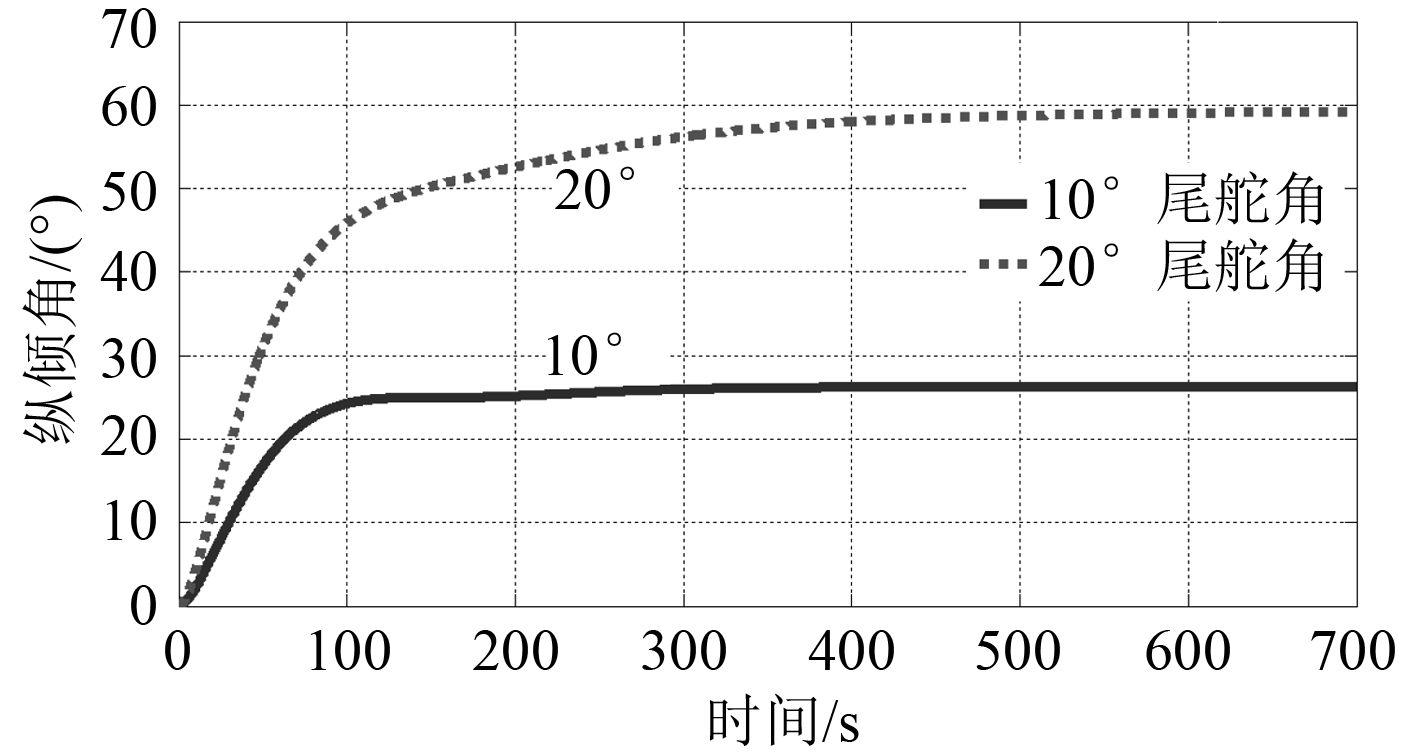
潜艇在定深航向时,当升降舵变为某一固定舵角,潜艇将作定常直线潜浮运动。定常潜浮运动能够反映潜艇的深度机动性。对潜艇操 10° 和 20° 尾升降舵的定常直线潜浮运动仿真,计算所得垂直面重心轨迹曲线如图 4 所示,纵倾角变化曲线如图 5 所示。
|
图 4 垂直面运动轨迹曲线 Fig. 4 Locus curves of motion in vertical plane |
|
图 5 垂直面运动纵倾角变化曲线 Fig. 5 Variation curves of pitch angle of motion in vertical plane |
4)垂直面超越机动运动
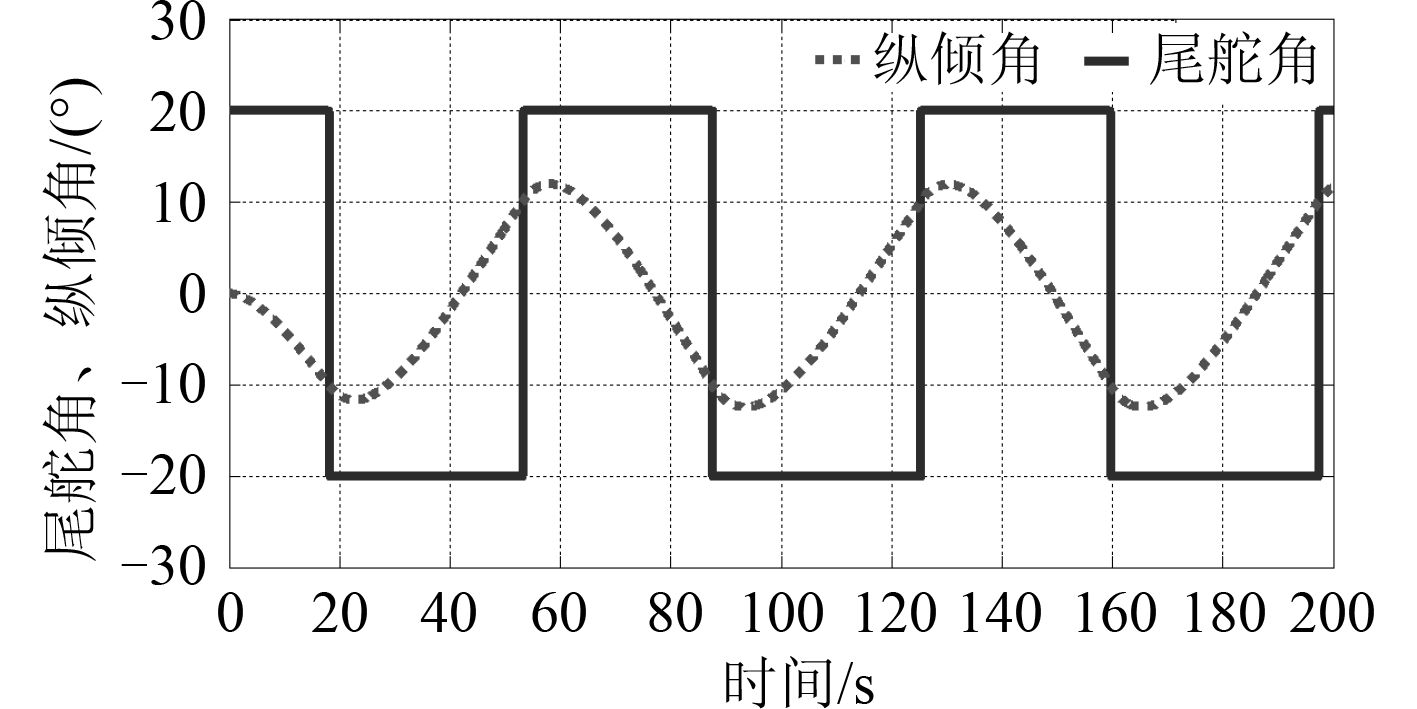
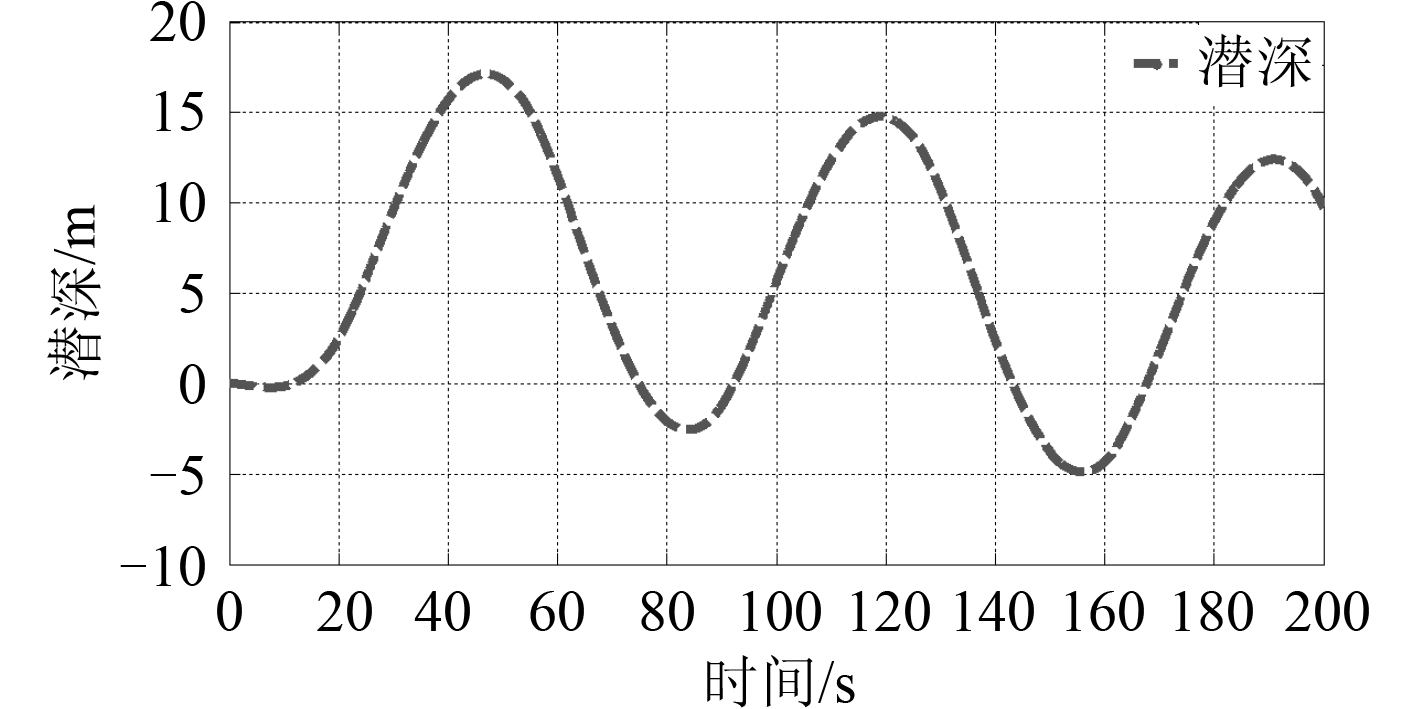
垂直面内周期性变化潜艇升降舵,潜艇将作超越机动运动,此时可以研究潜艇对升降舵的应舵能力。对潜艇在 δ s /θ = 20°/10° 时的超越机动运动,计算所得舵角、纵倾角变化曲线如图 6 所示,潜深变化曲线如图 7 所示。
|
图 6 垂直面运动舵角、纵倾角变化曲线 Fig. 6 Variation curves of rudder angle and pitch angle of motion in vertical plane |
|
图 7 垂直面运动潜深变化曲线 Fig. 7 Variation curves of diving depth of motion in vertical plane |
5)空间定常螺旋运动
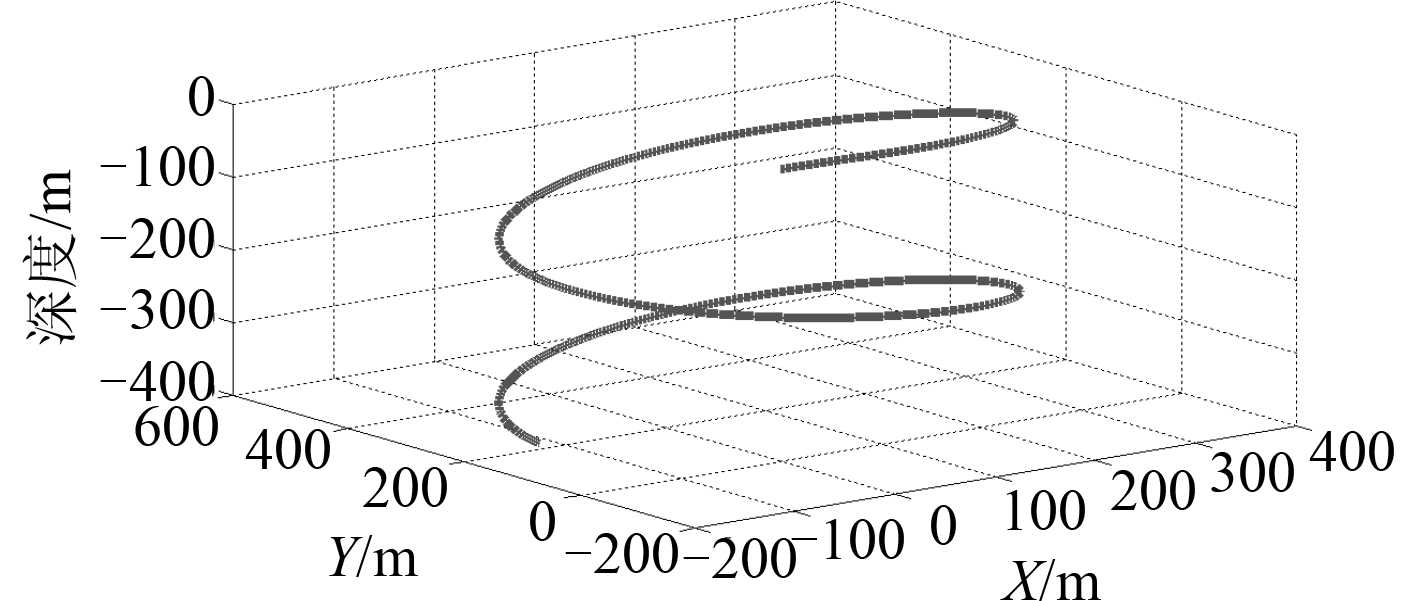
当固定潜艇某一方向舵角和升降舵角,或者只固定方向舵角,潜艇将绕 Eζ 轴以等角速度回转,其重心的三维运动轨迹为螺旋线,此时潜艇的运动称为空间定常螺旋运动。空间定常螺旋运动可用来研究潜艇的空间机动性。对潜艇在操舵条件:δ r = 30°,δ b = 10° 及δ s = 0° 时的空间定常螺旋运动进行仿真,得到的重心轨迹曲线如图 8 所示。
|
图 8 空间定常螺旋运动轨迹曲线 Fig. 8 Locus curves of spatial helical motion |
5 种典型运动的仿真结果表明:仿真结果反映出来的潜艇运动规律基本符合客观实际,所建立的潜艇六自由度数学模型基本正确,可用来预报外挂武器模块之后潜艇的运动。
2 潜艇外挂武器模块后的水动力系数近似估算潜艇外挂载武器模块后的水动力系数会发生改变,为此必须要确定外挂的武器模块的水动力系数。潜艇外挂武器后的水动力系数获取可采用实验测定、理论计算或近似估算等方法[10],本文在初步论证阶段,采用近似估算方法。近似估算方法[11]是根据在大量船模试验结果基础上整理得出的半经验的图谱经过估算得到的,能在允许一定误差的情况下较快的推算出水动力系数的近似值。这种方法假设潜艇外挂武器模块后的水动力系数等于潜艇和外挂的武器模块的水动力系数之和。
2.1 武器模块的加速度系数近似估算潜艇外挂的武器模块一般可有一个或多个。本文所研究的为潜艇外部外挂一个武器模块情况(见图 9)。武器模块长 L 取 10 m,宽 B 和高 H 取 1.5 m,水下全排水容积
|
图 9 武器模块外挂示意图 Fig. 9 Schematic diagram of submarines carrying weapons module |
流线形的武器模块可以用 1 个三轴椭球体代替,以主尺度 L,B,H 作为椭球体的三轴 2a,2b,2c。由于椭球体的 λ ij = 0(i ≠ j),故所需计算的附加质量只有 λ ij = 0(i = j)。
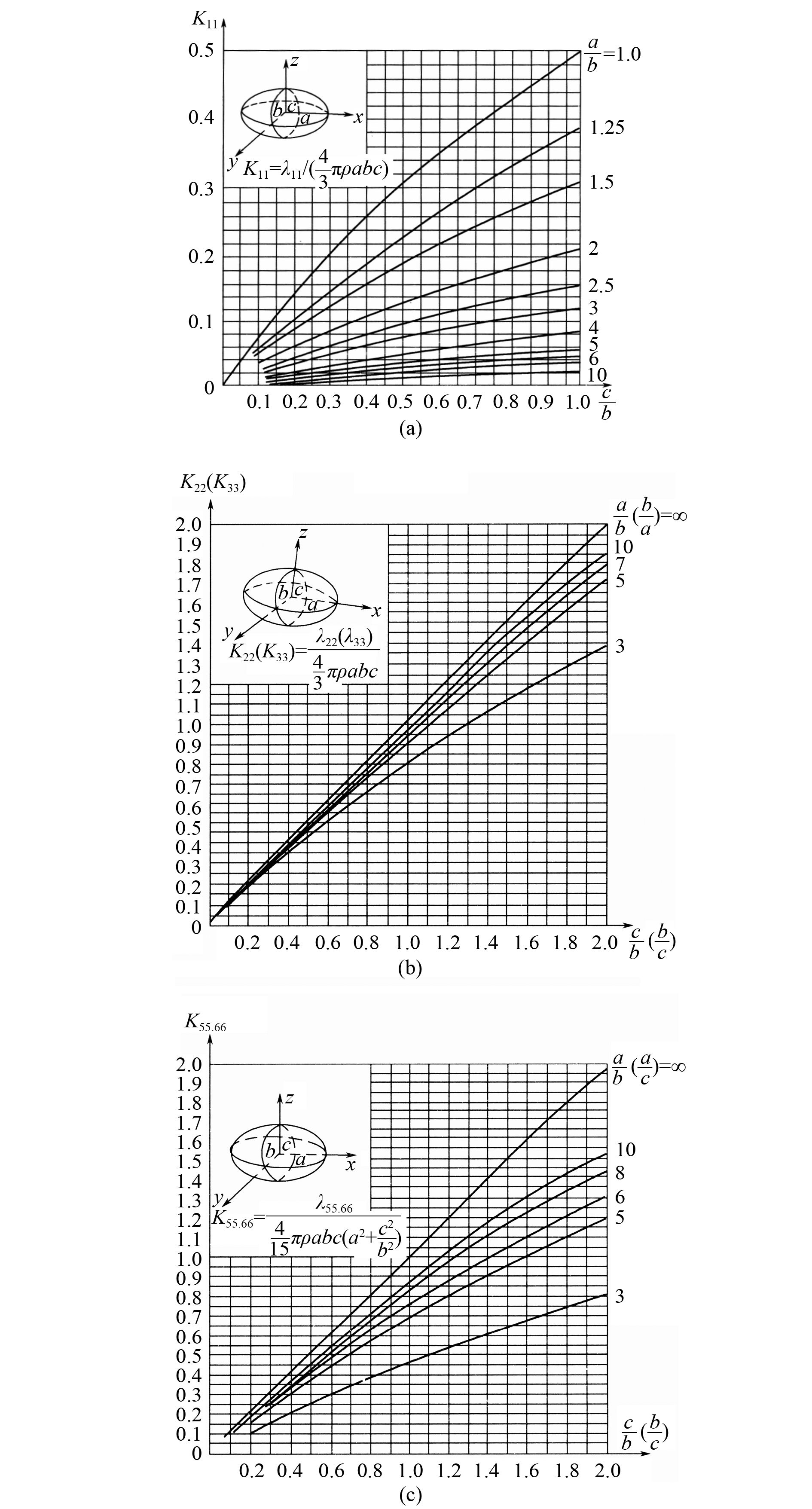
椭球体的附加质量系数曲线是兰姆(Lamb)根据势流理论得到的[11]。当已知椭球体的半轴长 a,b,c 时,在图 10 曲线就可以查得椭球体的附加质量。图中的 K 11,K 22,K 33 分别是椭球体附加质量 λ 11,λ 22,λ 33 的相对值,K 55,K 66 为椭球体附加转动惯量 λ 55,λ 66 的相对值。
|
图 10 椭球体附加质量系数曲线 Fig. 10 Added mass coefficient curves of ellipsoid |
由 L/B = 10.0,H/B = 1.0 查椭球体的附加质量系数曲线(见图 10),得到附加质量系数:K 11 = 0.02,K 22 = 0.96,K 33 = 0.96,K 55 = 0.87,K 66 = 0.87,将得到的质量系数通过计算得到武器模块的加速度系数:
| $\begin{aligned}{\left( {{{X'}_{\dot u}}} \right)_{wq}} = - \frac{\pi }{3}\frac{B}{L}\frac{H}{L}{K_{11}} = - 2.09 \times {10^{ - 4}},\\{\left( {{{Y'}_{\dot v}}} \right)_{wq}} = - \frac{\pi }{3}\frac{{BH}}{{{L^2}}}{K_{22}} = - 1.005 \times {10^{ - 2}},\\{\left( {{{Z'}_{\dot w}}} \right)_{wq}} = - \frac{\pi }{3}\frac{{BH}}{{{L^2}}}{K_{33}} = - 1.005 \times {10^{ - 2}},\\\end{aligned}$ |
| $\begin{aligned}{\left( {{{M'}_{\dot q}}} \right)_{wq}} = - \frac{\pi }{{60}}\frac{{BH}}{{{L^2}}}\left[ {1 + {{\left( {\frac{H}{L}} \right)}^2}} \right]{K_{55}} = - 4.60 \times {10^{ - 4}},\\{\left( {{{N'}_{\dot r}}} \right)_{wq}} = - \frac{\pi }{{60}}\frac{{BH}}{{{L^2}}}\left[ {1 + {{\left( {\frac{B}{L}} \right)}^2}} \right]{K_{66}} = - 4.60 \times {10^{ - 4}}\text{。}\end{aligned}$ |
|
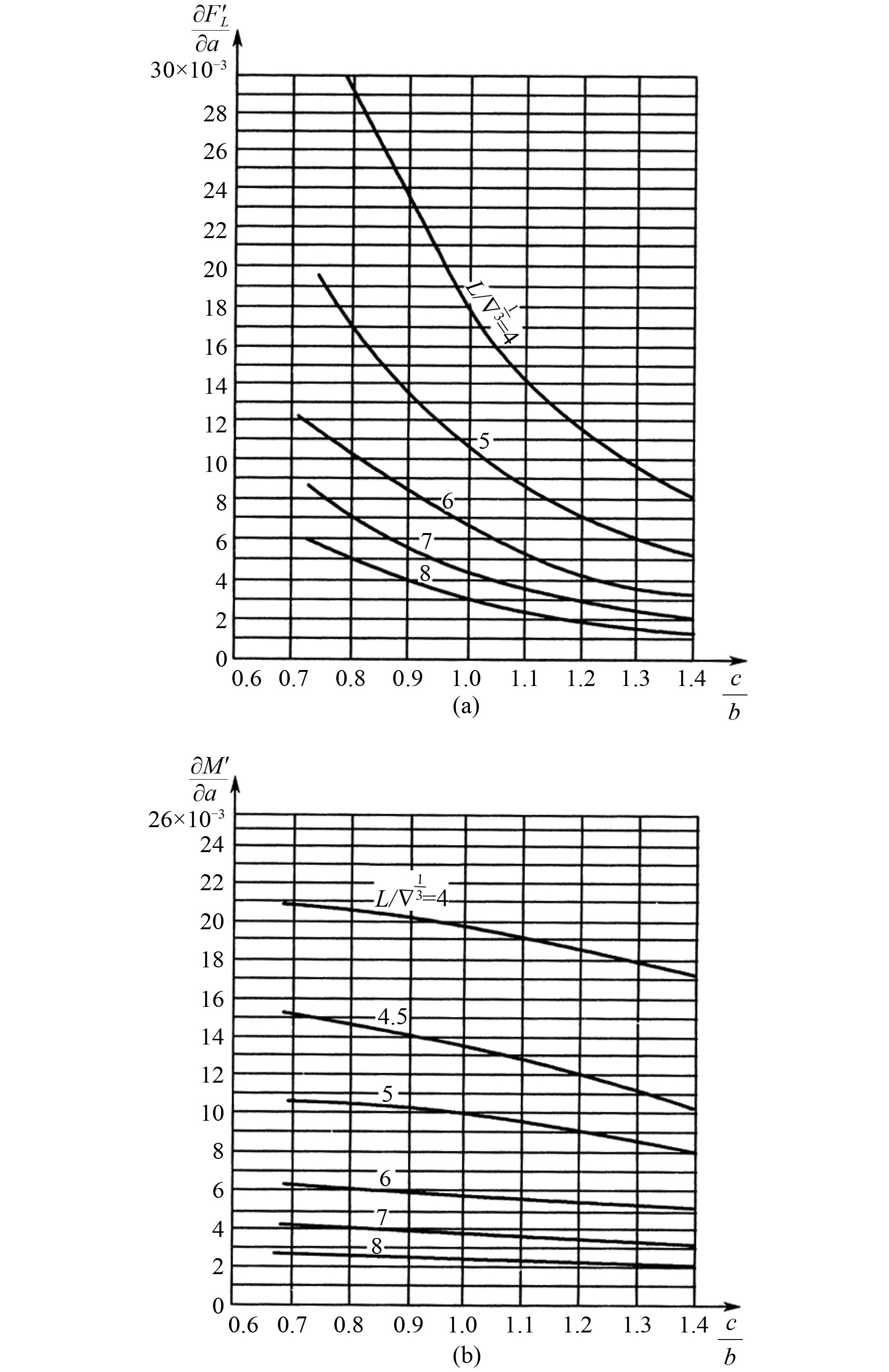
图 11 椭球体冲角导数曲线 Fig. 11 Attack angle derivation curves of ellipsoid |
用
| $\frac{{\partial {{F'}_L}}}{{\partial \alpha }} = 1.05 \times {10^{ - 2}},\;\;\;\;\frac{{\partial M'}}{{\partial \alpha }} = 1.03 \times {10^{ - 2}};$ |
椭球体的阻力系数取
| ${F'_D} = 0.05 \times \frac{{\pi {B^2}}}{{4{L^2}}} = 0.39 \times {10^{ - 3}},$ |
计算得到武器模块的速度水动力系数:
| $\begin{array}{l}{\left( {{{Y'}_v}} \right)_{wq}} = {\left( {{{Z'}_w}} \right)_{wq}} = - \left( {\displaystyle\frac{{\partial {{F'}_L}}}{{\partial \alpha }} + {{F'}_D}} \right) = - 1.09 \times {10^{ - 2}},\\[5pt]{\left( {{{N'}_v}} \right)_{wq}} = {\left( {{{M'}_w}} \right)_{wq}} = \displaystyle\frac{{\partial M'}}{{\partial \alpha }} = 1.03 \times {10^{ - 2}}\text{。}\end{array}$ |
|
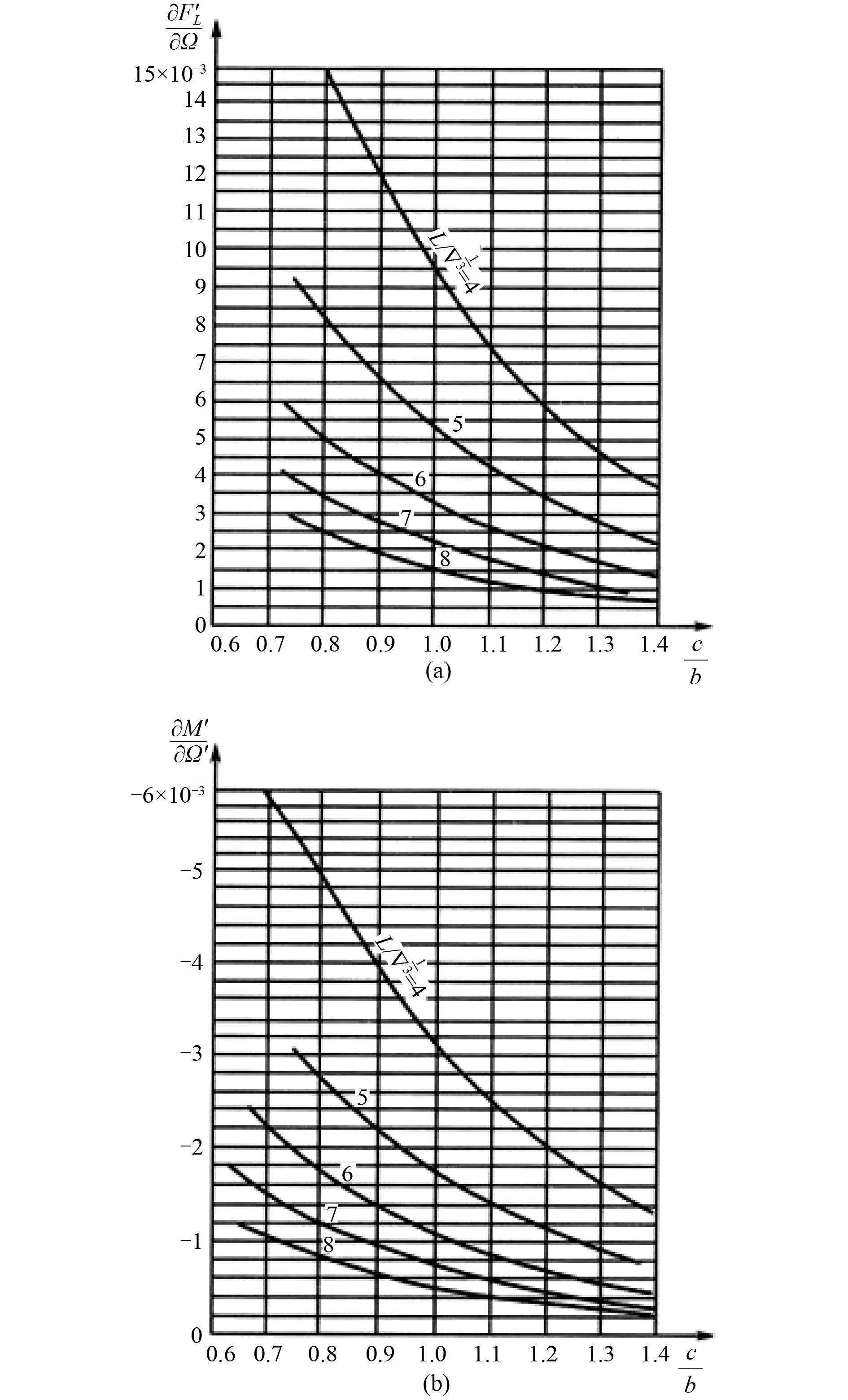
图 12 椭球体角速度导数曲线 Fig. 12 Angular velocity derivation curves of ellipsoid |
用
| $\frac{{\partial {{F'}_L}}}{{\partial \Omega }} = 5.3 \times {10^{ - 3}},\;\;\;\;\frac{{\partial M'}}{{\partial \Omega }} = - 1.66 \times {10^{ - 3}};$ |
假设武器模块的重心 G 在模块正中,即浮心位置修正系数为 1,则武器模块的角速度系数为:
| $\begin{array}{l}{\left( {{{Y'}_r}} \right)_{wq}} = - {\left( {{{Z'}_q}} \right)_{wq}} = \displaystyle\frac{{\partial {{F'}_L}}}{{\partial \Omega }} = 5.3 \times {10^{ - 3}},\\[10pt]{\left( {{{N'}_r}} \right)_{wq}} = {\left( {{{M'}_q}} \right)_{wq}} = \displaystyle\frac{{\partial M'}}{{\partial \Omega }} = - 1.66 \times {10^{ - 3}}\text{。}\end{array}$ |
根据估算得到的外挂后潜艇的水动力系数,结合建立的潜艇运动数学模型,便可以对外挂后的潜艇 5 种典型运动进行仿真。
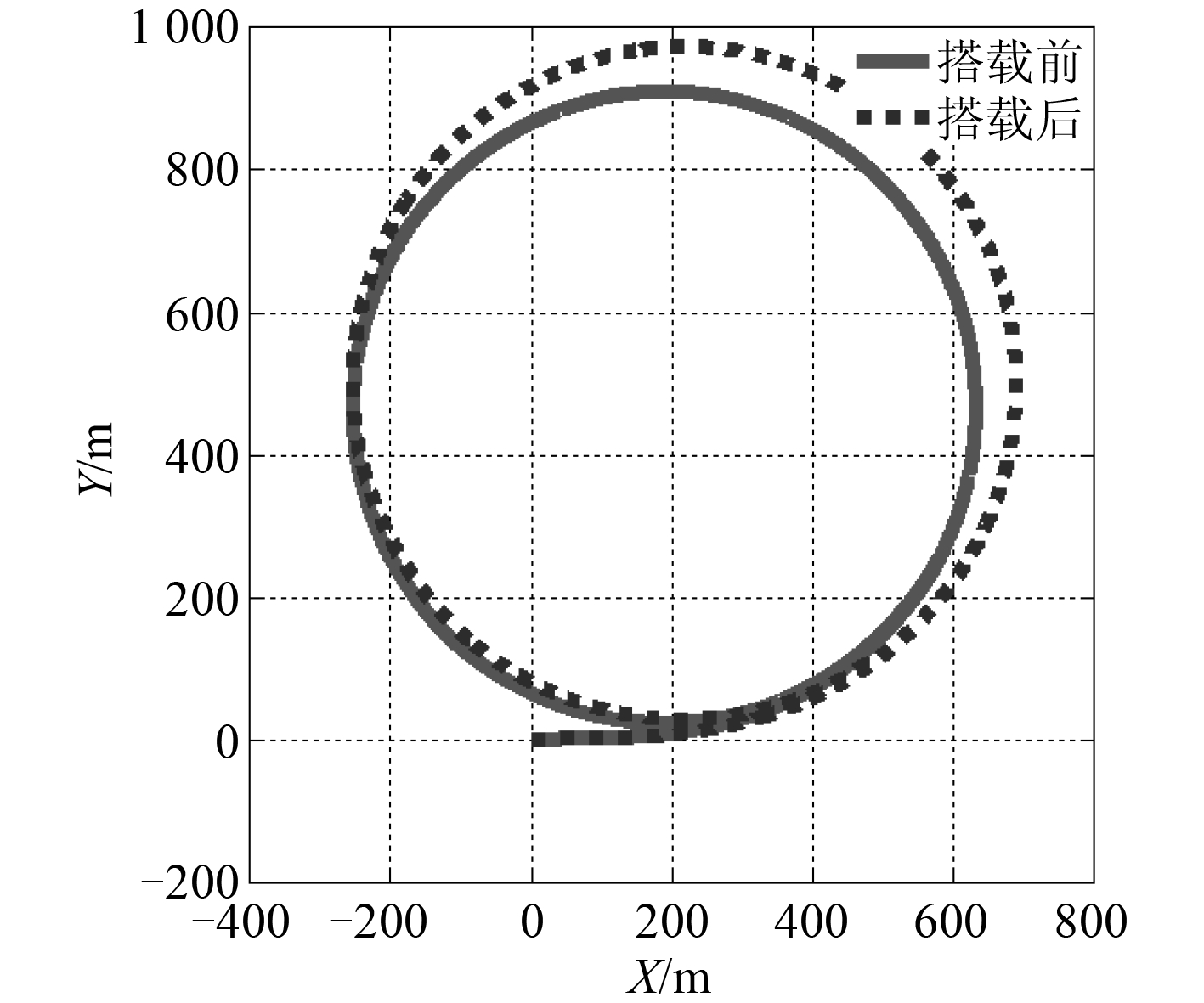
3.1 水平面定常回转运动对比对潜艇操 15°,25°,35° 方向舵 3 种情况分别进行运动仿真,这里给出 15° 方向舵时外挂前后的潜艇重心轨迹曲线如图 13 所示。
|
图 13 水平面运动轨迹对比曲线 Fig. 13 Comparison curves between motions in horizontal plane |
通过重心轨迹曲线计算得到外挂武器模块前后潜艇的操纵性能指标如表 1 所示。
|
|
表 1 外挂前后的水平面操纵性能指标对照表 Tab.1 Contrast on performance indexes of maneuverability in horizontal plane before & after carrying weapons module |
从表 1 可知:潜艇外挂武器模块后的回转直径、潜艇从打舵开始至达到定常状态的稳定时间、回转周期以及回转角速度等操纵性能指标均比操舵前的指标大,说明外挂武器模块后潜艇的水平面操纵性能减低。另外,通过外挂前后的性能指标的绝对变化量分析,潜艇在小舵角时外挂前后的操纵性变化较大、在大舵角时的变化较小。
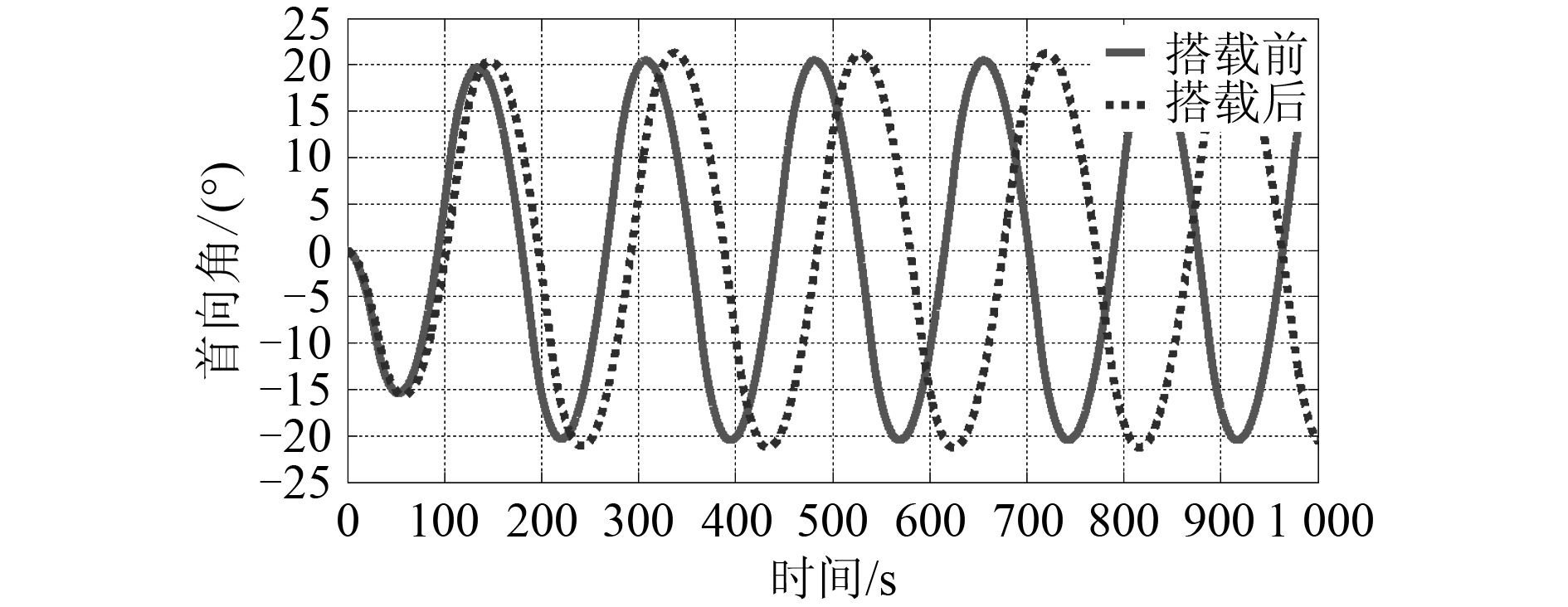
3.2 水平面 Z 型操舵运动对比仿真得到的潜艇外挂武器模块前后的首向角对比曲线如图 14 所示。
|
图 14 水平面运动首向角对比曲线 Fig. 14 Comparison curves between heading angles in horizontal plane |
计算结果表明:外挂武器模块前潜艇的初转期为 31.0 s、超越首向角为 11°,外挂后的潜艇的初转期为 33.7 s、超越首向角为 12°。外挂前后初转期的绝对变化量为 8.71%、超越首向角的绝对变化量为 4.76%。分析可知外挂武器模块后潜艇的应舵性降低了。
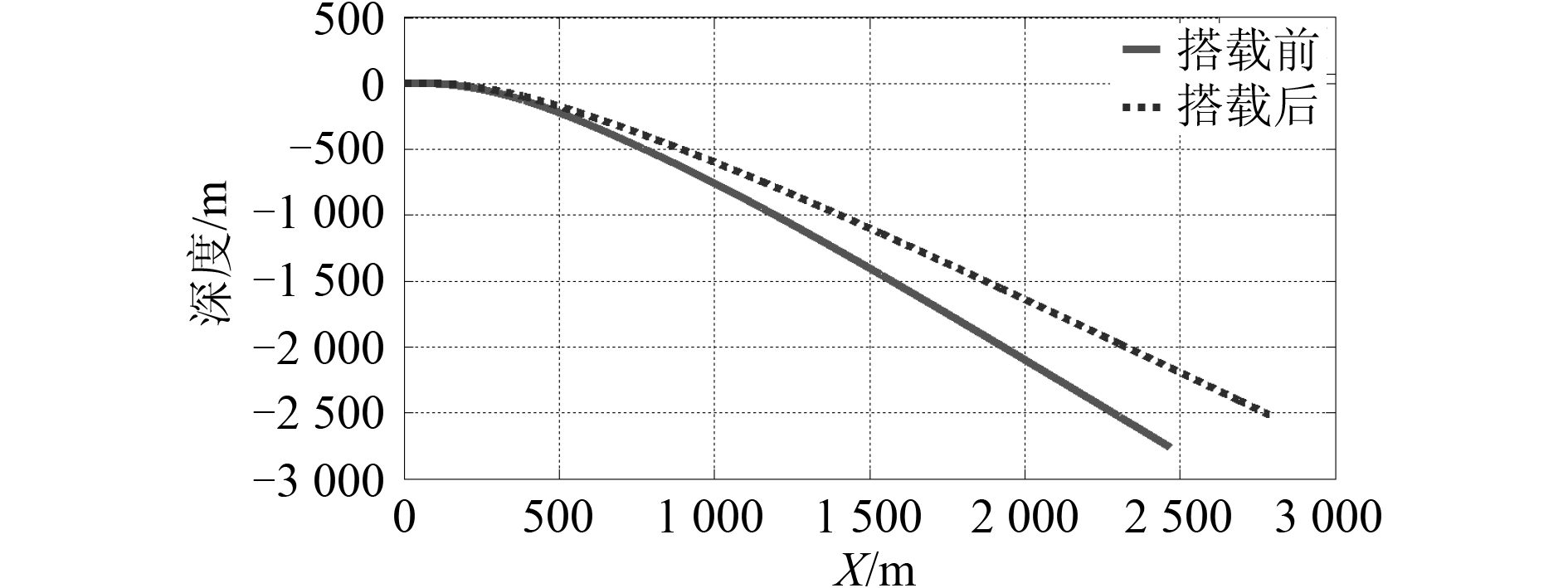
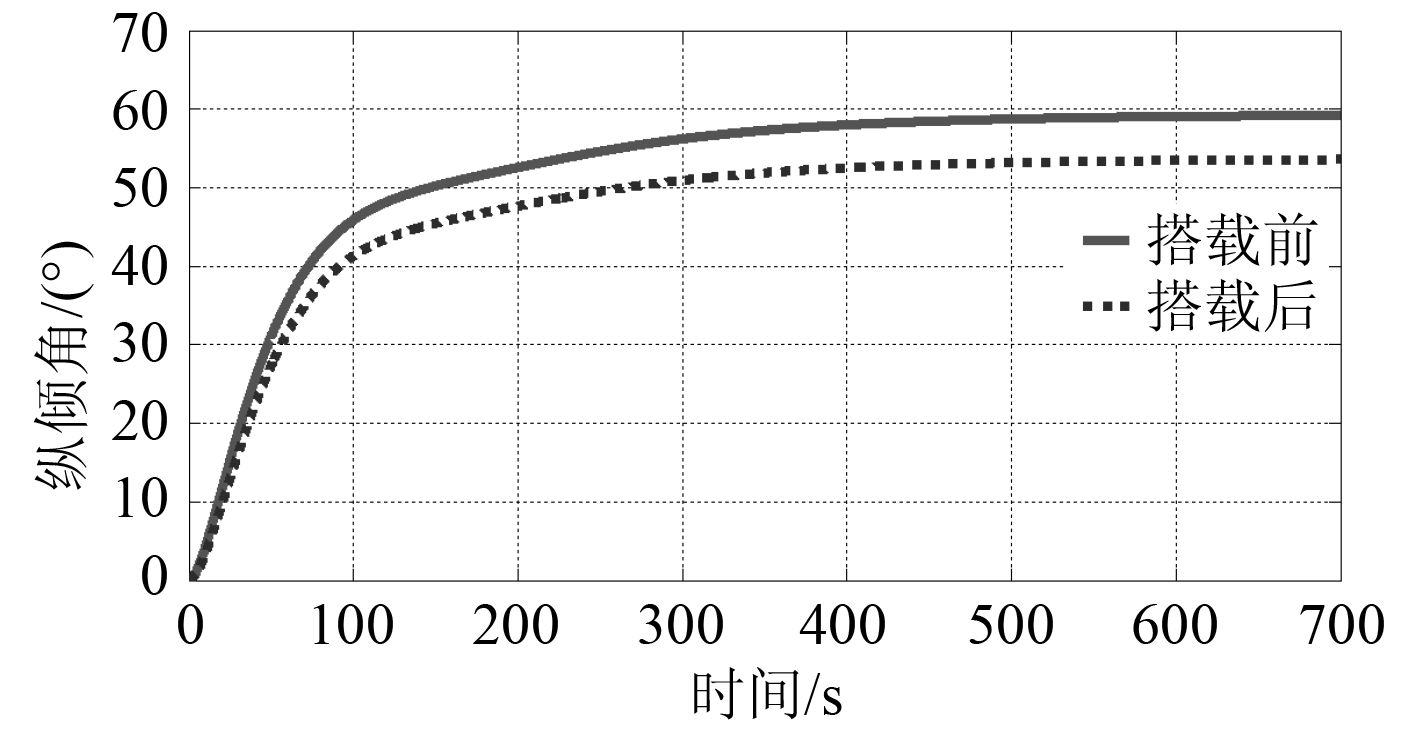
3.3 垂直面定常直线潜浮运动对比对潜艇(尾升降舵 20°)在外挂武器模块前后的定常直线潜浮运动进行仿真,得到的重心轨迹对比曲线(见图 15)和纵倾角对比曲线(见图 16)。
|
图 15 垂直面运动轨迹对比曲线 Fig. 15 Comparison curves of motion in vertical plane |
|
图 16 垂直面运动纵倾角对比曲线 Fig. 16 Comparison curves between pitch angles of motion in vertical plane |
从图 15 和图 16 分析可知:潜艇在外挂前的稳定时间为 46.2 s、最大纵倾角为 59°;外挂后的稳定时间为 50.1 s、最大纵倾角为 52°。分析可知外挂的武器模块对潜艇在垂直面上的操纵性能指标也有较大的影响,特别是纵倾角变化很大。
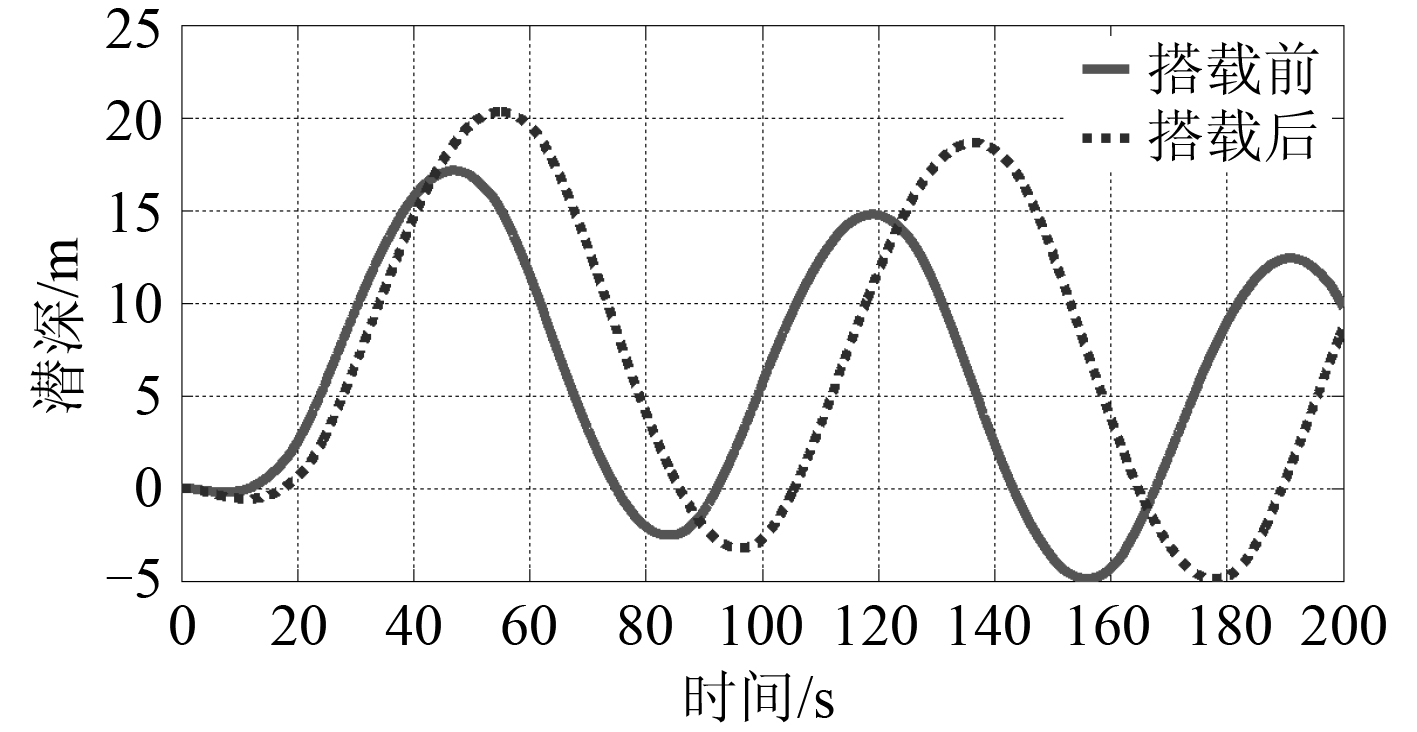
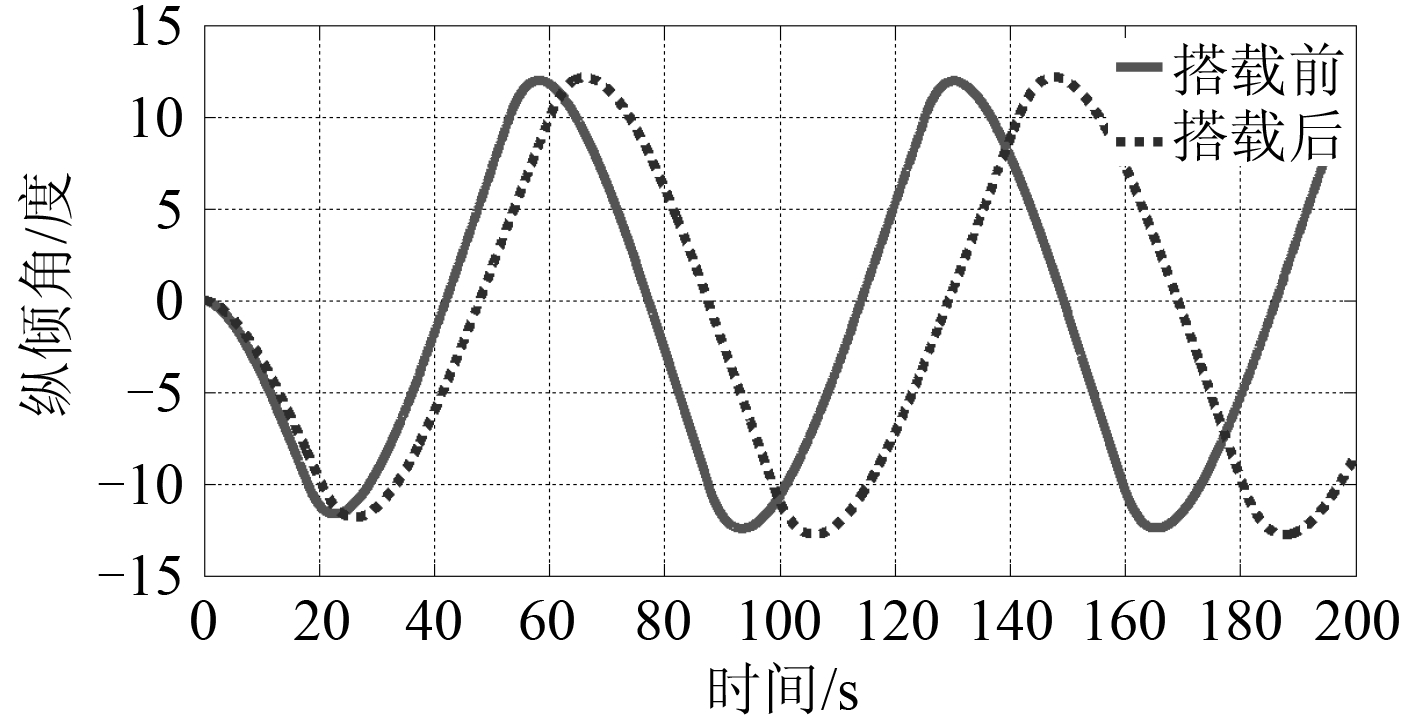
3.4 垂直面超越机动运动对比对潜艇外挂前后在 δ s /θ = 20°/10° 时的超越机动运动仿真计算,所得的深度对比曲线和纵倾角对比曲线如图 17 和图 18 所示。
|
图 17 垂直面运动潜深对比曲线 Fig. 17 Comparison curves of diving depth of motion in vertical plane |
|
图 18 垂直面运动纵倾角对比曲线 Fig. 18 Comparison curves of pitch angles of motion in vertical plane |
计算结果表明:外挂武器模块前潜艇的初转期为 17.8 s、超越深度为 0.4 m、超越纵倾角为 2.5°,外挂后的初转期为 20.0 s、超越深度为 0.5 m、超越纵倾角为 3.2°。计算可知搭载前后初转期的绝对变化量为 15.7%、超越深度的绝对变化量为 25.0%、超越纵倾角的绝对变化量为 28.0%。分析各性能指标的绝对变化量可知搭载的武器模块对潜艇垂直面的应舵性影响比对水平面的影响更大,潜艇在垂直面的机动能力将损失更多。
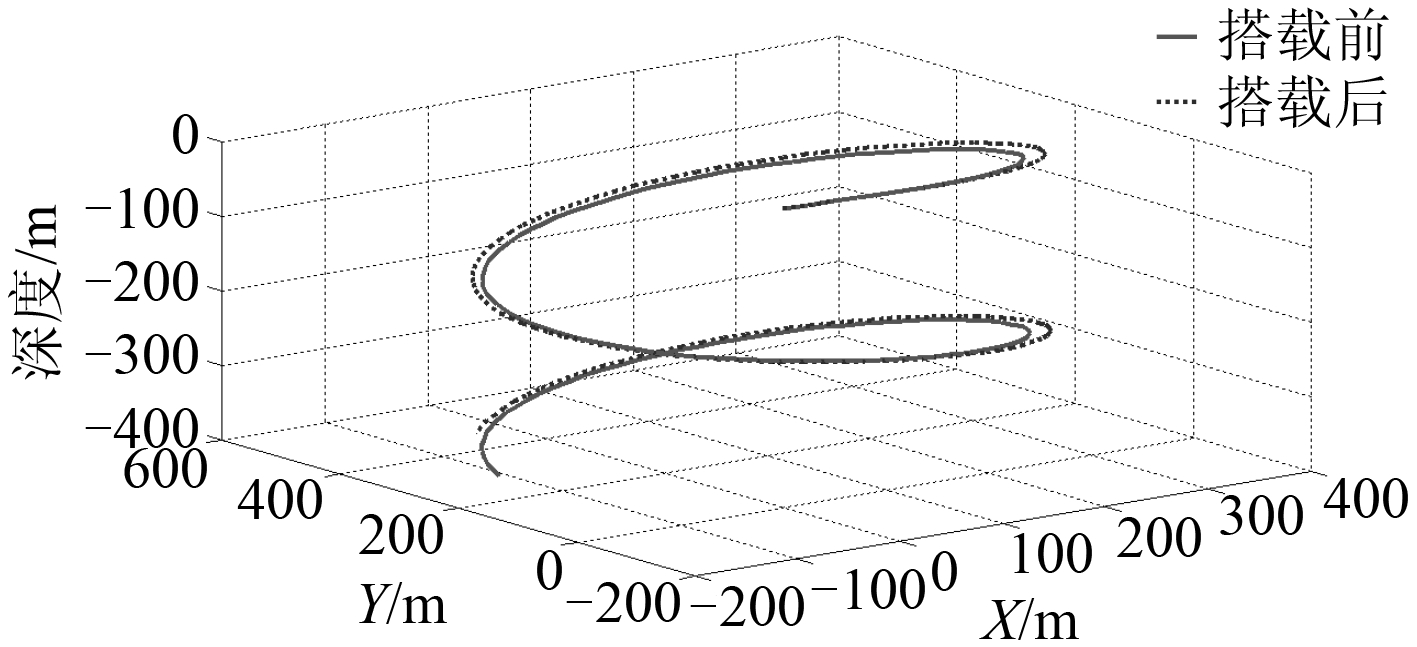
3.5 空间定常螺旋运动对比在 δ r = 30°,δ b = 10°,δ s = 0° 操舵条件下,对潜艇外挂武器模块前后的空间定常螺旋运动进行仿真,得到的潜艇外挂武器模块前后的重心运动轨迹对比曲线如图 19 所示。
|
图 19 空间螺旋运动轨迹对比曲线 Fig. 19 Comparison locus curves of spatial helical motion |
仿真得出的潜艇外挂武器模块前后的回转直径、回转周期、升距、相对升速等主要特征参数如表 2 所示。
|
|
表 2 外挂前后空间操纵性能指标对照表 Tab.2 Contrast on performance indexes of spatial maneuverability before and after carrying weapons module |
由表 2 可知:潜艇外挂武器模块前后的空间操纵性能有较大的变化,特别是回转直径和回转周期,这说明潜艇外挂武器模块后的空间操纵能力下降了,空间机动能力降低了。
4 结 语本文结合 5 种典型运动对外挂武器模块后的潜艇运动进行了仿真,结果表明外挂后的潜艇的机动性降低,相关的操纵性能指标下降。仿真结果符合潜艇本身的运动特性,说明所建立的模型合理。本文的仿真研究为下一步潜艇外挂武器模块的可行性论证奠定了一定的理论基础。
| [1] | 范乃忠. 现代潜艇的外挂布雷装置[J]. 现代舰船, 1995, 6 (2): 32–34. |
| [2] |
钱东. 美国未来的大型UUV-MANTA[J]. 鱼雷技术, 2003 (01): 41–50.
QIAN Dong. The Large-scale Unmanned Undersea Vehicles by the US in the Future[J]. Torpedl Tochnology, 2003 (01): 41–50. |
| [3] | SIRMALIS J E. Pursuing the MANTA vision: recent at-sea technology demonstration results[C]//UDT 2001 |
| [4] | 杨路春. 潜艇在有外部外挂情况下操纵性水动力导数的数值计算方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2009. |
| [5] | 付延辉, 万延橙. 潜艇空间运动研究进展[C]//国内外潜艇操纵性研究评述, 北京: 国防科工委水动力学专业组, 1992: 13–31 |
| [6] | 夏飞, 陈源. 潜艇操纵性预报评述[A]. 国内外潜艇操纵性研究评述, 北京: 国防科工委水动力学专业组, 1992: 1–12 |
| [7] | JOHN T H. Development of a six degee of freedom motion Simulation model for use in subma-rine design analysis[R]. ADA078410. USA: DTNSRDC, 1978: 1–20 |
| [8] | 胡坤, 张洪刚, 徐亦凡. 潜艇水下空间机动仿真与分析[J]. 北京: 计算机仿真, 2006, 23 (5): 10–13. |
| [9] | MARTLON G, GRANT P H. Standard equations of motion for submarine simulation. AD653861 June 1967, Naval Ship Research and Development Center. |
| [10] | 陈厚泰, 徐玉如, 黄锡荣. 关于深潜艇六自由度运动的流体动力系数测定和推算[J]. 船工学报, 1980(1). |
| [11] | 李殿璞. 船舶运动与建模(第二版)[M]. 北京: 国防工业出版社, 2008. |
 2017, Vol. 39
2017, Vol. 39
