近年来,人们的环保意识逐渐加强,对环境的保护越来越重视。水润滑轴承正在逐渐取代油润滑轴承成为新的研究方向。水润滑船舶尾轴承具有无污染、成本低、良好的减震和消音等优点[1]。阶梯腔动静压轴承具有运行平稳、损耗较低、承载力强等特点[2]但船舶尾轴承在启动、停车及低速运转的状态之下,常处在干摩擦或者半干摩擦状态,造成尾轴承的严重磨损。伴随着船舶尾轴承向高速重载方向的发展,解决轴承在运转过程中的摩擦磨损问题刻不容缓。
目前,国内许多专家学者在这方面做过科研工作[3 – 4]。郭胜安等[5]利用 CFD 软件研究了深浅腔动静压轴承的工作和结构参数对轴承的承载特性的影响。并运用理论与实验相结合的方法,验证了结果的正确性。文章只研究了动静压轴承的热动力润滑问题,对轴承的静力学问题鲜有涉及。戴攀等[6]针对高速机床主轴出现的热变形问题,提出了一种新型水润滑动静压混合轴承,运用有限元求解雷诺方程。研究了不同型腔结构轴承的刚度和温升性能,结果证明了新结构的有效性。文章重点是运用数学模型计算的方法,没有进行有限元仿真模拟。
为了解决上述问题,本文对尾轴承加以改造创新,在船舶尾轴承内部开设型腔结构,将尾轴承设计成一种新型的阶梯腔动静压轴承。新结构避免了主轴与轴承直接接触,从而形成液体润滑。并对这个新结构进行有限元静力分析,研究不同腔角和腔深对船舶尾轴承力学性能的影响。
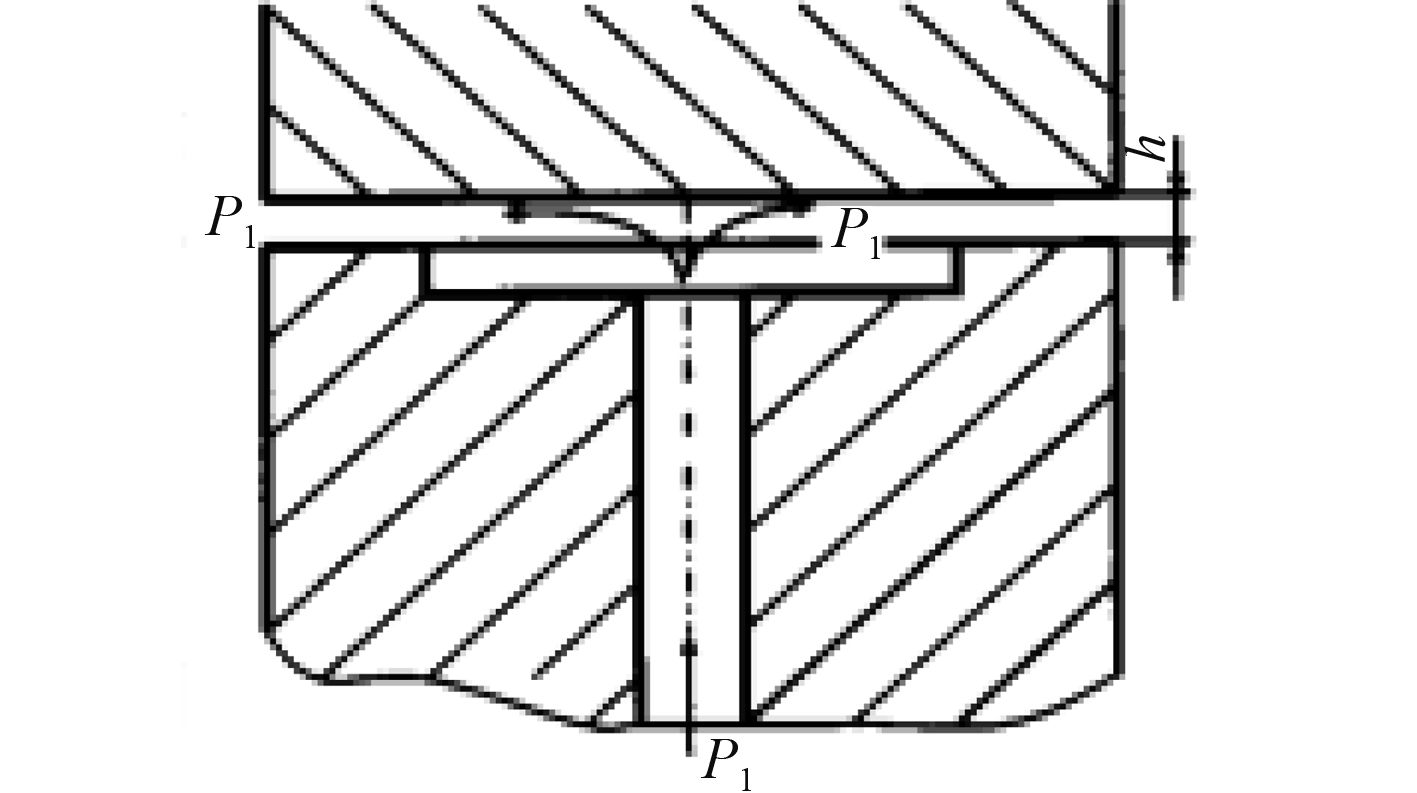
1 水润滑动静压尾轴承工作原理水润滑动静压轴承系统分为外部供水系统和轴承本身2部分构成。外部供水设备将一定压力的水通过进水孔送入到轴承静压腔内,从而建立起压力水膜,将轴承顶起,使得轴承主轴在预定载荷和任意转速下,与轴承处于完全液体润滑状态[7 – 8]。当轴承正常运转时,依靠主轴与轴承之间产生的动压压力和外部供油压力,支撑轴承的运转。如图 1 所示,将压力为 p 1 的润滑液注入到静压腔内,并顺着静压腔和四周的封油面流出到外界。图中P 1为供油压力,P 0为端泄压力,h为轴承间隙。
|
图 1 动静压轴承工作原理图 Fig. 1 Working principle of the static pressure bearing |
船舶尾轴承由轴套和外圈钢套2部分构成。对尾轴承的单元属性和材料属性进行定义:外圈钢套为合金钢,其中,密度为 7 800 kg/m3,弹性模量为 2.061 011 Pa,泊松比为 0.25;轴套材料为硬橡胶,密度为 1 850 kg/m3,弹性模量为 7.481 06 Pa,泊松比 0.4。同时,为了减小计算量对模型的其他几何尺寸进行相应的简化处理,如表 1所示。
|
|
表 1 模型几何尺寸 Tab.1 Model geometry size |
根据表 1所给出模型的基本参数,利用 Solidworks 三维绘图软件分别绘制了腔角分别为 20°,25°,30° 的 6 腔阶梯腔动静压船舶尾轴承基本模型。并且在腔角为 20° 的 6 腔阶梯腔模型基础上,分别绘制了深浅腔腔角比例为 1 : 3,1 : 4,1 : 5 的尾轴承模型。

|
图 2 尾轴承实体模型 Fig. 2 Stern bearing entity model |

|
图 3 尾轴承三维模型网格划分图 Fig. 3 Stern bearing mesh model figure |
将建好的模型导入到有限元软件中进行分析,以腔角为 20° 的 6 腔阶梯腔尾轴承模型为例(见图 2) ,其中坐标系中的Z轴为尾轴承的轴向方向,顺时针为轴承的运转方向。
|
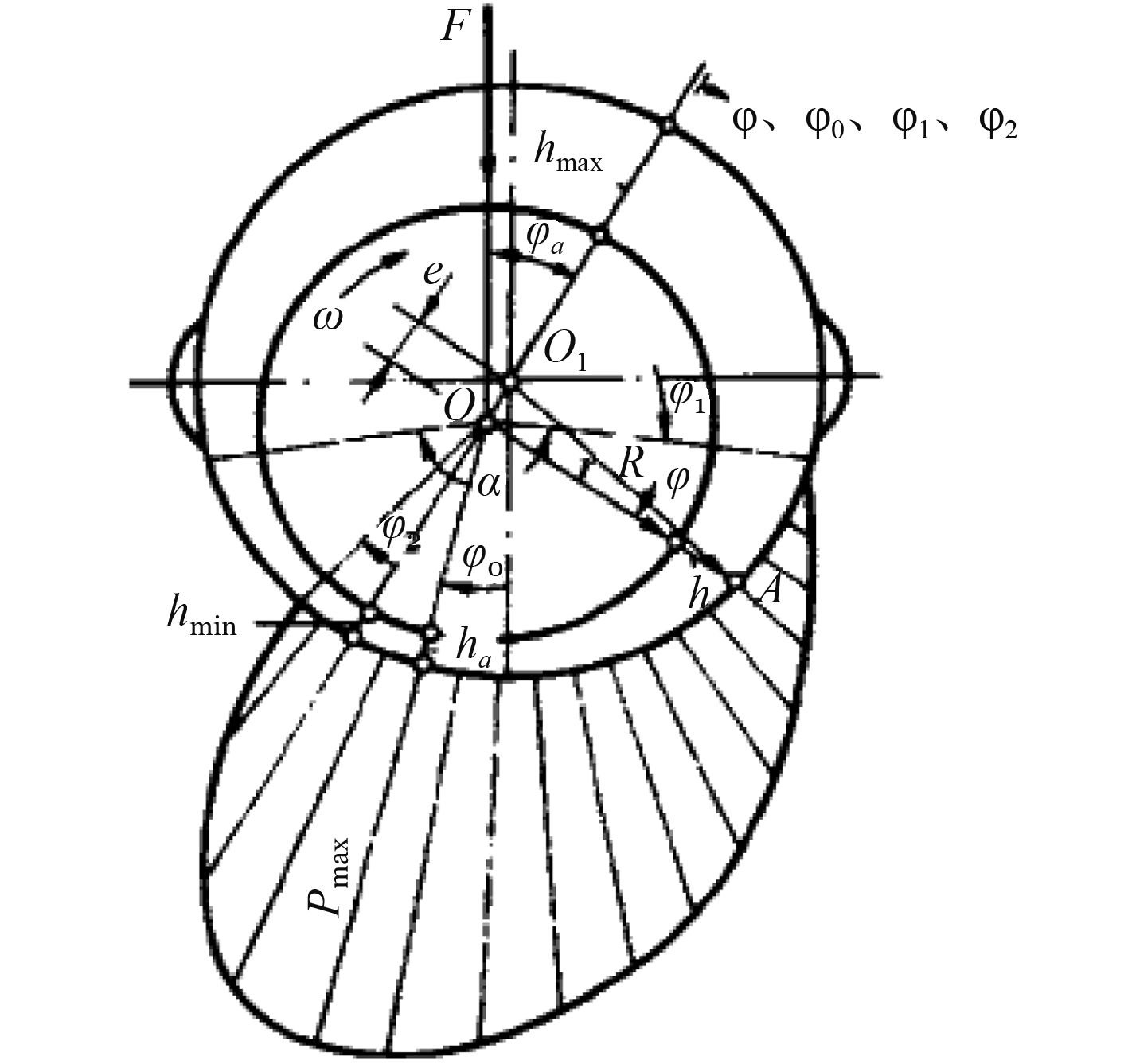
图 4 动压润滑压力分布 Fig. 4 The pressure distribution of dynamic pressure lubrication |
将建好的模型导入到 Ansys Workbench 软件中进行静力分析,设置好材料类型和单元属性。对所建模型按照边界尺寸大小为 0.015 mm 进行网格划分(见图 3),设定运行温度为 22°,然后对模型进行添加约束载荷并最终进行求解和计算。本文以图 2 所示的腔角为 20° 的 6 腔阶梯形腔尾轴承为例,划分后得到如下结果:节点 122 352 个和单元 69 808 个。对轴承的外表面施加全约束,以防止轴承沿轴向滑动,更接近实际情况。当尾轴承内部无沟槽和型腔情况下,动压润滑压力分布[1]如图 4 所示,图中,F为外载荷,ω为角速度,e为偏心距,Φ为偏位角,h为油膜厚度,p为油膜压力。由于深浅腔轴承可以在转速较低的情况之下形成连续完整的润滑油膜[7 – 9]。所以假设开设沟槽和型腔的尾轴承的压强分布近似满足图 4 所示的压力分布,先将轴承分割成许多较小的区域,根据图 4 所示的压力分布进行离散取值,将取好的压力值施加到相应的区域内。输入数值进行运算,最后模拟得出应力,应变和位移三维模型图。假设本文中尾轴承运动状态是动静压润滑状态,运行工况为稳态环境,轴承在轴向方向不发生位移,不考虑海水的惯性力。
|
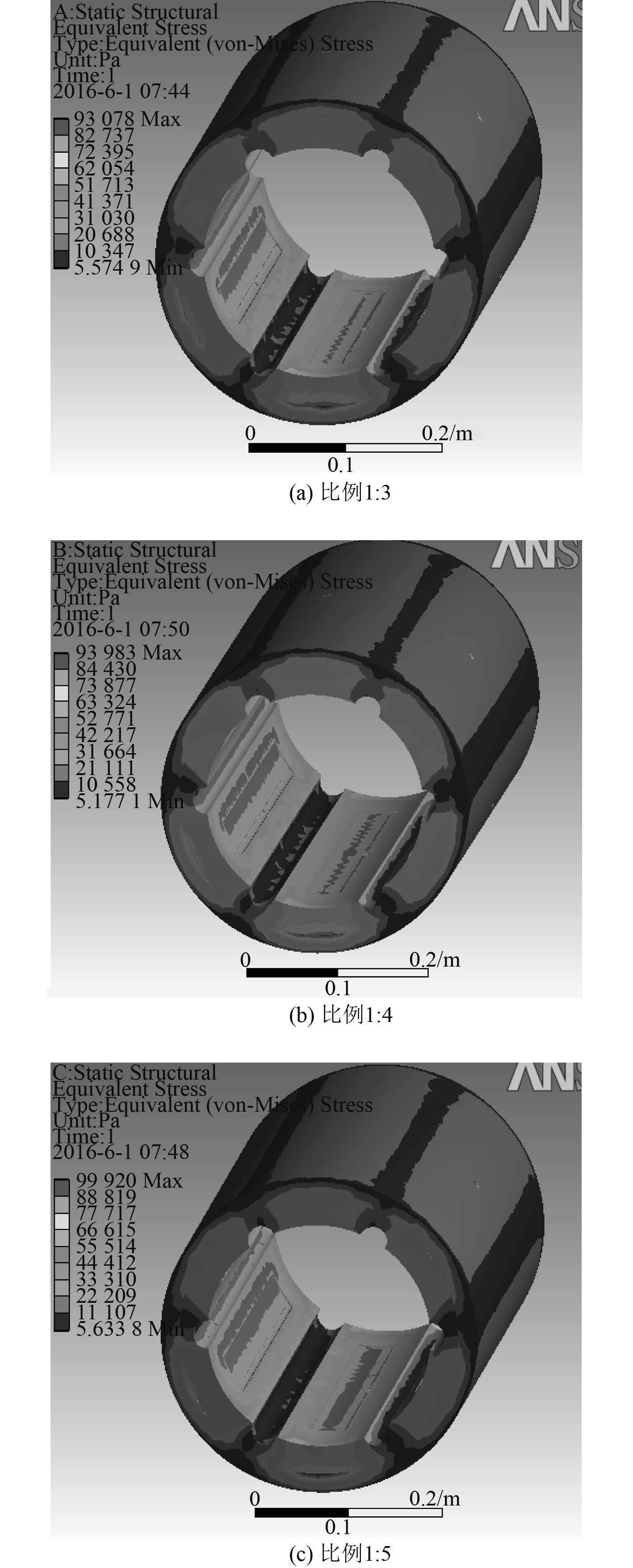
图 5 不同腔角比例尾轴承应力图 Fig. 5 Different chamber angle proportion stern bearing stress |
|
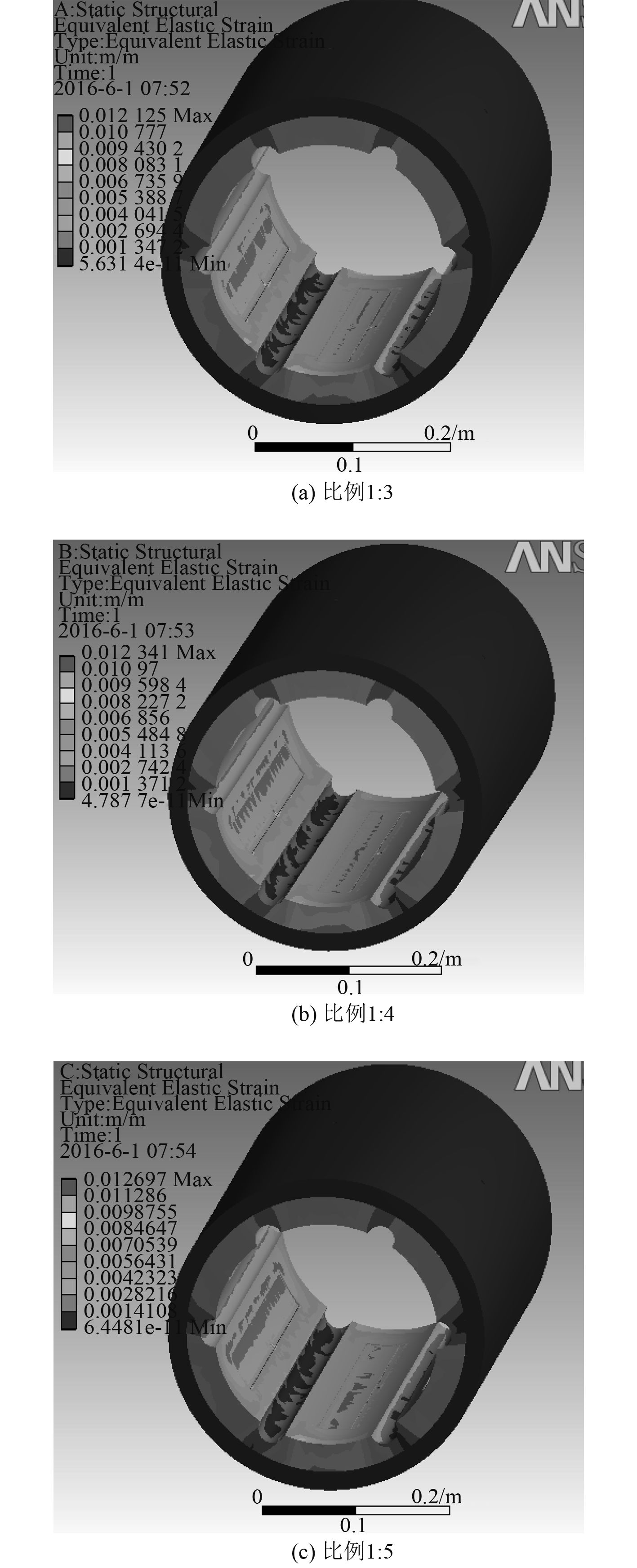
图 6 不同腔角比例尾轴承应变图 Fig. 6 Different chamber angle proportion stern bearing strain |
建立腔角分别为 20°,25°,30° 的阶梯形腔尾轴承模型,为了控制变量,保证深浅腔的腔角比例固定不变,按照 1:4 的比例[7]进行设置,其他几何尺寸都相同,并导入 Ansys Workbench 软件中,施加相同大小的载荷进行静力学分析,设定最大载荷为 3 600 N。分别得到应力、应变和位移 3 个影响因素的变化情况如表 2 所示。
|
|
表 2 不同腔角艉轴承力学性能 Tab.2 Different chamber angle stern bearing mechanics performance |
从表 2 中可看到,在 3 组最大应力的对比中,腔角为 20° 时应力值最小,此时的数值为 106 560 Pa。同样,比较最大应变值发现,腔角为 20° 时最大应变值最小,数值为 1.151 × 10–2。而对比分析最大位移值的变化时发现,3 组数值大小相差不大,腔角的变化对位移的影响较小。所以,综合对比发现,当腔角为 20° 时,尾轴承的力学性能最优。
3.3 不同腔角比例尾轴承力学性能选用腔角大小为 20° 的尾轴承,研究在总腔角大小不变的情况之下,不同深浅腔腔角比例尾轴承的力学性能。建立深浅腔腔角比例分别为 1 : 3,1 : 4,1 : 5 的阶梯腔尾轴承模型,并将建好的模型导入到 Ansys Workbench 有限元软件中进行分析。分别得到应力、应变和位移的分布情况。
通过对比不同深浅腔腔角比例尾轴承应力分布图发现(见图 5 ),当深腔和浅腔的比例为 1 : 3 时,在尾轴承的左侧和下侧都存在最大应力集中现象,而其他 2 种轴承的最大应力集中现象只在下侧比较明显。单独比较腔角比例 1 : 4 和 1 : 5 的应力集中情况发现,当腔角是 1 : 5 时,下侧最大应力集中区域比较狭长;从数值上作比较,腔角比例是 1 : 4 时的最大应力值为 94 983 Pa,而腔角比例是 1 : 5 时的最大应力值为 99 920 Pa。出现这个现象的原因是,由于腔角比例增大,深腔所占面积比例减小而浅腔比例增加,深腔的深度大而面积小,会使得深腔变成了一道深沟,类似轴承表面出现了损伤,从而导致尾轴承应力增大。
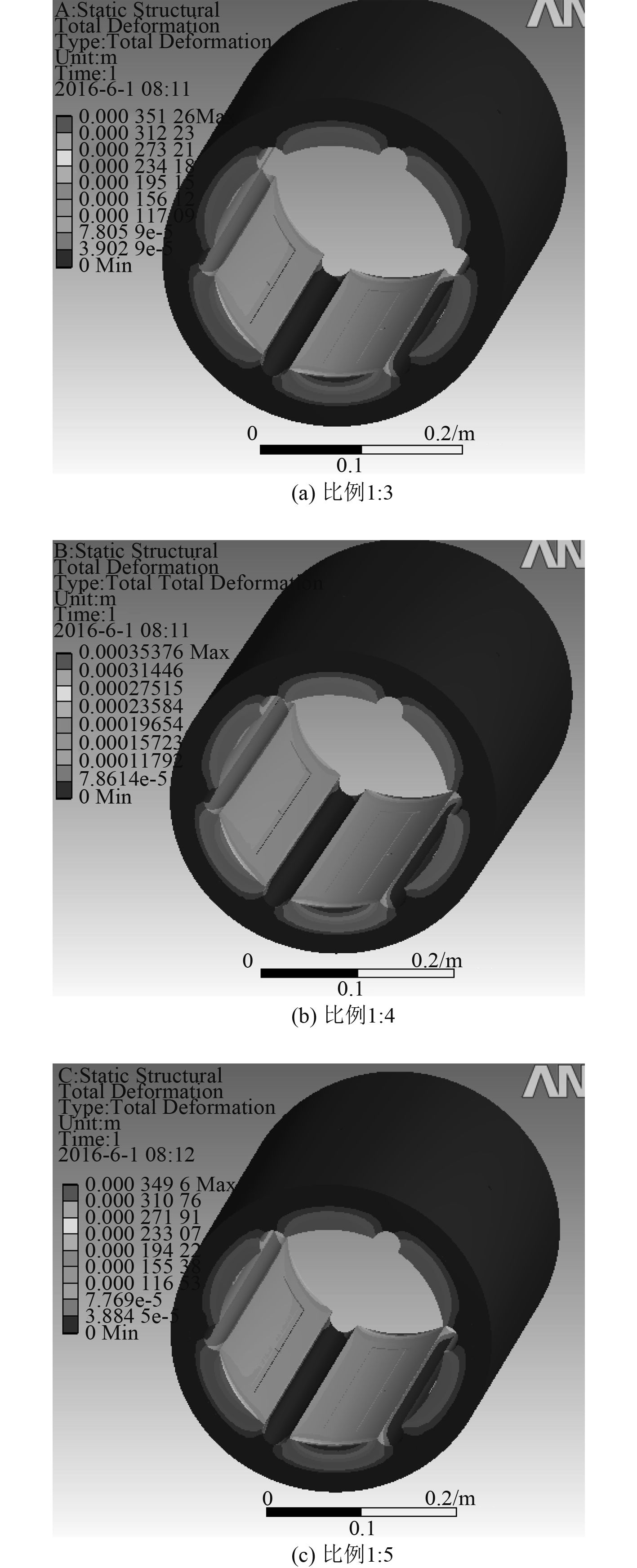
|
图 7 不同腔角比例尾轴承位移图 Fig. 7 Different chamber angle proportion stern bearing displacement |
图 6 为不同腔角比例的尾轴承应变图。从图中可看出,3 种不同比例的尾轴承应变主要集中出现在低端和左侧边缘处,这是由于低端承受了主轴的大部分力,而左侧由于动压效应的作用,受力也相对增大,所以这 2 个地方的应变现象比较明显。腔角比例为 1 : 3 和 1 : 4 的应变图比较相似,最大应变值也较接近,前者为 0.012 1,后者为 0.012 3。从图 6 可看出,腔角比例为 1 : 5 时的应变集中变化较平缓,但它最大应变值达到 0.012 7。
|
图 8 不同腔深尾轴承最大应力折线图 Fig. 8 Different cavity deep stern bearing maximum stress |
图 7 为不同腔角比例下尾轴承位移图,分析对比 3 张图发现,位移变化较大的位置均出现在了尾轴承的两端的边缘处,且位移的变化差距不大。从数值上比较,3 种轴承的最大位移值差距不大,腔角比例为1 : 5 时最大位移值为 0.349 6 mm,腔角比例 1 : 3和 1 : 4 的最大位移值分别为 0.351 3 mm 和 0.353 8 mm。
|
图 9 不同腔深尾轴承最大应变折线图 Fig. 9 Different cavity deep stern bearing maximum strain |
综合考虑应力、应变和位移的变化情况发现,当深浅腔的腔角比例为 1 : 4 时,此时力学性能最优。阶梯腔的深浅腔腔角比例对尾轴承的力学性能有着十分重要的影响,合适的腔角比例能有效的改善尾轴承的力学性能,提高轴承的使用寿命,增加轴承的稳定性。
3.4 不同腔深对尾轴承力学性能的影响研究深腔腔深为 1.2 mm,1.4 mm,1.6 mm,1.8 mm,2 mm 以及浅腔腔深为 0.2 mm,0.4 mm,0.6 mm,0.8 mm,1.0 mm 的尾轴承类型,根据数学对应关系总共建立 25 种尾轴承模型。除了腔深不同之外,轴承的其他尺寸都相同,将建好的模型导入到 Ansys Workbench 软件中进行有限元分析,其他步骤如上所述。分别得到应力、应变和位移3个影响因素的变化情况,并将结果绘制成折线图。
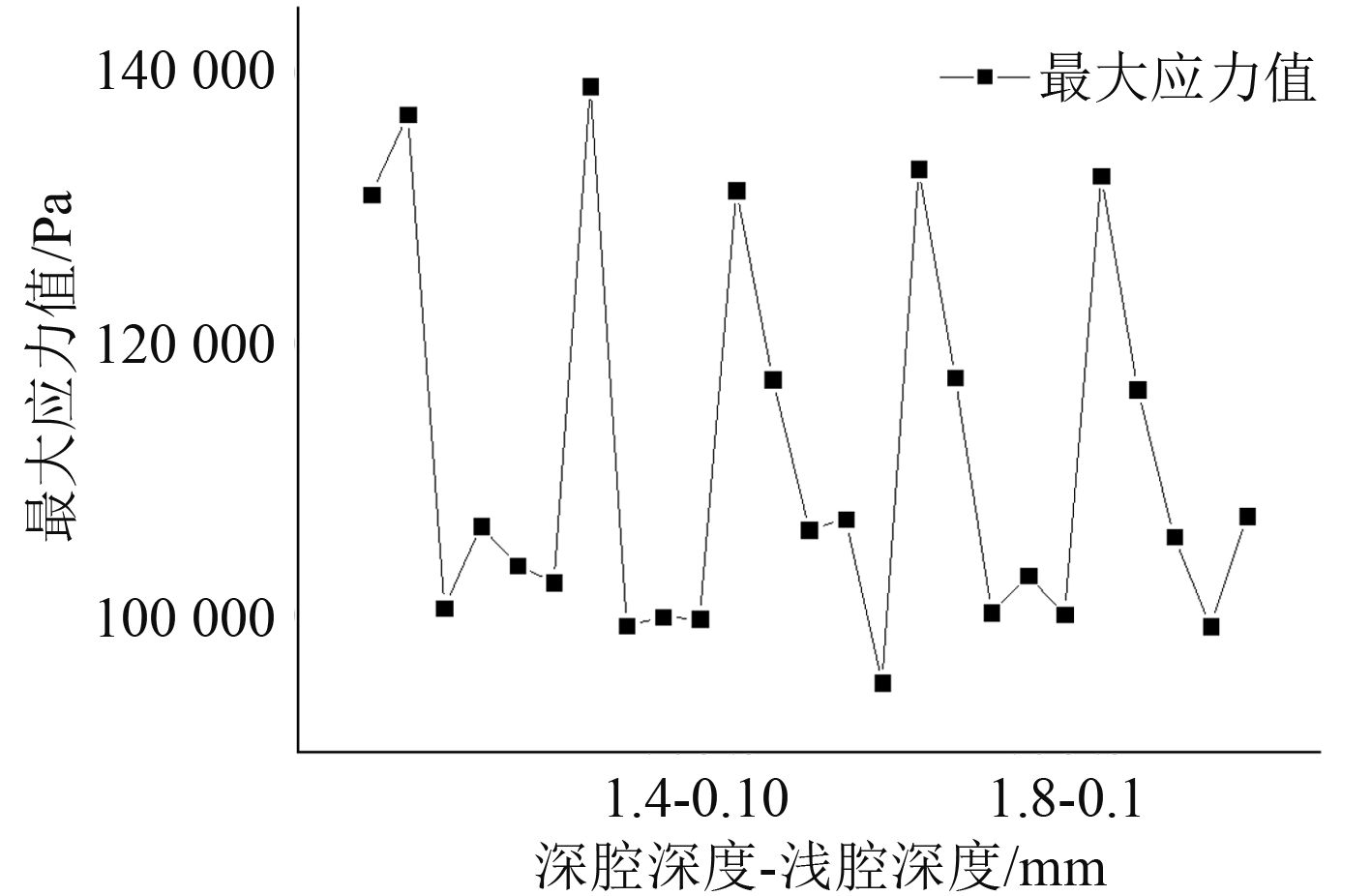
图 8 所示为不同腔深尾轴承最大应力折线图,由图 8 可发现,随着横坐标的增大,最大应力值呈现波浪式的变化。波峰的位置分别出现在 1.2~0.4 mm,1.4~0.4 mm,1.6~0.2 mm,1.8 ~ 0.2 mm 和 2.0~0.2 mm 五个位置,波峰出现的位置基本上是在2个深腔腔深数值交换处,也就是说,当深腔腔深增大 0.2 mm(比如由 1.8 增大到 2.0)时,最大应力值会突然变化,随后随着浅腔腔深不断增大,最大应力值逐渐减小这样的规律。出现波峰的原因是,由于深腔和浅腔腔深差距过大,导致过渡变化较大,表面出现断崖式的不连续现象,应力变化较大。当深腔腔深不变时,随着浅腔腔深不断增大,最大应力值逐渐减小。出现这种现象的原因是,随着浅腔腔深的增大,两腔之间的差距被缩小,由深腔到浅腔的过渡比较的平缓,所以最大应力值减小。在设计深浅腔动静压轴承时,在保证承载力的前提下,应该尽量使得两腔的腔深差距不要过大,保持过渡平缓。当 1.6~1 mm(即深腔腔深为 1.6 mm,浅腔腔深为1 mm)时,此时的最大应力值最小为 95 172 Pa。
|
图 10 不同腔深尾轴承最大位移折线图 Fig. 10 Different cavity deep stern bearing maximum displacement |
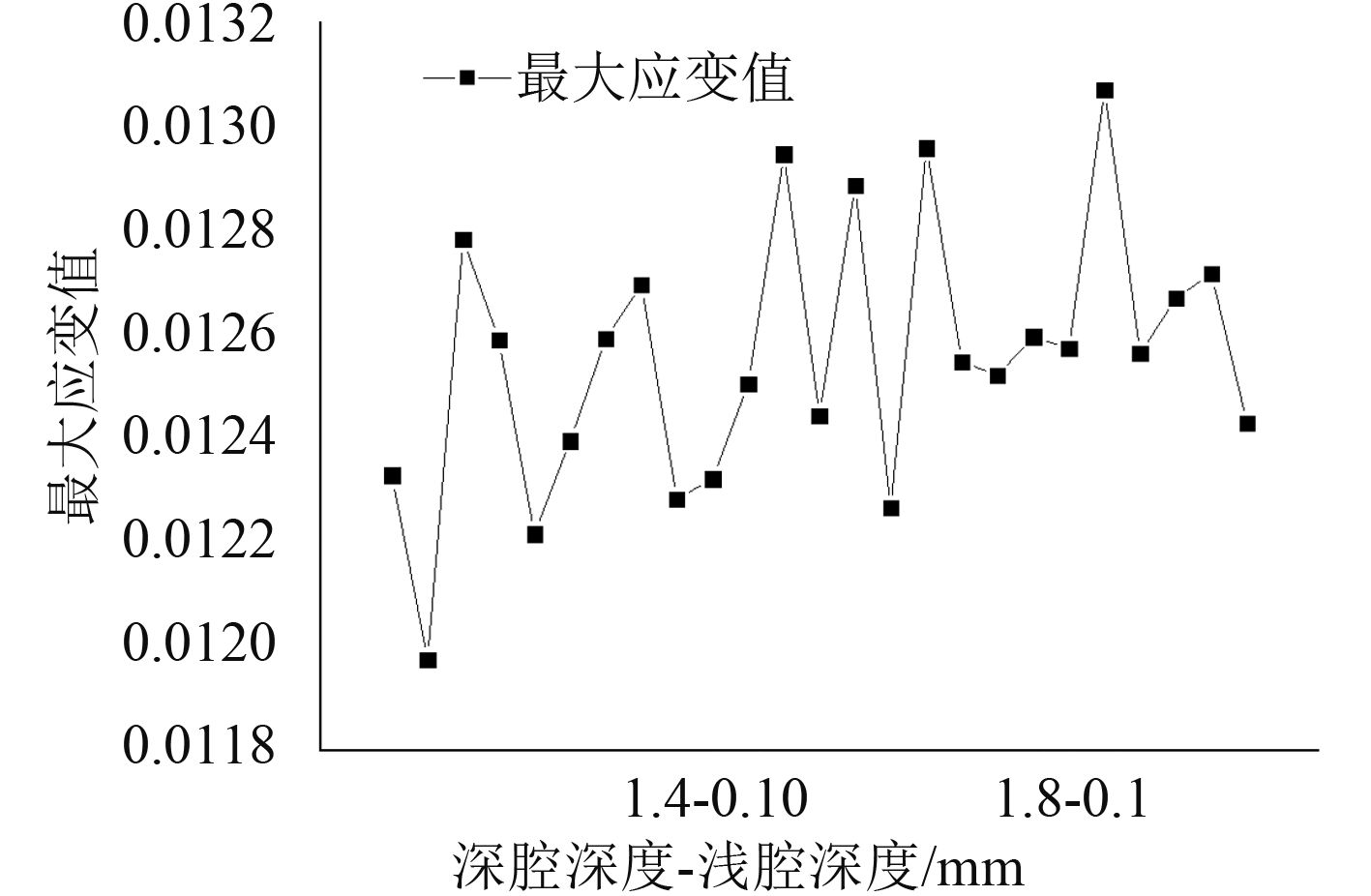
图 9 所示为不同腔深尾轴承最大应变折线图。从图 9中可看出,随着横坐标的增大,最大应变值呈现波动上升的趋势。说明无论是深腔还是浅腔,腔深过大都会导致尾轴承应变的增加,所以,设计腔深时尽量使得尾轴承腔深较浅,从而达到最佳的力学性能。当 1.6~1 mm(即深腔腔深为 1.6 mm,浅腔腔深为1 mm)时,尾轴承的最大应变值较小为 0.012 25。
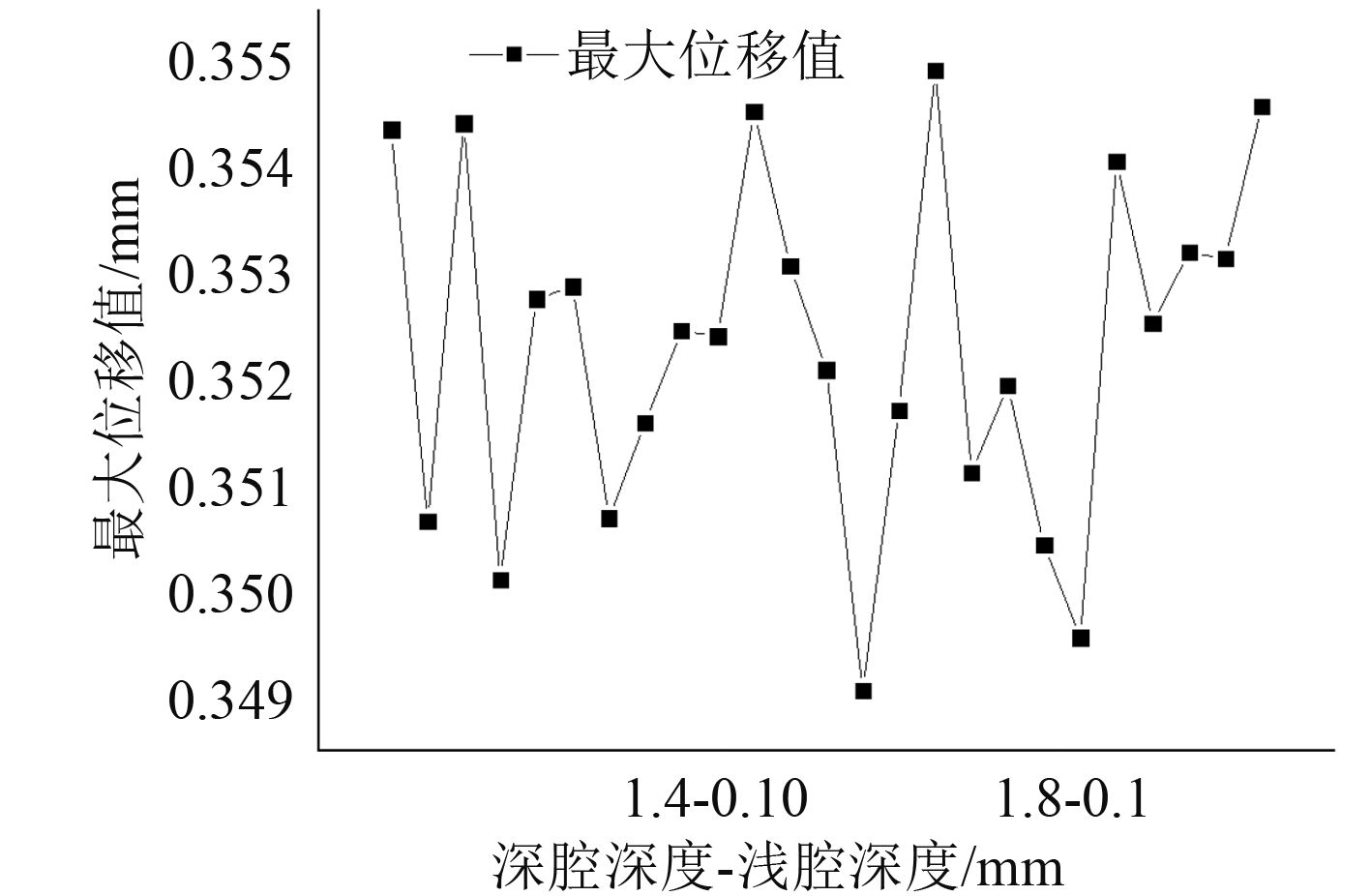
图 10 所示为不同腔深尾轴承最大位移折线图。从图 10 中可看出,最大位移值波动变化,波峰出现的位置基本上是在 2 个深腔腔深数值交换处。从图上看变化比较剧烈,但比较数值大小可以发现,最大值与最小值之间只相差了 0.005 86 mm,所以轴承腔深对位移的影响较小。
综上所述,在设计深浅腔动静压轴承时,保证承载力的前提下,应该尽量使得两腔的腔深差距不要过大,保持过渡平缓。综合考虑应力、应变和位移3个因素得出,当深腔腔深为 1.6 mm,浅腔腔深为 1 mm 时,轴承的力学性能较优。
4 结 语1)阶梯腔的腔角对尾轴承的力学性能有比较大的影响,影响着应力、应变和位移的分布,并且呈现出各自特有的规律。当腔角为 20° 时,尾轴承的力学性能最优。
2)合适的腔角比例能有效改善尾轴承的力学性能,当深浅腔的腔角比例是 1 : 4 时,此时力学性能要优于其他腔角比例的尾轴承。
3)在保证承载力的前提下,应该尽量使得两腔的腔深差距不要过大,保持过渡平缓,避免应力集中现象的发生。当深腔腔深为 1.6 mm,浅腔腔深为 1 mm 时,此时轴承的力学性能较优。
| [1] |
律辉, 王优强, 卢宪玖, 等. 基于Ansys的不同螺旋槽艉轴承的结构静力分 析[J]. 润滑与密封, 2014 (3): 57–62.
LV Hui, WANG You-qiang, LU Xian-jiu, et al. The Static Structural Analysis of the Various Spiral Groove Stern Bearing Based on Ansys[J]. Lubrication Engineering, 2014 (3): 57–62. |
| [2] |
刘豪杰, 郭红, 张绍林. 基于FLUENT的深浅腔动静压轴承油膜压力研究[J]. 润滑与密封, 2013 (10): 35–38.
LIU Hao-jie, GUO Hong, ZHANG Shao-lin. Research on Static Characteristics of Deep/Shallow Pockets Hybrid Bearing Based on FLUENT[J]. Lubrication Engineering, 2013 (10): 35–38. DOI: 10.3969/j.issn.0254-0150.2013.10.008 |
| [3] |
杨俊, 王隽, 周旭辉, 等. 水润滑橡胶轴承结构设计[J]. 舰船科学技术, 2011 (8): 103–107.
YANG Jun, WANG Jun, ZHOU Xu-hui, et al. Research on Static Characteristics of Deep/Shallow Pockets Hybrid Bearing Based on FLUENT[J]. Lubrication Engineering, 2011 (8): 103–107. |
| [4] |
姚世卫, 胡宗成, 马斌, 等. 橡胶轴承研究进展及在舰艇上的应用分析[J]. 舰船科学技术, 2005, 27 (S1): 27–30.
YAO Shi-wei, HU Zong-cheng, MA Bin, et al. Research progress of rubber bearing and its application on the ship[J]. ship science and technology, 2005, 27 (S1): 27–30. |
| [5] |
郭胜安, 侯志泉, 熊万里, 等. 基于CFD的深浅腔液体动静压轴承承载特性研究[J]. 制造技术与机床, 2012 (9).
GUO Sheng-an, HOU Zhi-quan, XIONG Wan-li, et al. Bearing characteristics study on liquid hybrid bearing based on CFD[J]. Manufacturing Technology & Machine Tool, 2012 (9). |
| [6] |
戴攀, 张亚宾, 徐华. 新型高速铣床主轴水润滑动静压轴承结构及性能研究[J]. 润滑与密封, 2009, 34 (2): 11–14.
DAI Pan, ZHANG Ya-bin, XU Hua. The Structure of New Journal Hybrid Bearing for High-speed Machine Spindle and Its Performance[J]. Lubrication Engineering, 2009, 34 (2): 11–14. |
| [7] |
邵俊鹏, 张艳芹, 李鹏程. 基于FLUENT的静压轴承椭圆腔和扇形腔静止状态流场仿真[J]. 润滑与密封, 2007, 32 (1): 93–95.
SHAO Jun-peng, ZHANG Yan-qin, LI Peng-cheng. Static Flow Simulation of Hydrostatic Bearing Ellipse and Sector Curve Based on FLUENT[J]. Lubrication Engineering, 2007, 32 (1): 93–95. |
| [8] | 陈燕生. 液体静压支承原理和设计[J]. 北京: 国家工业出版社, 1980. |
| [9] |
王芳芳, 陈渭, 张友峰. 新型水润滑动静压高速主轴轴承的流场模拟[J]. 润滑与密封, 2010, 35 (12): 28–31.
WANG Fang-fang, CHEN Wei, ZHANG You-feng. Flow field simulation of a new type of hydrostatic high speed spindle bearing[J]. lubrication and seal, 2010, 35 (12): 28–31. DOI: 10.3969/j.issn.0254-0150.2010.12.006 |
 2017, Vol. 39
2017, Vol. 39
