应力集中是导致轴系断裂破坏的主要因素之一,船舶轴系应力集中主要发生在法兰与轴之间的过渡区域。轴肩即该过渡部位,良好的轴肩过渡曲线设计有助于缓解应力集中。目前普遍采用一个1/4圆弧作为轴肩过渡曲线,通常情况下此种设计已能够满足轴系安全平稳运行的要求。但对于某些特殊情况,比如阶梯轴之间轴径差过大、轴材料强度不足等,单曲率圆弧过渡曲线已经不能将应力集中系数减小到足够小的程度,此时不得不采用一些特殊形式的过渡曲线[1]。近年来,在对 38 000 t 绿色海豚系列散货船的研发设计过程中,为确保轴系安全运转,研究了多种轴肩过渡曲线。
本文主要分析多种轴肩过渡曲线的设计方法,以有限元软件 Abaqus 为工具建立轴肩模型,研究这些曲线下轴肩应力集中的情况。除了本文涉及到的 5 种形式,其他形式的轴肩过渡曲线还有 3 次样条、B 样条和圆弧蜕变等多种复杂曲线,由于这些曲线形状加工难度高,不利于工程上的应用,故本文不做研究。另外,轴肩应力集中系数的大小与加载方式有关,拉压和扭转 2 种情况下的应力集中系数是有不小差别的。轴系设计的关键参数——扭振合成许用应力只与扭转应力集中系数相关,故本文只研究不同轴肩过渡曲线下的扭转应力[2]。
1 轴肩过渡曲线设计本文分析单曲率圆弧、双曲率圆弧、三曲率圆弧、椭圆和流线形等 5 种轴肩过渡曲线的设计方法。
1.1 单曲率圆弧过渡曲线单曲率圆弧是目前最常用的轴肩过渡曲线,如图 1所示。其中,D,h,d,r,L,e 分别为法兰直径、法兰厚度、轴径、轴肩过渡半径、轴肩过渡长度和轴肩过渡高度。点 P 为应力最大的点,点 Q 为轴肩与轴的切点,θ 为点 P 到点 Q 之间圆弧对应的角度,称之为应力集中角度。
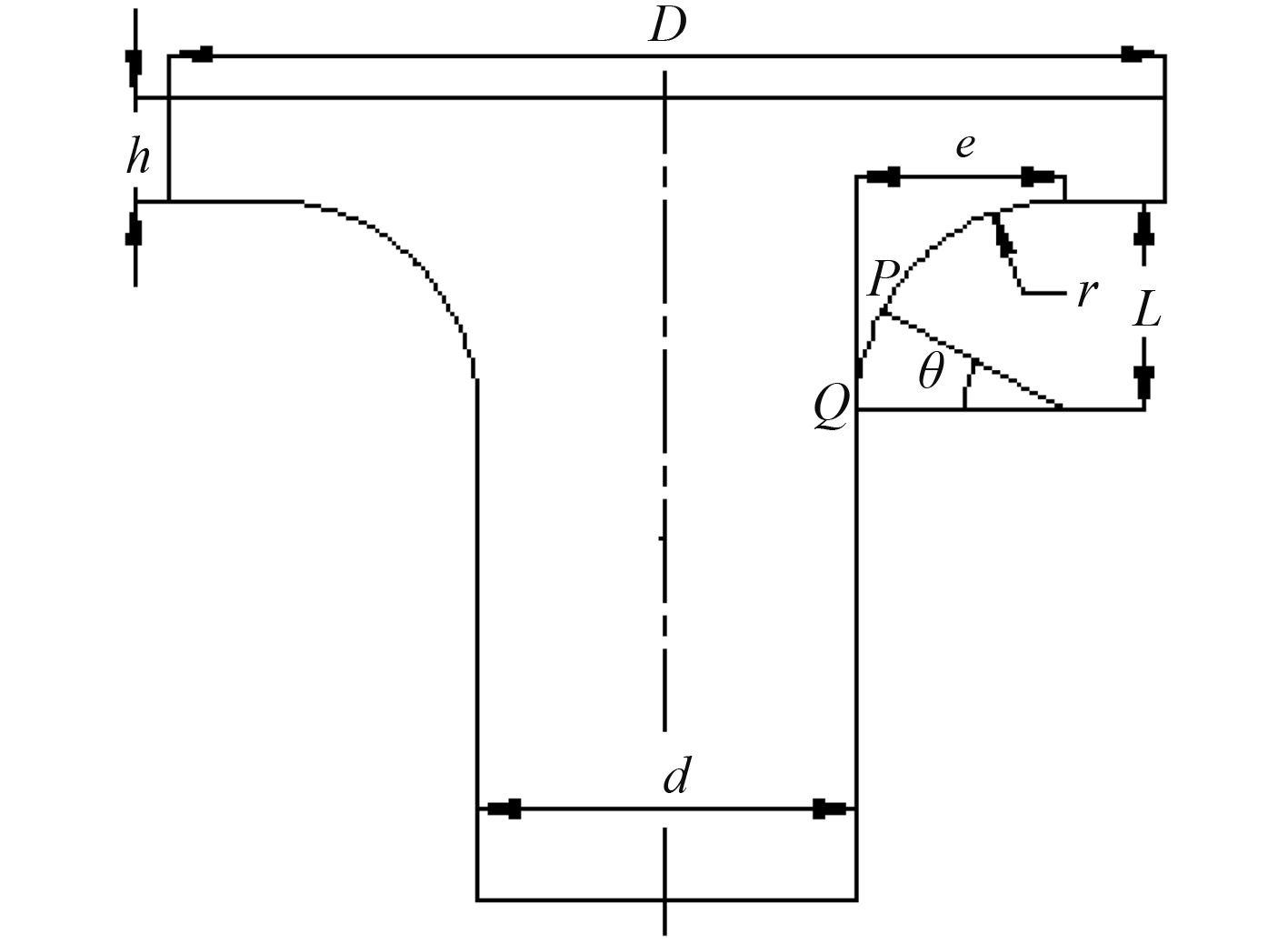
|
图 1 单曲率圆弧轴肩过渡曲线 Fig. 1 Single-radius shoulder transition curve |
过渡半径 r 越大,过渡越平缓,应力集中系数越小。理论上可以通过加大过渡半径来将应力集中降低到可以忽略的程度,但是随着半径的增大,法兰和轴肩也不断变大,一方面增加了轴系的重量和成本,另一方面占据过大空间而不利于布置[3]。
研究表明,轴肩上最大应力点 P 从圆弧切点 Q 起,对于圆心,处于 15° 之内,即P 与 Q 是紧邻着的。因此一般认为,只要局部地将 PQ 之间的半径加大,便可达到既减小应力集中系数又不增大轴肩和法兰尺寸的目的,这也便是双曲率和三曲率过渡曲线的设计理念由来[4]。
1.2 双曲率圆弧过渡曲线双曲率圆弧过渡曲线如图 2 所示,AB 段是半径较小的圆弧,BC 段是半径较大的圆弧,两圆弧在 B 点相切。其中,r 1 和 r 2 分别是两段圆弧的半径。根据不同的r 1 和 r 2,可以设计出无数条双曲率圆弧。文献[5]对于很多种不同形式的双曲率过渡曲线进行了光弹性实验,通过试凑的方法给出了1条效果良好的曲线。
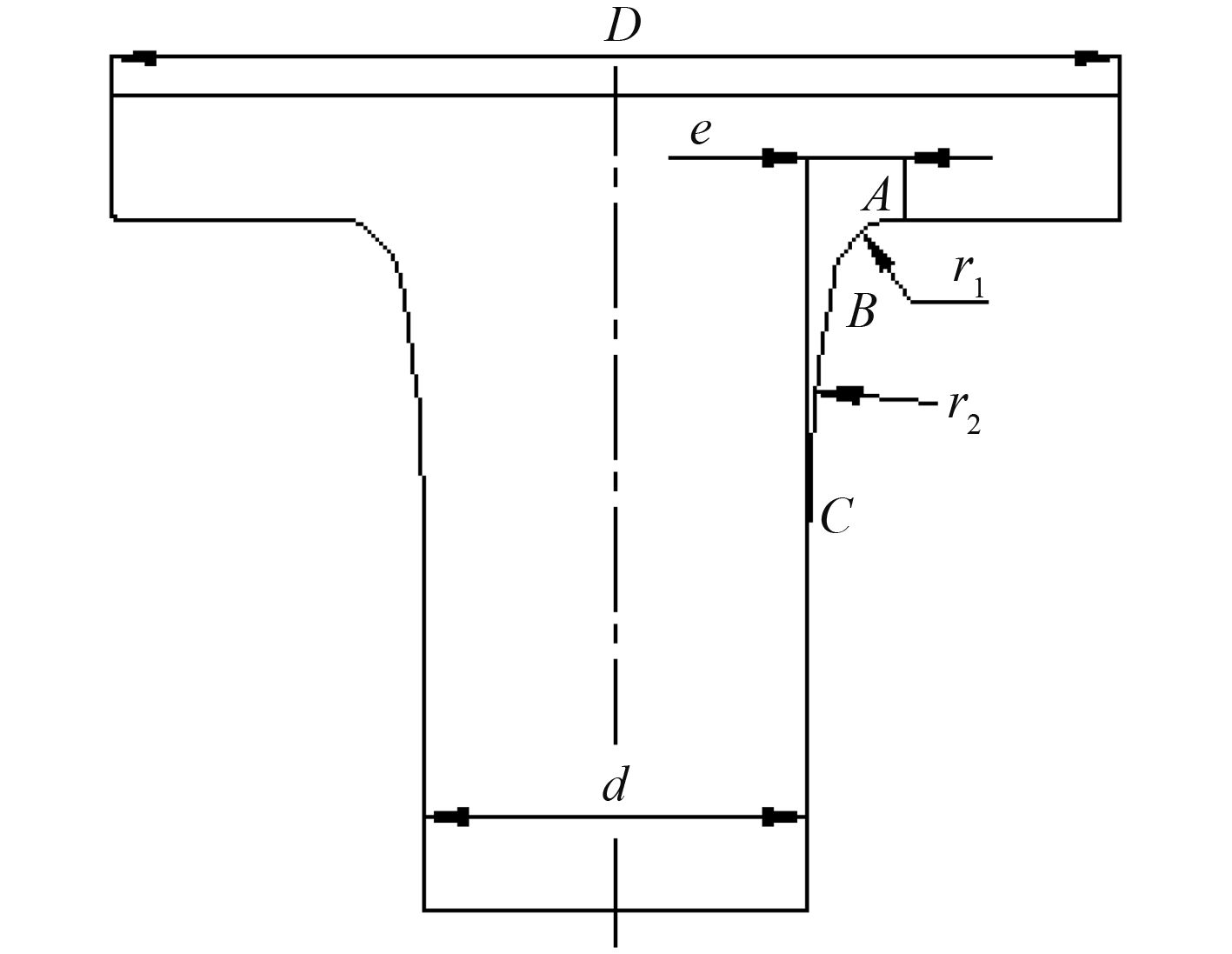
|
图 2 双曲率圆弧轴肩过渡曲线 Fig. 2 Two-radii shoulder transition curve |
| $e = d/2\text{,}$ | (1) |
| $r_1 = 0.75e\text{,}$ | (2) |
| $r_{{}_2} = 16r_{{}_1}\text{。}$ | (3) |
光弹性实验结果表明,它的扭转应力集中系数几乎接近于 1.0(1.00~1.02)[5]。双曲率圆弧过渡曲线在不增加轴肩过渡高度 e 的情况下,仅依靠延长轴肩过渡长度即可达到有效减小应力集中系数的目的。
1.3 三曲率圆弧过渡曲线三曲率圆弧过渡曲线如图 3 所示,它进一步加大了最大应力点与切点间的过渡圆弧半径。
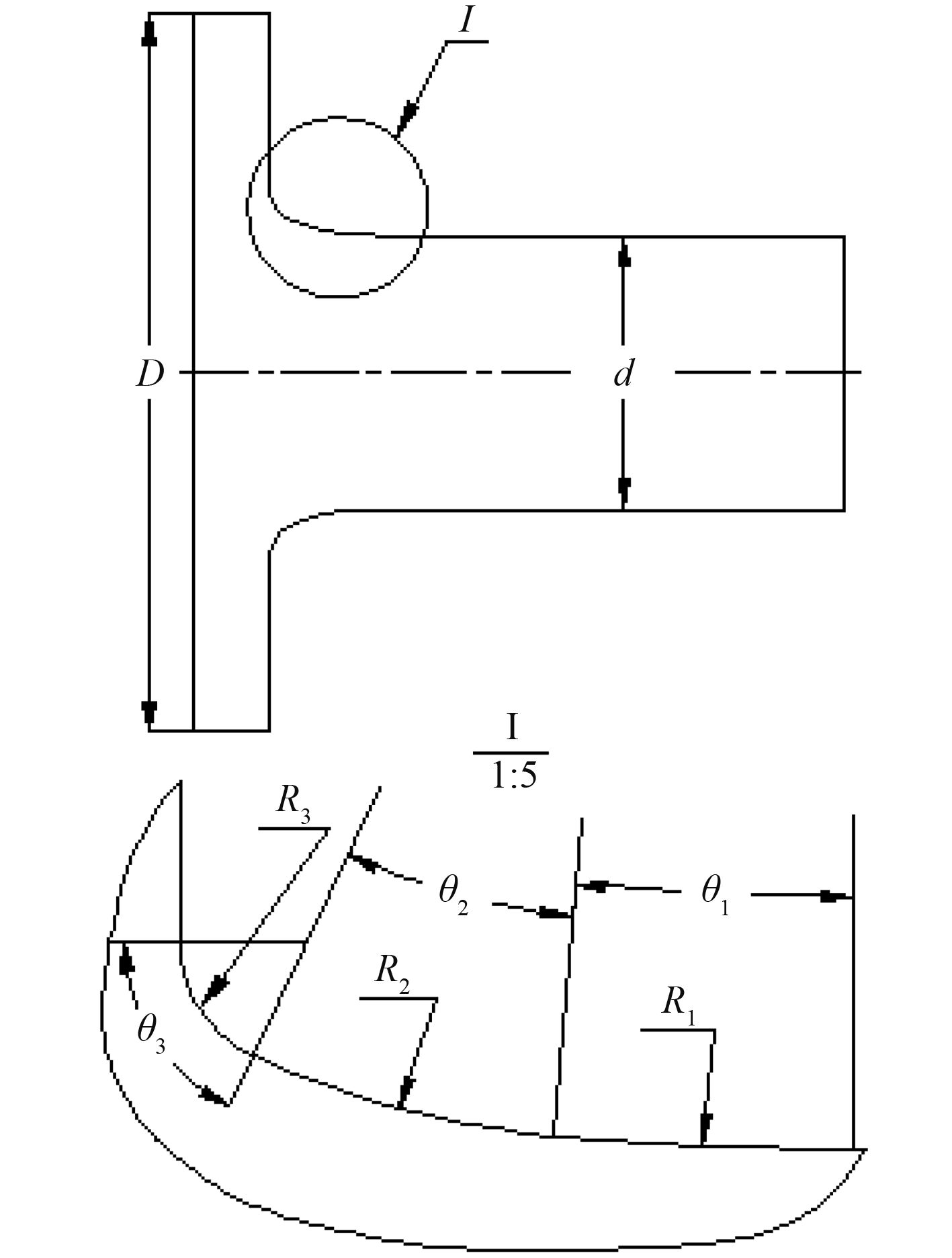
|
图 3 三曲率圆弧轴肩过渡曲线 Fig. 3 Three-radii shoulder transition curve |
根据不同的参数,三曲率圆弧也可以设计出无数种形式。挪威船级社凭其丰富的工程经验给出了一种效果良好的三曲率圆弧过渡曲线,设计该曲线的各参数如式(1)~ 式(3)所示[6]。
| ${R_1} = 2.5d,\;\;\;\;\;\;\;\;{\theta _1} = 5^\circ \text{;}$ | (4) |
| ${R_2} = 0.6d,\;\;\;\;\;\;\;\;{\theta _2} = 20^\circ\text{;} $ | (5) |
| ${R_3} = 0.09d,\;\;\;\;\;\;\;\;{\theta _3} = 65^\circ \text{。}$ | (6) |
式中:R 1,R 2 和 R 3 分别为三段圆弧的半径;θ 1,θ 2 和 θ 3 分别为三段圆弧对应的圆心角。
1.4 椭圆过渡曲线椭圆过渡曲线如图 4 所示,将1/4椭圆作为轴肩过渡曲线,图中轴肩曲率从上至下逐渐减小。当椭圆长轴和短轴的长度比值(b/a)等于相邻两轴段截面尺寸比值(D/d)时,应力集中系数最小[7]。
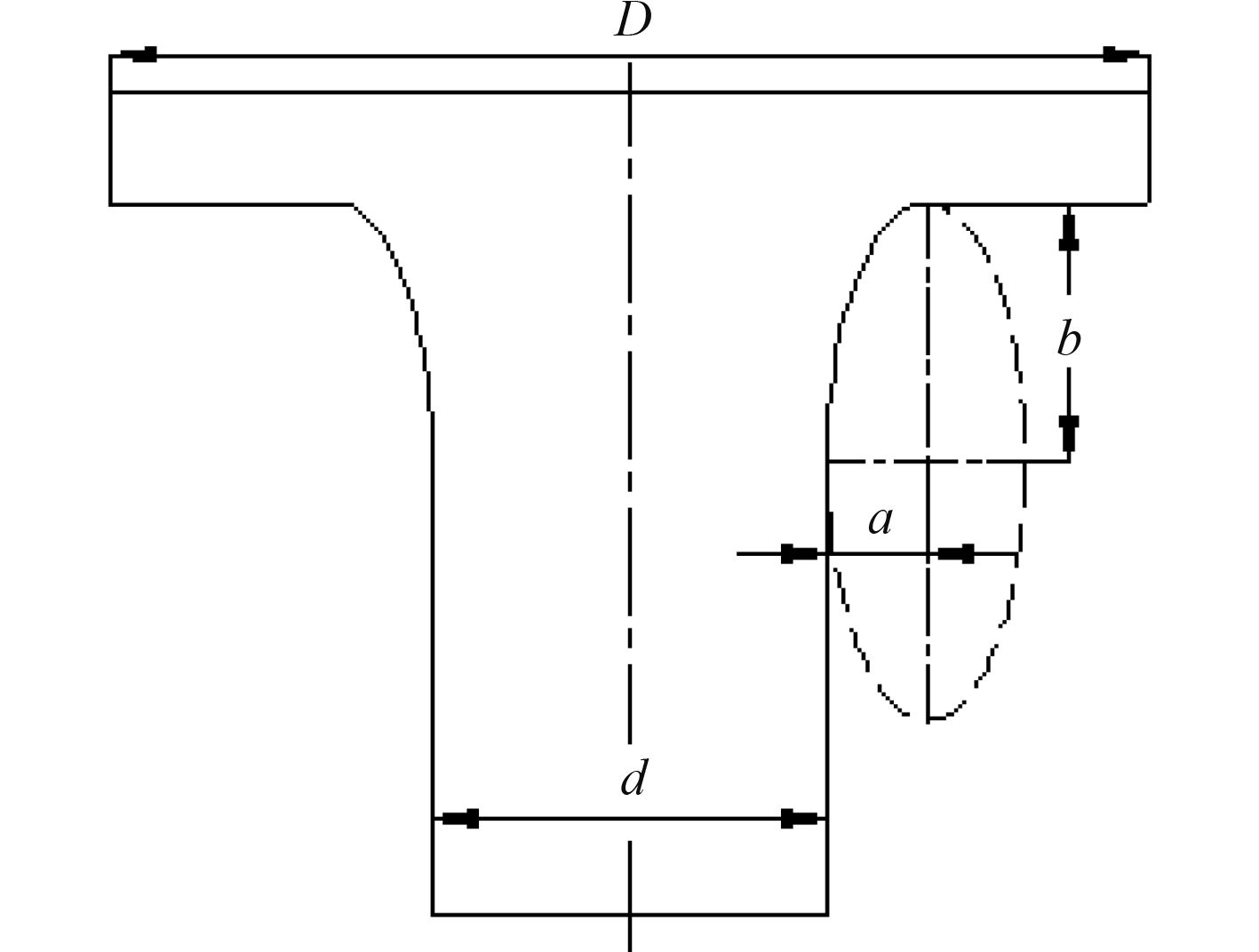
|
图 4 椭圆轴肩过渡曲线 Fig. 4 Elliptical shoulder transition curve |
文献[8]提出了一种流线形轴肩过渡曲线,带有圆角的圆棒承受拉力或压力时,如果采用一种无摩擦的理想流体从容器底部的圆孔流出时的线型(如图 5 所示),则表面的正应力均匀,因而可以避免应力集中。拉压情况下的流线形轴肩过渡曲线可以通过理论计算推导得到。

|
图 5 理想流体流线模型和流线形轴肩过渡曲线 Fig. 5 Streamline model of ideal fluid and streamline shoulder transition curve |
适用于具有圆角的圆棒承受扭转时的流线形曲线与拉伸情况下的流线形曲线有所不同,通过实验可以建立与拉伸情况的换算公式,并加以利用。
扭转情况下,流线形曲线沿纵向变化的直径 d(y)如表 1 所示。在 y/d = ∞(即液体流到无限远处)时,d(y)/d = 1,这不适于工程设计。当 y/d = 1.6 时,d(y)/d = 1.003,d(y)非常接近轴径 d,所以从这一点起往下可加工成等直径[8]。
|
|
表 1 流线形过渡曲线参数 Tab.1 Parameters of streamline transition curve |
本文用有限元软件 Abaqus 对以上过渡曲线进行建模分析,其中单曲率圆弧轴肩模型(D = 945 mm, d =360 mm,h = 100 mm,r = 50 mm)的应力分布剖面图如图 6 所示。计算结果表明,切应力是关于轴中心对称分布的。在同一个圆截面上,相同半径处的切应力大小相等,并且切应力随着半径的增大而增大,在轴的外沿切应力达到最大,最大切应力为 1.390 04 × 10–4 GPa。在远离轴肩的区域,应力均匀分布;在轴肩区域,出现了应力集中的现象。应力集中导致的最大应力出现在过渡弧与轴相切的位置附近,这与理论分析结果一致,也就进一步证明双曲率和三曲率过渡的可行性。

|
图 6 单曲率圆弧过渡的应力分布剖面图 Fig. 6 The sectional view of stress distribution of single-radius shoulder transition curve |
理论应力集中系数是最大局部应力与名义应力的比值,名义应力是未发生应力集中时的应力。
名义切应力的理论计算公式为:
| $nominal\;shear\;stress = \frac{{16M}}{{\pi {d^3}}}\text{,}$ | (7) |
式中:M = 1 000 Nm为施加的扭矩,d = 360 mm为轴径,代入上式得到名义切应力 nominal shear stress = 109 160 Pa。
应力集中系数 scf(stress concentration factor)计算如下:
| $\begin{split}scf = & {\rm maximum}\;{\rm shear}\;{\rm stress}/{\rm nominal}\;{\rm shear}\;{\rm stress}=\\& 139 \,\, 004/109 \,\, 160 = 1.273\text{。}\end{split}$ | (8) |
随着过渡半径 r 的增大,轴肩扭转应力集中系数逐渐减小,如图 7 所示。当过渡半径达到 200 mm 时,应力集中系数才减小至 1.09,此时轴肩过渡长度和过渡高度过大,导致法兰尺寸过大,不利于轴系设计。因此对于单曲率圆弧过渡,依靠增大过渡半径来减小应力集中系数的效果有限。
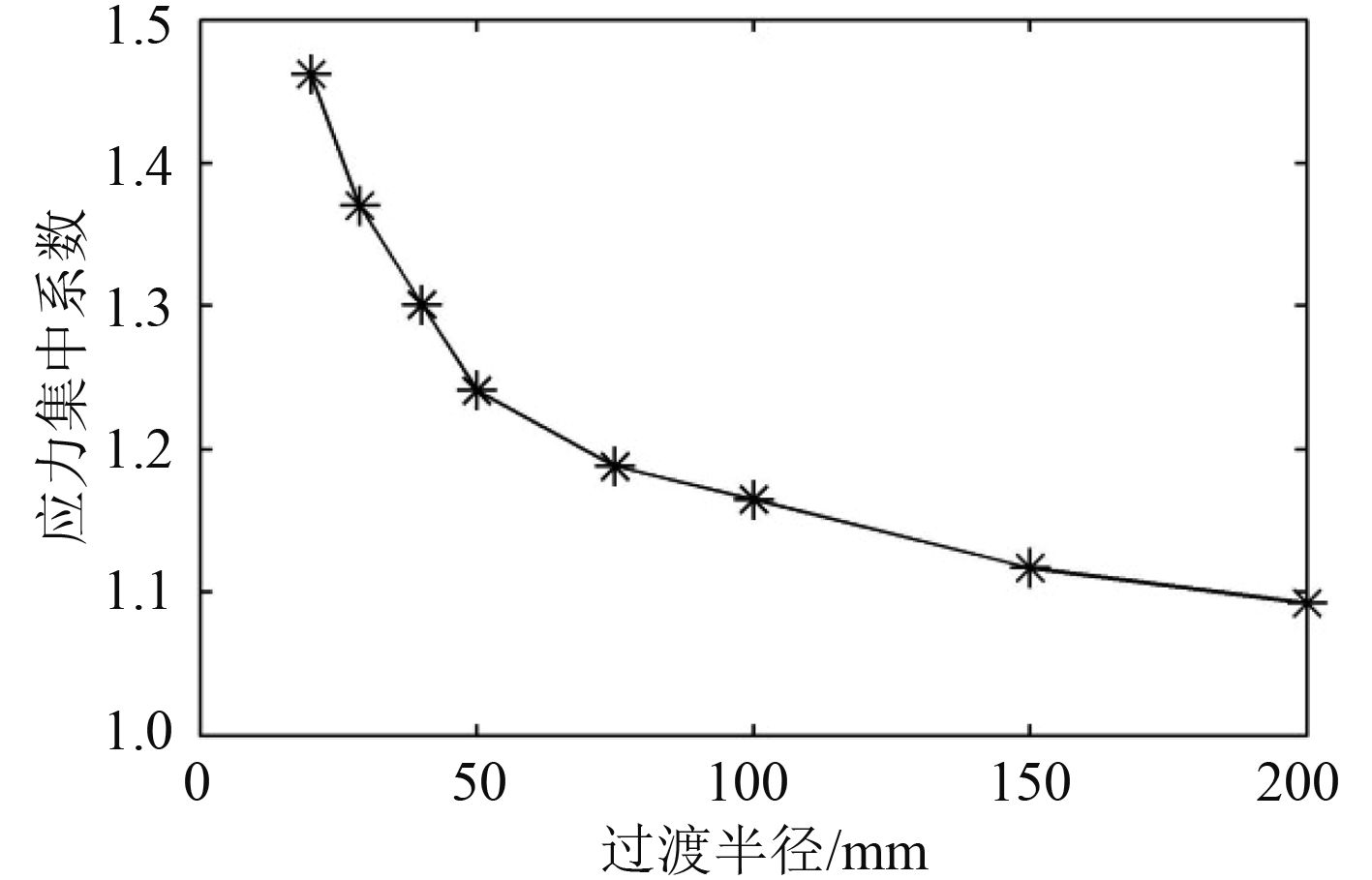
|
图 7 应力集中系数变化图 Fig. 7 The change chart of stress concentration factor |
另外,应力最大点出现位置所对应的角度随过渡半径的变化而变化,如图 8 所示。

|
图 8 应力集中角度变化图 Fig. 8 The change chart of stress concentration angle |
结果表明,应力集中角度随半径增大而减小,半径越大,应力最大点越靠近轴肩与轴的切点。
各种型式轴肩过渡曲线的应力集中系数如表 2 所示。
|
|
表 2 多种轴肩过渡曲线的应力集中系数 Tab.2 The stress concentration factors of several shoulder transition curves |
单曲率圆弧过渡消除应力集中的效果最差,流线形过渡的效果最好,其应力集中系数几乎约等于 1,表明应力集中接近于被完全消除。双曲率、三曲率和椭圆过渡的效果基本相当,理论上相当尺寸的情况下三曲率过渡的效果优于双曲率过渡,但是因为本文模型中双曲率过渡尺寸略大于三曲率过渡,故其效果略优于三曲率过渡。
3 结 语轴肩过渡曲线的优化设计有助于保障轴系安全运行和为船舶减重及降低成本。双曲率、三曲率、椭圆和流线形是比单曲率更优的轴肩过渡曲线,流线形几乎完全消除了应力集中的现象,在非常严苛的设计条件下可以采用流线形过渡,但它会给加工制造带来一定的难度。双曲率、三曲率和椭圆曲线的加工难度较小,而且具有较好的削弱应力集中的效果。尤其是三曲率过渡,已经获得了挪威船级社、中国船级社等多家权威船检机构的认可,特别适用于船舶轴系设计。
| [1] |
雷继军, 韩致信. 异形截面轴肩的应力集中特征[J]. 兰州理工大学学报, 2010, 36 (4): 44–47.
LEI Ji-jun, HAN Zhi-xin. Stress Concentration Character at Shaft Shoulder with Abnormal Cross-section[J]. Jorurnal of Lanzhou University of Technology, 2010, 36 (4): 44–47. |
| [2] |
吴凤林. 一种新型轴肩过渡曲线[J]. 工程设计, 1997, 04 : 35–37.
WU Feng-lin. A New Type of Shoulder Transition Curve[J]. Journal of Engineering Design, 1997, 04 : 35–37. |
| [3] |
陈科, 殷磊, 陈振华. 万向十字轴轴根过渡结构的优化设计和分析[J]. 中国机械工程, 2014, 25 (23): 3155–3159.
CHEN Ke, YIN Lei, CHEN Zhen-hua. Optimization and Analysis of Transition Curves for Roots of Universal Cross shaft[J]. China Mechanical Engineering, 2014, 25 (23): 3155–3159. DOI: 10.3969/j.issn.1004-132X.2014.23.007 |
| [4] | TAYLOR D, KELLY A, TOSO M, et al. The Variable-Radius Notch: Two New Methods for Reducing Stress Concentration[J]. Engineering Failure Analysis, 2011, 18 (3): 1009–1017. DOI: 10.1016/j.engfailanal.2010.12.012 |
| [5] |
西田正孝. 应力集中[M] 北京: 机械工业出版社, 1986: 96–103.
Nishida Masataka. Stress concentration[M]. Beijing: Machinery Industry Press, 1986: 96–103. |
| [6] | Det Norske Veritas. Calculation of shafts in marine applications[M]. Norway: Norway Classification Society Press, 2007. |
| [7] | MARSDEN B J, BLAKEMORE R H. Stress Concentration around Elliptical Fillets in Stepped Flat Bars[J]. Journal of Strain Analysis for Engineering Design, 1981, 16 (4): 227–233. DOI: 10.1243/03093247V164227 |
| [8] | R. Fillets without Strees Concentration[J]. Proc. SESA, 1955, 13 (1): 97–104. |
 2017, Vol. 39
2017, Vol. 39
