随着新世纪我国海洋强国战略的实施,海洋工程不断向深海推进,海洋结构物所处的海洋环境将会更加恶劣。其中,内孤立波作为一种特殊的非线性内波,其振幅大、周期短、能量巨大,对跨越密跃层的水下潜器会产生剪切作用,使潜器运动稳定性或运动姿态发生变化,甚至将潜器拖至海底,若处理不当会造成巨大损失。因而开展海洋内孤立波与水下潜器相互作用问题研究,对提高水下潜器设计水平和在水下作业时的安全性具有重要意义。
大量学者对内孤立波的数值生成进行研究,取得了一些关键性的成果。内孤立波的 Kdv 理论最早由 Korteweg 和 G. de Vries[1]提出,之后学者们又相继提出了内孤立波的 eKdv,mKdv 和 MCC[2 – 3]理论模型。在此基础上,黄文昊[4]实验研究了这四类内孤立波理论的适用性条件。方舟、王旭等[5 – 6]构造了双推板、速度入口、质量源三类内孤立波数值造波模型,得到了高效的内孤立波数值生成方法。
关于内孤立波与水下潜器相互作用问题,付东明[7]基于内孤立波的 Kdv 理论最早研究了回转潜器在不同潜深时的受力特性。陈杰等[8]鉴于此,利用 CFD 方法数值模拟了有航速潜器在内孤立波中的受力特性。关晖[9]同时对比了上凸型与下凹型 2 种内孤立波对潜器的受力影响。魏岗等[10 – 11]通过密度分层水池,实验研究了内孤立波与固定潜器相互作用问题。SHEN Hui 和 HOU YiJun[12]基于内孤立波的 Kdv 理论和莫里森公式,提出了一个计算大振幅内孤立波作用于 ROV 上受力的方法。
以上成果都是基于内孤立波的单一理论或者单一幅值的研究,本文依据内孤立波的 Kdv、eKdv 和 mKdv 理论,建立高效率内孤立波数值波浪水池,数值模拟了不同波幅、不同潜深以及不同上下层流体深度比对水下潜器载荷的变化影响,以期对水下潜器在内孤立波中的载荷问题提供更有价值的参考。
1 数学模型 1.1 流体运动控制方程采用 RANS 方程为流场控制方程,数值模拟内孤立波诱导流场。控制方程为:
| $\begin{array}{l}\displaystyle\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\text{,}\\\displaystyle\frac{{\partial {u_i}}}{{\partial t}} + {u_j}\displaystyle\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \displaystyle\frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \displaystyle\frac{\partial }{{\partial {x_j}}}\left( {\nu \displaystyle\frac{{\partial {u_i}}}{{\partial {x_j}}}} \right) + {f_i}\text{。}\end{array}$ | (1) |
式中:
熟知的 Kdv 理论适用于小振幅内孤立波,其方程如下:
| ${\zeta _t} + {c_0}{\zeta _x} + {c_1}\zeta {\zeta _x} + {c_2}{\zeta _{xxx}} = 0\text{,}$ | (2) |
方程(2)解为:
| $\zeta = a{\mathop{\rm sech}\nolimits} \left( {\displaystyle\frac{{x - {c_k}t}}{\lambda }} \right)\text{,}$ | (3) |
在方程(2)中加入一个 O(ε2)阶的非线性项,可得 eKdv 方程,它可以适用于较大振幅的内孤立波,其方程如下:
| ${\zeta _t} + \left( {{c_0} + {c_1}\zeta + {c_3}{\zeta ^2}} \right){\zeta _X} + {c_2}{\zeta _{XXX}} = 0\text{,}$ | (4) |
方程(4)解为:
| $\zeta = \displaystyle\frac{a}{{B + \left( {1 - B} \right){{\cosh }^2}\left[ {{\lambda _{eKdv}}\left( {x - {c_{eKdv}}t} \right)} \right]}}\text{,}$ | (5) |
当
| $\zeta = \displaystyle\frac{{a{{{\mathop{\rm sech}\nolimits} }^2}\left[ {{\lambda _{mKdv}}\left( {x - {c_{mKdv}}t} \right)} \right]}}{{1 - \mu {{\tanh }^2}\left[ {{\lambda _{mKdv}}\left( {x - {c_{mKdv}}t} \right)} \right]}}\text{。}$ | (6) |
水下潜器壁面为无滑移边界条件,水池顶部及底部满足如下壁面条件:
| $w\left| {_{z = {h_1}} = 0} \right.,w\left| {_{z = - {h_2}} = 0} \right.\text{,}$ | (7) |
若内孤立波波幅为a,相速度为 c,上下层入口速度分别为:
| ${\overline u _1} = - c\displaystyle\frac{\zeta }{{{h_1} - \zeta }},\;{\overline u _2} = c\displaystyle\frac{\zeta }{{{h_2} + \zeta }}\text{。}$ | (8) |
两层流体界面变化采用 VOF 法追踪。
在 Fluent 中,采用有限体积法对控制方程进行离散,压力方程选用加权体积力格式(Body Force Weighted),压力速度耦合方式采用 PISO 算法,动量方程的离散采用二阶迎风格式。
2 结果与分析 2.1 计算模型文中所采用的计算模型如图 1 所示。水池尺寸参考上海交通大学国家海洋实验室内孤立波水槽[4],长 30 m,宽 0.4 m,深 1 m,上层流体为淡水,密度 ρ 1 = 998 kg/m3,下层流体为海水,密度 ρ 2 = 1 025 kg/m3。水下潜器以中国“潜龙一号”的裸艇体为原型,缩尺比为 1:10,固定在水池中。

|
图 1 计算域示意图 Fig. 1 Diagram of computational domain |
模型总长 0.46 m,直径为 0.08 m,是典型的鱼雷型单体轴对称回转细长体,潜器重心距离水池入口处 10 m。
2.2 内孤立波数值模拟结果为了验证内孤立波生成与传播特性,图 2 给出了当 h 1:h 2 = 2:8,内孤立波设计振幅 a d = 0.1 m,选用 eKdv 理论时,在数值水槽工作区x = 5 m,10 m,15 m 处内孤立波的时历曲线。从图中可以看出随着传播距离增加,内孤立波波形比较稳定,损耗很小,粘性对其影响较小。
|
图 2 内孤立波数值模拟结果 Fig. 2 The numerical results for the internal solitary waves |
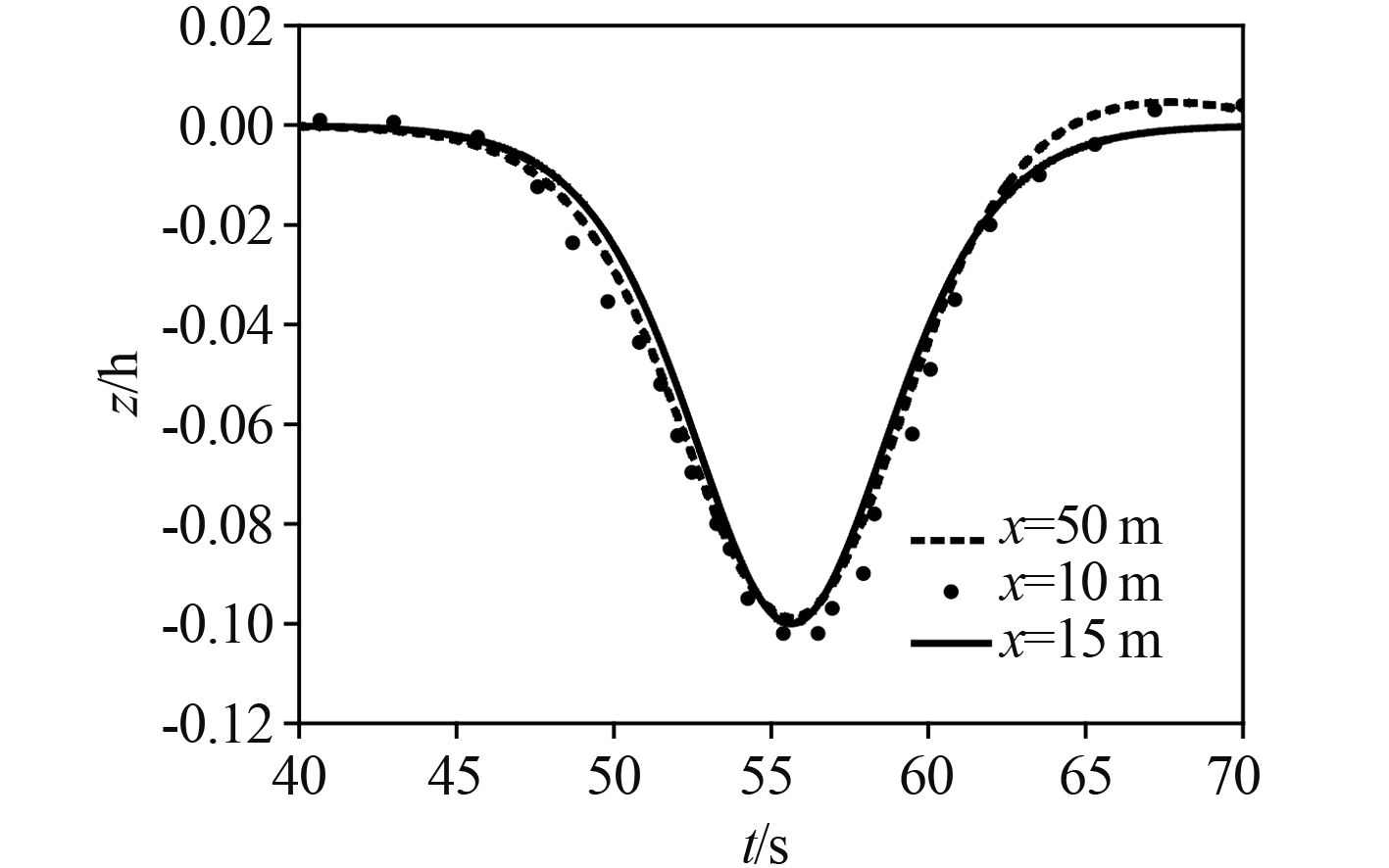
图 3 给出了此种情况下数值结果与其相应理论和实验的对比结果,实验结果取自文献[4]。总体而言,数值模拟所得内孤立波波形与其对应的理论解和实验相吻合。

|
图 3 内孤立波波形数值模拟结果与理论和实验结果比较 Fig. 3 Comparisons of the numerical results for the internal solitary wave waveforms with theoretical and experimental ones |
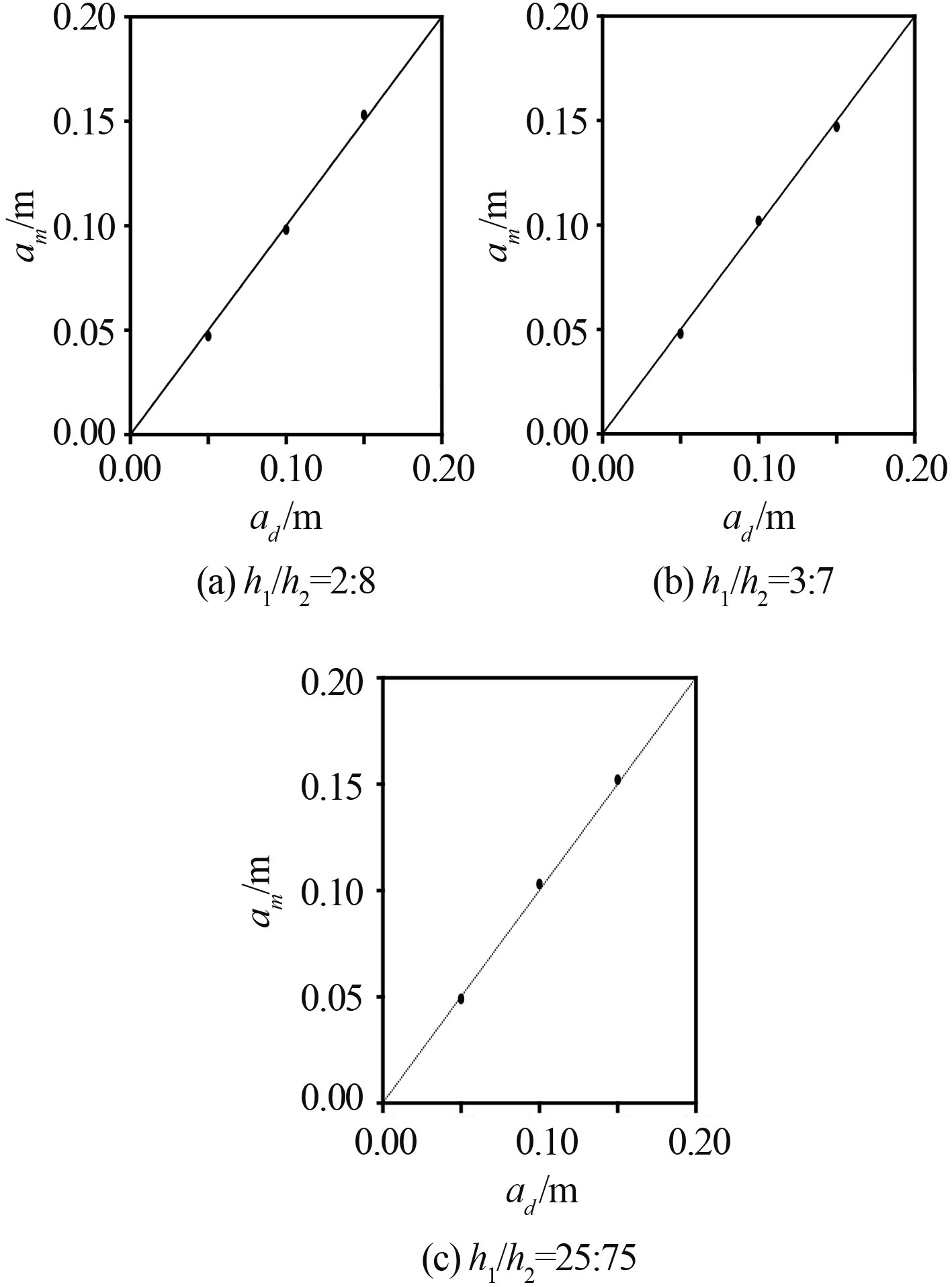
图 4 为 h 1:h 2 = 2:8,25:27 和 3:7 时内孤立波的设计振幅 a d 与其数值模拟振幅 a m 之间的关系。直线为设计振幅,圆点为数值模拟振幅。当 a d 分别为 0.05 m,0.1 m 和 0.15 m 时,分别对应选择 Kdv 理论、eKdv 理论和 mKdv 理论计算其速度入口。
|
图 4 内孤立波振幅数值模拟结果 Fig. 4 The numerical results of the waves amplitudes for the internal solitary waves |
由图可知,数值模拟所得内孤立波波幅在各种工况下都与其相应理论解符合良好,两者之间的相对误差不高于 5%,以上结果表明各工况下本文采用的内孤立波数值生成方法准确可行。
2.3 内孤立波对水下潜器作用分析记 F x ,F z 和 M xz 分别为内孤立波作用下水下潜器所受到的水平力、垂向力和力矩,力矩转动中心为潜器重心。定义 C X ,C Z 和 C XZ 为其无因次水平力,垂向力和力矩,表达式如下:
| ${C_X} = \displaystyle\frac{{{F_x}}}{{\rho gAD}},{C_Z} = \displaystyle\frac{{{F_z}}}{{\rho gAD}},{C_{XZ}} = \displaystyle\frac{{{M_{xz}}}}{{\rho gADB}}\text{。}$ |
式中:A 为潜器水平迎流面积;B 为潜器长度。水平力以向右为正,垂向力以向上为正,力矩以逆时针为正。
2.3.1 内孤立波作用下潜器载荷验证算例为验证本文计算方法的有效性,下面将对内孤立波与潜器的相互作用进行数值模拟,并将计算结果与文献[10]中的实验进行比较。
1)计算模型说明
数值水池与模型结构的尺寸和参数与文献[10]中保持一致,如图 5 所示,图中水池长 12 m,水深 0.8 m,其中上层水深 h 1 = 0.05 m,密度 ρ 1 = 995 kg/m3,下层水深 h 2 = 0.75 m,流体密度 ρ 1 = 1 023 kg/m3。潜器为长 0.8 m,直径 0.09 m 的细长体,放置于水下 0.05 m 处(即 2 层流体交界面上)。内孤立波设计波幅为 0.051 m,基于 Kdv 理论造波。

|
图 5 计算域示意图 Fig. 5 Diagram of computational domain |
2)计算结果
图 6 为数值模拟结果与实验结果对比图,图中可知,由数值模拟得到内孤立波与潜器相互作用的无因次水平力、垂向力和力矩的时历曲线与实验结果大致吻合。由此可以验证文中的计算方法可行有效。其中垂向力曲线略有误差是由于实验水池中内孤立波尾波对潜器造成影响,使得垂向力曲线呈波动衰减,而数值模拟中尾波影响并不明显。

|
图 6 潜器内孤立波受力 Fig. 6 The force on the submerged body |
在上下层水深比 h 1:h 2 = 2:8,内孤立波设计波幅为 a d = 0.1 m 时,考虑 5 种潜深,分别为 d = –0.1 m,即潜器位于上层流体中;d = –0.2 m,即潜器位于 2 层流体交界面上;d = –0.3 m,即潜器位于下层流体中穿越内孤立波位置;d = –0.4 m 和 d = –0.5 m,即潜器位于内孤立波波谷以下。图 7 为这 5 种情况下潜器的受力结果。

|
图 7 不同潜深下潜器的受力 Fig. 7 The force on the submerged body at different depths |
由图 7(a)可知,当潜器位于上层流体中和位于 2 层流体交界面处时,其受到的水平力方向都是先向右后向左。当潜器位于下层流体时,其受到的水平力方向是先向左后向右。这是由于在上层流体中,内孤立波的流速方向向右,下层流体中内孤立波的流速方向向左,当内孤立波波谷传播至潜器中心附近时,水平力达到最值,之后在某一时刻潜器前后压差力的绝对值与内孤立波流速方向相反使得潜器所受水平力反方向增加。
图中还可知,水平力的幅值在潜器位于上层流体中达到最大。穿越内孤立波时由于波面上下方速度相反而使得水平力最小。之后随着潜深的增加,水平力幅值又逐渐增大,其幅值小于潜器位于上层流体的情况原因是上层流体的流速比下层流体流速大。
图 7(b)可看出,潜器位于穿越内孤立波位置时,其所受垂向力方向都是向下,并且当潜器位于两层流体交界面处时达到最大。而潜器没有穿越内孤立波时,其所受垂向力方向向上,且其幅值远远小于穿越内孤立波时的情况。原因不难解释,当潜器穿越内孤立波时,其位于上层流体的体积开始增大,这使得潜器所受的浮力发生变化而导致其垂向力急剧增加。潜器不穿越内孤立波时,其所受垂向力只由内孤立波本身提供,故此时潜器所受垂向力要小得多。
图 7(c)可看出,潜器位于上层流体和穿越内孤立波时,其力矩方向都是先顺时针方向再逆时针方向,而潜器位于下层流体不穿越内孤立波时,其受到的力矩方向为先逆时针再顺时针。其幅值与垂向力幅值变化趋势相同,在潜器位于跃层处时达到最大,潜器不穿越内孤立波时受到的力矩幅值同样远小于穿越内孤立波时的情况。
综上所述,潜器位于穿越内孤立波位置时,其垂向力比水平力大了近两个量级,实际情况下有可能会使其稳定性和悬停姿态突然改变而导致栽入海底。然而当潜器不穿越内孤立波时,其受到的垂向力虽然小很多,但此时潜器所受的水平力增大,量级与垂向力相当,潜器的纵荡运动也不容小觑,若操作不当,同样会造成巨大损失。
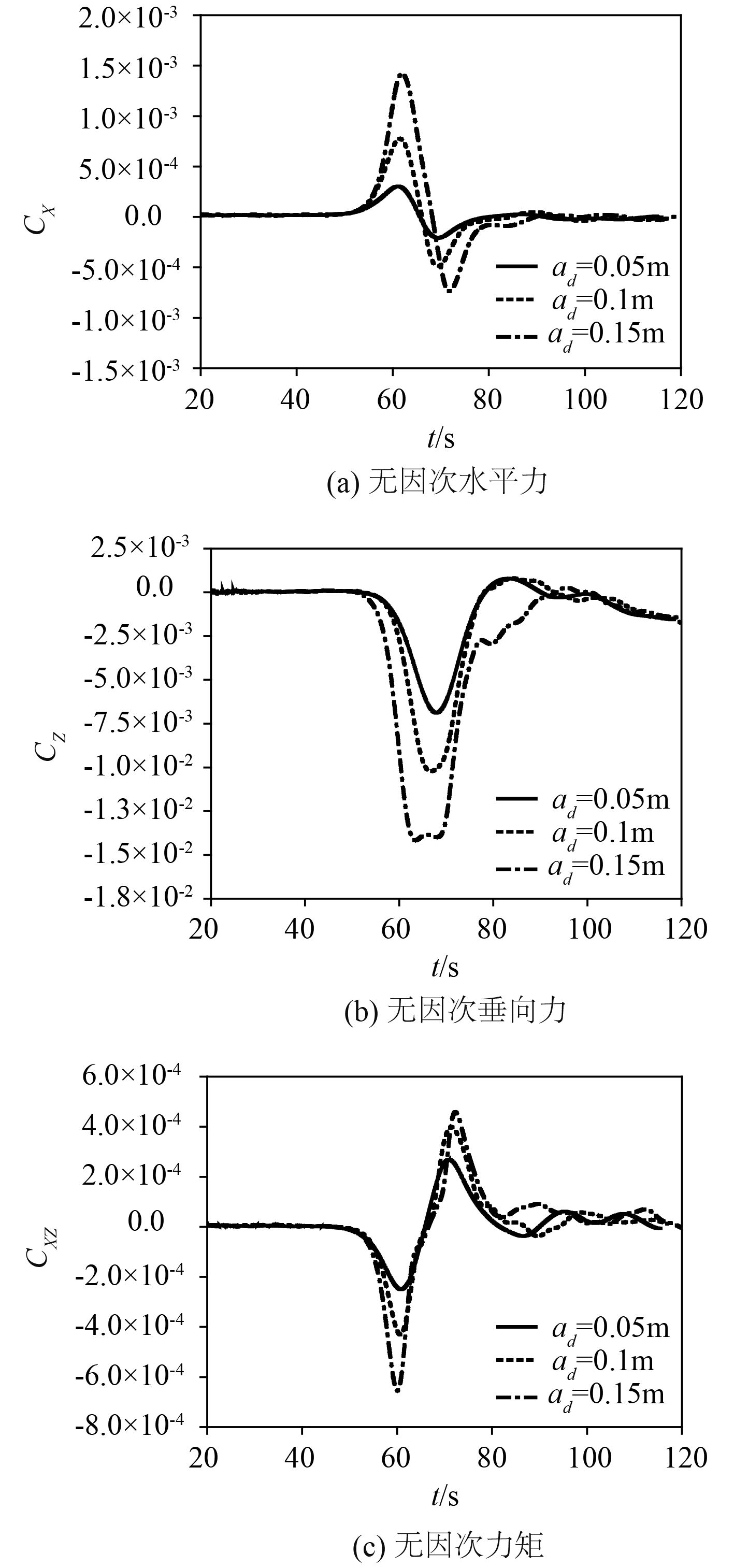
2.3.3 潜器在不同波幅下的波浪力图 8 给出了上下层流体水深比 h 1:h 2 = 2:8,潜器放置于潜深 d = –0.2 m(即跃层处)时,内孤立波设计波幅分别为 a d = 0.05 m,0.1 m 和 0.15 m 作用下的受力结果。从图中可看出,潜器在同一潜深不同波幅的作用下,各个力的变化趋势与前文分析的相一致,但力的大小随着内孤立波波幅的增大而增大。因此,波浪的幅值会对潜器的稳性造成显著影响,小振幅内孤立波会使得潜器颠簸,对其壳体造成损失,而大振幅内孤立波在极端情况下很可能会将潜器拖至海底,造成艇毁人亡的巨大伤害。
|
图 8 不同波幅下潜器的受力 Fig. 8 The force on the submerged body for different wave amplitudes |
图 9 为 a d = 0.15 m,潜器在上下层水深比分别为 h 1:h 2 = 2:8,27:75 和 3:7 三种情况下,潜器位于跃层处以下 0.15 m 位置时的受力结果。图中表明,水深比对潜器受到的载荷变化趋势没有影响,但 h 1:h 2 越大,内孤立波诱导的上层流体水平和垂向速度越小,这使得穿越内孤立波位置的潜器受到的力也随之减小。还可以发现随着 h 1:h 2 的增大,潜器受到的力的作用时间也越长,这是因为 h 1:h 2 大,内孤立波的波长长,潜器的受力时间长。由于海水的分层情况受到温度和日照影响显著,潜器在水下作业前若能获取海水的分层情况信息,则能尽量减小内孤立波对潜器的伤害。
3 结 语

|
图 9 不同上下层水深比下潜器的受力 Fig. 9 The force on the submerged body in different upper and lower layer depths |
基于 Fluent 的二次开发功能,依据内孤立波的 3 种理论,通过速度入口造波方法,成功建立内孤立波数值水槽,实现了内孤立波与水下潜器相互作用的数值模拟。
1)依据内孤立波的 Kdv,eKdv 和 mKdv 理论,模拟了不同波幅以及不同上下层水深比情况下的内孤立波,并与文献中实验和其对应理论做对比,验证了造波方式的可行性和有效性。
2)对于潜器在不同潜深时的载荷变化进行研究,发现潜器位于穿越内孤波位置时由于浮力的变化使得垂向力占主导,造成潜器失稳甚至破损。而潜器位于内孤立波波面上方或下方时,水平力也不容小觑。
3)模拟了不同内孤立波波幅以及不同上下层水深比对潜器载荷的影响,结果表明波幅越大,潜器受力越大;而 h 1:h 2 越大,穿越内孤立波位置的潜器受力越小,但力的作用时间越长。潜器在水下作业时,应合理规划其作业区域以减小内孤立波造成的损失。
| [1] | KORTEWEG D J, DE VRIES G. On the c-hange of form of longwaves advancing in a rectangle canal, and on a new t-ype oflong stationary waves[J]. Philos Mag Ser, 1895, 39 (5): 422–443. |
| [2] | HELFRICH K R, MELVILLE W K. Long n-onlinear internal waves[J]. Ann Rev Fl-uid Mech, 2006, 38 : 395–425. DOI: 10.1146/annurev.fluid.38.050304.092129 |
| [3] | CHOI W, CAMASSA R. Fully nonlinear internal waves in a two-fluid system[J]. Fluid Mech, 1999, 396 : 1–36. DOI: 10.1017/S0022112099005820 |
| [4] |
黄文昊, 尤云祥, 王旭, 等. 有限深两层流体中内孤立波造波实验及其理论模型[J]. 物理学报, 2013, 62 (8): 1–14.
HUANG Wen-hao, YOU Yun-xiang, WANG Xu, et al. Wave-making experiments and theoretical models for internal soli-tary waves in a two-layer fluid of fini-te depth[J]. Acta Phys. Sin., 2013, 62 (8): 1–14. |
| [5] |
方舟, 严圣甫, 王旭. 两层流体中三类内孤立波数值造波方法比较研究[J]. 热带海洋学报, 2015, 34 (4): 31–36.
FANG Zhou, YAN Sheng-fu, WANG Xu. Co-mparative study of three wave-generati-ng methods for internal solitary waves in a two-layer fluid[J]. Journal of Trop-ical Oceanography, 2015, 34 (4): 31–36. DOI: 10.11978/j.issn.1009-5470.2015.04.004 |
| [6] |
王旭, 林忠义, 尤云祥. 两层流体中内孤立波质量源数值造波方法[J]. 上海交通大学学报, 2014, 48 (6): 850–855.
WANG Xu, LIN Zhong-yi, YOU Yun-xiang. A Mass Source Method for Numerically Generating Internal Solitary Waves in Two-Layer Fluid[J]. Journal of Shangh-ai Jiao Tong University, 2014, 48 (6): 850–855. |
| [7] |
付东明, 尤云祥, 李巍. 两层流体中内孤立波与潜体相互作用的数值模拟[J]. 海洋工程, 2009, 27 (3): 38–44.
FU Dong-ming, YOU Yun-xiang, LI Wei. Numerical simulation of internal solitar-y waves with a submerged body in a two-layer fluid[J]. The Ocean Engineer-ing, 2009, 27 (3): 38–44. |
| [8] |
陈杰, 尤云祥, 刘晓东, 等. 内孤立波与有航速潜体相互作用数值模拟[J]. 水动力学研究与进展, 2010, 25 (3): 343–351.
CHEN Jie, YOU Yun-xiang, LIU Xiao-dong, et al. Numerical simulation of interaction of internal solitary waves with a movi-ng submarine[J]. Chinese Journal of H-ydrodynamics, 2010, 25 (3): 343–351. |
| [9] |
关晖, 魏岗, 杜辉. 内孤立波与潜艇相互作用的水动力学特性[J]. 解放军理工大学学报, 2012, 13 (5): 577–582.
GUAN Hui, WEI Gang, DU Hui. Hydrody-namic properties of interactions of thre-e-dimensional internal solitary waves w-ith submarine[J]. Journal of PLA Uni-versity of Sceince and Technology (Na-tural Science Edition), 2012, 13 (5): 577–582. |
| [10] | WEI Gang, DU Hui, XU Xiao-hui, et al. Experimental investigation of the g-eneration of large-amplitude internal s-olitary wave and its interaction with a submerged slender body[J]. Physics, Mechanics & Astronomy, 2014, 57 (2): 201–310. |
| [11] | DU Hui, WEI Gang, GU Meng-meng, et al. Experimental investigation of the lo-ad exerted by nonstationary internal s-olitary waves on a submerged slender body over a slope[J]. Applied Ocean Research, 2016 (59): 216–223. |
| [12] | SHEN Hui, HOU Yi-jun. Effects of large-amplitude internal solitary waves on ROV operation—A numerical study[J]. Earth Sciences, 2016, 59 (5): 1074–1080. |
 2017, Vol. 39
2017, Vol. 39

