船体结构在海水等介质的腐蚀作用下容易产生凹坑,影响结构强度[1]。对于较大面积和深度坡口的厚壳体凹坑,目前国内缺乏修理技术文件和标准,而整体更换船体结构牵连工程较大,时间长,费效比低。采用焊补修复方法,可快速完成缺陷修复工作,牵连工程小,费效比高,但受材料老化、施工环境有限等因素限制,修复过程中残余应力过大,将产生裂纹等新缺陷。
国内外相关研究人员对腐蚀凹坑修复开展了大量研究,提出了一些分析方法,日本的上田幸雄等[2]以有限元法为基础,分析了厚板腐蚀凹坑焊接修复后的残余应力;WEN S W 等[3]利用 Abaqus 软件分析了厚板凹坑焊接过程。前期相关人员在研究过程中,主要考虑凹坑的深度,对凹坑面积分析较小。本文针对较大面积和深度坡口的厚壳体凹坑焊接修复问题,采用双椭球三维热源模型和热弹塑性材料模式[4],对较大面积和深度坡口的厚壳体凹坑多道焊接过程进行模拟计算,并进行试验分析,验证计算结果的有效性。
1 缺陷物理模型根据我国船体结构使用的主要材料和尺寸结构,取钢板厚度为 30 mm,凹坑深度为 20 mm,凹坑面积为 200 mm× 200 mm,凹坑形状为方形,如图 1 所示。腐蚀凹坑深度已达到板厚度的 2/3,腐蚀面积远超出现有相关修复标准要求。

|
图 1 缺陷大小及形状示意图 Fig. 1 Schematic diagram of defect size and shape |
对于三维焊接热传导模型,传导方程为:
| $\frac{\partial }{{\partial {x_i}}}\left[ {{\lambda _{ij}}\frac{{\partial T}}{{\partial {x_j}}}} \right] + Q - \rho c\frac{{\partial T}}{t} = 0,$ | (1) |
式中:t 为时间;λ 为材料的导热系数;T 为时间;ρ 为单位体积的质量密度;c 为材料的比热容;Q 为焊接单位体积的热生成率。
对于熔化极气体保护电弧焊、高能束流焊和厚板开坡口焊接,采用 Goldak 提出的双椭球三维热源模型更能真实体现这些焊接的热过程。前半部分的椭球热源表达式为:
| ${q_f}\left( {x,y,z,t} \right) = \frac{{6\sqrt 3 Q{f_f}}}{{ab{c_f}\pi \sqrt \pi }}{\rm exp}\left[ { - 3\left( {\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{c_f^2}}} \right)} \right],$ | (2) |
后半部分的椭球热源表达式为:
| ${q_r}\left( {x,y,z,t} \right) = \frac{{6\sqrt 3 Q{f_r}}}{{ab{c_r}\pi \sqrt \pi }}{\rm exp}\left[ { - 3\left( {\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{c_r^2}}} \right)} \right]\text{。}$ | (3) |
式中: q f 和 q r 为焊接熔池内前后单位体积的焊接热流率;Q = ηUI 为输入的能量;a 为焊接熔宽;b 为焊接熔深;c f 和 c r 为指沿焊接方向热源前后距离。f f 和 f r 为热流密度分布系数,满足 f f + f r = 2。
2.2 焊接应力计算模型船体结构腐蚀凹坑修复的关键是掌握焊接热、弹塑性应力应变关系。当材料处于弹性或塑性状态时,应力和应变关系一般为
| ${\rm d}\sigma = {\textbf{\emph{D}}}{\rm d}\varepsilon - {\textbf{\emph{C}}}{\rm d}T,$ | (4) |
式中: D 为弹塑性矩阵; C 为与温度有关的量。在弹性区
| $ {\textbf{\emph{D}}} ={\textbf{\emph{D}}} _\varepsilon $ | (5) |
| $ {\textbf{\emph{C}}} ={\textbf{\emph{C}}}_\varepsilon= {\textbf{\emph{D}}}_\varepsilon\left( {\left\{ \alpha \right\} + \frac{{\partial {\textbf{\emph{D}}} _\varepsilon ^{ - 1}}}{{\partial T}} \sigma} \right),$ | (6) |
式中:α 为线性膨胀系数;T 为温度。在塑性区,设材料屈服条件为:
| $f\left( \sigma \right) = {f_0}\left( {{\varepsilon _p},T} \right),$ | (7) |
式中:f 为屈服函数;f 0 为与温度和塑性应变有关的屈服应力的函数。应变增量 {dε} p 一般为:
| ${\left\{ {{\rm d}\varepsilon } \right\}_p}=\xi \left\{ {\frac{{\partial f}}{{\partial \sigma }}} \right\},$ | (8) |
当 ξ > 0 时,为加载过程;当 ξ = 0 时,为中性过程;当 ξ < 0 时,为卸载过程。
根据有限元原理,可以得到平衡方程:
| ${\textbf{\emph{K}}}{\rm d}\delta ={\rm d}F\text{,}$ | (9) |
式中: K 为整体刚度矩阵;dF 为整体载荷向量;dδ 为整体位移向量。利用静力学原理,得到
| ${\rm d}F = {\sum {{\rm d}F}^e} + {\sum {{\rm d}R}^e},$ | (10) |
式中 dRe 为单元等效节点应变增量。
2.3 边界条件在温度场分析过程中,实际计算中需要考虑对流和辐射的综合影响,在焊接过程中,熔池附近辐射放热占主导;而远离焊接熔池对流散热是热流损失的主要方式。采用整体焊接对流散热系数。取初始温度为预热温度,不考虑熔化潜热的影响。
在应力分析过程中,边界条件由根据实验条件确定,通过采用施加对称位移约束方式,来实现添加边界条件。
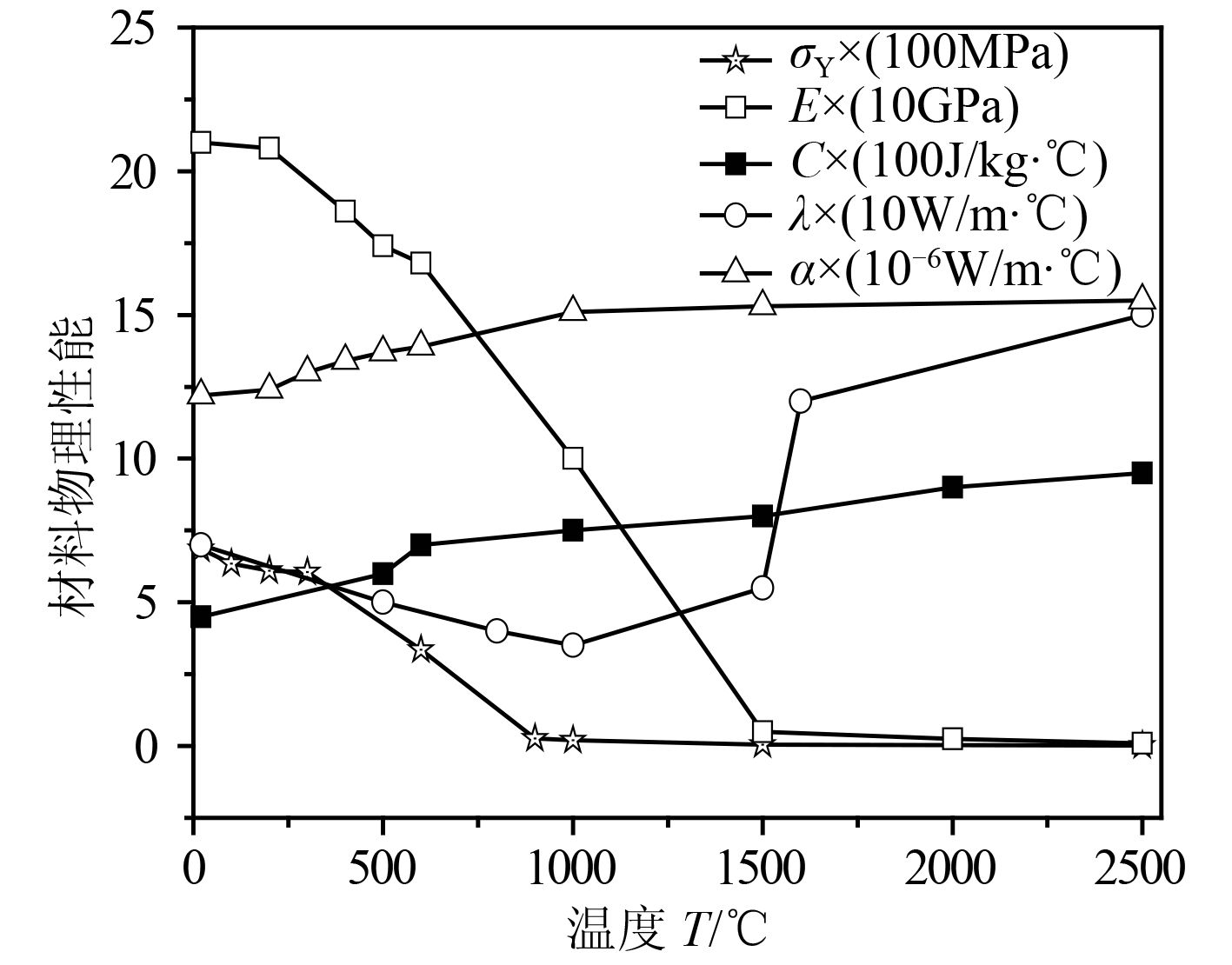
2.4 材料参数图 2 是母材和焊缝金属材料性能参数与温度的对应关系。材料密度为 7 850 kg/m3,泊松比为 0.3。
|
图 2 钢材料物理性能参数 Fig. 2 Physical properties of steel materials |
热、弹塑性有限元分析的求解过程为:首先把构件划分成有限个单元,然后逐步加上温度增量。每次温度增量加载后,由式(10)可求得单元位移增量 dδ。每个单元内的应变增量 dεe 和单元位移增量 dδe 的关系为:
| ${\rm d}\varepsilon^e = {\textbf{\emph{B}}}{\rm d}\delta^e$ | (11) |
由本构关系可进一步得到每个单元的应力增量 dσe,从而得到整个焊接过程中动态应力应变的变化过程和最终的残余应力和变形的状态。在每个增量步开始时将几何形状更新,在新的拉格朗日坐标下分析温度场方程。采用非线性方程迭代解法求解热传导方程的等效温度场递推关系式。收敛后,在同一增量步中,更新温度值,评价材料力学性质和热应变,迭代求解力平衡方程,收敛后,进行下一增量步的分析直至所需的增量步结束。
3.2 参数选取母材选取国产低碳调质高强钢[5],电流 130 ~ 135 A,焊接能量控制在 10 ~ 15 kJ/cm;中间 4 至 6 层采用 ϕ 4 mm 焊条,电流 165 ~ 170 A,焊接能量控制在 15 ~ 18 kJ/cm;盖面采用 ϕ 3.2 mm 焊条,退火焊道,以防止盖面层淬硬组织。
3.3 计算模型及计算结果针对图 1 所示缺陷,建立如图 3 所示的焊接结构 1/4 计算模型,在凹坑附近的单元结构单元总数 19 320 个,计算时间为 49 h。其中 A-B 路径方向为轧向,C-D 为垂直轧向方向。1,2 和 3 点分别位于间隔 2 个焊道的焊缝金属上,沿 C-D 路径排列。

|
图 3 焊接计算模型示意图 Fig. 3 Schematic diagram of welding calculation model |
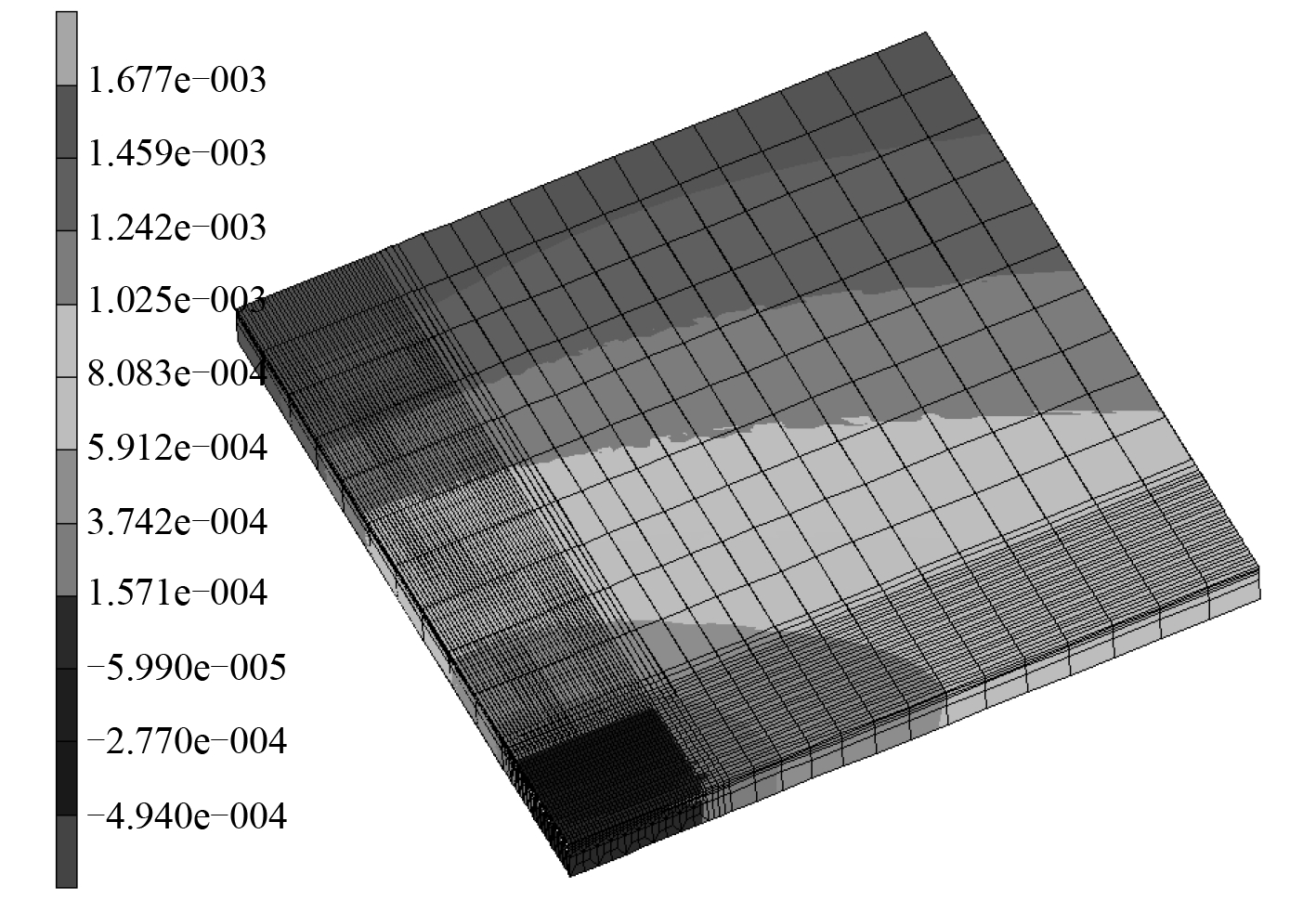
焊接残余变形如图 4 所示,焊接完成后的最大变形为 1.7 mm,变形值以腐蚀凹坑中心为基准,基本按照椭圆面的方式大小分布,整体焊接变形小。
|
图 4 焊接残余变形分布云图 Fig. 4 Distribution of welding residual deformation |
焊接过程中的焊接温度场和熔池形态的分布如图 5~图 7 所示。由图 5 可知,熔池温度附近温度达到 2 300 °C。在焊缝表面以椭圆形等温线,拖长尾分布 [6]。

|
图 5 焊接过程中温度场分布图 Fig. 5 Distribution of temperature field during welding |

|
图 6 焊接过程中沿轧向应力分布云图 Fig. 6 Stress distribution along the rolling direction during welding |

|
图 7 焊接过程中垂直轧向应力分布云图 Fig. 7 Distribution of stress in vertical rolling direction during welding |
由图 6 和图 7 可看出,在堆焊后残余应力分布在腐蚀凹坑及其周围的较小区域内,局部区域的残余应力达到了母材的屈服强度。距离凹坑边缘处有一定的距离后残余应力的值变得很小。在凹坑长边处附近,沿轧向方向的残余应力分布,由焊缝到母材从拉应力变为压应力,而垂直轧向方向残余应力基本上都是拉应力;在凹坑短边附近,沿轧向方向的残余应力基本为拉应力,而垂直轧向方向的残余应力由焊缝到母材从拉应力变为压应力。
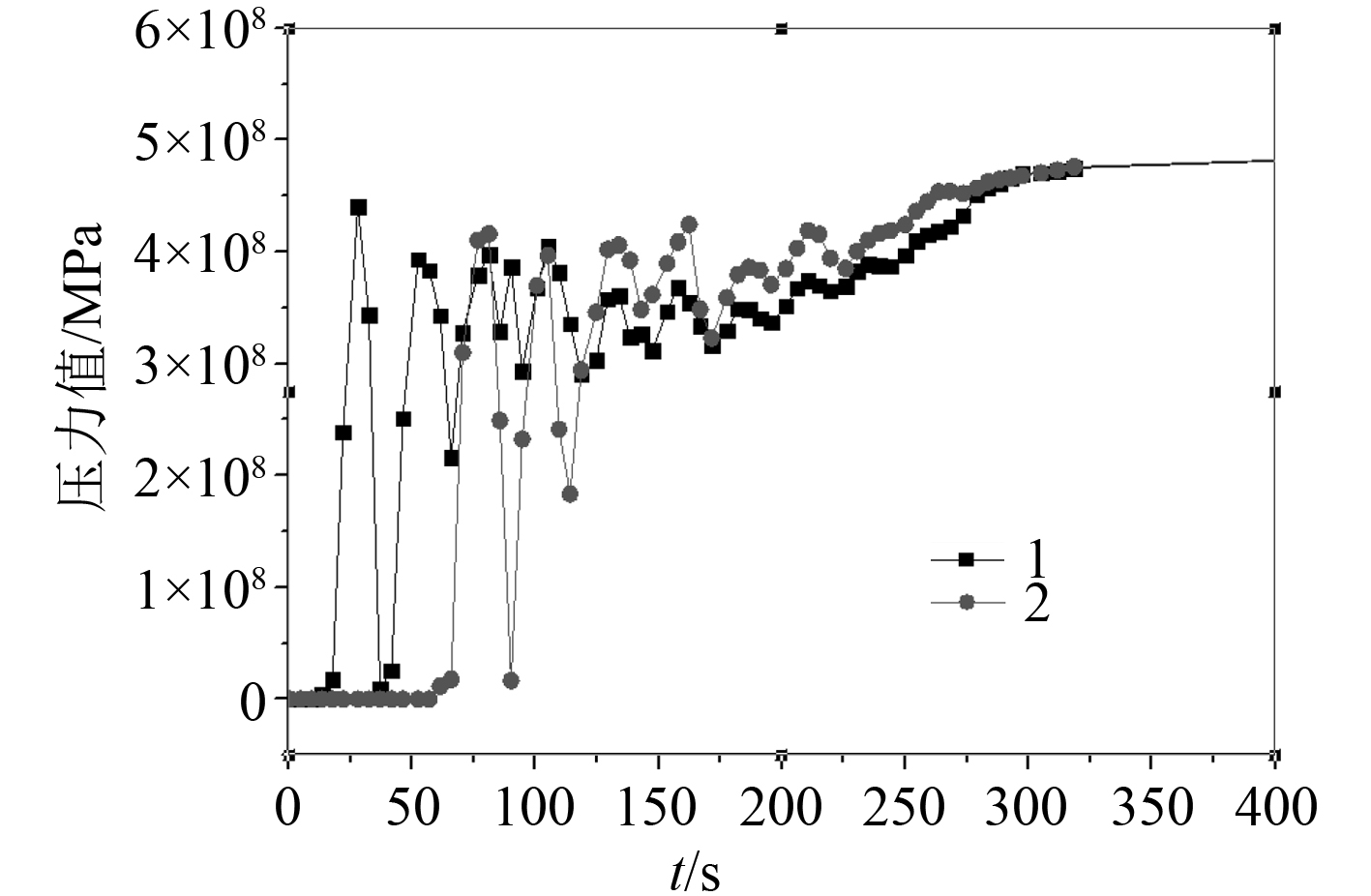
位置 1 和位置 2 等效焊接应力-时间历程曲线如图 8 所示。由图可知,随着焊缝金属的不断填入,焊缝沿轧向和垂直轧向的应力相继产生,1 点位置要比 2 点早些产生,因焊接位置 1 点时的焊道时,2 点位置处的焊道还未出现。焊接热应力时间历程过程的总体趋势一致,最终达到平衡状态,即常温下的残余应力状态[7]。
|
图 8 位置 1 和 2 等效焊接应力-时间历程曲线 Fig. 8 Equivalent welding stress-time history curves for positions 1 and 2 |
综合分析数值计算结果发现:使用手工电弧焊方法堆焊腐蚀凹坑的焊接残余变形较小;焊接热循环曲线表明,堆焊过程中,先焊焊道受到后焊焊道的热作用。焊接达到准稳态时,不同焊道的热循环曲线形状基本相似;焊接残余应力较大值分布在腐蚀凹坑及附近母材的较小区域内,母材和焊缝熔合的凹坑边缘局部位置残余应力达到母材的屈服强度水平。在焊缝金属内的残余应力均为拉应力,且分布均匀;在腐蚀凹坑的附近区域由残余压应力的存在。建议采用后热处理,降低残余应力的峰值。
4 试验分析 4.1 试验方案试验钢板为 30 mm 连铸 921A 钢,用碳弧气刨在钢板中间刨出如图 1 所示的坑,打磨修整后,采用 CW66J 焊条补焊。焊道与钢板轧向平行。多层多道焊接。焊后进行无损检测检查内部缺陷,渗透无损检测检验表面裂纹。焊缝采用退火焊道布置,表面打磨平整后,沿熔合线进行表面焊接残余应力测试。
4.2 缺陷修补试验钢板模拟缺陷补焊连续焊接,采用短弧、小摆动、多层多道焊,每一层焊道交替改变施焊方向,焊接共持续了 20 h,整个补焊过程尽量采用小规范焊接,其中ϕ 3.2 mm 焊条采用 130~135 A 的电流,焊接能量控制在 10.5~14.8 kJ/cm,ϕ 4.0 mm 焊条采用 165~170 A 的电流,焊接线能量控制在 15.4~18.2 kJ/cm。
4.3 修后检验补焊完成后,试板整体未发生明显变形。X 射线探伤前,将焊接区打磨至与钢板平齐。X 射线检测表明,在熔合线附近有一近 ϕ 2 mm 气孔,评片结果为I级。同时对堆焊层表面进行渗透检查,未发现表面裂纹。
将焊缝磨平后标出熔合线,在沿熔合线边缘 5 mm 的钢板一侧和焊缝一侧分别进行残余应力测试,发现钢板一侧大部分为拉应力,在堆焊区四边的中心部位残余应力最大,达 620 MPa;焊缝一侧全部为拉应力,应力大小则无明显规律,最大值位于拐角处,为 460 MPa[8]。
5 结 语1)利用数值计算方法可较准确模拟较大面积和深度缺陷厚钢板缺陷焊补过程修复过程,并优化施工工艺参数。
2)采用短弧、小摆动、多层多道焊补方式,有效控制缺陷结构焊补后的残余应力,模拟缺陷补焊试验结果来看,对于 921A 钢板存在的缺陷,采用上述方法修补后,接头各向强度能够满足技术指标要求。
| [1] | 秦广冲. 腐蚀坑对钢材应力集中系数及疲劳损伤影响研究[D]. 西安: 西安建筑科技大学, 2014. |
| [2] | 王强. 厚板焊接温度场与残余应力场有限元分析[D]. 武汉: 湖北工业大学, 2015: 5–7. |
| [3] | 庞艺, 雷永平, 林健. 厚板对接残余应力的三维有限元模拟与验证[J]. 热加工工艺, 2014, 11 : 10–13. |
| [4] | 李培麟, 陆皓. 双椭球热源参数的敏感性分析及预测[J]. 焊接学报, 2011, 32 (11): 13–19. |
| [5] | 于兆斌. 921A船板钢动态断裂力学性能研究[J]. 哈尔滨工程大学, 2005 : 1–12. DOI: 10.3969/j.issn.1006-7043.2005.01.001 |
| [6] | 汪建华. 焊接残余应力形成机制与消除原理若干的问题讨论[J]. 焊接学报, 2002, 23 (3): 75–79. |
| [7] | 孙志明. 中厚板焊接有限元数值模拟及其参数优化[D]. 北京: 北京交通大学, 2011. |
| [8] | 魏海滨. 船体结构焊接残余应力消除装置设计研究[J]. 中国水运月刊, 2014, 14 (12): 21–22. |
 2017, Vol. 39
2017, Vol. 39
