2. 哈尔滨工程大学 多体船技术国防重点学科实验室,黑龙江 哈尔滨 150001
2. Harbin Engineering University, Multihull Ship Technology Key Laboratory of Fundamental, Harbin 150001, China
自钢制船产生之日起,疲劳破坏就一直是科研人员们的研究重点[1]。世界上几大船级社都对疲劳强度校核进行了相关规定,总的来说,疲劳损伤计算方法可分为简化计算和直接计算2种。
简化计算法主要包括疲劳载荷计算、各应力范围分量的计算、应力范围的合成以及许用应力衡准。该方法的优点是按照规范给出的经验公式计算载荷,形式简单、工作量相对较小[2]。
疲劳评估的直接计算法是相对于简化方法而言,这类方法的主要思想是直接由波浪载荷程序计算疲劳载荷,然后通过结构有限元分析或其他方法得到疲劳应力范围。直接计算又分为设计波法和谱分析法。谱分析方法所得到的结果普遍被人们所承认,谱分析的理论也越来越完善,因而谱分析方法在疲劳寿命预测中被认为是最为准确合适的[3]。
目前疲劳校核一般采用四节点壳单元的嵌入式细化模型。有关多节点和体单元模型的相关计算较少。本文选择某船舱口角隅部分作为疲劳强度分析对象,在热点区域采用嵌入式模型和外部模型对舱口角隅进行细化。其中外部模型分别采用 4 节点壳单元、8 节点壳单元、8 节点实体单元、20 节点实体单元进行建立,嵌入式模型使用 4 节点壳单元。通过外部模型的计算分析比较单元类型、热点应力的选取对疲劳热点应力的影响,结合嵌入式模型利用谱分析法对热点的疲劳损伤进行计算。
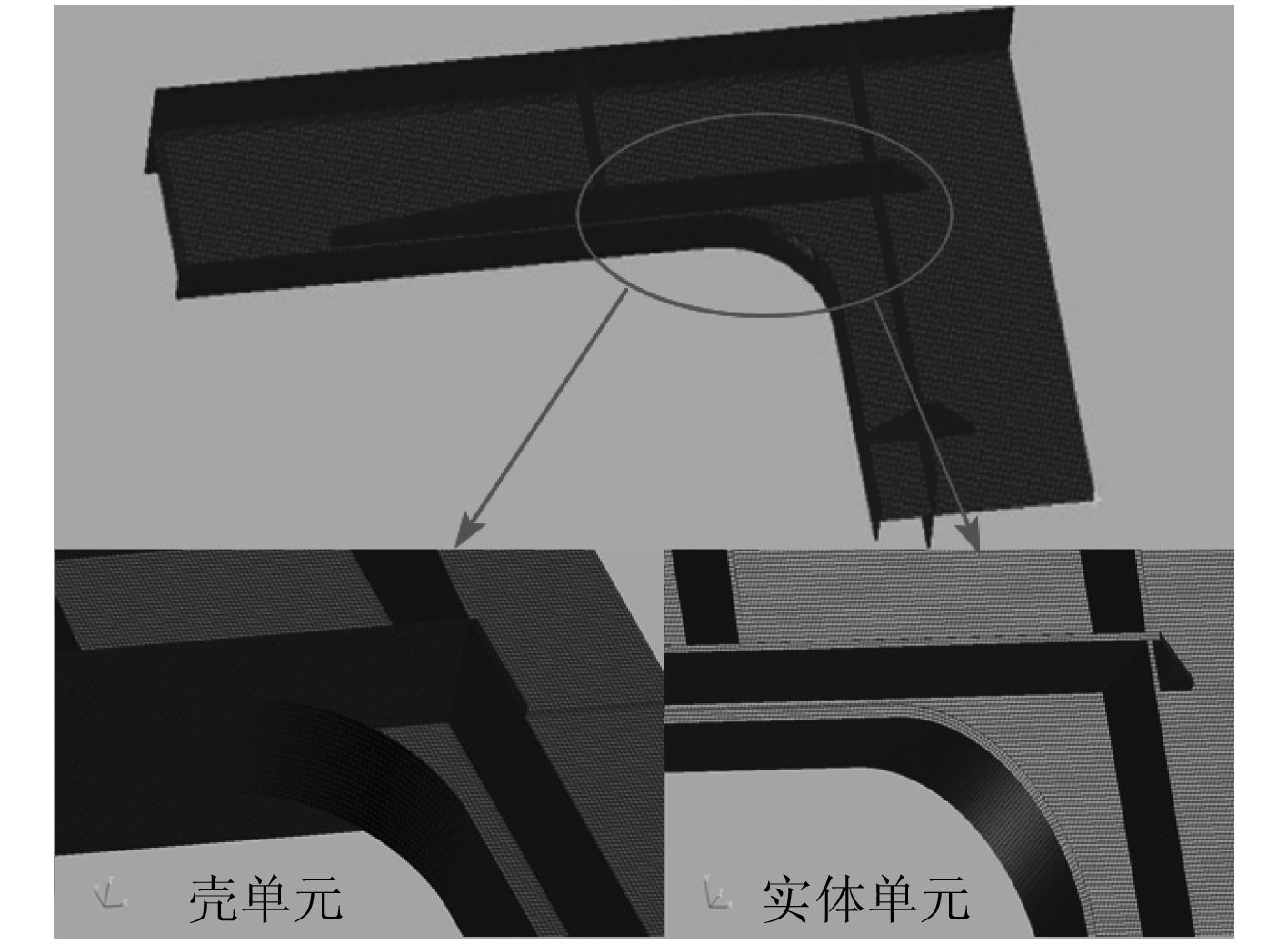
1 有限元模型的建立 1.1 细化模型的建立根据 CCS《船体结构疲劳强度指南》[4]中有限元建模的相关要求,通过 MSC.PATRAN 软件建立了某船的有限元模型并对舱口角隅及其相邻构件处使用精细有限元网格进行细化。建立的嵌入式细化区域模型和外部细化模型如图 1 和图 2 所示。

|
图 1 嵌入式细化区域模型 Fig. 1 Embedded refined region model |
|
图 2 外部细化区域模型 Fig. 2 External refined region model |
对外部模型施加的载荷和边界条件要保证外部模型与嵌入式模型高应力区域应力分布相似,为此本文计算了全船模型在迎浪、斜浪和横浪下舱口角隅处应力分布,如图 3~图 6 所示。

|
图 3 0° 迎浪下舱口角隅应力分布图 Fig. 3 Hatch corner stress distribution at 0 degrees |

|
图 4 30° 斜浪下舱口角隅应力分布图 Fig. 4 Hatch corner stress distribution at 30 degrees |

|
图 5 60° 斜浪下舱口角隅应力分布图 Fig. 5 Hatch corner stress distribution at 60 degrees |

|
图 6 90° 横浪下舱口角隅应力分布图 Fig. 6 Hatch corner stress distribution at 90 degrees |
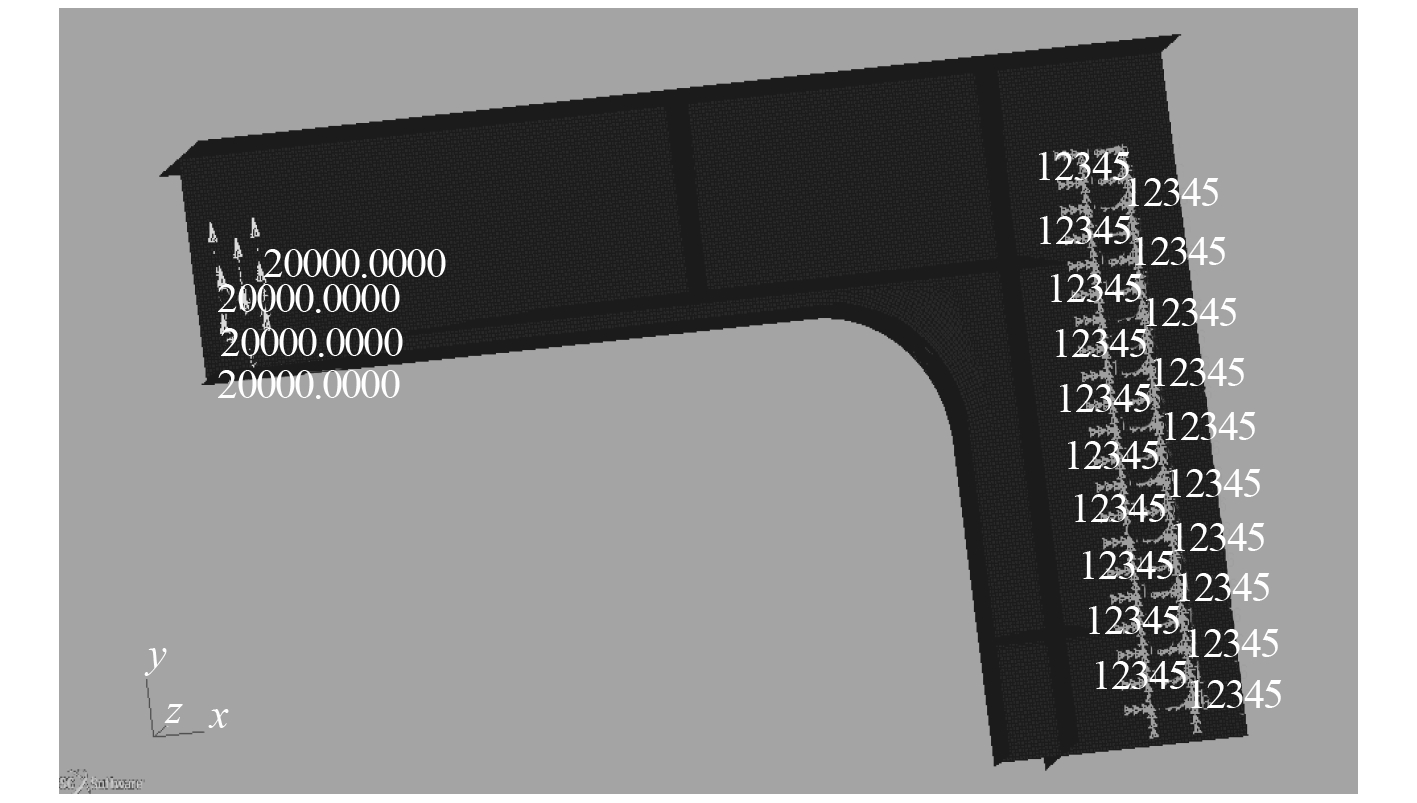
从图 3~图 6 可看出,无论何种浪向下角隅区域热点应力分布大致相同,因此本文中外部模型的边界条件如图 7 所示。图7中一侧刚固另一侧施加拉力,其中拉力的合力大小为 160 kN。模型的应力分布如图 8所示。图 9 为距热点 0.5 t(t 为热点区域处板厚)处嵌入式模型在各个浪向下主应力方向与外部模型主应力方向的对比。
|
图 7 载荷及边界约束条件 Fig. 7 Load and edge-restraint condition |

|
图 8 外部模型应力分布图 Fig. 8 Stress distribution diagram of external model |

|
图 9 主应力方向的对比 Fig. 9 Comparison of principal stress direction |
从图 8 和图 9 可看出,外部模型的应力分布与嵌入式模型相似并且热点附近主应力方向也在相近的范围内。这说明外部模型施加的载荷和边界条件合理。
2 热点应力分析目前热点应力的界定并没有一个统一的标准,外推方式和热点应力成分的选取都有着不同方法。本文采用有限元方法计算热点应力时使用精细网格建模,精细网格的热点应力由位于 0.5 倍和 1.5 倍净厚度处的应力线性外插到热点位置得到[5],而热点应力成分的选取采用方疲劳热点应力取最大主应力[4]和疲劳热点应力取焊缝法线左右 45°区域内的主应力[6]2种方式,并对它们的计算结果进行分析比较。
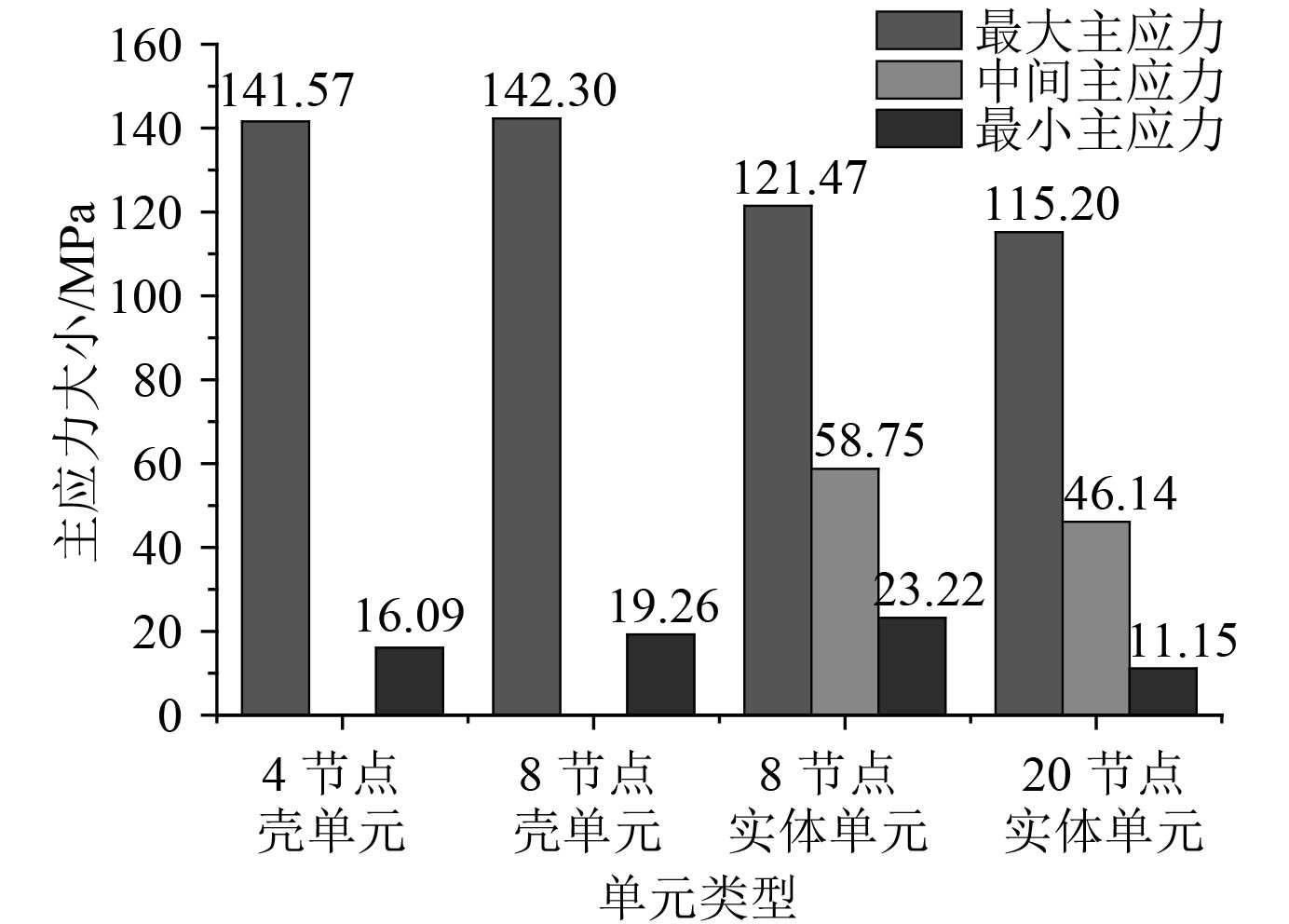
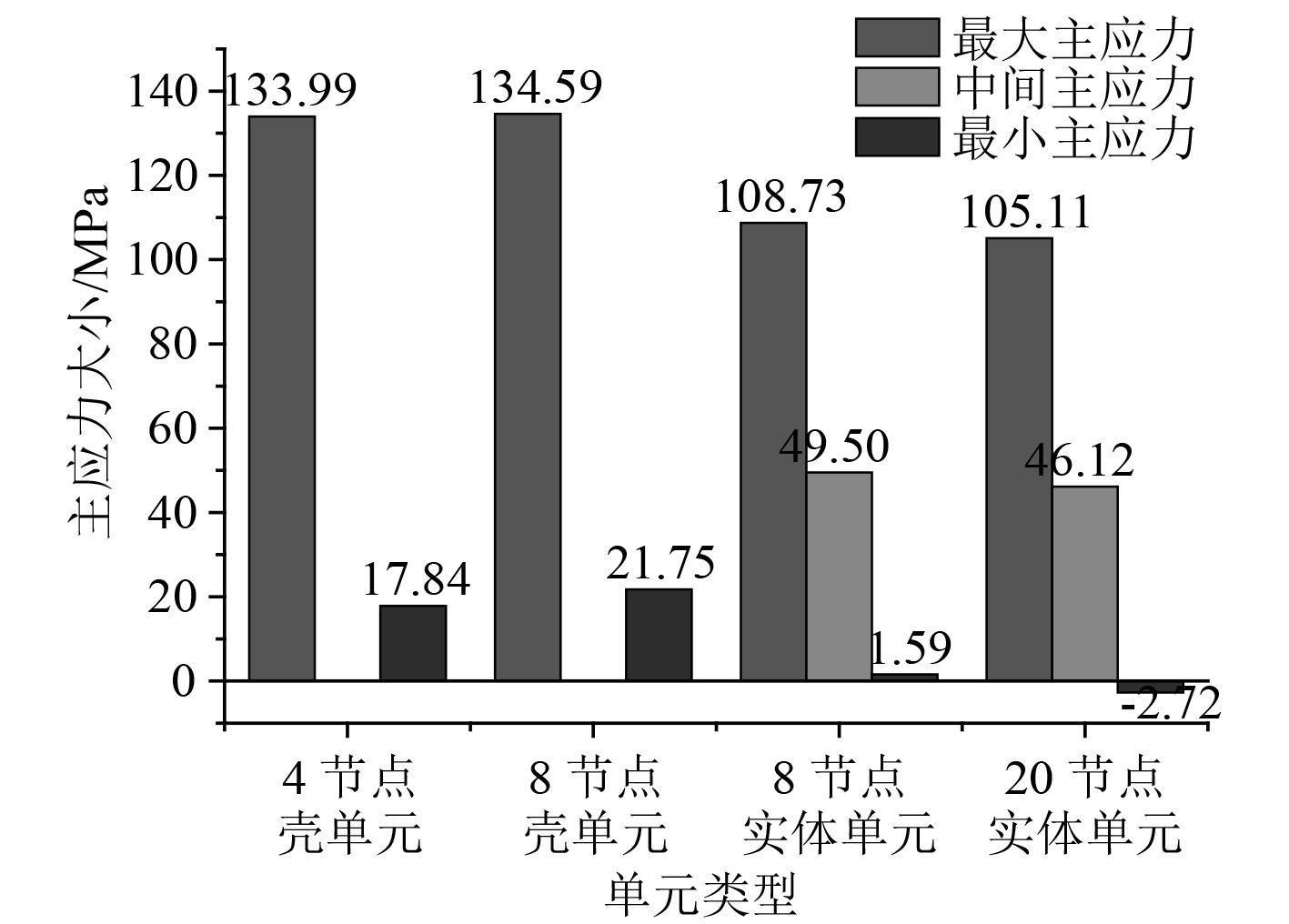
通过 MSC.PATRAN 软件计算得到外部模型不同类型单元下距热点 0.5 t 和 1.5 t 处的主应力大小如图 10 和图 11 所示。
|
图 10 0.5 t 处主应力大小 Fig. 10 Principal stress magnitude at 0.5 t |
|
图 11 1.5 t 处主应力大小 Fig. 11 Principal stress magnitude at 1.5 t |
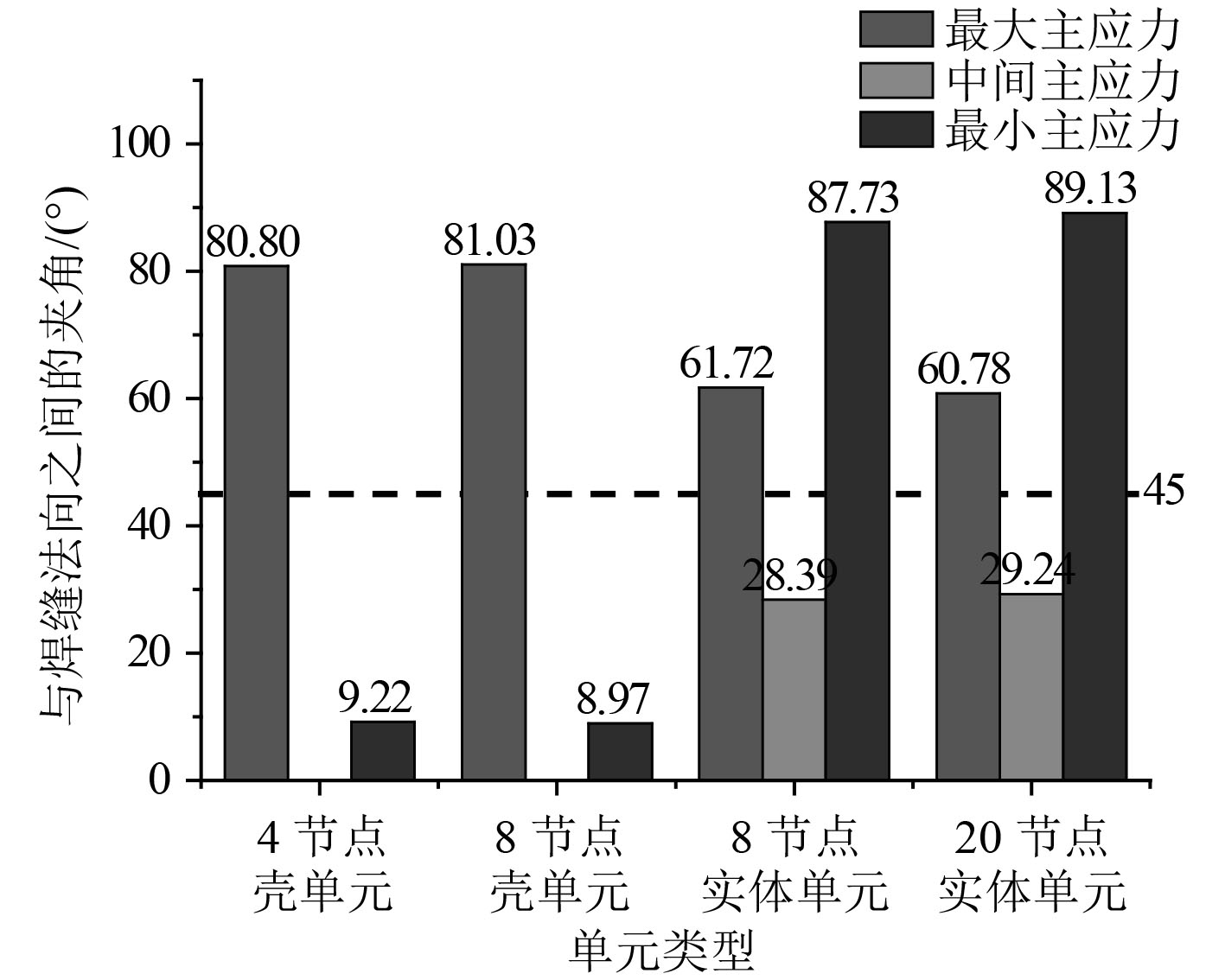
计算得到的距热点 0.5t和 1.5 t处各主应力与焊缝法向之间的夹角如图 12 和图 13 所示。

|
图 12 0.5 t 处各主应力与焊缝法向之间的夹角 Fig. 12 Angle between the principal stress and the normal of the weld line at 0.5 t |
|
图 13 1.5 t 处各主应力与焊缝法向之间的夹角 Fig. 13 Angle between the principal stress and the normal of the weld line at 1.5 t |
从图 12 和图 13 可看出,当采用方式 2 计算热点应力时,壳单元使用最小主应力进行插值计算,实体单元采用中间主应力进行插值计算,2种方式计算得到的热点应力结果见表 1。以 4 节点壳单元采用方式 1 计算得到的热点应力大小为基准,其余各种情况下的热点应力与其大小的比较见表 2,该计算结果也为下文各类型单元的频率响应函数的计算提供依据。
|
|
表 1 热点应力大小 Tab.1 Hotspot stress(单位:MPa) |
|
|
表 2 热点应力大小的比较 Tab.2 Comparison of hot spot stress |
从表 2 可看出,热点应力采用最大主应力时壳单元计算得到的热点应力较实体单元计算得到的热点应力要偏大。同类型的壳单元和实体单元,节点数目的不同对热点应力的影响不大。热点应力采用焊缝法线左右 45°区域内的主应力时,由于最大主应力不在该范围内,因此热点应力比最大主应力的计算结果偏小很多。同时由于壳单元选入的是最小主应力,而实体单元选入的是中间主应力,因此计算得到的壳单元热点应力比实体单元热点应力要小。这导致当采用方式 2 的方法计算热点应力时不同类型单元之间计算结果偏差较大,文献[7]中为了避免这种情况对最大主应力不在焊缝法向 45° 范围内时,采用对最大主应力进行修正的办法来计算热点应力。
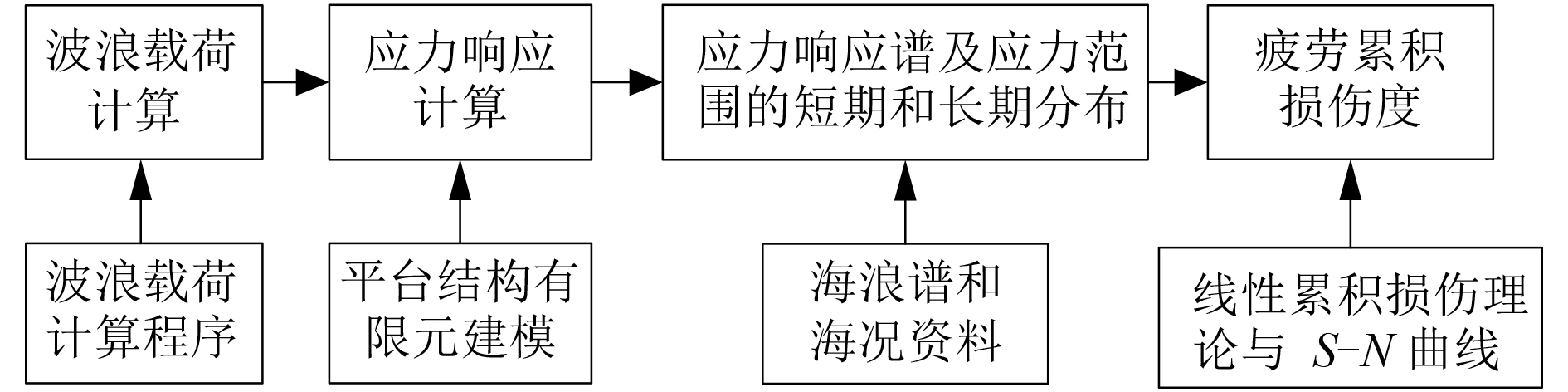
3 谱分析直接计算 3.1 谱分析计算原理基于谱分析的直接计算法是船舶与海洋工程中一种常用的研究载荷和结构响应的方法,谱分析方法首先计算目标船不同装载工况、浪向和计算频率下的波浪载荷以及船体结构应力响应,进而得到应力传递函数;然后结合特定海域的海浪谱和海况资料获得应力响应谱及应力的短期分布。最后基于线性累积损伤理论并选取相应的 S-N 曲线,计算得到疲劳评估部位总的累积损伤度。谱分析方法的流程如图 14 所示。
|
图 14 谱分析疲劳的计算流程 Fig. 14 Spectrum analysis of fatigue calculation process |
本文利用 WALCS 软件计算该船舶满载状态单位规则波下所受到的舷外水动压力和惯性力。航向角从迎浪(0°)到斜浪(330°)以 30° 步长递增,波浪频率的范围是从 0.1 ~ 1.6 Rad/s 以 0.1 Rad/s 步长递增,个别频率上以 0.05 Rad/s 递增计算,如表 3 所示。划分的水动力网格如图 15 所示。
|
|
表 3 计算工况 Tab.3 Calculation condition |

|
图 15 Walcs 划分的水动力网格 Fig. 15 Hydrodynamic grid by Walcs |
本文将船舶受到的舷外水动压力和货物造成的惯性力按照实部虚部分别加载到模型上,计算单位规则波下的热点应力。大多数船级社对于全船有限元分析所采用的边界条件都有相应的规定。本文采用惯性释放技术,可以简单且很好地处理全船有限元模型。加载过程中由于工况数目较多,手动加载非常困难,本文利用 MSC.PATRAN 提供的 PCL 语言编制波浪载荷和惯性力自动加载程序,实现载荷的自动加载,如图 16 所示。
|
图 16 疲劳载荷的加载 Fig. 16 The fatigue load |
对每一工况(给定航向、遭遇频率、单位波幅)分别得到角隅部位的应力响应余弦项
本文利用嵌入式模型按方式 1 计算了频率响应函数,其频率响应函数幅值如图 17所示。其他类型单元的频率响应函数幅值可参照表 2 中的比例关系换算得到。

|
图 17 频率响应函数幅值 Fig. 17 The amplitude of frequency response function |
在船舶结构疲劳强度分析的谱分析方法中,频率响应函数求出之后,结合波浪的功率谱密度函数即可求得应力的响应谱。波浪的功率谱密度一般采用国际船舶结构会议(ISSC)推荐的双参谱作为波浪的功率谱密度函数。
船舶应力范围的长期分布采用分段连续模型模拟,每个分段连续模型都对应一个短期分布,其结构应力幅值服从 Rayleigh 分布,疲劳计算回复期 T L 的疲劳累积损伤度 D 可直接采用各短期分布疲劳累积损伤度的组合得到[9]:
| $D \!\!=\!\!\! \displaystyle\frac{{\delta \cdot {T_L}}}{{\overline a }}\Gamma (1 \!\!+\!\! \frac{m}{2})\!\!\!\!\sum\limits_{n = 1}^{{N_{load}}} {{p_n} \!\!\cdot \!\!\sum\limits_{i = 1}^{{n_S}} {\sum\limits_{j = 1}^{{n_H}} {{p_i}{p_j}{\nu _{ijn}}} } {{\left( {2 \!\! \sqrt {2{m_{0ijn}}} } \right)}^m}}\!\!\! \text{。}$ |
式中:
本文采用全球航行海域的波浪散布图进行结构的疲劳分析,结合 Miner 线性累积损伤理论计算损伤值如表 4 所示。
|
|
表 4 疲劳损伤 Tab.4 Fatigue damage |
在得到的疲劳计算回复期的疲劳累积损伤度 D 之后,实际的疲劳寿命可按下式计算:
| ${T_d} = \displaystyle\frac{1}{D} \times {T_L}\text{,}$ |
式中:T L 为疲劳计算的回复期,一般取为 20 年;T d 为船舶的实际疲劳寿命,年。
计算得到的疲劳寿命如表 5 所示。
|
|
表 5 疲劳寿命(单位:年) Tab.5 Fatigue life |
1)该舱口角隅无论采用何种类型单元和热点应力计算方式得到的疲劳强度均符合要求,但计算得到的损伤值差别很大。
2)对于同种热点应力计算方式,当采用方式 1 计算热点应力时,实体单元得到的热点应力约为壳单元计算得到的热点应力的 80%,同种单元节点数目的不同对热点应力大小影响不大。而采用方式 2 计算热点应力时,由于实体单元和壳单元参与计算的主应力不同,二者的热点应力大小相差很大,但同种单元,节点数目对疲劳热点应力大小影响也不大。
3)对于同一类型单元,2种热点应力计算方式得到的热点应力差别较大,利用方式 2 计算得到的热点应力较方式 1 明显偏小,这也造成的疲劳损伤与方式 1 计算的差别较大。
4)舱口角隅在各个浪向下最大主应力均不在焊缝法向 ±45° 内,这种情况下方式 2 计算得到的不同类型单元的热点应力差别较大,因此在计算舱口角隅处的疲劳强度时建议采用方式 1 计算热点应力。
| [1] |
冯国庆. 船舶结构疲劳评估方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2003.
FENG Guo-Qing. The fatigue assessment methods for ship structures[D]. Harbin: Harbin Engineering University, 2003. |
| [2] |
程玉芹, 罗广恩. 超大型集装箱船上甲板舱口角隅疲劳强度评估[J]. 船海工程, 2013, 01 : 24–27+31.
CHENG Yu-Qin, LUO Guang-En. Fatigue Assessment of the Upper Deck Hatch Corners in Very Large Container Ship[J]. Ship and sea engineering, 2013, 01 : 24–27+31. DOI: 10.3963/j.issn.1671-7953.2013.01.007 |
| [3] |
冯国庆. 船舶结构疲劳强度评估方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.
FENG Guo-qing. Resrarch on fatigue strength assessment methods of ship structures[D]. Harbin: Harbin Engineering University, 2006. |
| [4] |
中国船级社. 船体结构疲劳强度指南[M]. 北京: 人民交通出版社, 2014.
China Classification Society. Guide of ship structures fatigue strength [M]. Beijing: China Communications Press, 2014. |
| [5] |
刘文华, 张弛. 基于CSR中热点应力的散货船疲劳强度分析[J]. 上海造船, 2009, 03 : 17–2041.
LIU Wen-Hua, ZHANG Chi. Fatigue strength analysis of bulk carriers based on hot spot stress in CSR[J]. Shanghai Shipbuilding, 2009, 03 : 17–2041. DOI: 10.3969/j.issn.1005-9962.2009.02.005 |
| [6] |
唐明非, 许汀. 基于DNV规范的结构疲劳强度谱分析方法[J]. 船舶设计通讯, 2011, 01 : 21–25.
TANG Ming-fei, XU Ting. Spectrum Analysis of Structural Fatigue Strength Based on DNV Rules[J]. Ship design communication, 2011, 01 : 21–25. |
| [7] |
任慧龙, 刘洋, 冯国庆. HCSR规范疲劳筛选方法研究[J]. 船海工程, 2014, 02 : 19–22.
REN Hui-long, LIU Yang, FENG Guo-qing. Research on the HCSR Fatigue Screening Method[J]. Ship and sea engineering, 2014, 02 : 19–22. DOI: 10.3963/j.issn.1671-7953.2014.02.006 |
| [8] |
刘敬喜, 唐永生, 楼丹平. 大型LNG船典型节点疲劳寿命谱分析评估[J]. 海洋工程, 2010, 03 : 86–90.
LIU Jing-xi, TANG Yong-sheng, LOU Dan-ping. Fatigue strength assessment of typical spots in a large LNG based on spectral method[J]. Oceanographic engineering, 2010, 03 : 86–90. DOI: 10.3969/j.issn.1005-9865.2010.03.013 |
| [9] |
胡毓仁, 李庆典, 陈伯真, 船舶与海洋工程结构疲劳可靠性分析[M]. 哈尔滨: 哈尔滨工程大学出版社, 2012.
HU Yu-ren, LI Qing-dian, CHEN Bo-zhen, Fatigue reliability analysis of ship and offshore structures[M]. Harbin: Harbin Engineering University Press, 2012. |
 2017, Vol. 39
2017, Vol. 39
