随着我国造船业迅速发展,许多新式舰船纷纷建造下水,对长期服役的老旧舰船船体结构技术状态的鉴定工作也逐渐开启,对舰船结构强度的校核是技术状态鉴定的重要组成部分。甲板作为舰船的重要结构之一,对甲板结构极限承载能力的分析是对舰船结构强度评估的重要组成内容。
加筋板被广泛应用于许多工程结构中,它大大提高了板的承载能力[1]。加筋板结构为船体甲板结构的基本构件,其承载能力直接影响整体结构的极限承载能力。舰船在中垂状态时甲板板架受总纵弯曲轴向压力,甲板板架是距离中和轴最远的主船体受压结构,所受的轴向压力最大,只有保证甲板的承载能力,才能保证舰船整体结构的安全性。加筋板作为船体甲板的主要结构单元,研究其受压状态下的极限承载能力十分必要。一般地,受到轴向压力作用的加筋板的可能破坏模式包括:总体屈曲后的总体破坏;加强筋之间的板格局部屈曲后引起的总体破坏;加强筋(无转动)局部屈曲或屈服后引起的总体破坏;加强筋弯扭屈曲(侧屈),整个加筋板随之丧失承载能力;加筋板的整体屈服[2]。
水面舰船在长期使用过程中,船体加筋板结构由于各种载荷的作用,会产生挠度变形,对后续载荷而言,这种挠度变形在加载之前就已经产生,故称为初始挠度。初始挠度对加筋板的极限承载能力会产生不利影响。因此,在加筋板的极限承载能力分析中,考虑初始变形等因素的影响,具有重要的工程意义。
国内外考虑初始挠度影响下,对加筋板极限强度的研究比较多。Ueda 等[3]推导了受双轴压应力、剪应力,并考虑初始变形和焊接残余应力情况下,板有效宽度的计算公式;Paik 等[4]考虑焊接导致的初始变形,对加筋板进行了非线性屈曲分析;万育龙等[5]分析了考虑多种应力组合模式及局部、整体初始缺陷组合模式下的加筋板的极限强度,归纳出了适用于 CSR-OT 加筋板屈曲和极限强度计算的替代方法;罗刚等[6]研究了不同外力工况下加筋板极限强度的响应特点,过程中考虑了加筋板初始挠度的作用。这些研究虽然都考虑了初始挠度的影响作用,但都只是考虑了焊接产生的初始挠度,并且在有限元计算中,直接取一阶失稳模态作为加筋板的初始挠度模式,没有考虑初始挠度的具体形态对加筋板承载能力的影响。本文从初始挠度的具体形态出发,计算含初始挠度加筋板在加强筋方向单向受压情况下的极限强度;考虑初始挠度幅值和半波数对加筋板极限承载力的影响,提出了计算公式修正系数;并研究分析了含初始挠度加筋板典型位置剖面的应力分布特性以及初始挠度对加筋板破环模式的影响。
1 含初始挠度加筋板的稳定性分析 1.1 模型建立本文根据某舰船的甲板结构,选取甲板典型位置处的某一加筋板作为研究对象。该加筋板具有 6 条纵向加强筋,板尺寸 a × b 为 1 500 mm × 2 800 mm,加强筋间距 s = 400 mm,加强筋均为角钢,角钢尺寸为
研究中,利用有限元分析软件 Ansys,根据加筋板的具体尺寸,建立合适的有限元模型,如图 1 所示。采用 shell181 单元,单元长度在 20 ~ 30 mm 之间,计算中假定板的材料是理想弹塑性,弹性模量 E = 2.1 × 10 5 MPa,泊松比 ν = 0.3。

|
图 1 有限元模型 Fig. 1 The finite element model |
加筋板的边界条件定义为四边简支,具体定义方法可以参照相关文献[7]:
1)加筋板的四周边界限制法向位移 U z = 0,即为 z 方向简支;
2)长度方向两端 AB,CD 边(x = 0和 x = a 处)限制转角位移 R x = R z = 0,即可沿 y 方向自由转动;宽度方向两端 AD,BC 边(y = 0 和 y = b 处)限制转角位移 R y = R z = 0,即可沿 x 方向自由转动;
3)AB,CD 边线保持沿 x 方向的直边约束,AD,BC 边线保持沿 y 方向的直边约束;
4)AB、CD 边线中点限制 y 方向位移,即 U y = 0,AD、BC 边线中点限制 x 方向位移,即 U x = 0。
加筋板的外载荷施加方式为在 AB,CD 两端截面同时施加轴向压力为 1 MPa 的集中力载荷,在有限元软件中转换施加到截面节点上。
1.2 初始挠度设计初始挠度这种结构上的缺陷可以分为整体和局部 2 种形态。整体初始挠度是指板和加强筋同时产生挠度变形;局部初始挠度是指仅板产生的挠度变形。初始挠度形态主要包括两方面因素,即幅值和半波数。在较长的跨度范围内,初始挠度是由多个半波所组成的曲面,而在较短的范围内(2 个加强筋之间)一般只有一个半波。船体加筋板初始挠度形态可以看成由多种半波形式叠加而成,可用如下公式表示:
| $w = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{A_{mn}}\sin \displaystyle\frac{{m\pi x}}{a}\sin \displaystyle\frac{{n\pi y}}{b}} } \text{。}$ | (1) |
也有用如下公式来表示焊接作用导致加筋板产生的挠度变形[8]:
| $\displaystyle\frac{{{w_0}}}{{{w_{opl}}}} = {B_{oi}}\sin \displaystyle\frac{{i\pi x}}{a}\sin \displaystyle\frac{{\pi y}}{b}\text{。}$ | (2) |
式中:w 0 为初始挠度,mm;w opl 为加强筋间板格的最大初始挠度,mm;B oi 为初始变形幅值,mm。
加筋板结构的一阶屈曲模态是最容易产生的失稳状态,对加筋板的稳定性有重要影响。一般认为,取一阶模态作为结构的初始缺陷比较合理。本文在考虑初始挠度时,并不是考虑焊接影响产生的挠度变形,而是考虑长期外载荷作用下产生的挠度变形,这种挠度变形在加载之前就已经存在,故称为初始挠度。根据舰船甲板实际情况,假设初始挠度为:
| $w = A\sin \displaystyle\frac{{i\pi x}}{a}\sin \displaystyle\frac{{\pi y}}{b}\text{。}$ | (3) |
考虑半波数对弹性失稳压力的影响时,限定 y 方向为一个半波,只考虑 x 方向半波数的影响。
本文拟采用式(3)的初始挠度形式模拟实际初始挠度情况,来研究整体初始挠度的幅值和半波数对加筋板极限承载力的影响。
根据生产实践,当强力甲板厚度在 7~10 mm 之间时,钢板的绝对变形量达到 35 mm 时,才会对钢板进行矫正修复;从甲板变形测量数据的统计结果来看,甲板变形一般在 8 mm 左右。为了使研究更具有实用性和有效性,本文将初始挠度幅值设定在 0~30 mm 之间进行研究。国内关于甲板板架变形的半波数测量研究内容较少,国外有针对船厂建造中船体变形情况测量的研究[9],初始挠度半波数一般在 3 个以内。本文根据初始挠度实际情况,决定最多取 6 个半波作为研究对象。
在有限元软件 Ansys 中,可以通过对各个节点施加具体的法向位移来实现初始挠度的设计。图 2 所示为具有 1 mm 幅值、一个半波初始挠度的加筋板。
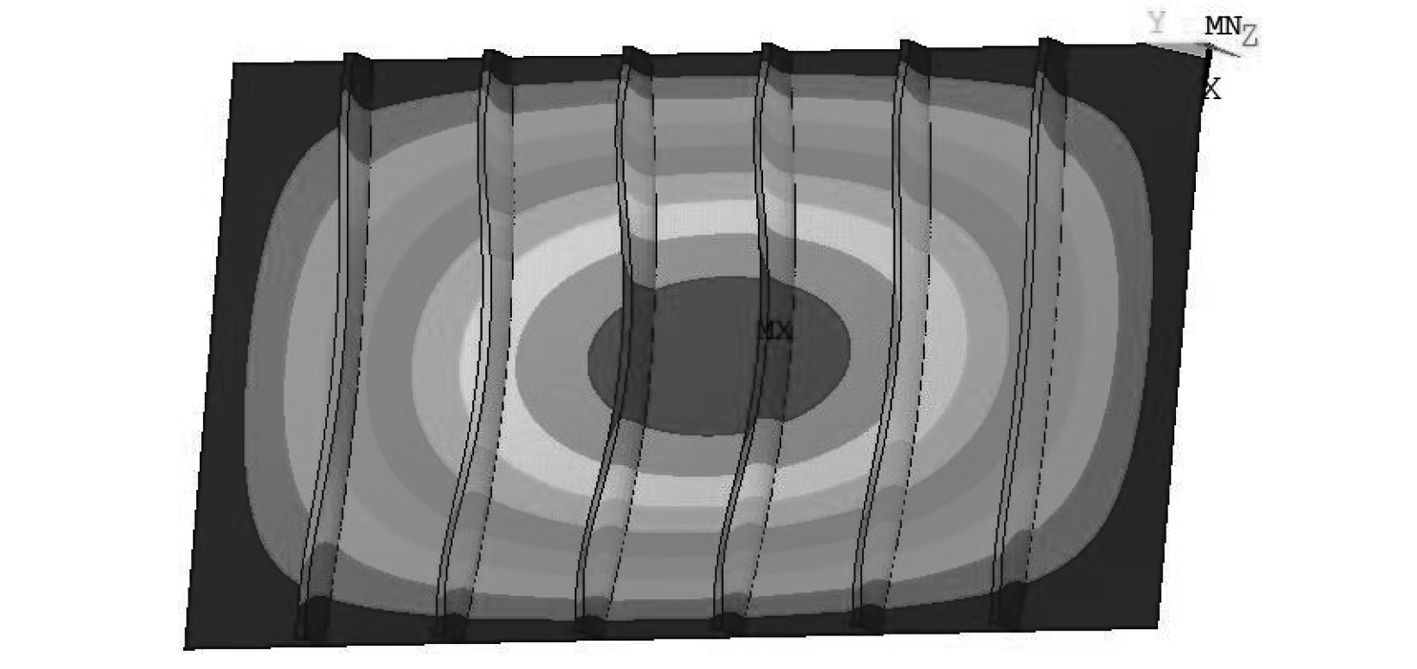
|
图 2 具有 1 mm 幅值、一个半波初始挠度的加筋板 Fig. 2 The stiffened plate with initial deflection of 1mm amplitude and 1 half-wave |
当计算模型不具有初始挠度时,计算所得极限载荷 σ ult 为 234.978 MPa。通过不断改变初始挠度的幅值和半波数,计算相应的极限载荷,计算数据见表 1。
|
|
表 1 含不同初始挠度加筋板的极限载荷(MPa) Tab.1 P of the stiffened plate with different initial deflections(MPa) |
根据计算数据可以绘制出极限载荷与初始挠度幅值的关系图,从而可以判定,在某一半波数情况下,极限载荷随初始挠度幅值的变化规律。为了更加方便比较不同半波数的初始挠度情况下,极限载荷随幅值的变化规律,将各个半波数下的曲线绘制到同一个坐标系下,并考虑将初始挠度幅值和极限载荷转化为无因次量,取初始挠度幅值 f 与加筋板厚度 t 的比值为自变量,取含初始挠度加筋板极限载荷 σ 与不含初始挠度加筋板极限载荷 σ ult 比值作为因变量,如图 3 所示。
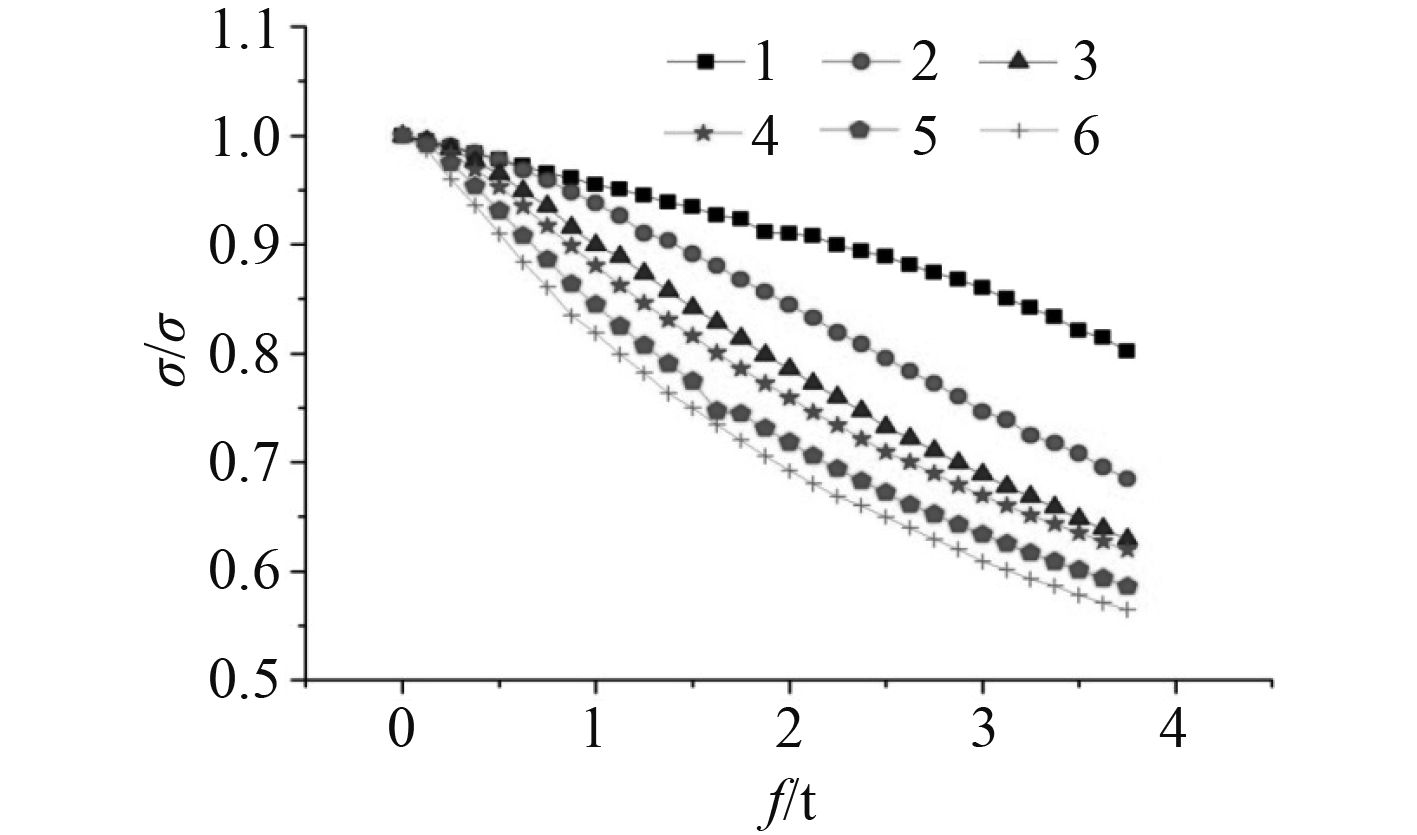
|
图 3 σ/σ ult 随 f/t 的变化规律 Fig. 3 σ/σ ult varies with f/t |
从图 3 中可以看出,虽然初始挠度的半波数不同,但是加筋板的极限载荷与初始挠度幅值的变化规律相似。随着初始挠度幅值的增大,极限载荷逐渐减小。当初始挠度半波数为 1 和 2 时,曲线变化近似于一次函数,极限载荷随初始挠度幅值的变化率基本保持不变;当初始挠度半波数大于 2 时,曲线变化近似于指数函数,极限载荷的变化率随初始挠度幅值的增大而减小。从整体来看,比值σ/σ ult 随着初始挠度半波数的增大而减小。
2.2 初始挠度半波数对加筋板极限载荷的影响由于计算数据较多,考虑初始挠度半波数对极限载荷的影响,只选取了含幅值为 5 mm,10 mm,15 mm,20 mm,25 mm 和 30 mm 初始挠度的数据进行分析,如图 4 所示。
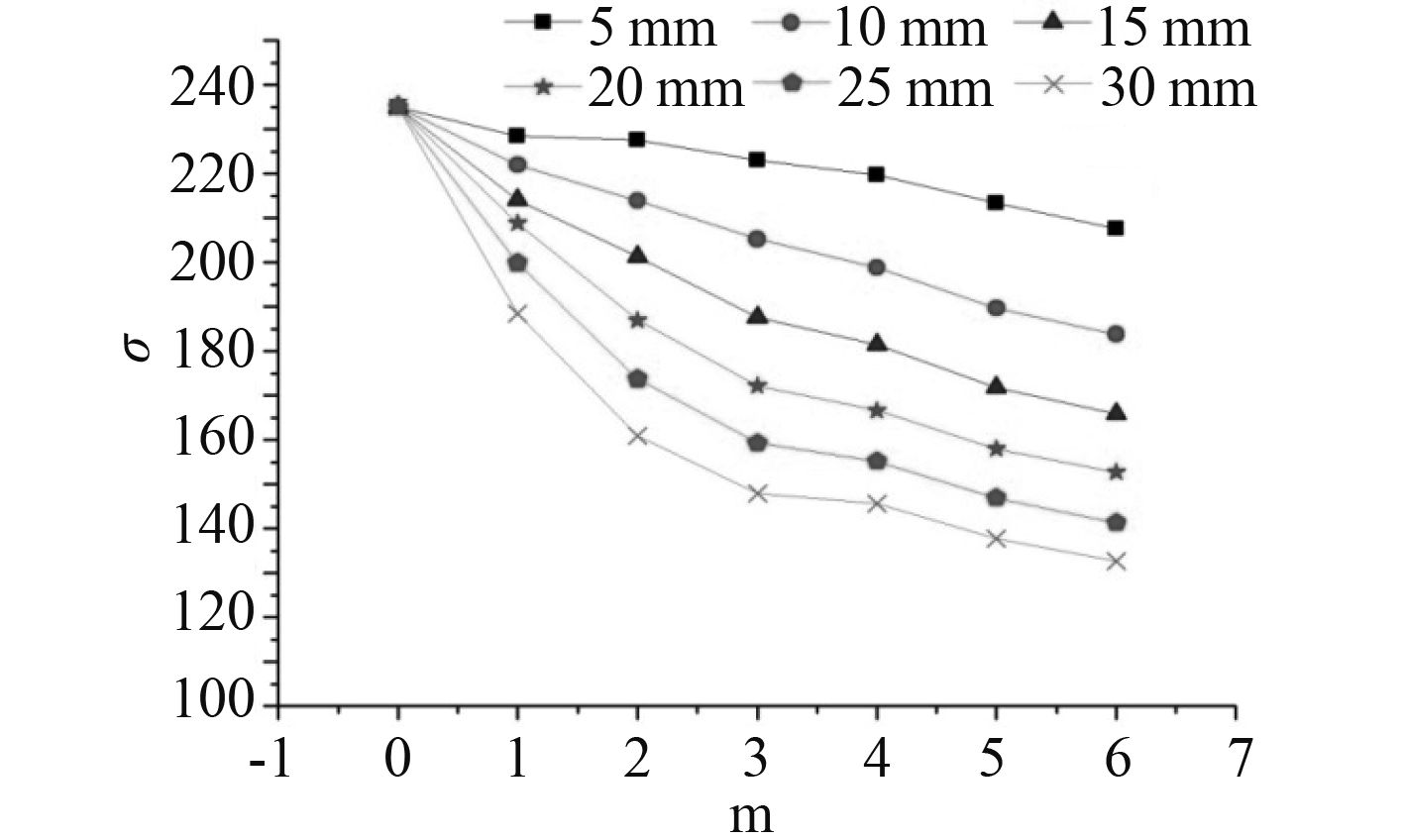
|
图 4 极限载荷随初始挠度半波数的变化规律 Fig. 4 P varies with the number of half-waves |
图 4 显示了当初始挠度幅值不变时,增加初始挠度的半波数,加筋板的极限载荷的变化情况。从图中可看出,不同半波数的初始挠度情况下,极限载荷的变化规律相似,载荷都是随着半波数的增加而减小。而且随着初始挠度半波数的增大,极限载荷的变化率逐渐减小。
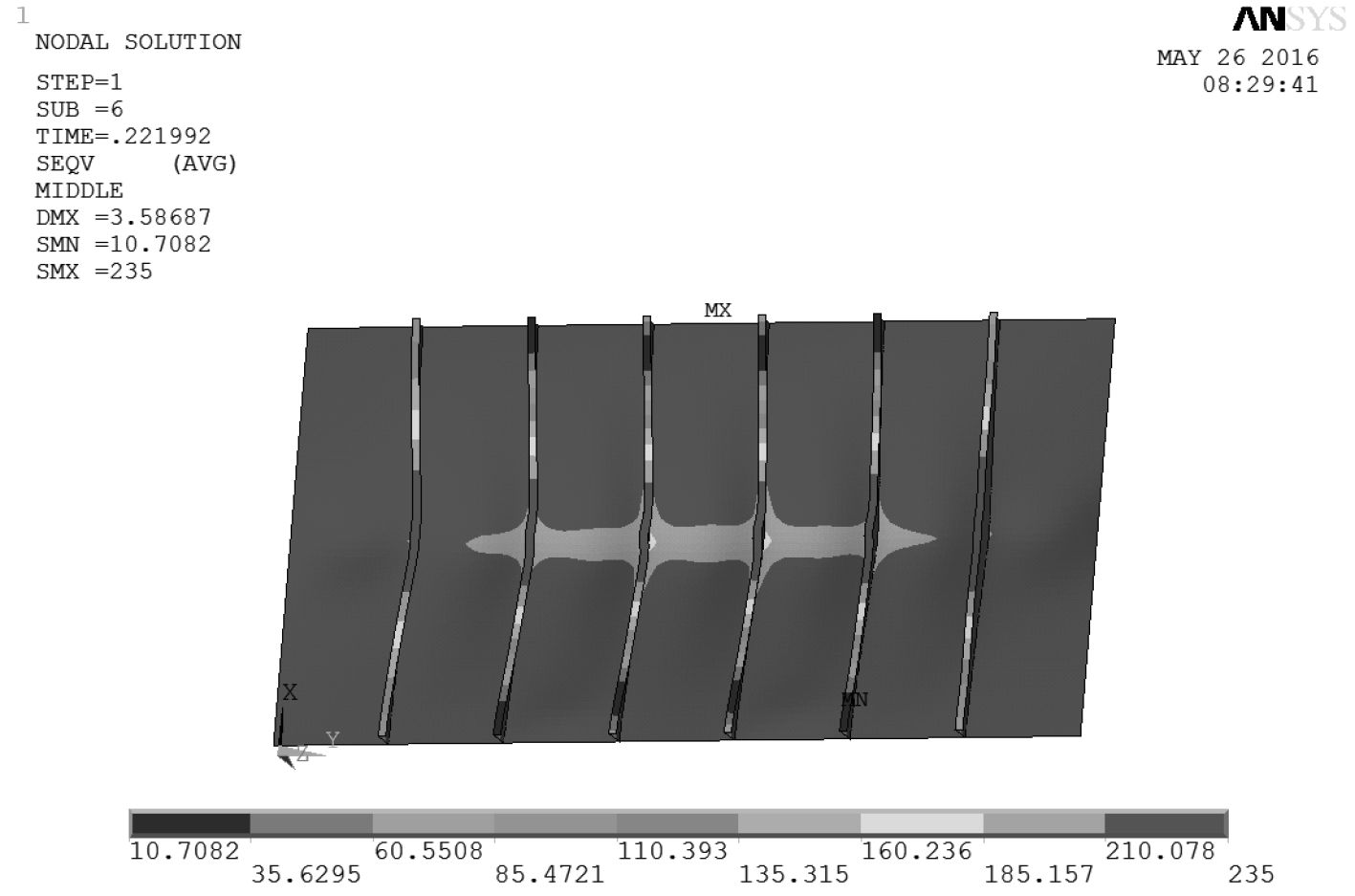
2.3 典型剖面的应力分布特点根据对中修船体甲板变形的勘验测量数据可知,船体加筋板出现的初始挠度幅值大部分在 10 mm 左右,具有一个半波形式,因此只讨论含有幅值 10 mm、具有一个半波初始挠度的加筋板应力分布特点。经过有限元计算,当含有一个半波、幅值 10 mm 初始挠度的加筋板达到其极限承载力时,其结构变形云图如图 5 所示,结构应力分布云图如图 6 所示。
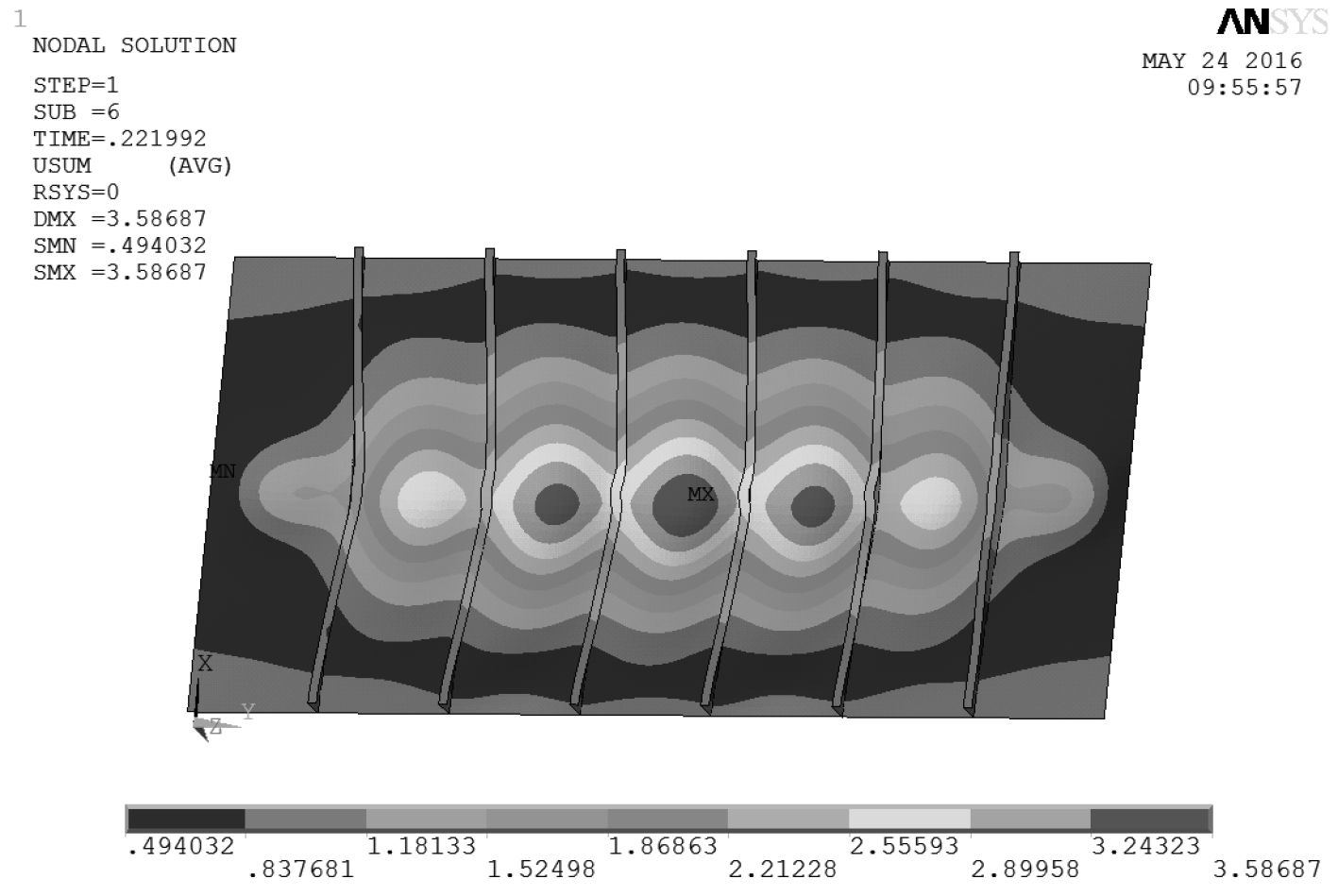
|
图 5 具有一个半波、10 mm 初始挠度的加筋板位移云图 Fig. 5 The displacement nephogram |
|
图 6 具有一个半波、10 mm 初始挠度的加筋板应力云图 Fig. 6 The stress nephogram |
从图 5 和图 6 可看出,加筋板 X 方向中横剖面处变形位移最大,且位移沿 Y 方向具有一定递变规律。此剖面也是加筋板初始挠度最大幅值位置,应力分布具有代表性。因此,取加筋板中横剖面的节点,观察其应力分布情况,如图 7 所示。
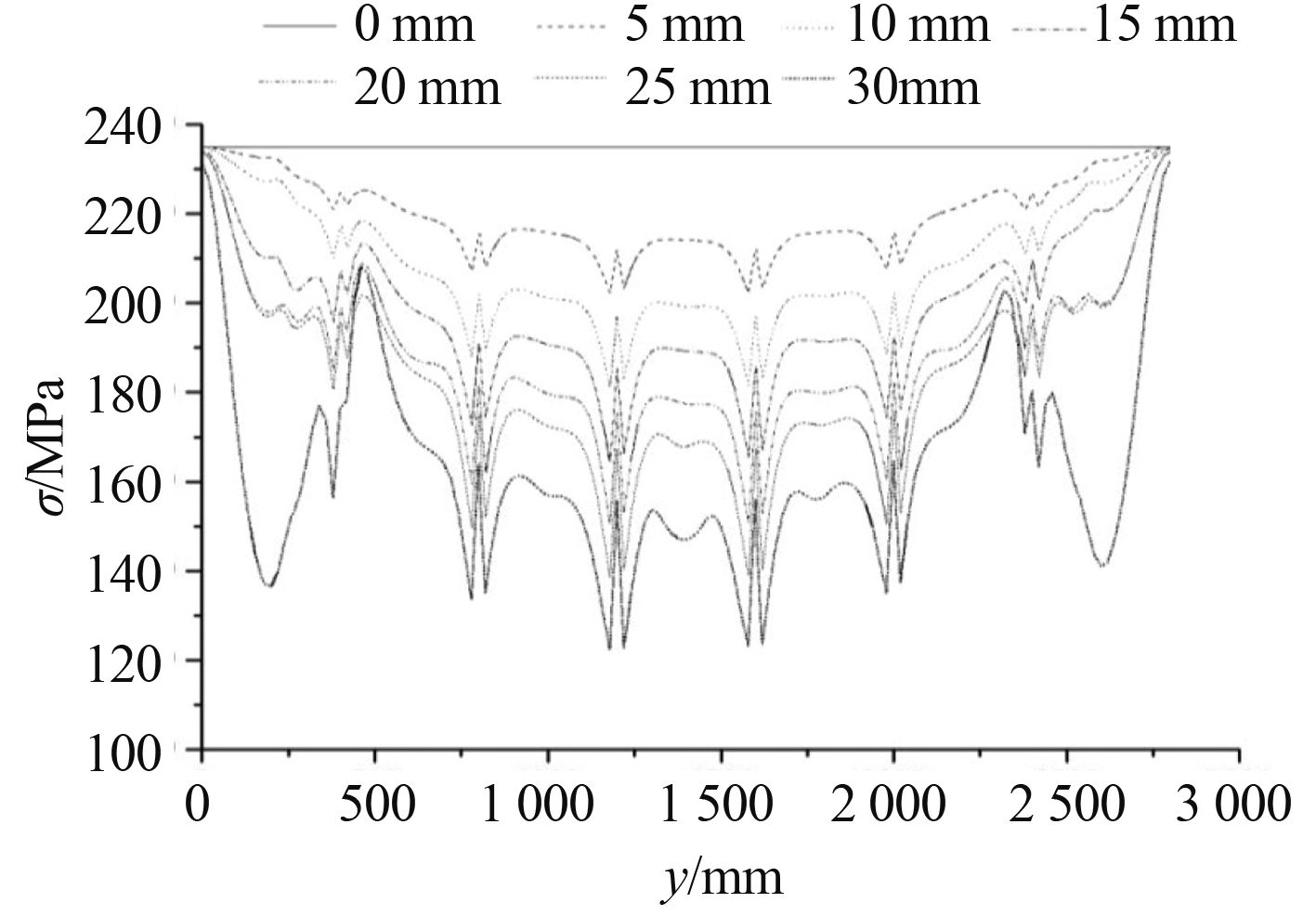
|
图 7 中间剖面应力分布 Fig. 7 The stress distribution in the mid-section |
图 7 显示了当初始挠度为一个半波时,不同挠度幅值下的加筋板中横剖面的应力分布情况。从图 7 中可以看出,与不含初始挠度加筋板的应力分布(图形比例导致分布规律显示为一条直线)相比,含初始挠度的加筋板中剖面的应力水平成曲线变化,应力分布成 U 字型。中间部分所受合应力较小,边界附近所受的合应力较大,应力整体变化规律是由中间向两边逐渐增大。随着初始挠度加筋板幅值增大,中横剖面处应力水平整体降低,且两侧边界处应力水平下降速率较大。
选取中横剖面中变形位移最大点,即含初始挠度加筋板达到极限承载力时的位移最大点,绘制该点的载荷位移曲线,以反映节点在加载过程中的位移变化,如图 8 所示。从图 8 可看出,随着初始挠度的增大,极限承载点降低,到达极限承载点的位移逐渐变大,曲线的变化率逐渐降低,趋于平缓。这说明对于初始挠度幅值较大的加筋板,在加载过程中更容易产生结构变形,更容易达到极限承载点。
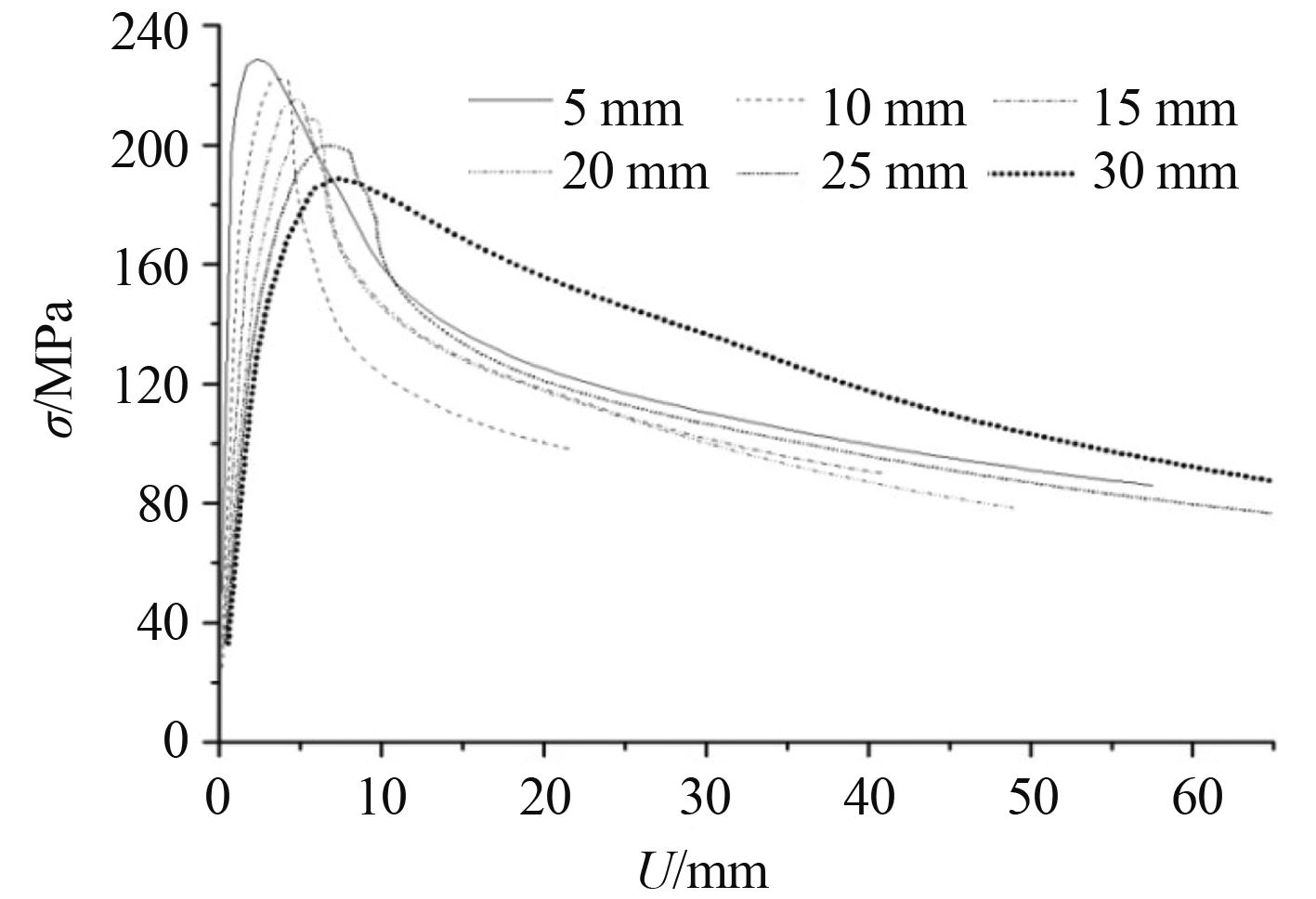
|
图 8 最大位移点载荷-位移曲线 Fig. 8 The load-displacement curve of the node with maximum displacement |
由计算可知,含初始挠度加筋板的极限载荷与不含初始挠度加筋板的极限载荷存在一定差距。后者与前者差值反映了初始挠度对加筋板极限载荷的影响,因此定义两者差值与后者的比值的绝对值为影响因子 λ(0 < λ < 1),即
| $\lambda = \displaystyle\frac{{{\text{差值}}}}{{{\text{正常加筋板极限载荷}}}}\text{。}$ | (4) |
参考相关文献对含有初始缺陷的加肋圆柱壳理论失稳压力修正系数研究的相关方法[10 – 11],可以首先初步假设影响因子与加筋板的长宽比、板厚、加强筋间距等几何尺寸有关,然后分析含初始挠度加筋板极限载荷与各主要尺寸参数的关系,计算模型是利用一节的有限元模型作为基础,进行相应的参数改变。下面将讨论含有幅值 10 mm、一个半波初始挠度的加筋板的影响因子。
3.1 加筋板长宽比与影响因子的关系根据相关对船体加筋板尺寸的统计数据[12],船体加筋板板长 a 与加强筋间距 s 的比值应该满足关系:2 ≤ a/s ≤ 6。因此,控制加强筋间距不变,通过改变加筋板的长度 a 来改变加筋板的长宽比 a/b。
已知加筋板计算模型加强筋间距 s = 400 mm,具有 6 根加强筋,加筋板宽度 b = 2 800 mm,所以加筋板长度取值范围为 800 ≤ a ≤ 2 400,均匀取值:800 mm,1 000 mm,1 200 mm,1 400 mm,1 600 mm,1 800 mm,2 000 mm,2 200 mm,2 400 mm。经过计算可以得到影响因子如表 2。可以将表 2 数据放在直角坐标系中显示,如图 9 所示。
|
|
表 2 λ 随加筋板长宽比 a/b 的变化 Tab.2 λ varies with a/b |
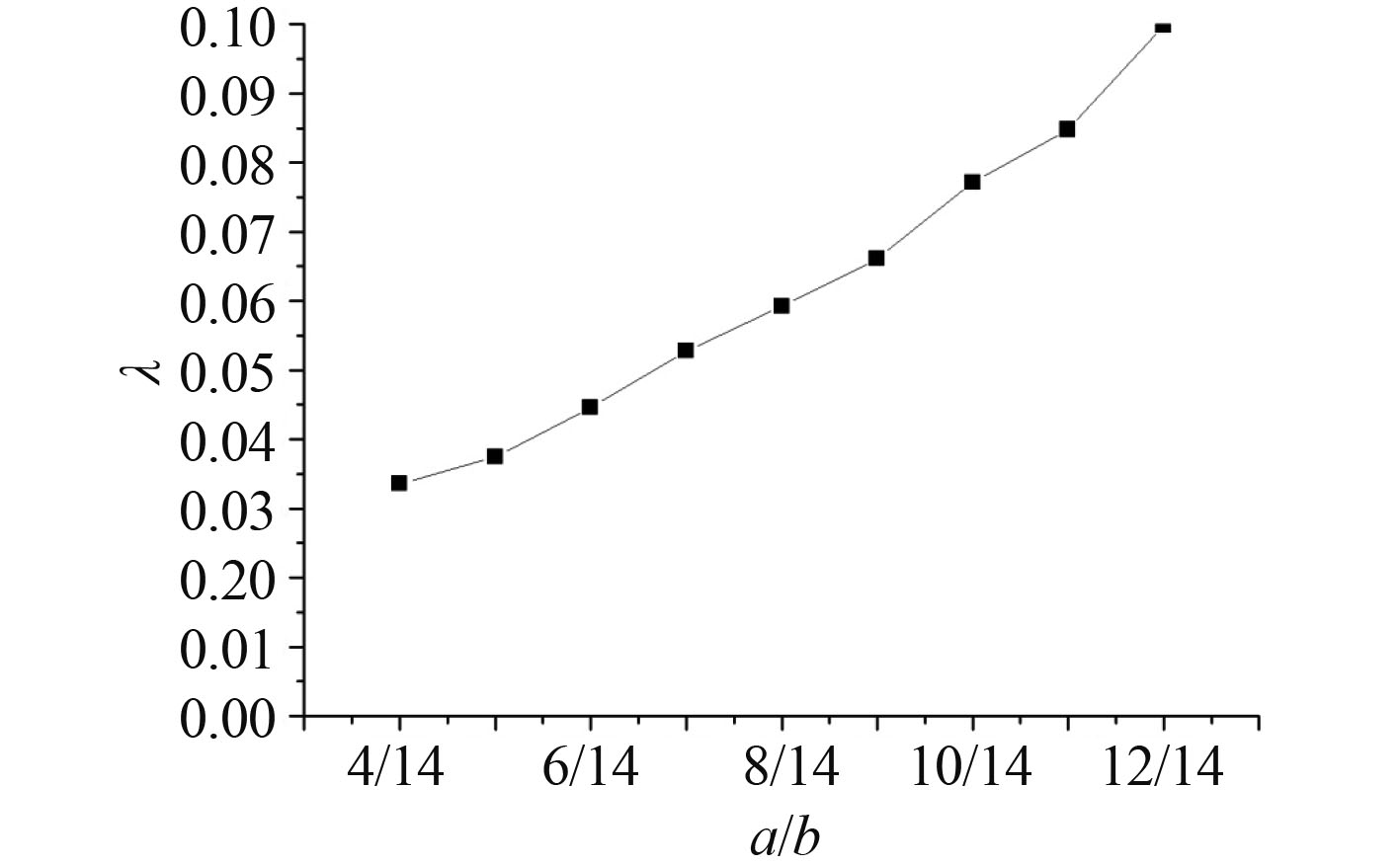
|
图 9 影响因子 λ 随加筋板长宽比 a/b 的变化规律 Fig. 9 λ varies with a/b |
从图 9 可看出,随着加筋板长宽比 a/b 增大,影响因子 λ 逐渐增大,且近似成二次函数规律变化。利用 Matlab 可以拟合二次函数表达式:
| $\lambda = 0.08738{\left( {a/b} \right)^2} + 0.01342\left( {a/b} \right) + 0.02253\text{。}$ | (5) |
拟合函数数据与原始数据最大误差在 0.5% 以内,符合工程要求,拟合函数符合实际情况。由变化规律可知,当加筋板长宽比a/b 增大时,加筋板初始挠度对其极限载荷影响增大。在满足钢板材料充分利用和结构强度的情况下,应尽量缩小加筋板的长宽比,以保持加筋板产生挠度变形时,其对加筋板极限承载力的影响较小。利用式(5)可以计算确定其最小值,在最小值附近选取合适的长宽比数值,从而将初始挠度的影响降到最低。
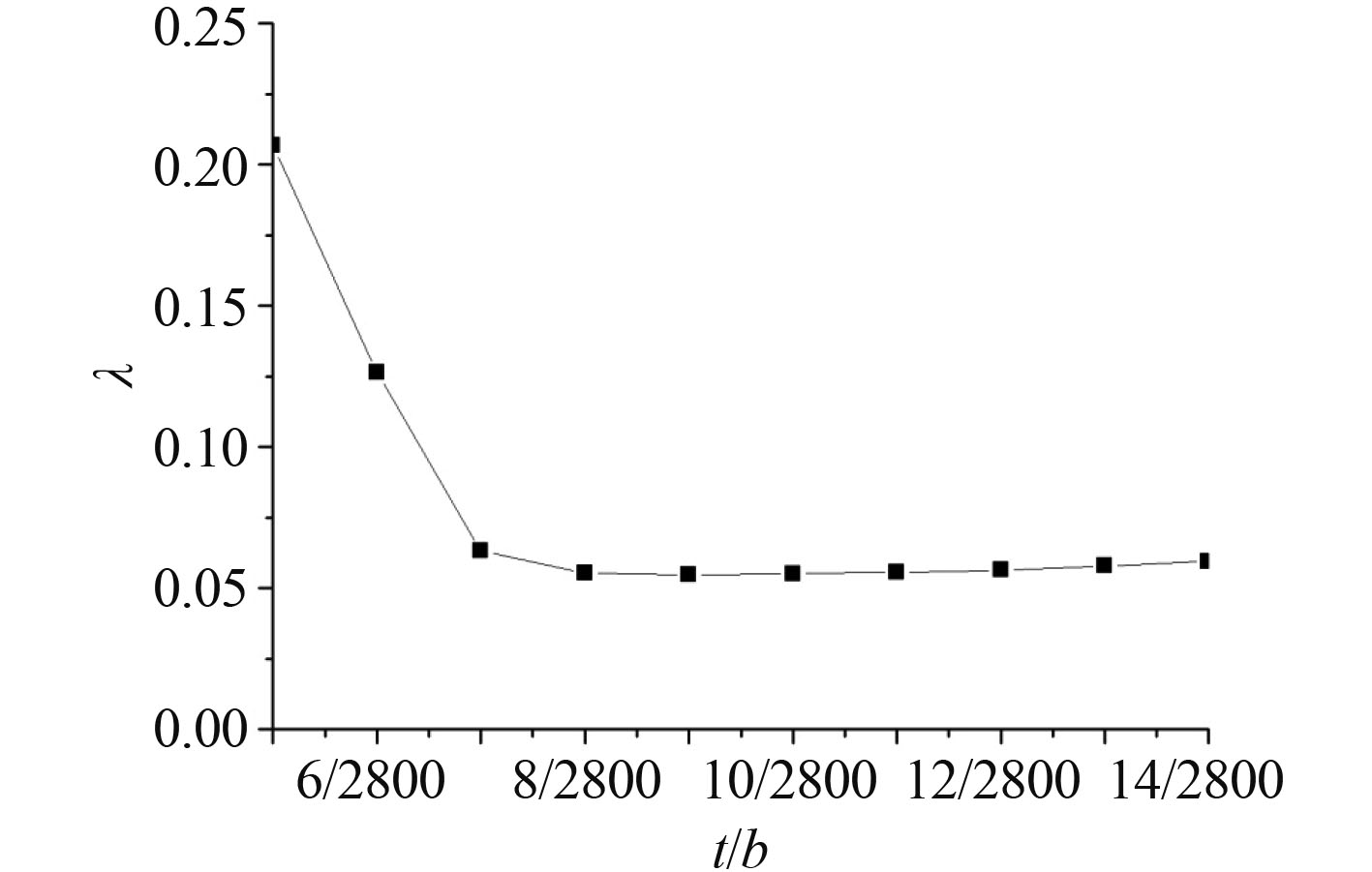
3.2 加筋板厚度与影响因子的关系船用加筋板的厚度一般在 8 mm 左右,对于特殊的大型船舶和军船,加筋板的厚度可能会超过 10 mm。因此,加筋板的厚度在 5 ~ 14 mm 之间均匀取值进行计算,计算结果见表 3。为了保持变量为无量纲因子,将加筋板厚度 t 与加筋板宽度 b 的比值作为因变量。将计算结果绘制成图,如图 10 所示。
|
|
表 3 λ 随 t/b 的变化规律 Tab.3 λ varies with t/b |
|
图 10 影响因子 λ 随 t/b 的变化规律 Fig. 10 λ varies with t/b |
从图 10 可看出,当板厚较小时,随着加筋板 t/b 增大,影响因子 λ 逐渐减小,且近似成一次函数规律变化;当板厚增大到一定厚度,影响因子开始逐渐增大,但是增加幅度非常小,可忽略不计。所以,在结构设计时,增加板厚不仅可以保证结构强度要求,而且可以减小初始挠度对加筋板极限承载力的影响。
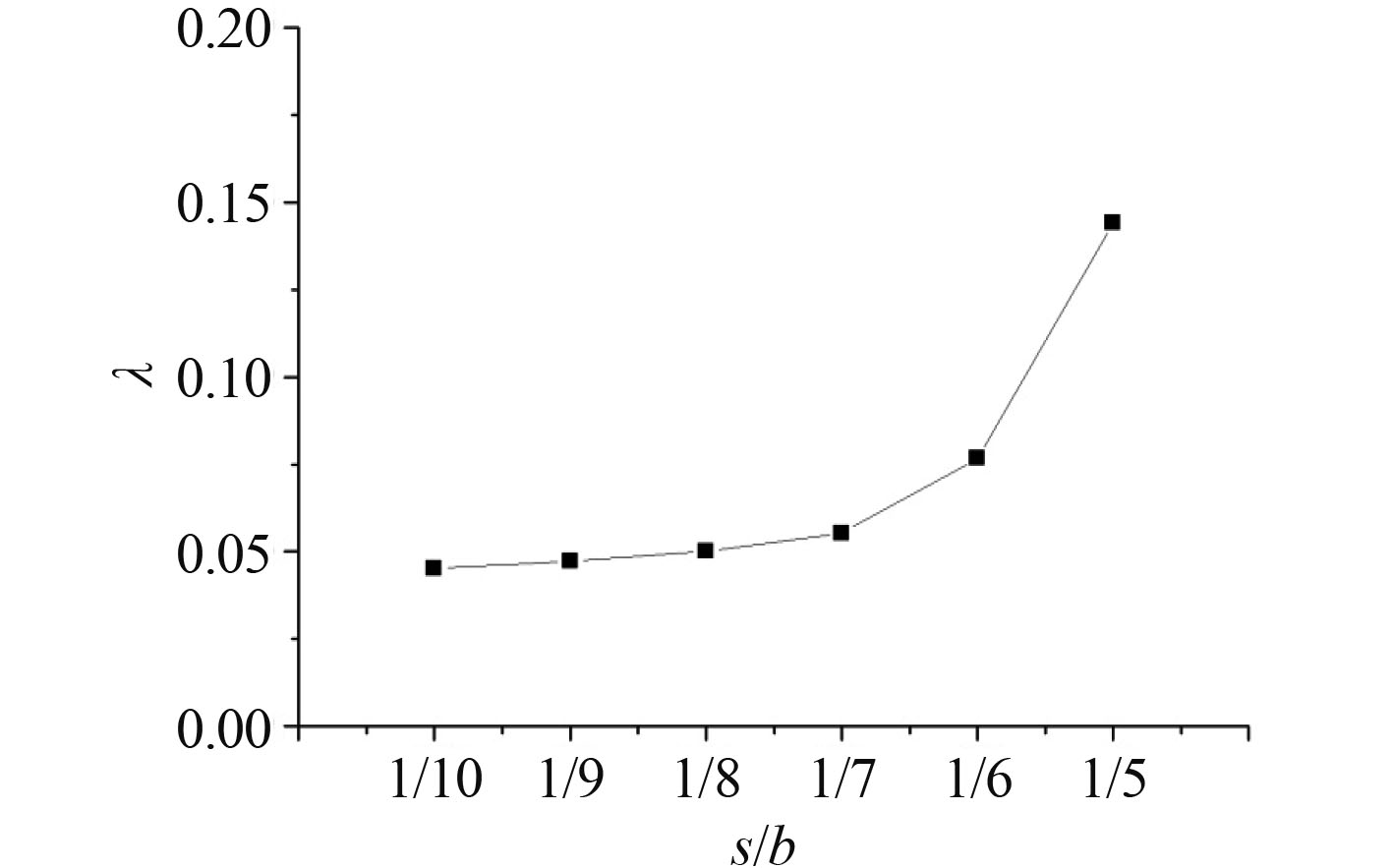
3.3 加强筋间距与影响因子的关系考虑加强筋间距对影响因子 λ 的影响,对加强筋间距的控制,主要是通过改变加强筋的数量来实现,即保持加筋板的宽度 b 保持不变。因此,加筋板数量取 4 ~ 9 进行计算,计算结果见表 4。为了保持变量为无量纲因子,将加强筋间距 s 与加筋板宽度 b 的比值作为因变量。将计算结果绘制成图,如图 11 所示。
|
|
表 4 λ 随 s/b 的变化规律 Tab.4 λ varies with s/b |
|
图 11 影响因子 λ 随 s/b 的变化规律 Fig. 11 λ varies with s/b |
从图 11 可看出,当加强筋间距较小时,影响因子随其变化不明显,近似为一条平行线;随着加强筋间距增大,影响因子 λ 逐渐增大,且增大速率也逐渐增大。即当加强筋数量较小时,影响因子数值较高,加筋板的极限承载力易受初始挠度影响。对于密加筋板(加强筋数量 n ≥ 6),影响因子可以保持较小的数值,且此时加强筋数量对影响因子变化影响较小。所以在结构设计时,应用密加筋板设计合适的加强筋数量,更有利于减小初始挠度对加筋板极限承载力的影响。
4 结 语本文利用非线性数值计算方法,对含有初始挠度的加筋板在轴向压力作用下的极限承载力进行了非线性分析,并得到以下结论:
1)初始挠度对加筋板的极限承载力影响较大,且随着初始挠度的幅值和半波数的增大,加筋板的极限承载能力会逐渐降低,在加筋板长期使用过程中,应尽量减小其挠度变形的幅值和半波数;
2)与不含有初始挠度的加筋板相比,当达到结构的极限承载力时,含初始挠度加筋板中横剖面内的应力分布成 U 字型,中间应力水平最低,依次向边界方向逐渐增大;
3)含初始挠度加筋板影响因子与加筋板的长宽比、板厚和加强筋间距有关;为了减小初始挠度对加筋板极限承载力的影响,可以在设计过程中,适当减小加筋板的长宽比和加强筋间距,增大板厚。
| [1] |
张涛, 刘土光, 赵耀, 等. 初始缺陷加筋板的屈曲与后屈曲分析[J]. 船舶力学, 2003, 7 (1): 79–83.
ZHANG Tao, LIU Tu-guang, ZHAO Yao, et al. Buckling and Postbuckling of Imperfect Stiffened Plates[J]. Journal of Ship Mechaniacs, 2003, 7 (1): 79–83. |
| [2] |
谭开忍, 李小平. 船体结构极限强度研究进展[J]. 船舶, 2006, 5 : 19–25.
TAN Kai-ren, LI Xiao-ping. Research Development of Ultimate Strength of Hull Structure[J]. Ship & Boat, 2006, 5 : 19–25. DOI: 10.3969/j.issn.1673-2278.2006.09.004 |
| [3] | UEDA Y, RASHED S M H, PAIK J K. Effective width of rectangular plates subjected to combined loads[J]. Journal of the Society of Naval Architects of Japan, 1986, 159 : 269–281. |
| [4] | Nonlinear finite element method models for ultimate strength analysis of steel stiffened-plate structures under combined biaxial compression and lateral pressure actions —Part I: Plate elements. |
| [5] |
万育龙, 朱旭光. 加筋板屈曲和极限强度有限元计算方法研究[J]. 船海工程, 2013, 42 (6): 17–21.
WAN Yu-long, ZHU Xu-guang. Studies on the Nonlinear Finite Element for Buckling and Ultimate Strength of Stiffened Panels[J]. Ship & Ocean Engineering, 2013, 42 (6): 17–21. |
| [6] |
罗刚, 吴国民, 汤刚, 等. 侧压对加筋板极限强度的影响分析[J]. 武汉理工大学学报(交通科学与工程版), 2014, 38 (6): 1400–1403.
LUO Gang, WU Guo-min, TANG Gang, et al. Analyse the Influence of Lateral Pressure on the Ultimate Strength of the Stiffen Plate[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2014, 38 (6): 1400–1403. |
| [7] |
单成巍. 循环载荷作用下船体结构的极限强度非线性有限元分析[D]. 武汉: 武汉理工大学, 2013.
SHAN Cheng-wei. Nonlinear finite element analysis for the ultimate strength of ship structures under cyclic loading[D]. Wuhan: Wuhan University of Technology, 2013. |
| [8] |
杨淼. 基于HCSR的加筋板格非线性屈曲研究[D]. 大连: 大连理工大学, 2011.
YANG Miao. Analysis of non-linear buckling strength of stiffened plate based on harmonized common structural rules[D]. Dalian: Dalian University of Technology, 2011. |
| [9] | TEIXEIRA A P, IVANOV L D, SOARES C G. Assessment of characteristic values of the ultimate strength of corroded steel plates with initial imperfections[J]. Engineering Structures, 2013, 56 : 517–527. DOI: 10.1016/j.engstruct.2013.05.002 |
| [10] | DONNELL L H. Effect of imperfection on buckling of thin cylinders under external pressure[J]. Journal of Applied Mechanics. Trans. ASME, 1956, 78. |
| [11] |
张二. 初始几何缺陷对锥-环-柱结合壳力学性能影响研究[D]. 武汉: 海军工程大学, 2015.
ZHANG Er. Research on the impact of initial imperfection to cone-toroid-cylinder combined shell’s mechanical property[D]. Wuhan: Naval University of Engineering, 2015. |
| [12] |
张晓丹, 杨平. 加筋板在轴向压力下的极限强度研究[J]. 武汉理工大学学报, 2011, 35 (2): 305–308.
ZHANG Xiao-dan, YANG Ping. Ultimate Strength of Stiffened Plate Under Axial Compression[J]. Journal of Wuhan University of Technology, 2011, 35 (2): 305–308. |
 2017, Vol. 39
2017, Vol. 39
