固体能够贮存剪切和压缩能量,所以会保持所有形式的波,即压缩波、弯曲波、剪切波和扭转波;流体只能贮存压缩能量,所以它仅能维持压缩波。紧邻固体表面的压力波动将在该表面上产生声辐射载荷。如果流体介质为空气,那么声辐射载荷通常非常之小;如果流体介质为液体,那么声辐射载荷可能变得很大,在流体和结构之间会建立起流固耦合。
求解流固耦合问题涉及到结构力学与流体力学两大力学体系,难度很大。在当今的国际学术界和工程界,这类流体-结构-声的耦合系统振动与声的研究,仍然十分活跃。
由于固体形状不规则、边界约束复杂,一般采用有限元对耦合方程进行求解。目前商用软件应用较为普遍,本文针对一个试验测量结果,采用 3 种软件进行计算,从而为工程应用提供一种参考。
1 水中模态法的一般表述板在液体中振动时,流体介质“阻挡”了弹性结构的振动,增加了结构的惯性质量,另外,结构振动的一部分能量泄漏到流体介质中转换成声能量,产生声辐射[1]。
1.1 结构在水下时振动和声的耦合矩形板在简支情况下无限介质中的自由振动与声[2],可以采用模态叠加的方法研究,稍微复杂的板、边界约束,可能尚且无法采用理论分析,但数值计算却可行有效。
对于静态流体介质中声波波动方程为:
| ${\nabla ^2}\varphi - \displaystyle\frac{1}{{c_0^2}}\displaystyle\frac{{{\partial ^2}\varphi }}{{\partial {t^2}}} = 0 ,$ | (1) |
其中: φ 为速度势函数;
v
在没有外力时,弹性结构体中密度为 ρ 的介质微元的运动方程为:
| $\rho \displaystyle\frac{{{\partial ^2}{\textbf{\emph{v}}}}}{{\partial {t^2}}} = (\lambda + \mu )\nabla (\nabla \cdot {\textbf{\emph{v}}}) + \mu {\nabla ^2}{\textbf{\emph{v}}},$ | (2) |
其中λ ,μ 为拉米(Lame)常数。任一向量可以表示成
| $\rho \displaystyle\frac{{{\partial ^2}\phi }}{{\partial {t^2}}} = (\lambda + 2\mu ){\nabla ^2}\phi ,$ | (3) |
| $\rho \displaystyle\frac{{{\partial ^2}\vec \psi }}{{\partial {t^2}}} = \mu {\nabla ^2}\vec \psi \text{。}$ | (4) |
这样成为了表示纵、横波传播的波动方程[3]。
弹性体与流体接触的界面上满足的条件是:切向应力等于 0;法向应力相等(连续);法向位移相等(连续)。对于有限长的板,存在的波是流固耦合作用下结构的固定(共振)频率下的辐射声。需要指出的是,在低于符合频率时也会辐射声。
在采用有限元办法来求解时,首先要形成结构的有限元方程,表达式为:
| ${\textbf{\emph{M}}}\{ \ddot \delta \} +{\textbf{\emph{C}}}\{ \dot \delta \} + {\textbf{\emph{K}}}\{ \delta \} =\left\{P\right\} ,$ | (5) |
其中: M , C 及 K 分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;{P}为介质声压形成的脉动压力。而在流体与物面上满足[4]:
| $\left\{ \begin{array}{l}\frac{1}{{{c^2}}}\displaystyle\frac{{{\partial ^2}\varphi }}{{\partial {t^2}}} - {\nabla ^2}\varphi = 0 ,\\\displaystyle\frac{{\partial \varphi }}{{\partial n}} = \dot \delta \cdot \mathord{\buildrel{\lower3pt\hbox{$$}} \over {{n}}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({\text{物面上}}),\\\mathop {\lim }\limits_{r \to \infty } r(\displaystyle\frac{{\partial \varphi }}{{\partial r}} + ik\varphi ) = 0 ,\end{array} \right.$ | (6) |
式中:
n
为物面法向矢量;δ 为物面振动位移;
Junger 分析了物体在水中的振动,指出如果一物体是前后缓慢地前后移动,流体几乎不可压缩,这里仅有局部前后区域的往复运动[2];如果运动加快,流体的压缩和稀疏就会变得明显。
根据这个说法,可以先求出附加质量,然后将附加质量附在结构上,再进行结构振动频率计算。
对于不可压缩无旋流体,速度势函数 φ 满足拉普拉斯方程为:
| $\Delta \varphi = 0 \text{。}$ | (7) |
对于一些规则物体的简单运动,可理论求解,复杂的可用数值求解。在获得附加质量后,将之均匀附在结构表面节点上,然后进行结构动力计算[5]。
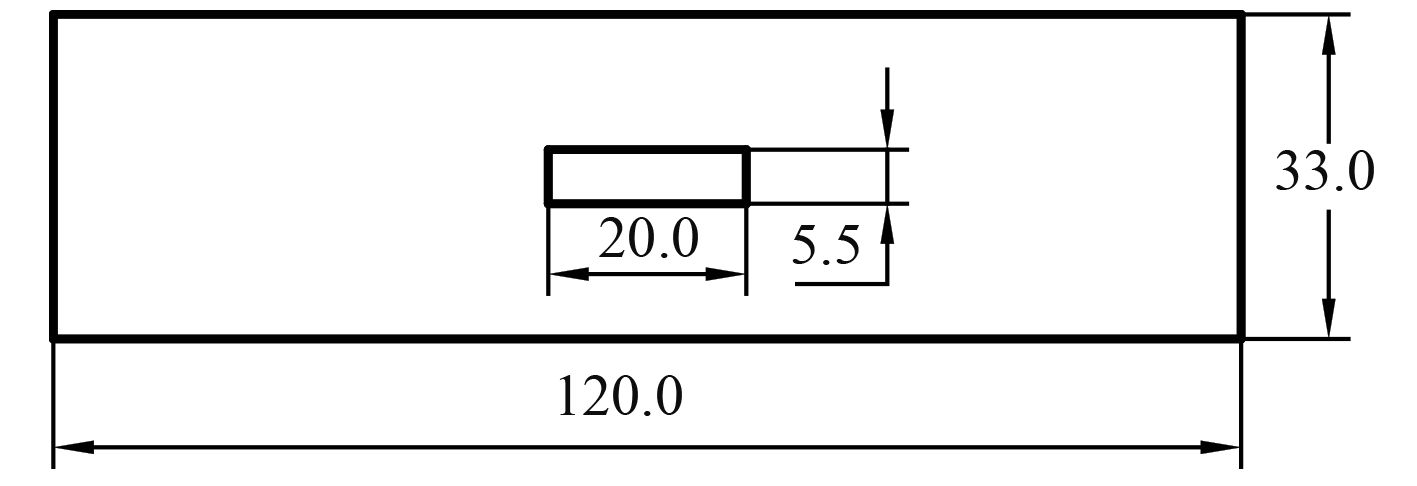
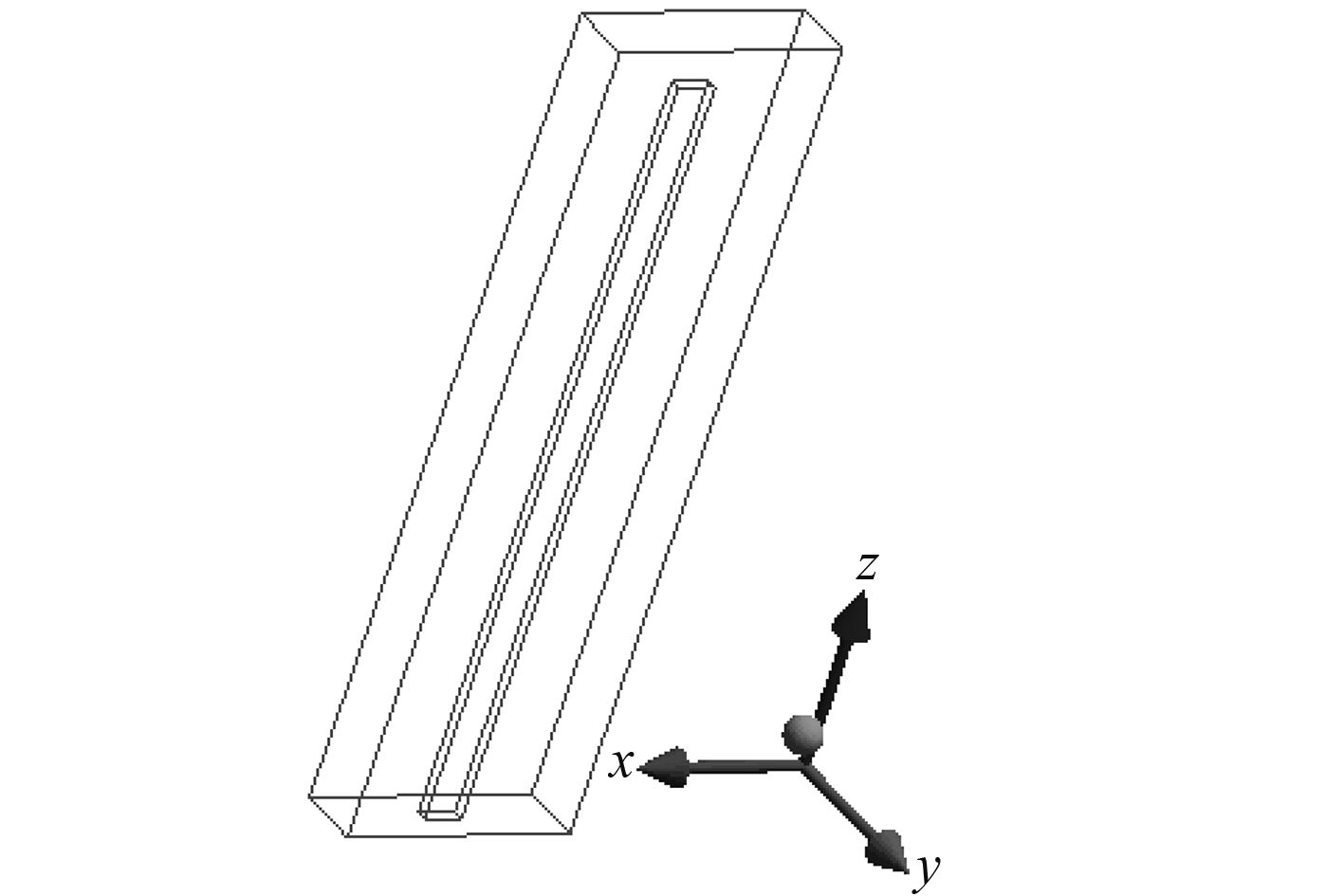
2 计算模型介绍薄板的尺寸:长度 20 mm,宽度 5.5 mm,高度 373 mm;水域:长度 120 mm,宽度 33 mm,高度 400 mm。底面尺寸如图 1 所示,模型示意图如 2 所示,其中底面在XOY 平面上,薄板在 XOY 平面的端面固定。
薄板参数:弹性模量为 210 GPa,密度为 7 850 kg/m3,泊松比为 0.3;水参数:密度为 998.2 kg/m3,声速为:1 460 m/s[6]。
|
图 1 模型底面尺寸 Fig. 1 The dimension of the model bottom |
|
图 2 模型示意图 Fig. 2 The sketch of the model |
对于上述计算模型,在不同软件中进行计算,为了与实验结果对比,只取在 YOZ 平面的振动。
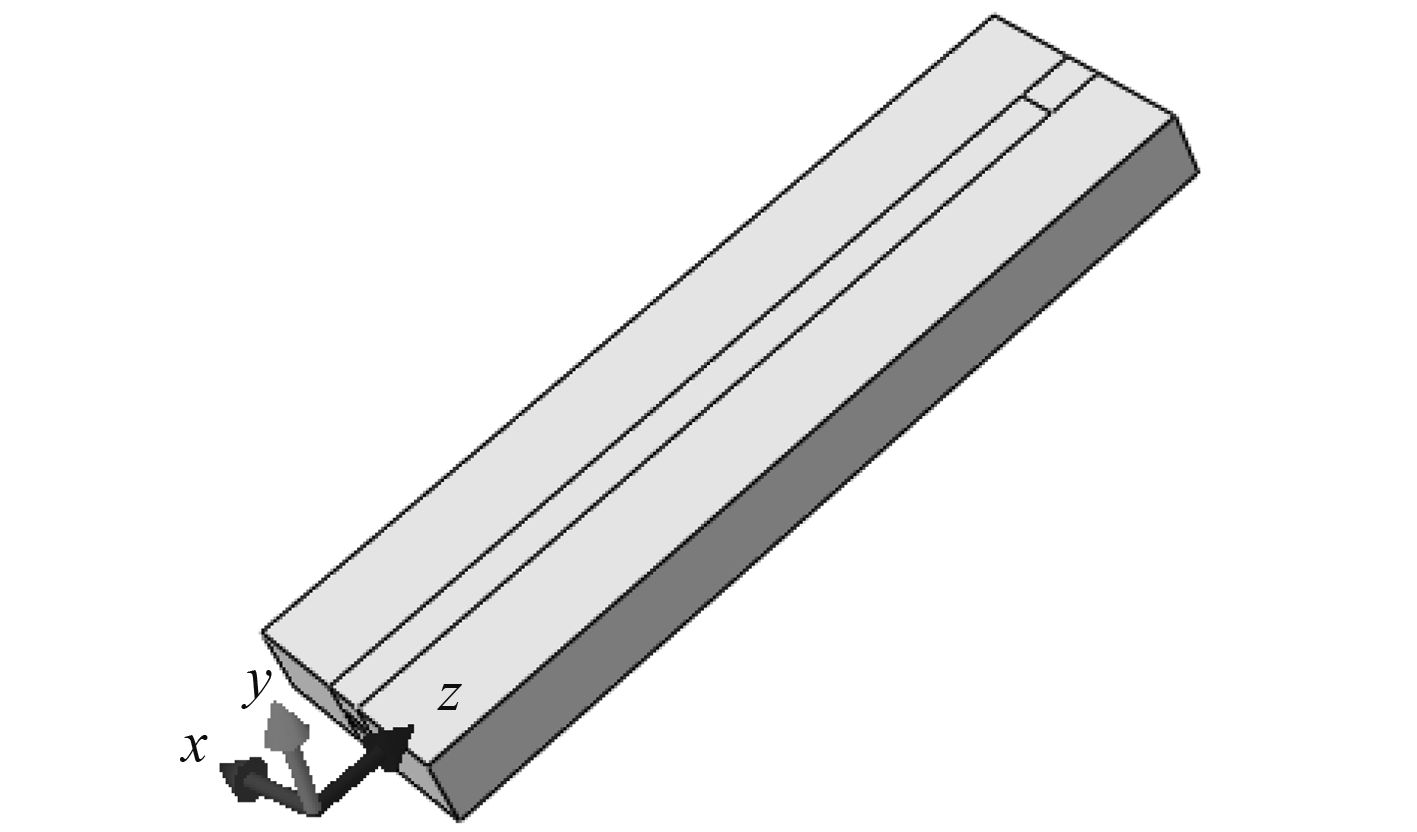
3.1 采用 Abaqus 计算1)在 Abaqus 建模。其中板采用草图直接拉伸形成。水域形成时,先用草图拉伸形成,再用剪切拉伸,并且将水体按图 3 所示剖分,以便将来将来绘制结构化网格。
|
图 3 水域模型 Fig. 3 The model of the water |
2)定义材料、截面属性。截面属性除了钢板、水的之外,还要有声学无限属性,并将截面属性分配到相应部件。
3)装配。将板和水体装配在一起,并且设置板与水接触的外表面,以及相应的水的外表面。
4)绘制网格。在各个部件中分别绘制网格。板网格采用 3D Stress 类型,几何阶次选择二阶。
5)水的网格类型选择 Acoustic,几何阶次选择二阶[7]。板的网格数为 240 个,水的网格数为 13 140 个。
6)设置分析步。过程类型为线性摄动,选择频率分析类型。输出变量选择应力、位移/速度/加速度、声。
7)进入 Interaction 模块。创建约束,约束类型为 Tie,分别将板的外表面与水的外面表设为主表面和从表面,共设 5 对。形成声阻抗面,表面为水的外表面,定义为无反射面,无反射类型为 Planar。
8)进入 Load 模块,设置边界条件。在板的底端设置固定支撑。
9)结果处理。运算结束后,频率为 27.249、170.85、479.41,其中一阶 Von Mises 应力云图如图 4 所示。

|
图 4 采用 Abaqus 计算的板的一阶振动 Fig. 4 The 1st vibration of the plate by Abaqus |
1)安装 Ansys Workbench 的插件 ACT_Acoustics.wbex。
2)建立 Modal 分析项目。
3)建立流体单元的实体模型,其中薄板与水是分开的部件。
4)标记流固耦合界面。薄板与水接触的面是除底面之外的 5 个面,因此接触面选此 5 个面,目标物体选为水,接触面是与薄板接触的 5 个面。
5)网格划分。由于网格难以使用结构化网格,所以这里采用四面体网格划分。
6)计算设置。不设置阻尼,求解类型为程序控制;将薄板在 XOY 平面上的端面设为固定支撑;采用工具中的根据接触自动生成 FSI(Fluid-solid interaction)条件。设置水域为声学体。
7)提交计算并查看结果。前三阶 Y 方面的固有频率为 27.912 Hz,175.04 Hz,491.66Hz。其中二阶总变形图如 图 5 所示。

|
图 5 采用 Ansys 计算的板的二阶振动 Fig. 5 The 2nd vibration of the plate by Ansys |
1)板在水中运动时的附加质量。板在水中运动时会产生附加质量,用 CFD 软件 Ansys Fluent,运用其中的动态网格技术,基于粘性流理论的 RANS 方程求解[9],计算模型中的薄板在 YOZ 平面的附加质量,计算结果为 0.126 6 kg。
2)网格与求解设置。进入 Ansys Workbench 的 Modal 模块,在几何中,将附加质量均匀加在薄板的 6 个面上,六面体网格个数为 5 610。在 XOY 平面内的薄板的端面约束设为固定支撑。
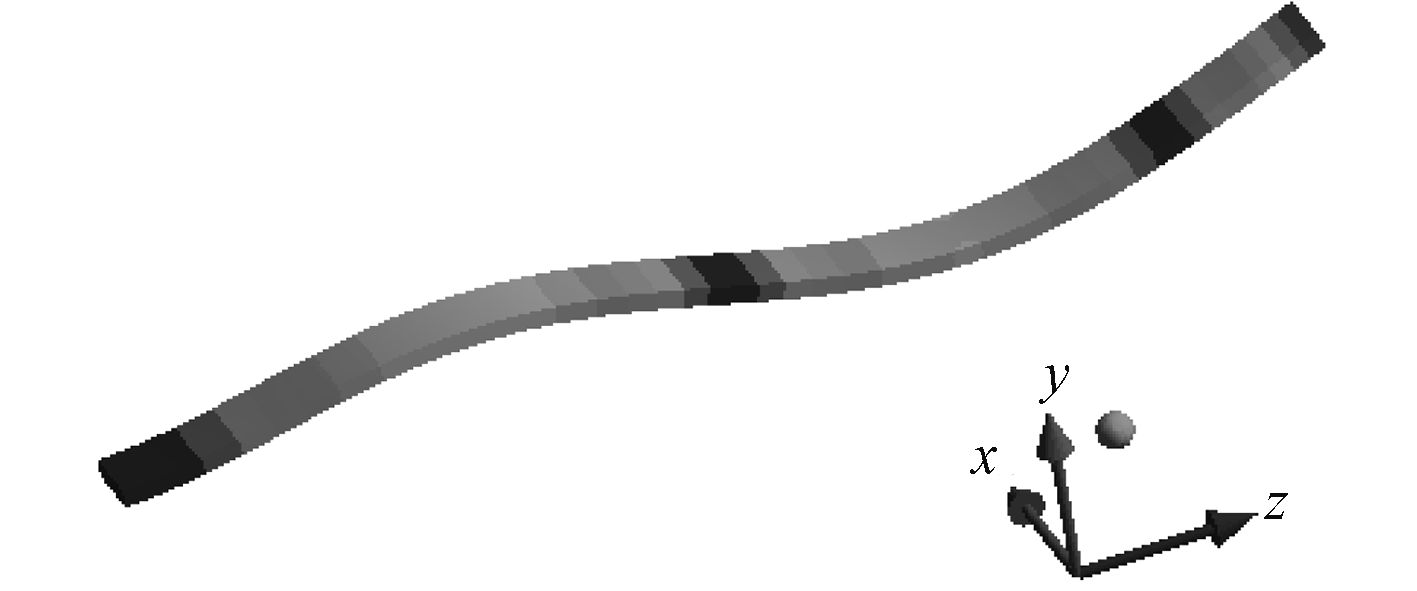
3)提交计算并查看结果。前三阶Y方面的固有频率为 28.013 Hz,175.35 Hz,490.16Hz。其中三阶总变形如图 6 所示。
|
图 6 采用附加质量法计算的三阶振型图 Fig. 6 The 3rd vibration of the plate by added mass |
1)网格绘制。在 UG NX 中建模,导入 ICEM 中,在 ICEM 中绘制结构化网格,其中板的网格个数为 4 998,水的网格数为 116 552。
2)网格导入。导入声学网格,导入时选择将网格分成多块,导入后水域的面包络网格自动形成。
3)设置材料并赋予相应的网格。
4)单元组。包括设置板底部端面,水域外表面(用来设置 AML 层,实现无反射边界条件的模拟),结构的外表面(共 5 个面),与结构外表面接触的水的表面。
5)建立约束。在板的底端建立固定支撑。
6)建立耦合面。将单元组中的结构外表面与水域外表面定义成 Coupling Surface。
7)插入力源。插入 Load Function Set,力的位置顶端,方向为 Y 方向,如图 7 所示。

|
图 7 模型约束与受力示意图 Fig. 7 The sketch of the restraint and the applied force |
8)求解。插入 Direct Vibro-acoustic Reponse analysis case,采用此模块直接进行声振耦合计算[8]。频率范围设为 15~600 Hz,步长为 5 Hz。
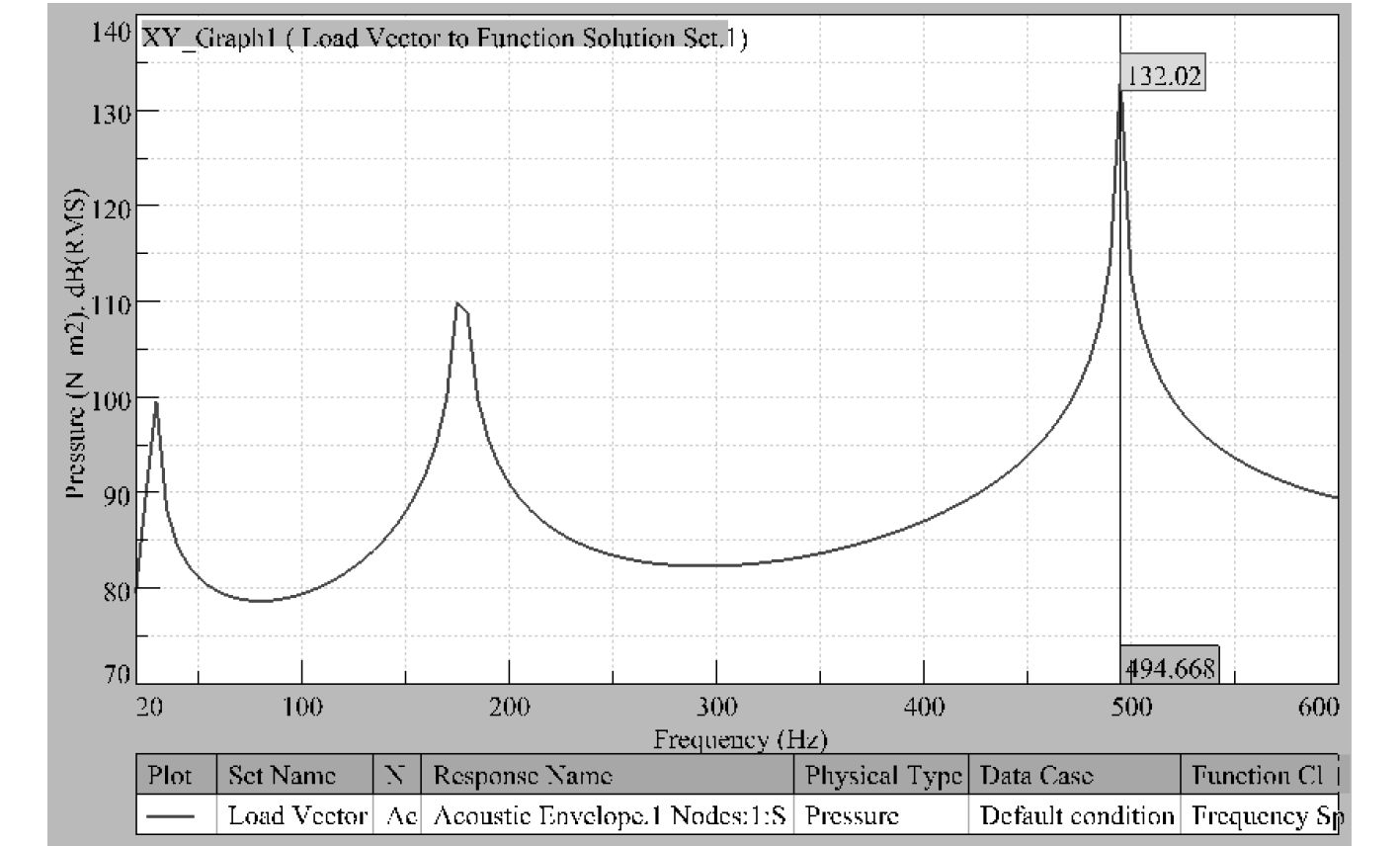
9)结果查看。插入 Vector to Function Conversion Case,输出点采用声学网格上的任意一点,格式采用 dB(RMS)[8]。其中频率分别为 29.977,175.911,494.668。
|
图 8 Virtual Lab 结果输出 Fig. 8 The result by Virtual Lab |
将上述计算结果集中到表 1 中,可以看出,对于 1阶、2 阶结果,各软件结果相差不大,对于第 3 阶,最大相差 4.6%
由于数值模拟中是理想的状态:水域无穷大、底部完全固定支撑,计算原理、耦合处理、网格类型、网格个数、数值计算中自身的误差,这些对计算结果都有一些影响。
|
|
表 1 数值计算的结果 Tab.1 The result by the numerical calculation |
利用多个软件对同一物理模型进行了数值计算,根据上面的分析可以得出以下结论:
1)计算的整体思路基本一致,除了常规的属性设置外,都要设置耦合面,以及水体外表面的无反射边界条件。
2)几种计算软件的计算结果比较接近,满足工程使用需要。
3)在数值计算时,水域外表而是无限元;但实验中水在一个箱体里,这个箱体内的混响场对声固耦合理应有一定影响。在这种情况下,两者结果接近,很有可能说明频率计算准确。
4)采用附加质量的思路是没考虑声固耦合,这也说明在 500 Hz 以下时还算是低频,物体仍算是“缓慢”地前后移动,流体几乎不可压缩。
5)采用此例不是在比较各软件,因为这个计算内容只是其强大功能的一方面,只是为从事相关研究的人员提供一些计算方法。
| [1] | 赵玫. 结构振动噪声源[D]. 上海: 上海交通大学. 2002年. |
| [2] | MIGUEL C, JUNGER, DAVID F. Sound, structures, and their interaction migual, second edition, 1976. |
| [3] | 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京: 南京大学出版社. 2001. |
| [4] | 何凌. 船舶螺旋桨涡发放噪声和唱音研究[D]. 无锡: 中国船舶科学研究中心, 2001. |
| [5] |
郑治国, 孙大成, 刘宪亮. 用湿模态法进行流固耦合分析时一个问题的探讨[J]. 华北水利水电学院学报, 1998. 19(2): 22–25.
ZHENG Zhi-guo, SUN Da-cheng, LIU Xian-liang. A Study on the fluid-structure interaction with wet model[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 1998. 19(2): 22–25. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hbsl802.005&dbname=CJFD&dbcode=CJFQ |
| [6] |
杨吉新, 张可, 党慧慧. 基于ANSYS的流固耦合动力分析方法[J]. 船海工程, 2008, 37 (6): 86–89.
YANG Ji-xin, ZHANG Ke, DANG Hui-hui. Dynamic Analysis Method for Fluid-Structure Interaction Based on ANSYS[J]. SHIP & OCEAN EN GINEERING, 2008, 37 (6): 86–89. |
| [7] |
缪旭弘, 钱德进, 姚熊亮, 等. 基于ABAQUS声固耦合法的水下结构声辐射研究[J]. 船舶力学, 2009, 13(2): 319–324.
MIAO Xu-hong, QIAN De-jin, YAO Xiong-liang, et al. Sound radiation of underwater structure based on coupled acoustic-structural analysis with ABAQUS[J]. Journal of Ship Mechanics, 2009, 13(2): 319–324. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=cblx200902022&dbname=CJFD&dbcode=CJFQ |
| [8] | 詹福良, 徐俊伟. Virtual. Lab Acoustics声学仿真计算从入门到精通[M]. 西安: 西北工业大学出版社, 2013. |
 2017, Vol. 39
2017, Vol. 39
