随着水下航行器、机器人技术及水下定位与导航技术越来越成熟,运用小平台进行近距离沉底及掩埋目标的探测逐渐受到重视。常规基阵由于体积、波束、旁瓣等的限制,不利于小平台、近距离进行沉底及掩埋目标的探测。而基于非线性声学原理的参量发射阵因其具有在小尺寸基阵下实现低频、窄波束、近乎无旁瓣、易获得较大的信号带宽等优点,有利于提高信混比、方位分辨力等,而且有高、低 2 个频段的回波数据,可以丰富探测结果的对比,非常适合运用在水下小平台上进行沉底及掩埋目标的近距离探测等。
本文依据参量发射阵理论Westervelt线源参量阵[1]、Berktay宽带参量阵[2 –3],结合参量阵的优势及截断参量阵的特点,设计一种应用于海底小目标近距离探测的系统,并开展系列试验——测试该系统在近距离的特性、利用该系统探测沉底及掩埋目标。结果表明,该参量阵系统能够实现近底小目标探测,在现有条件下所做的探索工作将对实际工程的实现具有一定的指导意义。
1 参量发射阵理论基础波与波的非线性作用,在互作用区内产生非线性的二次量,从而在此区域中形成与原波频率不同的差频波与和频波[4]。声学参量阵就是利用声波在介质中传播的非线性特性,使 2 个沿同一方向传播的高频初始波
Westervelt提出的参量阵是一种线源参量阵,认为源是分布在一条直线上,在理论推导过程中,其假设介质是理想流体、小振幅传播、介质对声波的衰减只引入衰减因子来表征,并且非线性声学方程只取到二级近似,得到:
| ${p_s} = \frac{{{\rho _0}}}{{4\pi }}\int_V {\frac{1}{r}\frac{\partial }{{\partial t}}\left[{q(t-\frac{r}{{{c_0}}})} \right]{\rm{d}}V}\text{,}$ | (1) |
式中:
p
s
为和、差频声压;
c
0 为介质中的声速;
| $q = \frac{1}{{{\rho _0}c_0^2}}\frac{\partial }{{\partial t}}\left( {{\rho _0}{u^2} + \frac{B}{{2A}}\frac{{{p^2}}}{{{\rho _0}c_0^2}}} \right)\text{,}$ | (2) |
式中: u 为质点振速; B/A 为非线性参数。由于和频波受到的吸收大,超过一定的距离后只有差频波存在,这里只考查二阶场中的差频波,则Westervelt远场解为:
| ${p_d} = \frac{{\omega _d^2{p_1}{p_2}\beta S}}{{8\pi {\rho _0}c_0^4r}}\frac{1}{{\sqrt {\alpha _0^2 + {k_d}{{\sin }^4}\frac{\theta }{2}} }}\text{,}$ | (3) |
式中:
p
1,
p
2 为两原频波振幅;
Berktay在Westervelt参量阵理论基础上提出包络自解调宽带参量阵,即使用幅度调制的原频信号来产生差频信号,其远场解为:
| ${p_d}(t) = \frac{{p_0^2\beta S}}{{16\pi {\rho _0}c_0^4{\alpha _0}r}}\frac{{{\partial ^2}}}{{\partial {t^2}}}\left[{{E^2}(t-\frac{r}{{{c_0}}})} \right]\text{。}$ | (4) |
式中
由式(4)可知:自解调得到的差频声压与包络函数幅度平方的2阶导数成正比[2]。设计复杂参量阵信号源波形通常参考该远场结论,并根据实际情况进行适当的补偿。
1.2 参量发射阵特性[2, 3]圆形活塞换能器经常出现在各种声呐系统中,比较适合搭载在UUV等水下小平台上,这里以单个圆形活塞辐射器辐射产生的参量阵声场为基础,同样只考查其声场中差频波的特性。
1.2.1 差频波声轴声压分布对于圆形活塞换能器辐射产生的参量阵声场,根据式(1)可知,其差频波声轴声压随距离变化的趋势:在离换能器很近的距离内,差频波随原波的变化较剧烈,但由于虚拟活塞换能器的能量积累效应,差频声压总体是增大的;随着距离的增加,当原波稳定后,差频波相应也稳定下来,在
在水介质中,对差频波来说,当原波的指向性非常尖锐,Berktay宽带参量阵理论的指向性函数与Westervelt线源参量阵理论的指向性函数表示上一致[7],可表示为:
| $D(\theta ) \approx \frac{1}{{\sqrt {1 + {{[(2{k_d}{{\sin }^2}\frac{\theta }{2})/2{\alpha _0}]}^2}} }}\frac{{2{J_1}({k_d}a\sin \theta )}}{{{k_d}a\sin \theta }}\text{。}$ | (5) |
为更好地理解参量阵的优势,这里先进行数值仿真以对比:假设都用相同尺寸(直径均为 200 mm)的圆形活塞换能器来辐射声波,原波(载波)频率为 200 kHz,差频波频率为 20 kHz,常规方式产生 200 kHz、20 kHz声波与参量阵方式产生 20 kHz差频波的声压指向性图如图 1所示。

|
图 1 常规阵与参量阵指向性对比 Fig. 1 Contrast of the directivity of regular array and parametric array |
从图 1中不难发现,常规阵辐射 200 kHz声波的指向性比辐射 20 kHz声波的指向性要尖锐很多,符合频率越高、指向性越好的规律,但频率越高旁瓣也增加。而利用参量阵方式产生 20 kHz差频波的指向性比常规方式好,而且近乎没有旁瓣。如果用常规阵形成如此尖锐的指向性,则阵的等效线度就很大,而且避免不了旁瓣的影响。显然,参量阵具有可在小孔径换能器下实现低频、高指向性、近乎无旁瓣波束的优势。
2 参量阵试验探测系统设计在利用小平台近距离探测海底目标时,参量阵所处的空间有限、原波声场被底界面截断,由于参量阵产生的声场由虚源存在的空间决定,所以有必要先考查截断参量阵的特性。
2.1 截断参量阵[8]如果一个活塞型换能器在瑞利距离
| ${p_d}' \approx \frac{{\beta p_0^2S{\omega ^2}}}{{4\pi {\rho _0}c_0^4}}\ln \frac{R}{{R-{R_1}}} \times {e^{j({\omega _d}t-kR)}}\text{,}$ | (6) |
从式(3)可知,远场轴向差频声压与频率的关系正比于
| $\left| {{p_d}'} \right| \propto \omega _d^2\ln \frac{R}{{R-{R_1}}}\text{,}$ | (7) |
按照远场理论,在差频波频率一定时,声压反比于原波中心处(或载波)频率的平方;但由上式来看,当
| $\left| {{p_d}'} \right| \propto \frac{{\omega _d^2{R_1}}}{R} \propto \omega _d^2{\omega _0}\text{。}$ | (8) |
由此可知,参量阵被截断的情况下,在可能的范围内,适当提高原波频率是有好处的,这一结论也已在实验中得到证实[9]。
2.2 试验探测系统设计探测沉底及浅掩埋的目标,为了一定的穿透能力,声呐探测信号的频率通常在 40 kHz以内,对于参量阵声呐系统来说,即差频的频率范围为 40 kHz以内;但是,影响参量阵应用的最主要因素是差频的转化效率,而差频的转化效率与频率下移比(原频频率与差频频率的比)成反比,根据截断参量阵的分析可知,近底探测时适当的提高原频频率对形成差频有利,所以差频的频率也不应该选择过低。综合考虑底质吸收、目标散射特征、差频波束分辨率等,本文将差频的频率范围选择在 5~35 kHz,主要频段为10~30 kHz;而原频的频率主要选择在 100~300 kHz。
本文采用的参量阵信号源波形是基于Berktay包络自解调理论的,为了探究参量阵应用于近底探测系统的可行性,根据现有条件,选择一个 180~220 kHz范围内阻抗平坦直径为 20 cm的宽带换能器,中心频率处(200 kHz)的波束宽度

|
图 2 试验采用的换能器 Fig. 2 The used transducer in experiments |
|
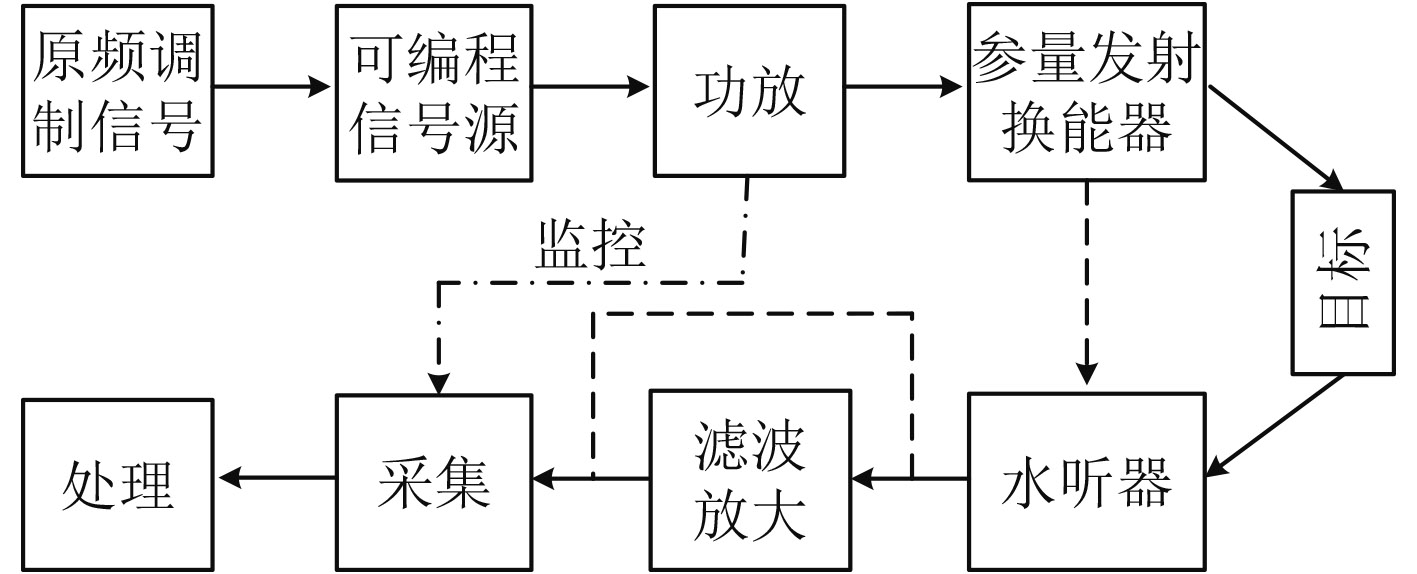
图 3 试验测试系统示意图 Fig. 3 Schematic diagram of the test system |
其中,原频调制信号是通过原频与包络信号相乘获得的,该方式可以节约换能器带宽、减少差频信号失真等,解调得到的差频信号频率为包络信号频率的 2 倍,而包络信号可以采用频率可控的单频脉冲信号、调频脉冲信号等[10]。
采用单频调制信号不但简化信号源设计,但是反映的目标散射特性相对单一。采用调频调制信号,丰富的差频频率成分可以获取更多的目标信息,低频成分利于穿透底质,同时宽带对抗起伏和混响有利,且可以进行脉冲压缩,提高距离分辨力。但是也相应地增加了信号源设计和信号接收处理的复杂度[10]。
3 实 验由于参量阵是声场的次级效应,有很多不确定的因素,加上用于近距离探测,对于具体的参量阵探测系统,差频的特性(尤其在参量阵近场)还是需要通过实验来研究的。
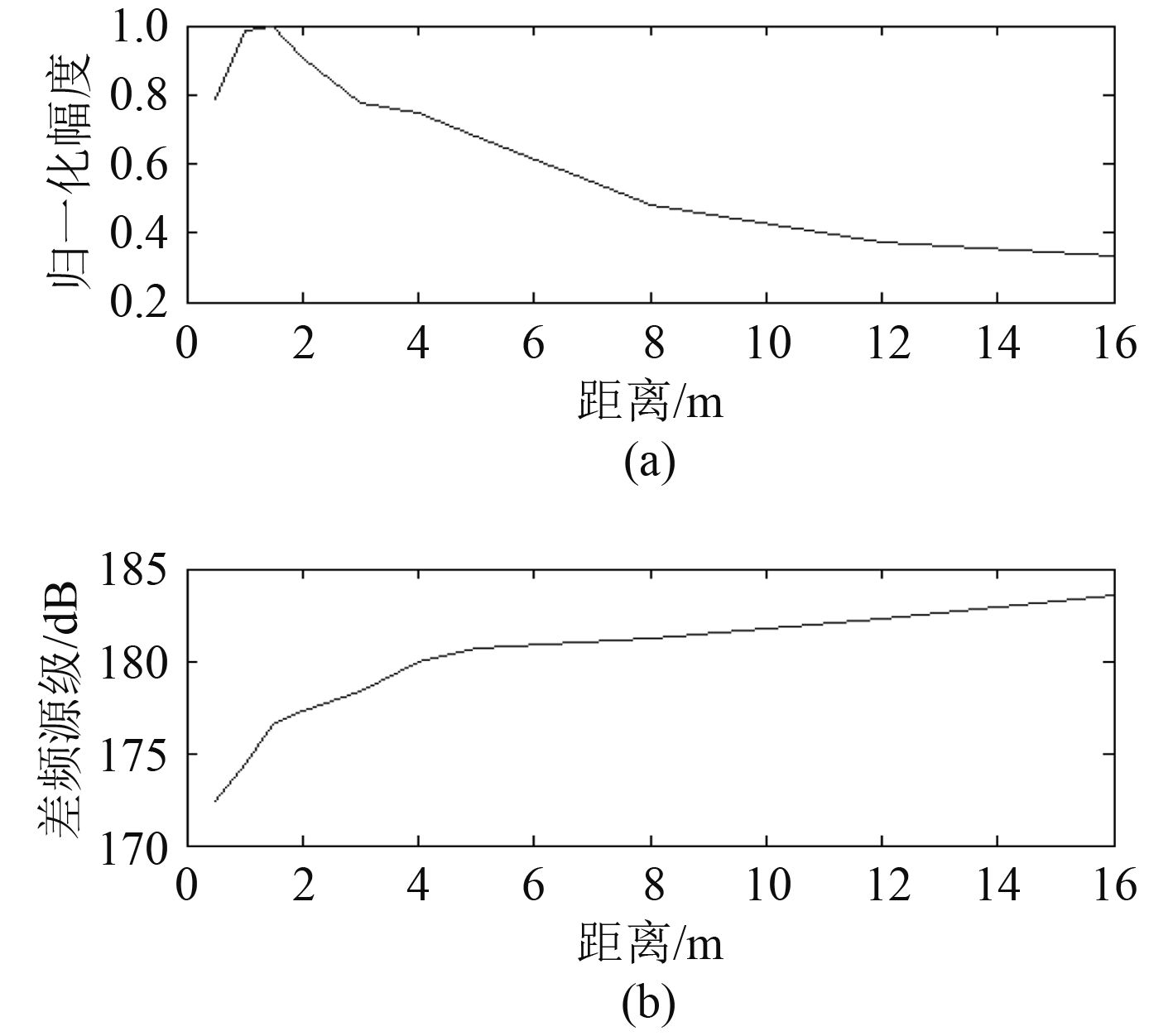
3.1 试验系统的差频特性测试试验在消声水池中进行,试验系统的原波声源级为 224 dB,双平衡调制获得频率为 20 kHz的差频波的声轴声压分布如图 4所示,图 4(a) 为差频声轴声压随距离的分布情况(这里幅度直接用水听器输出的电压幅值归一化后来表示,不影响声轴声压分布的趋势),图 4(b) 为归算到 1 m处的差频源级随距离的变化曲线。
|
图 4 差频波声轴声压分布 Fig. 4 Acoustic axis pressure distribution of difference frequency |
由图 4可知,在换能器原频的瑞利距离内,差频的声压变化比较大,在 1~1.5 m范围其值较大;而在换能器原频的瑞利距离之外,差频的声压变化较小,差频积累效应逐渐减弱,差频源级也逐渐趋于稳定。
指向性通常是从远场来考查的,由于系统只用在近距离探测,在有限的距离内,该测试系统的指向性用波束宽度来考查(近场可能测不准)。原波声源级仍为 224 dB,双平衡调制获得频率为 20 kHz的差频波的指向性如图 5所示,图 5(a) 为 16 m处测得的指向性图,图 5(b) 为差频波束宽度随距离的变化曲线。

|
图 5 差频波声压指向性 Fig. 5 Sound pressure directivity of difference frequency |
由图 5可知,该测试系统获得的差频波的波束宽度在换能器原频瑞利距离内,随距离增加逐渐减小;超过瑞利距离后,波束宽度基本稳定在 3.6°。总体看,差频波束宽度总体都是比较小的。
另外,在载波频率(这里为 200 kHz)一定时,实验测得的差频波频率为 10 kHz,30 kHz的波束宽度变化趋势基本与图5一致,且与差频波频率为 20 kHz的波束宽度相差不大。
3.2 试验系统的探测能力测试为初步论证在有限空间环境中开展参量阵近距离探测掩埋目标实验的可行性,也为了解目前条件下所搭建的测试系统产生的差频信号穿透底质的能力,先在室内小水箱进行了参量阵掩埋目标的探测实验。
实验在电解水箱(盐水)中进行,如图 6所示。细沙,厚度为 30 cm,沙是往盛水的水箱中加的、近似为自沉方式,使沙层较均匀。掩埋圆盘目标(直径 15 cm、厚 2 cm)距水-沙界面 20 cm、距底 8 cm,换能器距水-沙界面 45 cm(拟收发合置)。功放采用 L 2、水听器B&K8104 接收,该实验接收回波时,未加滤波、放大电路,主要想避免接收系统的干扰和方便原频及差频回波的同时接收(理论上,原频、差频回波应该分别滤波、放大接收)。

|
图 6 实验环境及换能器布放 Fig. 6 The experiment environment and transducer’s placement |
由于水箱的空间有限(1 m × 0.7 m × 1 m),为了一定的穿透深度和较高的距离分辨力,参量阵获得频率为 5~35 kHz的宽带差频信号,脉宽为 1 ms,距离分辨率理论上可达 2.5 cm。
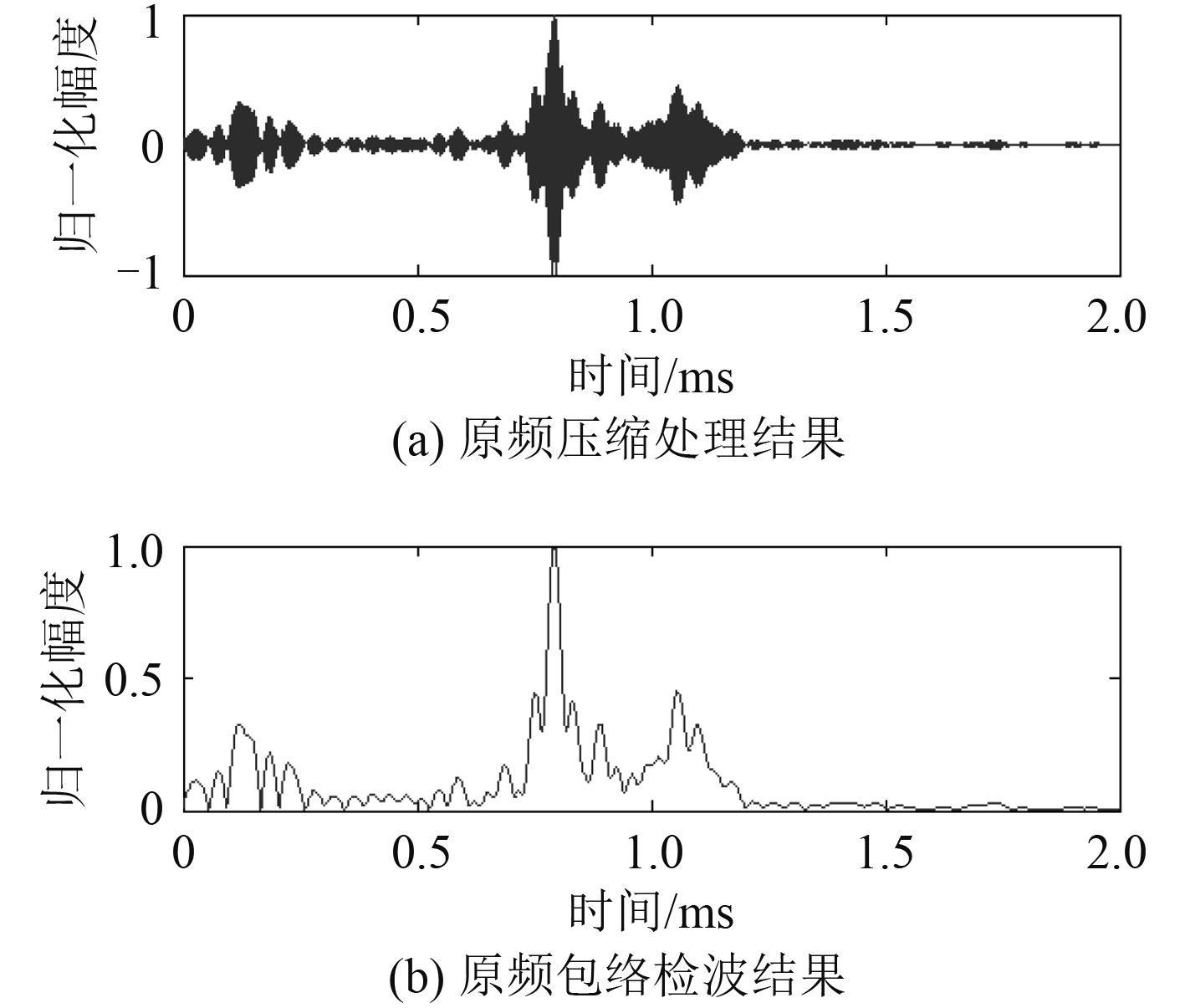
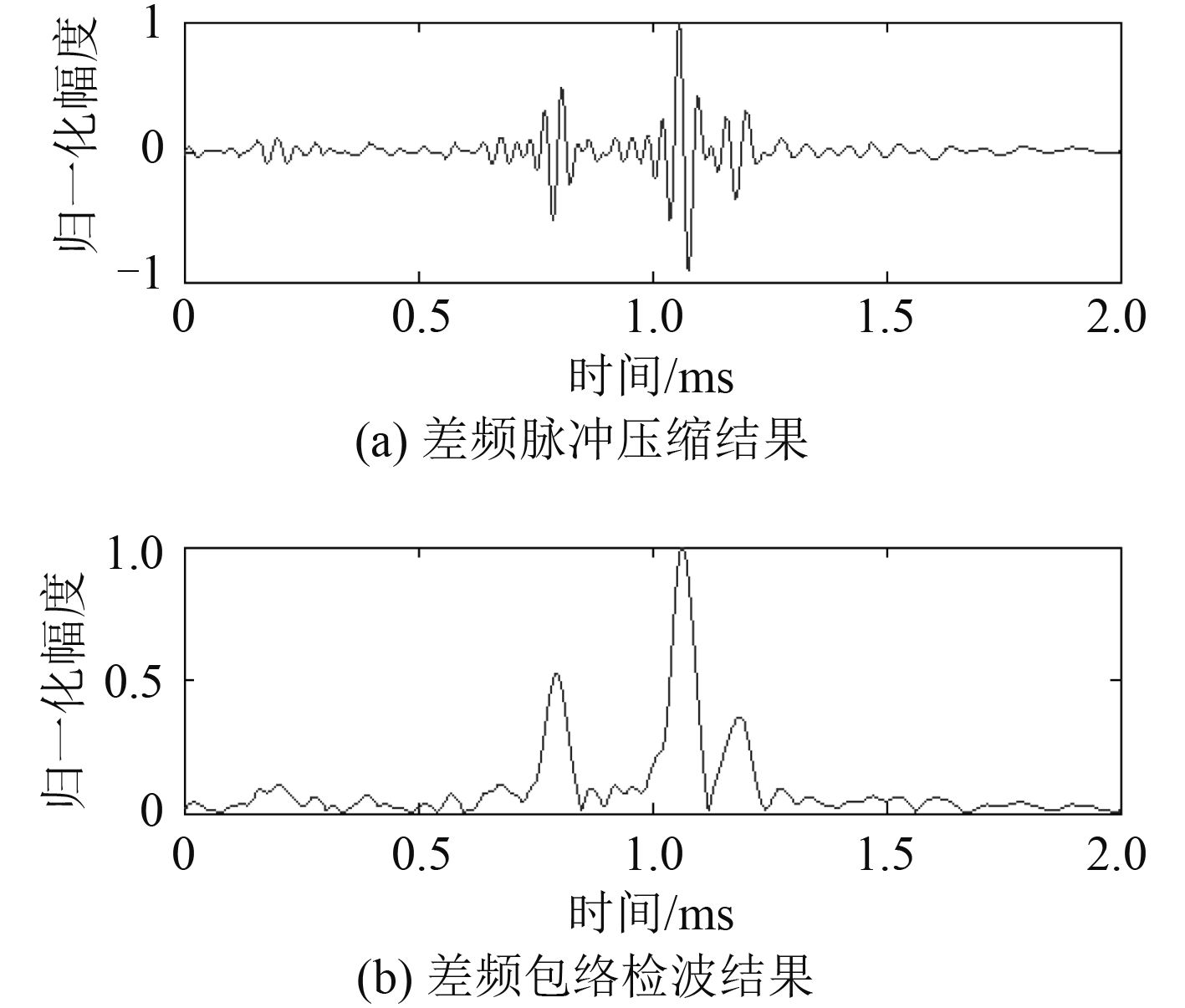
对接收信号中的原频及差频成分经数字滤波后再进行压缩处理,并对压缩后的信号经Hilbert变换求取包络,结果如图 7和图 8所示。 图 8的各峰分别对应旁瓣的直达信号、水-沙界面反射信号、目标反射信号、箱底反射信号(圆盘目标不完全挡住发射波束)。
|
图 7 掩埋目标原频实验结果 Fig. 7 The result of primary frequency of buried target experiment |
|
图 8 掩埋目标差频实验结果 Fig. 8 The result of difference frequency of buried target experiment |
由图 7和图 8可知,高频信号很难穿透沙层,而该参量阵测试系统形成的差频可以穿透。由于为尽量利用水域空间以形成差频信号,换能器和水听器都被布放在水面附近,可能导致各反射信号中含有经水面再反射的部分进而影响了压缩效果,而且由于水-沙界面存在一层约 1 cm厚的浮泥层,导致水-沙界面的回波信号压缩变差了一些,这些影响对原波更大些,从图中即可发现这点。
综上,该利用参量阵近场的海底小目标近距离探测试验系统能够在有限水域中近距离探测掩埋目标,发射宽带信号有助于浅掩埋目标的探测。
上述实验限于条件,只是获得了目标在特定方位上的回波信息,实际应用中,显然很难只通过某一方位的信息来实现目标的识别,获取目标越多方位的回波信息,越有利于海底小目标的识别。对于单波束的近距离参量探测系统,可以采用小平台走航的方式或者换能器机械扫描的方式来获取海底小目标更多的方位信息。对于多波束的近距离参量探测系统,若搭载在水下小平台上,不适合成较大规模的阵,且由于参量阵对源级要求较高,为了能量集中发射,一般采用电子扫描的方式。
4 结 语虽然参量阵有转换效率低而差频声源级不高的问题,但其能在小孔径下得到高指向性低频声波且近乎无旁瓣和具有宽频带等优点,若搭载在水下小平台上进行海底小目标的近距离探测,能够提高信混比等,具有其应用优势。本文设计的系统在试验阶段实现了预期目标,但需要进一步细化,以利于工程设计及应用:本文在现有条件下选择了原频中心频率在 200 kHz的宽带换能器搭建测试系统进行试验探索,进一步工作要优化原频频率及差频频率的选择;参量阵近场获得的宽带差频信号的特性未详细探究,了解这类宽带信号的特性有利于该方式下获取目标更多的散射特征、提高小目标的识别率。
| [1] | Westervelt P.J.. Parametric Acoustic Array[J]. The Journal of the Acoustical Society of America, 1963, 35 (4): 535–537. DOI: 10.1121/1.1918525 |
| [2] | Berktay H.O.. Possible exploitation of nonlinear acoustics in underwater transmitting applications[J]. J. Sound Vibration, 1965, 2 (4): 435–461. DOI: 10.1016/0022-460X(65)90122-7 |
| [3] | Berktay H.O.. Farfield performance of parametric transmitters[J]. The Journal of the Acoustical Society of America, 1974, 55 (2): 539–546. |
| [4] | 何祚镛, 赵玉芳. 声学理论基础[M]. 北京: 国防工业出版社, 1985, 420–431. |
| [5] | 姚培锋. 指向性声源的理论与实验研究[D]. 济南: 山东科技大学, 2005. |
| [6] | Moffett Mark B., Mellen Robert H.. Nearfield characteristics of parametric acoustic sources[J]. J. Acoust. Soc. Am., 1981, 69 (2): 404–409. DOI: 10.1121/1.385467 |
| [7] |
叶超, 吴鸣,等. 参量阵差频波指向性的研究[C]// 2009全国环境声学学术会议文集, 195–164.
YE Chao, WU Ming, et al. The research of the directivity of difference frequency of parametric array[C]// The 2009 National Conference on Environmental Acoustics Corpus, 195–164. |
| [8] | 钱祖文. 非线性声学(第 2 版)[M]. 北京: 科学出版社, 2009. |
| [9] |
钱祖文, 邵道远. 关于浅海参量阵的应用[J]. 物理学报, 1986, 35 : 1374–1377.
QIAN Zuwen, SHAO Daoyuan. About the application of shallow sea parametric array[J]. Journal of physics, 1986, 35 : 1374–1377. DOI: 10.3321/j.issn:1000-3290.1986.10.015 |
| [10] |
刘亮, 王锦柏. 一种参量阵浅地层剖面仪及实验研究[J]. 声学技术, 2015, 34(4), 202–205.
LIU Liang, WANG Jin-bo. One kind of parametric sub-bottom profiler and its experiment research[J]. Technical Acoustics, 2015, 34(4), 202–205. |
 2017, Vol. 39
2017, Vol. 39
