在舰载机试飞(飞行)取证过程中,甚至舰载机飞行员训练过程中,对试飞(飞行)数据进行分析处理是性能评价的重要环节。通过数据处理可得出飞行试验(训练)的结果[1],另外,实际试飞(训练)中采集的仅仅是一些离散的数据点,多数性能数据需通过数据的计算分析得到,其结果可以作为取证的依据。例如,通过试飞(飞行)数据得到的起飞着落性能曲线可为修正并提高舰载机起降训练水平提供参考依据。虽然舰载机的试飞或飞行训练科目有其特点,但就数据分析角度而言,常规飞行试验数据的处理方法和特点也适用于舰载机。
近年来,随着先进飞行器技术性能的提高,对参数测量精度要求越来越高,对先验知识和数据的依赖也越来越强,导致飞行试验数据量急剧膨胀。例如某新型飞机每架次试验数据基于统计规律的误差修正方法有时难以满足要总量平均超过了 50 GB[2],预计未来新型飞机单架次试验数据总量将在 100~500 GB。因此,在对数据分析时往往需要分段处理。例如,对数据按训练(试验)科目截取时,需要结合单点及其邻近数据才能确定分割点[3]。本文提出一种逐点分析与多点分析相结合的非常规误差处理方法,能够为舰载机基于飞行数据的性能分析提供良好预处理手段,也为飞行(试验)数据的高效利用奠定基础。
1 移动基准区间误差消除与平滑算法 1.1 飞行试验数据特点一般而言飞行试验数据是由测量仪器按预设的时间间隔对被测参数采样所得离散数据。具备以下特点:
数据量大,需分段加载与截取。目前,常规参数采样频率按 8 Hz,16 Hz,32 Hz,64 Hz系列设置,例如:按 64 个测量点整数类型 32 Hz采样,飞行试验 1 h产生的数据量为 64 × 32 × 3 600 = 7 372 800 个数据点,按 32 位整数类型表达折合存储容量为 225 M,若被测参数是单精度或双精度数,其容量更大。
多参数可按时间系列组织处理。单架次飞行器试飞数据均是基于同一授时系统实时采集,因而在数据分析与处理时,多个参数可以按时间序列组织。如 t i – 2 , t i – 1 , t i , t i + 1 , t i + 2 时刻某参数对应的测量值为 X i – 2 , X i – 1 , X i , X i + 1 , X i + 2 。
使用前需要预处理。数据系列除含有参数的有用信息及仪器测量误差外,还含有各种由于噪声、干扰、信息传送、编码方法及显示处理方法等因素造成的误差(偏差)。这些误差明显地影响二次处理结果,尤其是在分析飞行不稳定状态时。 图 1所示为某次平飞状态时高度数据在 8 320 m处上下波动,在分析平飞性能时,为了能够在整个数据段中快速智能截取平飞状态的数据,需要对其预处理,使数据点均在图中理想区间内。此外,还涉及有效数据提取问题。

|
图 1 平飞状态高度数据示例 Fig. 1 Example of horizontal flight altitude data |
误差点数据不能删除,只能修正。由于试飞数据一个时间点涉及多个参数,而且在性能分析时,这些参数可能彼此相关联,因此对某个参数处理时,即使出现大的误差,为了保证测试数据的完整性(其他参数可能是准确的),也不能直接删除。
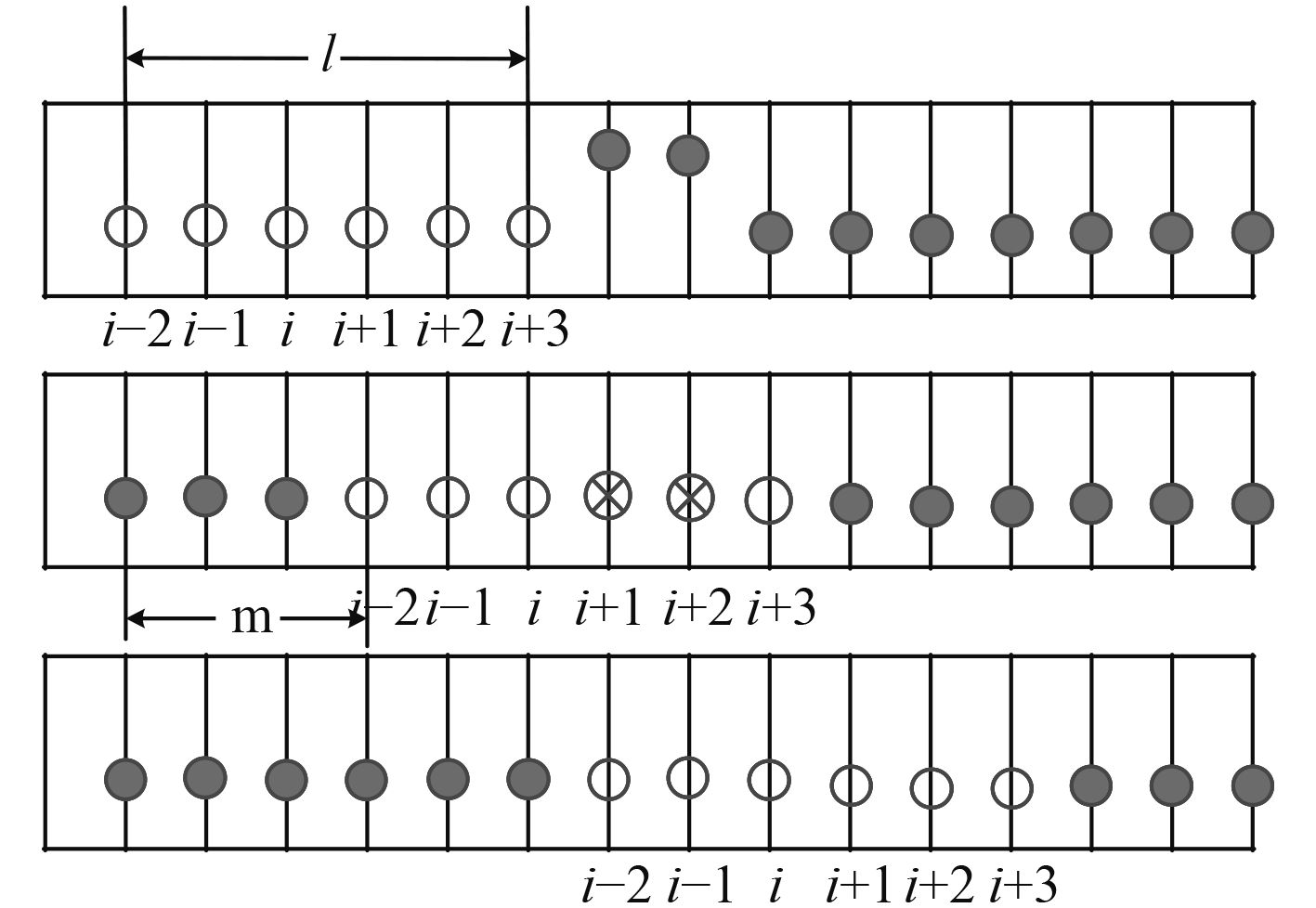
1.2 移动基准区间误差消除对每个被测参数 X i ,设定相邻 l 个测点(一般为 5 个点)为一个基准区间,在分析处理过程中,基准区间随时间逐次移动 m 个测量点,并对每个试验值进行分析比较。其过程如图 2所示,图中取 l = 6, m = 3。
|
图 2 移动基准区间 Fig. 2 Moving reference section |
若已知相邻测点之间的允许极限增值为Δ(一般可通过测点的物理特性求得),则对每个试验值的
| $\begin{array}{l}x_i' = \displaystyle \frac{{{x_{i - j}} + ({x_{i + j}} - {x_{i - j}})}}{k} \text{。}\\\end{array}$ | (1) |
其中
j 为大于
常用实验数据处理方法有Lagrange多项式插值[4]、牛顿插值、Hermite插值[5]、分段插值和样条插值。考虑试飞数据分析需要处理的数据量大[6- 7],重复计算多,在基准区间内采用牛顿插值方法逐点修正测量点的值,然后再逐次移动基准区间,直到完成全部数据的处理。
根据牛顿插值算法可知,对于数据序列
| $\begin{array}{l}f\left[ {{x_i},{x_{i + 1}}, \cdots {x_{i + k}}} \right]{\rm{ = }}\\\displaystyle \frac{{f\left[ {{x_{i + 1}}, \cdots {x_{i + k}}} \right]{\rm{ - }}f\left[ {{x_i},{x_{i + 1}}, \cdots {x_{i + k{\rm{ - 1}}}}} \right]}}{{{x_{i + k}} - {x_i}}}\text{,}\end{array}$ | (2) |
基准区间内的牛顿插值公式(不经过 i 点)为:
| $\begin{split}\\[-11pt]& {N_i}\left( x \right) = f\left( {{x_0}} \right) + f\left[ {{x_0},{x_1}} \right]\left( {x - {x_0}} \right) + \cdots + \\& f\left[ {{x_0},{x_1}, \cdots {x_{i - 1}},{x_{i + 1}}, \cdots {x_l}} \right]\times\\& \left( {x - {x_0}} \right) \cdots \left( {x - {x_{i - 1}}} \right)\left( {x - {x_{i + 1}}} \right) \cdots \left( {x - {x_{l - 1}}} \right) \text{,}\end{split}$ | (3) |
| $\begin{split}\\[-12pt] E\left( x \right) = f\left( x \right) - {N_i}\left( x \right) = & f\left[ {{x_o},{x_1} \cdots {x_{i - 1}},{x_{i + 1}} \cdots {x_l}} \right]\\ & \mathop \prod \limits_{j = 0,j \ne i}^l \left( {x - {x_j}} \right),x \in \left[ {a,b} \right] \text{,}\end{split}$ | (4) |
则经 k 次移动后, 基准区间内第 i 点的插值公式为:
| $\begin{split}\\[-12pt]& {N_{km + i}}\left( x \right) = f \left( {{x_{km}}} \right) + f\left[ {{x_{km}},{x_{km + 1}}} \right]\left( {x - {x_{km}}} \right) + \cdots + \\& \quad f \left[ {{x_{km}},{x_{km + 1}}, \cdots ,{x_{km + i - 1}},{x_{km + i + 1}}, \cdots {x_l}} \right]\left( {x - {x_{km}}} \right) \\& \quad \cdots (x - {x_{km + i - 1}})(x - {x_{km + i + 1}}) \cdots \left( {x - {x_{km + l - 1}}} \right)\text{,}\end{split}$ | (5) |
最终该点的平滑处理公式为:
| $ x{'_i} = {N_{km + i}}\left( x \right){\rm{ + }}\frac{{{N_{km + i}}\left( x \right) - {x_{i - 1}}}}{{{x_i} - {x_{i - 1}}}} \times \Delta \text{。}$ | (6) |
其中 Δ 为允许极限增量。
2 移动基准区间牛顿插值法在飞行试验数据处理中的应用表 1数据是某型号进行平飞加速性能实验的高度实测数据片段,从左到右按序编号,3 行共计 30 个数据。
|
|
表 1 某试飞GPS高度实测数据片段(单位:m) Tab.1 A flight test GPS height test data segment (unit: m) |
在试验中, GPS高度传感器的数据发送频率为 16 Hz,因此可以预设相邻 2 点高度的允许极限增值Δ为 6.25 m(可根据飞行器最大过载确定),基准区间长度
l = 5,逐点移动
m = 1,区间内数据首先应该满足允许极限增值条件即

|
图 3 非常规误差的消除 Fig. 3 Calculation result for grubbs criterion |
对表 1的数据采用式(1)和式(6)进行误差修正与平滑,计算结果见表 2。
|
|
表 2 某试飞GPS高度修正数据片段(单位:m) Tab.2 A flight test GPS height corrected data segment(unit: m) |
按 15 个数据点分组对表 2数据用格拉布斯准则分析,其结果见表 3,没有发现需要再次修正的数据点,误差消除结束。
|
|
表 3 格拉布斯准则计算结果 Tab.3 Calculation result for Grubbs Criterion |
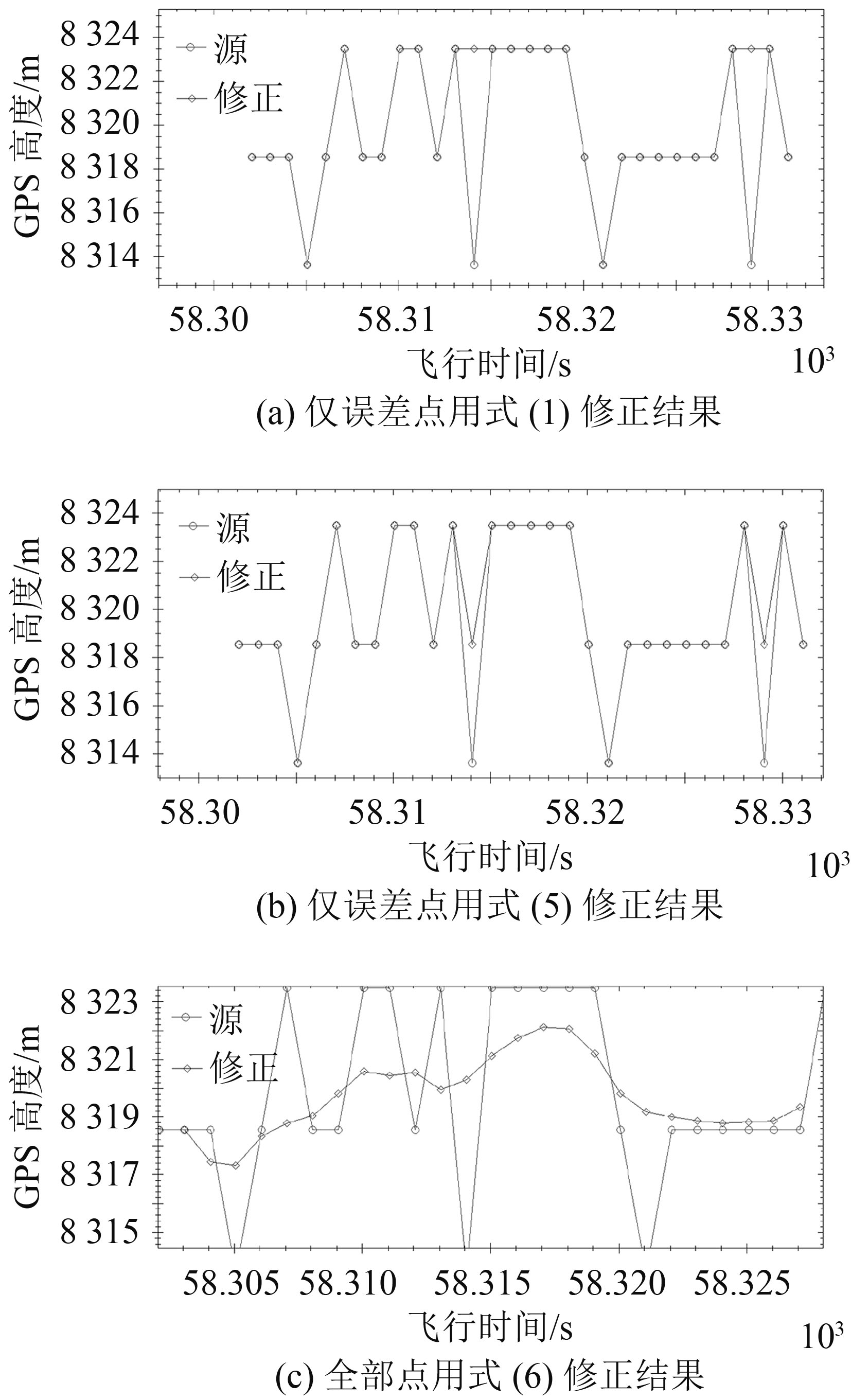
对表 1及其数据分析结果曲线如图 4所示,可见式(1)和式(5)对非常规误差发现与修正有较好的效果,其修过过程中把修正点的测量值看着错误,修正中不予采用,其结果见图 4(a);而式(6)综合可考虑了修正点的测量值,其结果见图 4(b),而图 4(c)则是平滑处理结果。
|
图 4 误差消除与平滑处理结果 Fig. 4 Error elimination and smoothing results |
试飞实测数据具有数据量大、多参数按时间组织、需预处理及误差修正的特点。在试飞数据分析过程中需要分段加载及截取,且在非常规误差的发现和修正中采用常规的统计方法有时难于满足要求,采用移动基准区和牛顿插值法相结合的方法进行 k重误差修正,效果良好。该法具有简单易行,计算量小,适应性强(可根据计算机性能要求动态调整单次数据处理长度),应用范围广(对于能够预设相邻测点最大极限增值情况均可采用)等特点,为试飞数据预处理提供了一条新途径。
| [1] |
陈增江. 动态试飞数据修正[J]. 飞行力学, 1994, 12 (1): 81–85.
Chen Zengjiang. Dynamic Flight Data Correction[J]. Flight mechanics, 1994, 12 (1): 81–85. |
| [2] |
李健翩, 李学仁. 多项式拟合在试飞数据预处理中的应用[J]. 弹箭与制导学报, 2005, 25 (4): 799–801.
Li JianjPian, Li Xueren. Application of Polynomial Fitting for Data Pre-processing Flight Test Data[J]. Journal of Missile and Guidance, 2005, 25 (4): 799–801. |
| [3] |
杨亚军, 李言俊, 邓建华. 多项式移动平滑算法及在试飞数据预处理中的应用[J]. 西北工业大学学报, 1998, 16 (4): 501–505.
Yang Yajun, Li Yanjun, Deng Jianhua. A New Smoother Algorithm for Pre-processing Flight Test Data[J]. Journal of Northwestern Polytechnical University, 1998, 16 (4): 501–505. |
| [4] | W Werner. Polynomial interpolation: Lagrange versus Newton[J]. Mathematics of Computation, 1984, 43 (167): 205–217. DOI: 10.1090/S0025-5718-1984-0744931-0 |
| [5] | VY Pan. An algebraic approach to approximate evaluation of a polynomial on a set of real points[J]. Advances in Computational Mathematics, 1995, 3 (1): 41–58. |
| [6] | C De Boor, K Llig, M Sabin. High accuracy geometric Hermite interpolation[J]. Computer Aided Geometric Design, 1987, 4 (4): 269–278. DOI: 10.1016/0167-8396(87)90002-1 |
| [7] |
张友民, 王培德, 张洪才. 估计理论在飞行数据相容性检验中的应用[J]. 航空学报, 1992, 13 (7): 398–402.
Zhang You-min, Wang Pei-de, Zhang Hong-cai. The Application Of Estimation Theory In Flight Data Compatibility Check[J]. Acta Aeronautica ET Astronautica Sinica, 1992, 13 (7): 398–402. |
| [8] | 张夏阳, 殷之平, 刘飞, 黄其青, 等. 飞机机动划分的数据挖掘方法[J]. 西北工业大学学报, 2016 (1): 33–40. |
| [9] | CT Han, TK Gaik. Newton’s divided difference interpolation using scientific calculator[J]. International Conference on Mathematics, 2016, 1775 (1): 030102. |
 2017, Vol. 39
2017, Vol. 39
