潜载导弹是潜艇作战平台最重要的武器之一,是潜艇作战能力的重要体现,发射装置作为潜艇导弹武器系统的重要组成部分[1],其战技性能指标、发射导弹数量和平台试装性能直接影响潜艇的作战能力。作为潜艇的重要组成部分,潜载导弹发射装置具备贮存和发射导弹的重要功能,当潜艇受到冲击时,发射装置对导弹武器起到一定保护作用。
随着计算机仿真技术的发展,基于响应面方法的有限元仿真计算及数值优化被广泛应用[2 –3]。余俊等[4]利用响应面法建立了开孔耐压球壳非线性稳定性近似公式,并联合采用多岛遗传算法和Hook-Jeeves法进行优化设计,得到满足强度和稳定性要求的重量最轻的耐压球壳设计方案。葛珅玮等[5]针对船体夹层板优化的问题,通过正交试验方法设计样本点,构建了神经网络响应面模型,并用改进后的遗传算法进行优化分析,验证了该方法的实用性和有效性;Marcus等[6]利用神经网络法建立响应面,实现了对吸能盒外形尺寸的优化设计。
响应面法是指通过一系列确定性的试验拟合一个响应面以模拟真实极限状态曲面的方法,与直接优化方法相比,优点如下:
1)响应面法可以消除目标函数的高频噪声,因此可期望得到全局的近似最优解;
2)在优化设计的过程中,针对不同的目标函数和约束条件,无需增加额外的计算量;
3)响应面法能够比较容易的应用于多学科、多目标的优化设计问题中。
本文以某型潜载垂直发射装置为研究对象,将响应面法应用到发射装置结构的优化设计中,在提高发射装置抗冲击能力的同时,尽量降低发射装置的重量。
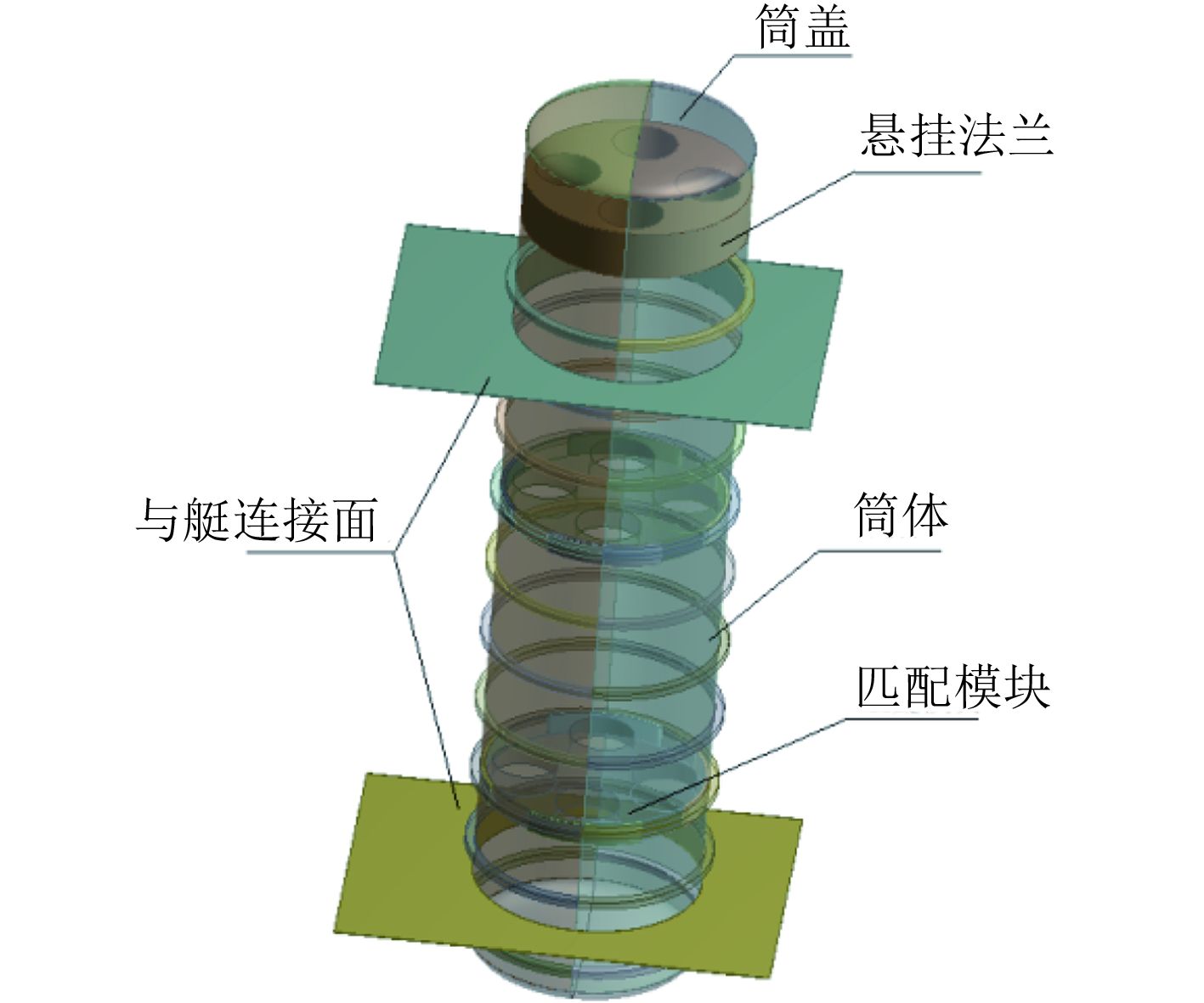
1 有限元模型针对某型潜载垂直发射装置的抗冲击性能,首先对发射装置进行简化建模,如图 1所示。发射装置由筒盖、悬挂法兰、筒体、匹配模块等组成,通过上下2层铺板与潜艇平台固定连接。当潜艇受到冲击时,发射装置与潜艇连接面随潜艇变形而发生位移,将潜艇变形载荷传递至发射装置,因此可将发射装置所受冲击载荷转化为与艇连接面的位移载荷,有限元模型网格与计算结果如图 2所示。
|
图 1 潜载垂直发射装置示意图 Fig. 1 Schematic diagram of submarine missile vertical launch |

|
图 2 有限元模型网格及计算结果 Fig. 2 FEM model and result |
响应面法(Response surface methodology,RSM)是一种通过采用试验设计理论对指定的设计点集合进行试验,得到目标函数和约束函数的响应面模型,来预测非试验点的响应值的方法。利用响应面法建立近似模型时,首先需要确定近似函数的形式,然后运用统计试验设计方法在空间内选取足够多的设计点,最后运用最小二乘法原理得到近似模型来拟合设计点的分析结果。
系统响应 Y 与设计变量 x 间的函数关系为:
| $Y = {\rm{y}}(x) + \varepsilon {\text{,}}$ | (1) |
式中:
通过试验设计,系统响应与设计变量之间的函数关系为:
| $Y = {\rm{\tilde y}}(x) + \delta{\text{,}} $ | (2) |
式中:
响应面可定义为:
| ${\rm{\tilde y}}(x) = {a_0} + \sum\limits_{i = 1}^N {{a_i}{\varphi _i}x}{\text{,}} $ | (3) |
式中:
1阶与2阶多项式近似模型的基函数分别为 1, x 1, x 2,… x n ,1, x 1, x 2,… x n , x 1 2, x 1 x 2,… x 1 x n ,… x n 2,其中 n 为设计变量个数。
根据式(3),可得1阶和2阶响应面近似模型的表达式分别为:
| ${\rm{\tilde y}}(x) = {a_0} + \sum\limits_{i = 1}^n {{a_i}{x_i}}{\text{,}} $ | (4) |
| ${\rm{\tilde y}}(x) = {a_0} + \sum\limits_{i = 1}^n {{a_i}{x_i}} + \sum\limits_{i = 1}^n {{a_{ii}}x_i^2 + } \sum\limits_{i = 2}^n {\sum\limits_{j = 1}^{i - 1} {{a_{ij}}{x_i}{x_j}} }{\text{。}} $ | (5) |
对设计变量 x 的 k( k > 1.5 N)个样本值( x 1, x 2,…, x k )进行仿真试验,得到 k 个响应量( y 1, y 2,…, y k ),则样本点试验值与近似响应面值之间的误差为:
| $\delta = \sum\limits_{i = 1}^k {{{[{y_i} - ({a_0} + \sum\limits_{i = 1}^k {{a_i}{x_i}} + \sum\limits_{i = 1}^k {\sum\limits_{j = i}^k {{a_{ij}}{x_i}{x_j}} } )]}^2}} {\text{,}}$ | (6) |
通过最小二乘法可计算得到基函数系数列阵:
| ${ a} = {({\varPhi ^{\rm T}} \varPhi )^{ - 1}}({\varPhi ^{\rm T}}y){\text{,}}$ | (7) |
式中
| $\varPhi = \left[ \begin{array}{l}1\quad {x_{1,1}}\quad {x_{1,2}}\quad \cdots \quad {x_{1,N}}\\1\quad {x_{2,1}}\quad {x_{2,2}}\quad \cdots \quad {x_{2,N}}\\ \vdots \quad \;\; \vdots \quad \;\;\;\; \vdots \quad \;\;\;\;\quad \;\;\;\; \vdots \\1\quad {x_{M,1}}\quad {x_{M,2}}\quad \cdots \quad {x_{M,N}}\end{array} \right]{\text{。}}$ | (8) |
从设计空间中的设计样本点确定矩阵
响应面近似模型的精度与设计样本点的选取有很大关系。拉丁超立方试验设计方法依据等概率随机正交分布的原则,可以通过很少的试验点得到较高精度的响应面,是一种高效的试验设计方法。对于设计变量较多的大型结构,工程中通常使用拉丁超立方试验设计方法[7 –9]。
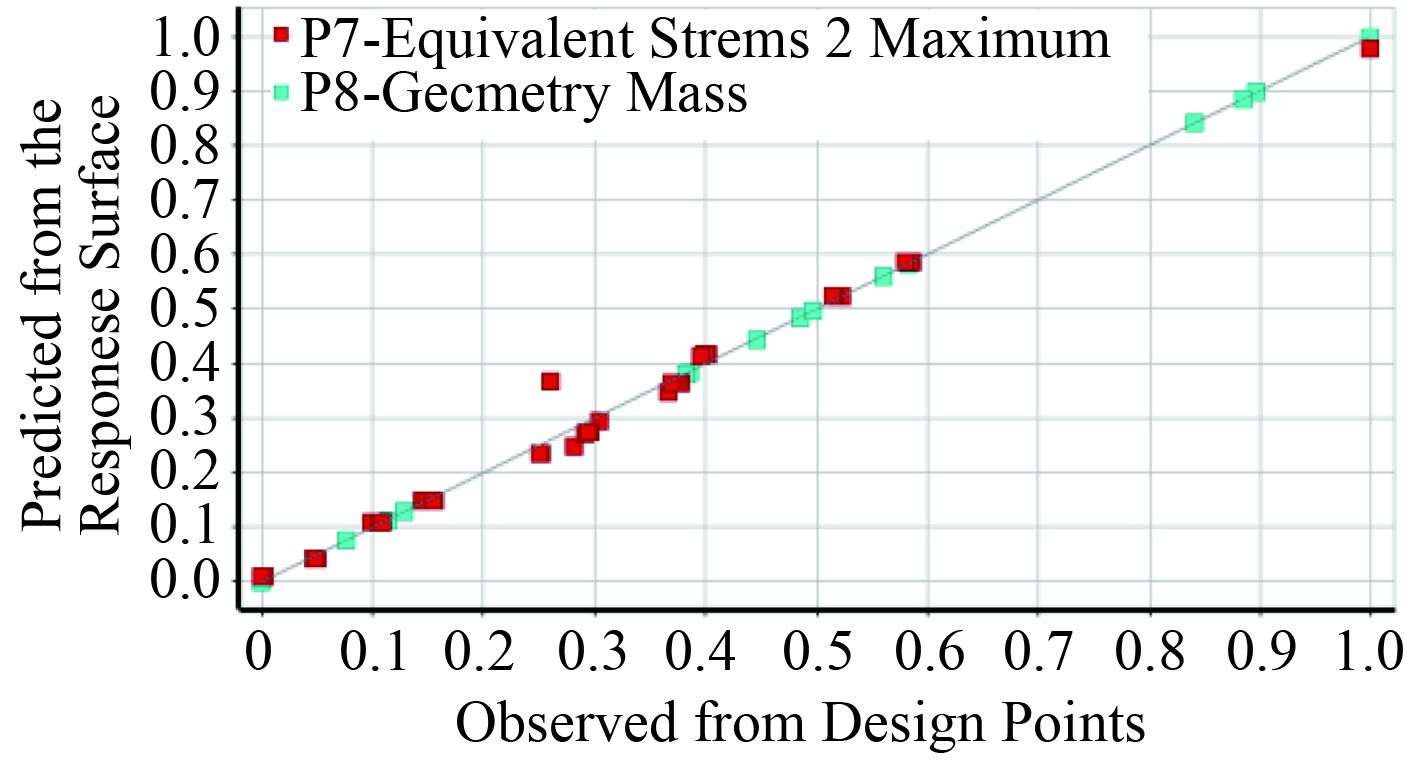
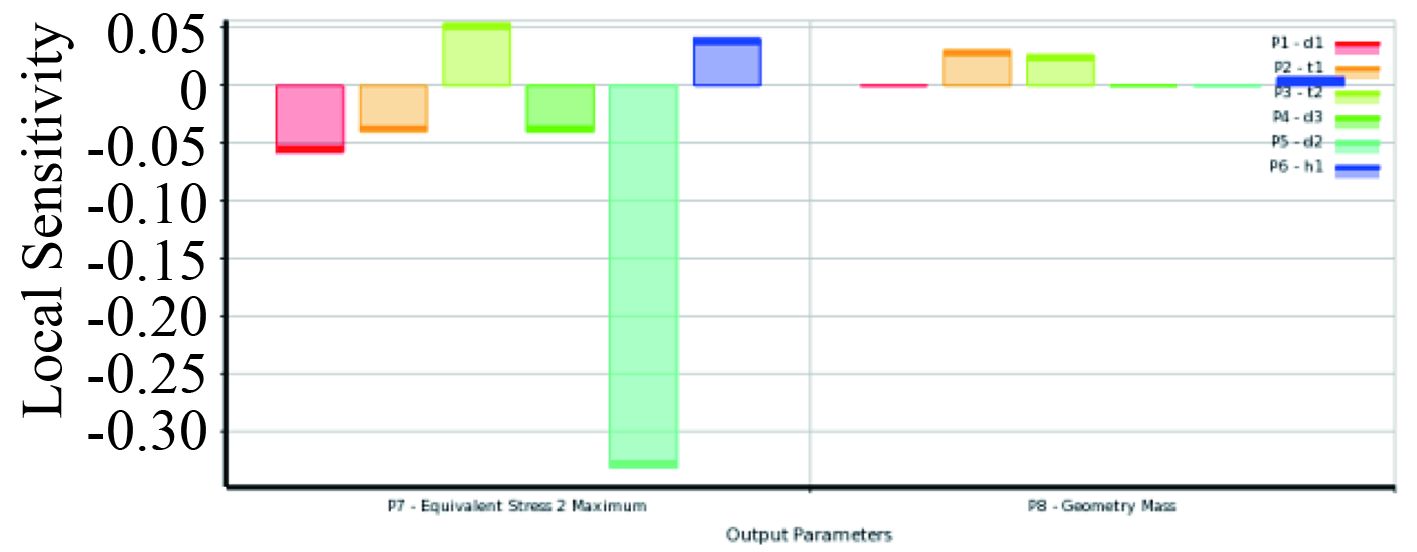
3 算 例基于发射装置有限元模型,在可优化参数范围内选取 6 个结构尺寸参数作为优化参数,如表 1所示。通过拉丁超立方试验设计,利用有限元法求解不同设计样本点的发射装置,建立发射装置所受载荷目标函数响应面,并将响应面预测值与仿真计算值进行对比,如图 3所示。获得结构参数对目标函数的灵敏度,如图 4所示。
|
图 3 响应面预测值与仿真计算值对比图 Fig. 3 Comparision of Predictive value and simulation value |
|
图 4 结构参数对目标函数灵敏度柱状图 Fig. 4 Columnar analysis diagram of the structure parameter sensitivity |
由图 3可看出,响应面模型预计值与仿真计算结果十分接近,响应面模型满足精度要求。由图 4可看出,对于发射装置抗冲击性能而言,仅肋骨宽度与匹配模块高度与其正相关,且影响较小;其余参数与其负相关,下匹配模块距筒底高度对其影响最大,即下匹配模块距筒底越高,发射装置抗冲击载荷性能越差。对发射装置重量而言,各参数对其影响均较小,其中肋骨的长度对发射装置重量影响最大。
根据发射装置结构参数灵敏度分析结果,确定各参数优化范围如表 1所示。
|
|
表 1 发射装置模型优化参数 Tab.1 The optimal parameters of the model |
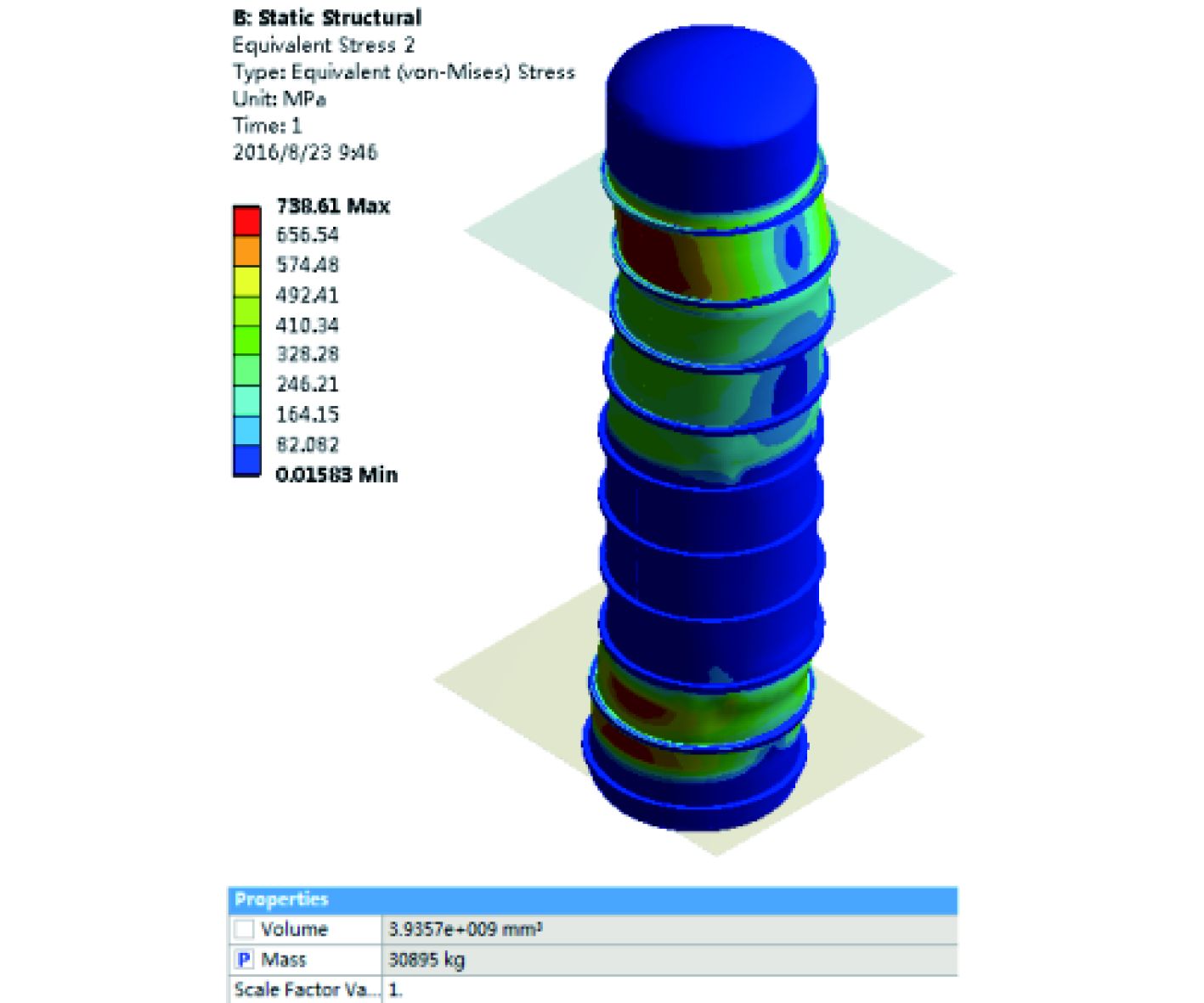
利用workbench目标驱动优化模块,对发射装置结构进行多目标优化,优化结果如表 2所示。发射装置抗冲击性能是我们首要优化的目标,因此选第 3 个优化结果为最优解,其应力云图如图 5所示。
|
|
表 2 发射装置模型优化结果 Tab.2 The optimization result of the model |
|
图 5 发射装置最优解应力云图 Fig. 5 The stress nephogram of the optimal solution |
由图 5可知,经过优化设计,发射装置所受载荷从 867.82 MPa降至 738.61 MPa,性能提升了 14.9%,整体重量由 31 559 kg降至 30 895 kg,降低了 2.1%。
4 结 语本文将试验设计、响应面模型、灵敏度分析及优化算法相结合,针对某型潜载垂直发射装置,以提高抗冲击性能和轻量化为目标进行整体优化,实现了发射装置设计参数动态优化,为工程产品快速优化设计提供了参考,得到结论如下:
1)基于响应面法的多目标优化方法快速准确,适合工程应用;
2)发射装置匹配模块距筒底高度对其抗冲击性能影响较大,匹配模块距筒底越高,发射装置抗冲击载荷性能越差;
3)通过基于响应面法的多目标优化设计,实现了发射装置抗冲击性能提升 14.9%,同时发射装置整体减重 2.1%,为潜载导弹垂直发射装置设计提供一定依据。
| [1] |
倪火才. 潜地弹道导弹发射装置构造[M]. 哈尔滨: 哈尔滨工程大学出版社, 1998.
NI Huo-cai. The structure of submarine-to-ground ballistic missile iauncher[M]. Harbin: Harbin Engineering University Press, 1998. |
| [2] |
孙光永, 李光耀, 钟志华, 等. 基于序列响应面法的汽车结构耐撞性多目标粒子群优化设计[J]. 机械工程学报, 2009, 45 (2): 224–230.
SUN Guangyong, LI Guangyao, ZHONG Zhihua, et al. Optimization Design of Multi-objective Particle Swarm in Crashworthiness Based on Sequential Response Surface Method[J]. JOURNAL OF MECHANICAL ENGINEERING, 2009, 45 (2): 224–230. |
| [3] |
熊俊涛, 乔志德, 韩忠华. 基于响应面法的跨声速机翼气动优化设计[J]. 航空学报, 2006, 27 (3): 399–402.
XIONG Jun-tao, QIAO Zhi-de, HAN Zhong-hua. Optimum Aerodynamic Design of Transonic Wing Based on Response Surface Methodology[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27 (3): 399–402. |
| [4] |
余俊, 王永军, 潘广善. 集体逃逸舱开孔耐压球壳优化设计[J]. 舰船科学技术, 2014, 36 (1): 104–110.
YU Jun, WANG Yong-jun, PAN Guang-shan. Optimal design of pressure spherical shell with openings in collective escape capsule[J]. SHIP SCIENCE AND TECHNOLOGY, 2014, 36 (1): 104–110. |
| [5] |
葛珅玮, 张延昌. 基于BP-GA算法实现船体结构多目标优化[J]. 舰船科学技术, 2013, 35 (9): 31–37.
GE Shen-wei, ZHANG Yan-chang. The multiple optimal design of ship structures based on BP—GA algorithm[J]. SHIP SCIENCE AND TECHNOLOGY, 2013, 35 (9): 31–37. |
| [6] | MARCUS R, LARSGUNNAR N, FREDRIK B, et al. Shape optimization of a vehicle crash-box using LS-OPT[C]// 5th European LS-DYNA User conference. Sweden: Engineering Research Nordic, 2005: 27–31. |
| [7] | PAPILLA M. Accuracy of response surface approximations for weight equations based on structural optimization[D]. Gainesville: University of Florida, 2001. |
| [8] |
刘文卿. 实验设计[M]. 北京: 清华大学出版社, 2005.
LIU Wen-qing. Design of experiments[M]. Bei Jing: Tsinghua University Press, 2005. |
| [9] | Mckay M D, Beckman R J, Conover W J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code[J]. Technometrics, 1979, 21 (2): 239–245. |
 2017, Vol. 39
2017, Vol. 39
