0 引　言

船用光电跟踪监视取证设备是进行海上搜救跟踪、执法取证的重要设备，为维护我国海洋权益发挥着重要作用。世界各国一直致力于研究先进的光电跟踪系统，由于伺服控制的优劣直接决定了光电跟踪系统的性能，伺服控制技术的研究一直备受关注。

传统伺服控制对受控转台进行精确模型分析，以此确定控制参数，控制性能受建模准确度影响大，由于光电跟踪系统结构复杂，还存在外界的不确定干扰，所以传统控制方法开发难度大，环境适应性较弱。

智能控制是一种很好的解决方案，其中模糊神经网络近年来发展迅速，模糊逻辑具有很强的非线性特性，结合神经网络强大的学习能力，使得模糊神经网络具有控制性能好、环境适应性强以及开发难度小等优点。

本文设计的模糊神经网络算法以神经网络为基础，根据模糊逻辑进行分层，通过对隶属度函数以及模糊规则进行自适应调节实现，不但具有参数学习能力，还具有结构学习能力，使得控制器拥有良好的动态、静态特性以及很强的适应性，与传统的模糊控制或者神经网络控制相比有较大的提高。

1 模糊神经网络控制器结构分析

小型光电跟踪系统的伺服部分一般采用永磁同步电机（PMSM），根据永磁同步电机矢量控制理论，本设计采用双闭环控制，内环为电流环，用PID控制使得电机直轴电流分量为 0，外环为速度环，输入量为理想速度与实际速度之差 e 及其变化率 $\dot e$ ，输出为理想的交轴电流参考，控制器的参数以及结构通过误差反向传播进行修正和调整，系统结构如图 1所示。

1.1 模糊神经网络算法的结构

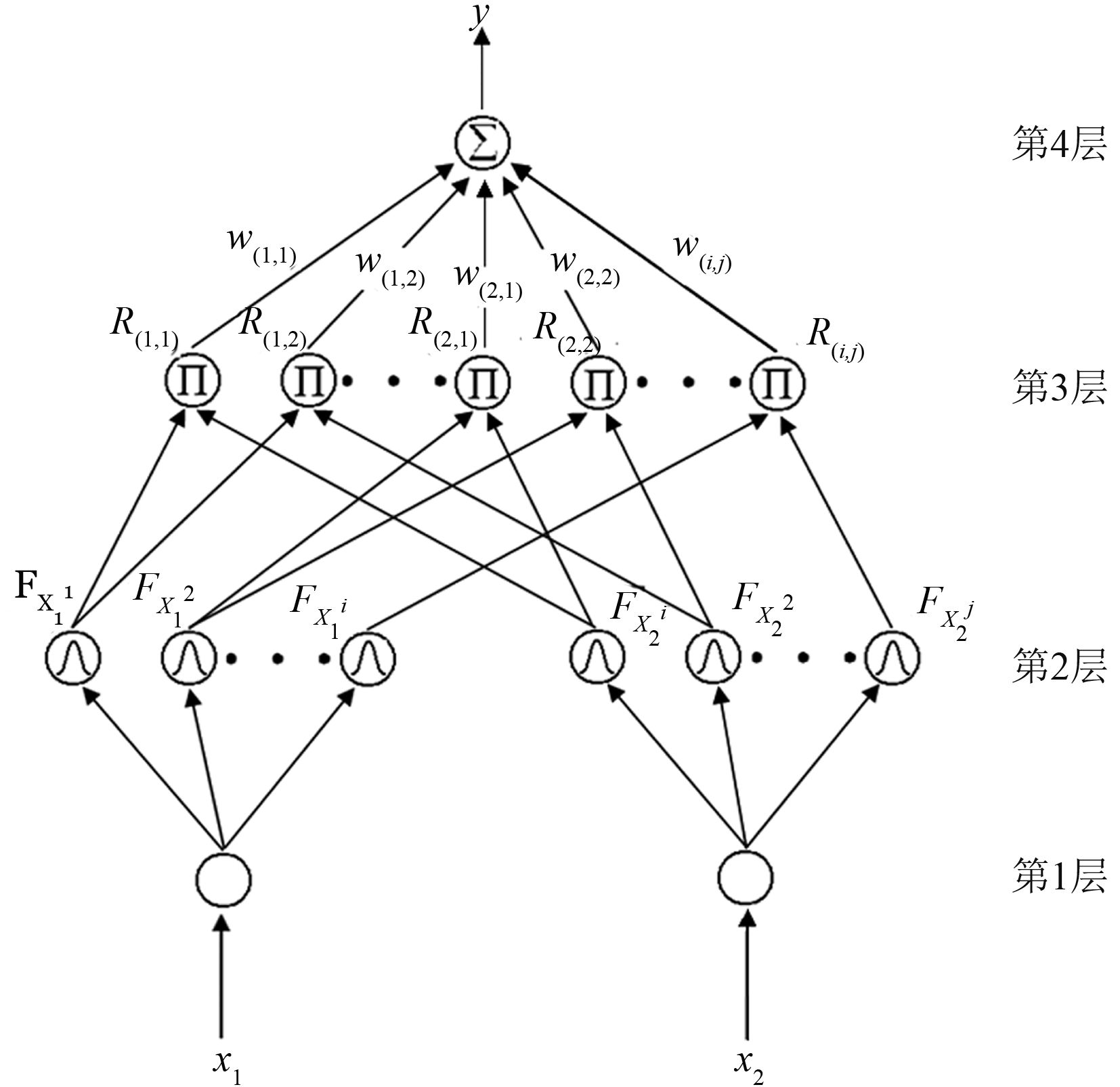
根据模糊控制的构成，结合反向传播网络的结构，本文提出的模糊神经网络控制器由4层前向网络组成，分别为输入层、隶属度函数层、模糊规则层和输出层，模糊神经网络控制器结构如图 2所示。

1）输入层

该层有2个神经元，其输入分别为参考速度与实际速度之差 e 及其变化率 $\dot e$ 的精确值，用 x ₁， x ₂ 来表示，信号不经处理直接传给下一层。

2）隶属度函数层

该层完成的是对模糊集合隶属函数的定义，对输入变量进行模糊化，这里规定隶属度函数统一采用高斯函数：

$\begin{array}{l}{F_{{X_1}^i}} = \exp ( - \displaystyle\frac{{{{({x_1} - {c_{1i}})}^2}}}{{2{\sigma _{1i}}^2}}),\\[8pt]{F_{{X_2}^j}} = \exp ( - \displaystyle\frac{{{{({x_2} - {c_{2j}})}^2}}}{{2{\sigma _{2j}}^2}}),\;\end{array}$

式中： x ₁， x ₂ 为输入信号； ${F_{{X_1}^i}}$ ， ${F_{{X_2}^j}}$ 分别为变量 x ₁ 对应的第 i 个隶属函数以及 x ₂ 对应的第 j 个隶属函数； ${c_{1i}},\;\;{c_{2j}},\;\;{\sigma _{1i}},\;\;{\sigma _{2j}}$ 为对应的隶属函数的均值和方差。

各个模糊集合隶属函数的均值和方差不同，均值反映了模糊集合的位置，方差反映了模糊集合的形状，隶属函数的个数、均值以及方差都可以自动调整。

3）模糊规则层

本设计采用一个神经元代表一个模糊规则，神经元的输入是模糊规则对应的 2 个条件，即 2 个模糊集合的隶属函数，模糊推理算法采用求乘积的形式，神经元的输出为：

${R_{(i,j)}} = {F_{{X_1}^i}} \times {F_{{X_2}^j}},$

式中： ${R_{(i,j)}}$ 表示的规则就是 x ₁ 的第 i 个模糊集合与 x ₂ 的第 j 个模糊集合共同发生时输出属于某个模糊集合。 ${R_{(i,j)}}$ 的大小反映了输出对各个输出模糊集合的隶属程度关系。

4）输出层

该层完成了模糊综合运算以及反模糊运算，计算出了精确的模糊输出，采用一个神经元完成上述功能，计算方法为：

$y = \sum {{R_{(i,j)}}} \times {w_{(i,j)}}\text{。}$

式中： y 为控制器的精确输出，是电流环交轴电流分量的参考， ${w_{(i,j)}}$ 为加权值，是用一个精确值来代表输出模糊集合，体现了各个输出模糊集合的相对关系。

1.2 模糊神经网络算法的自学习

本文设计的模糊神经网络具有 2 种学习调整能力，一种是参数学习，包括对隶属度函数层均值和方差的调整，还有就是对输出层的加权系数的调整，目的是使得系统性能不断的改善；另一种就是结构学习，即对模糊规则的个数以及隶属函数个数的调整，调整的目的是在保证性能的基础上使得系统的结构尽可能的简单，减少计算量。

1）参数学习

参数学习是为了使得系统性能不断优化，系统性能通过定义能量误差函数来表示，表达式为：

$E = \frac{1}{2}{({\omega _r} - \omega )^2} = \frac{1}{2}{e^2}\text{，}$

式中： ω _r ， ω 分别为理想转速和实际转速； E 为能量误差。

参数学习采用梯度下降算法，将误差从最后一层反向推导，从后往前各层的计算依次如下：

① 输出层

反向传播的误差为：

$ \quad\quad \delta = - \displaystyle\frac{{\partial E}}{{\partial y}}\text{，} $

输出层的加权值改变量为：

$\Delta {w_{(i,j)}} = - {\eta _w}\displaystyle\frac{{\partial E}}{{\partial {w_{(i,j)}}}} = $ $- {\eta _w}(\displaystyle\frac{{\partial E}}{{\partial y}}\displaystyle\frac{{\partial y}}{{\partial {w_{(i,j)}}}}) = {\eta _w}\delta {R_{(i,j)}}\text{。}$

式中 η _w 为输出层加权值学习步长，人为设定，决定学习的速度。

② 隶属度函数层

隶属度函数的均值：

$\begin{split}\\[-12pt]\Delta {c_{1i}} &= - {\eta _c}\displaystyle\frac{{\partial E}}{{\partial {c_{1i}}}} = - {\eta _c}(\frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial {R_{(i,j)}}}}\frac{{\partial {R_{(i,j)}}}}{{\partial {c_{1i}}}}) = \\&\sum\limits_j {{\eta _c}\delta {w_{(i,j)}}{R_{(i,j)}}\displaystyle\frac{{({x_1} - {c_{1i}})}}{{{\sigma _{1i}}^2}}} \text{，}\\\Delta {c_{2j}}& = - {\eta _c}\displaystyle\frac{{\partial E}}{{\partial {c_{2j}}}} = - {\eta _c}(\frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial {R_{(i,j)}}}}\frac{{\partial {R_{(i,j)}}}}{{\partial {c_{2j}}}}) = \\&\sum\limits_i {{\eta _c}\delta {w_{(i,j)}}{R_{(i,j)}}\displaystyle\frac{{({x_2} - {c_{2j}})}}{{{\sigma _{2j}}^2}}} \text{；}\end{split}$

隶属度函数的方差：

$\begin{split}\\[-12pt]\Delta {\sigma _{1i}}& = - {\eta _\sigma }\displaystyle\frac{{\partial E}}{{\partial {\sigma _{1i}}}} = - {\eta _\sigma }(\frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial {R_{(i,j)}}}}\displaystyle\frac{{\partial {R_{(i,j)}}}}{{\partial {\sigma _{1i}}}}) = \\&\sum\limits_j {{\eta _\sigma }\delta {w_{(i,j)}}{R_{(i,j)}}\displaystyle\frac{{{{({x_1} - {c_{1i}})}^2}}}{{{\sigma _{1i}}^3}}}\text{，} \\\Delta {\sigma _{2j}}& = - {\eta _\sigma }\displaystyle\frac{{\partial E}}{{\partial {\sigma _{2j}}}} = - {\eta _\sigma }(\frac{{\partial E}}{{\partial y}}\displaystyle\frac{{\partial y}}{{\partial {R_{(i,j)}}}}\frac{{\partial {R_{(i,j)}}}}{{\partial {\sigma _{2j}}}}) = \\[3pt]&\sum\limits_i {{\eta _\sigma }\delta {w_{(i,j)}}{R_{(i,j)}}\displaystyle\frac{{{{({x_2} - {c_{2j}})}^2}}}{{{\sigma _{2j}}^3}}} \text{。}\end{split}$

式中 η _c ， η _σ 分别为均值和方差的学习速度，人为设定。

通过以上分析发现，参数学习很重要的一点就是计算反向传播的误差 δ，根据公式有：

$\delta = - \frac{{\partial E}}{{\partial y}} = - (\frac{{\partial E}}{{\partial e}}\frac{{\partial e}}{{\partial y}}) = - (\frac{{\partial E}}{{\partial e}}\frac{{\partial e}}{{\partial \omega }}\frac{{\partial \omega }}{{\partial y}})\text{。}$

最后问题归结到求实际转速 ω 对交轴参考电流 y 的偏导，由于系统参数的不确定性以及外界干扰等因素的影响，很难精确求出反向传播误差项，本文通过采用切换策略来给出 δ 一个合适的值。

首先定义切换策略条件 $s\dot s$ ，其中 $s = e + c\dot e$ ， c 是人为定义的，要求 c > 0，从 s 的定义可看出切换条件与速度误差以及误差变化率都有关系，通过 c 值来表现关系的比重，切换策略的切换点选择为 0。分为 2 种： $s\dot s \geqslant 0$ ，此时误差幅值有增大的趋势，应该有比较大的修正，此时反向传播的误差项为 $\delta = cs$ ； $s\dot s < 0$ ，此时误差幅值有减小的趋势，此时反向传播的误差项为 $\delta = cs\beta $ ，其中 β 是一个很小的正数。

通过以上的策略切换给出了一个比较合适的误差项 δ，然后根据梯度下降法对参数进行修正，实现控制参数自学习功能。

2）结构学习

结构学习发生的条件是通过参数调整系统性能还是没有达到指定标准，这种标准一般为 $|e| < {e_{\max }}$ 或者 $|\dot e| < {\dot e_{\max }}$ ，其中 ${e_{\max }}\;\;{\text{和}}\;\; {\dot e_{\max }}$ 是人为设置的可以接受的最大速度误差以及误差变化率，结构学习都是通过增加或减少模糊规则神经元以及隶属函数层神经元实现的。

① 增加神经元

结构学习首先是规则层的学习，规则层增加一个神经元相当于增加了一个模糊规则，一般情况下系统模糊规则的个数没有达到饱和，增加规则层神经元的时候先对个数进行判断，如果没有饱和就按照相邻一个时间段内隶属度高低从输入的模糊集合中选取2个隶属度高的组成新的模糊规则，然后对应的增加一个加权系数 w，继续进行参数学习。

通过规则层的结构学习如果还是达不到性能指标需要增加隶属函数层的神经元，增加一个隶属函数层的神经元就是增加一个输入模糊集合，新增的隶属函数的均值和方差可以提前设定预设值 ${c_r},\;\;{\sigma _r}$ ，然后通过参数学习进行调整。

② 精简神经元

结构学习还涉及的另一个问题是结构的精简，因为过于复杂的结构会使得运算很复杂，对执行单元是一种负担，结构的精简也包括两个方面，一是规则层神经元的精简，该神经元的输出可以理解为输入信号属于对应的模糊集合的程度，如果该神经元的输出太小，说明该模糊规则的作用很小，可以考虑将其精简掉，将规则层各个神经元最近的 N 个输出取其最大值，记为：

${R^{\max }}_{(i,j)} = \max {R^n}_{(i,j)},\;n = 1,2,3,...,N\text{。}$

如果有 ${R^{\max }}_{(i,j)} < R$ ，就需要将这个规则神经元精简掉，其中 R 是人为设定的临界值，关乎规则层的神经元个数。

结构精简的另一个方面是对隶属函数层神经元的精简，因为该层神经元的个数直接决定了规则层神经元的个数，采用的方法相同，取各个神经元最近的 N 个输出的最大值，记为：

$\begin{array}{*{20}{c}}{{F_{{X_1}^i}}^{\max } = \max {F^n}_{{X_1}^i}}\text{，}\\[5pt]{{F_{{X_2}^j}}^{\max } = \max {F^n}_{{X_2}^j}}\text{，}\end{array}\;\;n = 1,2,3......N\text{。}$

如果有 ${F_X}^{\max } < F$ ，就需要将这个神经元精简掉，其中 F 是人为设定的临界值，关乎隶属函数层的神经元个数。

2 Matlab仿真实验

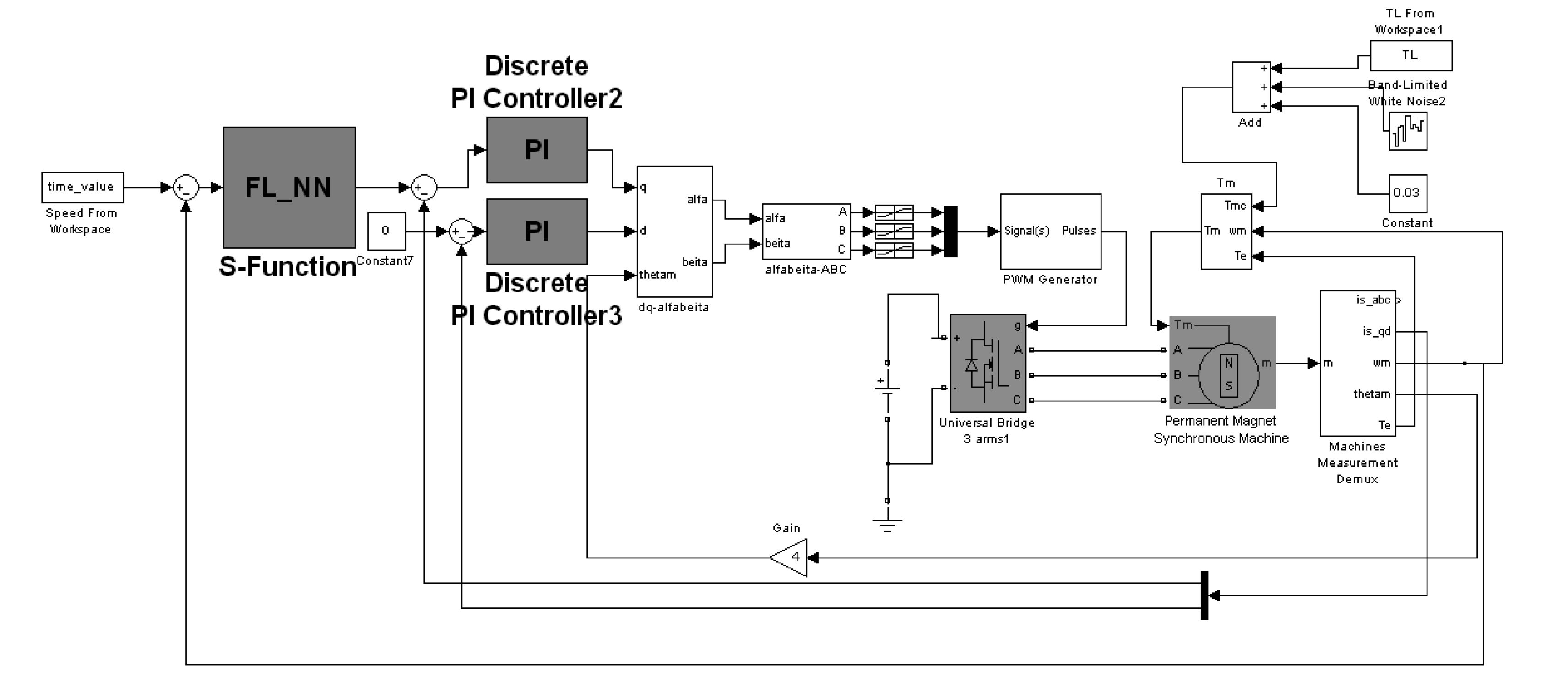
通过以上分析，在Matlab软件中搭建伺服控制系统仿真模型如图 3所示。实验参数设置为：定子等效电阻 R = 1.285 Ω，直轴等效电感 L _d = 9.8 × 10 ^–4 H，交轴等效电感 L _q = 9.8 × 10 ^–4 H，转动惯量 J = 1 × 10 ^–4 kg·m ²，摩擦因数 F = 5 × 10 ^–6 N·m·s，极对数 p = 4，转动时负载力矩 T = 0.03 N·m；

为了验证该模糊神经网络控制算法的动、静态控制性能，设置理想参考速度为 11 rad/s，并且在 t = 0.02 s的时候突加外部力矩 T _F = 0.1 N·m，通过与普通PI控制以及普通模糊控制做对比来验证其控制性能，仿真图如图 4所示。

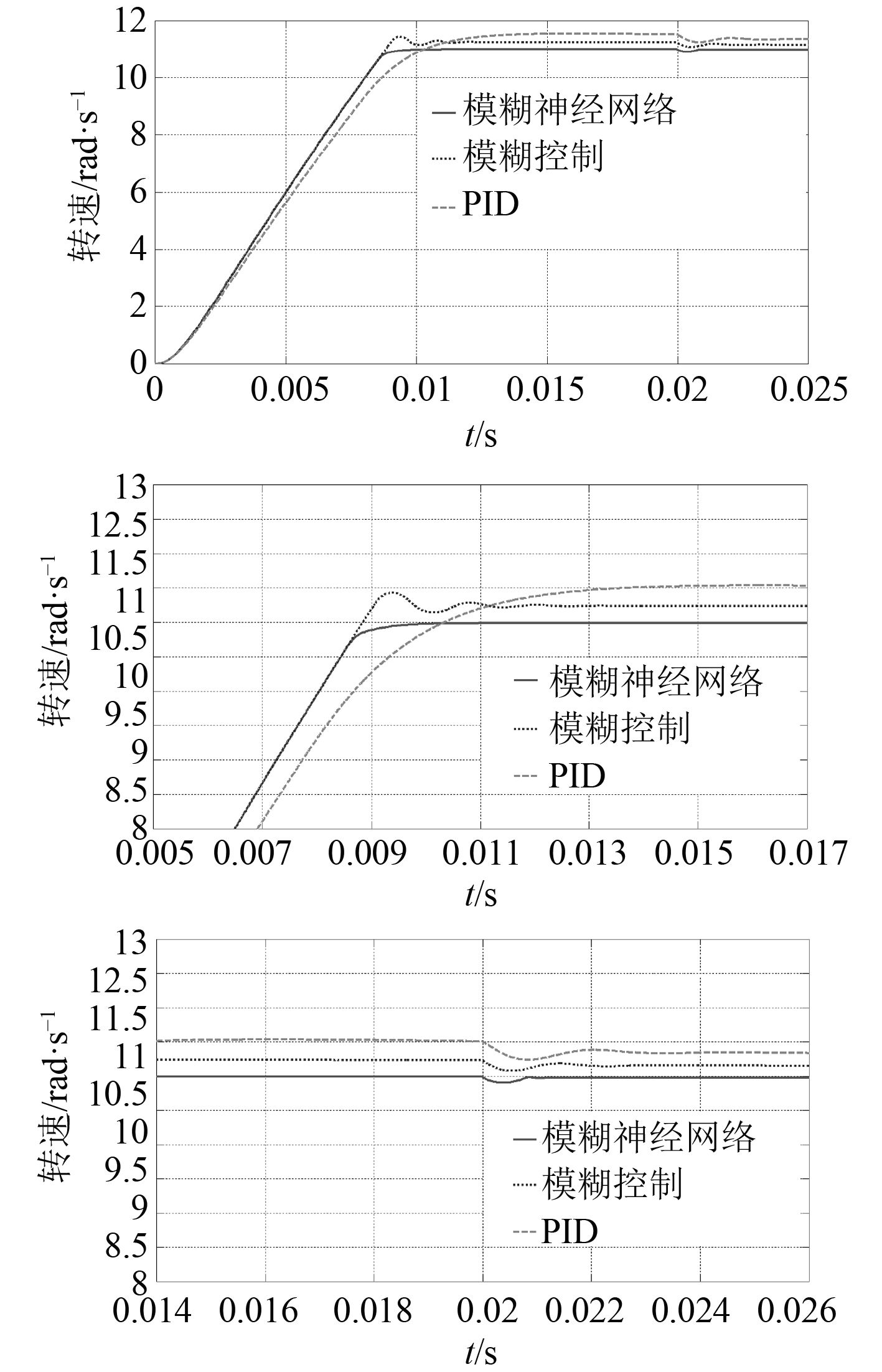
为了验证控制器的鲁棒性，改变电机模型的参数，使得转动惯量变为原来的 2 倍，仿真对比结果如图 5所示。

通过第 1 组仿真结果可以发现在系统固定不变的情况下，通过人为的调整控制参数，用传统PID控制可以获得性能一般的响应曲线，这主要是由于PID控制是一种线性控制，各个参数相互制约，性能的好坏最后是一个折中考虑的问题，相比之下模糊控制和模糊神经网络控制性能表现要好很多，因为他们都是非线性控制，可以达到较高的控制性能，而且可以发现，模糊神经网络比模糊控制性能要好一些，这主要是因为模糊控制的隶属函数以及模糊规则等都是人为设置的，存在较大的主观因素，控制器的性能不一定可以达到最优，而模糊神经网络可以通过神经网络的反向修正不断趋近最优，通过离线训练可以达到很高的性能。

通过第 2 组仿真结果可看出，在系统参数变化的时候，PID控制受影响最大，动态性能以及稳态误差都变差了，这也是由PID控制的特点决定的，模糊控制受影响也比较明显，出现了一些震荡，稳态误差也变大了，这是由于模糊控制的鲁棒性很有限，相比之下模糊神经网络受影响很小，这是由于神经网络的学习能力使得控制器通过在线修正可以很快的实现参数调整，适应外界变化。

3 结 　语

具有参数和结构学习能力的模糊神经网络控制器在动、静态性能以及鲁棒性上都要优于传统PID控制以及模糊控制，能够在线调整控制器内部参数，适应外部环境变化并且使得控制性能不断趋近最优，满足光电跟踪系统伺服控制的准确性以及实时性要求，为伺服控制设计提供了一种可行的技术方案。