2. 三峡大学 新能源微电网湖北省协同创 新中心, 湖北宜昌 443002;
3. 三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002
2. New Energy and Micro Grid Collaborative Innovation Center in Hubei Province, China Three Gorges University, Yichang 443002, China;
3. Hubei Key Laboratory of Hydroelectric Machinery Design and Maintenance, China Three Gorges University, Yichang 443002, China
随着工业发展,在武器装备、雷达、工程机械、起重运输机械、森林灭火机械、机器人等装备机械,俯仰系统广泛运用于不同的领域。绝大多数设备受到随时间和空间变化的负载作用(如力、扭矩等)及意外冲击的影响,甚至设备本身就是变质量系统[1]。
进行仿真研究时,由于变质量系统的负载存在严重的非线性[1],在不同的运动状态下,模型负载参数变动较大,其转动惯量存在严重的不确定性,使得数学模型难以精确地反映实际运动控制过程中被控对象的特征和运动属性。因此,建立仿真模型及变质量俯仰系统位置伺服控制策略尤其重要。
现代工业和军事对齿轮传动系统和滚柱丝杠传动系统的传动性能要求的提高,研究复合传动动力学及伺服控制问题,有利于指导和提高变速器及其控制系统的研发效率。研究变质量俯仰系统位置伺服控制策略,旨在为变质量俯仰系统的实际控制过程提供参数参考。
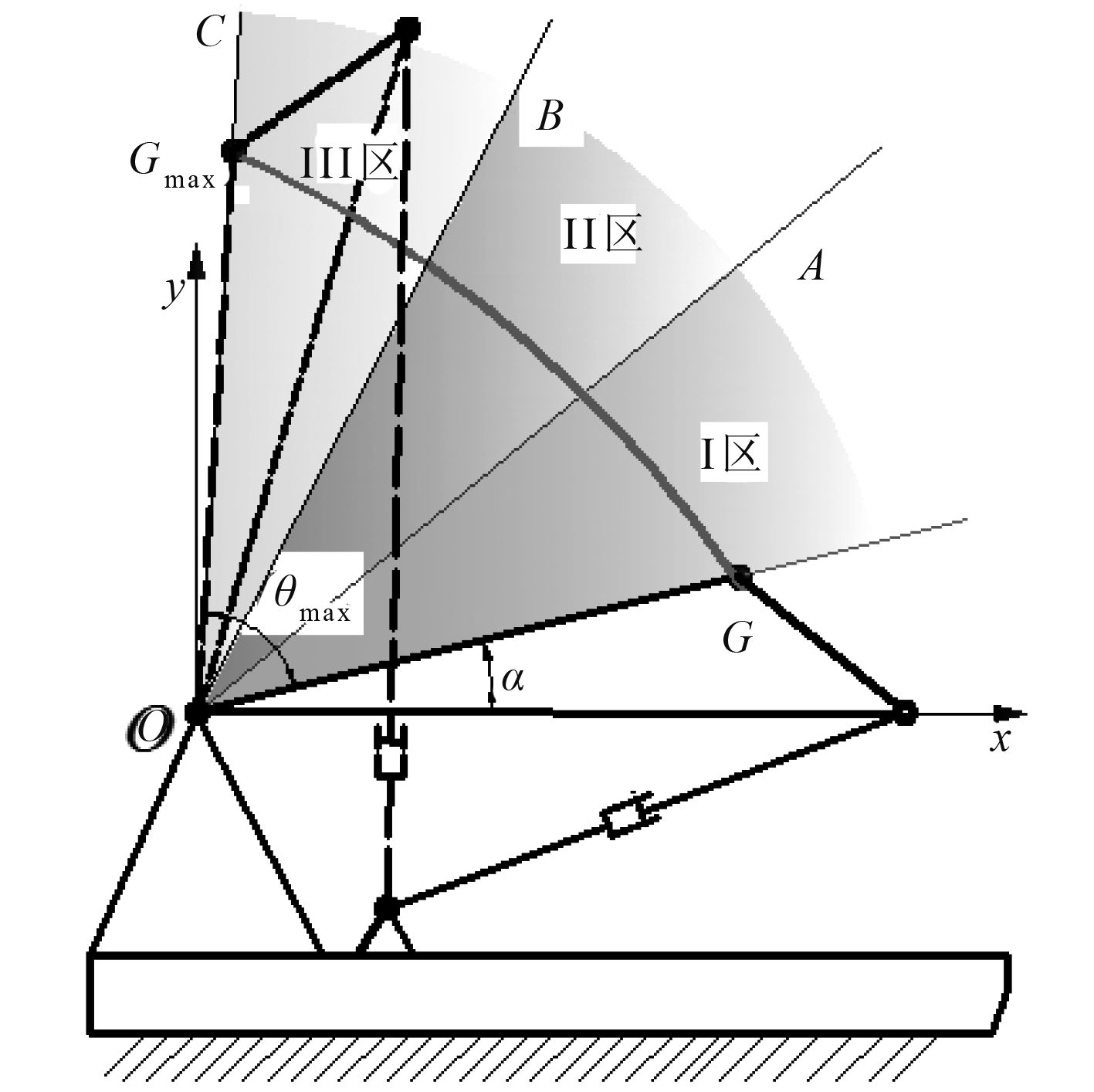
1 变质量俯仰系统特性如图 1所示为变质量俯仰系统机构简图,俯仰系统机构主要由底座、俯仰传动油缸、俯仰体组成。以俯仰体与底座铰接点处建立
xOy 坐标系,
G 点为俯仰体的重心,
θ 为任意时刻系统的俯仰角,任意时刻俯仰角位移的变化量与质心的角位移变化量相等,
a 为俯仰体质心的结构角,
|
|
表 1 俯仰体各区间驱动转矩参数变化过程 Tab.1 Change process of driving torque parameters in different range of pitch |
|
图 1 变质量俯仰系统机构简图 Fig. 1 Variable mass pitch system mechanism diagram |
位置伺服系统是基于位置误差和误差变化控制的系统,传统的伺服驱动器和运动控制器等受硬件和控制算法复杂度的制约,仍采用了PID或改进的PID控制器。常规PID控制原理简单、容易实现,在控制具有确定模型的线性过程中也取得了良好的控制效果。但位置伺服系统运行情况复杂,具有参数的时变性和模型的不确定性,系统辨识与建立模型涉及诸多因素,如摩擦特性、扰动扭矩、机械系统的刚度和惯量,难以建立精确的数学模型。传统PID控制参数在线实时整定困难,对不确定性的非线性过程的系统难以进行有效控制[2 –5]。
通过大量的仿真实验发现,当俯仰角不同的区间内,通过补偿和修正一些参数,可以使得更接近预期的效果。本文针对具有参数不确定性的一类热工对象,提出变质量俯仰系统分区间PID位置跟踪控制方法。
2 分区间PID三环控制策略 2.1 控制策略变质量俯仰系统位置控制所研究的被控制量是俯仰体的角位移。当俯仰位置给定变化时,控制系统的任务是使系统输出快速而准确地复现输入,即要求俯仰体能够及时地复现俯仰位置输入的变化[6 –7]。
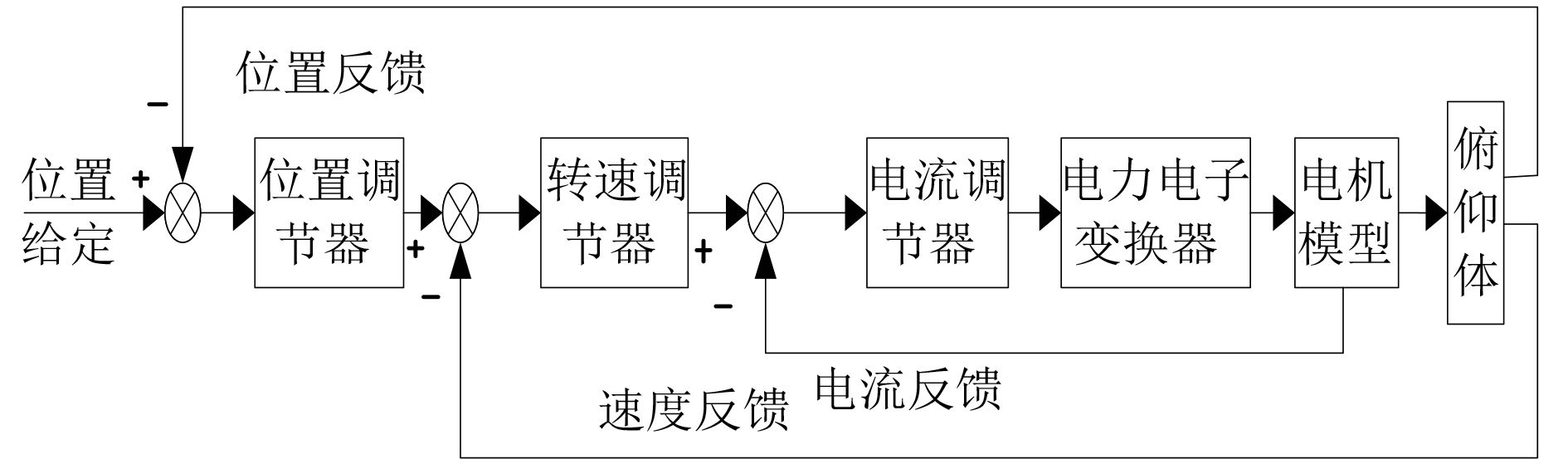
典型的的三闭环PID控制系统由位置环、速度环和电流环组成,如图 2所示,根据系统要求,选择直流电机作为驱动电机,采用三闭环PID控制系统以提高变质量俯仰系统的位置响应精度。由位置给定和位置检测信号的差值经过位置调节器输出,作为转速给定;转速给定值和转速检测值的差值经过转速调节器输出,作为电流给定;电流环作为最内环,可以快速的跟踪电流给定。其中电流环和速度环的给定来自速度反馈和位置反馈,位置环的给定来自电机的转速输出,电流经过PWM脉宽调制之后得到控制电压,控制电机的转速,电机即通过减速器后带动负载转动,达到控制位置的目的。
|
图 2 俯仰传动机电三环控制系统组成 Fig. 2 Diagram of pitch drive electromechanical system |
多闭环控制系统调节器的设计方法是从内环到外环,逐个设计各环的调节器。在本系统中,先将ASR和ACR设计好后,再设计APR。这样的逐步设计保证了每个控制环都是稳定的,从而保证了整个系统的稳定性。当电流环和转速内环的对象参数变化或者受到扰动时,电流反馈和转速反馈能起到及时的抑制作用,使之对位置环的影响较小。
2.2 三环控制系统设计1)电流环调节器设计
电流环调节器一般设计为PI控制器,需要考虑启动电流超调的问题。电流环控制对象为PWM逆变器(包括PWM信号形成、延时、隔离驱动及逆变器)、电机的电枢回路、电流采样和滤波电路。电流环主要作用是限制电流,因而电流的跟随作用尤为重要,一般将电流环校正成典型 Ⅰ 型系统。电流环PI控制器传递函数为:
| ${W_{ACR}}(s) = {K_{pi}} + \frac{{{K_{ii}}}}{s} = \frac{{{K_{pi}}({\tau _i}s + 1)}}{{{\tau _i}s}}\text{,} $ | (1) |
式中:
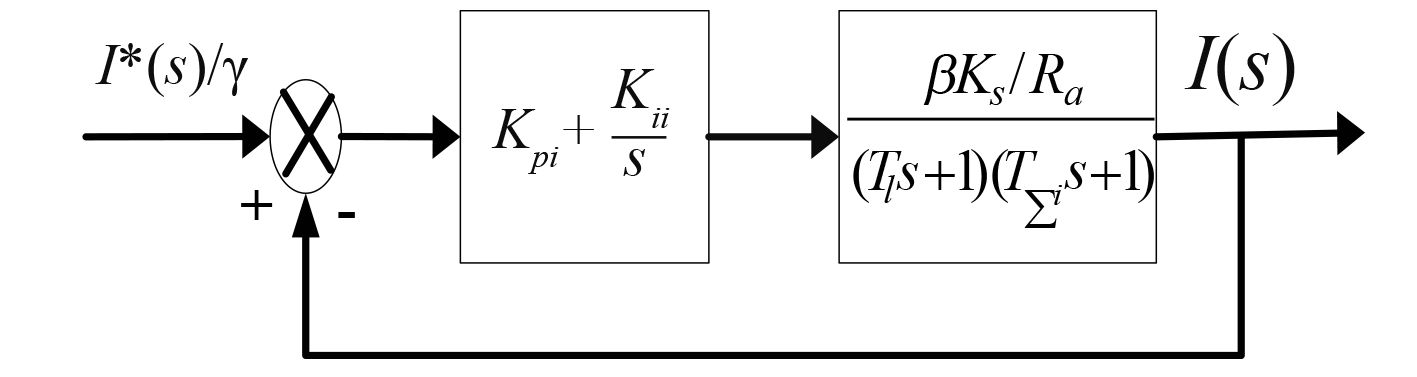
图 3所示为电流环动态结构图。
|
图 3 电流环动态结构图 Fig. 3 Current loop dynamic structure |
则电流环开环传递函数为:
| ${W_{opi}} = \frac{{I(s)}}{{{I^ * }(s)/\gamma }} = \frac{{{K_{pi}}({\tau _i}s + 1)}}{{{\tau _i}s}}\frac{{\beta {K_s}/{R_a}}}{{({T_l}s + 1)({T_{\sum i }}s + 1)}}\text{。} $ | (2) |
式中:
2)速度环调节器设计
为实现速度环输出控制无静差,在负载扰动前必须有一个积分环节,因此,速度控制器一般设计为PI控制器,考虑到实际系统的调试中,电机有额定的最高转速,需要考虑限速的问题。一般将速度环校正成典型 Ⅱ 型系统。速度环PI控制器的传递函数为:
| ${W_{ASR}}(s) = {K_{pn}} + \frac{{{K_{in}}}}{s} = \frac{{{K_{pn}}({\tau _n}s + 1)}}{{{\tau _n}s}}\text{,} $ | (3) |
式中:
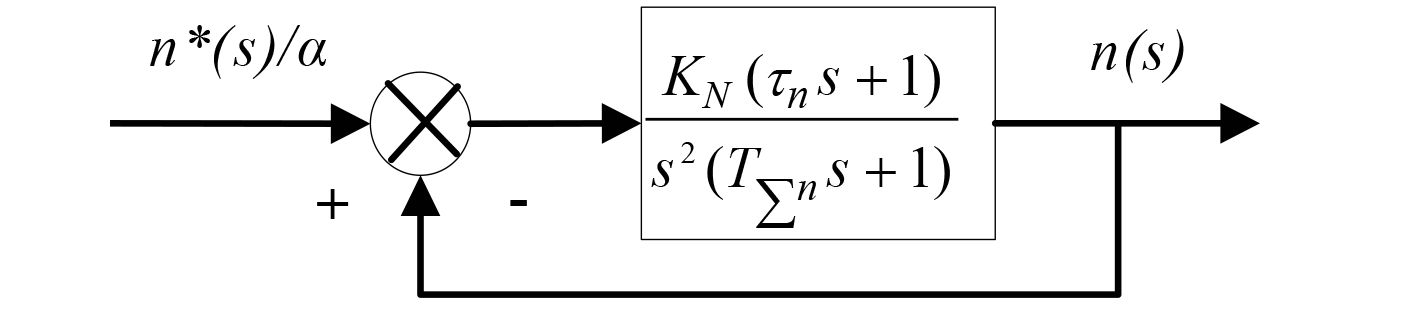
如图 4,则速度环开环传递函数为:
| ${W_{opn}}(s) = \frac{{{K_N}({\tau _n}s + 1)}}{{{s^2}({T_{\sum n }}s + 1)}}\text{。} $ | (4) |
式中:速度开环增益公式为
|
图 4 速度环动态结构图 Fig. 4 Speed loop dynamic structure |
3)位置环调节器设计
随动系统要求输出量准确跟随给定量的变化,输出响应要求具有快速性、灵活性、准确性等特征。位置随动系统的主要结构特征是位置环,即主导控制器是位置控制器,它的作用是使位置信号 θ 跟随给定信号 θ ref 的变化,其性能直接决定了系统的控制性能。根据经验,一般将位置环设计成典型 Ⅰ 型系统,位置环设计成一个比例放大环节 K p ,比例作用 K p 使得控制器的输入与输出成一一对应比例关系,一有偏差立即会产生控制作用。因此,比例控制基于偏差进行调节,为了尽量减小偏差同时也为了加快响应速度,缩短调节时间,就需要增大 K p ,但是 K p 又受到系统稳定性的限制,不能任意增大,可保证系统无超调且具有良好的跟随性能。变PI控制的思想是由工程实践中产生,PID控制针对俯仰系统变质量变负载的复杂工况,存在一定的局限性[8]。当一组固定的 K p 参数不能更好的获取准确地、快速地的响应时,根据变质量俯仰系统俯仰角不同的工作区间,对应不同的 K p 参数,从而大大提高了控制的性能。位置环控制器传递函数为:
| ${W_{APR}}(s) = {K_p} = \left\{ {\begin{array}{*{20}{c}}{{K_{p1}},\quad \theta \in I}\text{,} \\{{K_{p2}},\quad \theta \in Ⅱ}\text{,} \\{{K_{p3}},\quad \theta \in Ⅲ}\text{。} \end{array}} \right.$ | (5) |
其中 K p1 , K p2 , K p3 分别为I,Ⅱ,Ⅲ 区间的位置环比例系数。
位置环闭环传递函数结构如图 5所示。

|
图 5 位置环动态结构框图 Fig. 5 Position loop dynamic structure |
位置控制系统是包括 1 个积分环节和 3 个小惯性环节。将时间常数分别为
| ${T_{\sum p }} = {T_{op}} + 1/{\omega _{cn}} + {T_{\sum n }}\text{,} $ | (6) |
| ${K_\theta } = 6N\gamma {K_p}/\alpha \text{,}$ | (7) |
位置环闭环传递函数可简化为:
| ${{\rm{W}}_{c\ln }}(s) = \frac{{\theta (s)}}{{{\theta ^ * }(s)/\gamma }} = \frac{{{K_\theta }/{T_{\sum p }}}}{{{s^2} + \frac{1}{{{T_{\sum p }}}}s + \frac{{{K_\theta }}}{{{T_{\sum p }}}})}}\text{。}$ | (8) |
式中,
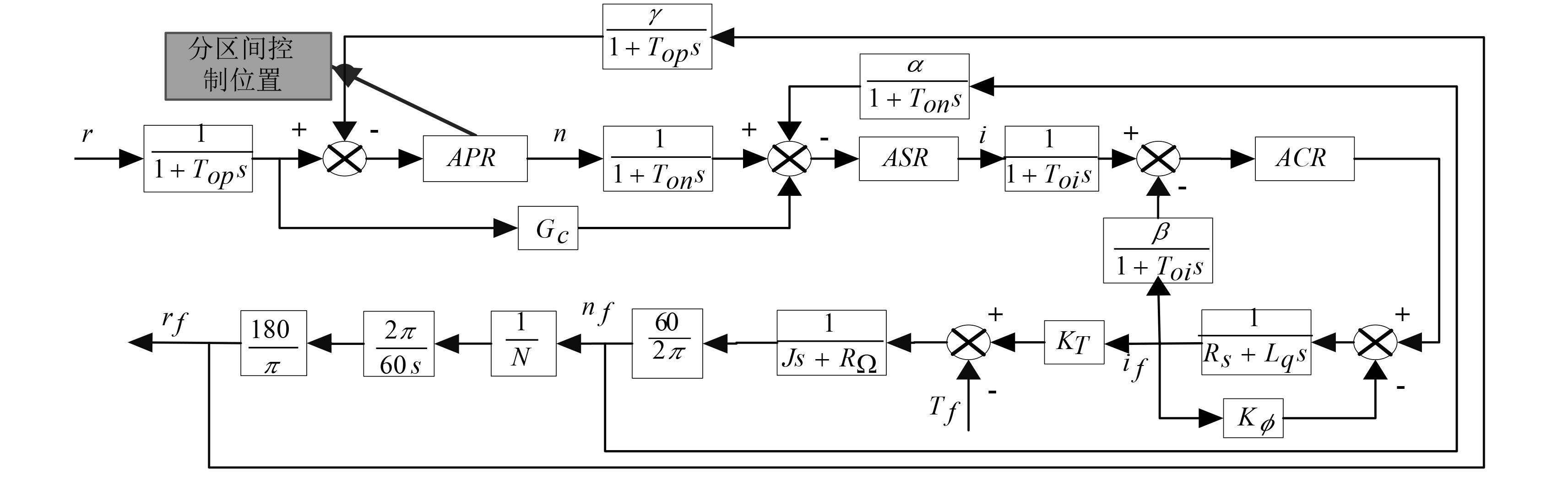
综上,如图 6所示为整个三环控制系统传递函数控制框图。图中
|
图 6 三环控制系统传递函数控制结构图 Fig. 6 Three-loop control system transfer function of control chart |
在进行大量仿真实验基础上,通过不断调试,得出表 2所示控制参数,变质量俯仰系统的俯仰角分为 3 个个区间,0°~ 20° 为第 Ⅰ 个区间;20°~40° 为第 Ⅱ 个区间;40°~ 60° 度为第 Ⅲ 个区间。其中无论是经典PID,还是分区间PID电流环的 K p 、 K i ,速度环的 K p 、 K i 的参数均固定不变,这是由于其参数跟所选俯仰电机的额定参数有关,不同的是经典PID位置环 K p 参数是固定的,而分区间PID位置环 K p 参数由控制器根据给定输入位置信号的大小来自行判断来给定。
|
|
表 2 经典PID和分区间PID各控制器参数 Tab.2 Controller parameters of classical PID and inter-partition PID |
基于ADAMS与Matlab/Simulink实现变质量俯仰机系统机械与控制联合仿真方法,机电联合仿真平台建模技术包括三维建模、动力学建模、控制系统建模以及接口技术。对机械系统采用PROE建模,动力学采用ADAMS建模,控制系统才Matlab软件的Simulink模块实现,联合仿真平台为ADAMS/View模块和ADAMS/Control模快。
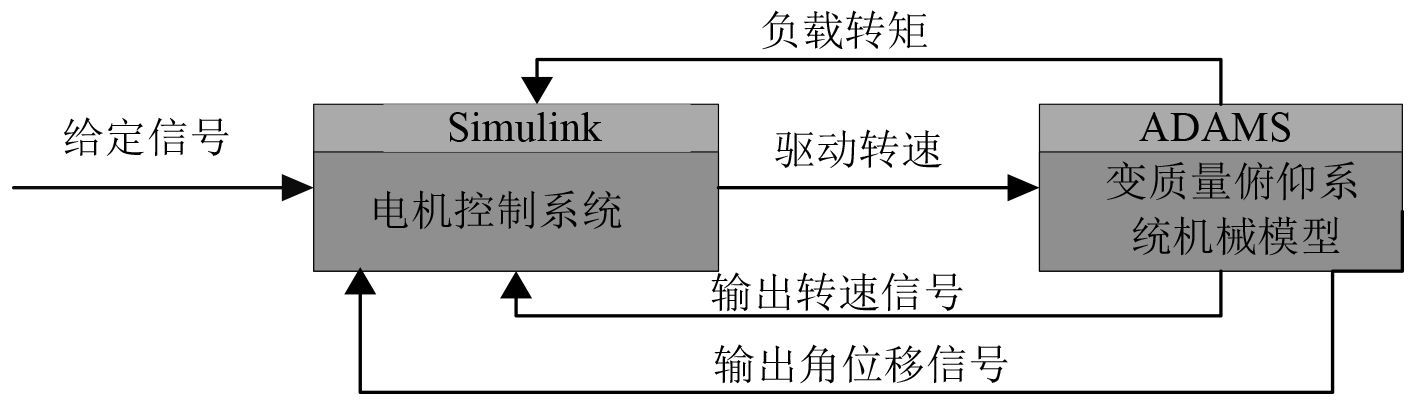
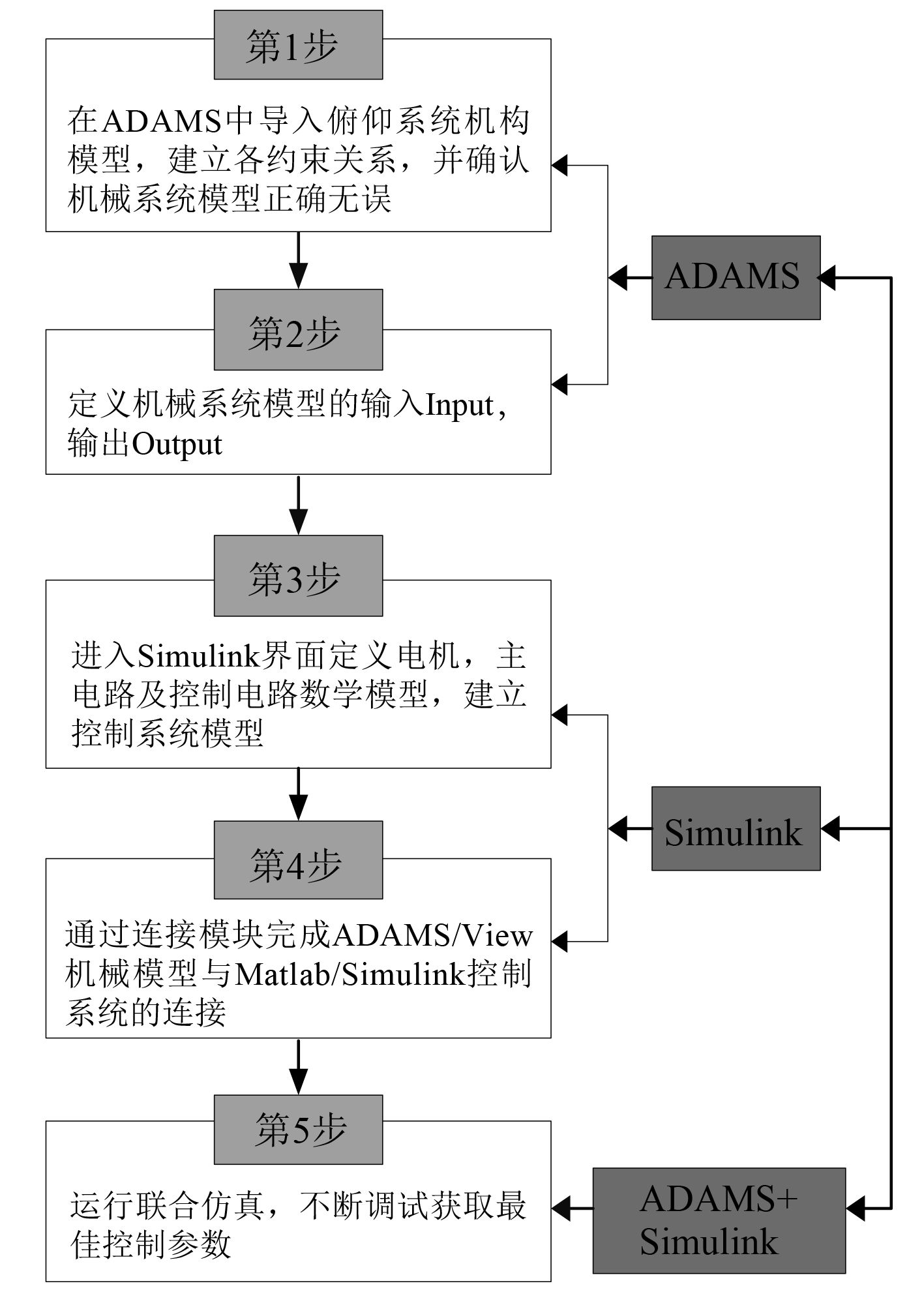
ADAMS/Controls模块可以将机械系统仿真分析工具(ADAMS)同控制系统设计仿真软件(MATLAB)有机连接起来,实现复杂机电系统联合仿真[9]。ADAMS和Simulink联合仿真原理图如7所示。在ADAMS中定义机械系统输入变量(包括电机角速度)、输出变量(包括俯仰体角位移、角速度及负载扭矩变量),具体实现步骤如图 8所示。
|
图 7 ADAMS与Simulink联合仿真控制原理图 Fig. 7 ADAMS and Simulink simulation control flow chart |
|
图 8 变质量俯仰系统机械与控制仿真步骤 Fig. 8 Variable mass luffing mechanism simulation steps of mechanical system and control system |
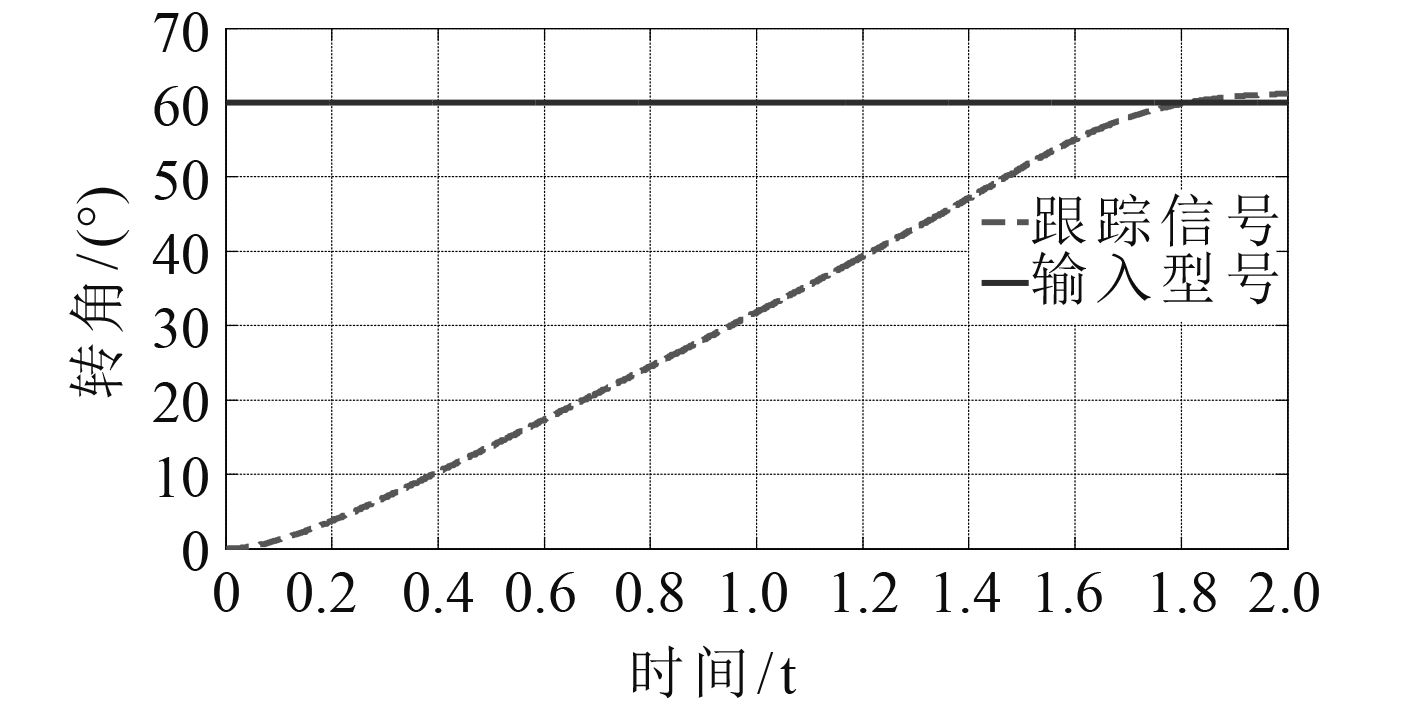
变质量俯仰系统经典PID控制和分区间PID控制仿真中,分别用俯仰角为给定的
|
图 9 阶跃信号的响应曲线(经典PID) Fig. 9 The response curve of the step signal(Classical PID) |
|
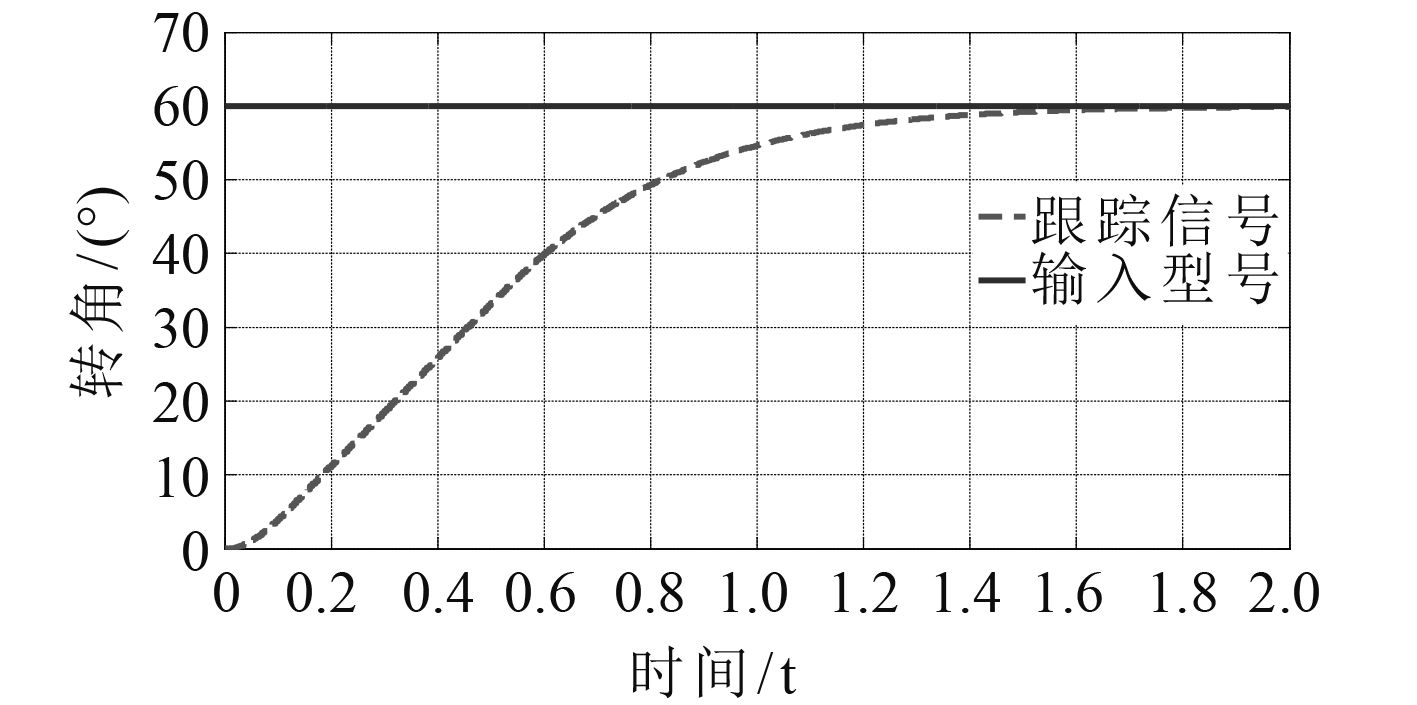
图 10 阶跃信号的响应曲线(分区间PID) Fig. 10 The response curve of the step signal(Inter-partition PID) |
|
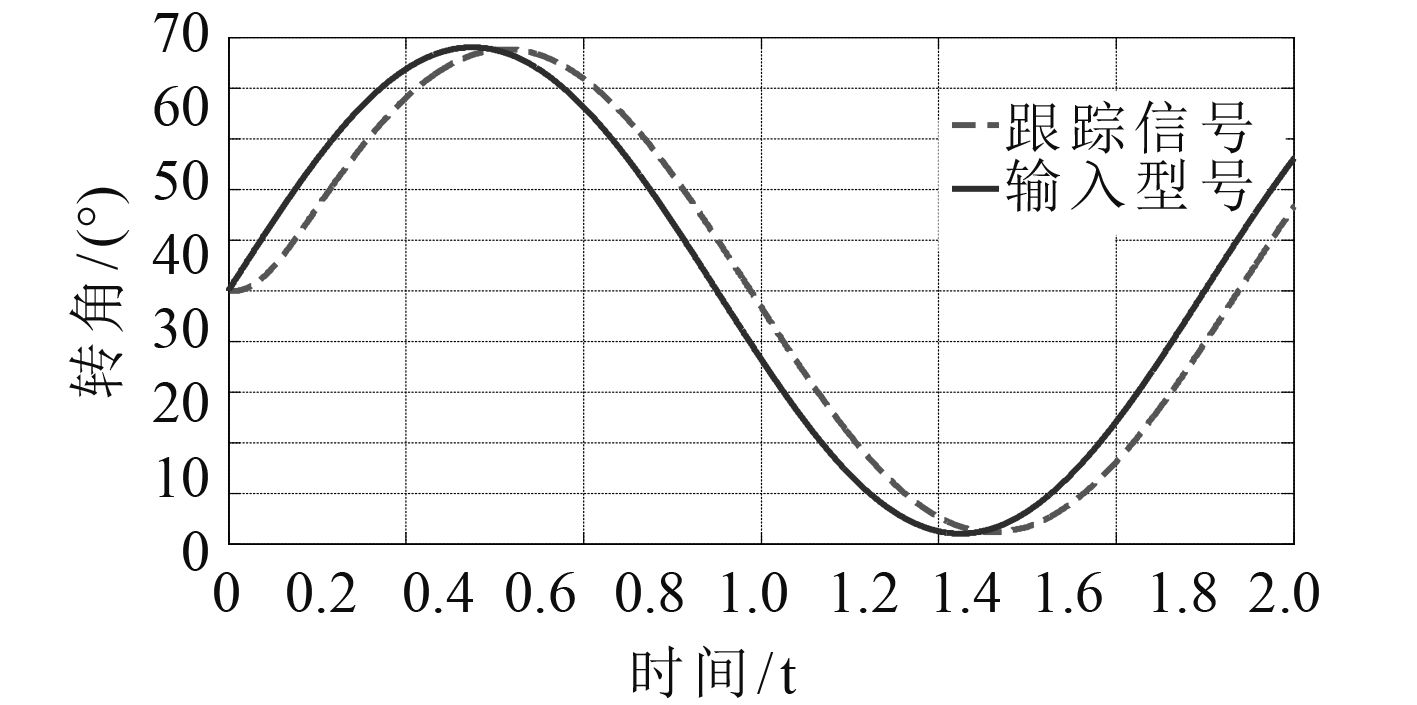
图 11 正弦信号的响应曲线(经典PID) Fig. 11 The response curve of the sinusoidal signal(Classical PID) |
|
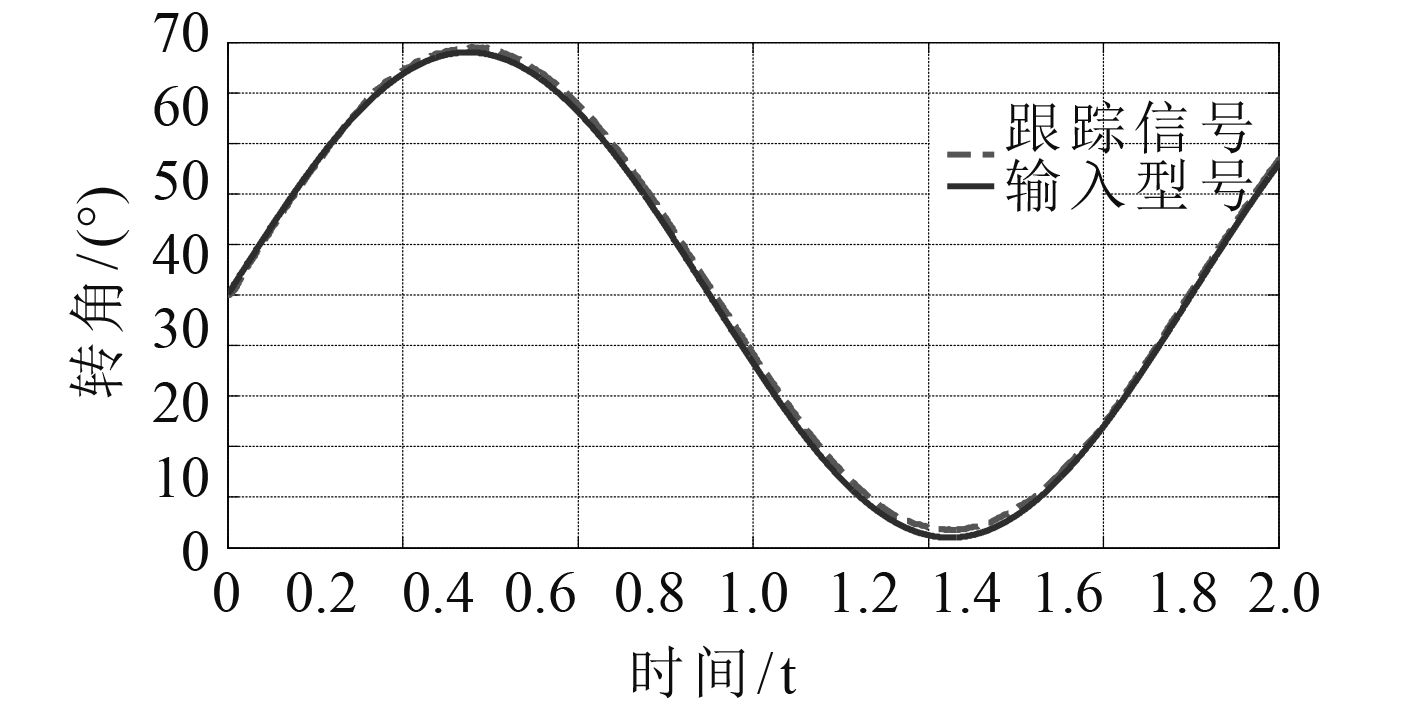
图 12 正弦信号的响应曲线(分区间PID) Fig. 12 The response curve of the sinusoidal signal(Inter-partition PID) |
如表 3和表 4,当给定输入
|
|
表 3 阶跃信号输入时俯仰系统俯仰运动位置响应曲线 Tab.3 The position response curve of the pitching system with the step signal input |
|
|
表 4 正弦信号输入时俯仰系统俯仰运动位置响应曲线 Tab.4 The position response curve of the pitching system with sinusoidal signal input |
不论是俯仰空载还是俯仰满载的反馈曲线,分区间PID的控制策略都能满足系统控制精度,满足系统负载要求。对比经典PID控制系统,分区间PID控制系统满足功能上的俯仰角度区间要大。
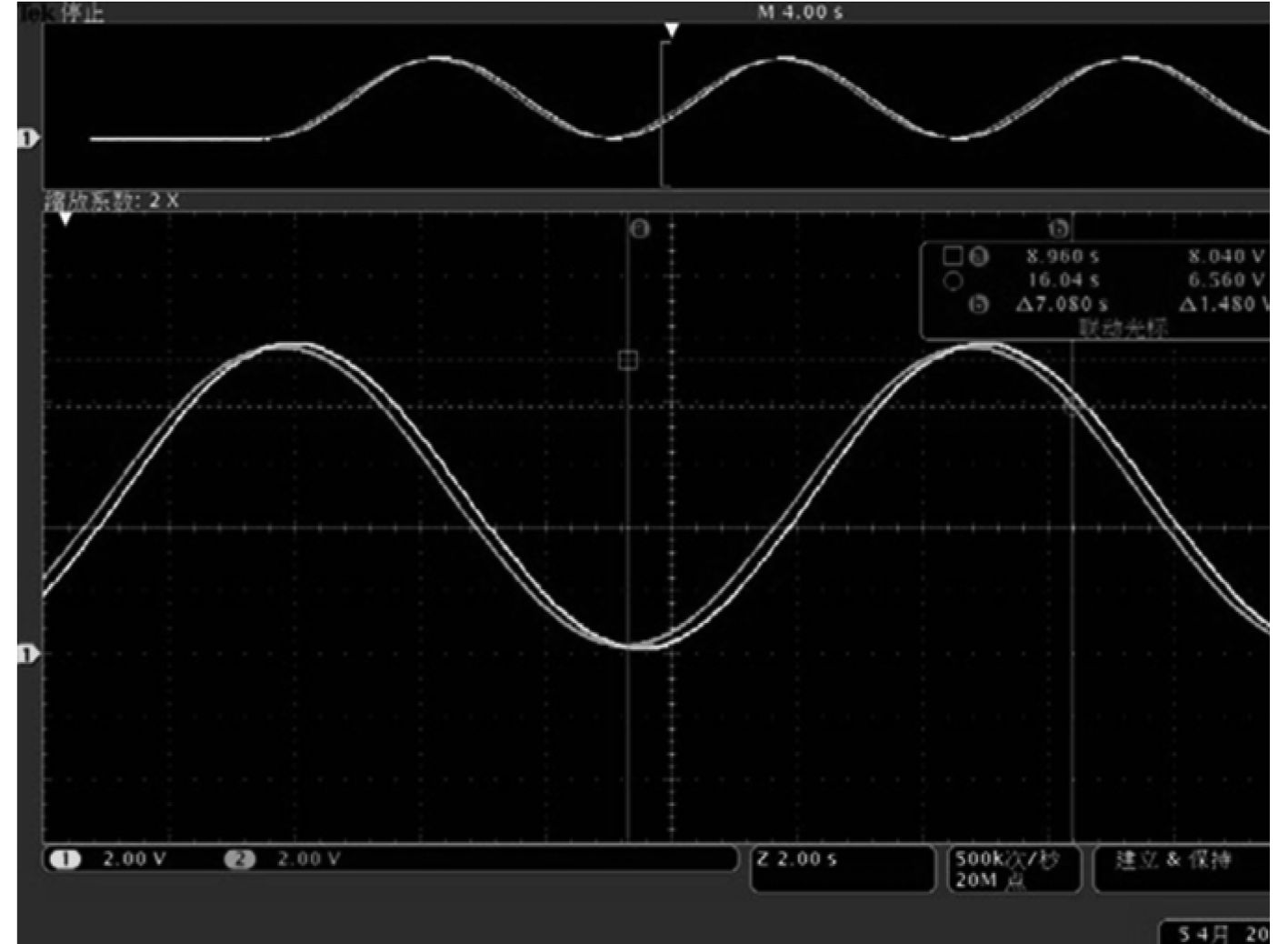
4 控制系统试验研究对变质量俯仰系统进行试验,驱动装置由SG7100 型交流伺服驱动器与 1FT5 型交流永磁同步电机构成。对控制系统进行样机控制系统调试试验,控制系统分区间PID控制系统,给定幅值 30°、周期为 10 s的角位移跟踪信号,变质量俯仰系统的俯仰运动试验跟踪信号试验结果如图所示。
|
图 13 变质量俯仰系统经典PID跟踪曲线 Fig. 13 The test curve of variable mass luffing system sine tracking (Classical PID) |
变质量俯仰系统装置物理样机模型分别满载工况和空载工况 2 种条件下进行测试,分别针对 2 种不同的控制算法,在给定正弦信号条件,得到如表 5和表6的正弦信号跟踪系统响应曲线相关数据统计。
|
|
表 5 经典PID正弦信号输入系统响应曲线 Tab.5 Classic PID sine signal input system response curve |
|
|
表 6 分区间PID正弦信号输入系统响应曲线 Tab.6 Inter-partition PID sine signal input system response curve |
从表中可看出,无论是满载工况,还是空载工况,2 种控制方式都能比较稳定、快速的跟踪正弦信号。但相对来说,经典PID的滞后时间明显比分区间PID的大。对变质量俯仰系统行联合仿真的大量实验基础上得到各种参数,设计出变质量俯仰系统实验模型。在经典PID控制算法和分区间PID控制算法进行了变质量俯仰系统的运动物理样机调试试验研究,试验结果与仿真结果基本一致,验证了所建立机械模型和控制方法的可行性、正确性、快速性和稳定性。

|
图 14 变质量俯仰系统分区间PID跟踪曲线 Fig. 14 The test curve of variable mass luffing system sine tracking (Inter-partition PID) |
在研究变质量俯仰系统在虚拟样机仿真技术的基础上,以变质量俯仰系统装置虚拟样机为研究对象,以提高传动系统的位置控制快速性和准确性及减小转速波动为主要目标,提出分区间PID控制算法,通过仿真与物理样机试验,对比分析经典PID和分区间PID控制算法的位置控制准确性和快速性。所做的研究工作和结论如下:
1)建立适用于永磁同步电机的三环PID控制系控制模型。
2)针对经典PID控制系统在工程实践中的缺点,提出了位置环分区间PID控制策略,通过大量的仿真实验和实物试验,验证了分区间PID控制策略的适用性、准确性。
3)物理样机试验,验证了分区间PID控制算法能有效提高变质量俯仰系统控制精度。
| [1] | 方子帆, 高术, 周刚, 等. 大俯仰机构布局方案优化方法及应用研究[J]. 机械设计与研究, 2015, 31 (1): 17–21. |
| [2] | 刘金琨.先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2004:102–128. |
| [3] | Xu Wujiao, Qin Datong, Shi Wankai. Research and development of a digital design system for hull structures[J]. Journal of Marine Science and Application, 2007, 02 (19): 37–43. |
| [4] | Dong-Chan Lee, Chang-Soo Han. CAE (computer aided engineering) driven durability model verification for the automotive structure development[J]. Finite Elements in Analysis and Design, 2009, 45 (5): 324–332. DOI: 10.1016/j.finel.2008.10.004 |
| [5] | JAULINL, LIEFFERMN, DIDRITO, et al.Applied interval analysis with examlples in parameter and state estimation, robust control and robotics[M]. springer-Verlag, 2001. |
| [6] | KharitonovVL. Asymptotic stability of an equilibrium position of a family of systems of linear differential equtions[J]. Differential Equtions, 1978, 14 : 2086–2088. |
| [7] | Chapellat H, Bhattacharyya S P. A generalization of Kharitonov’s theorem:Robust stability of interval plants[J]. IEEE-Tr-Auto-Control, 1990, 34 (3): 306–311. |
| [8] | 徐峰, 李东海, 薛亚丽, 李政, 等. 基于区间多项式稳定性理论的PID控制器[J]. 清华大学学报(自然科学版), 2003, 12 : 1642–1645. DOI: 10.3321/j.issn:1000-0054.2003.12.017 |
| [9] | 李斌茂, 钱志博, 程洪杰, 等. AUV发动机的ADAMS/MATLAB联合仿真研究[J]. 系统仿真学报, 2010, 22 (7): 1668–1673. |
 2017, Vol. 39
2017, Vol. 39
