水下航行器在高速航行时,由于质量不大而动力较大以及外形原因,使得单边横滚转矩明显,严重影响航行器的稳定且易引起侧翻。所以像鱼雷等中小型水下航行器大都采用对转螺旋桨推进结构,由两同轴螺旋桨,1部正转1部反向旋转构成,分别产生 2 个大小相等方向相反的单边扭矩,如果电机控制合理,2 个单边扭矩就可以完全抵消,达到消除横滚和侧翻且提高动力的目的[1]。
在风力发电和水下航行器中常会用到此种对转结构,此外电动航模直升机等一些需要消除横滚转矩的地方,都可考虑使用对转推进结构,但需要 2 个转子同时对转[2]。实现双转子对转目前有 3 种方法:1)反向安装 2 台完全一样的普通电机。此种方法简单易实现,但是体积过大,成本较高;2)只安装 1 台电机,通过复杂的机械变速结构将 1 台电机的动力转换成 2 个异向旋转的动力。但此方法使系统过于复杂机械磨损大,鲁棒性降和效率降低;3)采用新型结构的对转式双转子永磁同步电机,该电机由 2 根轴传递动力效率高、体积小,提高了航行器推进系数并可增强推进装置功能[3]。
本文对水下航行器推进用新型对转式双转子永磁同步电机进行研究,该电机的最大特点是有 1 个电输入和 2 个独立的机械输出。 1 台电机就可实现对转双机械端口输出,不仅体积小、重量轻,降低了成本,而且没有电刷,安全可靠性高[4]。通过内外推进轴直接带动正反转螺旋桨转动,在有效避免中小型水下航行器发生侧滚现象和保证航行器前进姿态的同时,还可明显降低推进系统的机械传动噪声,整体运行效率提高。对转螺旋桨(CRP)系统之所以高效的原因在于,前桨产生的涡动能量则可以通过后桨加以回收。此外,对于相同的推力要求,对转螺旋桨降低了单个桨所承受的负荷,减少了空泡噪声,因而也改善了螺旋桨的效率。经研究表明,对转螺旋桨推进系统的节能效果可达 10%~20%[5 –6]。因此,它被广泛应用于各种水上、水下装备中。
1 电机工作原理与数学模型双转子电机的内外转子与定子是由 2 个旋转磁场耦合在一起的,这与传统电机有很大不同。在定子内外两侧的三相对称绕组中通入三相对称电流,产生旋转磁场。定子磁通被分为两部分,分别穿过内外气隙与 2 个转子交链,此时可在转子侧产生各自的电磁转矩。 2 个旋转磁场的磁通都经过定子铁心,它们分别与定子内外绕组交链,而定子内外绕组又是串联在一起的,故可以把这种电机简化看作为 2 个电机的串联。
|
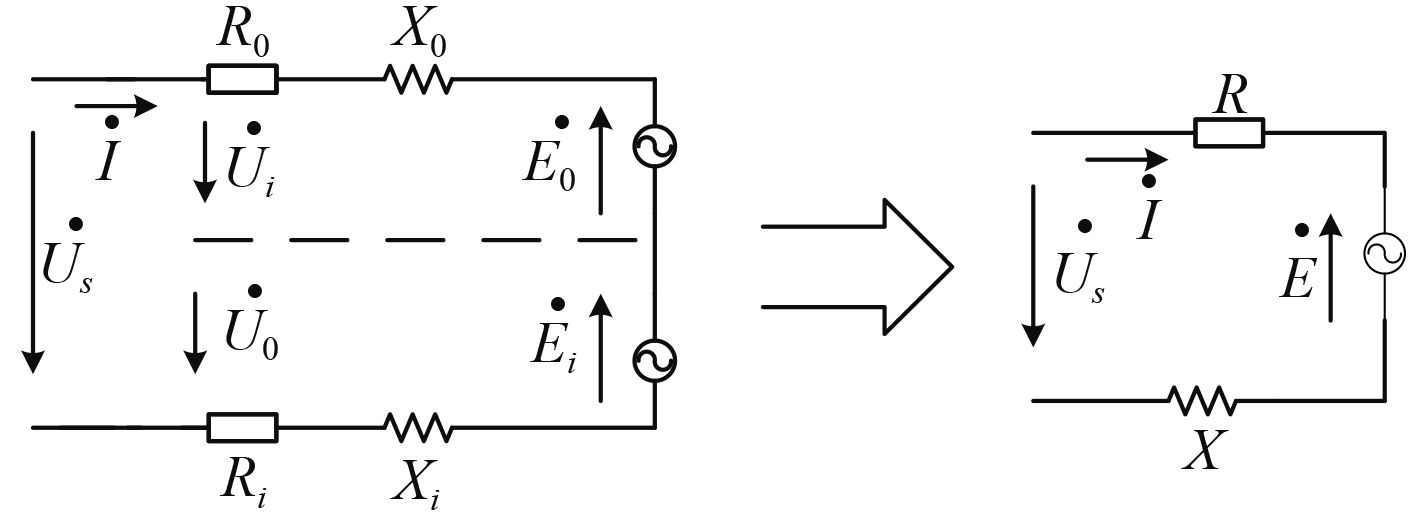
图 1 双转子电机等效电路 Fig. 1 Double rotor motor equivalent circuit |
对转式双转子永磁同步电动机的定子绕组可以等效成内、外永磁电动机的定子绕组相串联,此时有
| $\left\{ \!\!{\begin{array}{*{20}{c}}{{u_d} \!= \!{u_{d1}} \!+ \!{u_{d2}} \!= \! ({R_{s1}} \!+ \! {R_{s2}}){i_d} \!+ \! \frac{{d({\psi _{d1}} \! + \! {\psi _{d2}})}}{{{d_t}}} \!- \! \left( {{\omega _{r1}}{\psi _{q1}} \!+ \! {\omega _{r2}}{\psi _{q2}}} \right)}\text{,} \\[5pt]{{u_q} \!= \! {u_{q1}} \!+ \! {u_{q2}} \!= \! ({R_{s1}} \!+ \! {R_{s2}}){i_q} \!+ \! \frac{{d({\psi _{q1}} \!+ \! {\psi _{q2}})}}{{{d_t}}} \! + \! \left( {{\omega _{r1}}{\psi _{d1}} \!+ \! {\omega _{r2}}{\psi _{d2}}} \right)}\text{,} \end{array}} \right.$ | (1) |
式中:
| ${T_{e1}} = 1.5{n_{p1}}({\psi _{d1}}{i_{q1}} - {\psi _{q1}}{i_{d1}})\text{,}$ | (2) |
| ${T_{e2}} = 1.5{n_{p2}}({\psi _{d2}}{i_{q2}} - {\psi _{q2}}{i_{d2}})\text{,} $ | (3) |
| $\left\{ {\begin{array}{*{20}{c}}{\frac{{{\rm d}\omega _{r1}}}{{{\rm{d}}t}} = \frac{{n_{p1}}}{{J_1}}(T_{e1} - T_{L1} - \frac{{\omega _{r1}}}{{n-p}}B_{m1})}\text{,}\\[5pt]{\frac{{\rm d}{\omega _{r2}}}{{{\rm{d}}t}} = \frac{{n_{p2}}}{{J_2}}(T_{e2} - T_{L2} - \frac{{\omega _{r1}}}{{n_{p2}}}B_{m2})}\text{,}\end{array}} \right.$ | (4) |
式中:
电磁转矩可以表示为:
| $\begin{split}\\[-12pt]{T_e} = {T_{e1}} + {T_{e2}} = 1.5[({\psi _{d1}} + {\psi _{d2}}){i_q} - ({\psi _{q1}} + {\psi _{q2}}){i_d}] = \\ 1.5({\psi _d}{i_q} - {\psi _q}{i_d}) = 1.5[{\psi _{mf}}{i_q} + ({L_d} - {L_q}){i_d}{i_q}]\text{。} \end{split}$ | (5) |
矢量控制具有线性转矩特性,控制效率高,调节器设计易于实现,具有良好的起动性能和较宽的调速范围[7 –9]。对转永磁同步推进电动机的数学模型经过坐标变换后, i d 和 i q 之间仍存在着耦合,要获得良好的动、静态性能,就必须实现 i d 和 i q 的解耦。对转永磁同步推进电动机可等效看成 2 个电机串联,只需有效地控制定子,就可实现转速和转矩控制。如能控制 i d = 0,整个控制过程中就没有电枢反应的去磁问题,不涉及电机参数,实时性高、鲁棒性好。双转子永磁同步推进电动机的状态方程式为:
| ${U_q} = {R_s}{i_q} + ({L_{q1}} + {L_{q2}})p{i_q} + ({\omega _1}{\psi _{mf1}} + w{\omega _2}{\psi _{mf2}})\text{,} $ | (6) |
| $\left\{ {\begin{array}{*{20}{c}}{\frac{{{\rm d}\omega_{ r1}}}{{{\rm{d}}t}} = \frac{{n_{p1}}}{{J_1}}(1.5{n_p}{i_q}{\psi _{mf1}} - T_{L1} - \frac{{\omega _{r1}}}{{np}}B_{m1})}\text{,} \\[5pt]{\frac{{{\rm d}\omega_{ r2}}}{{{\rm{d}}t}} = \frac{{n_{p2}}}{{J_2}}(1.5{n_p}{i_q}{\psi _{mf2}} - T_{L2} - \frac{{\omega _{r1}}}{{np2}}B_{m2})}\text{。} \end{array}} \right.$ | (7) |
根据电机数学模型设计系统的状态变量为:
| $\left\{ \begin{array}{l}{x_1} = {\omega ^*} - \omega \text{,}\\[5pt]{x_2} = \int_{ - \infty }^t {{x_1}} {\rm{d}}t = \int_{ - \infty }^t {({\omega ^*} - \omega ){\rm{d}}t} \text{。}\end{array} \right.$ | (8) |
式中
对上式求导可得:
| $\left\{ \begin{array}{l}\mathop {{x_1}}\limits^ \cdot = - \mathop \omega \limits^ \cdot = - \frac{{3p\psi }}{{2J}}{i_q} + \frac{1}{J}{T_L}\text{,}\\[5pt]\mathop {{x_2}}\limits^ \cdot = {x_1} = {\omega ^*} - \omega \text{,}\end{array} \right.$ | (9) |
文献[8] 中所取滑模面包含速度误差的微分量,会引入高频噪声。本文在常规滑模面的基础上加入状态量的积分量,得到积分滑模面为:
| $s = {x_1} + c{x_2}\text{,}$ | (10) |
选取积分初始值:
| ${I_0} = \int_{ - \infty }^0 {{x_1}} (\tau ){\rm{d}}\tau = - \frac{{{x_0}}}{c}\text{。}$ | (11) |
式中: x 0 为 x 1 初始状态; I 0 为积分初始值; c 为积分常数。当 t = 0 时, s = 0,此时系统开始在滑模面上运动,使系统具有全局鲁棒性。另外,积分作用可以消除稳态误差。
3.2 控制律的选取对式(10)求导得:
| $\dot s = \mathop {{x_1}}\limits^ \cdot + c{x_1} = - \frac{{3p\psi }}{{2J}}{i_q} + \frac{B}{J}\omega + \frac{1}{J}{T_L} + c{x_1}\text{。}$ | (12) |
为提高系统的动态品质,采用指数趋近律法设计控制器。指数趋近律的表达式为:
| $\dot s = - \varepsilon {\mathop{\rm sgn}} (s) - ks\text{,}$ | (13) |
由式(12)和式(13)可得:
| ${i_q} = \frac{{2J}}{{3p\psi }}[c{x_1} + \frac{B}{J}\omega + \frac{1}{J}{T_L} + \varepsilon {\mathop{\rm sgn}} (s) + ks]\text{,}$ | (14) |
滑模控制系统中高频抖振问题不可避免,对抖振的合理抑制是实现精确控制的关键。指数趋近律法减弱滑模抖振效果良好。此外,采用饱和函数
| ${\rm{sat}}(s,\delta ) = \left\{ {\begin{array}{*{20}{c}}{1,}&{s > \delta }\text{,}\\{s/\delta ,}&{\left| s \right| < \delta }\text{,}\\{ - 1,}&{s < - \delta }\text{,}\end{array}} \right.$ | (15) |
| ${i_q} = \frac{{2J}}{{3p\psi }}[c{x_1} + \frac{B}{J}\omega + \frac{1}{J}{T_L} + \varepsilon {\rm{sat}}(s,\delta ) + ks]\text{。}$ | (16) |
根据以上对转永磁电机数学模型与控制研究, 利用Matlab/Simulink建立电机的仿真模型, 对 2 个转子分别进行空载、加平衡负载和不平衡负载, 模拟航行器在水下受到水流扰动时 2 个螺旋桨的受力。当航行器受到干扰时,两转子转速发生变化,若不能有效地减弱和消除扰动,航行器会失去平衡。对内外 2 个转子采用相同的参考转速, 分别进行PI调节。
|
|
表 1 对转永磁同步电机参数 Tab.1 Counter rotating permanent magnet synchronousr motor parameters |
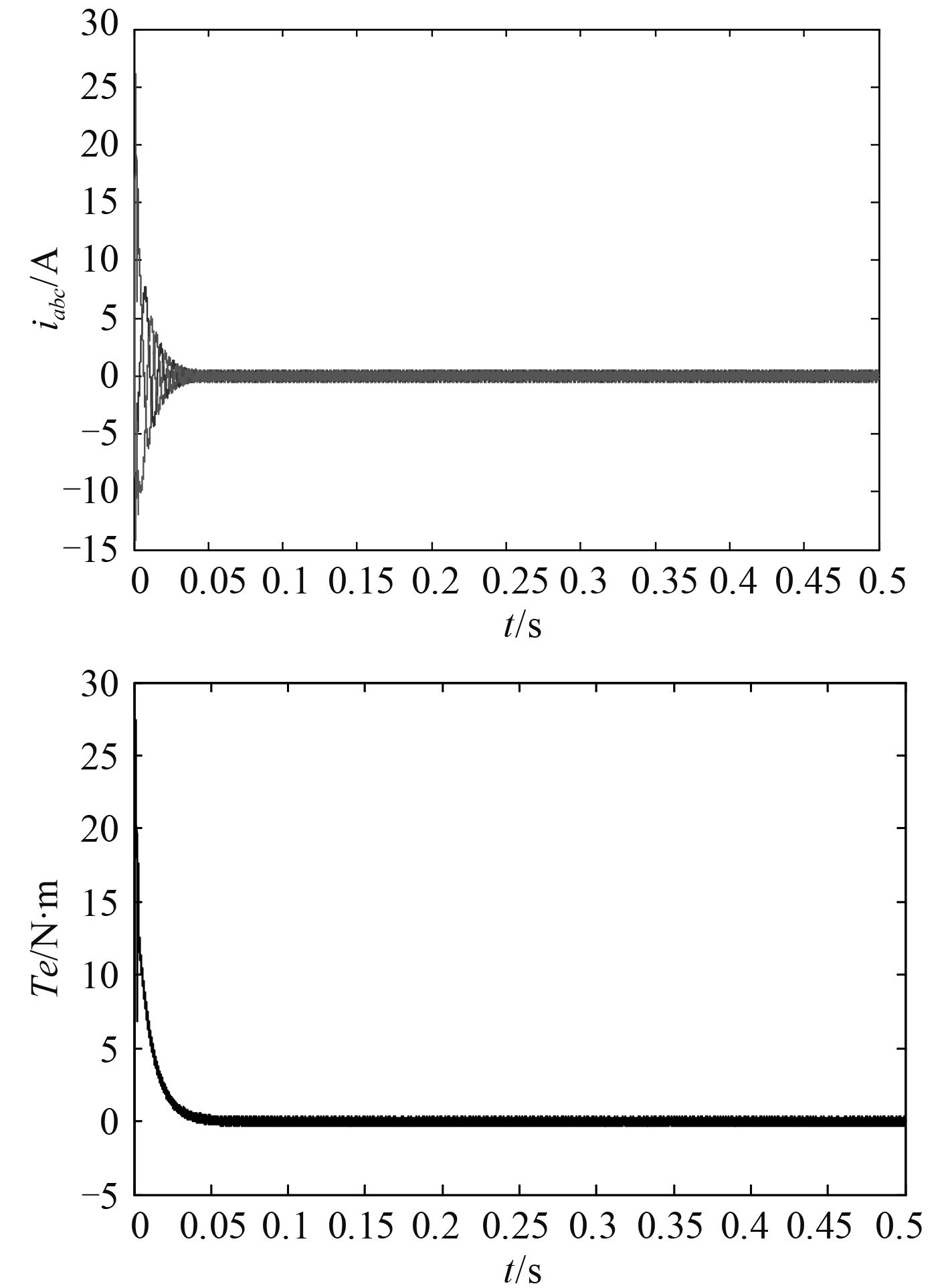
电机运行时,逆变器输出的调制波在进行滤波后保持三相对称是系统稳定的基本条件。 图 2为电机在额定转速下空载运行时电流和转矩波形,电流三相对称且纹波小。
|
图 2 空载电流、转矩波形 Fig. 2 No-load current, torque waveform |
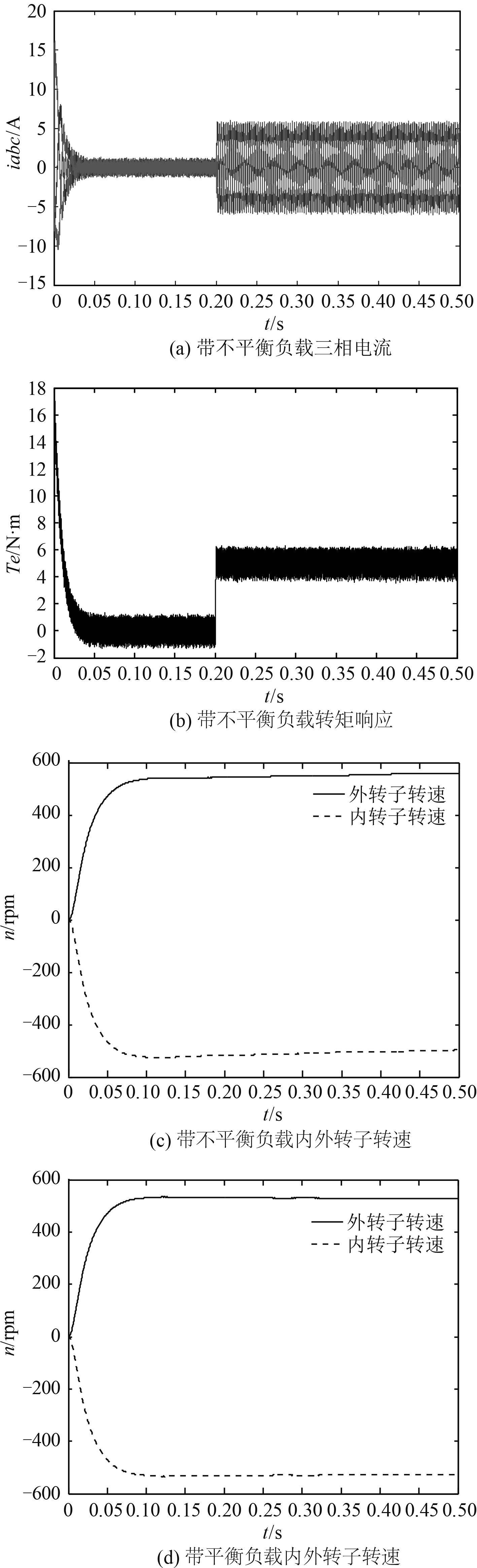
图 3是矢量控制下对电机内外转子轴加负载时电流、转矩和转速响应波形。当加不平衡负载时可以明显看出电机电流波动且纹波增加,波动的原因主要是电机两边永磁转子磁链在定子绕组中感应出的电动势包含在电机电动势中,因此当电机加不平衡负载运行时,转子运行并非一直同步,所以导致电流波形较大的原因在于转子磁链在定子感应出的反电动势在变化。即使在不平衡负载下运行,三相电流虽有波动,但仍保持在允许范围内对称,电机运行较稳定。从图 3(b)可以明显看出转矩波动增大, 图3(c)和图 3(d)对比可以看出转速有稍微变化相对较稳定。
|
图 3 带不平衡负载电流、转矩转速和平衡负载转速 Fig. 3 With unbalanced load current, rotational speed and torque balance load speed |
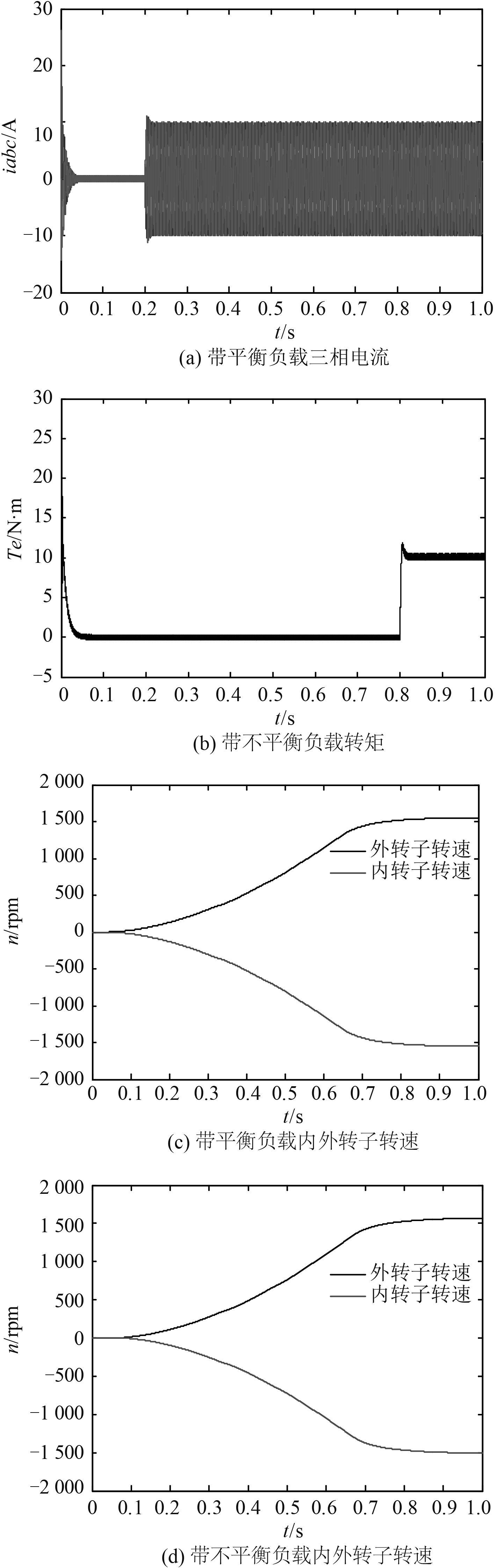
图 4利用积分型滑模面设计的滑模控制器与矢量控制相比增强了系统的稳定性,积分滑模面的引入使系统具有了全局鲁棒性。在 0.8 s突加 10 N负载,电流、转速和转矩响应波形如下。三相电流纹波明显减小,表面双转子基本同步。转矩响应波形良好,当加不平衡负载时双转子转速如图 4所示,响应时间有稍微延迟,转速虽有波动,但在允许范围内,说明系统具有很强鲁棒性。滑模控制的稳定性使航行器工作环境扩大,成本降低。
|
图 4 滑模控制电流平衡负载转速转矩和不平衡负载转速 Fig. 4 The sliding mode control current balance load speed torque and unbalanced load |
本文根据水下航行器对转螺旋桨推进原理,提出采用双转子对转永磁电机,首先对该电机矢量控制进行建模,仿真结果证明,电机矢量控制可以很好解决双转子速度调节问题,响应快,只是在双转子带不平衡负载时会出现扰动。为解决以上问题,设计一种积分滑模控制器,让系统全局鲁棒性提高,加不平衡负载仿真,结果显示系统扰动较小。可使水下航行器推进电机实现无传感控制,工作环境适应度大大提高且系统稳定性高。
| [1] | 孟昭鹤. 水下航行器用双转子永磁同步电机控制器的研究与实现[D]. 沈阳: 沈阳工业大学, 2009. |
| [2] |
饶志蒙, 黄守道, 成双银. 对转螺旋桨用永磁盘式对转电机磁场仿真分析[J]. 湖南工业大学学报, 2014, 28 (1): 39–41.
RAO Zhimeng, HUANG Shoudao, CHENG Shuangyin. The contra-rotating propeller disc counter rotating permanent magnet motor magnetic field simulation analysis[J]. Journal of hunan university of technology, 2014, 28 (1): 39–41. |
| [3] |
张凤阁, 刘光伟, 陈进华. 异向旋转双机械口永磁电机磁路建模与场分析[J]. 电机与控制学报, 2009, 13 (6): 804–809.
ZHANG Fengge, LIU Guangwei, CHEN Jinhua. Double mechanical differential rotation mouth permanent magnet motor magnetic circuit modeling and field analysis[J]. Journal of motor and control, 2009, 13 (6): 804–809. |
| [4] |
孙广贵, 张凤阁, 王凤翔. 一种新型结构的内外转子感应电机[J]. 辽宁工程技术大学学报, 2005, 24 (6): 874–877.
SUN Guanggui, ZHANG Fengge, WANG Fengxiang. A new type of structure of outer rotor induction motor[J]. Journal of liaoning university of engineering science, 2005, 24 (6): 874–877. |
| [5] | PAVANI G. Comparitive study of double-rotor permanent-magnet brushless motors with cylindrical and disc typeslot-less stator[D]. Baton Rouge: Louisiana State Univer-sity, 2007. |
| [6] |
王玉, 林秀桃, 宋诗军. 矢量推进自主水下航行器动力学建模及仿真[J]. 天津大学学报, 2014, 47 (2): 144–148.
WANG Yu, LIN Xiutao, SONG Shijun. Vectored thrust of autonomous underwater navigation line vehicle dynamics modeling and simulation[J]. Journal of tianjin university, 2014, 47 (2): 144–148. |
| [7] |
徐海珠, 谢顺依, 张林森, 等. 对转永磁同步推进电动机的矢量控制[J]. 微特电机, 2011 (10): 55–57.
XU Haizhu, XIE Shunyi, ZHANG Linsen. Counter rotating permanent magnet synchronous push into motor vector control[J]. Micro & special motor, 2011 (10): 55–57. DOI: 10.3969/j.issn.1004-7018.2011.10.017 |
| [8] | GIERAS J F, WANG Rong-jie, KAMPER M J. Axial flux permanent magnet brushless machine[M]. New York: Springer, 2008: 11–12. |
| [9] |
鲁文其, 黄文新, 胡育文. 永磁同步电动机新型滑模观测器无传感器控制[J]. 控制理论与应用, 2009, 26 (4): 429–432.
LU Wenqi, HUANG Wenxin, HU Yuwen. New type of sliding mode observer for sensorless control of PMSM[J]. Control theory and using, 2009, 26 (4): 429–432. |
 2017, Vol. 39
2017, Vol. 39
