2. 海军潜艇学院,山东 青岛 266199
2. Navy Submarine Academy, Qingdao 266199, China
远程UUV工作时间长,控制节点多,进行及时有效的指挥控制是保障其任务完成的重要前提。由于远程UUV应用领域少、工作流程复杂,目前针对远程UUV的指挥控制研究相对还不多。建立准确恰当的模型是从事性能研究的基础,远程UUV指挥控制流程具有分布、并行、异步、协调等特点,是典型的离散系统,传统流程建模方法主要有UML、活动网络及事件驱动过程链等。UML方法适用于以案例为驱动,以体系结构为中心的系统建模,一般灵活性较弱,语义清晰度差,难以应对复杂系统[1 –2]。复杂网络法多应用于工作流建模及生产系统的建模中,虽具有较强的语义清晰度,但不具备层次分析能力[3 –4]。事件驱动过程链语义清晰度弱,无法处理动态系统,不具备系统分析能力[5 –6]。由于远程UUV指控流程复杂,传统的研究方法很难对其各个环节进行详细描述和分析。Petri网建模方法能够完成复杂系统建模并具备强大的分析能力,其较强的层次分析能力,在描述和分析动态复杂系统流程上具有独特的优势[7 –9]。Petri网的灵活性强,可方便引入时间参数,为分析远程UUV指挥控制流程的延时特性提供了有力的分析工具。针对远程UUV指挥控制流程的复杂性及指挥决策延时时间要求,本文采用分层Petri网解决复杂流程建模及分层结构下的延时分析的问题。
1 分层延时Petri网 1.1 分层延时Petri网概念分层Petri网(Hierarchical Petri Net,HPN)建模方法为复杂系统建模分析提供了高效的解决方案,其不但可以降低模型复杂度,而且可以提高模型利用率,降低模型分析难度[10 –11]。HPN包括库所分层和变迁分层 2 部分内容,其定义如下。
库所分层定义:设
变迁分层定义:
由经典Petri网概念可知,系统中事件的发生需要一定的时间,因此本文所说的延时只与变迁相关联,而与状态即库所无关。为解决层次化后的延时问题,提出分层延时Petri网(Hierarchical Timed Petri Net,HTPN)概念。
分层延时Petri网定义:满足以下条件的网
1)
2) K 是 N 的容量函数;
3) W 是 F 的权函数;
4) M 0 为初始标识;
5)
I 是变迁集的时间函数
延时Petri网用户可以根据不同应用定义不同的触发条件[12 –13], UUV指控过程延时是事件发展所经历的时间,定义变迁触发条件:对于
不同的网络结构下,延时运算规则如下:
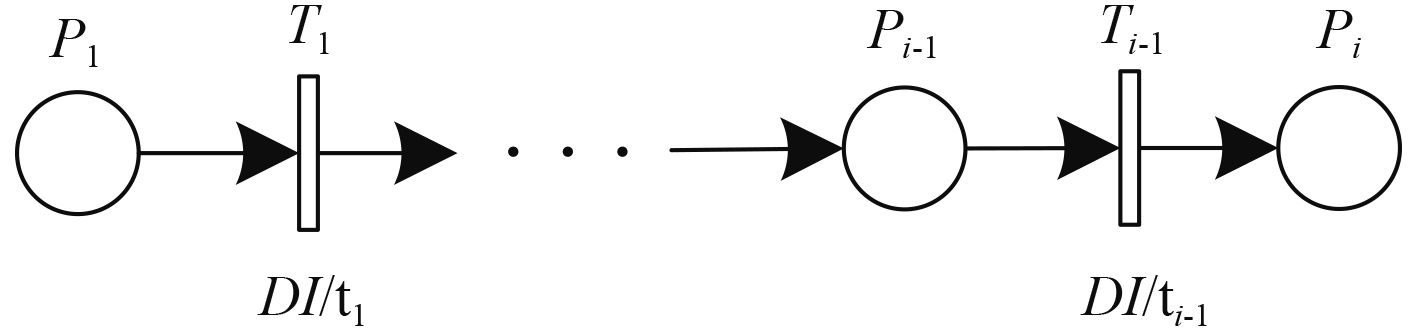
1)运算规则 1:顺序结构的延时
图 1所示顺序结构的延时计算公式为:
| $DI\left( {{\sum _1}} \right) = \mathop \sum \limits_{j = 1}^{i - 1} DI\left( {{t_j}} \right)\text{。}$ | (1) |
|
图 1 顺序结构延时Petri网 Fig. 1 Sequence structure timed Petri net |
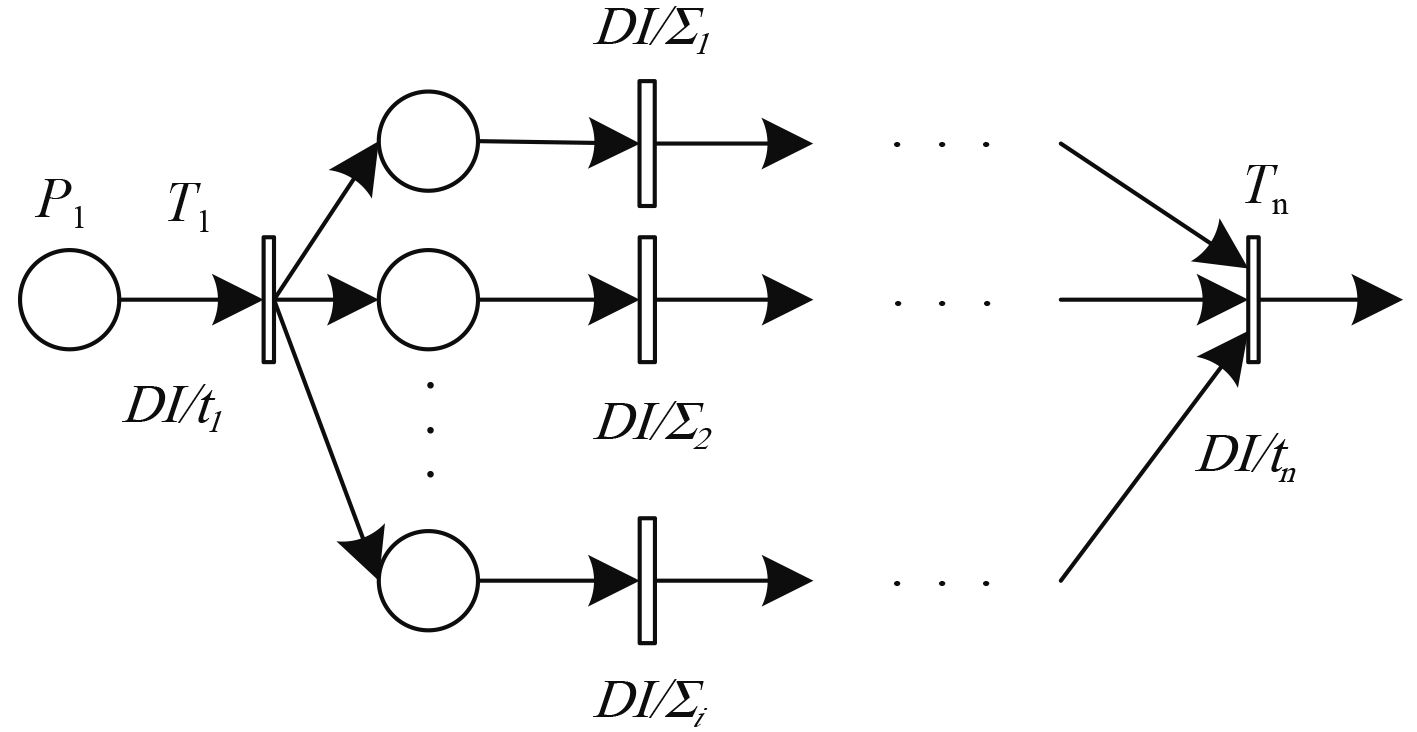
2)运算规则 2:并行结构的延时
图 2所示的Petri网经过变迁
| $DI\left( {{\sum _2}} \right) = DI\left( {{t_1}} \right) + \mathop {\max }\limits_{j = 1}^i DI\left( {{\sum _j}} \right) + DI\left( {{t_n}} \right)\text{。}$ | (2) |
|
图 2 并行结构延时Petri网 Fig. 2 Parallel structure timed Petri net |
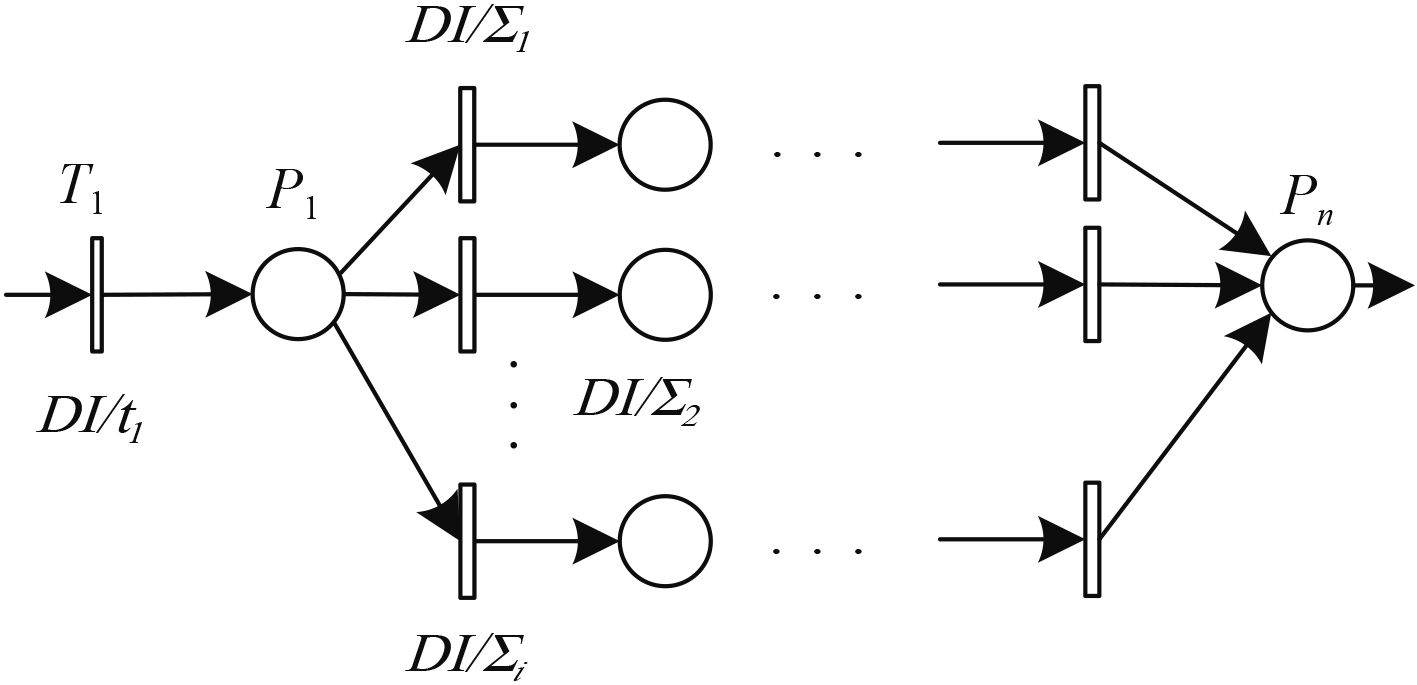
3)运算规则 3:选择结构延时
图 3所示的Petri网依库所
| $DI\left( {{\sum _3}} \right) = DI\left( {{t_1}} \right) + DI\left( {{\sum _j}} \right)\text{。}$ | (3) |
|
图 3 选择结构延时Petri网 Fig. 3 Selective structure timed Petri net |
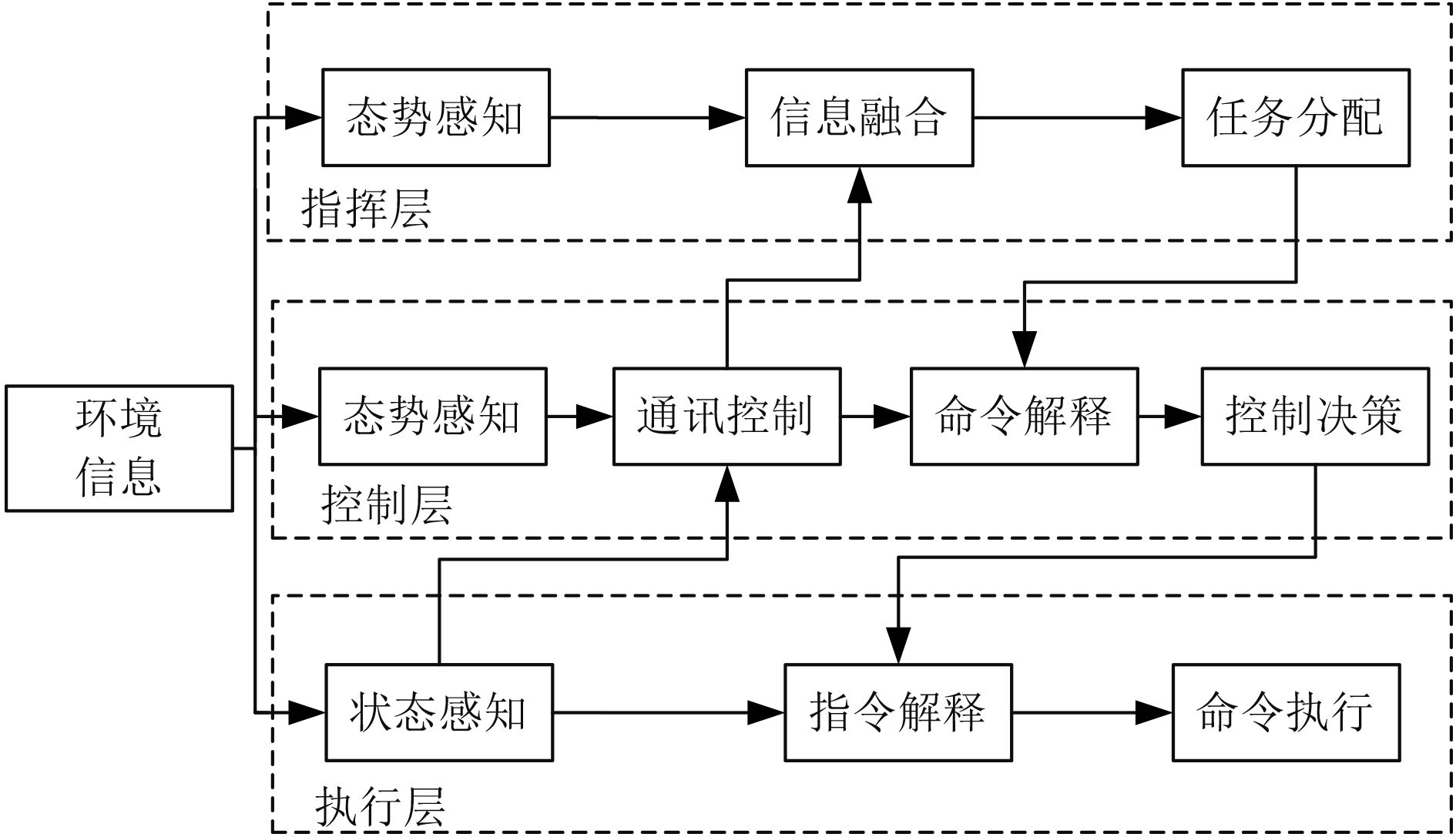
信息化条件下指挥控制过程一般有状态感知、信息融合、命令解释及决策输出 4 个基本过程。远程UUV指挥控制的 4 个过程由 3 个职能层共同完成,分别为指挥层、控制层及执行层,如图 4所示。指挥层实现对远程UUV的指挥和环境态势掌控,进行环境态势分析和判断,负责UUV和各协同伙伴的联合行动。控制层负责远程UUV任务规划、远程控制、状态监控和情况上报。执行层负责上传UUV状态及环境态势信息等,接收控制层发送的遥控和任务更新信息,并最终实现决策执行。
|
图 4 远程UUV指挥控制模式 Fig. 4 Remote UUV command and control mode |
远程UUV指挥控制流程如下:
1)指挥中心根据情报信息网提供的环境态势,协调各个协同伙伴,定下决心,下达行动命令。
2)待命状态下的远程UUV接到行动命令后完成技术准备, UUV装载,发射平台完成各项出航准备。
3)指挥中心向UUV控制系统发送作战命令,控制系统完成环境态势评估及武器任务规划并向UUV传送预置信息。
4)发射平台按计划出航,到达发射海域,待机等待发射。
5)经参数装订并发射后,远程UUV进入工作状态, UUV向目标区域航渡。
6)UUV发射后武器控制台实时监测UUV的工作状态,远程监测侦察平台实时监测海情信息, UUV工作状态及海情实时上传指挥中心。
7)当UUV偏离预定航路时,武器控制系统控制其按规划航路航行,当环境态势发生变化时,根据指挥中心指令适时调整UUV航路或目的海域。
8)UUV到达目的海域,进入任务模式, UUV按照预定程序自主执行任务。
9)任务执行完毕, UUV将任务完成情况经控制系统上传指挥中心,指挥中心评估任务执行效果,以便再次组织任务或任务结束。
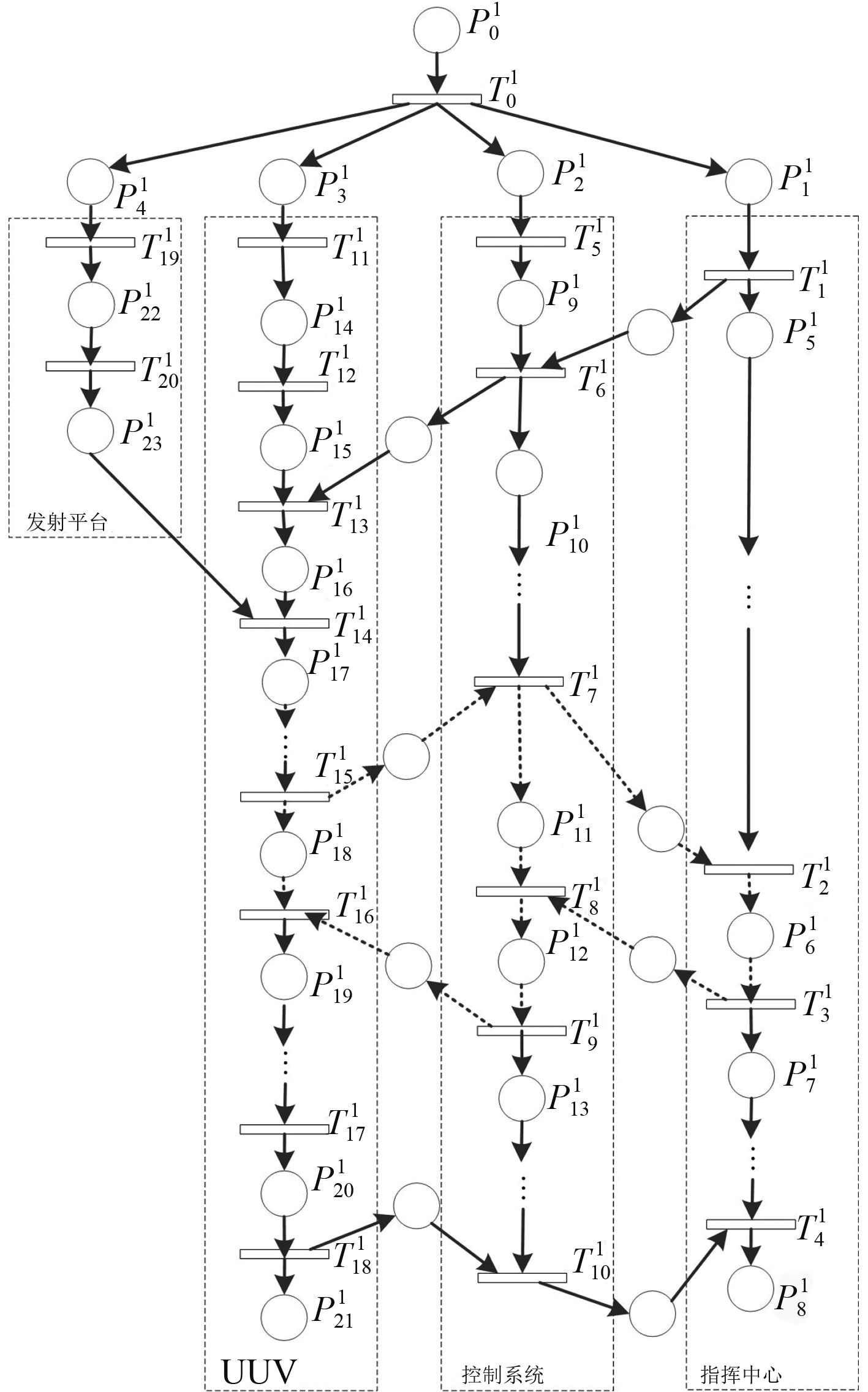
3 远程UUV指挥控制流程建模由以上指挥控制流程可知,远程UUV指控系统主要包含指控中心、控制系统、UUV及发射平台 4 个对象,指挥控制过程主要就是对象间的交互协调通讯、指挥、控制过程。为降低模型复杂度,采用面向对象的分层Petri网建模方法,所建立的顶层Petri网模型如图5所示,模型中库所及变迁含义如表 1所示。
|
|
表 1 顶层库所及变迁含义 Tab.1 Meaning of top level places and transitions |
根据研究需求,
图 5所示的模型中多个变迁可进一步层次化,其中虚线有向弧表示的是UUV状态监测及控制过程,在远程UUV指挥决策过程中,状态监测及控制是及时感知UUV工作状态,根据环境态势需求及时调整应对策略的过程,其对实时性要求较高,对UUV的性能有重要影响。本文以这一过程为例进行深入分析,其变迁
|
图 5 远程UUV指挥控制流程顶层Petri网 Fig. 5 Top Petri net of remote UUV command and control process |
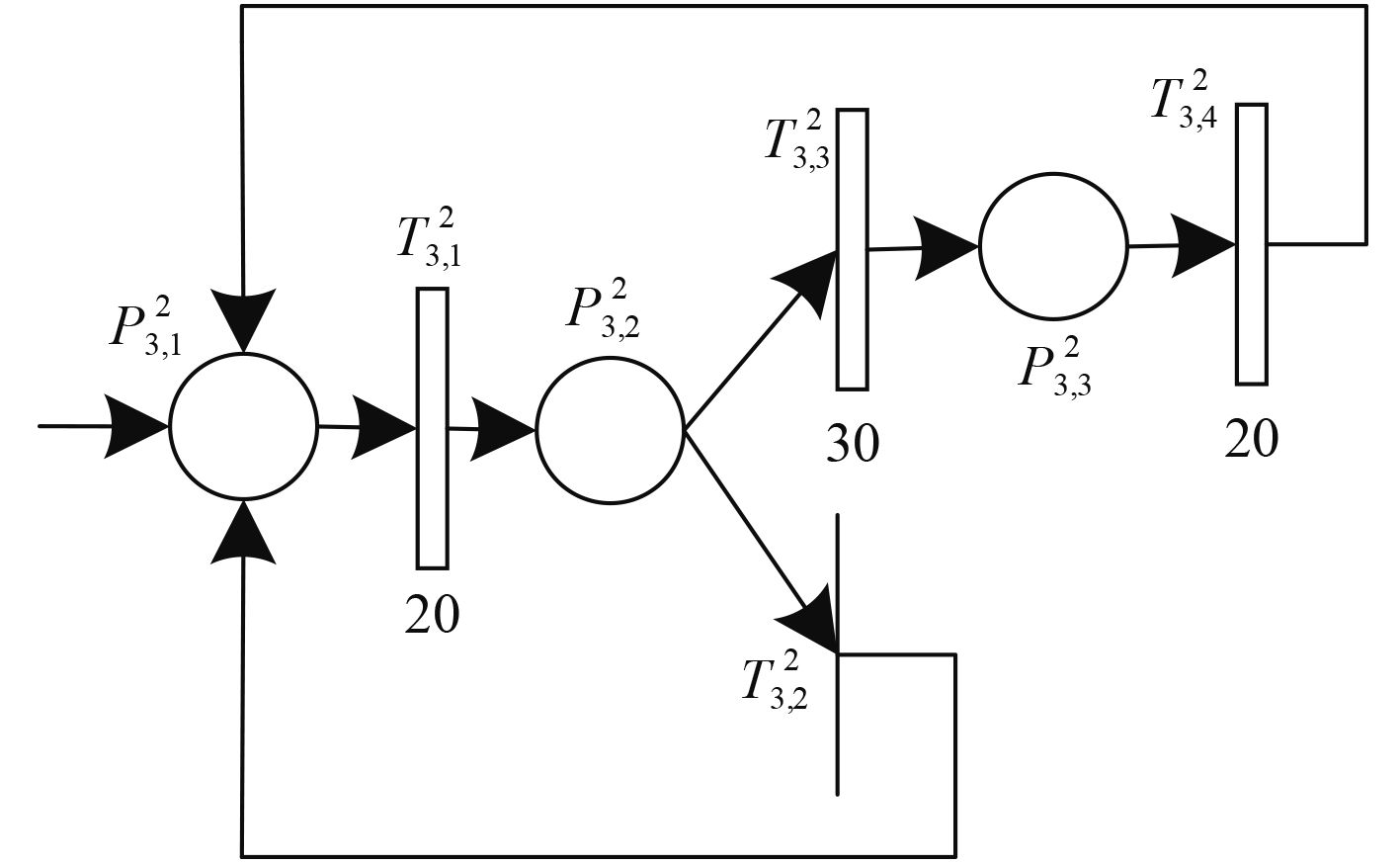
|
图 6 任务调整变迁模型 Fig. 6 Task adjustment transition hierarchical model |
|
|
表 2 任务调整变迁模型含义 Tab.2 Meaning of task adjustment transition hierarchical model |
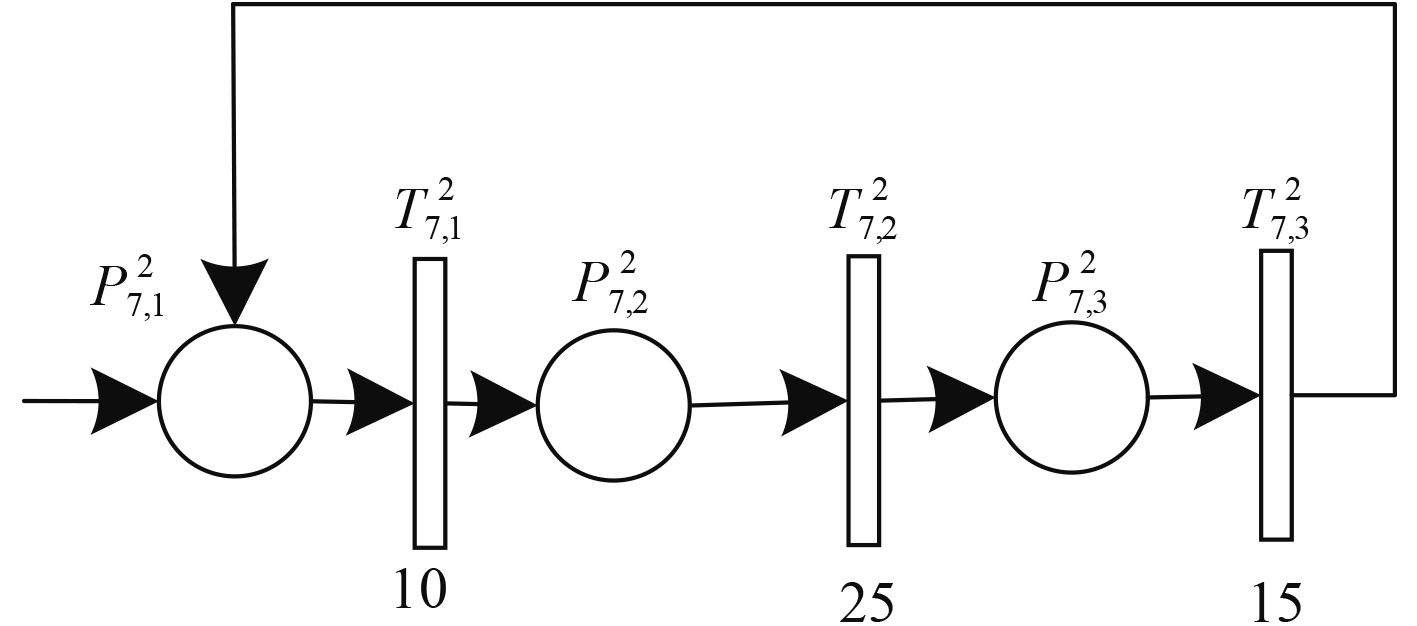
|
图 7 状态及态势感知变迁分层模型 Fig. 7 State and situational awareness transition hierarchical model |
|
|
表 3 状态及态势感知变迁分层模型含义 Tab.3 Meaning of state and situational awareness transition hierarchical model |
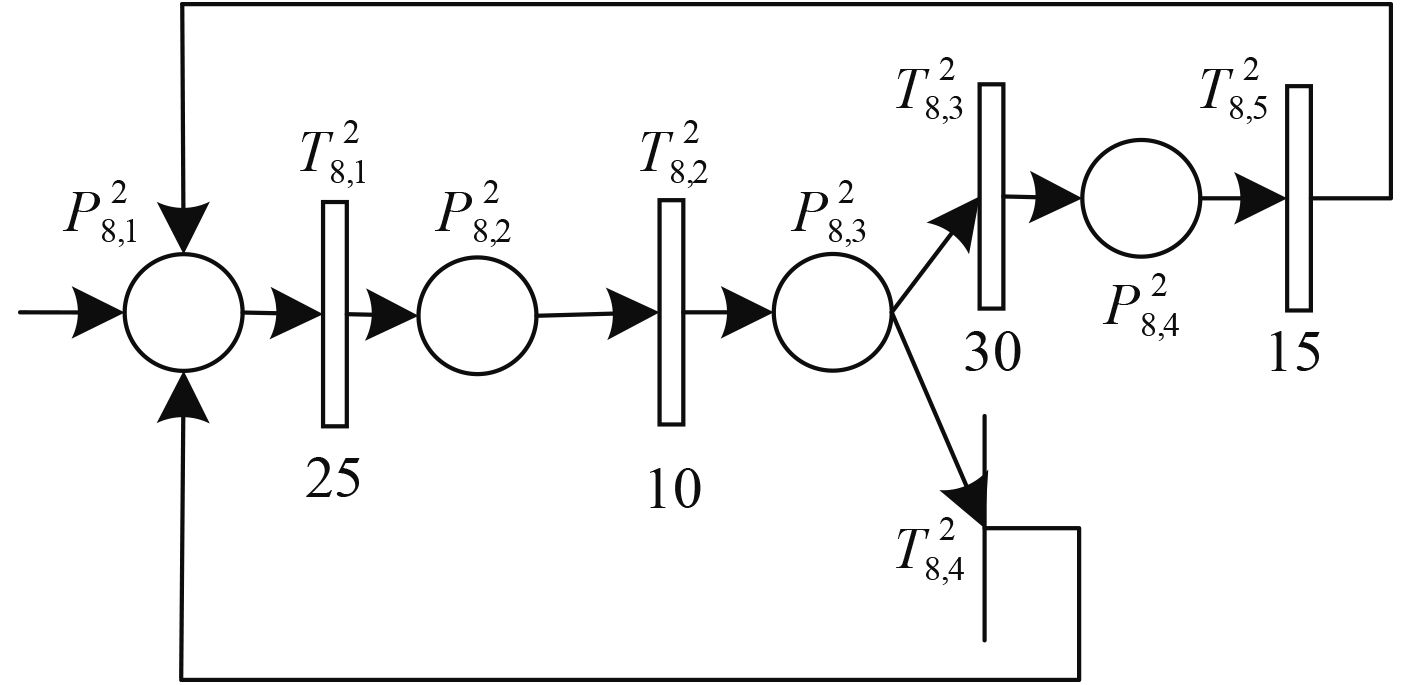
|
图 8 命令解释变迁分层模型 Fig. 8 Command interpretation transition hierarchical model |
|
|
表 4 命令解释变迁分层模型含义 Tab.4 Meaning of command interpretation transition hierarchical model |
|
图 9 状态参数上传变迁分层模型 Fig. 9 State parameters upload transition hierarchical model |
|
|
表 5 状态参数上传变迁分层模型含义 Tab.5 Meaning of state parameters upload transition hierarchical model |
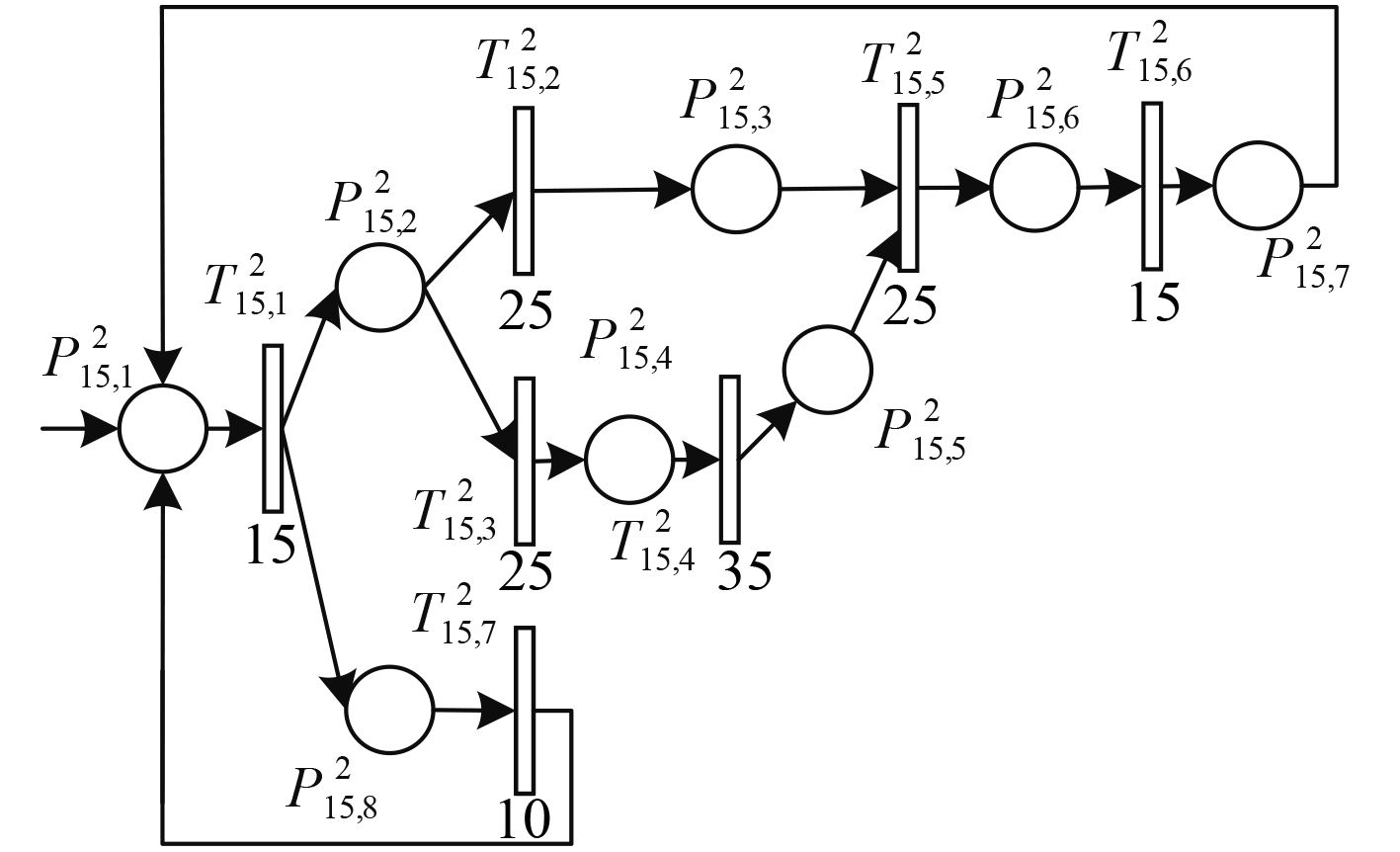
|
图 10 状态调整变迁分层模型 Fig. 10 State adjustment transition hierarchical model |
|
|
表 6 目标状态修正变迁分层模型含义 Tab.6 Meaning of state adjustment transition hierarchical model |
为仿真分析指控流程延时特性,本文使用Simulink环境下的Stateflow工具包进行仿真,Stateflow将状态转移图和流程图等理论相结合,采用面向对象的编程思想,适合用来对Petri网进行仿真[14 –15]。
以上远程UUV指挥及控制流程延时时间是基于各个阶段所需时间为常数的假定,由于实际指控过程中依据任务不同,战场态势不同,其所用时间是随机的,一般呈正态分布。假设
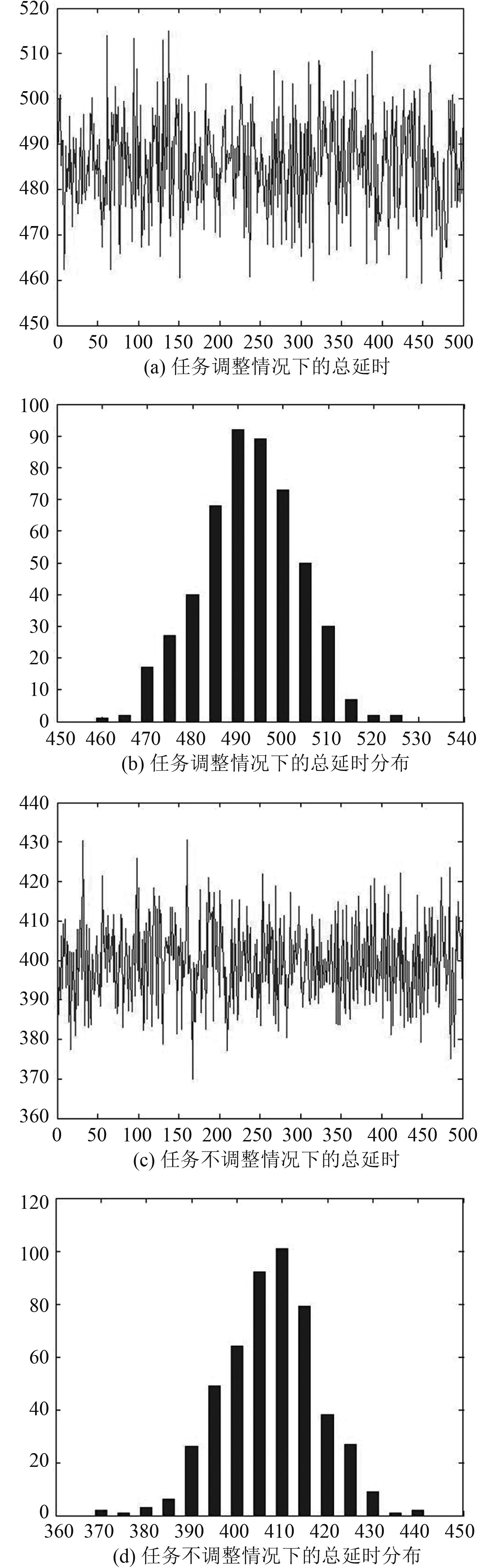
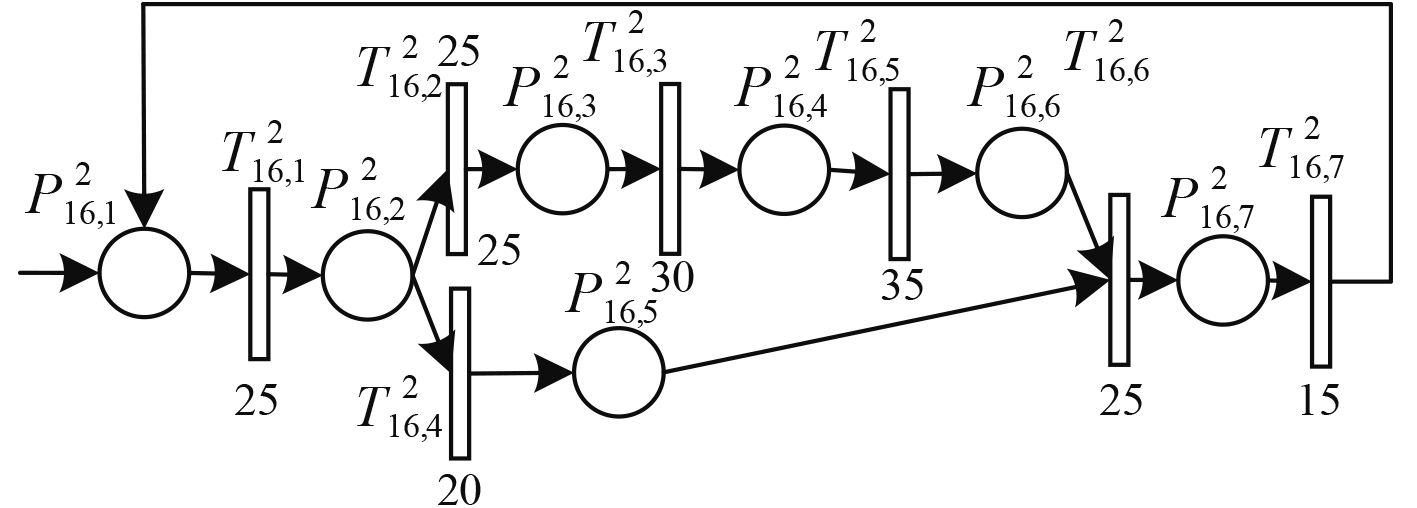
|
图 11 总延时情况及其分布规律 Fig. 11 Total time delay and its distribution |
建模及分析过程表明所建模型可详细描述远程UUV指挥控制流程,适用性较好。通过以上 2 种情况的总延时及延时分布规律可以发现,在各离散事件延时满足正态分布的情况下,总延时时间大致符合正态分布,与实际延时规律相符。模型对延时时间有良好的描述和分析功能,可以基于此模型进一步对整个指挥控制流程的时间特性进行定量及定性分析。所提出的分层延时Petri网可以方便对复杂流程进行建模,且降低了模型分析难度。
5 结 语为降低模型复杂度,增强分析便利性,本文结合分层Petri网及延时Petri网的概念,提出了分层延时Petri网的概念,建立了远程UUV指挥控制流程分层延时Petri网模型,并对模型的延时特性进行了仿真分析。仿真结果表明所建模型准确描述了远程UUV的指挥控制流程,延时情况分析结果能够反映实际规律。基于所建模型不但可以对指挥控制系统其他特性进行深入分析和研究,也可为UUV科研人员分析指挥控制流程的合理性提供决策依据,同时为描述和分析复杂流程提供了一种便利的方法。
| [1] | 卫红春. UML软件建模教程[M]. 高等教育出版社, 北京, 2012.08. |
| [2] | David B, Jurgen D, Torsten L. Model driven security: From UML models to access control infrastructures[J]. ACM Trans on Software Engineering and Methodology(TOSEM), 2006, 15 (1): 39–91. DOI: 10.1145/1125808 |
| [3] | 付伟. 基于活动网络的工作流模型设计与实现[D]. 天津: 天津大学, 2007. |
| [4] | 蔡冽, 李世其. 基于活动网络的生产系统仿真集成模型研究[J]. 计算机应用研究, 2005, 22 (12): 63–65. DOI: 10.3969/j.issn.1001-3695.2005.12.020 |
| [5] | Mending Jrr, Neuman G. Towards Workflow Pattern Support of Eent-driven Process Chains[J]. Proc of Workshop Xm14bpm, 2005 : 23–38. |
| [6] | 于晓浩, 刘俊先, 陈涛, 罗雪山, 等. 事件驱动过程链在军事信息系统建模中的应用[J]. 火力与指挥控制, 2011, 36 (07): 21–24. DOI: 10.3969/j.issn.1002-0640.2011.07.006 |
| [7] | 张耀鸿, 樊建才, 廖晓林. 基于Petri网的指挥控制流程仿真方法[J]. 系统仿真学报, 2012, 24 (7): 1418–1421. |
| [8] | 朱敏洁, 张伟. 作战指挥工作流程的建模与仿真[J]. 火力与指挥控制, 2008, 33 (12): 45–48. DOI: 10.3969/j.issn.1002-0640.2008.12.012 |
| [9] | 杨志华, 刘顺利, 刘己斌. 基于Peter网的防空兵群指挥信息结构建模分析[J]. 兵工自动化, 2012, 31 (4): 39–42. |
| [10] | Hao K, Ding J. Hierarchical Petri nets[J]. Journal of Frontiers of Computer Science & Technology, 2008, 5 (91): 281–290. |
| [11] | Dai X., Li J., Meng Z.. Hierarchical Petri net modelling of reconfigurable manufacturing systems with improved net rewriting systems[[J]. International Journal of Computer Integrated Manufacturing, 2009, 22 (2): 158–177. DOI: 10.1080/09511920802014904 |
| [12] | ZUBEREK W M. Invariant-based performance analysis of timed petri net models[M]. Dependability Engineering and Complex Systems. 2016. |
| [13] | Toyoshima I, Nakano S, Yamaguchi S. Reduction Operators Based on Behavioral Inheritance for Timed Petri Nets[J]. Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences, 2014, E97.A (2): 484–489. |
| [14] | 陶继平, 徐文艳, 杨根科, 等. 基于Stateflow的Petri网仿真方法[J]. 计算机仿真, 2006, 23 (12): 96–99. DOI: 10.3969/j.issn.1006-9348.2006.12.026 |
| [15] | Feng-Yu L V. Research and Application of Stateflow Modeling Method Based on Petri Nets[J]. Measurement & Control Technology, 2014 . |
 2017, Vol. 39
2017, Vol. 39
