目前,大多数船舶安装有侧推装置,用于产生船舶横向推力,从而顺利离靠码头、进出水闸或通过狭窄航道和水域等,作用巨大,其中可调桨可以很方便地通过改变桨叶角度实现柴油机负荷增加或减小,改善船舶在不同航行工况下的推进效率和操作性能,从而获得设计者的认可。
传统意义上侧推系统螺距调节采用闭环反馈的PID控制理念,近些年随着我国工业经济的飞速发展,新兴控制理论逐渐应用于工业控制,其中模糊控制理论越来越受到学者的关注。本文运用模糊PID控制理论,通过对船舶可调桨系统仿真建模,设计出螺距模糊PID控制器,并通过实验验证其较好的控制效果,从而提高船舶自动化性能。此课题具有较高的研究意义和应用价值,开创了模糊控制理论在船舶驾驶领域研究应用的先河。
1 模糊PID控制理论模糊系统理论由美国加利福尼亚大学扎德教授于 1965 年提出,随着模糊系统理论在工业上的成功运用,很多学者开始对模糊系统理论进行研究,这大大促进了模糊理论的发展。20 世纪 90 年代,经过实际应用和理论创新,模糊控制从理论上解决了2个问题:一是如何从实验数据中获得模糊规则;二是如何实现模糊系统的稳定性。这一领域的研究成果随后被广泛应用在核电发电系统、汽车控制系统、机器人控制系统等。
模糊控制之所以得到广大研究学者的认可和亲睐,归功于模糊控制的如下显著特点[1]:
1)运用模糊控制理论,不需要研究系统的精确数学模型,因为很多复杂的工控过程难以得到精确描述。
2)模糊规则多从专家知识和实际经验中总结得到,所以即使是非控制专业的人也可以很容易地掌握模糊控制理论。
3)模糊控制器构造起来容易。实际模糊控制算法可以通过PLC进行实现,也可以通过单片机进行构造。
4)模糊控制是一种人工智能控制,有很好的动态响应品质,并且对过程参数变化有很强的适应性,方便调节。
在现实工控中,固化的PID控制参数很难取得很好的控制效果,因为控制对象的参数常常会发生变化。那么把PID控制和模糊控制结合起来,实现控制参数的在线自动化调整,从而构造模糊PID控制算法,设计出来的控制器具有诸多优点。
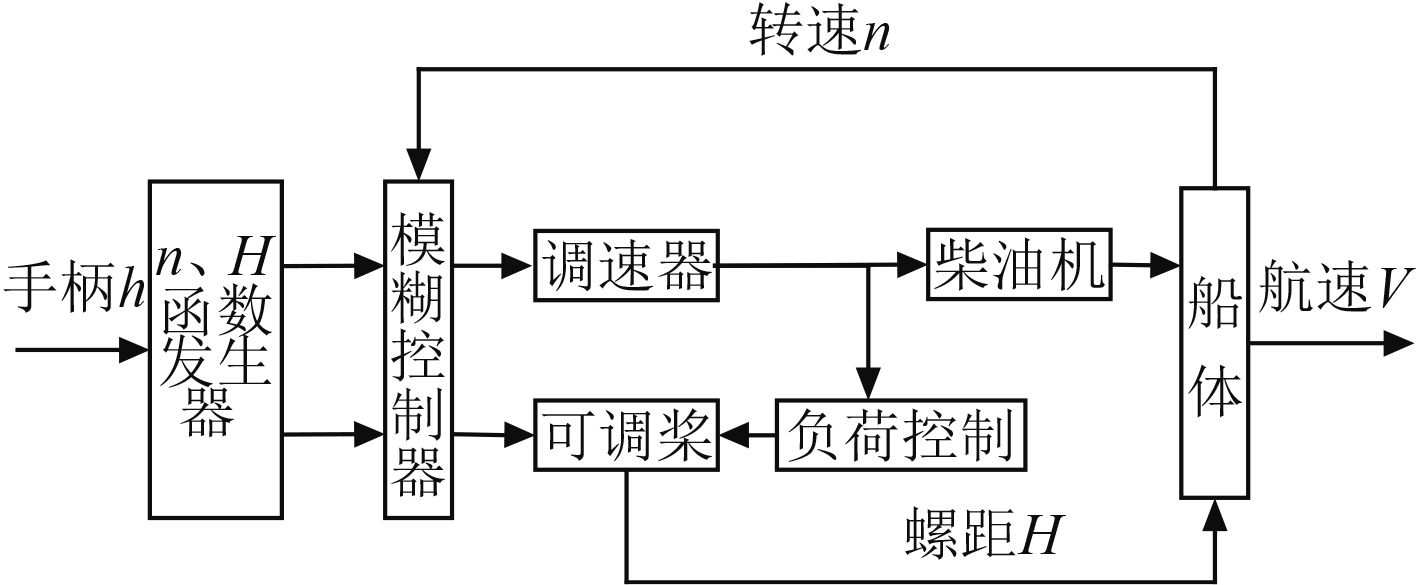
2 可调桨推进系统建模 2.1 船桨系统模型对于船舶可调桨推进系统,主机通过传动设备带动螺旋桨转动,从而产生推力作用在推力轴承上,船舶最终运动。整个系统可分解为多个子系统[2],简化处理形成图 1。
|
图 1 可调桨推进系统组成图 Fig. 1 Composition diagram of controllable pitch propulsion system |
根据螺旋桨工作原理,螺旋桨淌水推力 T 和水力矩 M P 分别为:
| $T = {K_T}\rho {n^2}{D^4}{\text{,}}$ | (1) |
| ${M_P} = {K_Q}\rho {n^2}{D^5}{\text{。}}$ | (2) |
式中: K T 为螺旋桨推力系数; K Q 为螺旋桨扭矩系数; n 为螺旋桨转速; D 为螺旋桨直径。
根据牛顿力学定理,船舶推进系统在无偏转作用时可由以下数学式描述[3]。
动力学关系:
| $M\frac{{{\rm d}{V_S}}}{{{\rm d}t}} = {T_e} - R{\text{,}}$ | (3) |
| $2\pi I\frac{{{\rm d}n}}{{{\rm d}t}} = {M_d}i - {M_p} - {M_f}{\text{。}}$ | (4) |
运动学关系:
| ${n_s} = ni{\text{,}}$ | (5) |
| ${V_P} = (1 - \omega ){V_S}{\text{。}}$ | (6) |
式中:
T
e
为可调桨有效推力,N;
R 为船体运动阻力;
M 为船体总质量,并考虑到随船一起运动的附着水的质量;
V
P
为螺旋桨的进速;
V
S
为船舶的航速;
I 为螺旋桨转动惯量,包括随它们一起转动的附着水的转动惯量;
n
s
为主机转速;
n 为螺旋桨的转速;
M
d
为主机输出扭矩,
柴油机系统的物理模型主要由柴油机本体和减速器组成。根据柴油机原理,柴油机本体模型为:
| ${P_S} = \frac{{30nm{g_c}}}{{{b_e}}}{\text{,}}$ | (7) |
| ${b_e} = \frac{{3\;600}}{{{H_u}{n_e}}}{\text{,}}$ | (8) |
| ${n_e} = {n_i}{n_m}{\text{。}}$ | (9) |
式中: b e 为柴油机有效燃油消耗率; P S 为柴油机有效功率; n 为柴油机转速; m 为气缸数目; g c 为柴油机循环供油量; H u 为燃油的低热值; n e 为柴油机有效效率; n i 为柴油机指示效率; n m 为柴油机机械效率。
减速器数学模型较简单,减速齿轮箱减速比为:
| $i = {n_s}/n{\text{,}}$ | (10) |
经过减速齿轮箱后主机输出力矩为:
| ${M_G} = {M_D}i{\text{。}}$ | (11) |
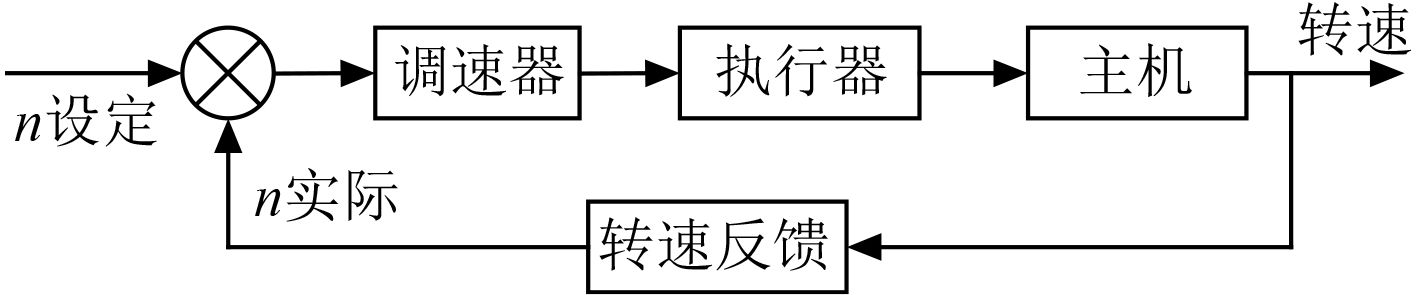
柴油机调速系统由柴油机、电子调速器、喷油泵和供油机构组成(见图 2)。
|
图 2 柴油机调速系统组成图 Fig. 2 Composition diagram of diesel engine governor system |
柴油机调速系统实现3个基本功能:
1)负荷增加,转速下降,实现减速增油调节动作;
2)负荷减少,转速上升,实现增速减油调节动作;
3)负荷不变,供油不变。
建立柴油机调速系统的数学模型,设执行器与输出轴位移的传递函数为:
| ${G_1}(s) = \frac{{L(s)}}{{u(s)}} = \frac{{{K_1}}}{{1 + {T_1}s}}{\text{,}}$ | (12) |
取拉普拉斯反变换:
| $\frac{{{\rm d}L}}{{{\rm d}t}} = - \frac{L}{{{T_1}}} + \frac{{{K_1}}}{{{T_1}}}u{\text{。}}$ | (13) |
式中: u 为执行器的控制信号,这里是柴油机油门的开度; L 为执行器的输出轴位移; T 1 为执行器的时间常数; K 1 为控制增益常数。
为使调速器调节响应较迅速,调节时间短,反应敏捷,本文中调速器传递函数为[4]:
| $G(s) = \frac{{2\;012.6500}}{{0.0012{s^3} + 0.0831{s^2} + 1.1001s + 2.7223}}{\text{。}}$ | (14) |
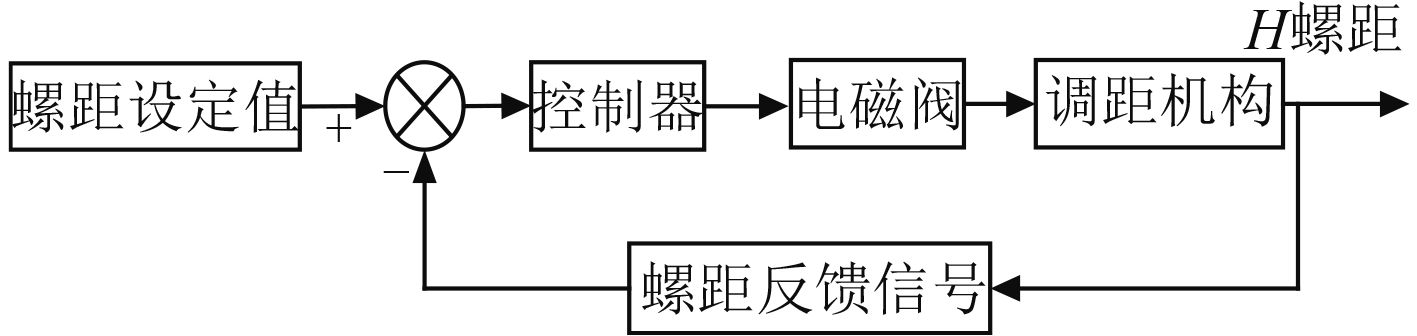
可调桨操作时,当控制台发出的螺距设定信号与螺距反馈信号进行比较得出偏差,经过控制器的运算处理,按照一定规律输出螺距调节控制信号,该信号驱动液压动力装置的电液比例阀,打开相应前进或倒退油路,控制调距机构调节螺距。
|
图 3 螺距调节原理图 Fig. 3 Principle diagram of adjusting pitch |
液压动力装置由油箱和伺服油泵系统组成。调距操作时启动油泵,伺服油压力调节阀保证最小的伺服油压力,安全阀设定系统的最大压力,液控单向阀保证螺距在伺服油中断情况下保持螺距稳定不变。
伺服油系统主要由伺服油泵、控制阀、油箱和管件组成。高压油由一个伺服油泵传动到高压滤器,经过由单向阀、安全阀、压力调节阀和电控比例阀组成的阀装置,从比例阀出来的伺服油流入油分配器,油分配器出来的高压油经过液控双单向阀到伺服活塞的一侧,从另一侧流出。
螺距调节机构的传递函数为:
| $\begin{aligned}& G(s) = \\ & \frac{{72\;997}}{{0.1704{s^5} \!\!+\!\! 10.47{s^4}\! \!+\!\! 312.8{s^3} \!\!+\!\! 4\;691{s^2} \!\!+\!\! 35\;859s \!\!+\!\! 39\;880}}{\text{。}}\end{aligned}$ | (15) |
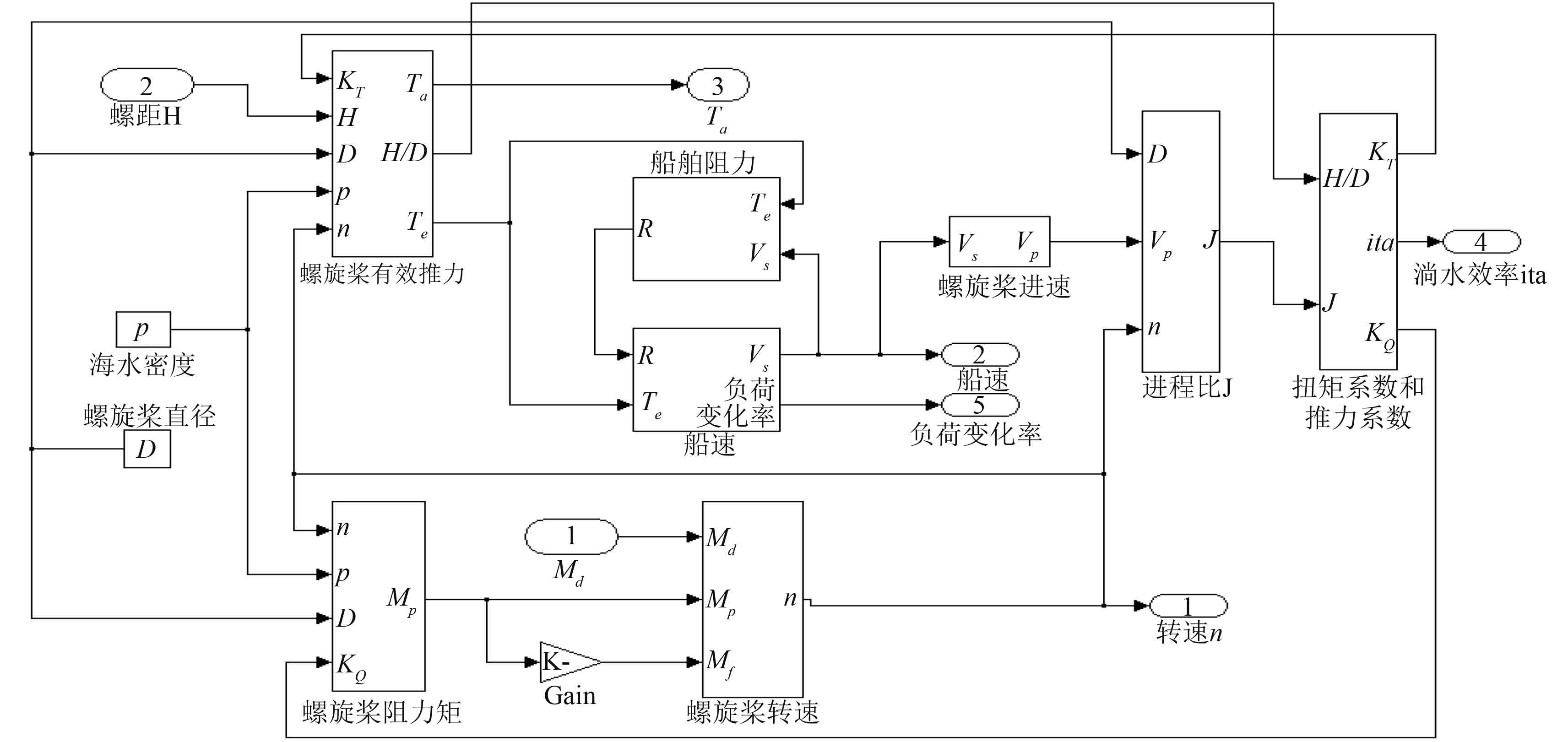
根据船桨系统数学模型,包含螺旋桨的淌水推力公式和水力矩公式,船舶运行动力学方程和运动学方程,结合推力系数、扭矩系数与螺旋桨进程比、螺距比的关系[5],在Matlab平台上利用Simulink进行模型搭建如图 4所示。
|
图 4 船桨系统模型 Fig. 4 Model of paddle system |
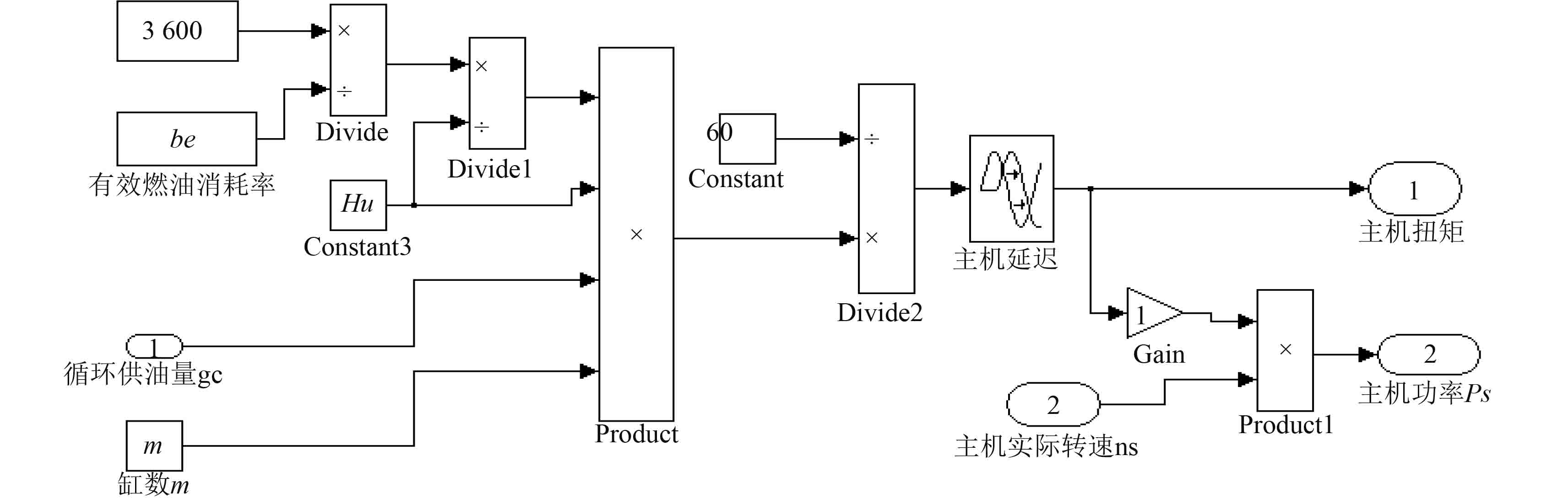
对于船用柴油机而言,在额定工况下指示效率一般取 0.43~0.50,机械效率一般近似取值 0.85~0.90。根据柴油机系统数学模型,搭建仿真模型如图 5所示。
|
图 5 柴油机系统模型 Fig. 5 Model of diesel engine system |
调速器与主机一起构成主机转速自动控制系统,调速器根据柴油机负载变化自动调节喷油泵的供油量,调速器仿真模型是推进系统建模及仿真研究中很重要的一部分,主机转速调节值由推进控制系统仿真输出,调速系统输出得循环供油量[6 –8],具体Simulink模型如图 6所示。

|
图 6 主机转速调节系统模型 Fig. 6 Model of main engine governor system |
螺距调节值匹配调节机构传递函数,最终实现螺距值输出,如图 7所示。

|
图 7 螺距调节系统模型 Fig. 7 Model of pitch controller system |
对于船舶推进控制系统,由驾驶台发出车钟指令,采集实际船速和实际螺距,根据柴油机负荷曲线获取当下最佳主机转速和螺距值,运用模糊控制理论设计模糊控制器,实现PID参数在线整定[9],最终输出主机转速调节值和螺距调节值。
模糊控制器检测到螺距角设定值 H 0,经过螺距反馈装置获取螺距角 H 实际值,两者比较分别计算出螺距角偏差值 e 及其变化率 ec。通过模糊控制规则推理,合成运算,模糊判决得到实际螺距调节值,从而控制伺服阀,驱动调距桨液压装置和机械装置,实现变螺距调节。模糊控制理论要求将输入变量偏差 e 和偏差变化率 ec 量化到模糊论域并划分为 13 个等级,模糊论域为 {– 6,– 5,– 4,– 3,– 2,– 1,0,1,2,3,4,5,6}。选择隶属度函数时,需要考虑很多因素,例如隶属函数的形状,模糊编辑器中隶属度函数曲线有三角形、钟形、阶跃型好正弦型等[10],这里输入变量偏差 e、偏差变化率 ec 和输出变量 △ H 隶属度如表 1~ 表 3所示:
|
|
表 1 偏差模糊集隶属度 Tab.1 Membership of deviation fuzzy set |
|
|
表 2 偏差变化率模糊集隶属度 Tab.2 Membership of deviation rate fuzzy set |
|
|
表 3 调节量模糊集隶属度 Tab.3 Membership of controller output deviation fuzzy set |
经过Matlab程序离线计算得到模糊控制器输出控制变量 △ K P 、△ K I 和 △ K D 的值,这些数值组成了模糊控制器输出控制量查询表。根据模糊控制器输出控制量查询表,可以利用S7-1200 编写模糊PID控制器程序[11],最终实现可调桨螺距的模糊PID控制器设计。

|
图 8 PID控制曲线 Fig. 8 The curve of PID control |
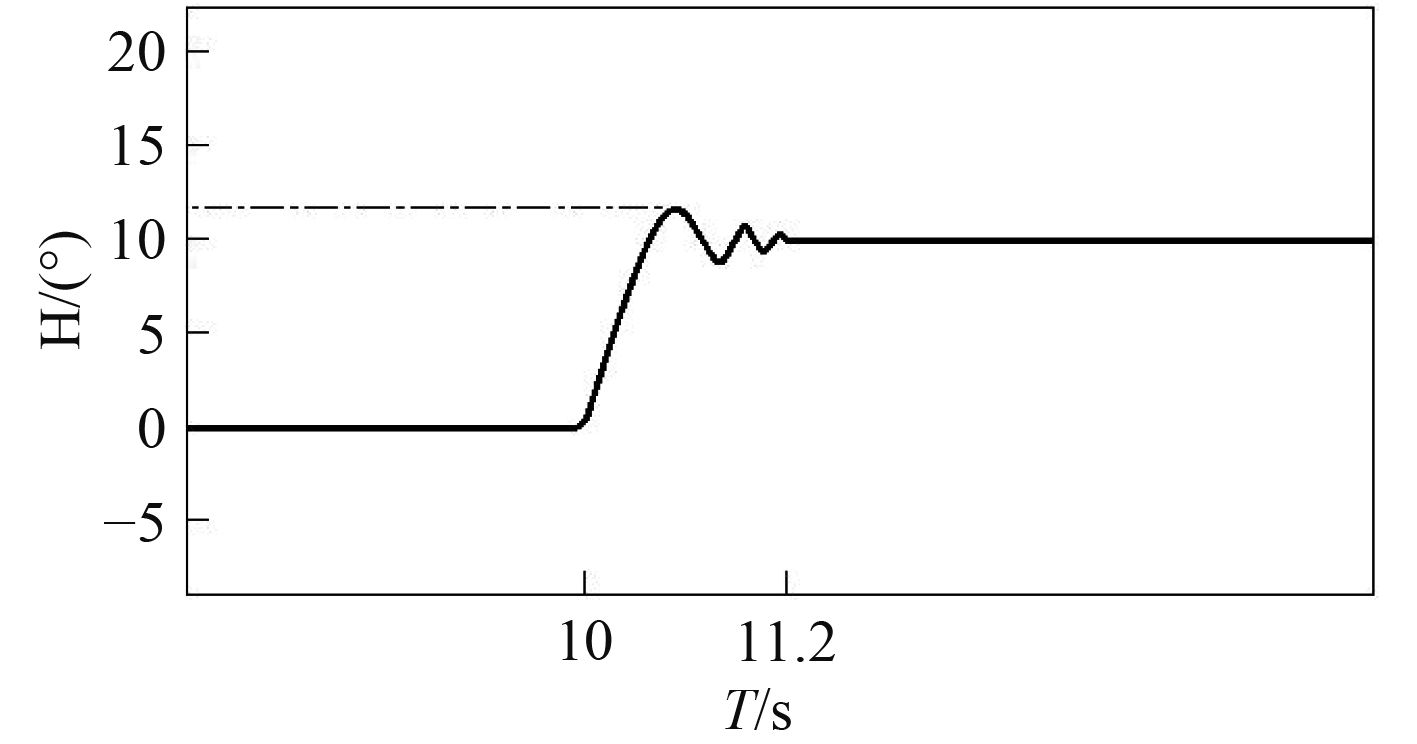
对于可调桨推进系统,通过控制手柄在 10 s时刻给定1个螺距指令 10°,同时引入1个脉冲干扰信号。从效果图 9和图 10对比可看出,模糊PID控制稳定明显性好于PID控制,但是其超调时间较久。指令发出后PID控制反应过渡时间为 0.8 s,实际桨角震荡波峰值为 14.3°,模糊PID控制反应过渡时间为为 1.20 s,实际桨角震荡波峰值为 11.8°。分析这种效果产生的原因,模糊PID控制是在PID控制器前面引入了模糊推理系统,经过输入量偏差和偏差变化率的模糊化,模糊规则的推理,模糊判决的决断和输出量的去模糊化,实现PID控制参数在线整定,控制效果相对较好,但是因为这一系列过程的进行,使得整个控制过程反应时间相对较长。
|
图 9 模糊PID控制曲线 Fig. 9 The curve of fuzzy PID control |
|
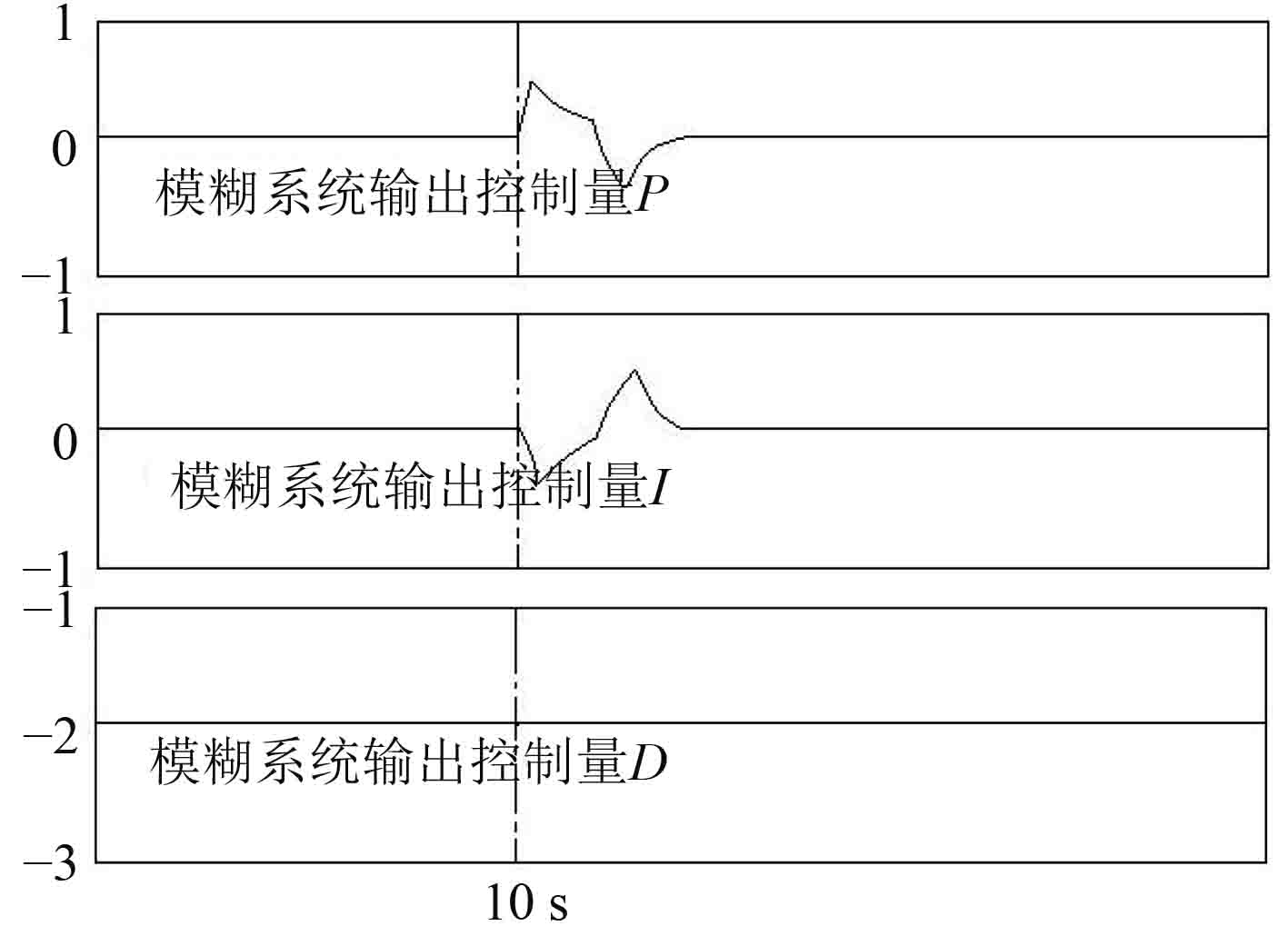
图 10 模糊推理机控制量输出曲线图 Fig. 10 The controller output curve of fuzzy inference machine |
在上述仿真过程中,模糊系统实现了PID控制参数 P, I 和 D 的在线整定,模糊推理机输出量的控制曲线如 图 11 所示。螺距调节过程中,输出量 △ K P 出现波动,先发生正跳变后发生负跳变,最后回归稳定值;输出量 △ K I 出现波动,先发生负跳变后发生正跳变,最后回归稳定值;输出量 △ K D 基本无波动。
5 结 语本文基于Matlab搭建可调桨推进系统仿真模型,设计用于调节螺距的模糊PID控制器,设计并进行相应实验得到控制曲线和实验数据。研究成果证实模糊PID控制器对于螺距的控制精度和稳定性比之PID控制器更有优势,且结构明确、实用、适应性更强,这为模糊PID控制理论在船舶可调桨上的应用提供了基础。
模糊控制理论广泛应用于汽车控制系统、机器人控制系统等,本文率先尝试将模糊控制理论用于船舶螺距调节,并在仿真过程中模糊PID控制器具有较好的跟踪性能和抗干扰能力,此研究促进船舶工业领域控制理论多样化应用。
实现模糊PID控制需要准确合理地获取PID参数的模糊校正规则,这需要进行精确离线仿真试验和现场调整。本文不足之处,有待于进一步将本文研究成果转化为实船应用,此为后续研究的切入点。
| [1] |
郭庆祝, 姜德金, 尹忠厚. 基于模糊智能控制的船用可调螺旋桨系统仿真研究[J]. 造船技术, 2006 (2): 41–43.
GUO Qing-zhu, JIANG De-jin, YIN Zhong-hou. Simulation research based on the fuzzy intelligent control of marine controllable pitch system[J]. Shipbuilding Technology, 2006 (2): 41–43. |
| [2] |
尚二国. 调距桨推进装置控制系统的研究与设计[D]. 武汉: 武汉理工大学, 2009.
SHANG Er-guo. Research and design of controllable pitch propulsion system[D]. Wuhan: Wuhan University of Technology, 2009. |
| [3] |
沈海云.可调侧推器设计与水动力性能仿真研究[D]. 杭州: 浙江大学, 2012.
SHEN Hai-yun. Simulation research of hydrodynamic performance and design on controllable pitch system[D]. Hangzhou, Zhejiang Universtity, 2012. |
| [4] | HU Ju-xi, SHI Qing-he, LI Yun-long. Simulation Analysis of Controllable Pitch Propeller Dynamics Modeling Considering Flexibility[J]. Ship Engineering, 02, 2014 . |
| [5] | HONG Shu-hua, CHEN Wei. An Optimal Starting Algorithm for Load Limiting Function Controller Pitch Propeller[J]. Ship Engineering, 02, 2014 . |
| [6] |
孙霄峰, 尹勇, 张秀凤. 可调螺距螺旋桨船舶的操纵运动数学模型[J]. 大连海事大学学报, 2007 (4): 21–23.
SUN Xiao-feng, YIN Yong, ZHANG Xiu-feng. Maneuvering mathematical model of ships with controllable pitch system[J]. Journal of Dalian Maritime University, 2007 (4): 21–23. |
| [7] |
徐鑫. 中速柴油机-可调螺距桨推进装置及其控制系统的仿真研究[D]. 大连: 大连海事大学, 2009.
XU Xin. Simulation research on control system of controllable pitch propulsion system with medium speed diesel engine. Dalian: Dalian Maritime University, 2009. |
| [8] | 肖清, 谢俊超, 花靖. 船用电动伺服舵机性能仿真研究[J]. 舰船科学技术, 2016, 38 (6): 118–121. |
| [9] | Millnko Godjevac. Towards High Performance Pitch Control[J]. Wartsila Technical Journal, 01, 2008 . |
| [10] | CHEN Wei, YAO Zhen-qiu. Numerical Analysis the flow field around JDC4-55 Controllable Pitch Propeller[J]. Ship Science and Technology, 05, 2012 . |
| [11] | SONG Fei, PENG Li-kun. The Mechanical efficiency and sensitivity analysis of typical hub mechanisms of controllable pitch propeller[J]. Ship Science and Technology, 04, 2015 . |
 2017, Vol. 39
2017, Vol. 39
