2. 重庆交通大学 航运与船舶工程学院,重庆 400074;
3. 重庆交通大学 建筑与城市规划学院,重庆 400074
2. College of Shipping and Marine Engineering, Chongqing Jiaotong University, Chongqing 400074, China;
3. College of Architecture and Urban Planning, Chongqing Jiaotong University, Chongqing 400074, China
南海拥有丰富的自然资源,海上风力平台的合理应用可以满足岛上居民的生活用电需求,相比于其他发电形式,海上风力发电具有绿色、清洁、风速高、风情稳定,可减轻用电压力,减少二氧化碳排放,推动国民经济可持续发展,将起到重要作用。
对于海上风力发电平台在波浪中的运动响应分析,国内外的专家做过相应研究。邹早建等[1] 对浮式风机平台在规则波作用下的动力响应分析指出,系泊平台的运动是由风机的风力和波浪参数大小共同决定的。Lee[2] 提出TLP型和Spar型 2 种浮式风机系统的概念设计,对其在风浪中的运动响应进行有效、合理的评估。Denis Matha等[3]在美国研发的TLP平台基础上对张力腿模型进行了系统分析,Denis Matha等根据海上风机的设计准则验证了改良之后的浮式风机TLP平台,结果表明张力腿式风机平台运动特性较好。Jason M.Jonkman and Marshall L.Buhl Jr.[4]通过全耦合进行分析模拟,对 5 MW的浮式风力发电机的初步载荷进行了分析,确定了经济和技术的可行性、动力响应、潜在的载荷以及不稳定性。叶小嵘等[5] 将浮式平台的运动响应结果对风机气动性能产生的影响考虑在内,并研究在风、浪、流联合作用下风机气动性能。李溢涵[6]以 5 MW风机为研究对象,考虑粘性阻尼矩阵和系泊系统回复刚度矩阵,考虑系泊系统与基础之间的耦合作用,对风机的整体模型进行时域分析。邓慧静[7] 根据三维势流理论和Morison方程求解三浮筒半潜平台波浪载荷和浮体在波浪中的运动响应。J.M. Jonkman等[8]对海上浮式风力发电结构的动力响应分析所采取的耦合方法进行了系统总结,并提出了动力响应的全耦合模拟分析方法;该方法不仅解决了频域和时域各自的局限性,而且可以考虑影响系统的所有可能载荷,同时也验证模型实验方法的可行性。
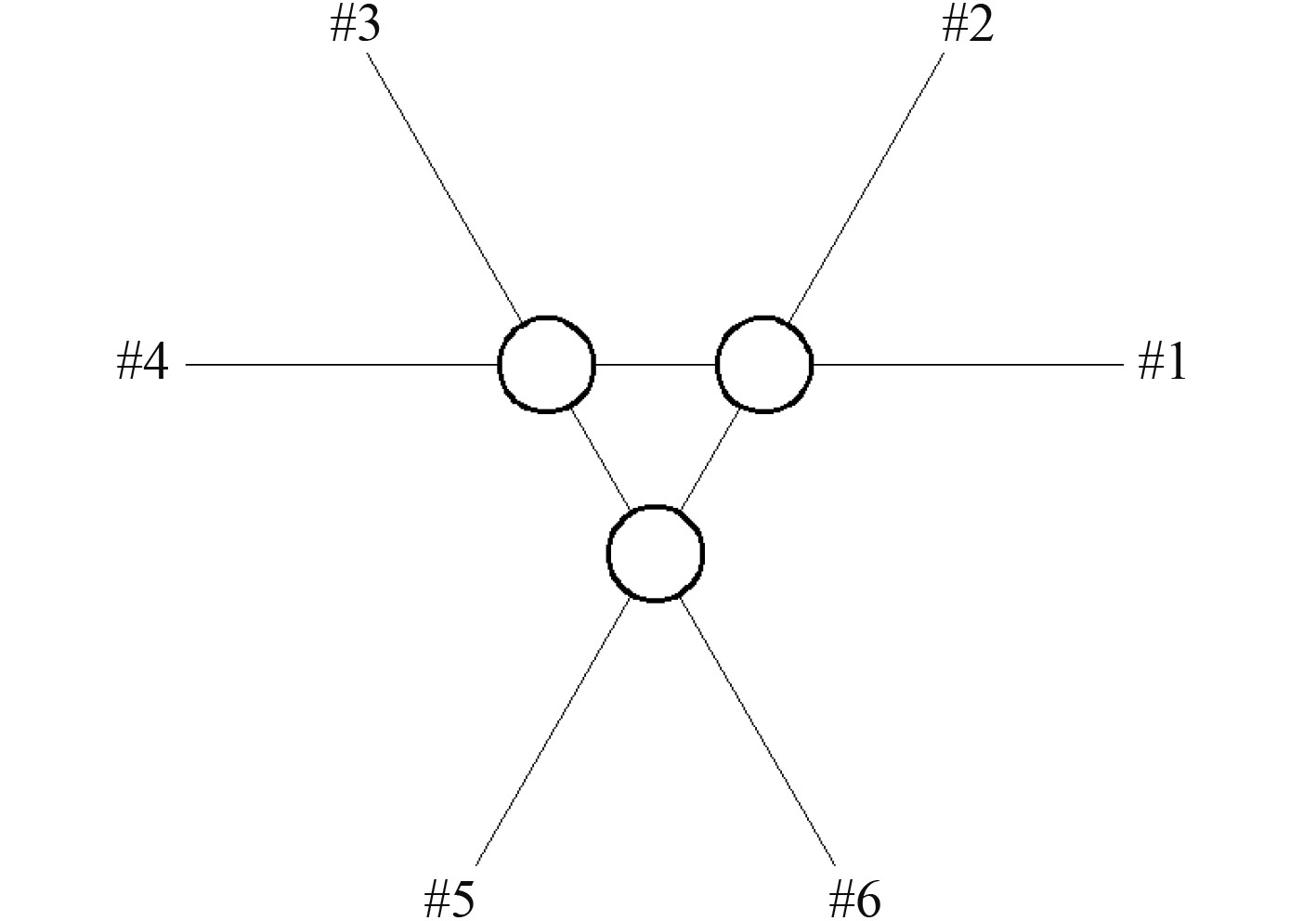
1 浮式风力发电平台及系泊定位系统设计浮式风力发电平台是由三立柱共同作用承载风力发电机组的重量,三立柱的特殊布置形式可以使浮式基础的稳性高度在 360° 内所有方向均相等。通过在三立柱下方各设置一压水板,一方面可以减小风力发电机组整体共振的不利影响,另一方面还可以增加浮式基础垂荡的粘性阻尼。同时,浮式风力发电平台设置若干横撑和斜撑,以更好的保持结构的连续性及防止局部区域应力集中。 表 1为浮式风力发电平台的主尺度要素, 图 1为浮式风力发电平台系泊系统布置示意图。
|
|
表 1 浮式风力发电平台主要要素 Tab.1 Main parameter of floating wind platform |
|
图 1 浮式风力发电平台系泊系统布置示意图 Fig. 1 Arrangement of the mooring lines |
对于浮式风力发电平台来说,耦合分析是需要考虑海洋结构物及其系泊系统的相互影响,建立整个系统的运动方程和动力方程进行求解,是一类复杂的非线性问题,需要考虑系泊系统的回复力、阻尼力及惯性力对结构物的平均位置及其动力响应所产生的影响[9]。
当完全时域耦合分析浮式风力发电平台运动时,需要将风力机、支撑平台和系泊系统的耦合效应考虑在内,平台的结构可以近似看成具有 6 个自由度的简单刚体。
浮式风力发电平台整体结构体系的运动方程为:
| $\begin{split}\\[-12pt]({ M} + { A})\ddot x + & ({{ B}_w} + {{ B}_m})\dot x + ({{ K}_w} + {{ K}_t} + {{ K}_m})x = \\[5pt]& {F_{hys}} + {F_{waveI}} + {F_{waveD}} + {F_{winds}}{\text{。}}\end{split}$ | (1) |
式中: M 为结构质量矩阵; A 为附加质量矩阵;
B w 和 B m 分别为波阻尼矩阵和系泊系统阻尼矩阵;
K w 为水动力恢复刚度矩阵;
K t 和 K m 分别为张力腿筋腱部分的刚度矩阵和锚缆部分的刚度矩阵;
F hvs 和 F winds 分别为静水力和风荷载力;
F waveI 和 F waveD 分别为入射波浪力和绕射波浪力。
当计入不规则波以及海流的作用时,此运动方程为:
| $\begin{split}\\[-12pt]\!\!\!\! ({ M} + { A})\ddot x + & ({{ B}_w} + {{ B}_m})\dot x + ({{ K}_w} + {{ K}_t} + {{ K}_m})x = \\[5pt] & {F_{hys}} \!+\! {F_{waveD}} \!+\! {F_{wavedift}} + {F_{winds}} \!+\! {F_{currents}}{\text{。}}\!\!\end{split}$ | (2) |
式中: F wavedift 为波浪慢漂力; F currents 为海流作用力。
3 数值算例 3.1 系泊缆索主要参数浮式风力发电平台在开阔的海洋环境中,会受到复杂的环境载荷,根据初步的风载荷、海流载荷和波浪载荷的计算,选取 6 根锚链形式的悬链线进行系泊定位,分析认为流体是无粘性、不可压缩的理想流体,考虑系泊缆索与浮式风力发电平台的相互耦合作用,系泊缆索的具体参数如表 2所示。
|
|
表 2 系泊缆索主要参数 Tab.2 Main parameter of the mooring lines |
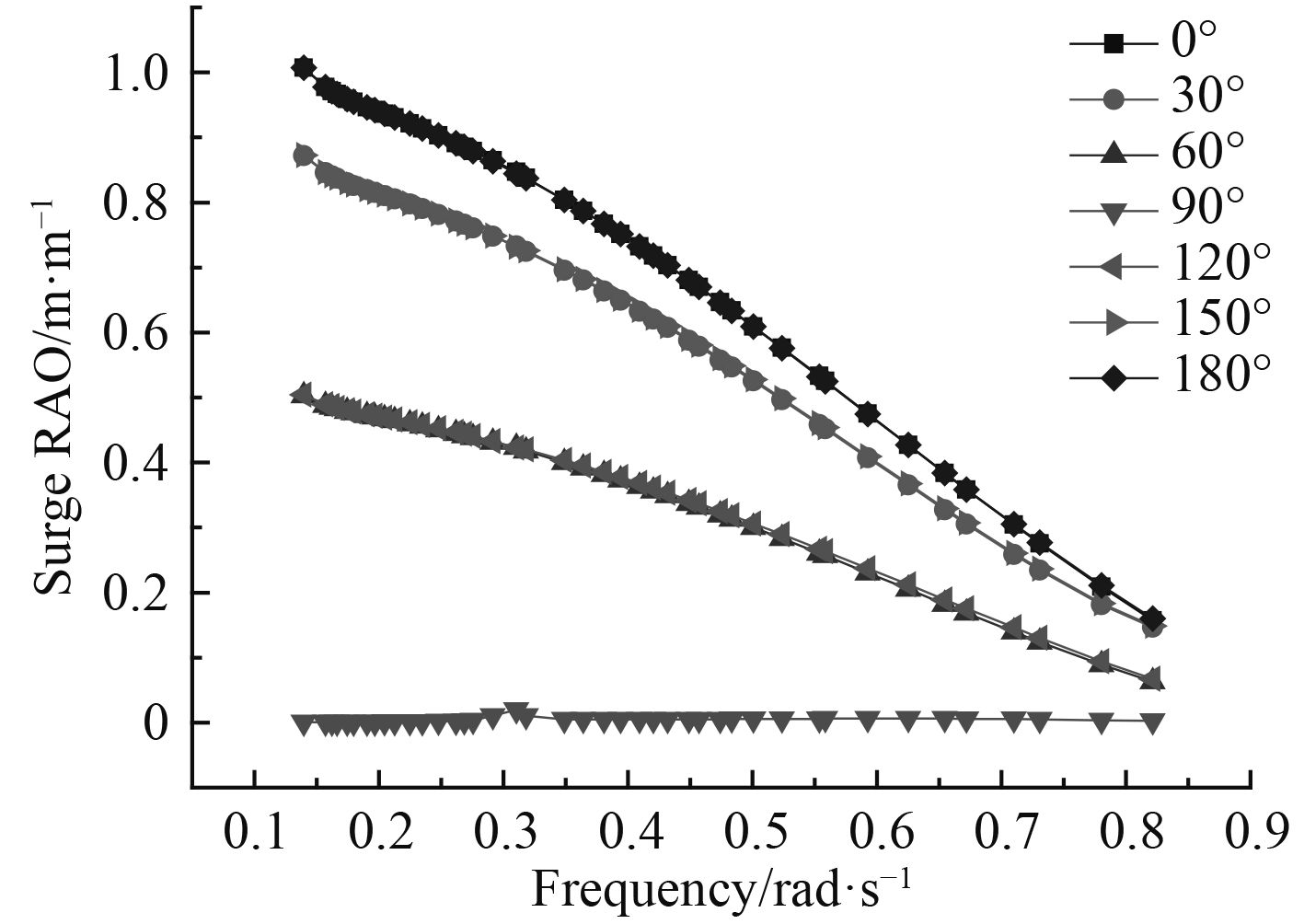
浮式风力发电平台的工作水深为 1 000 m,不考虑风速的影响,只考虑粘性阻尼力和系泊系统回复力的作用,主要研究浮式风力发电平台六自由度幅值响应算子随浪向角的变化规律,定义浪向角增量步长为 30°,分析平台在 0°,30°,60°,90°,120°,150°和 180°浪向角下的运动响应幅值算子的变化规律,如图 2~ 图 7所示。
|
图 2 纵荡RAO随浪向角的变化曲线 Fig. 2 The curve of surge RAO with the wave direction angle |
|
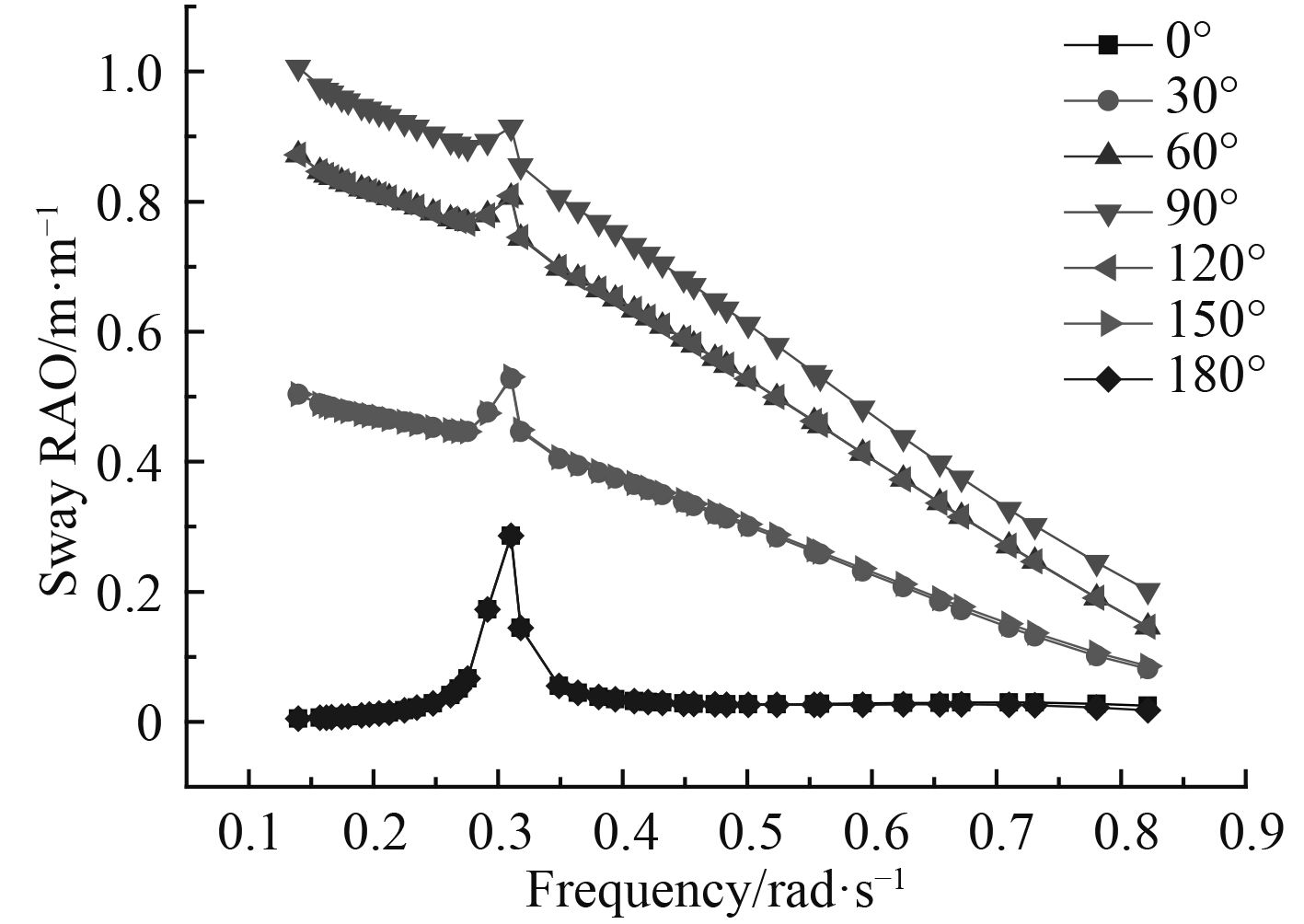
图 3 横荡RAO随浪向角的变化曲线 Fig. 3 The curve of sway RAO with the wave direction angle |
|
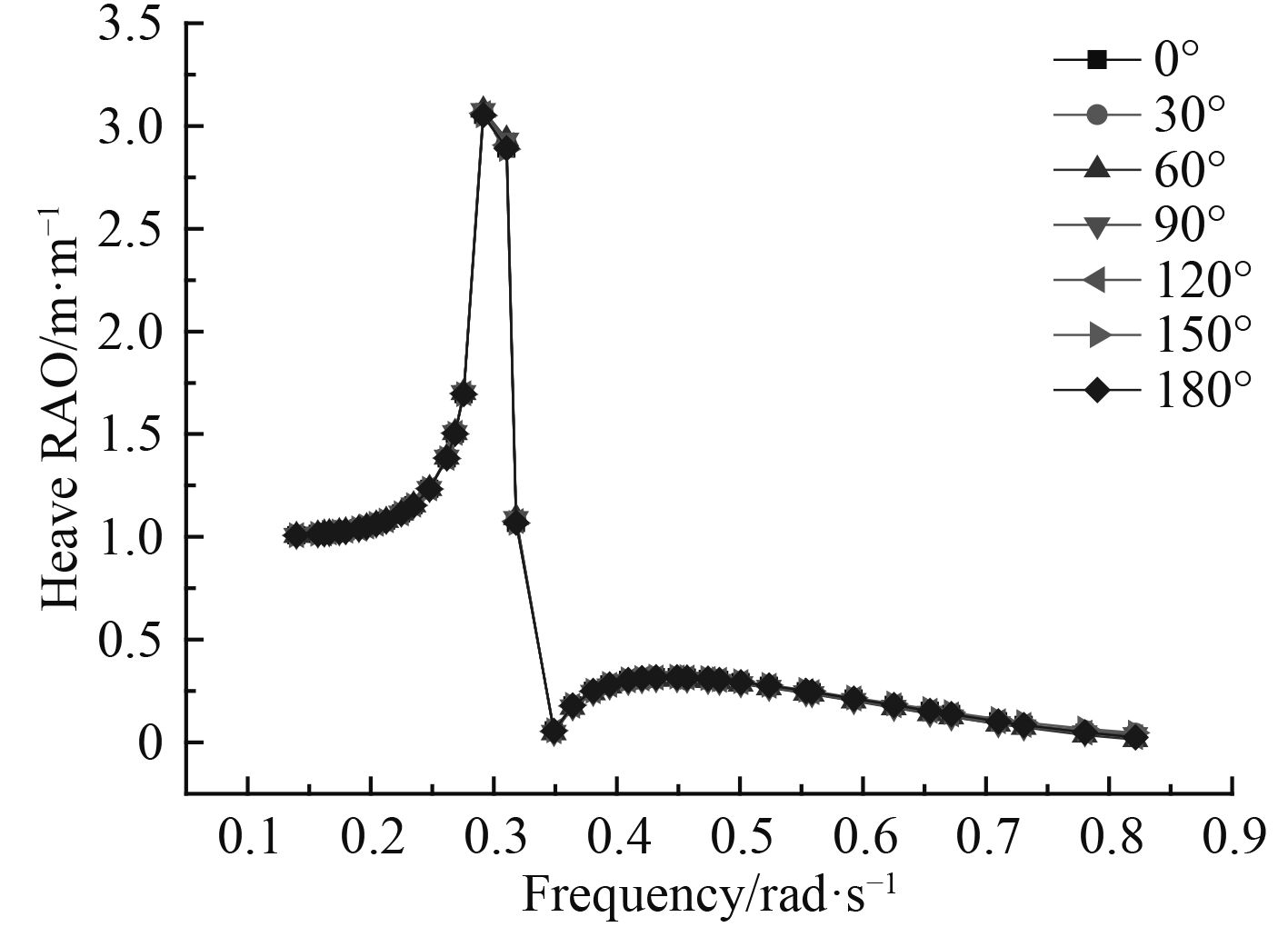
图 4 垂荡RAO随浪向角的变化曲线 Fig. 4 The curve of heave RAO with the wave direction angle |
|
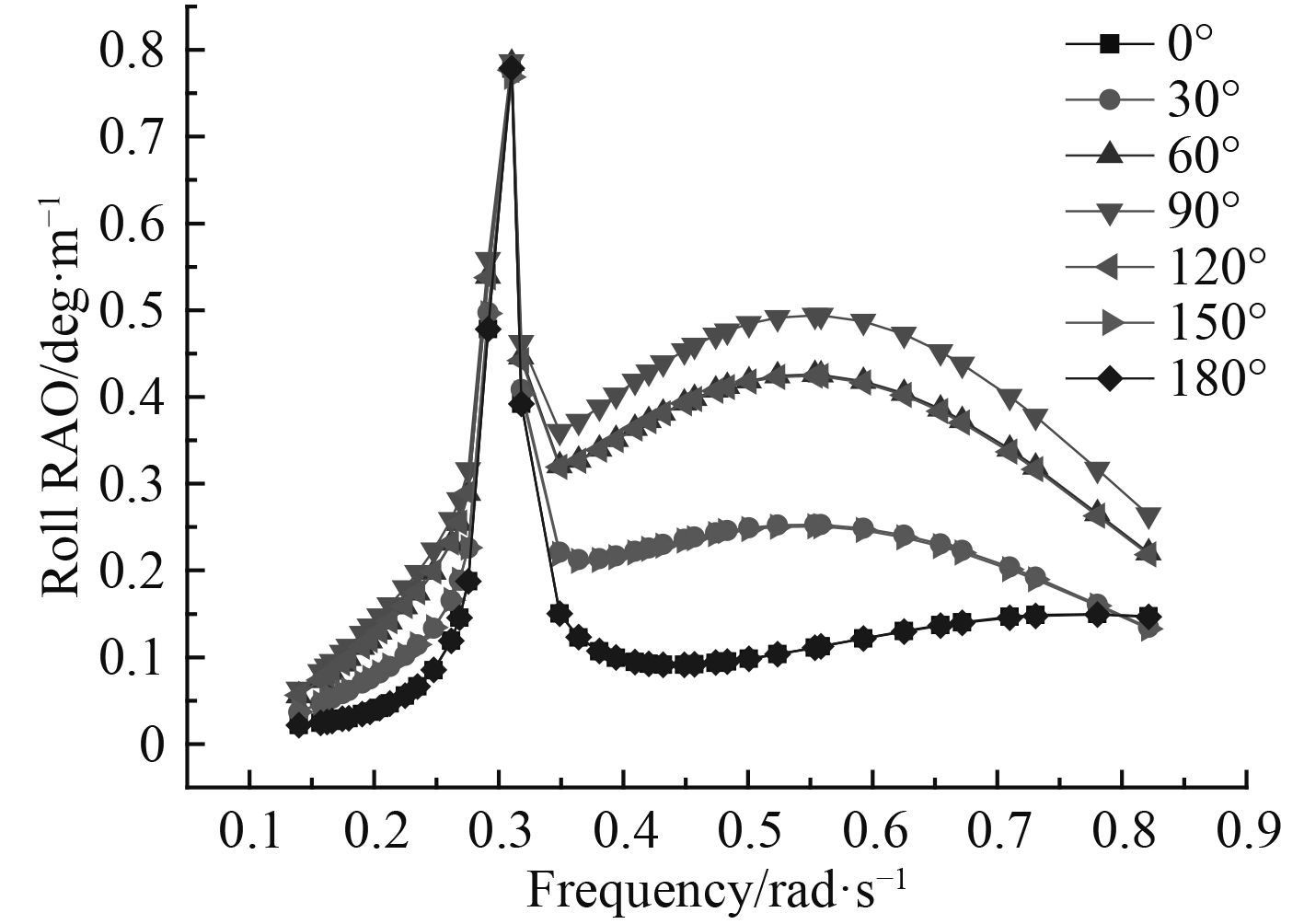
图 5 横摇RAO随浪向角的变化曲线 Fig. 5 The curve of roll RAO with the wave direction angle |
|
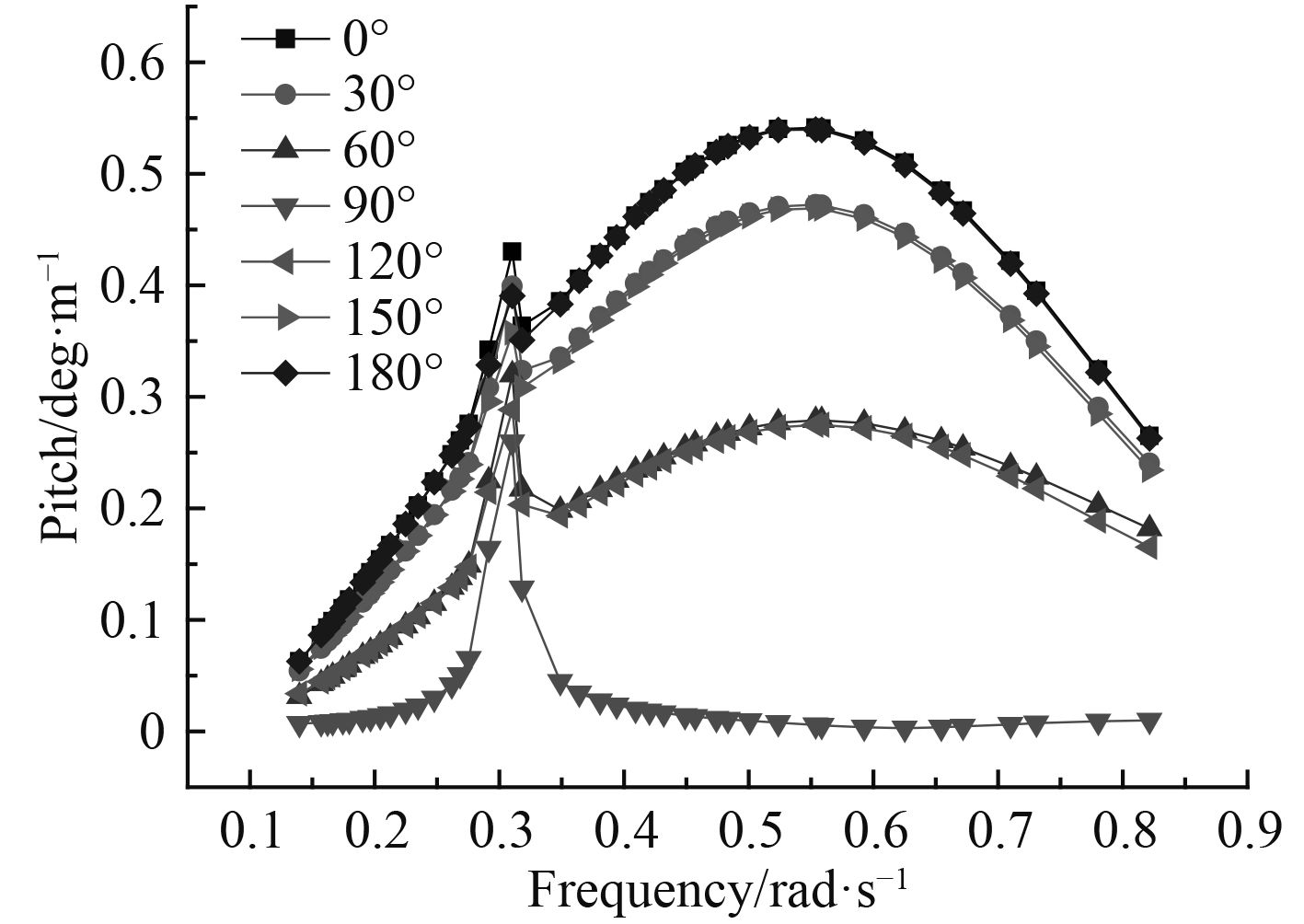
图 6 纵摇RAO随浪向角的变化曲线 Fig. 6 The curve of pitch RAO with the wave direction angle |
|
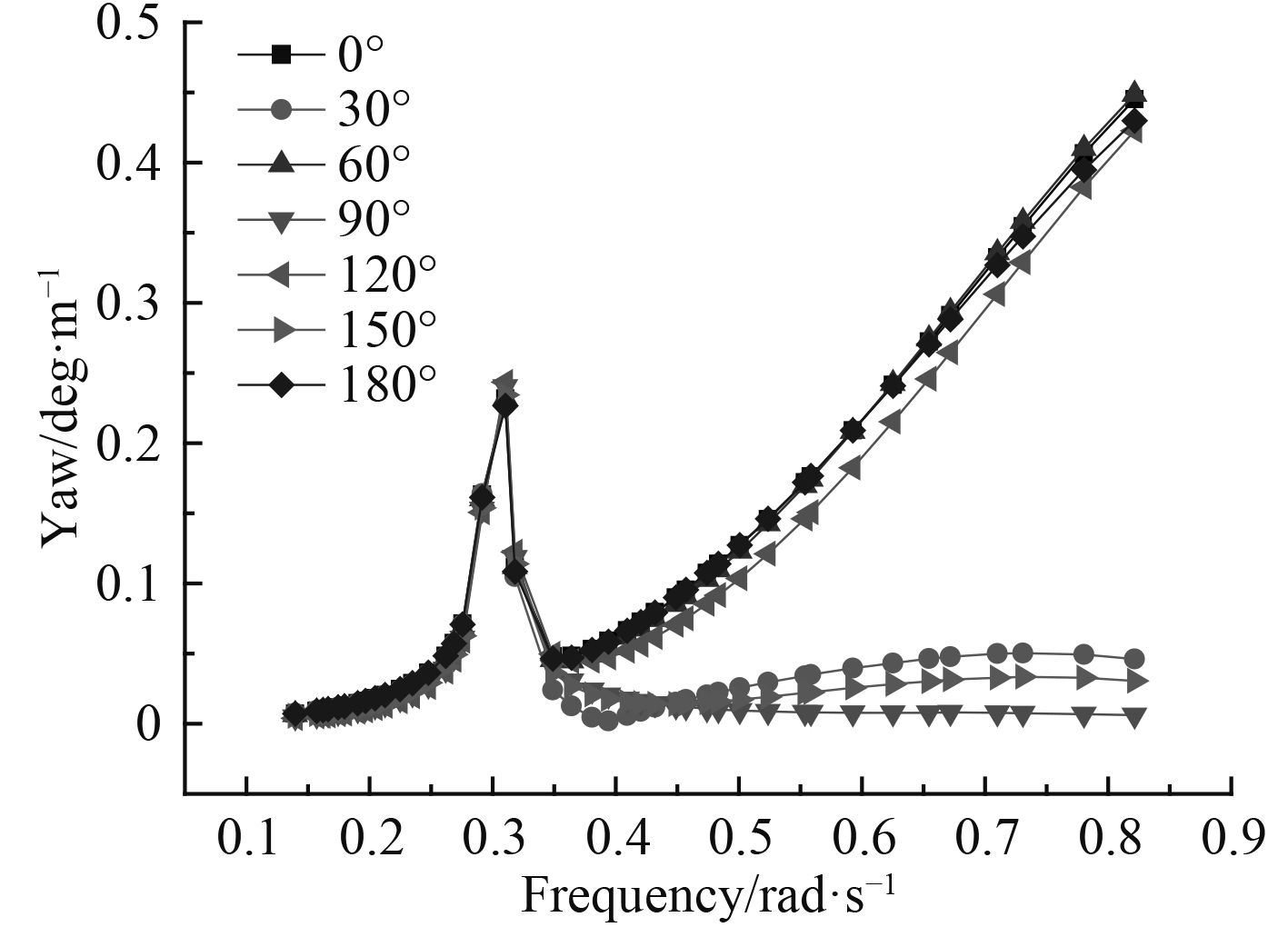
图 7 首摇RAO随浪向角的变化曲线 Fig. 7 The curve of yaw RAO with the wave direction angle |
由图 2纵荡RAO随浪向角变化曲线可知,纵荡RAO从 0°~180° 呈现先减小后增大的趋势;由图 3可知,横荡RAO随浪向角变化可知,横荡RAO从 0°~180° 呈现先增大后减小的趋势,无论在任何浪向作用下,都是在 0.3 rad/s处出现极值;由图 4可知,垂荡RAO随浪向角变化可知,无论在任何浪向作用下,垂荡RAO基本不发生变化,且在 0.3 rad/s处出现极值,同时也表明垂荡RAO与波浪入射方向基本无关。由图 5横摇RAO随浪向变化可知,随着浪向角的增加,横摇RAO表现出先增大,后减小的趋势,且在 0.3 rad/s处出现极值;由图 6纵摇RAO随浪向变化可知,随着浪向角的增加,横摇RAO表现出先减小,后增大的趋势,在浪向角是 90° 时为单峰值,在其他角度为双峰值。
3.3 时域分析结果本文以风、浪、流组合环境为例,通过对本模型 10 800 s的数值模拟结果可知,风、浪、流 3 种载荷在同一方向时,系泊缆索的顶端张力出现最大值,浮式风力发电平台的运动响应幅值出现最大值,由于结构的特殊稳定形式,纵荡运动幅值的最大为 0.2 m,纵摇运动幅值最大为 0.65°,首摇运动幅值最大 0.65°,在浮式风力发电平台的六自由度中,横荡、垂荡和横摇为主要的运动模态,运动响应时间历程曲线如图 8~ 图 10所示。
|
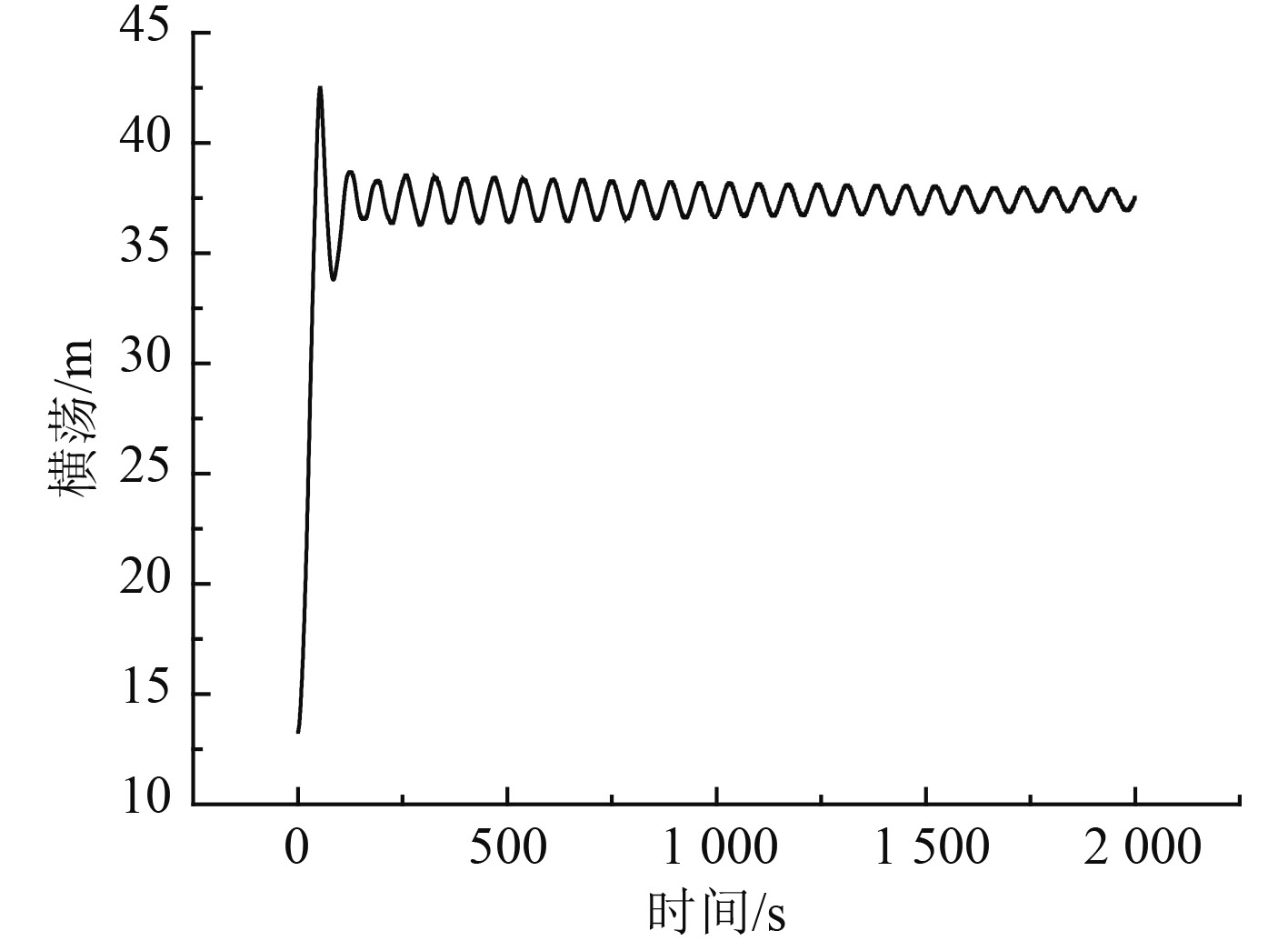
图 8 风力发电平台横荡时间历程曲线 Fig. 8 Time series of floating wind platform sway |
|
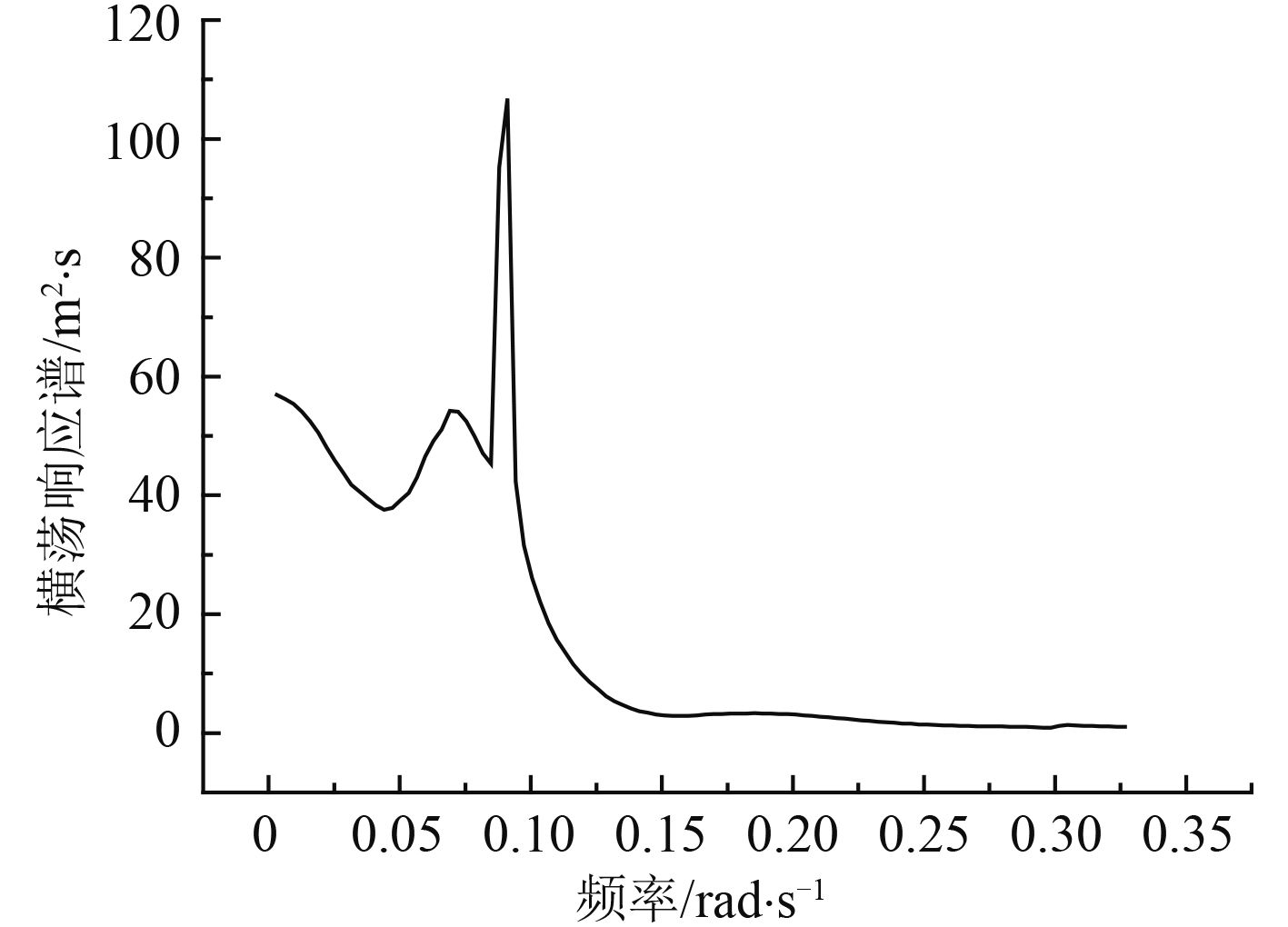
图 9 风力发电平台横荡响应谱 Fig. 9 Response spectrum of floating wind platform sway |
从图 8风力发电平台横荡时间历程曲线可看出,由于风浪流同向 90° 入射,风力发电平台的运动幅值会不断增大,并且呈现出大周期、不规则的运动形式,系泊系统提供水平回复力,使风力发电平台围绕相对平衡位置做往复运动。从图 9风力发电平台横荡响应谱可看出,横荡表现为明显的低频特性,能量主要集中在 0.75 rad/s附近处,在 0.1 rad/s处出现峰值。
|
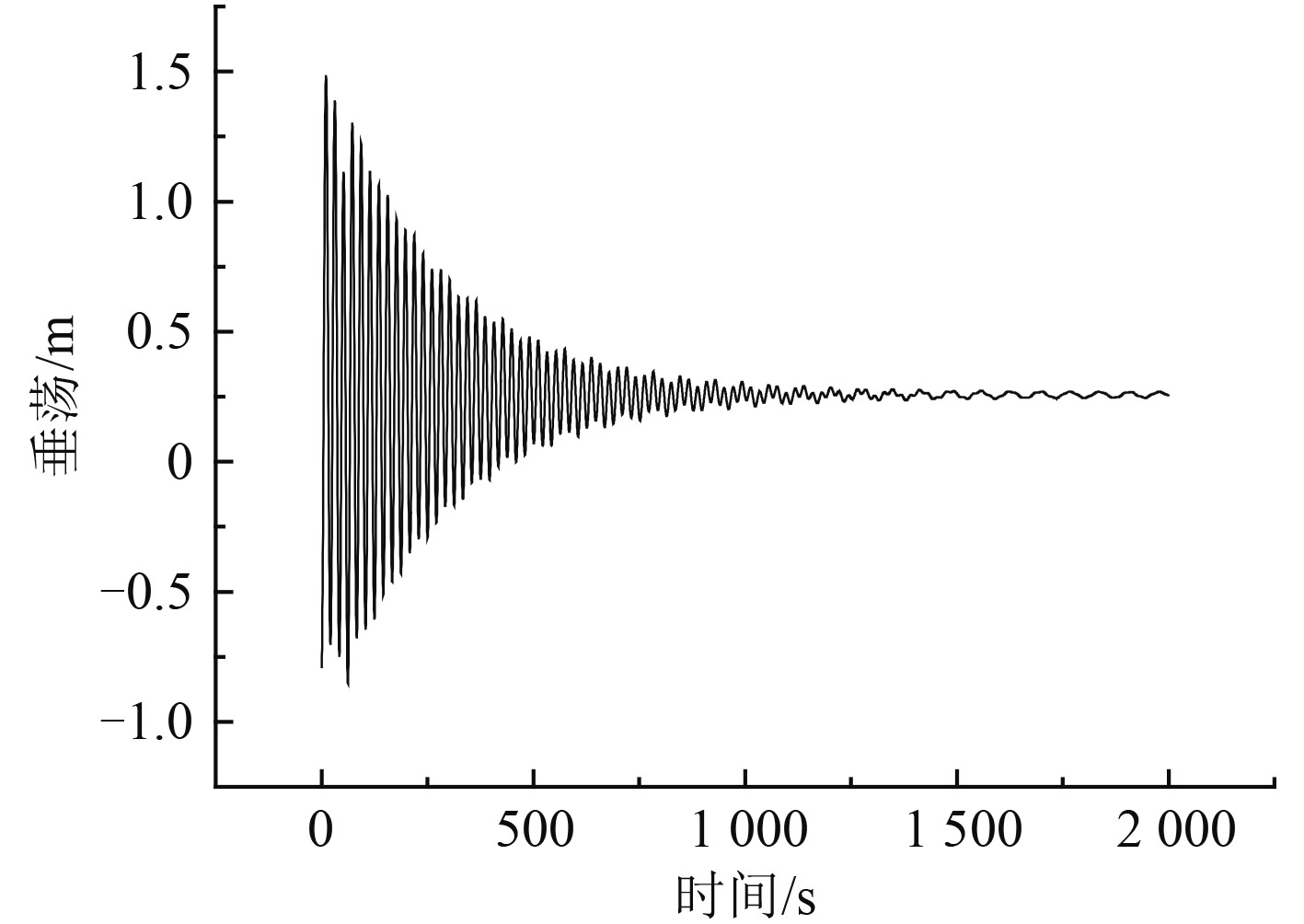
图 10 风力发电平台垂荡时间历程曲线 Fig. 10 Time series of floating wind platform heave |
|
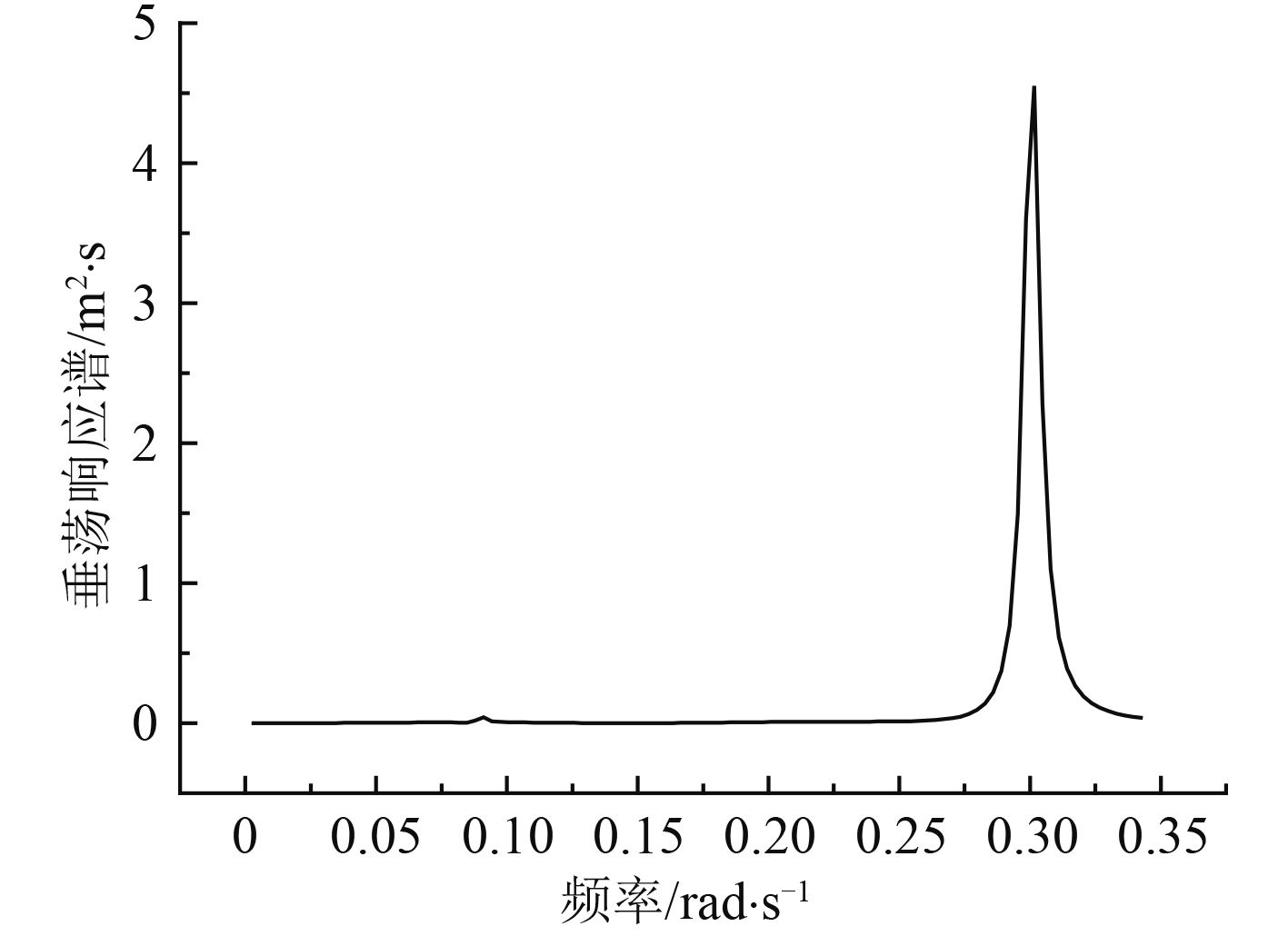
图 11 风力发电平台垂荡响应谱 Fig. 11 Response spectrum of floating wind platform heave |
从图 10风力发电平台垂荡时间历程曲线可看出,由于风浪流同向 90° 入射,浮式风力发电平台在平衡位置处往复运动,风力发电平台的运动受到系泊系统回复力、重力和浮力等外力共同作用,使其运动幅值逐渐减小。从图 11风力发电平台垂荡响应谱分析出,垂荡表现为明显的波频特性,能量在 0.08 rad/s处略微有变化,但是能量主要集中 0.30 rad/s附近处,且在 0.3 rad/s处出现峰值。
|
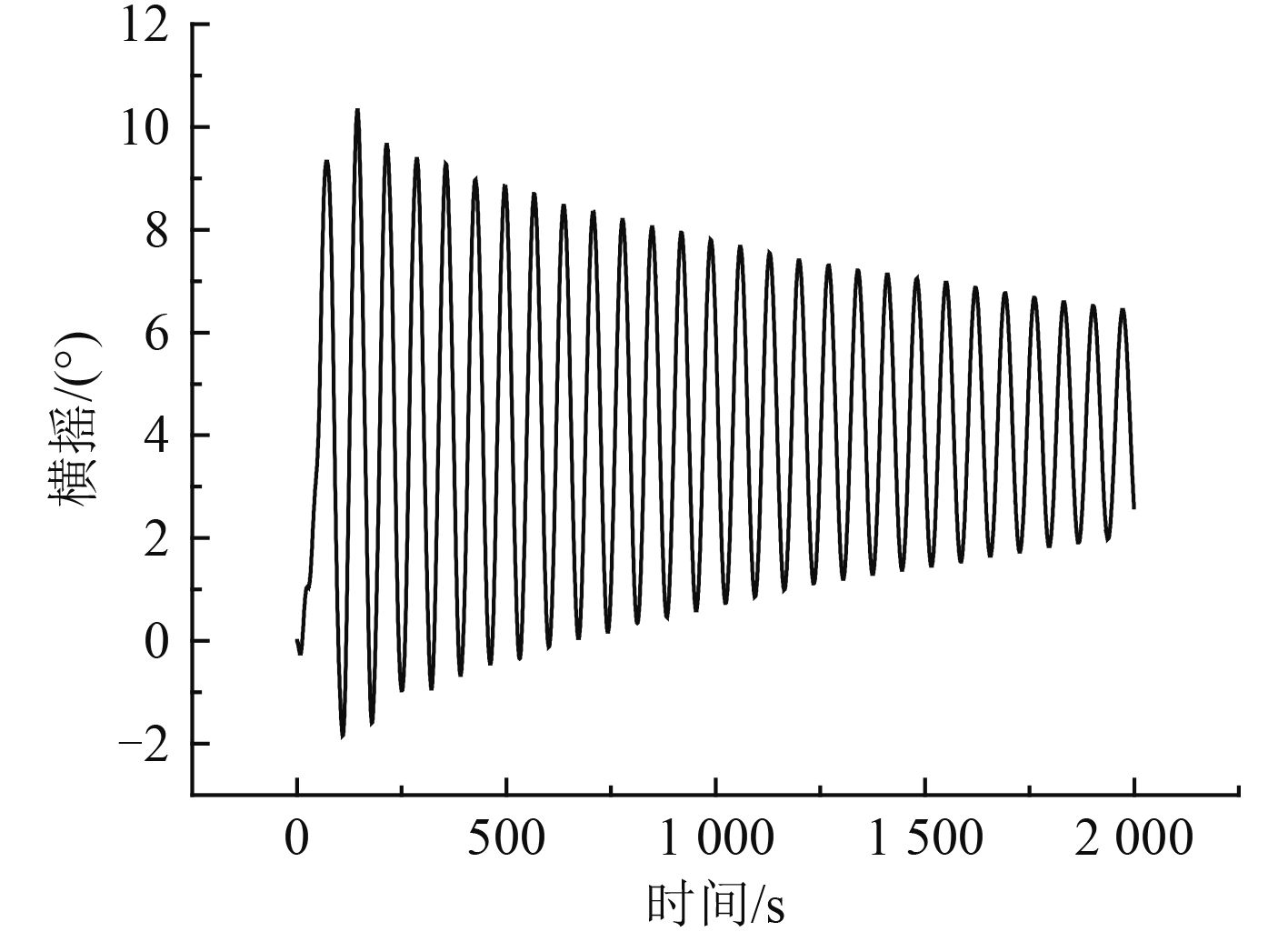
图 12 风力发电平台横摇时间历程曲线 Fig. 12 Time series of floating wind platform roll |
|
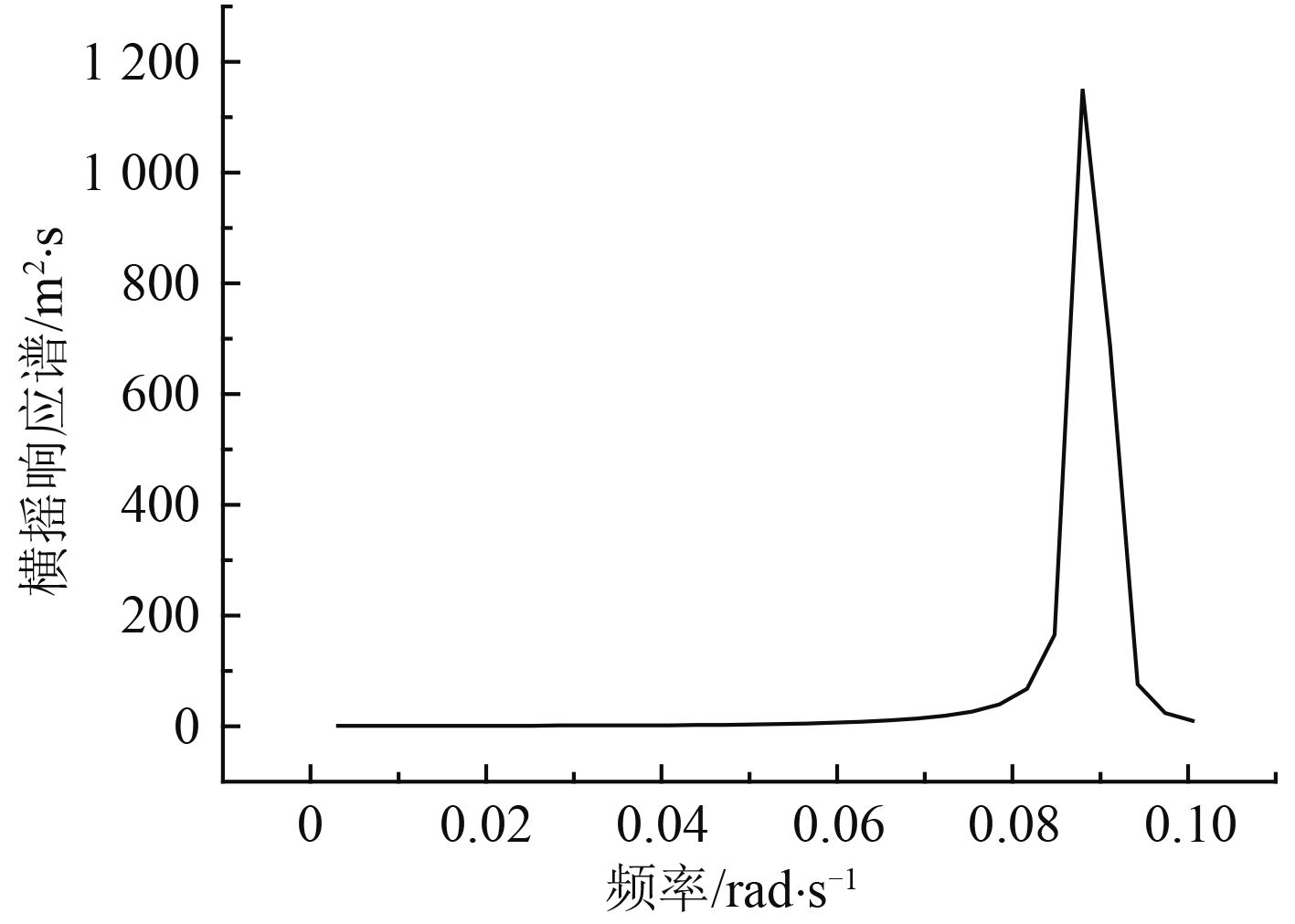
图 13 风力发电平台横摇响应谱 Fig. 13 Response spectrum of floating wind platform roll |
从图 12风力发电平台横摇时间历程曲线可看出,由于风浪流同向 90° 入射,浮式风力发电平台的横摇角有很大的幅值变化,风力发电平台的运动受到系泊系统提供水平回复力,使其运动幅值逐渐减小。从图 13风力发电平台横摇响应谱分析出,横摇表现为明显的低频特性,能量主要集中 0.09 rad/s附近处,且在 0.09 rad/s处出现峰值。
4 结 语通过完全时域耦合的分析方法,对作业水深 1 000 m的风力发电平台及其系泊系统的响应进行求解,得出风力发电平台及其系泊系统的动力响应特性。同时,本文描述风力发电平台概念设计的基本流程及其系泊系统设计的参数,考察风力发电平台幅值响应算子随浪向角的变化及求解风力发电平台在系泊系统的作用下,主要运动模态的运动响应幅值及运动响应谱,为实际工程的应用、系泊系统的设计提供一定的参考价值,具体结论如下:
1)从纵荡和纵摇RAO随浪向角变化曲线可知,纵荡和纵摇RAO从 0°~180° 变化过程中呈现出先减小后增大的变化趋势,且纵摇在 0.3 rad/s和 0.55 rad/s处出现双峰值;
2)浪向任意角度入射,垂荡RAO各曲线基本重合,幅值基本不发生变化;横荡和横摇的幅值响应算子从 0°~ 180° 变化过程中呈现出先增大后减小的变化趋势,且横摇也在 0.3 rad/s和 0.55 rad/s处出现双峰值;
3)对于海上风力发电平台作业海况下,风浪流同向作用,横荡、横摇和垂荡运动响应十分显著,横荡的最大幅值为 43 m,垂荡运动最大幅值为 1.5 m,横摇运动最大幅值为 1.5°,满足响应规范的要求;
4)从海上风力发电平台主要运动模态响应谱可知,横荡运动具有显著的低频运动特性;而垂荡的谱峰集中在 0.3 rad/s附近,主要呈现波频运动的特性;横摇运动的谱峰能量集中在 0.09 rad/s附近,主要呈现低频运动的特性。
总之,风力发电平台是深海能源开发最主要的形式之一,也为新型能源风力发电机的主要载体,合理的平台型式设计及系泊系统的优化,可以有效避开波浪能量集中的频率,使得风力发电平台的主要运动模态幅值明显改善,大大增强平台的适用范围、舒适度和安全性。
| [1] |
唐耀, 范菊, 邹早建, 等. 浮式风机平台在规则波和定常风作用下的动力响应分析[J]. 中国海洋平台, 2014, 29 (1): 50–56.
TANG YAO, FAN JU, ZOU ZAO-jian, et al. The response analysis of floating wind platform in regular wave and steady wind[J]. China offshore platform, 2014, 29 (1): 50–56. |
| [2] | LEE K H. Responses of floating wind turbines to wind and wave excitation[D]. Massachusetts, USA: Massachu-setts Institute of Technoloqy, 2005. |
| [3] | MATHA D, FISCHER T, KUHN M. Model development and loads analysis of a windturbine on a floating offshore tension leg platform. NREL/CP-500-46725. Golden, CO: National Renewable Energy Laboratory, 2010: 22–25. |
| [4] | JONKMAN, J. M, a BUHL M L, Jr., ‘Loads analysis of a floating offshore wind turbine using fully coupled simulation.’ NREL/CP-500-41714, Golden, CO: National Renewable Energy Laboratory, June3-6, 2007: 6–10. |
| [5] |
叶小嵘, 张亮, 吴海涛, 等. 平台运动对海上浮式风机的气动性能影响研究[J]. 华中科技大学学报, 2012, 40 (3): 123–126.
YE XIAO-rong, ZHANG LIANG, WU HAI-tao, et al. Influence of platform motion response on aerodynamic performance of floating offshore wind turbine[J]. J. Huazhong Univ. of Sci. & Tech. (Natural Science Edition), 2012, 40 (3): 123–126. |
| [6] | 李溢涵. 海上风机Spar型浮式基础的运动特性研究[D], 天津: 天津大学, 2011. |
| [7] | 邓慧静. 海上浮式风机平台稳性及锚泊系统性能研究[D], 哈尔滨: 哈尔滨工程大学, 2012. |
| [8] | JONKMAN J M, BUHL JR M L. Development and verification of a fully coupled simulator for offshore wind turbines[A]. The 45th AIAA Aerospace Sciences Meeting and Exhibit, Wind Energy Symposium. Nevada, 2007: NREL/CP-500-40979. |
| [9] |
黄祥鹿, 陆鑫森. 海洋工程流体力学及结构动力响应[M]. 上海: 上海交通人学出版社, 1992.
HUANG XIANG-lu, LU XIN-sen. Hydromechanics of marine engineering and dynamic response of structure[M]. Shanghai: SHANGHAI Jiao Tong University Press, 1992. |
 2017, Vol. 39
2017, Vol. 39
