由于海上风电具有诸多陆上风电不可比拟的优势而受到很多国家重视,但海上风机支撑结构成本高、服务周期长、工作环境恶劣,因此其安全性不容忽视[1 –2]。支撑结构属细长柱体结构,长期承受交变随机载荷,属典型的高周疲劳结构,容易产生疲劳损伤,结构疲劳破坏是其主要失效形式[3]。且一旦发生疲劳破坏,后果将不堪设想。因此,在设计阶段对支撑结构进行疲劳寿命计算尤为重要。
目前,海上风机支撑结构疲劳寿命计算有采用时域法,即先通过动力响应分析得到危险节点的应力时程曲线、试验统计得到材料的S-N曲线,然后对应力时程曲线进行雨流计数得到应力循环次数,最后结合Palmgren-miner线性累计损伤法计算出结构的疲劳寿命[4]。但随着装机容量越来越大,工作海域越来越深,支撑结构受到的环境载荷也将十分复杂。用时域法计算其疲劳寿命时需处理的数据庞大,耗时长、效率低[5 –6]。频域法通过动力学仿真和有限元分析计算出支撑结构危险节点的功率谱密度(Power spectral density function,PSD),结合Dirlik概率模型计算出结构的疲劳寿命,省去了时域法中统计应力循环次数这一复杂繁琐过程,可大大缩短计算时间,适用于受长期随机交变载荷作用下的海洋风机支撑结构疲劳寿命计算[7]。为了探索频域法在海上风机支撑结构疲劳寿命计算中的应用,本文首先建立海上三脚架固定式风机有限元模型,利用FAST软件对 5MW风机叶轮附近空气流场进行仿真,计算得到作用于风机叶片上的气动力载荷。并用Stokes五阶波理论和Morison方程计算出浪流联合载荷。然后分别用时域法和频域法计算出支撑结构危险节点的疲劳寿命,并对 2 种方法的计算结果进行对比分析。
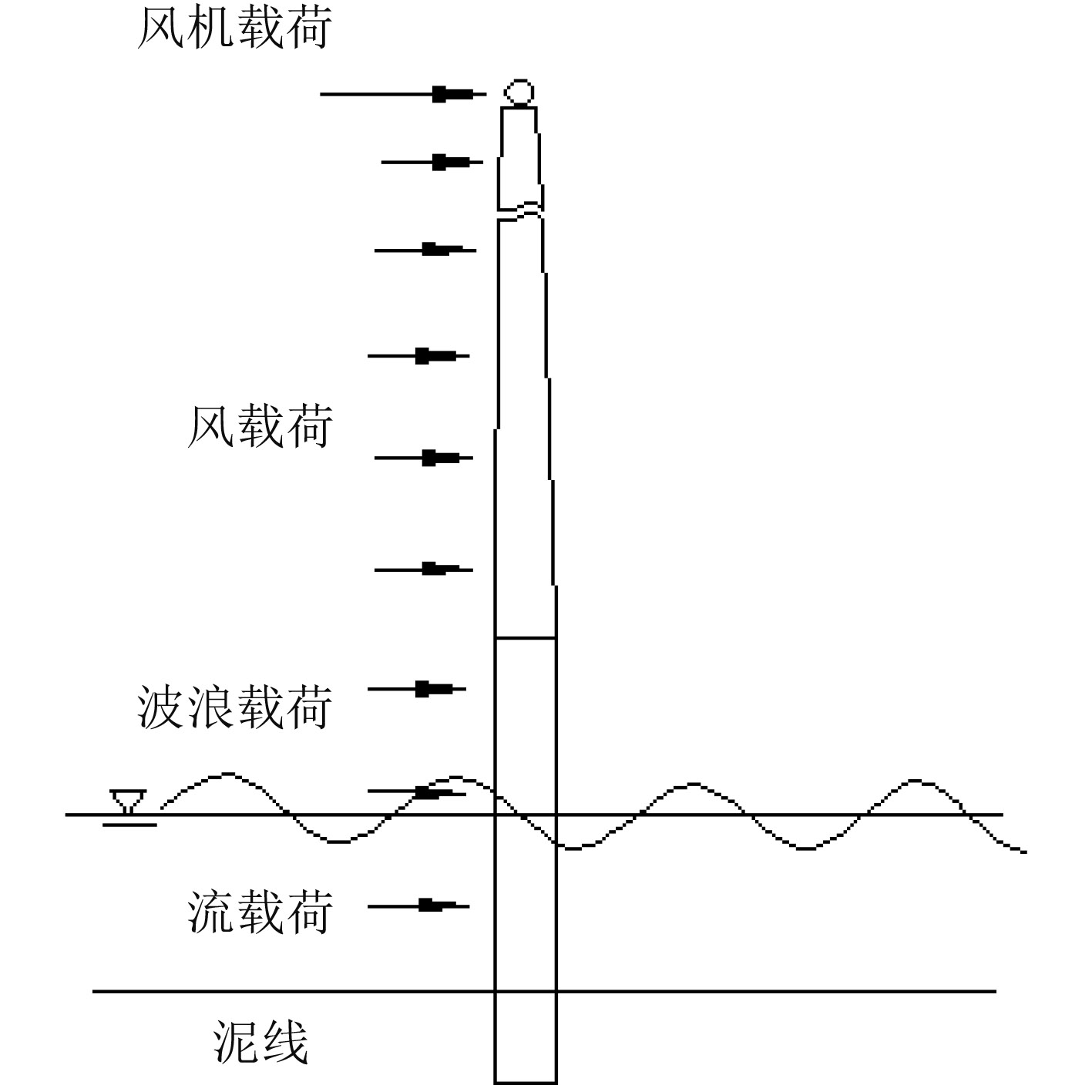
1 疲劳载荷三脚架式支撑结构受力形式如图 1所示。包括作用于塔柱上的风机载荷、风载荷;作用于斜撑及三脚架桩腿结构上的浪流联合载荷等。其中最主要的载荷是风机载荷和浪流联合载荷[8]。
|
图 1 海上风机支撑结构受力形式 Fig. 1 Force form of support structure |
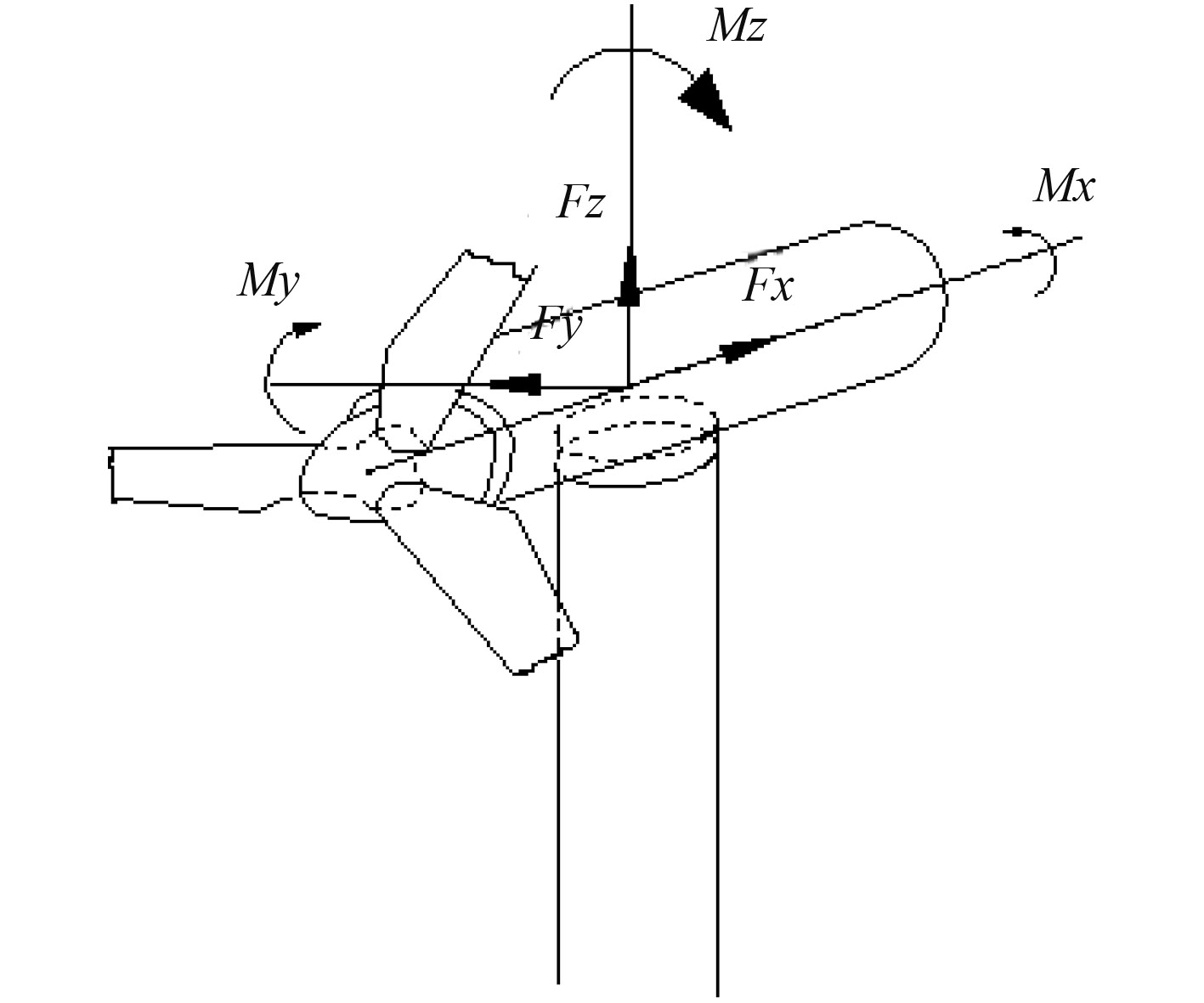
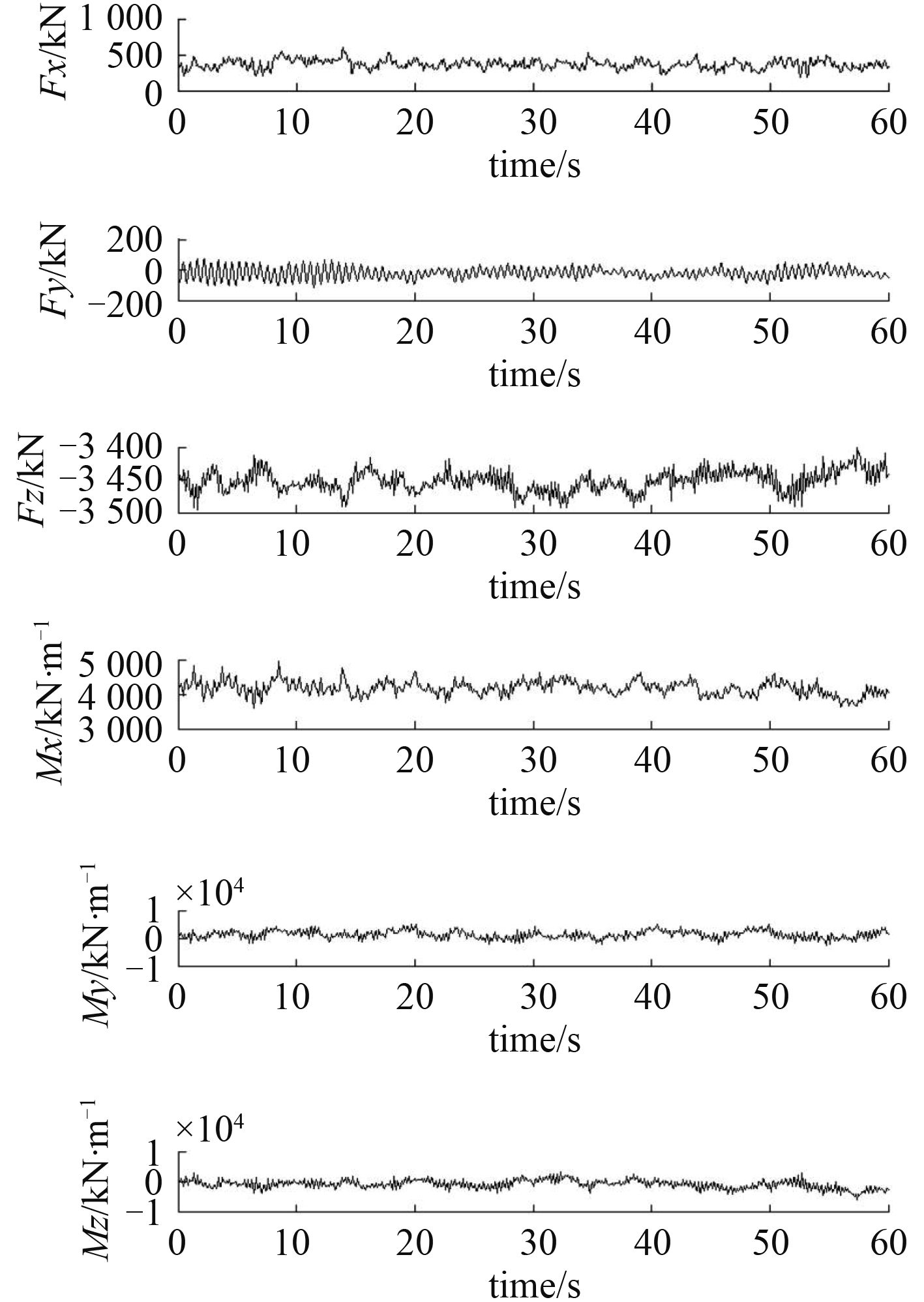
当叶轮转动发电时,会产生作用于塔柱顶部 3 个方向上的力和转动力矩。风机载荷作用形式如图 2所示。按照IEC 64100-3 标准,利用FAST软件建立风场模型,采用a级湍流强度的卡曼湍流模型[9]。轮毂高度为 90 m,风轮附近空气流场网格面积为 145 m × 145 m,叶片为柔性单元,桨距角自动调节。计算得到风机载荷如图 3所示。
|
图 2 风机载荷作用形式 Fig. 2 Form of wind turbine load |
|
图 3 风机载荷 Fig. 3 The wind turbine forces |
因为风机支撑结构为细长柱体,
|
|
表 1 100 年回归周期海洋环境 Tab.1 100 years return wave conditions of Atlantic region 2 |
|
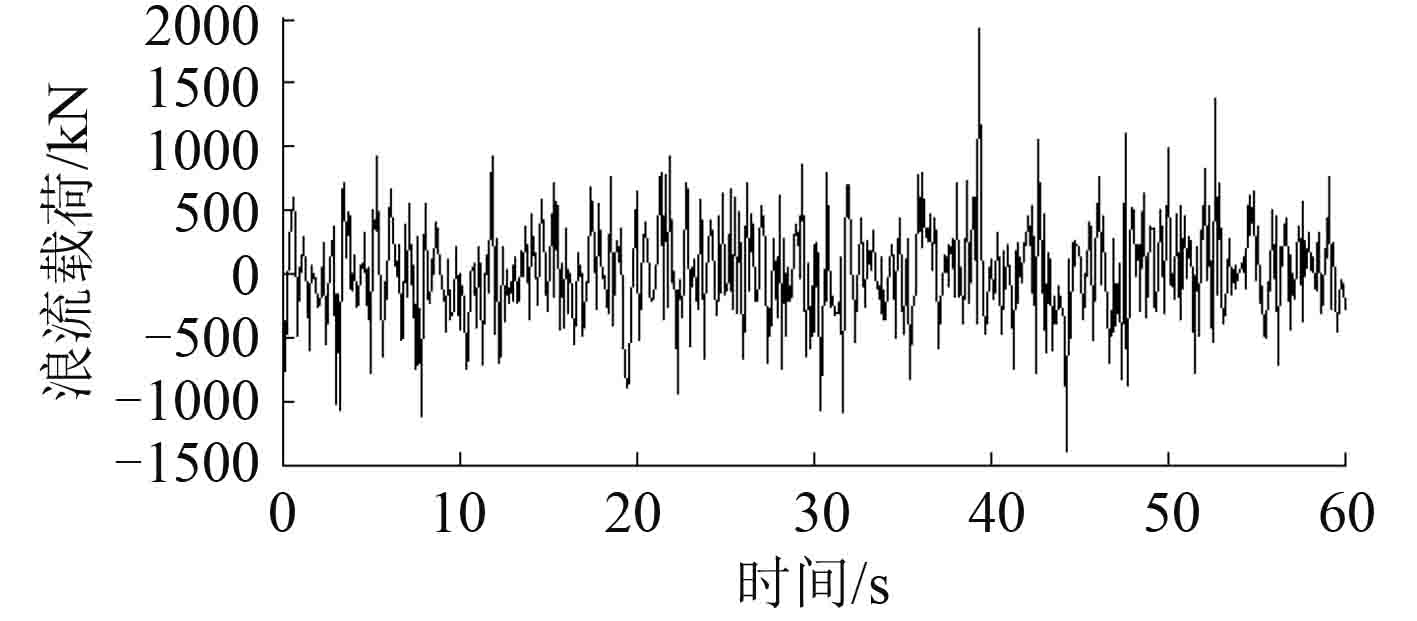
图 4 浪流联合载荷 Fig. 4 The wave and current loads |
本文采用的风机模型是NREL的 5MW海上风机模型[11],基本参数如表 2所示。
|
|
表 2 5MW海上风机基本参数 Tab.2 Properties of the NREL 5MW offshore wind turbine |
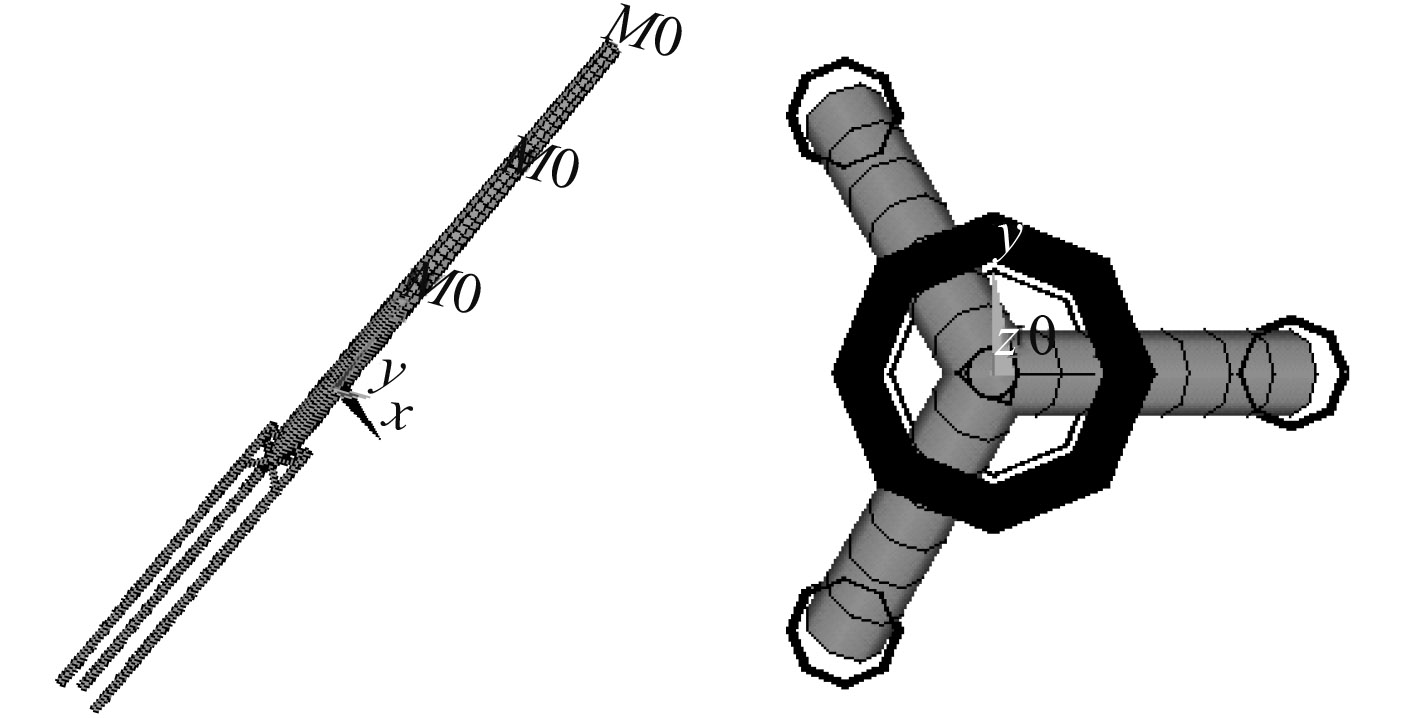
风机的支撑结构模型为三脚架式结构模型,它由位于中心的塔柱、斜撑及 3 根插入海床的桩腿组成。三脚架式基础结构简单,建造和施工方便,可减少海底冲刷、波浪流载荷,有良好的强度和稳定性,因此适用于水深较大且海床较为坚固的海域[12]。其有限元模型如图 5所示。
|
图 5 海上风机支撑结构有限元模型 Fig. 5 The finite element model of offshore wind turbine support structure |
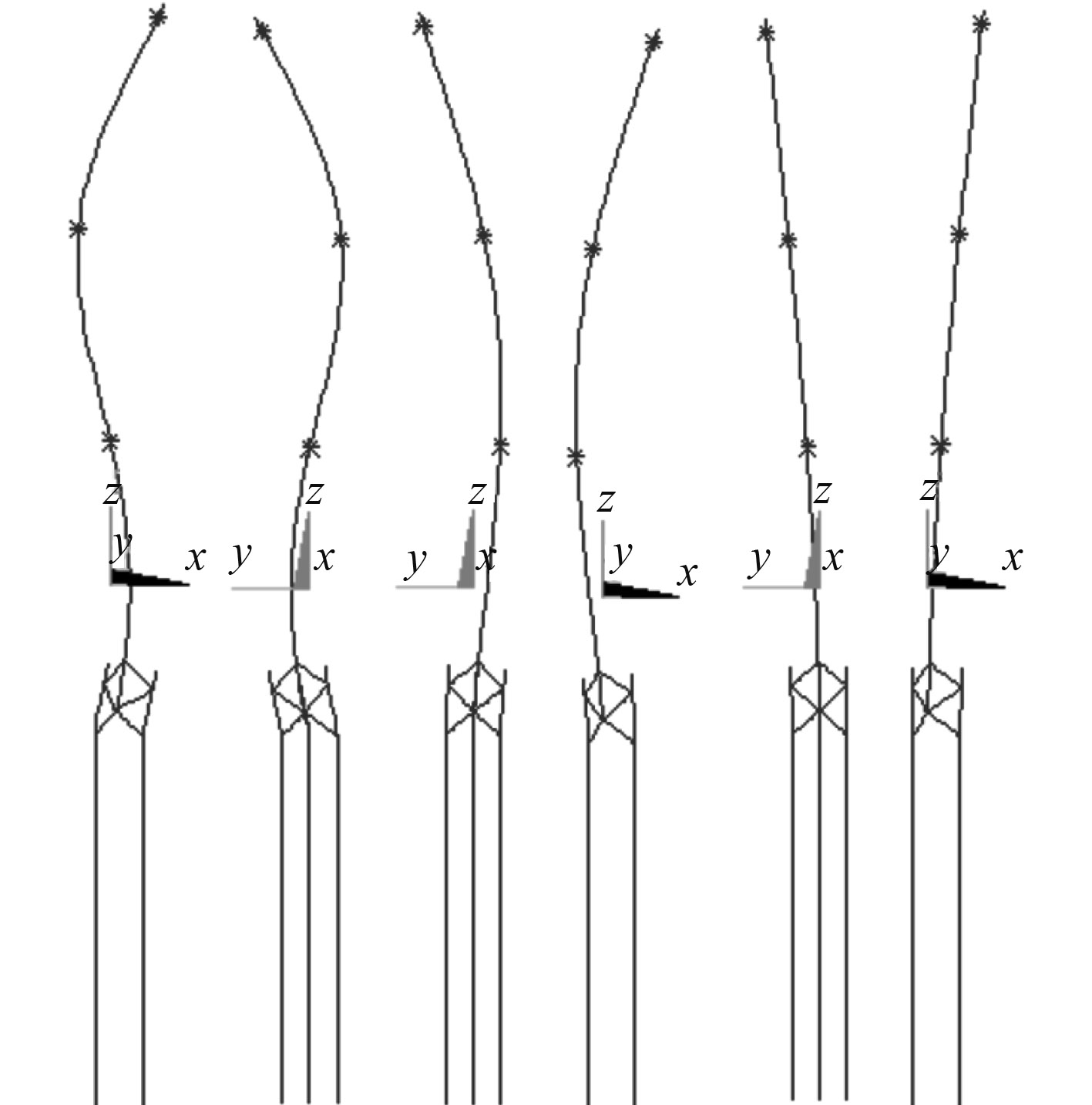
当风机工作时,支撑结构不仅受到风轮旋转所产生的周期性激励,还会受到风浪流载荷的作用,因此,支撑结构会产生振动,当结构的激励频率和固有频率接近时,结构会产生共振,造成极大的破坏。因此,在进行疲劳分析前,需先对其进行模态分析。 图 6为模态分析的前六阶模态振型,对应的自振频率如表 3所示。
|
图 6 前六阶模态振型 Fig. 6 Structural models of support structure |
|
|
表 3 前六阶自振频率 Tab.3 Structure natural frequencies |
本文使用的风机叶轮为三叶片式,每转 1 周塔柱受到 3 次激励振动,所以共振的激励源为 1 P和 3 P,3 P为作用在塔柱上的轴向推力频率[10]。塔柱固有频率必须避开激励振动频率。风机模型正常工作时的叶轮转速为 12.1 r/min,则
目前,海上风机支撑结构的疲劳寿命分析多采用时域法,即通过动力响应分析得到的应力时程曲线和试验统计得到的S-N曲线,应用Palmgren-miner线性累计损伤法计算结构的疲劳寿命。
3.1 Palmgren-miner法则支撑结构在多级循环应力作用下的疲劳损伤是一个累积的过程,每一级应力水平都会产生一组疲劳损伤,从而消耗掉一定分量的疲劳寿命。当结构总的损伤达到某一值时,结构就会发生疲劳破坏。目前最常用的疲劳损伤理论是Palmgren-miner线性累计损伤理论。这一理论认为结构受多级循环应力作用时,各级循环应力造成的损伤可以线性累加[10]。对于单一循环应力 s i 作用产生的损伤度为
| ${D_i} = \frac{{{n_i}}}{{{N_i}}}{\text{,}}$ | (1) |
式中: n i 为应力范围 s i 的实际循环次数; N i 为结构在应力范围 s i 作用下产生疲劳破坏所需的循环次数。
若有 k 级循环应力,那么总损伤度为
| $D = \sum\limits_{i = 1}^k {{D_i}} = \sum\limits_{i = 1}^k {\frac{{{n_i}}}{{{N_i}}}}{\text{。}} $ | (2) |
当 D = 1 时,结构便产生疲劳破坏。
3.2 应力时程曲线处理及雨流计数用Ansys对有限元模型做动力响应分析,可以得到所有单元节点的应力时间历程,其中最大等效应力时程曲线如图 7所示。

|
图 7 最大等效应力时程曲线 Fig. 7 The equivalent stress of support structure |
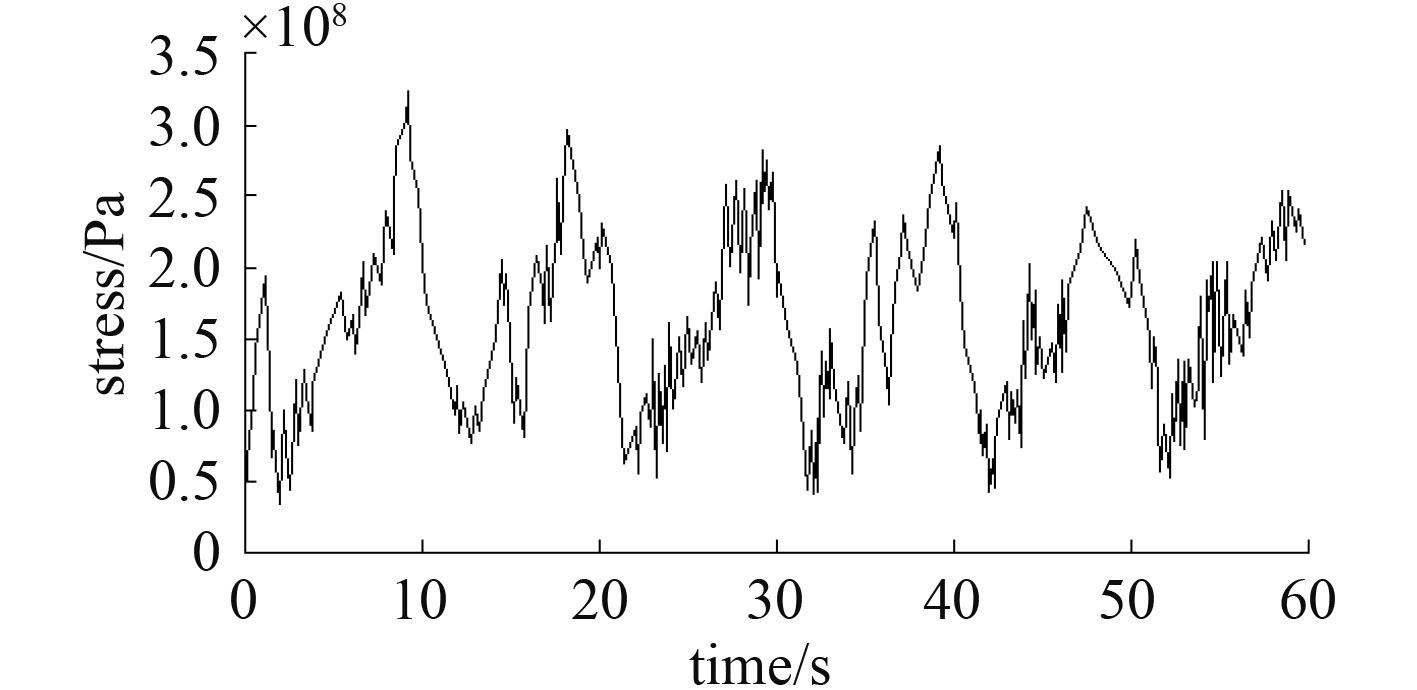
从应力时程曲线可看出,应力时程存在一些不会产生疲劳损伤的小应力循环,为了减少处理的数据,提高计算效率,需要对其进行小载荷处理,删除不必要的小应力循环。本文建立一个取舍标准,处理后的应力时程曲线如图 8所示。
|
图 8 小载荷处理后的应力时程曲线 Fig. 8 The equivalent stress of support structure after processing |
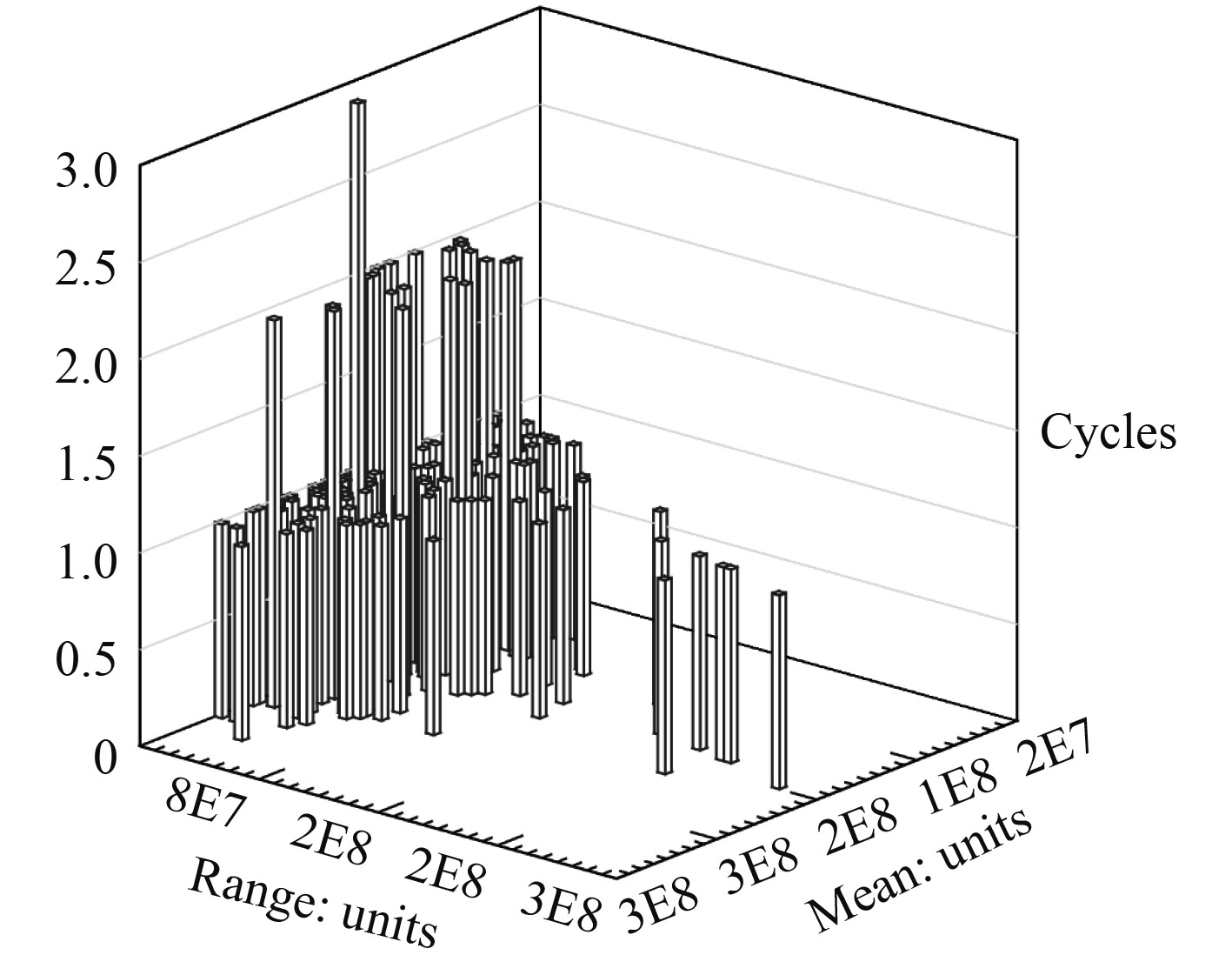
因为分析处理得到的载荷是随机不规则的,不能直接用于疲劳寿命的计算,需先对其应力循环进行计数,本文采用的是工程上应用较为广泛的雨流计数法。根据此方法,可以得到应力幅值、应力均值和对应的循环次数,支撑结构最危险节点的应力循环统计图如图 9所示。
|
图 9 应力循环统计图 Fig. 9 Stress cycle statistics |
根据统计处理得到的应力循环统计图和S-N曲线,利用Palmgren-miner线性累计损伤理论,可以求出风机支撑结构最危险节点的疲劳寿命。
4 频域法计算支撑结构疲劳寿命在使用频域法计算疲劳寿命时,需先对有限元模型加载求得最危险节点的动应力响应,由动应力响应经过傅里叶变换可得到应力的功率谱密度函数
在频域疲劳分析方法中,得到应力功率谱密度后,可进而求各阶矩 m n [14]。
| ${m_n} = \int {{f^n}} \cdot G\left( f \right){\rm d}f {\text{,}}$ | (3) |
式中
因为风电支撑结构的应力属于宽带随机过程,故可选择Dirlik公式作为评估模型,对支撑结构进行疲劳分析。Dirlik通过运用门特卡罗技术做了大量计算机模拟,得出峰值概率密度函数[15]。其表达式为:
| $p\left( S \right) = \frac{{\frac{{{D_1}}}{Q} \cdot {g^{ - \frac{Z}{Q}}} + \frac{{{D_1} \cdot Z}}{{{R^2}}}{e^{ - \frac{{{Z^2}}}{{2{R^2}}}}} + {D_3} \cdot Z \cdot {e^{ - \frac{{{Z^2}}}{2}}}}}{{2\sqrt {{m_0}} }}{\text{,}}$ | (4) |
式中:
其中,
结构最危险节点应力循环计算式为
| $N{S^m} = C{\text{。}}$ | (5) |
式中
C 和
m 为材料
由式(4)和式(5)可推导出宽带随机载荷作用下疲劳寿命的计算公式为:
| $\begin{split}\\[-12pt]{N_p} = & C/{\left\{ {(2\sqrt {{m_0}} )} \right.^m}\left[ {{D_1}} \right.{Q^m}{e^{ - \frac{{{S_0}}}{{2Q\sqrt {{m_0}} }}}} \cdot \left( {{{\left( {\frac{{{S_0}}}{{2Q\sqrt {{m_0}} }}} \right)}^m} + } \right.\\& \left. {\sum\limits_{k = 1}^m {\frac{{m!}}{{(m - k)!}}{{\left( {\frac{{{S_0}}}{{2Q\sqrt {{m_0}} }}} \right)}^{m - k}}} } \right) + 2\frac{{m - 2}}{2}\Gamma \left( {\frac{{m + 2}}{2}} \right) \times \\& \left( {{R^m}{D_2}Q_\chi ^2\left( {\frac{{{S_0}}}{{4{R^2}{m_0}}},m + 2} \right) + } \right.\left. {{D_3}Q_\chi ^2\left( {\frac{{{S_0}}}{{4{m_0}}},m + 2} \right)} \right){\text{。}}\end{split}$ | (6) |
式中,
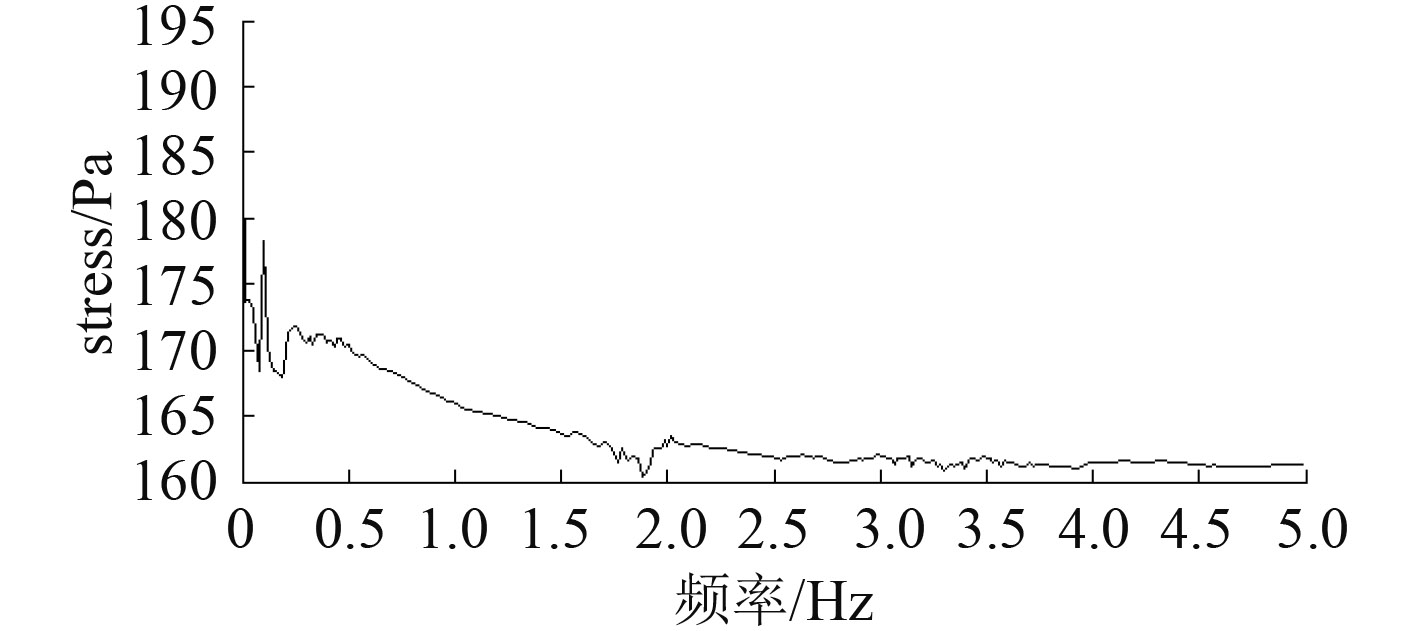
由应力时程经傅氏变换可得功率谱密度函数如图 10所示。
|
图 10 功率谱密度函数 Fig. 10 Power spectral density function |
将功率谱密度代入式(3)、式(4)和式(6)可得到风机支撑结构最危险节点的疲劳寿命。
5 计算结果对比分析采用雨流循环计数的时域法和Dirlik载荷概率密度函数的频域法分别计算海上风机支撑结构的疲劳寿命,计算结果如表 4所示。
|
|
表 4 时域法和频域法计算结果 Tab.4 Calculation results in time and frequency domain |
从计算结果可看出,采用Dirlik载荷概率密度函数的频域法计算结果比较准确,与时域法计算结果相对误差在可接受范围内。因为频域法省去了时域法中应力循环计数这一过程,故相对于时域法,频域法在计算结构疲劳寿命过程中具有耗时短的优势,对于受长期交变载荷的复杂结构,这一优势更加明显。但需要注意的是,频域法适用范围较窄,目前仅适用于线性系统,对于非线性系统,需采用时域法进行疲劳寿命的计算。
6 结 语通过对海上风机支撑结构动力响应分析得到危险节点应力时程曲线,进而求出功率谱密度函数,结合Dirlik概率模型,计算出支撑结构的疲劳寿命,并与时域法计算结果作对比分析。得到基本结论如下:
1) 采用Dirlik概率模型的频域法能够较为准确地计算出复杂交变载荷载荷作用下海上风机支撑结构的疲劳寿命,频域法和时域法计算结果相对误差在可接受范围内。
2)采用Dirlik载荷概率密度函数的频域法替代雨流计数的时域法,可省去统计应力循环次数这一繁琐过程,缩短计算时间,在受长期随机交变载荷作用下的结构疲劳寿命的计算过程中尤为明显。
| [1] |
朱云, 杨和振, 何炎平. 海洋风力电机支撑结构在风机故障状态下的动力响应研究[J]. 船海工程, 2013 (06): 131–135.
ZHU Yun, YANG He-zhen, HE Yan-ping. Dynamic response analysis of supporting structure of an offshore wind turbine under diagnosisstate[J]. Ship & Ocean Engineering, 2013 (06): 131–135. DOI: 10.3963/j.issn.1671-7953.2013.06.033 |
| [2] |
卢其进, 杨和振. 海洋风电支撑结构的随机性动力优化设计[J]. 振动与冲击, 2013 (17): 47–51.
LU Qi-jin, YANG He-zhen. Probabilistic dynamic optimization design for support structure of offshore wind turbines[J]. Journal of Vibration and Shock, 2013 (17): 47–51. |
| [3] |
莫继华, 何炎平, 李勇刚, 等. 近海风电机组单桩式支撑结构疲劳分析[J]. 上海交通大学学报, 2011, 45 (4): 565–569.
MO Ji-hua, HE Yan-ping, LI Gang, et al. Fatigue analysis of offshore wind turbine mono-pile support structure[J]. Journal of Shanghai Jiaotong University, 2011, 45 (4): 565–569. |
| [4] |
朱志松, 朱龙彪, 季采云. 风波联合载荷下海上风力机塔筒的疲劳寿命预测[J]. 机械科学与技术, 2013, 32 (6): 714–717.
ZHU Zhi-song, ZHU Long-biao, JI Cai-yun. Fatigue life prediction of the offshore wind turbine tower under combining load of wind and wave[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32 (6): 714–717. |
| [5] | KVITTEM M I, MOAN T. Frequency versus time domain fatigue analysis of a semi-submersible wind turbine tower[C]// In ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, 2014: V09AT09A021–V09AT09A021. |
| [6] | ARANY L, BHATTACHARYA S, MACDONALD J, et al. Accuracy of frequency domain fatigue damage estimation methods for offshore wind turbine support structures[C]// In Second International Conference on Vulnerability and Risk Analysis and Management (ICVRAM) and the Sixth International Symposium on Uncertainty, Modeling, and Analysis (ISUMA), 2014. |
| [7] | Halfpenny A. A frequency domain approach for fatigue life estimation from finite element analysis[J]. Key Engineering Materials, 1999, 167 : 401–410. |
| [8] |
陈建东, 王晶. 国外海上风电的发展现状, 趋势与展望[J]. 世界科技研究与发展, 2014, 36 (4): 458–464.
CHEN Jian-dong, WANG Jin. Development status, trends and prospects of offshore wind power in some foreign countries[J]. World SCI-TECH R&D, 2014, 36 (4): 458–464. |
| [9] | Philippe M, Babarit A l, Ferrant P. Comparison of time and frequency domain simulations of an offshore floating wind turbine[J]. In ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering[C], 2011 : 589–598. |
| [10] | Long H, Moe G. Preliminary design of bottom-fixed lattice offshore wind turbine towers in the fatigue limit state by the frequency domain method[J]. Journal of Offshore Mechanics and Arctic Engineering, 2012, 134 (3): 031902. DOI: 10.1115/1.4005200 |
| [11] | Chow R, Dam C. Verification of computational simulations of the NREL 5 MW rotor with a focus on inboard flow separation[J]. Wind Energy, 2012, 15 (8): 967–981. DOI: 10.1002/we.v15.8 |
| [12] | 李益, 张宏战, 马震岳. 基于土-结构相互作用的海上风机模态分析[J]. 水电与新能源, 2013, 106 : 70–73. DOI: 10.3969/j.issn.1671-3354.2013.01.022 |
| [13] | 杨平, 吕彭民, 王刚, 等. 混凝土泵车疲劳寿命预测方法[J]. 长安大学学报(自然科学版), 2011 (04): 102–106. |
| [14] | Du J, Li H, Zhang M, et al. A novel hybrid frequency-time domain method for the fatigue damage assessment of offshore structures[J]. Ocean Engineering, 2015, 98 : 57–65. DOI: 10.1016/j.oceaneng.2015.02.004 |
| [15] | Andrew Halfpenny, LIN Xiao-bin. A frequency domain approach for fatigue life estimation based on power spectral density[J]. China Mechanical Engineering, 1998, 9 (11): 16–19. |
 2017, Vol. 39
2017, Vol. 39
